«Площади»
| Вид материала | Документы |
СодержаниеЗадачи с параметрами Преподавание математики Ответ: a = 0 или a < 0. Задача 5 |
- ТемЫ рефератов по мерчендайзингу, 204.9kb.
- Разработка урока по теме «Понятие площади многоугольника», 32.86kb.
- Механика Жидкостей и Газов, 12.81kb.
- Блиц (матан и триг.) блиц (геометрия) Вопросы по планиметрии, 56.04kb.
- Лабораторная работа №1 Тема: «Разработка простейших программ линейных структур», 169.83kb.
- Городские тематические экскурсии, 85.03kb.
- Урок-сказка по теме "Площади и объемы". 5-й класс, 87.63kb.
- Урок геометрии в 8 классе по теме «Площади многоугольников», 52.25kb.
- Об изучении площади в начальной и средней школе, 56.34kb.
- Доклад заместителя министра лесного хозяйства, 82.14kb.
Задачи с параметрамиссылка скрыта Статья отнесена к разделу: ссылка скрыта  Работа со школьниками показывает, что задачи с параметрами являются наиболее сложным в логическом и техническом планах разделом математики. Умение решать эти задачи является необходимым условием для поступления в вуз. Предлагаемые задачи собраны из разных источников и, предназначены для школьников, будущих абитуриентов, учителей математики. Их можно использовать на уроках, факультативных занятиях, для самостоятельного решения. Задача 1. При каких значениях параметра а система уравнений 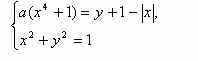 имеет единственное решение? имеет единственное решение?Решение: Заметим, что если пара чисел ( хо, уо ) решение системы, то пара (-хо,уо), так же является решением. Необходимым условием для существования единственного решения является равенство хо=0. Положим х =0. 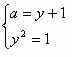 , получаем a=0 или a=2. , получаем a=0 или a=2.Итак, искомые значения параметра следует выбирать из множества { 0;2}. Если a=0,то 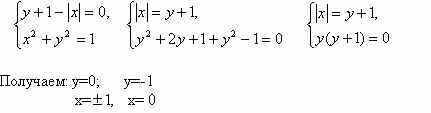 Система имеет 3 решения ( 1; 0), (-1;0), (0; -1) .Следовательно, a не может быть равно нулю. Если a=2. 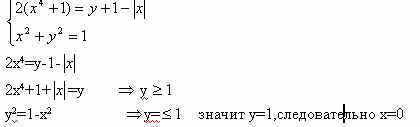 При a=2 система имеет единственное решение. Ответ: a=2. Задача 2. Решите систему уравнений 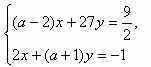 Решение:  Задача 3 Определить количество решений системы  Задача 4 При каких a уравнения х2 - a = 0 и 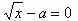 равносильны? равносильны?Решение: 1).Если a >0, то первое уравнение х2 - a =0 имеет два корня, а второе уравнение – только один, и в этом случае о равносильности речь идти не может. 2).При a = 0 решения уравнений совпадают. 3).При a < 0 ни первое, ни второе уравнения решений не имеют. А ведь, как известно, такие уравнения такие уравнения считаются равносильными. Ответ: a = 0 или a < 0. Задача 5 При каких a уравнение aх = a2 равносильно неравенству 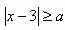 ? ?Решение: 1). При a, не равном нулю, уравнение ах =а2 имеет единственное решение, т.е. х =а, а неравенство 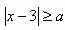 - бесконечно много. - бесконечно много.2).Если а = 0, то решение как неравенства, так и уравнения является все множество действительных чисел. 3). Таким образом, требованию задачи удовлетворяет только а=0. Ответ: а=0. Задача 6 Решить неравенство 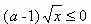 (1) (1)Решение: 1).Понятно, что область определения 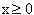 ; ;2). Понятно также и следующее, что ответ зависит от знака (a -1). 3). При 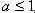 очевидно, неравенству (1) удовлетворяет любое значение из области определения, то есть очевидно, неравенству (1) удовлетворяет любое значение из области определения, то есть 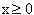 . .4). При a -1>0 левая часть неравенства (1) неотрицательна, в одном случае х=0 - единственное решение. Ответ: если 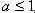 , то , то 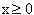 ; если a>1, то х=0. ; если a>1, то х=0.Задача 7 При каких a неравенство (х-a) (х-2) 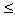 (1) имеет единственное решение? (1) имеет единственное решение?Решение: 1) Если a=2, то требование задачи удовлетворяется. И действительно, при a= 2 получаем неравенство (х-2)2 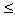 0 (2) имеющее единственное решение. 0 (2) имеющее единственное решение.2).А для случая, когда a  2, решение неравенства (1), очевидно, будет отрезок. 2, решение неравенства (1), очевидно, будет отрезок.Ответ: a= 2. Задача 8  Задача 10  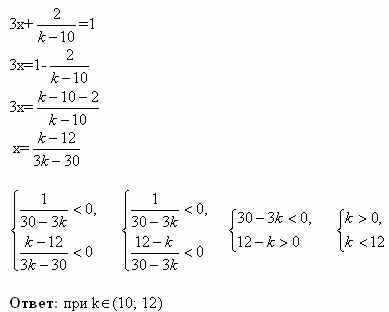 Задача 11  Задача 12.  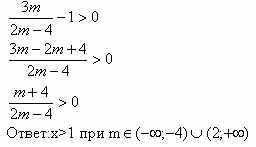 Задача 13.  Задача 14.  Задача 15  Литература: Андреев А.Н. варианты письменных экзаменационных заданий по математике в КемГУ с анализом их решений, Кемерово, 2001. Гарнштейн П.И., Полонский В.Б., Якир М.С. Задачи с параметрами. М.: Илекса, Харьков: Гимназия, 1999. Дорофеев Г.В. Квадратный трехчлен в задачах //Квантор, Львов, 1991. Рурукин А.Н. Единый государственный экзамен. Математика. Пособие для подготовки. М.: ВАКО, 2004. |
