Авторы: Чебоксаров А. Б. Откидычев П. А

Вид материала

Анализ

Содержание 2. Рассеяние низкоэнергетических квантовых частиц в центально-симметричном поле. 3. Моделирование процесса конвективной диффузии.

Подобный материал:

• Авторы: М. В, 27.16kb.
• Авторы: М. В, 36kb.
• Рекомендации по написанию реферата: (соответствуют последовательности изложения материала, 12.57kb.
• Государственный контроль и защита предпринимательства москва 2009 Авторы: Бут, 5788.38kb.
• Авторы: Жиряков И. Г, 1280.34kb.
• Авторы-составители: Мурзина, 1796.81kb.
• Программа дисциплины экономика труда для специальности 080504. 65 «Государственное, 313.47kb.
• Учебное пособие Авторы: Э. О. Леонтьева В. В. Грибунин Т. А. Лидзарь > Ю. А. Леонтьев, 2402.05kb.
• Программа дисциплины «Конъюнктура и прогнозирование мировой экономики и мировых товарных, 123.93kb.
• Авторы: Фиданка Бачева, cee bankwatch Network, 514.95kb.

Авторы: Чебоксаров А.Б. Откидычев П.А.

Толокольников Е.А.


Моделирование некоторых физических процессов в нелинейных средах

Аннотация: разработанный авторами метод аналитического решения дифференциальных уравнений в частных производных позволяет создавать математические модели физических процессов в нелинейных средах



1. Распространения тепловых возмущений от двух мгновенных точечных источников в нелинейной среде с объемным поглощением


Для описания процесса используем уравнения:,

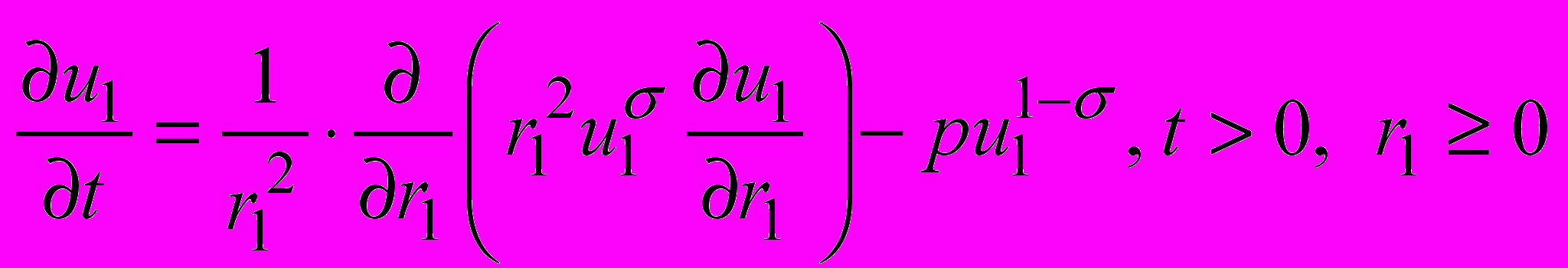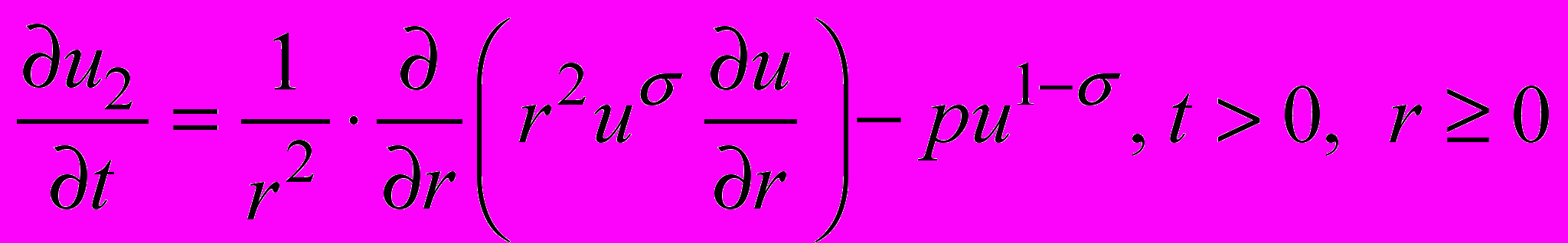
А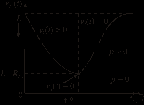налитическое решение данных уравнений дает картины эволюции тепловых фронтов:




А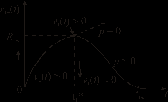нализ показывает поведение волн разогрева и охлаждения в любой момент времени и в любой точке пространства.


2. Рассеяние низкоэнергетических квантовых частиц в центально-симметричном поле.


Рассмотрим низкоэнергетическое s – рассеяние электронов на нелинейном потенциале, имеющий вид:



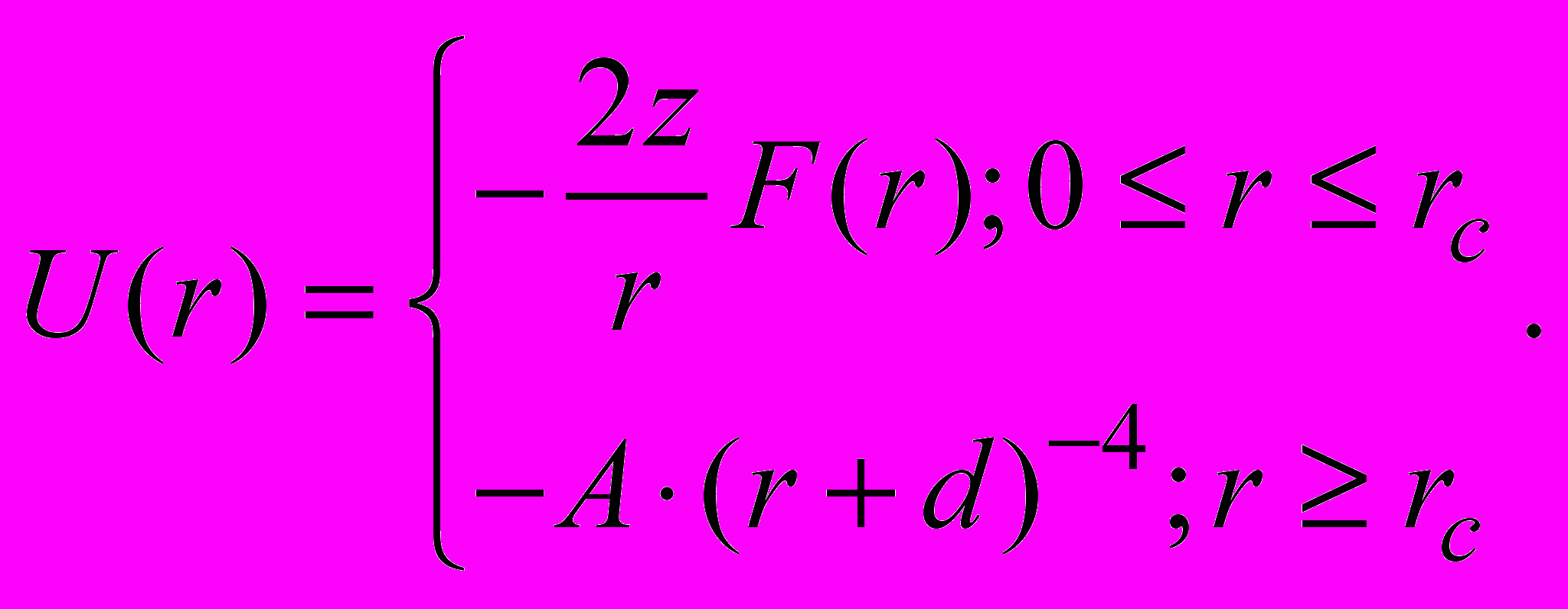
Для эффективной длины рассеяния электронов на потенциале получаем оценку:



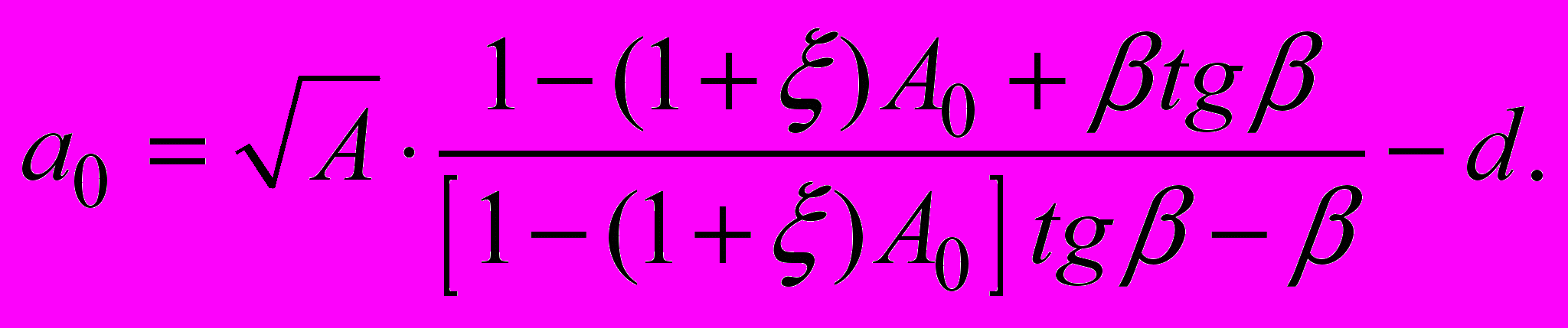
Вычисление численными методами и аналитическими дают примерно одинаковые результаты:

Z	Оценка аналитическая		Оценка численная
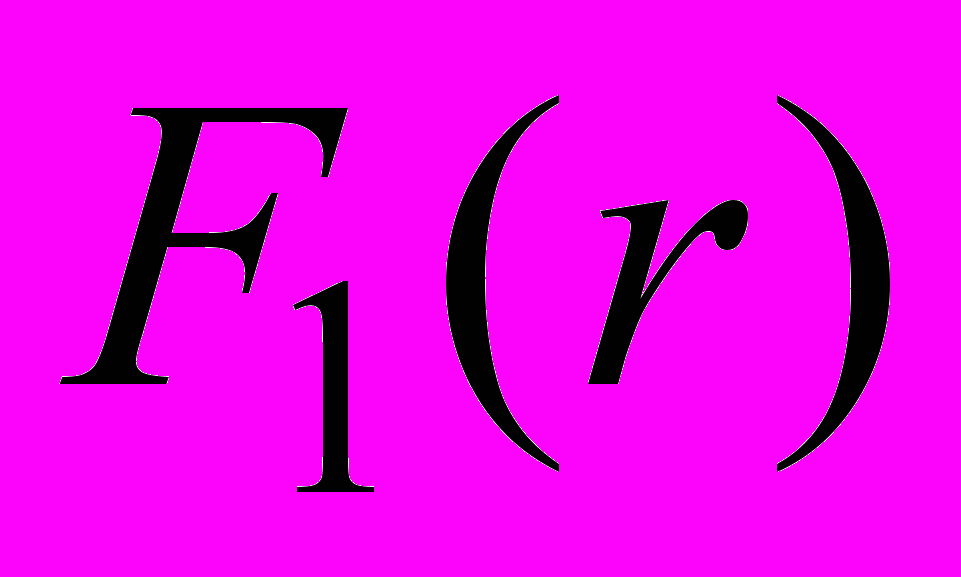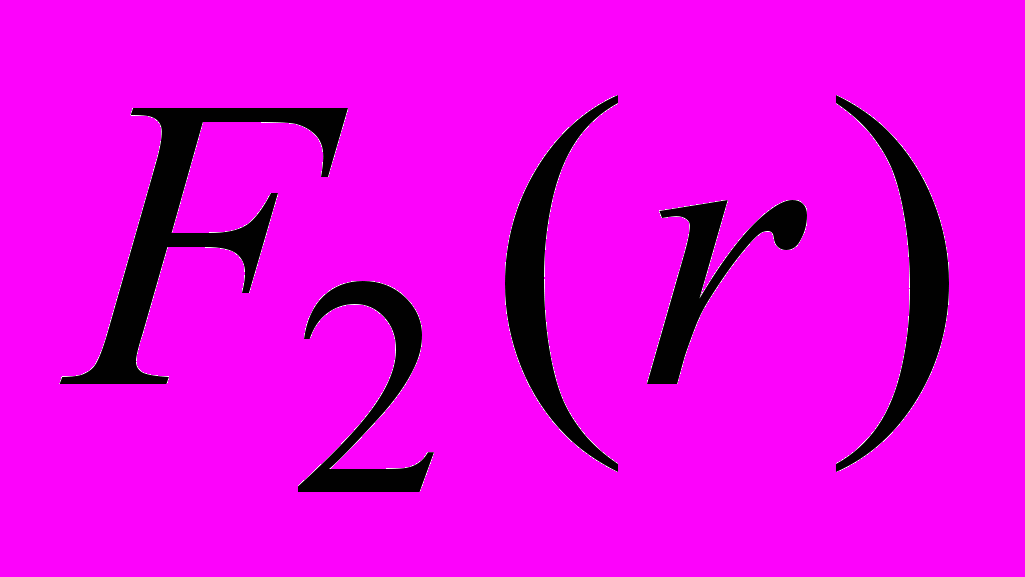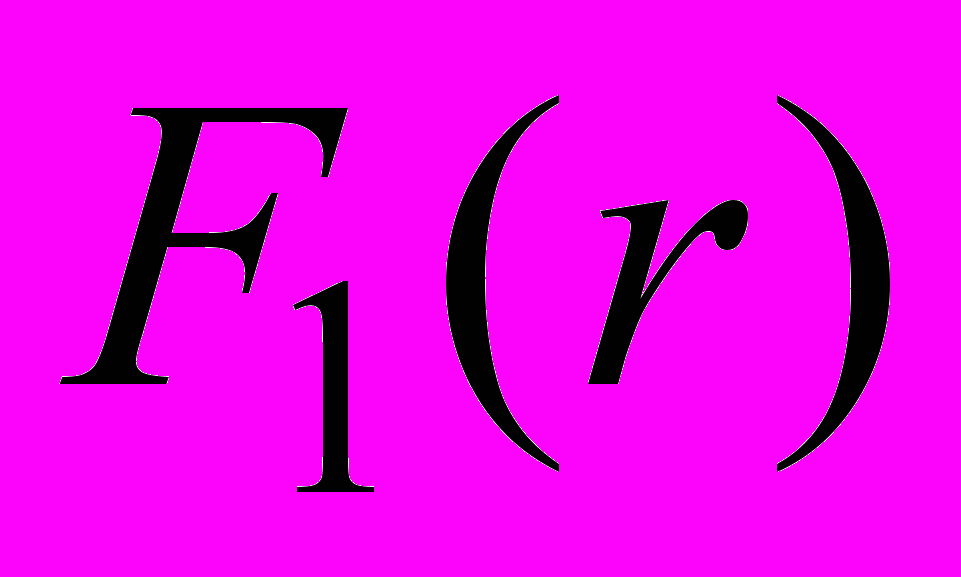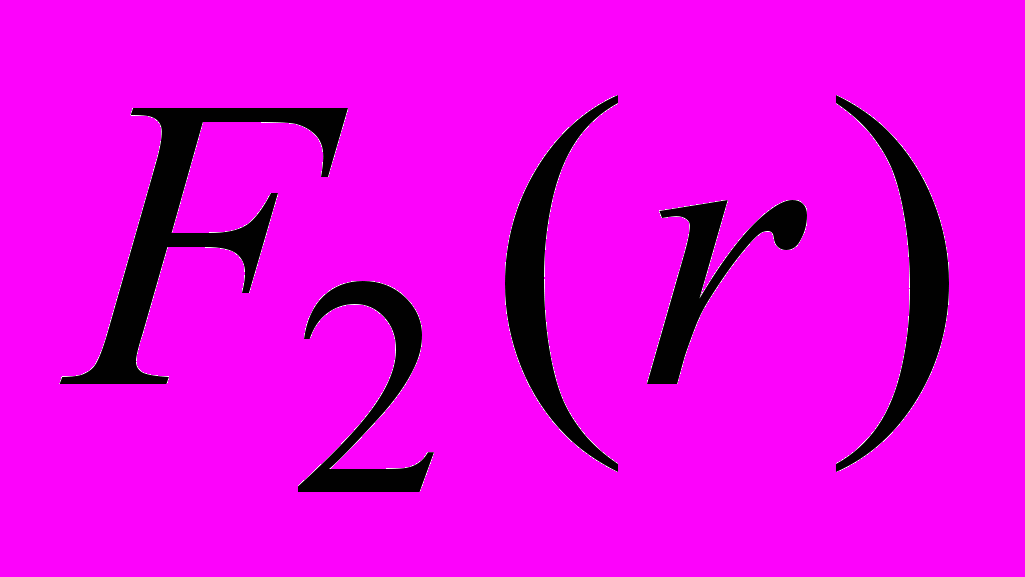2	1,194	1,077	1,236	1,063
10	-0,086	-0,295	-0,067	-0,278

3. Моделирование процесса конвективной диффузии.


Рассмотрим конвективную диффузию частиц наполнителя из падающей в жидкости капли суспензии и определим концентрацию частиц наполнителя 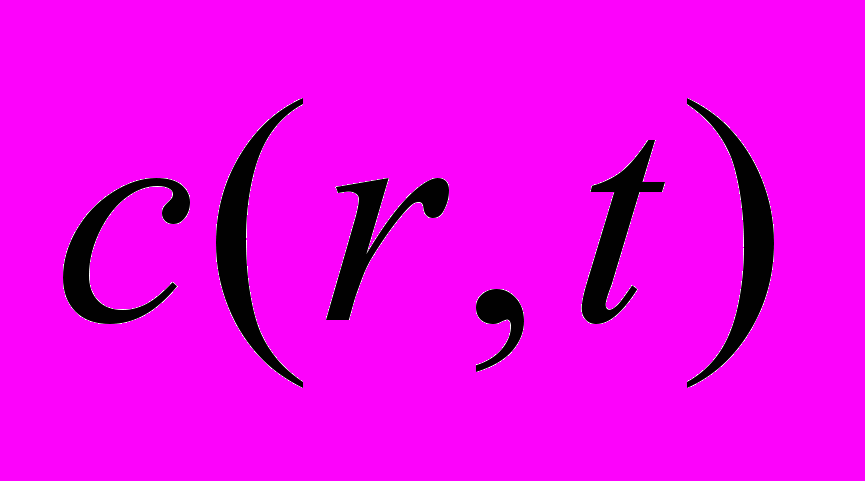в капле суспензии как функцию радиальной координаты 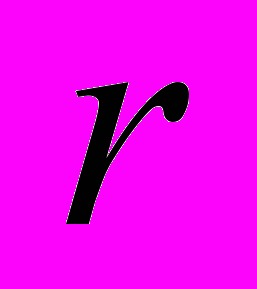и времени 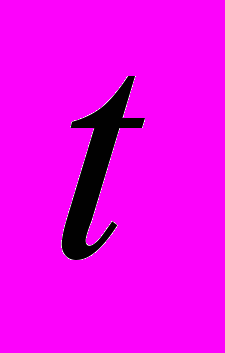. Для нахождения 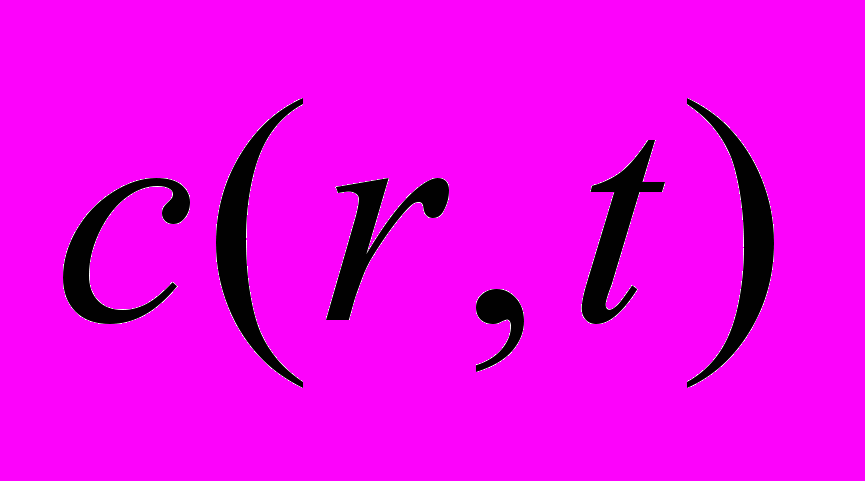необходимо решить нелинейное уравнение диффузии 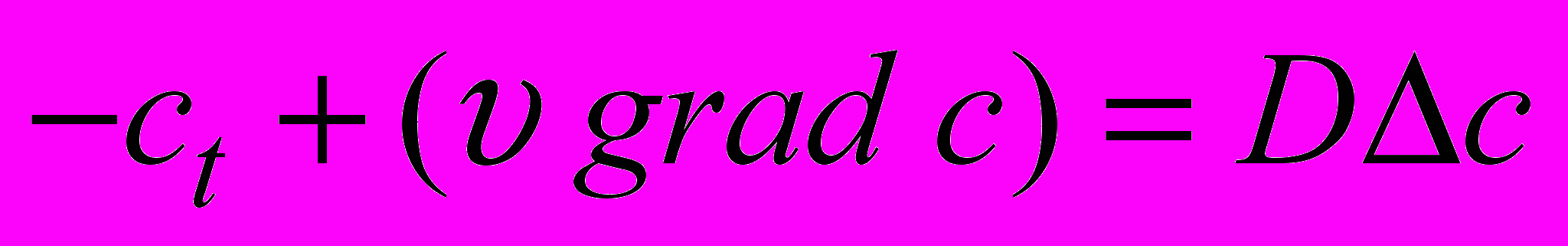с начальными и граничными условиями следующего вида: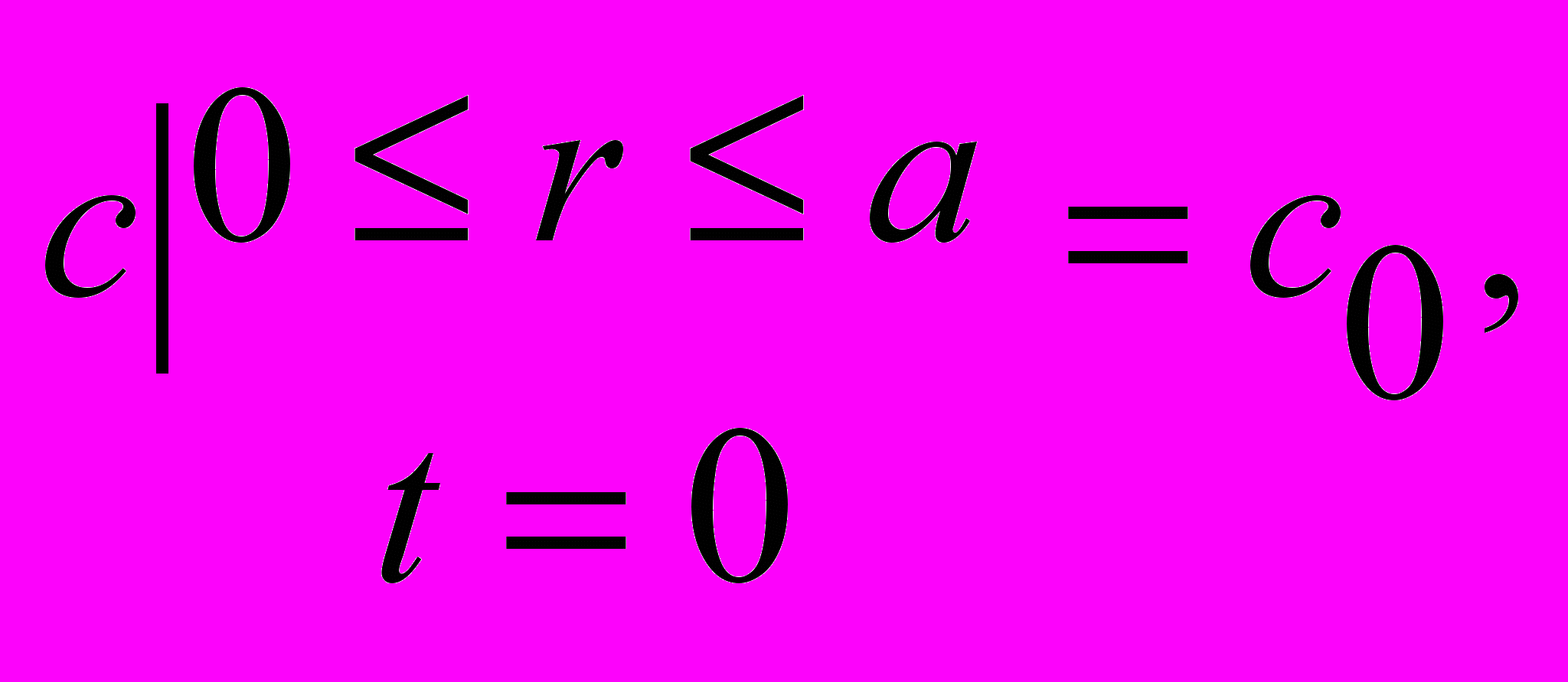



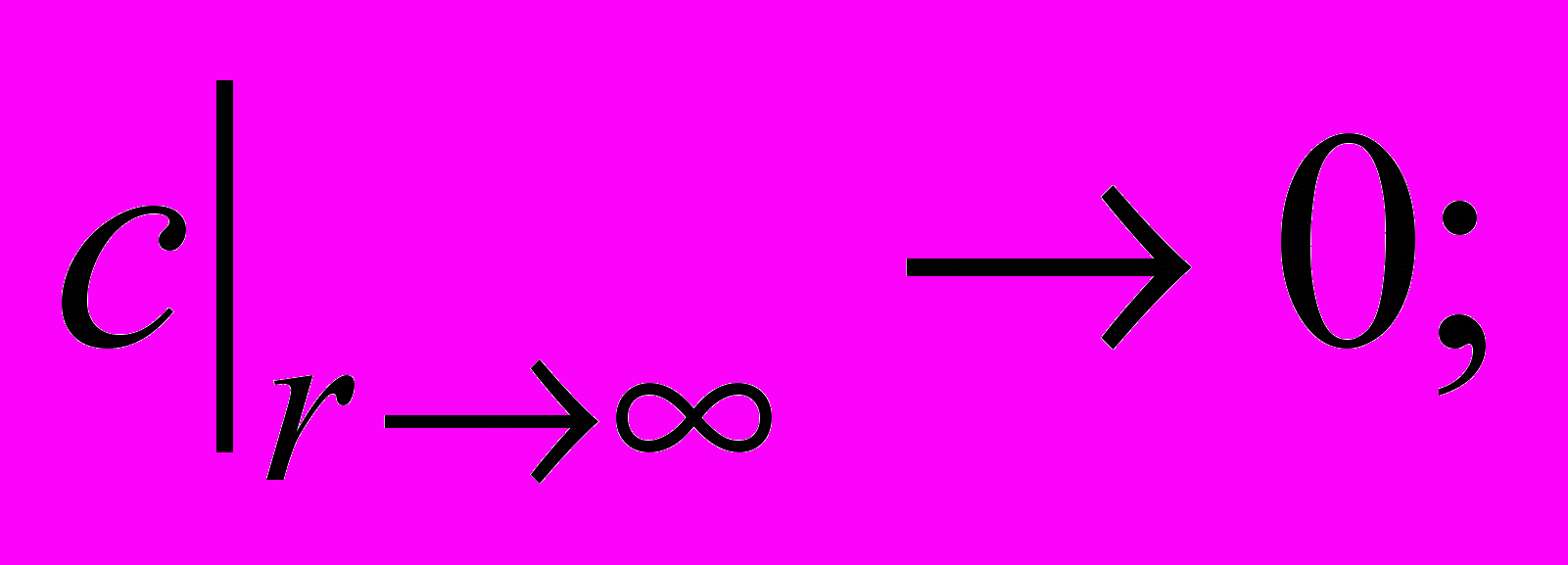
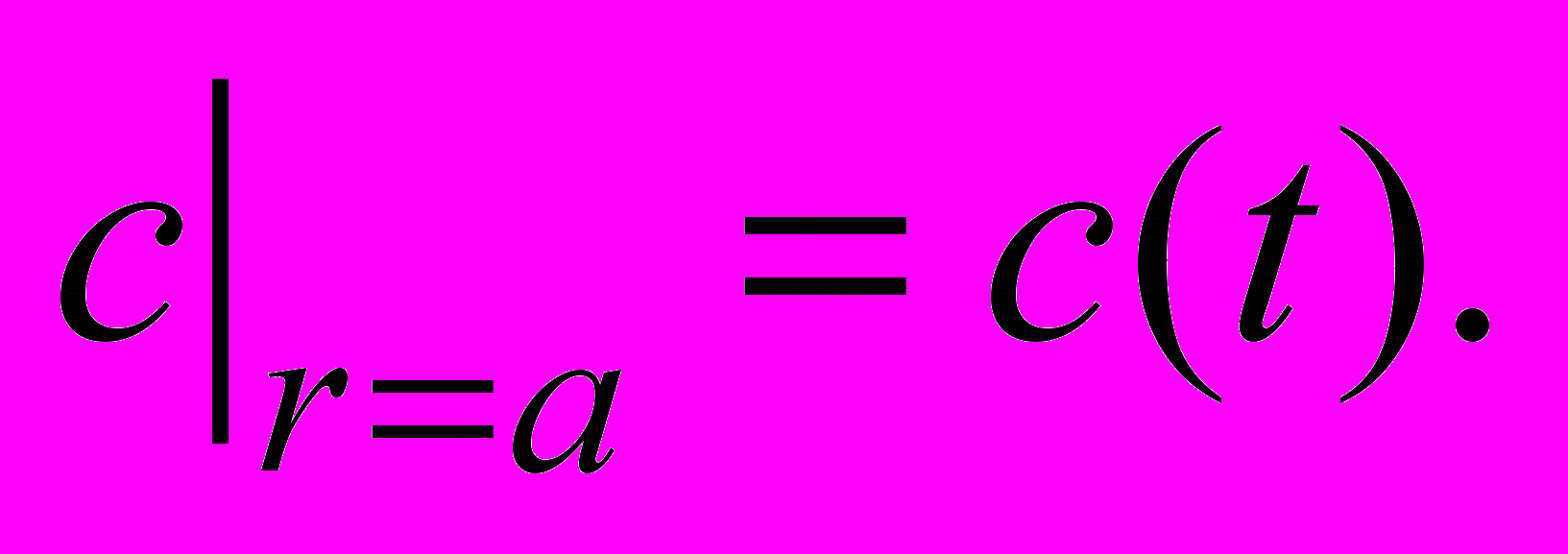
Решение задачи методом эталонного моделирования дает выражение для полного потока диффундирующих частиц наполнителя:

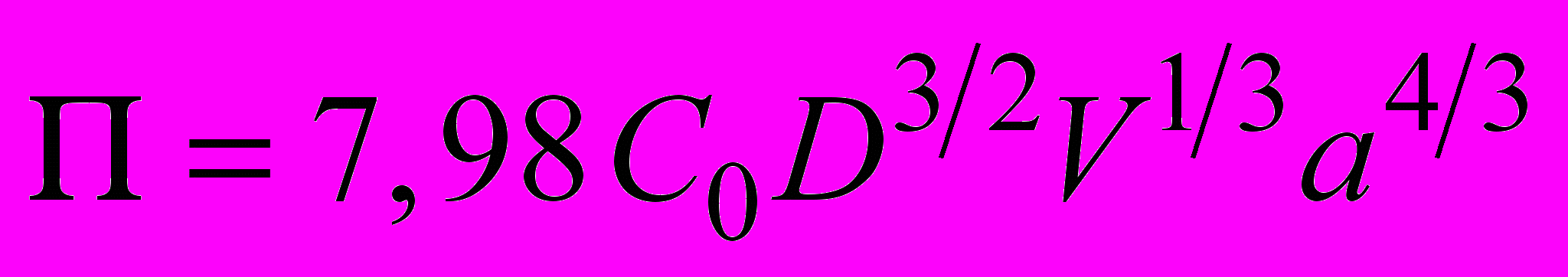(3.2.28)

Таким образом, полный поток частиц носителя, диффундирующих из капли суспензии, погружающейся в жидкость с малой скоростью, пропорционален концентрации частиц 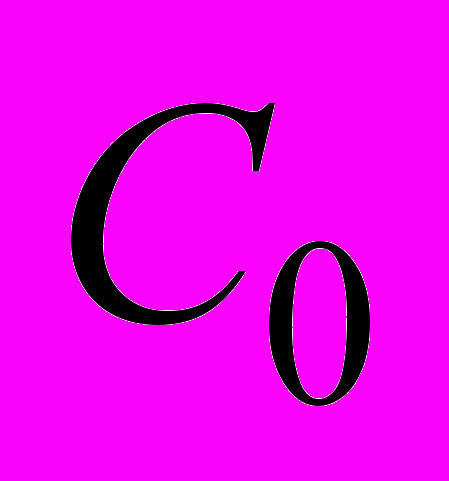в капле, коэффициенту диффузии 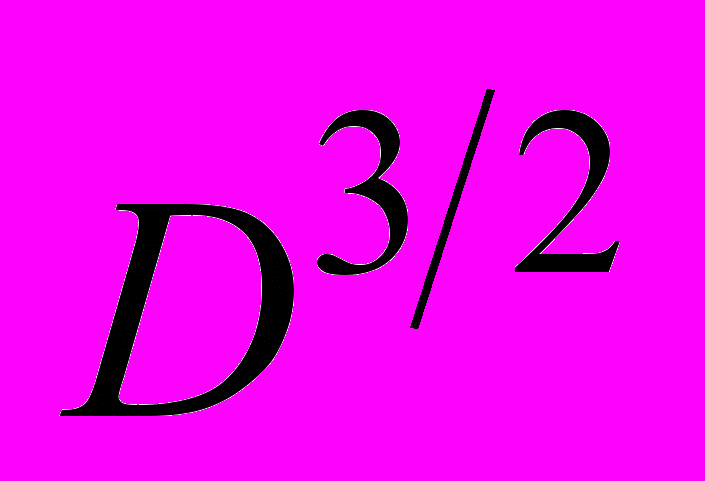, скорости погружения 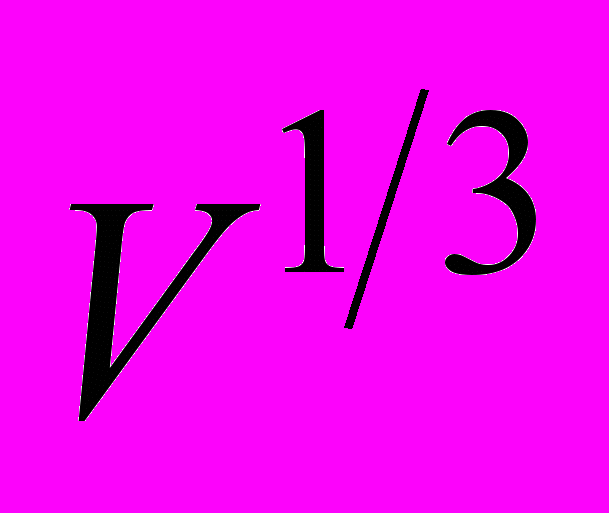и радиусу капли .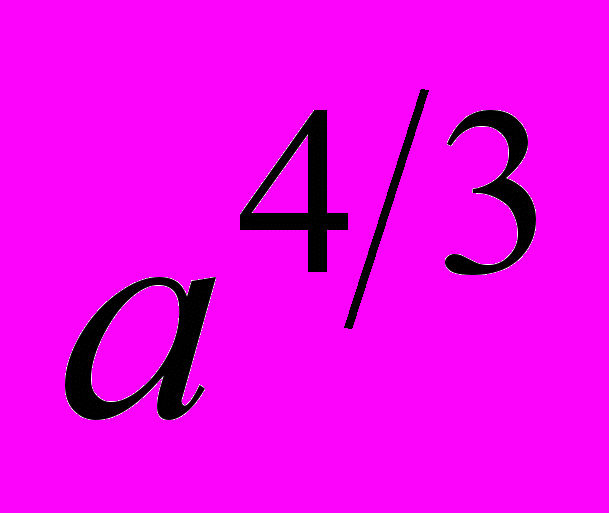