Ема урока. Свойство медианы равнобедренного треугольника
| Вид материала | Урок |
- План урока: Организационный момент. Рассказ сказка о медианах, высотах и биссектрисах., 161.11kb.
- Тема: Измерение углов, 29.65kb.
- Контрольная работа по алгебре №1 Тема «Алгебраические уравнения. Системы нелинейных, 13.42kb.
- Урок сказка по математике 6 класс «Умножение одночлена на многочлен», 304kb.
- Неравенство треугольника один из важнейших геометрических фактов, 212.21kb.
- Программы: эстетика жилища т разработала: тарасенко елена александровна, учитель обслуживающего, 385.96kb.
- Урок геометрии в 8 классе по теме «Площади многоугольников», 52.25kb.
- Тема урока: «Переместительное свойство сложения», 49.06kb.
- А. С. Пушкина р п. Колышлей Пензенской области Геометрия и сказки А. С. Пушкина Повторительно, 36.32kb.
- Курсовая работа по линейной алгебре (1 курс, 1 семестр), 18.82kb.
ТЕМА УРОКА. СВОЙСТВО МЕДИАНЫ РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА.
ЦЕЛИ. Знать формулировку и доказательство теоремы о медиане равнобедренного треугольника, проведенной к основанию, и уметь применять ее при решении задач.
Продолжить развитие познавательных и творческих способностей учащихся.
Воспитывать самостоятельность, трудолюбие, активную жизненную позицию.
ХОД УРОКА.
Класс разделён на три группы.
1. Доклад консультантов о качестве выполнения домашней работы.
2. Фронтальный опрос.
В
L
К
к
А) По данным , обозначенным на рисунках, указать медианы треугольников.
O
О
т
Р
С
м
о
А
Д
Е
K
M
М
д
д
т
с
Б) Укажите высоты в следующих треугольниках.
с
с
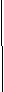
в
т
о
в
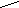
н
в
с
в
с
о
в
д
н
В) Укажите биссектрисы в следующих треугольниках.
в
у
к
в
в
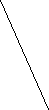
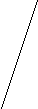
н
с
с
с
о
р
к
м
в
р
р
к
х
д
м
Г) Какой треугольник называется равнобедренным?
Д) Как называются стороны этого треугольника?
Физкультминутка.
3. Изучение нового материала.
Начертите равнобедренный треугольник. Проведите в этом треугольнике медиану к основанию.
ПРОБЛЕМА 1.
1) Является ли проведенная медиана биссектрисой? Для решения этой проблемы используется транспортир.
2) Является ли проведенная медиана высотой? Для решения этой проблемы используется треугольник.
ПРОБЛЕМА 2.
1) Правдоподобно ли утверждение, что медиана равнобедренного треугольника является биссектрисой и высотой?
2) А для произвольного треугольника?
Для решения этой проблемы выполняются следующие действия:
А) Начертите равнобедренный треугольник.
Б) Проведите медиану к боковой стороне.
В) Измерьте транспортиром углы.
Г) Треугольником проверьте, является ли медиана высотой.
Д) Начертите произвольный треугольник. Проведите медиану. Проверьте, является ли она биссектрисой и высотой.
ПРОБЛЕМА 3.
Верно ли , что медиана равнобедренного треугольника, проведенная к основанию является биссектрисой и высотой?
А) На доске начерчен рисунок 53 из учебника.
Б) Заполните места с вопросами верной информацией.
1. АС ВС, т.к. …
2. АД ВД, т.к. …
3.
А В, т.к. …
САД СВД ( по …) , тогда АСД ВДС, значит СД- …
АДС ВДС
АДС + ВДС =…, т.к. значит АДС=ВДС=… , СД-…В) Запишите доказательство теоремы.
ПРОБЛЕМА 4.
Как в равнобедренном треугольнике ОМК с основанием ОК провести высоту из вершины М , используя только линейку с делениями?
Обсудите результат своей работы. (Самооценка.)
Решите задачу самостоятельно, если необходимо- обратитесь за помощью.
В
МРК, 
, Р=100º, РА- медиана. Определите углы МРА.Решите задачу 28 стр. 47.
4. Домашнее задание.
П.26, № 20(1),21(2).