Geum.ru

Курсовая работа

Вид материалаКурсовая

Содержание


13. Предпосылки и решение
Подобный материал:
1   2   3   4   5   6   7   8   9   10   11

13. Предпосылки и решение


Итак, игроки объединились в коалиции и играют “стенка на стенку”. Что же они могут в результате получить?

Пусть образовалась коалиция , которая играет против коалиции , и пусть средний доход (или убыток, в зависимости от знака) 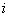-го игрока равен 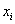. Какие ограничения накладываются на 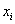? Достаточно разумными выглядят следующие ограничения:
  1. . Действительно, кто же будет вступать в коалицию, в которой он получит меньше, чем получил бы, играя в полном одиночестве.
  2. . Весь доход коалиции распределяется между игроками.
  3. . Игра с постоянной суммой и весь доход игроков должен быть равен этой сумме.

Набор , удовлетворяющий этим ограничениям, называется предпосылкой. В принципе, любая предпосылка имеет право на реализацию в виде соответствующих коалиций. Вот только какие из них реализуются?

Чтобы понять идею, рассмотрим пример. Пусть дана игра трёх лиц с постоянной суммой. В (0, 1) нормализации мы имеем:
  1. ;
  2. .  С другой стороны, так как, например, ,то .
  3. .

Рассмотрим множество A, состоящее из следующих трёх предпосылок

, , .

Давайте предположим, что реализовалась первая предпосылка, игроки 1 и 2, объединившись в коалицию, получают по 1/2, третьему игроку остаётся круглый ноль.

А теперь допустим, что первый игрок пожадничал и ему хочется большего. Он идёт к третьему игроку и предлагает ему коалицию {1, 3}, в которой доходы будут выглядеть так: . Всё разумно  оба игрока, первый и третий, увеличили свои доходы на 1/4.

Но теперь, когда реализовалась предпосылка , в обиде второй игрок. Он идёт к третьему игроку и предлагает ему новую коалицию {2, 3}, в которой доходы будут делиться поровну, . Третьему игроку это выгодно, он соглашается и возникает коалиция {2, 3} c распределением доходов

.

Что же произошло? Первый игрок пожадничал и в результате потерял всё, как говорится, “жадность фраера сгубила”. А мы снова оказались во множестве A.

Получается, что множество A обладает своеобразной внутренней устойчивостью, уходя из него, в него же и возвращаются. Кроме того, ни одна предпосылка из множества A не лучше другой. Подобные множества Дж. фон Нейман и О. Моргенштерн и предложили считать решением игры n лиц.

Формализуем эти идеи. Пусть имеются две предпосылки и . Говорят, что предпосылка y доминирует над предпосылкой x по отношению к коалиции T, если T  непустое множество и если выполняются следующие условия:

 1. ;

 2. .


Другими словами, игрокам выгодно объединиться в коалицию T все они от такого объединения выигрывают.

Говорят, что коалиция y доминирует над x (обозначение ) если имеется по крайней мере одно непустое множество T такое, что y доминирует над x по отношению к коалиции T.

Если имеются две предпосылки x и y, то могут быть следующие случаи:
  1. y доминирует над x, но x не доминирует над y;
  2. y доминирует над x и x доминирует над y (естественно, по отношению к разным коалициям);
  3. ни одна из предпосылок x и y не доминирует одна над другой.

Решение игры n лиц определяется как любое множество A. такое, что
  1. если x и y  предпосылки, входящие в A, то ни одна из них не доминирует над другой;
  2. если z  предпосылка, не входящая в A, то найдётся по крайней мере одна предпосылка x принадлежит A, которая доминирует над z.

Практическое значение всех этих понятий невелико. Во-первых, трудно вычислить характеристическую функцию игры. Во-вторых, решение в данном выше смысле неоднозначно, существует целое множество решений. И, в третьих, коалиции в жизни образуются совсем по другим правилам, и в их образовании большую роль играет психология, личные отношения между людьми. Так что теория игр и реальная жизнь  это пока что две большие разницы.