Курсовая работа
| Вид материала | Курсовая |
Содержание4. Смешанные стратегии 5. Нахождение смешанной стратегии |
- Методические рекомендации по выполнению курсовых работ курсовая работа по «Общей психологии», 54.44kb.
- Курсовая работа Социокультурные лакуны в статьях корреспондентов, 270.94kb.
- Курсовая работа, 30.27kb.
- Курсовая работа тема: Развитие международных кредитно-финансовых отношений и их влияние, 204.43kb.
- Курсовая работа+диск + защита, 29.4kb.
- Курсовая работа+диск + защита, 118.7kb.
- Курсовая работа на математическом, 292.45kb.
- Методические указания к выполнению курсовой работы курсовая работа по курсу «Менеджмент», 159.91kb.
- Курсовая работа по предмету "Бухгалтерский учёт" Тема: "Учёт поступления и выбытия, 462.23kb.
- Курсовая работа по управлению судном, 128.72kb.
4. Смешанные стратегииСедловая точка в матричных играх всё-таки скорее исключение, чем правило. А что же может гарантировать себе игрок, если седловой точки нет? Давайте снова рассмотрим игру с платёжной матрицей 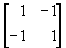 . .Здесь 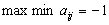 , , 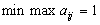 и между и между 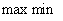 и и 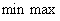 образуется “дыра” образуется “дыра” 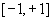 Как можно её заполнить и чем? Как можно её заполнить и чем? Представим себя в позиции первого игрока. Он имеет гарантированный выигрыш (скорее, проигрыш), равный (-1). Как он может его повысить? Конечно, если игра повторяется много раз, то он может изучить своего партнёра, придумывать всякие схемы игры и т.д. и т.п., но вряд ли это даст какие-то гарантии, если число партий невелико. Тут никакие схемы не помогут. В такой ситуации единственный выход выбирать свой ход случайным образом. Например, взять и подбросить монету. Упадёт она кверху орлом делать ход i=1, выпадет решка делать ход i=2. Что же это даст? Выигрыш станет случайной величиной и оценивать его надо по математическому ожиданию. Пусть второй игрок делает ход j=1. Тогда математическое ожидание выигрыша первого игрока будет 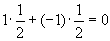 . .Если второй игрок делает ход j=2, то математическое ожидание выигрыша первого игрока равно 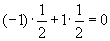 . .Таким образом, выбирая свой ход случайно, первый игрок гарантирует себе (правда, в среднем, а не в каждой партии), выигрыш, равный нулю. А это всё-таки лучше, чем гарантированный выигрыш, равный (-1) . Аналогично, второй игрок, бросая монету и выбирая ход в соответствии с её “указанием”, гарантирует себе в среднем проигрыш, равный 0. Это тоже лучше, чем проигрыш, равный 1. Таким образом, оказывается, что случайный выбор хода повышает наши шансы на успех, хотя бы в среднем. И это является одной из основных идей теории игр выбирать свой ход случайно. Подобный случайный выбор хода получил название смешанной стратегии. Конечно, с обычных житейских позиций, случайный выбор хода не всегда приемлем. Вообразите себе военачальника, который выиграл сражение. Он даёт интервью по TV и на вопрос о том, как же он принял правильное решение, говорит: “Ну, я бросил монету, она упала орлом кверху, и поэтому я … ”. Как посмотрит на него телезритель? А если он проиграл битву, то как отнесётся к такому ответу его начальство? И тем не менее, случайный выбор хода смешанная стратегия имеет право на существование, даже в реальной жизни. Когда не знаешь, как действовать выбирай свой ход случайным образом! Иногда помогает. По крайней мере, никто не разгадает стратегии твоего поведения и не предугадает твоего хода. 5. Нахождение смешанной стратегииЦена игры Оформим теперь всё сказанное выше математически. Рассмотрим сначала ситуацию, когда все 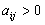 . Это гарантирует нам, что выигрыш первого игрока (и, соответственно, проигрыш второго) всегда будет положительным. . Это гарантирует нам, что выигрыш первого игрока (и, соответственно, проигрыш второго) всегда будет положительным.Пусть в распоряжении первого игрока имеется 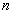 ходов ходов 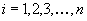 и он выбирает их случайным образом, так что ход номер и он выбирает их случайным образом, так что ход номер 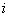 делается с вероятностью делается с вероятностью 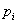 . Набор чисел . Набор чисел 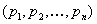 и называется смешанной стратегией первого игрока. Так как и называется смешанной стратегией первого игрока. Так как 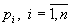 вероятности, то вероятности, то 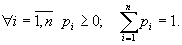 Пусть 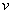 есть гарантированный средний выигрыш первого игрока. Но что значит гарантированный? Это означает, что при любом ходе второго игрока первый игрок получит в среднем не меньше, чем есть гарантированный средний выигрыш первого игрока. Но что значит гарантированный? Это означает, что при любом ходе второго игрока первый игрок получит в среднем не меньше, чем 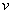 . Математически это означает, что . Математически это означает, что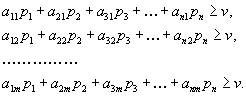 (4) (4)Заметим, что 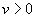 . Перейдём от величин . Перейдём от величин 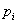 к величинам к величинам 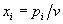 . Тогда, деля все уравнения на . Тогда, деля все уравнения на 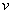 , получим систему неравенств , получим систему неравенств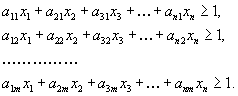 Но у нас есть еще условие нормировки 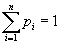 . Переходя к . Переходя к 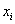 , запишем его в виде , запишем его в виде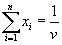 . .В чем же заключается задача выбора оптимальной смешанной стратегии? Она заключается в том, чтобы так выбрать числа 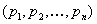 , чтобы гарантированный средний выигрыш , чтобы гарантированный средний выигрыш 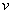 был максимальным. Но тогда был максимальным. Но тогда 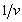 будет минимальным и задача приобретает вид будет минимальным и задача приобретает вид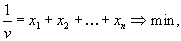 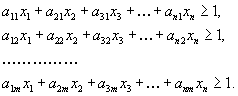 (5) (5)Это типичная задача линейного программирования. Решая её, мы найдём 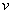 и и 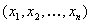 , откуда затем найдём и , откуда затем найдём и 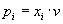 . Заметим, что для . Заметим, что для 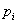 можно написать и другую формулу можно написать и другую формулу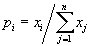 . .Встанем теперь на точку зрения второго игрока. Он ведь тоже может применить смешанную стратегию, выбирая свои ходы случайным образом с вероятностями 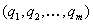 , для которых тоже верно , для которых тоже верно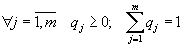 . .Он тоже имеет некоторый максимальный средний проигрыш 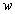 ; слово “максимальный” означает, что при любом ходе первого игрока он не должен ; слово “максимальный” означает, что при любом ходе первого игрока он не долженпроиграть в среднем больше, чем 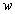 .Математически это означает, что .Математически это означает, что 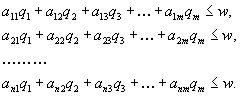 (6) (6) Заметим, что 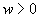 . Перейдём от величин . Перейдём от величин 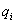 к величинам к величинам 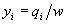 . . Тогда,деля все уравнения (6) на 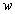 , получим систему неравенств , получим систему неравенств Условие нормировки 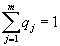 примет теперь вид примет теперь вид 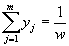 . . Задача выбора оптимальной смешанной стратегии вторым игроком заключается, очевидно, в том, чтобы выбрать 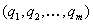 так, чтобы так, чтобы 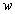 было минимальным. Это приводит к задаче было минимальным. Это приводит к задаче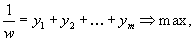  (7) (7)Это также стандартная задача линейного программирования. Решая её, мы найдём 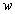 и и 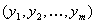 , откуда легко найти и интересующие нас величины , откуда легко найти и интересующие нас величины 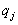 : : 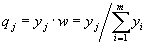 . .Тем самым определяется и оптимальная смешанная стратегия второго игрока. А теперь обратите внимание на самый важный момент в этих рассуждениях. Задачи (5) и (7) являются ссылка скрыта! Но тогда, в силу первой теоремы двойственности, экстремальные значения линейных форм этих задач должны быть равны, то есть при оптимальных смешанных стратегиях обеих игроков должно выполняться соотношение 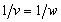 ,или ,или 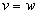 . . Это общее значение 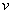 и и 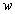 называется ценой игры. Системы (5) и (7) позволяют, таким образом, найти оптимальные смешанные стратегии обеих игроков и цену игры, то есть они позволяют решить игру. называется ценой игры. Системы (5) и (7) позволяют, таким образом, найти оптимальные смешанные стратегии обеих игроков и цену игры, то есть они позволяют решить игру.Обратите внимание на то, какую задачу мы решили. От смешанных стратегий средний выигрыш первого игрока (и, соответственно, средний проигрыш второго) будет равен 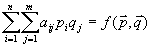 , ,где 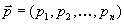 и и 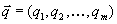 . Находя . Находя 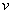 , мы решали задачу , мы решали задачу 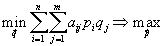 , ,то есть задачу нахождения 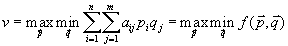 . .Находя 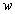 мы решали задачу мы решали задачу  , ,то есть задачу нахождения 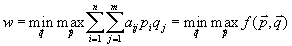 . .У нас получилось, что 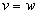 , то есть, что , то есть, что 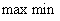 и и 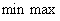 совпадают! Это позволяет говорить о том, что в смешанных стратегиях всякая игра двух лиц с нулевой суммой имеет седловую точку. Это положение является основной теоремой, касающейся игр двух лиц с нулевой суммой. совпадают! Это позволяет говорить о том, что в смешанных стратегиях всякая игра двух лиц с нулевой суммой имеет седловую точку. Это положение является основной теоремой, касающейся игр двух лиц с нулевой суммой.Как и всякая седловая точка, пара стратегий 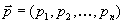 и и 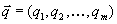 является уравновешенной парой. Это означает, что если противник знает, что я применяю стратегию, соответствующую седловой точке, то ему нет смысла менять свою смешанную стратегию смена стратегии ничего не даст. Игроки, так сказать, могут “играть в открытую”. является уравновешенной парой. Это означает, что если противник знает, что я применяю стратегию, соответствующую седловой точке, то ему нет смысла менять свою смешанную стратегию смена стратегии ничего не даст. Игроки, так сказать, могут “играть в открытую”.В заключение этого раздела отметим, что делать, если не выполняется условие 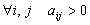 . В этом случае следует перейти к игре с платёжной матрицей . В этом случае следует перейти к игре с платёжной матрицей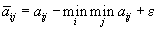 (8) (8)где 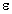 произвольное положительное число. Для новой игры стратегии игроков останутся теми же, то есть мы найдём произвольное положительное число. Для новой игры стратегии игроков останутся теми же, то есть мы найдём 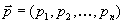 и и 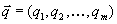 . Что касается цены новой игры . Что касается цены новой игры 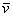 , то она связана с ценой , то она связана с ценой 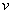 старой игры тем же соотношением, что и (8) старой игры тем же соотношением, что и (8)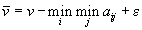 , ,то есть 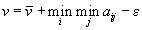 , ,что и решает исходную задачу. |
