Соответствует программе тридцатичасового курса лекций по логике, читаемого студентам Брестского педагогического института. Рассмотрены основные элементы логического мышления применительно к педагогической деятельности.

Вид материала

Лекция

Содержание Дизъюнкцией двух высказываний Аи В называется сложное высказывание Строгой дизъюнкцией высказываний Импликацией двух высказываний Эквиваленцией двух высказываний Вопросы для повторения Лекция тринадцатая. формулы логики Формула В называется логическим следованием формул Лекция четырнадцатая. Нейронные сети.

Подобный материал:

• Развитие логического мышления в процессе внеклассной и факультативной деятельности, 170.98kb.
• Учебно-методическое пособие по дисциплине «Основы педагогического мастерства» 2004, 2489.05kb.
• Муниципальное общеобразовательное учреждение, 478.25kb.
• Формирование логического мышления у школьников происходит, в первую очередь, в учебно-познавательной, 83.51kb.
• Программа дисциплины Введение в специальность: история наук о культуре для направления, 141.91kb.
• Доклад: Формирование логического мышления младших школьников на уроках математики, 40.14kb.
• Тема умозаключение как форма мышления, 341.63kb.
• Паpаллельные алгоpитмы в задачах вычислительной гидpодинамики, 191.67kb.
• Календарно-тематический план по магистерской программе «Мировая экономика» по дисциплине, 128.78kb.
• 12. Основные подходы к пониманию и исследованию мышления в психологии. Характеристика, 132.4kb.

Дизъюнкция. Третья операция, которая употребляется в логи­ке высказываний, соответствует союзу „или". Здесь следует сразу отметить то обстоятельство, что союз „или" имеет в русском языке (и во многих других европейский языках) два различных значе­ния. В одном случае мы говорим об исключающем „или", в дру­гом - о неисключающем „или". Разница заключается в следую­щем. Если мы имеем два высказывания А и В и оба они ложны, то, несомненно, сложное высказывание „А или В" следует считать ложным. Если Л - истинно, а В - ложно (А - ложно, В - истинно), то также понятно, что „А или В" следует рассматривать как истинное высказывание, так как это вполне соответствует смыслу слова '„или" в русском языке. Но как следует рассматривать сложное вы­сказывание „А или В", если А и В оба истинны: как истинное или как ложное? Поясним сказанное примерами. Рассмотрим высказы­вание „Студент Иванов способен или прилежен". Это сложное вы­сказывание истинно, когда истинно хотя бы одно из составляющих его высказываний, т. е. когда истинно высказывание „Студент Иванов способен", либо истинно высказывание „Студент Иванов прилежен". Оно истинно и тогда, когда студент Иванов и способен, и прилежен одновременно. Рассматриваемое высказывание ложно лишь тогда, когда оба высказывания ложны, т. е. студент Иванов неспособен и неприлежен. В приведенном примере союз „или" применяется в неразделительном смысле.

Если же рассматривать высказывание „Завтра в 12 часов я буду в институте или на заводе", то здесь союз „или" понимается в другом, разделительном смысле, он взаимно исключает соеди­няемые части, так как невозможно быть одновременно и в инсти­туте, и на заводе. Если хотят подчеркнуть разделительный смысл, то вместо „или" говорят „либо..., либо".

72

Таблица 6

у\	в	A v&
и	и	И
и	л	И
л	и	И
л	л	л

Рассмотрим логическую операцию, соответствующую неразде­лительному союзу „или". Она называется дизъюнкцией и обозна­чается символом V, который ставится между высказываниями. Если А и В высказывания, то их дизъюнкция обозначается А V В и читается „А или В".

Исходя из значения неразделительного союза „или", разумно дать следующее определение дизъюнкции.

Дизъюнкцией двух высказываний Аи В называется сложное высказывание А V В, которое истинно тогда и только тогда, когда истинно хотя бы одно из этих высказываний.

Определение дизъюнкции можно записать в виде истинност­ной таблицы (табл. 6).

Из таблицы следует также, что дизъюнкция двух высказыва­ний ложна лишь тогда, когда оба высказывания ложны.

Определение дизъюнкции так же, как и определение конъ­юнкции, естественным образом распространяется на любое число высказываний. Так, дизъюнкция высказываний А₁\/А₂У ... У А„ считается истинной, когда истинно хотя бы одно из высказываний ai. A₂₎ .._g) а„, и ложной, когда ложно каждое из этих высказыва­ний. Дизъюнкция п высказываний А _ь А₂,..., А„ кратко обозначает-

ся

V А,.-

п *» I

Приведем примеры дизъюнкции. Пусть А - высказывание „Река Днепр впадает в Черное море", а В - высказывание „Река Днепр впадает в Азовское море", тогда А V В - высказывание , „Река Днепр впадает в Черное или в Азовское море". Эта дизъюнк­ция истинна, так как истинно одно из высказываний. Дизъюнкция „Город Брест расположен на реке Днепр или на реке Волга" явля­ется ложной, поскольку оба высказывания (Город Брест располо­жен на реке Днепр; Город Брест расположен на реке Волга) явля­ются ложными.

Рассмотрим логическую Операцию, соответствующую раздели­тельному союзу „или". Она называется строгой дизъюнкцией и

73

Таблица 7

А	. в
И	и
И	л
Л	и
л	л

А

Л И И

л

обозначается символом V, который ставится между высказыва­ниями. Если А и В два высказывания, то их строгая дизъюнкция обозначается А V В и читается „либо А, либо В".

Исходя из значения разделительного союза „или", строгую дизъюнкцию разумно определить следующим образом.

Строгой дизъюнкцией высказываний А и В называется выска­зыванием А В, истинное тогда и только тогда, когда высказыва­ния А и В имеют различные истинностные значения.

Определение строгой дизъюнкции можно записать в виде истинностной таблицы (табл. 7).

Рассмотренные операции отрицания, конъюнкции и дизъюнк­ции называются булевыми операциями. Такое название они полу­чили в честь ирландского математика Джорджа Буля (1815-1864), в трудах которого математическая логика оформилась как своеоб­разная алгебра, впоследствии также названная булевой алгеброй или алгеброй Буля.

Импликация. К многозначным союзам естественного языка наряду с „или" относится также союз „если, то". В грамматике он причисляется к условным союзам. С помощью этого союза часто выражают то, что одно явление является условием для другого.

Обычно высказывание вида „если А, то В" понимается в смыс­ле следования В из А и часто вместо „если А, то В" говорят: „из А следует В" или „А влечет В" и др.

В определенной мере союзу „если, то" соответствует операция импликации высказываний. В качестве знака для импликации бу дем употреблять символ ^э, который ставится между высказы­ваниями. Если А и В - два высказывания, то их импликация обо­значается А и В и читается: „А имплицирует В" или „если А, то В".

Импликация, двух высказываний определяется следующим образом.

Импликацией двух высказываний А и В называется такое сложное высказывание А = В, которое ложно тогда и только тогда, когда высказывание А истинно, а В- ложно.

74

Таблица 8

А	&	Л=>£
И	и	и
И	л	л
Л	и	и
л	л	и

Тем самым операция импликации высказываний задается сле­дующей истинностной таблицей (табл. 8).

Из истинностной таблицы видно, что перестановка членов импликации может привести к изменению этой таблицы, т. е. высказывания А и В в импликации А => В нельзя менять местами так, как это можно было делать для рассмотренных выше опера­ций конъюнкции и дизъюнкции. В связи с этим каждый член импликации имеет свое название. Так, в импликации АВ, выска­зывание А называется антецедентом, а В - консеквентом.

Как отмечалось выше, импликация до некоторой степени соот­ветствует союзу „если, то", однако это соответствие весьма при­близительное. Чтобы выяснить, в каком смысле обычно приме­няется логическая связка „если, то", рассмотрим конкретные при­меры.

а). Если 6 делится на 3 и 9 делится на 3, то и их сумма делится на 3 - это истинная импликация.

б). Если 4 делится на 3 и 5 делится на 3, то их сумма делится на 3 - это истинная импликация, хотя антецедент ее ложный.

в). Если 4 делится на 3 и 7 делится на 3, то и их сумма делится на 3 - это истинная импликация, в которой антецедент и консе-квент ложные.

г). Если 6 делится на 3 и 9 делится на 3, то их сумма не делится на 3 - это ложное высказывание, так как не существует двух таких чисел, которые делятся на 3, а их сумма не делится на 3 (антеце­дент истинный, консеквент ложный).

Смысл приведенных примеров еще в определенной мере согласуется с пониманием союза „если, то".

Теперь возьмем для построения импликации такие простые высказывания: „Береза - дерево" - И; „Орешник - дерево" - Л; „Дважды два - четыре" - И; „Дважды два - семь" - Л.

Интерпретируя импликацию как союз „если, то", получаем следующие высказывания: „Если береза - дерево, то дважды два -четыре" - истинно; „Если орешник - дерево, то дважды два -

семь" - истинно; „Если береза - дерево, то дважды два - семь" -ложно.

Как видно, эти предложения совсем не соответствуют привыч­ному употреблению союза „если, то". Причина такого несоответ­ствия кроется в многозначности некоторых слов русского языка.

Союз „если, то" может описывать причинно-следственную связь между двумя высказываниями, например, „Если некоторое тело нагревать (причина), то оно увеличивается в объеме (след­ствие)".

Несколько иной смысл союз „если, то" имеет в следующем предложении: „Если все деревья имеют ствол и ясень - дерево, то ясень имеет ствол". Здесь союзом „если, то" выражается отноше­ние логического следования: высказывание „Ясень имеет ствол" следует из высказывания „Все деревья имеют ствол и ясень -дерево".

Несмотря на существенную разницу в понимании союза „если, то", имеется одна общая черта: он указывает на некоторую связь между содержанием высказываний А и В.

Из вышеизложенного следует, что высказывание А => В не сов­падает по смыслу с высказыванием „если А, то В". Поэтому, во из­бежание недоразумений, уместно читать сложное высказывание А = В не „если А, то В", а „А имплицирует В" и понимать эту опера­цию так, как это установлено соответствующей таблицей истин­ности.

Эквиваленция. Введем, наконец, еще одну логическую опера­цию - эквиваленцию. В качестве знака для эквиваленции будем употреблять символ „~", который ставится между высказывания­ми. Если А и В - два высказывания, то их эквиваленция обознача­ется так: „А ~ В" и читается" А тогда и только тогда, когда В" или „А эквивалентно В".

Эквиваленция двух высказываний определяется следующим образом.

Эквиваленцией двух высказываний А и В называется сложное высказывание А ~ В, которое истинно тогда и только тогда, когда оба высказывания А и В имеют одно и то же значение истинности.

Таблица 9

А	В	А~в
и	и	и
и	л	л
л	и	л
л	л	и

76

По определению, эквиваленция двух высказываний может быть задана следующей истинностной таблицей (табл. 9).

Из таблицы истинности следует также, что эквиваленция двух высказываний ложна лишь тогда, когда высказывания А и В име­ют различные истинностные значения.

Эквиваленция примерно соответствует употреблению выраже­ния „тогда и только тогда, когда". Но, так же, как и для имплика­ции, это соответствие далеко не полное. О связи логической опе­рации эквиваленции и языкового выражения „тогда и только тогда, когда',' можно в основном повторить то, что было сказано о связи импликации с союзом „если, то".

ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ

1. Дайте определение логических операций над высказываниями, приведите примеры.

2. Постройте истинностные таблицы для каждой логической операции.

3. В чем различие между законом двойного отрицания в логике и законом отри­цания в математике?

ЛЕКЦИЯ ТРИНАДЦАТАЯ. ФОРМУЛЫ ЛОГИКИ

Переменные и постоянные высказывания. Формулы логики,

их запись и чтение. Истинностные таблицы. Равносильность

и логическое следование. Равносильности, выражающие

свойства логических операций.

Понятие о логической формуле. Высказывание, истинностное значение которого не задано, будем называть переменным и обо­значать буквами А, В, С и т. д.

Высказывание с заданным истинностным значением будем называть постоянным и обозначать буквами И или Л.

Сложное высказывание, образованное из постоянных и пере­менных высказываний с помощью логических операций будем называть логической формулой или формулой логики.

Более точно логическую формулу можно определить следую­щим образом:

l.Bce переменные и постоянные высказывания являются логи­ческими формулами.

2. Если А и В - формулы, го (ТА), (А Л В), (A VB), (А=>В), (А~В) -также логические формулы.

3. Только те выражения являются логическими формулами, которые строятся на основании пунктов 1 и 2.

Таким образом, логическая формула записывается в виде ко­нечной последовательности больших латинских букв, символов И и Л, знаков логических операций, скобок путем последовательно­го применения правил Г и 2.

Примеры (A), (BVH), (А =>В),((А~В) =>( 1C))-логические формулы.

Ввиду того, что большое количество скобок усложняет запись и чтение логических формул, в математической логике, как и в алгебре, условились придерживаться-следующих правил: а) внешние скобки при записи формул опускаются;

77

б) при наличии скобок в первую очередь выполняются операции, заключенные во внутренних скобках, затем во внутренних из оставшихся скобок и т. д.;

в) при отсутствии скобок логические операции выполняются в сле­дующей последовательности: отрицание, конъюнкция, дизъюнк­ция, импликация и эквиваленция;

г) если без скобок записаны одна за другой несколько одинаковых операций, то они выполняются последовательно слева направо.

Пример. Формулу (A = ((]B)V(CA А)) в соответствии с приведен­ными выше правилами можно записать в виде А=1В V С Л А.

При записи формулы необходимо следить за тем, чтобы число открывающихся скобок было равно числу закрывающихся.

Зная истинностные значения высказываний, образующих данную формулу, можно установить истинностное значение слож­ного высказывания, представленного данной формулой. Напри-мер,пустьвф6рмуле1(А=В) = (А~СЛД)А~И,В-И, С-Л, Д -И. Тогда сложное высказывание, определяемое этой формулой, может быть записано в виде: 1(И=>И) => (И~ Л Л И). Значение этого вы­сказывания И, т. к. И=И - И, "1И - Л, Л ЛИ-Л, И~ Л - Л, Л = Л - И.

Истинностная таблица формулы. Если мы зададим всевозмож­ные наборы значений переменных, то для каждого случая по'лу-чим соответствующее истинностное значение формулы. Таким об­разом каждая формула определяет некоторую функцию, аргумен­тами которой являются переменные простые высказывания, а зна­чениями - И или Л. Поскольку каждый из аргументов может принимать лишь два значения, то такие функции могут быть опи­саны конечными таблицами. Как и прежде, их называют истин­ностными таблицами.

Пример. Построить истинностную таблицу для формулы А Л В=> 1CV А. Таблица имеет следующий вид (табл. 10).

В принципе для любой логической формулы можно построить истинностную таблицу, однако на практике это реально выполни­мо только лишь для формул, содержащих менее пяти простых высказываний. Дело в том, что число всевозможных наборов зна­чений переменных равно 2^П, где п - число переменных в формуле. Так, при п = 4, имеем 2⁴ = 16, при п = 5, будет 2^s = 32, а при п = 10 уже2^!" = 1024. Понятно, что нерационально строить истинностную таблицу с 32 строками. В подобных случаях формулу упрощают путем выполнения преобразований на основании правил, о кото­рых будет сказано ниже. Такие преобразования логических фор­мул в некоторой степени напоминают тождественные преобразо­вания алгебраических выражений.

Равносильные формулы. Две формулы будем называть равно­сильными, если при любых наборах значений переменных, входя­щих в эти формулы, они принимают одинаковые истинностные значения. Отсюда следует, что истинностные таблицы для равно­сильных формул совпадают.

78

Таблица 10

А	в	с	АлВ	1C	iCvA	Дл£ 1С\/А
и	и	И	и	л	и	и
и	и	л	и	и	Е	и
и	л	и	л	л	И	и
и	л	л	л	и	И	и
л	и	и	л	л	Л	и
л	и	л	л	и	и	и
л	л	и	л	л	л	и
л	л	л	л	и	и	и

противоречие,

Равносильность логических формул будем обозначать знаком „=". Например, как показано выше, формулы А и ЦА - равносиль­ны, т.е. A s "Ц д.

Логическая формула, равносильная формуле И, называется тождественно-истинной, или законом логики, или тавтологией, а логическая формула, равносильная формуле Л, называется тожде­ственно ложной или противоречием. Формулы, не относящиеся ни к одному, ни к другому виду, называются выполнимыми.

Например: АЛВЬ] CVA -тавтология, АЛ] А -C- выполнимая формула.

Тот факт, что первая формула является тавтологией, показано выше с помощью истинностной таблицы. Противоречивость второй и выполнимость третьей формулы читателю рекомендуется прове­рить самостоятельно.

Таким образом, последний столбец истинностной таблицы тавтологии содержит только значения И, а противоречия - только значения Л.

Очевидно, любые две тавтологии, как и любые два противоре­чия всегда равносильны, и любая тавтология равносильна отрица­нию противоречия.

Между понятием равносильности и операцией эквиваленции существует следующая связь: две формулы логики равносильны тогда и только тогда, когда их эквивалениия является тавтоло­гией. Справедливость этого утверждения непосредственно следу­ет из определения эквиваленции.

При определении равносильности двух формул не обязательно предполагать, что они содержат одни и те же переменные. Так, формула (AA"|A)VB равносильна формуле В, формула AV]A равно­сильна BV1B. Вместе с тем, очевидно, что если какая-либо пере­менная входит только в одну из двух равносильных формул, то эта формула при всех значениях переменной принимает одно и то же значение, если значения других переменных фиксированы. Ины­ми словами, хотя эта переменная и входит в формулу, но функция, определенная рассматриваемой формулой, от этой переменной не зависит.

Логическое следование. Пусть А1, аз,..., А_п - формулы логики высказываний.

Формула В называется логическим следованием формул A_lf А₂,..., А„, если при любом наборе истинностных значений перемен­ных, входящих в формулы ai, А2,..., А„, формула В принимает зна­чение И каждый раз, когда такое значение принимает каждая из формул ai, А₂,..., А„.

Используя истинностные таблицы, можно заметить, что форму­ла В является логическим следованием формул А₁₍ А₂,..., А„, если она имеет значение И во всех тех строках таблицы, в которых ai, А2, »», А„ имеет одновременно значение И.

Например, формула 1А является логическим следованием

80

Таблица It

k	£	а=> а	Alfl	1А
и	и	и	л	л
и	л	л *	и	л
л	и	и	и	и
л	.л	и	и	и
		1	"

формул А=зВи А=>1В, что подтверждается следующей истинност­ной таблицей (табл. 11).

Отметим также, что тавтология логически следует из любой формулы логики, а любая формула логически следует из противо­речия.

Между понятием логического следования и импликацией существует следующая связь: формула В является логическим сле­дованием формул ai, А₂,..., А_п , тогда и только тогда, когда форму­ла A_tA А₂А... Л А„=> В -тавтология. Справедливость этого утверж­дения непосредственно следует из определения импликации. Так, из предыдущего примера видно, что формула (АВ) Л (A=>]B)=>1 A является тавтологией.

Отношение логического следования будем обозначать симво­лом =» и записывать А =» В, если В логически следует из А.

Очевидно, что А =* В и В =» А, то A ^SB.

Свойства логических операций. Логические операции обла­дают целым рядом важных свойств. Некоторые из них подобны аналогичным свойствам алгебраических операций, а другие суще­ственно отличаются от них. При этом будем учитывать, что конъ­юнкцию иногда называют логическим умножением и обозначают знаком „•" или вообще не обозначают (пишут А -В или АВ вместо А Л В), а дизъюнкцию - логическим сложением и обозначают зна­ком „+" (пишут А + В вместо AVB). Такие названия и обозначения чаще всего встречаются в приложениях математической логики, где, кстати, отрицание ТА обозначают А и называют инверсией.

В дальнейшем будем считать высказывания А, В, С произволь­ными, а свойства логических операций записывать в виде равно-' сильностей.

Назовем основные свойства логических операций, доказатель­ство их справедливости будем проводить с помощью истинностных таблиц. Основную массу таких доказательств предлагается в качестве несложных упражнений осуществить самим читателям.

а) Коммутативность конъюнкции и дизъюнкции

81

Следует из определения соответствующих операций.

б) Ассоциативность конъюнкции и дизъюнкции (А Л В)Л С s АЛ (ВАС); (AVB)VC = AV(BVQ.

Справедливость ассоциативного закона конъюнкции проверим с помощью истинностной таблицы (табл. 12).

Совпадение двух последних столбцов истинностной таблицы и подтверждает справедливость доказываемого.

Ассоциативность дизъюнкции рекомендуется читателю про­верить самостоятельно.

в) Дистрибутивность конъюнкции относительно дизъюнкции

AA(BVC) э (AAB)V(AAC); дистрибутивность дизъюнкции относительно конъюнкции

AV(BAC)s(AVB)A(AVC). Докажите самостоятельно.

г) АЛ as А; АЛИ = А; АЛЛЛ; AVAsA; AVHsH; АУЛнА.

Справедливость этих равносильностей очевидна.

д) A A] as Л; А VI as И; ЦАаД. Докажите самостоятельно.

е) Отрицание конъюнкции (дизъюнкции) двух высказываний равносильно дизъюнкции (конъюнкции) отрицаний этих выска­зываний:'

1(АЛВ)з]АУ1В; 1(А V В) = ]А А 1В.

Рекомендуется доказать самостоятельно.

Приведем пример применения этого свойства.

Отрицанием высказывания „Солнце светит и греет" является высказывание „Солнце не светит или не греет".

Отрицанием высказывания „А. С. Пушкин или М. Ю. Лермон­тов написал роман „Евгений Онегин" является высказывание: „А. С. Пушкин не написал роман „Евгений Онегин" и М. Ю. Лер­монтов не написал роман „Евгений Онегин".

На основании сформулированного свойства е) конъюнкцию (дизъюнкцию) двух высказываний можно заменить отрицанием и дизъюнкцией (конъюнкцией).

Например: А А В а Ц(А А В) а ](]А V ]В),

Доказательство проведите самостоятельно.

На основании этого свойства операцию импликации можно за­менить операциями отрицания и дизъюнкции.

Например, импликация: „Если данный треугольник правиль­ный, то в него можно вписать окружность" равносильна сложному высказыванию: „Данный треугольник не является правильным, или в него можно вписать окружность".

Этим свойством часто пользуются и тогда, когда из контекста не совсем ясно, в каком значении употреблен союз „если, то".

з) А ~ В з (А => В) А (В => А).

82

Таблица 12

А	&	с	А/\В	ВлС	(А л В) л С	А А (В А С )
и	и	и	и	и	и	и
и	и	л	и	л	тт J л	Л
и	л	и	л	л	Л.	Л
и	л	л	л	л	Л	Л
л	и	и	• Л	и	Л	Л
л	и	л	л	л	Л	Л
л	л	и	-' л	л	Л	Л
л	•Л	л	л	л	Л	Л

Эта равносильность свидетельствует о том, что эквиваленцию двух высказываний можно заменить операциями импликации и конъюнкции. Свойство з) иногда используют в качестве опреде­ления эквиваленции: „Конъюнкция двух импликаций А=> В и В = А называется эквиваленцией высказываний А и В".

Например, эквиваленция: „Данное число делится на 3 тогда и только тогда, когда сумма цифр в его записи делится на 3" равно­сильна конъюнкции высказываний: „Если данное число делится на 3, то и сумма цифр в его записи делится на 3" и „Если сумма цифр в записи данного числа делится на 3, то само это число де­лится на 3".

и)А = В = 1В = 1А.

Действительно, учитывая последовательно свойства ж), д), а), ж) логических операций, будем иметь:

-

Равносильные преобразования. С помощью вышеуказанных свойств логических операций можно осуществлять равносильные преобразования произвольных логических формул. Пример такого преобразования приводится в пункте и). Такие преобразования вызываются не только потребностями самой математической ло­гики, но и многочисленными ее техническими приложениями. Более подробно на вопросах преобразования логических формул останавливаться не будем.

Анализируя приведенные выше свойства логических опера­ций, можно сделать вывод, что любую логическую формулу можно свести к формуле, содержащей только отрицание и конъюнкцию, либо отрицание и дизъюнкцию.

Естественно возникает вопрос: если все логические операции могут быть сведены, к двум, то почему логика высказываний поль­зуется многими операциями?

Причины этого кроются в следующем:

а) при исключении некоторых логических операций формулы становятся более длинными и менее обозримыми. Ведь и в ариф­метике натуральных чисел можно было бы обойтись без умноже­ния, и вместо 3 • 7 писать 3 + 3 + 3 + 3 + 3 + 3 + 3. Ясно, что это мало способствовало бы обозримости и удобочитаемости формул;

б) введенные нами логические операции играют определен­ную роль при описании! закономерностей логических заключений. Особенно это относится к операции импликации;

в) излагаемый здесь раздел логики высказываний далеко не исчерпывает проблематику логики высказываний. Он является одним из самых элементарных ее разделов. Имеются другие об­ласти, в которых не все приведенные равносильности имеют место и тем самым в них не всегда допустимы указанные нами выраже­ния одних операций через другие, но на этом мы останавливаться не будем.

Как уже было отмечено выше, всякую равносильность двух формул можно записать в виде тавтологии или закона логики.

84

Так, например, равносильность А V В е В V А выражает коммута­тивный закон дизъюнкции, поскольку формула AVB~BVA- тав­тология.

В математической логике формула Ц А ~ А называется законом двойного отрицания, 1(А Л ]А) ~ И -законом противоречия, AV]A~ '~И-законом исключенного третьего, а формулы ](AAB)~TAV|.B и 1(А V В) ~ А Л 1В - законами де Моргана. Можно также говорить об ассоциативном (п.б), дистрибутивном (п.в) законах, законе контра-позиции (п.и).

Вместе с тем, следует иметь ввиду, что обычно законами логи­ки называют не любые тавтологии, а лишь те из них, которые наи­более часто употребляются в умозаключениях при определении истинности или ложности некоторого суждения.

В заключение отметим, что нельзя путать логическое проти­воречие между высказыванием и его отрицанием с диалектиче­ским противоречием. В то время, как логическое противоречие вообще не существует в объективной реальности, диалектическое противоречие является движущей силой развития, играет в нем решающую роль. Если стороны диалектического противоречия обусловливают друг друга, то стороны логического противоречия исключают друг друга.

Закон исключенного третьего отражает тот факт, что некото­рая объективная связь между явлениями действительности либо существует, либо нет. Он сохраняет силу только для абсолютно истинных высказываний. Так как относительно истинные выска­зывания являются одновременно относительно ложными, то за­кон исключенного третьего к ним неприменим. Кроме них имеют­ся абсолютно истинное и абсолютно ложное высказывания о рас­смотренном объективном отношении между предметами.

вопросы для повторения

1. Что такое формула логики? Приведите примеры таких формул.

2. Перечислите виды логических формул. Приведите примеры.

3. Как определить в простейших случаях вид логической формулы?

4. Что понимают под отношением логического следЬвания одной формулы из другой?

5. Перечислите основные свойства логических операций.

6. В чем различие между законами исключенного третьего (противоречия) в ло­гике и философии?

ЛЕКЦИЯ ЧЕТЫРНАДЦАТАЯ. ПРИМЕНЕНИЕ ЛОГИКИ

ВЫСКАЗЫВАНИЙ

Синтез и анализ контактных схем. Нейронные сети

Синтез и анализ контактных схем. Высказывания и электри­ческие контакты - объекты совершенно различной природы, и, ка­жется, что никакой срязи между ними нет. Но эхо не так. В дейст­вительности они сходны между собой: высказывания могут прини­мать только два значения (И, Л), а электрические контакты могут находиться только в двух положениях („замкнуто", „разомкнуто").

85

Это сходство служит основой для применения алгебры выска­зываний к задачам, связанным с контактными схемами. При рас­смотрении контактных схем нас не будет интересовать, каким спо­собом переводятся контакты из одного положения в другое: с по­мощью электромагнитного реле, электронных ламп, транзисторов или иных электронных устройств.

Идея использования алгебры высказываний для построения автоматических устройств, основанных на контактных схемах, было высказано уже в 1910ГОДУ крупным физиком П. Эренфестом. Нб эта ценная мысль долгое время не привлекала к себе должного внимания. Дело в том, что для конструирования простейших схем (а другие тогда и не выполнялись) инженеры вполне обходились своим повседневным опытом и не нуждались в общей теории и математическом аппарате. Положение существенно изменилось в 30-х годах нашего столетия. К этому времени автоматические уст­ройства достигли такого уровня сложности, что создание научных теорий для их конструирования стало насущной необходимостью. С тех пор область применения математической логики в теории и практике контактных схем непрерывно расширяется. В нее вклю­чаются и более высокие разделы математической логики. С дру­гой стороны потребности теории автоматического регулирования стимулируют интенсивное развитие новых разделов математиче­ской логики. Эта тенденция особенно усилилась в эпоху создания электронно-вычислительных машин и возникновения кибернети­ки.

В теории контактных схем рассматриваются две задачи: синтез и анализ схемы.

Под синтезом понимают конструирование схемы по заданным условиям ее работы. Под анализом схемы понимают обратную за­дачу: определение условий работы заданной схемы. Параллельно с этими двумя задачами возникает и третья задача: упрощение схемы, т. е. конструирование „эквивалентной" схемы, но с мень­шим числом контактов.

Применение аппарата алгебры высказываний к синтезу и ана­лизу контактных схем основано на возможности установления соответствия между формулами логики высказываний и контакт­ными схемами.

Сущность этого соответствия заключается в следующем:

а) каждому высказыванию, которое может быть истинным или ложным, ставится в соответствие контакт, который может быть замкнут или разомкнут;

б) истинному высказыванию ставится в соответствие замкну­тый контакт, а ложному - разомкнутый.

Исходя из сказанного, легко выяснить, какие схемы соответ­ствуют конъюнкции, дизъюнкции и отрицанию высказываний.

1. Конъюнкции двух высказываний А и В соответствует схема, составленная из двух контактов А и В так, чтобы она была замкну­та тогда и только тогда, когда оба контакта замкнуты. Такая схе-

86



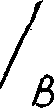
Рис.14

ма состоит из последовательно соединенных контактов АиВ, как показано на рис. 14.

4

4

Рис. 15

2. Дизъюнкции двух высказываний А и В соответствует схема, составленная из двух контактов АиВ так, чтобы она была замкну­та тогда и только тогда, когда замкнут хотя бы один из контактов А или В (или разомкнута тогда и только тогда, когда разомкнуты оба контакта А и В). Такая схема состоит из параллельно соеди­ненных контактов АиВ так, как показано на рис. 15.

3. Отрицанию 1А высказывания А соответствует схема, состав­ленная так, чтобы она была замкнута, когда контакт А разомкнут, и разомкнута, когда контакт А замкнут. Такая схема состоит из контакта А, контакта А, называемого инверсией и управляемого тем же элементом, что и контакт А, так, что А замкнут, когда А разомкнут и А" разомкнут, когда А замкнут. Схема, соответствую­щая отрицанию высказываний, изображена на рис. 16.

Так как каждая формула логики высказываний может быть выражена с помощью операций конъюнкции, дизъюнкции и отри­цания, то описанное выше соответствие сопоставляет с каждой такой формулой контактную схему, составленную из контактов и их инверсий с помощью параллельных и последовательных со­единений.

Очевидно, что соот­ветствие между форму­лами логики высказыва- О ний и контактными схе­мами является взаимно однозначным, т. е. каж­дой формуле логики вы­сказываний, составлен-

А

А

Рис.16

87

ных с помощью указанных выше операций соответствует точно одна контактная схема, составленная из контактов и их инверсий с помощью параллельных и последовательных соединений и на­оборот.

Установленное взаимно-однозначное соответствие обладает важным для приложений свойством: оно переводит равнозначные формулы логики высказываний в эквивалентные контактные схе­мы, т. е. в такие схемы, которые при любых наборах положений входящих в них контактов принимают одинаковые состояния. Например, равнозначным формулам логики высказываний А V (В Л С) и (А V В) Л (А V С) соответствуют эквивалентные схемы, изображенные на рис. 17.

Нетрудно заметить, что обе схемы замкнуты, когда замкнут контакт А или одновременно замкнуты контакты В и С и разомк­нуты, если разомкнут контакт А и один из контактов В или С. ,

Таким образом, с помощью установленного взаимно-однознач­ного соответствия:

а) анализ контактной схемы сводится к определению значе­ний соответствующей логической формулы при всевозможных зна­чениях входящих в эту формулу переменных;

б) упрощение контактной схемы сводится к упрощению соот­ветствующей 'логической формулы;

в) синтез схемы по условиям его работы сводится к составле­нию логической формулы по этим условиям, переведенным в истинностную таблицу, упрощению этой формулы и конструирова­нию соответствующей схемы.

Более подробно на вопросах, связанных с теорией контактных схем, останавливаться не будем. •

Нейронные сети. Остановимся на другом, не менее важном, применении логики высказываний. Речь пойдет о логике выска­зываний в нейронных сетях.

Чрезвычайно трудно исследовать принцип действия головного мозга человека. До сих пор нет никакой возможности непосред­ственно проследить, что происходит в головном мозге человека, когда он думает. Задача усложняется и тем, что нельзя экспери­ментировать непосредственно с головным мозгом человека, мож­но создать его модель, исследуя которую, ученые пытаются сде­лать заключение в отношении самого объекта. Такая модель дея­тельности мозга была создана в сороковых годах нашего столетия



л

•4