Методичн вказвки до виконання розрахунко роботи "дослдження за допомогою еом коливань системи з одним ступенем вльност"

Мнстерство транспорту кра

Днпропетровський державний технчний нверситет

залзничного транспорту

Кафедр У Теоретичн механка У

МЕТОДИЧН

ВКАЗ

ВКИ

ДО ВИКОНАННЯ РОЗРАХУНКООп

РОБОТИ УДОСЛ

ДЖЕННЯ ЗА ДОПОМОГОЮ

ЕОМ КОЛИВАНЬ СИСТЕМИ З ОДНИМ

СТУПЕНЕМ В

ЛЬНОСТ

Ф

Вльн коливання т вимушен коливання точки

при не гармончному збуренн

Частина ²

Укладач:а Л. А. Манашкн

Л. Г. Маслºва

Д. Б. Астраханцев

.Ю. Журавльов

Для студентва другиха курсв

спецальностей : 7.092107,

7.100501, 7.092202, 7.090603,

7.092203, 7.100502

Днпропетровськ 2001

Змст.

Вступ.......................................................................................................

1. Постановка задач
2. Складання диференцального рвняння вимушених коливань механчно� системи
3. Визначення амплтудно- та фозово- частотних характеристик системи
4. Розкладання функц�� ав ряд ФурТ

та визначення параметрв гармонк збурюючо� сили

Дослдження вимушених коливань механчно� системи.

            Визначення (за допомогою ЕОМ) Уточного ршення диференцального рвняння. Аналза ршення.

            Пдбр (за допомогою ЕОМ) рацонально

            Побудова аналтичного ршення диференцального рвняння. Пдбр рацонально

6. Стисла характеристика програми
7. Порядок пдготовки вихдних даних для виконання розрахунку на ЕОМ.
8. Схемиа механчниха система т розрахункова дана до них.
9. Перелка лтератури.

Вступ.

Друга частина розрахунково

Методичн вказвки мстять приклад виконання розрахунково

Виконання розрахунково

-          складання диференцального рвняння руху механчно

-          виконання розрахунку на ЕОМ;

-          визначення аналтичного ршення;

-          зставлення результатв розрахункв на ЕОМ аналтичного ршення.

1. Постановка задач

 

Методику дослдження малих коливань системи при дÿ негармончно

Механчна система, що зображена на рис.1, склада

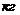
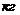
ться з трьох тл масою ата

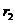
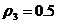
Така механ<чна система ма

один ступнь вльност.

Нехай рух системи виклика

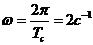
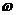ться перодичною збурюючи силою а ) з параметрами а<- амплтуда збурюючой сили, а<

Будемо вважати, що рух системи почина

ться з положення статично

Розрахунки проведемо у наступному порядку:

1.1.  З допомогоюа рвняння Лагранж <²-го роду складемо рвняння руху механчно

Початков умови задач взьмемо нульовими, так як рух системи почина

ться з положення статично

1.2.  Визначимо (за допомогою ЕОМ) амплтудно-частотну (АЧХ) та фазово-частотну (ФЧХ) характеристики системи.

1.3.  Розкладемо функцю ав ряд ФурТ

визначимо (за допомогою ЕОМ) параметри гармонк в розкладенн.

1.4.  Визначимо (за допомогою ЕОМ) ршення адиференцального рвняння руху механично

Розглянемо також випадок, коли сила азада

ться сумою агармонк. При цьому встановимо, при якому рацональному значенн афункця авизнача

ться з 5% точнстю (по вдношенню до точного ршення).

Проналзу

мо характер коливального процесу при рзних значеннях <

1.5.  Користуючись АЧХ и ФЧХ системи та знайденими параметрами гармонк у розкладенн сили адиференцального рвняння, руху механчно

При цьому встановимо, при якому рацональне значен налтичне ршення визнача

ться за 5% точнстю по вдношенню до Уточного ршення.

Спвставлення ршень будемо проводити для контрольного моменту часу

2.       Складання диференцального рвняння вимушених коливань механчно

Рвняння вимушених коливань задано

( )

де а< а<- загальнена координата та швидксть, а< а<- кнетична потенцальна енергÿ системи вдповдно, 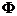а<- функця розсювання, а<- загальнена непотенцальна сила.

Складемо вираз кнетично

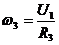
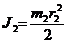
У вираз 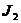ата а<- моменти нерцÿ тл 2 3 вдносно центрально

Позначимо коефцúнт 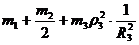а<- зведена маса системи. Тод:

( )

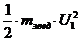
Складемо вираз потенцально

Обчислемо потенцальну енергю системи в ? довльному положенн як роботу потенцальних сил на перемщенн системи з довльного положення в положення статично

де аа

тут а<- статичн подовження пружин; 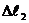а<- змна довжини вдповдно

Враху

мо, що

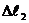
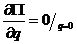
Вираз потенцально

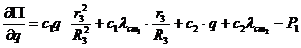
При рвноваз системи (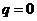

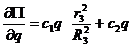
Тод вираз потенцально

а ( )

де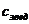

Функцю розсювання 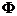абудемо вважати залежною вд загальнено

де а<- коефцúнт вТязкост (дисипативний коефцúнт).

До непотенцальних сил, що дють на систему, вдноситься тльки збурююча сила

Взьмемо вдповдн похдн складемо рвняння Лагранжа для задано

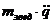
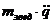
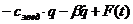
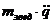
( а)

де а<

Диференцальне рвняння ( ) представля

собою неоднордне диференцальне рвняння другого порядку вдносно загальнено

Ршення задач про дослдження вимушених коливань системи зводиться до ршення цього диференцального рвняння при заданих початкових мовах задач. Оскльки у розглянутому випадку рух системи почина

ться з стану статично

при ( )

Як вдомо, аналтичне ршення рвняння ( ) склада

ться з суми двох ршень 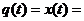а

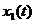
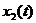
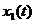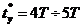
Слд зауважити, що ршення ав даному випадку (при вдповдному пдбор коефцúнта 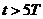а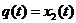

Визначимо чисельн значення параметрв системи та коефцúнтв в рвнянн ( ):

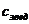
^.м ^Ц1;

^Ц1;

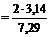
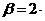
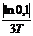
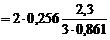^.с^.м ^Ц1;

с ^Ц1.

Для переврки врност визначення коефцúнту арекоменду

ться пдрахувати значення спвмножника 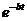ав ршенн 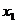апри ^.0,861 = 4,31с:

Таке значення спвмножника (наближене до нуля) в ршенн 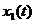азнайдено врно.

3.       Визначення амплтудних- та фазово-частотних характеристик системи.

 

Шляхом виведення, за допомогою ЕОМ, для задано

4.       Розкладання функцÿ F(t) в ряд ФурТ

та визначення параметрв гармонк збурюючо

 

Розкладемо функцю ав ряд ФурТ

:

( )

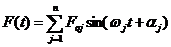де

Визначимо (за допомогою ЕОМ) параметри гармонк: амплтуди , частоти 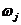ата початково

Для задано

Таблиця 1.

Номер гармонки,	кН		рад.
1	0,764	2	0
2	0,255	6	0
3	0,153	10	0
4	0,109	14	0
5	0,085	18	0

5.       Дослдження вимушених коливань механчно

 

5.1.  Визначення (за допомогою ЕОМ) точного ршення диференцального рвняння. Аналз ршення.

Визначимо за допомогою ЕОМ точне ршення адиференцального рвняння для випадку, коли сила апредставлена однúю гармонкою (адля вдповдних випадкв виводяться на екран ЕОМ. Перед виводом графкв на друкарський пристрй

з графкв видно, що функцÿ аполучаються перодичними, тобто рух механчно

5.2.  Пдбр (за допомогою ЕОМ) рацонально

Визначимо (за допомогою ЕОМ) функцÿ адля випадкв адля точного ршення, а лнями 2 - графки тих же функцй для випадкв апрактично не вдрзня

ться вд точного ршення.

Значення вдповдних функцÿ при D = 5,7%, при D = 3,7%.

За одержаним результатам можна зробити висновок, що для отримання ршення аз 5% точнстю достатньо взяти кльксть гармонк <= 3а ва розкладенна збурюючо

5.3.  Побудова аналтичного ршення диференцального рвняння. Пдбррацонально

Побуду

мо аналтичне ршення диференцального рвняння ( ), представивши збурюючу силу арозкладенням в ряд ФурТ

:

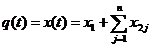
Врахуемо, що при 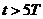аршення 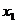апрактично згаса

. Тод для цих моментв часу:

( ).

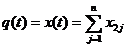
Вдмтимо, що ршення азмню

ться з частотою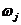

Користуючись даними табл. 1 та графками АЧХ ФЧХ системи, визначимо значення коефцúнта динамчност ата зсуву фаз адля а

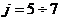
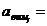
гармонк (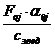, що вдповдають цим гармонкам.

Значення знайдених величин зведемо у табл. 2.

Таблиця 2.

Номер гармонки,	-1
1	2	0,274	1,08	0,0562	0,0607	0,088
2	6	0,823	2,63	0,0188	0,0497	0,076
3	10	1,37	1,06	0,0113	0,012	3,09
4	14	1,92	0,366	0,008	0,0029	3,09
5	18	2,47	0,195	0,006	0,0012	3,09

<

з табл. 2 виплива

, що визначальними

амплтуди аколивань першо

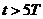
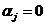
Обмежимося значенням адля випадку сталених вимушених коливань (ама

вигляд:

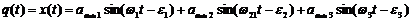
=а(м).

Знайдемо значення загальнено

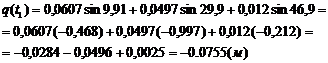
D = 4,2%.

<

з розрахункв виплива

, що визначальними

значення ршення для перших двох гармонк. При <= 3 аналтичне ршення 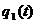адобре збга

ться з Уточним ршенням на ЕОМ (вдхилення ршення не перевищу

D = 5%).

6.       Стисла характеристика програми

Если надо -