Лекция 1 Среднеквадратичное приближение функции

Вид материала

Лекция

Содержание 1.6. Классические ортогональные многочлены и их применение в задачах приближения функций. С другой стороны 1.7. Некоторые общие свойства ортогональных полиномов.

Подобный материал:

• Лекция №1 Вычисления в Excel. Формулы и функции, 94.38kb.
• Лекция Производная функции, 30.86kb.
• Лекция 11. Индивидуальный и рыночный спрос, 58.12kb.
• Курс лекций. Лекция Финансы и их функции. План. Сущность финансов и их функции. Роль, 1021.27kb.
• Лекция 1 Лекция Бухгалтерский учет, его сущность и функции в системе управления хозяйствующим, 59.7kb.
• Лекция Виртуальные функции. Дружественные функции, 70.17kb.
• Лекция (4 учебных часа – 2 ч 40 мин) Концепции распределенной обработки в сетевых, 527kb.
• Лекция Дифференцирование функций, 25.58kb.
• Лекция 21. Экстремум функции нескольких переменных, 60.44kb.
• Интерполяция и приближение данных в matlab, 230.62kb.

Лекция 4.

1.5. Среднеквадратичное приближение функции.


Рассмотрим задачу наилучшего среднеквадратичного приближения функции 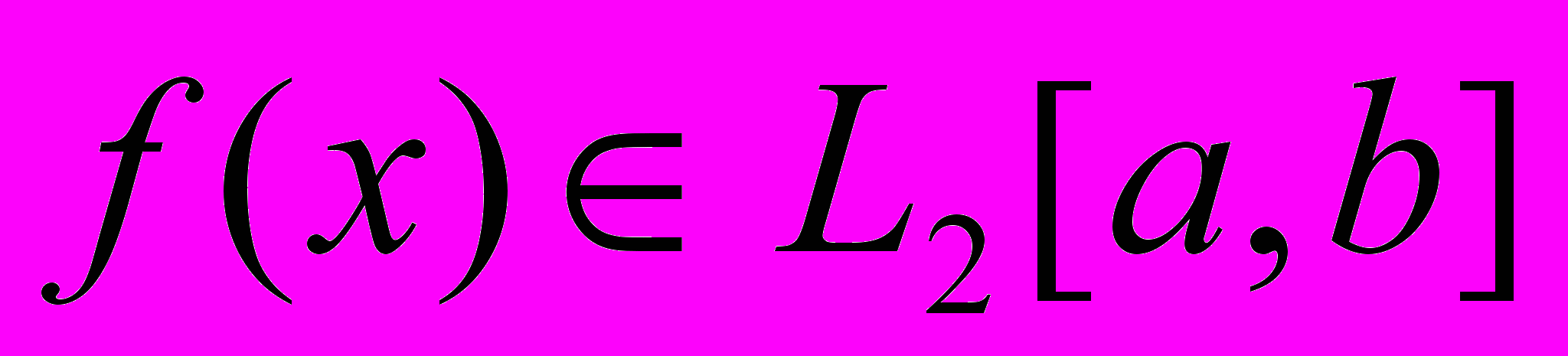полиномом 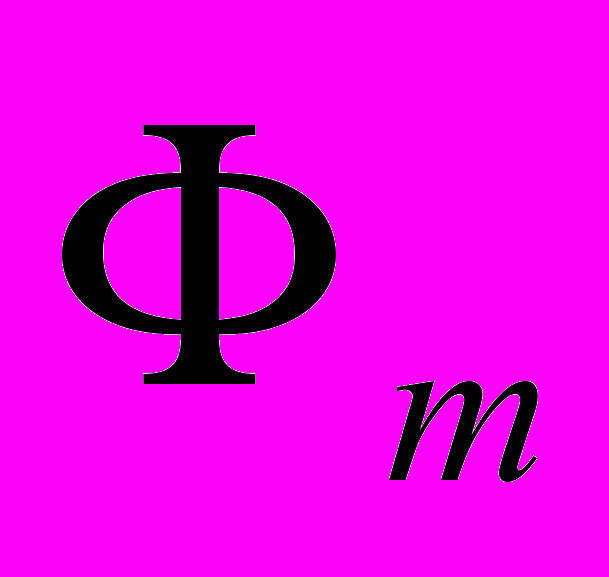по системе .

Определение 1.

Обобщенным полиномом порядка m по системе {_k} называется линейная комбинация



где C_k – произвольные вещественные коэффициенты.

Задача. Найти полином 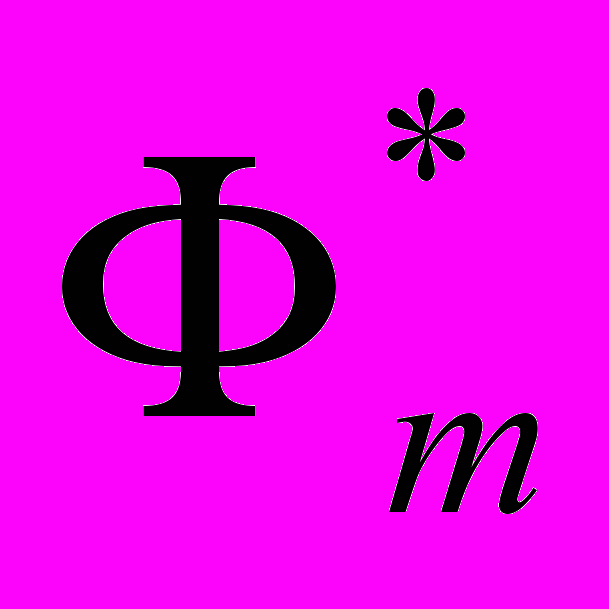, наименее уклоняющийся от функции f в метрике L₂, т.е. удовлетворяющий условию: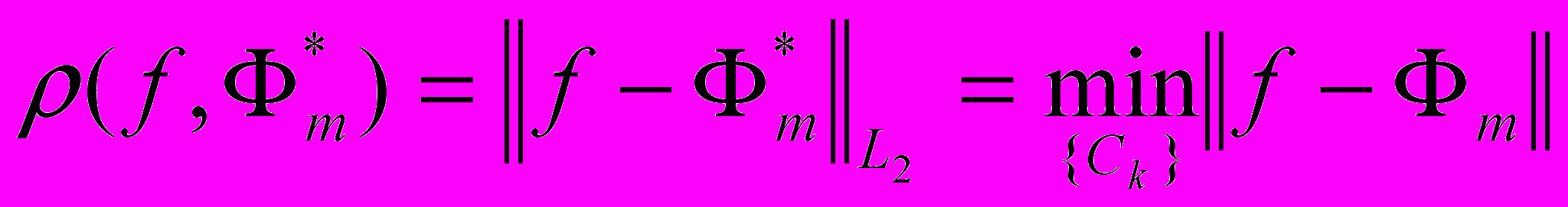



Теорема 1.

Если система 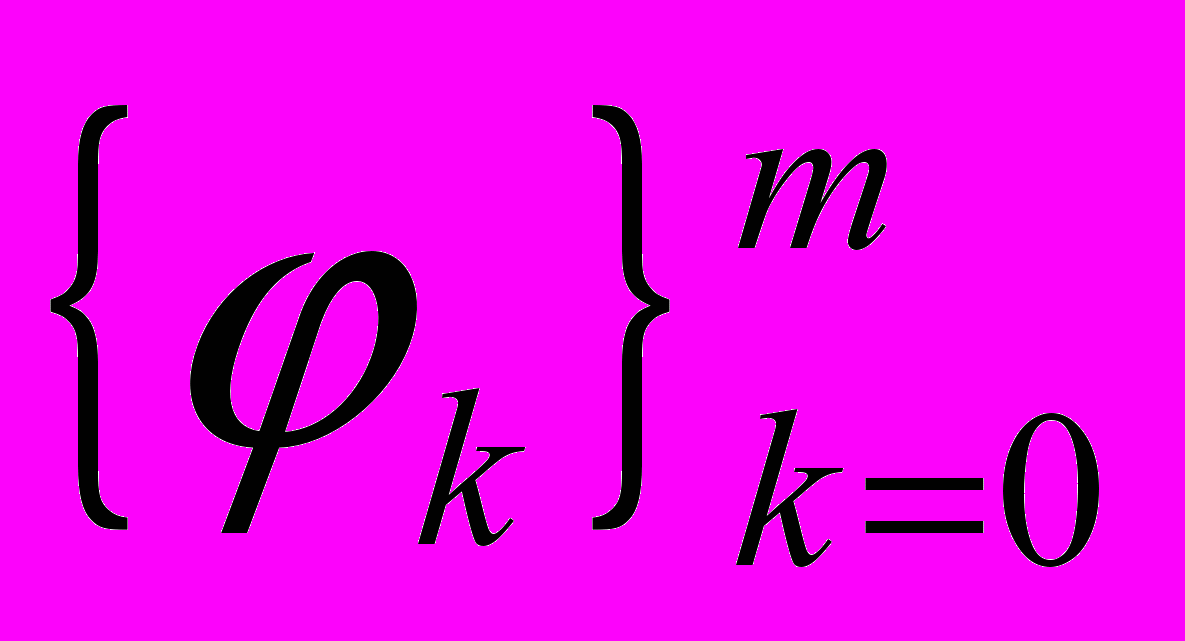линейно независима, то задача наилучшего среднеквадратичного приближения по этой системе однозначно разрешима.

Запишем квадрат расстояния между функцией и полиномом: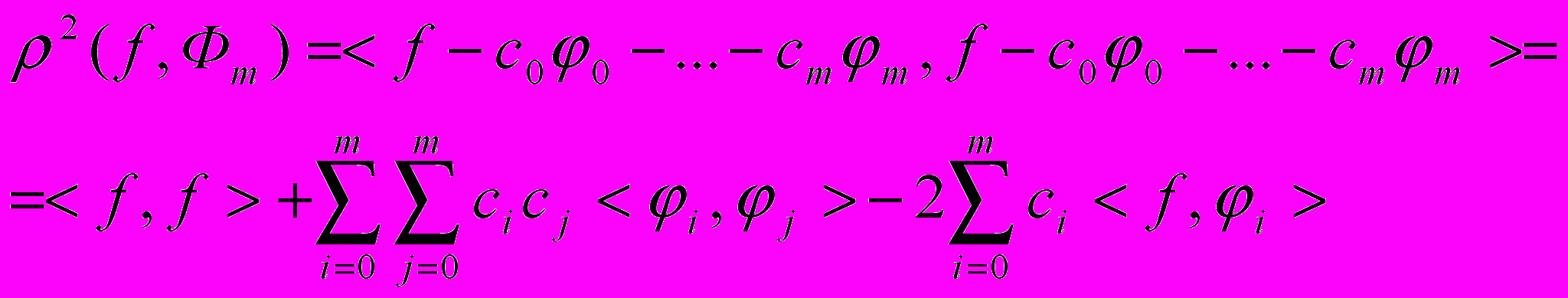

(1)

Очевидно, что величина 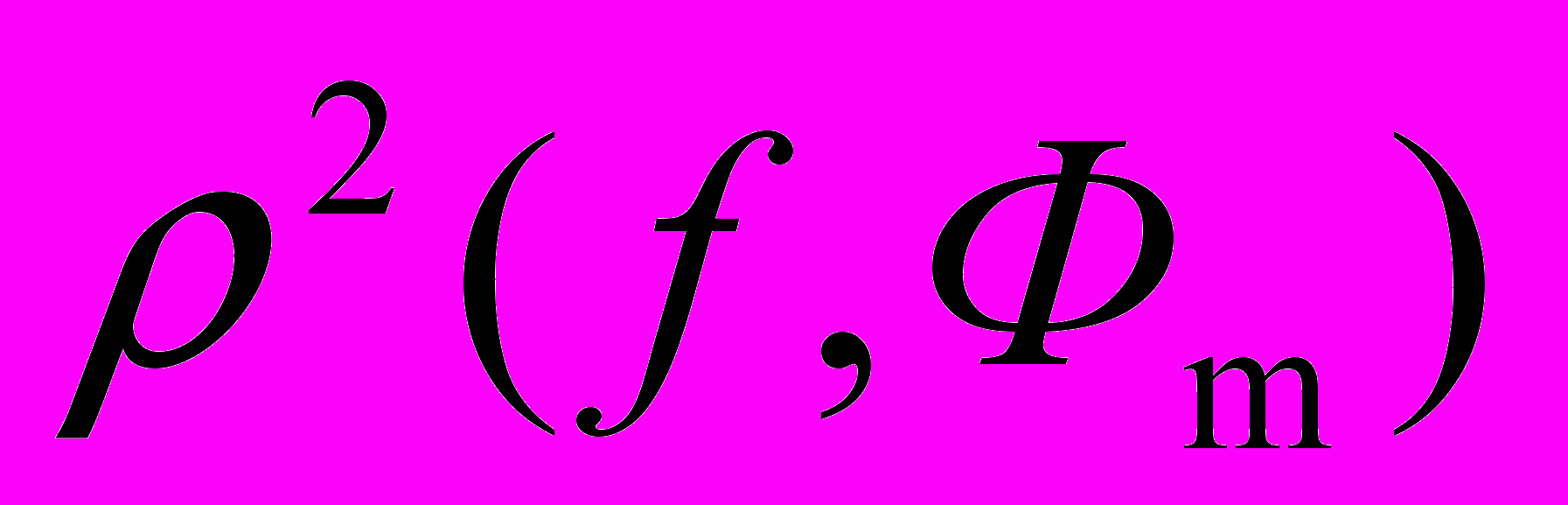- неотрицательно определенная квадратичная функция переменных 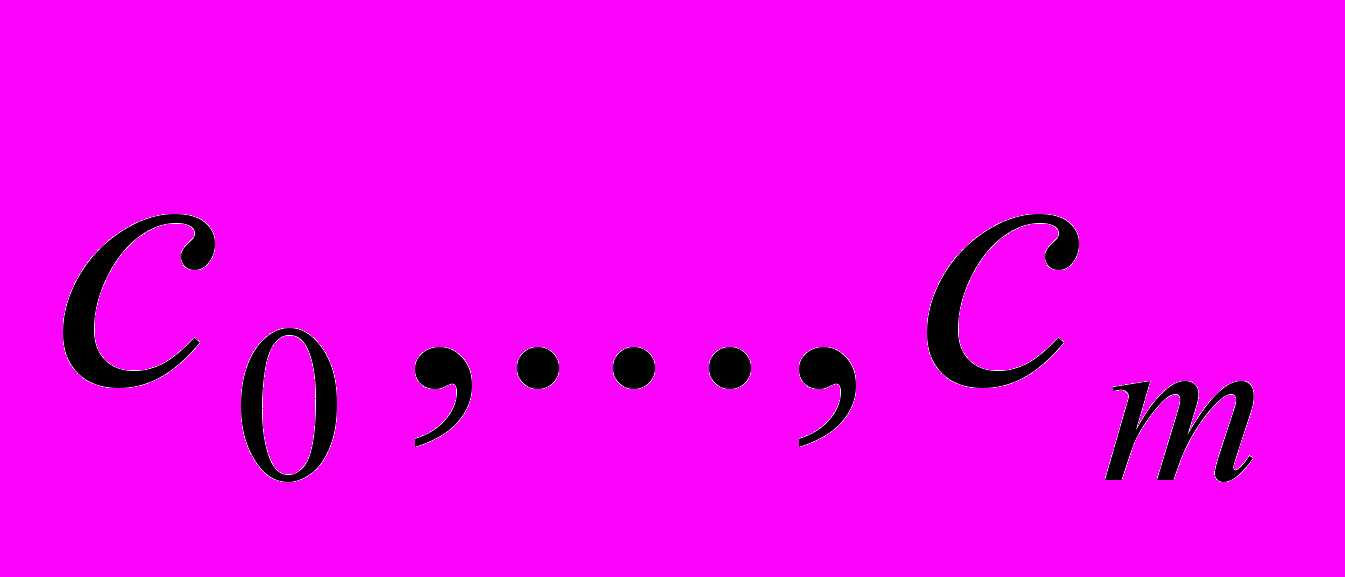, а такая функция достигает минимального значения. Таким образом, решение задачи среднеквадратичного приближения существует.

Докажем единственность решения.

Запишем необходимые условия минимума:

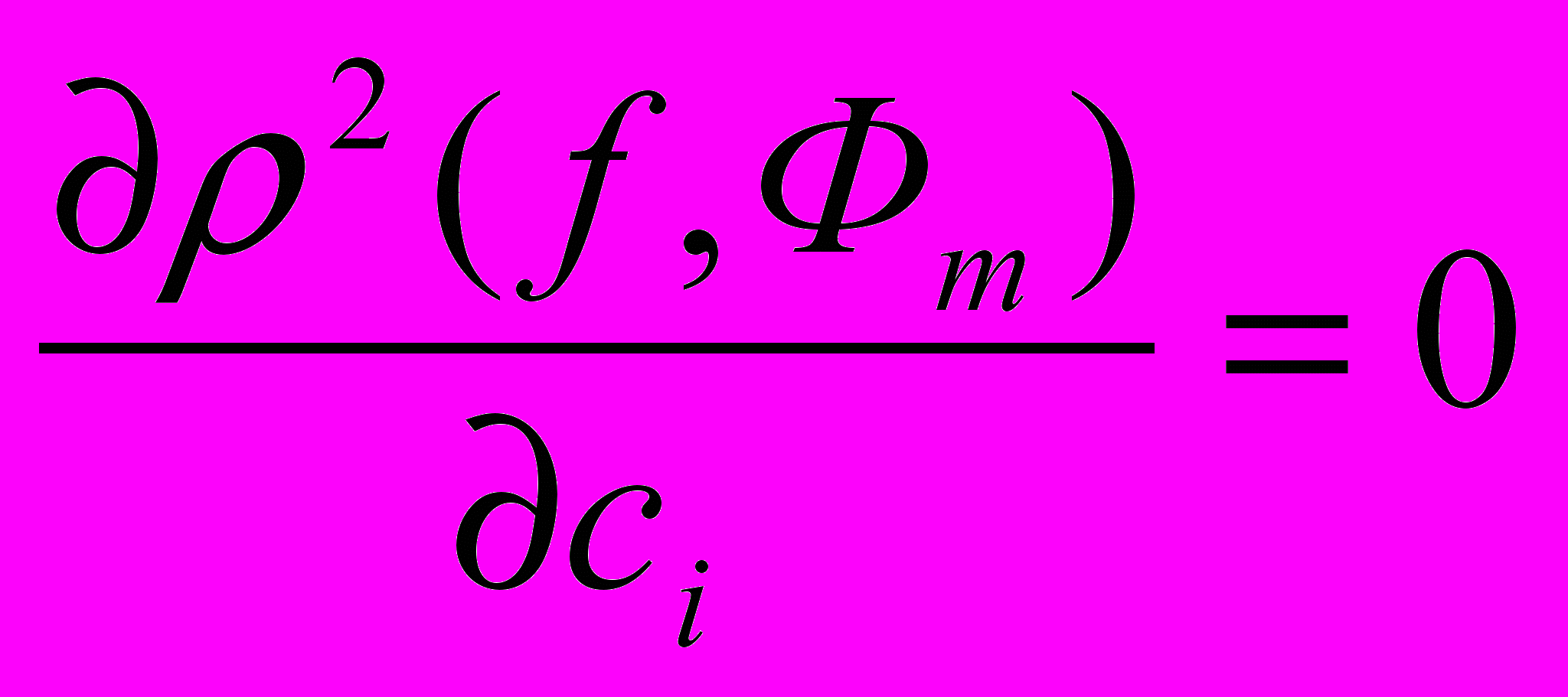, i=0,…,m.

Вычисляя частные производные по c_i выражения (1), получим линейную cистему уравнений:

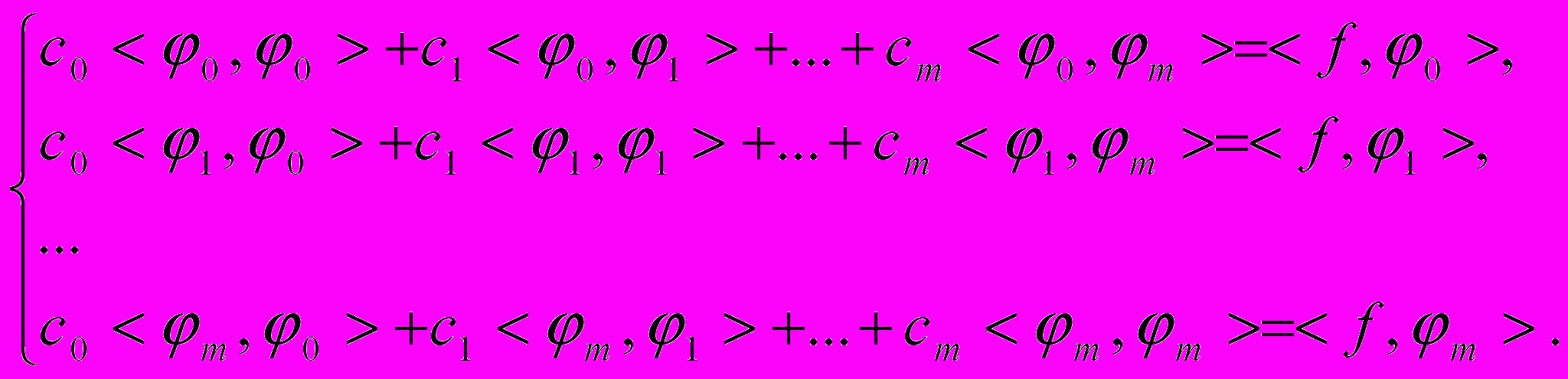(2)

Система (2) называется нормальной системой.

Выпишем определитель этой системы

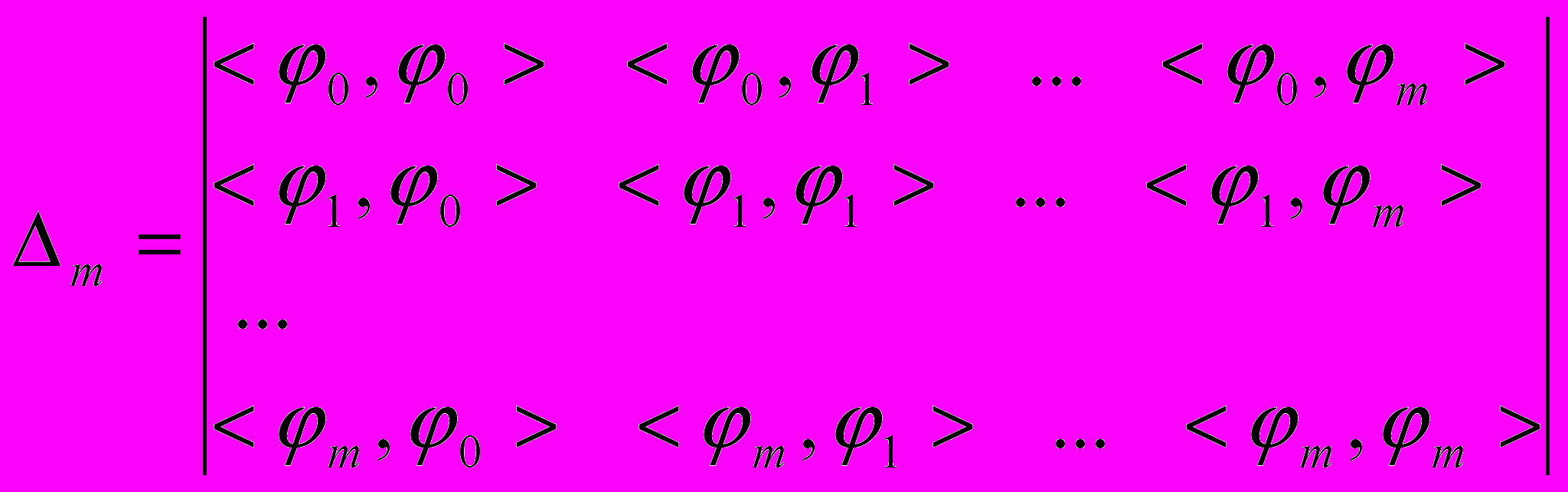(3)

Определитель системы (3) – так называемый определитель Грама системы 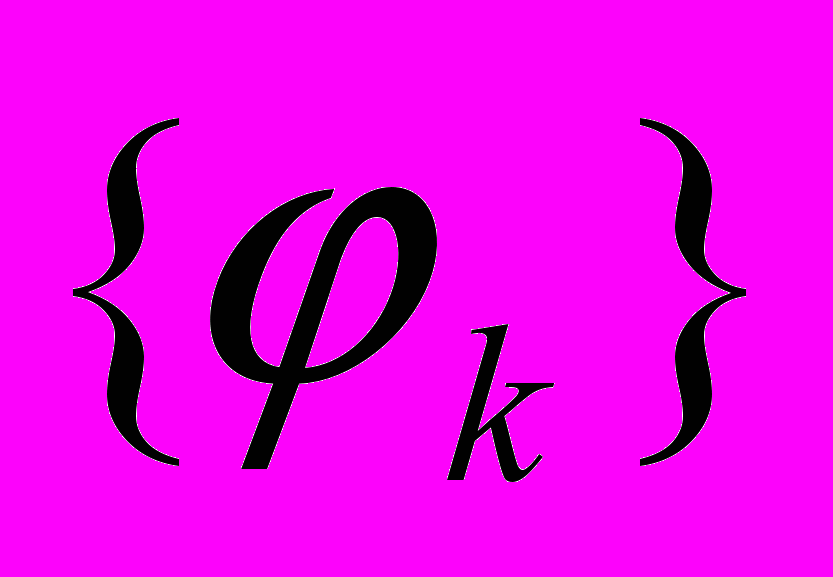. Известно, что если система 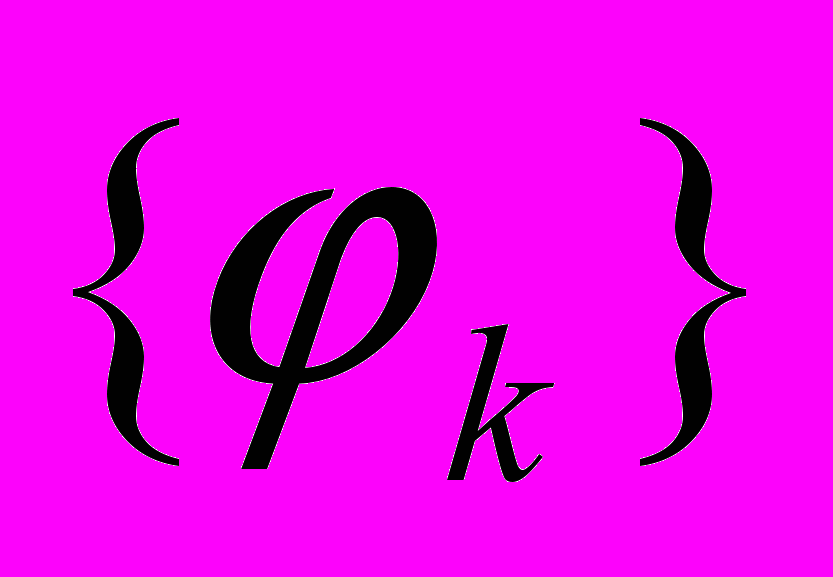- линейно независима, то определитель 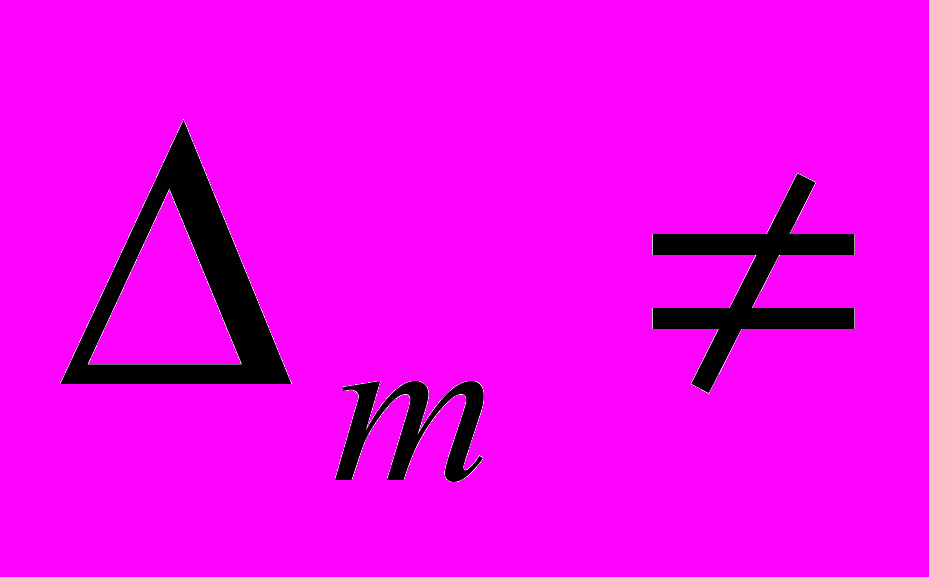0 (легко доказывается от противного). Согласно условию теоремы 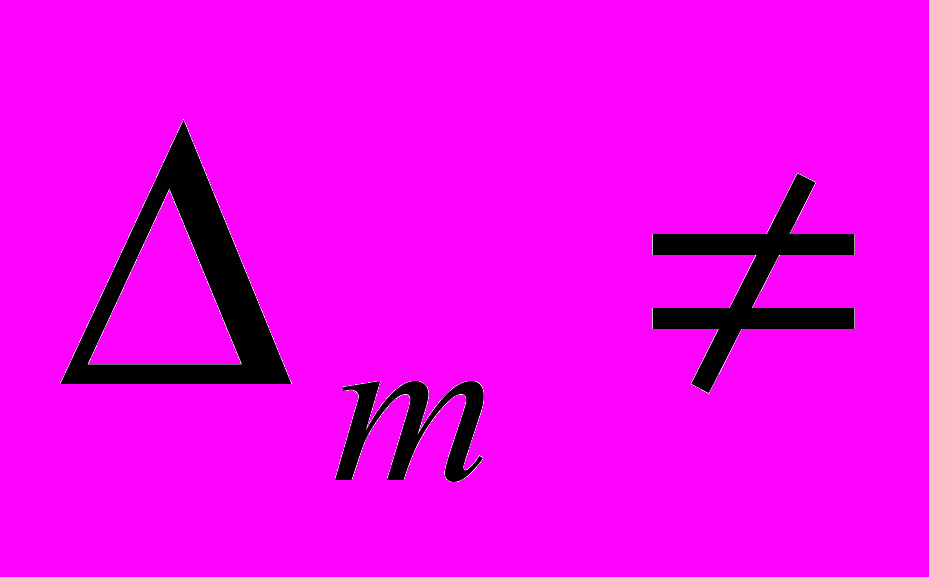0 и система (2) имеет единственное решение.


^

1.6. Классические ортогональные многочлены и их применение в задачах приближения функций.

Пусть H- гильбертово пространство со скалярным произведением 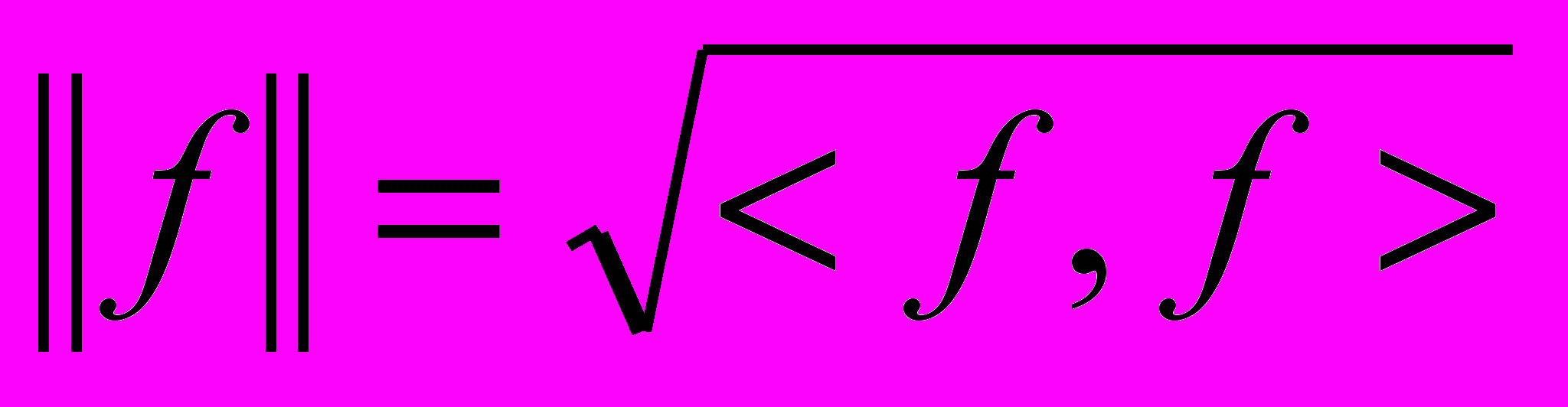и, соответственно, нормой . Важным примером такого пространства является так называемое пространство 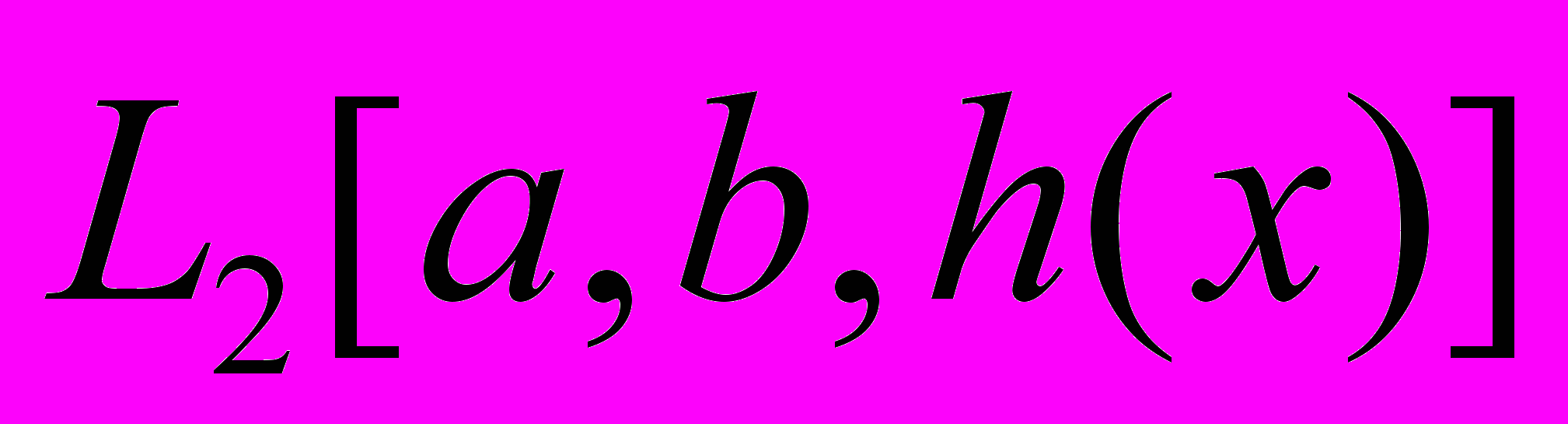- пространство функций f(x), для которых конечен интеграл:

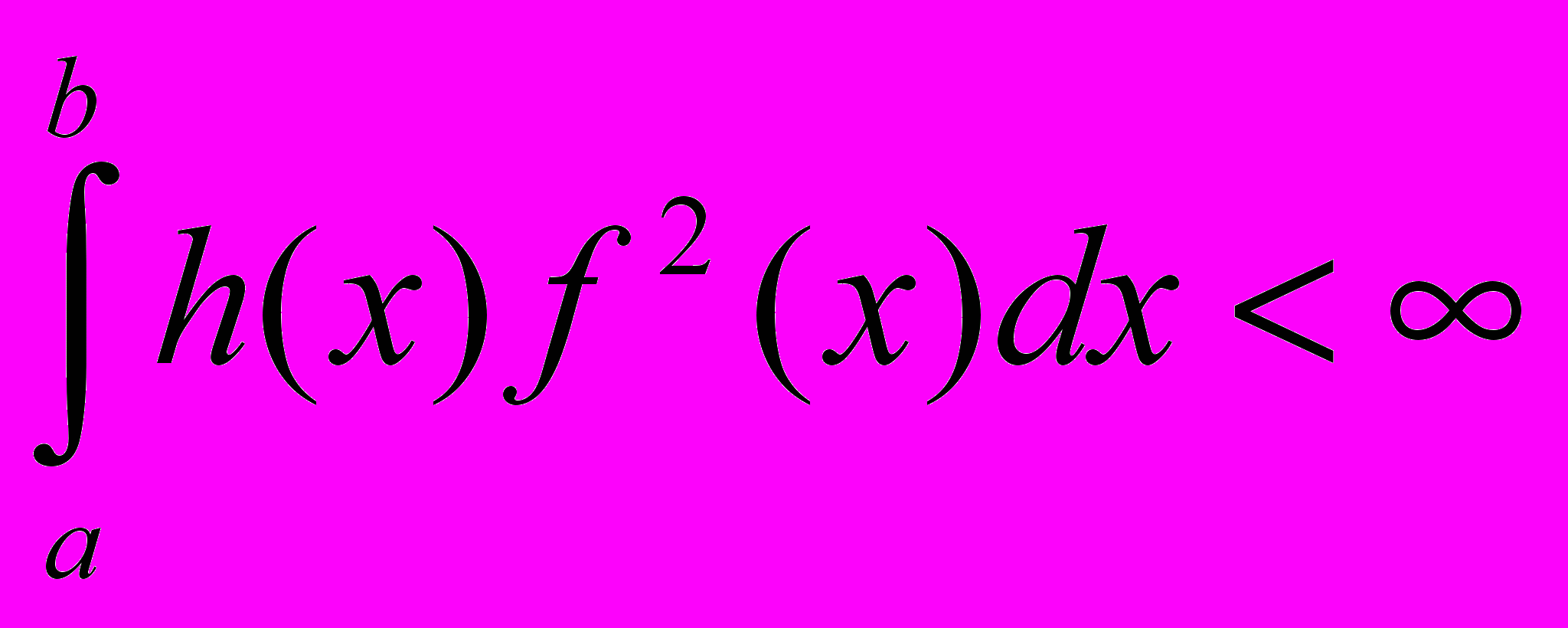(1)

Здесь h(x)- так называемая весовая функция, удовлетворяющая условиям:

1. h(x)0 на [a,b].
   
2. Если промежуток [a,b]- конечный, то существует и конечен;
   

Если же [a,b]=(0,+), то должно выполняться условие:



т.е. должны существовать любые моменты весовой функции.

Определение 1.

Для определено скалярное произведение: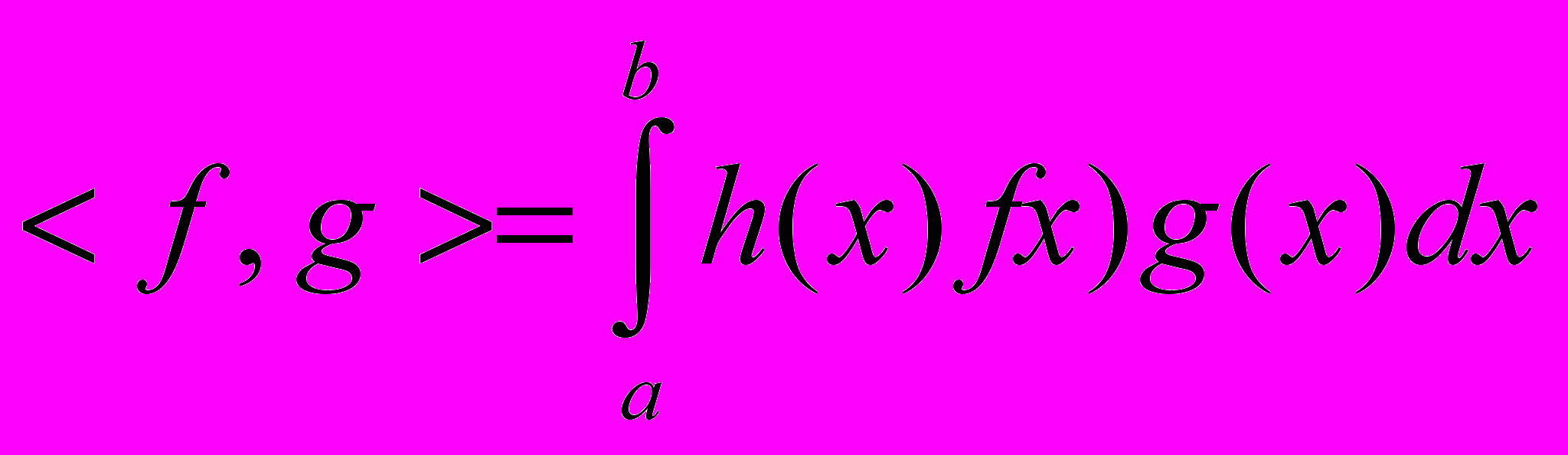

(2)

и соответственно норма:



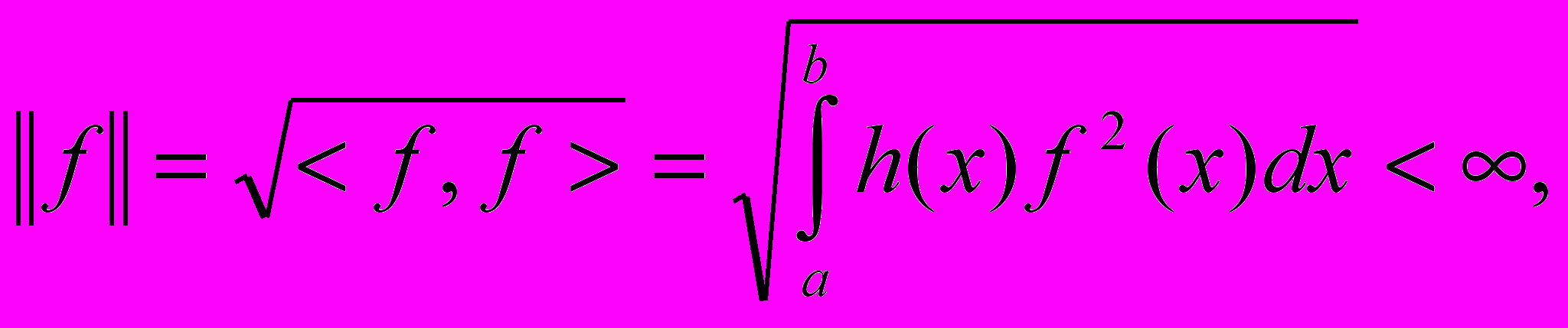
согласно условию (1).

Используя неравенство Коши – Буняковского - Шварца, получаем



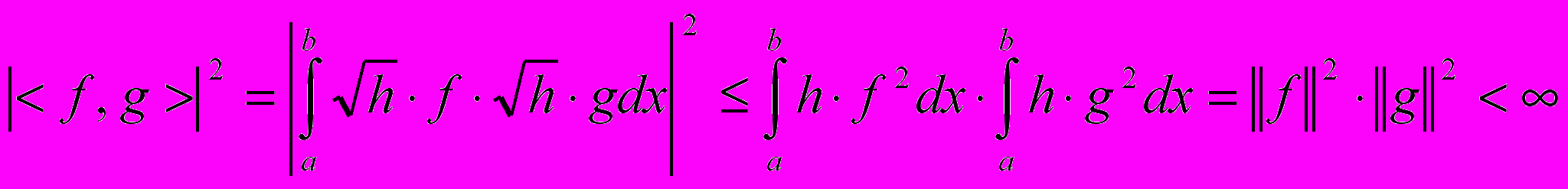
Поэтому скалярное произведение существует для

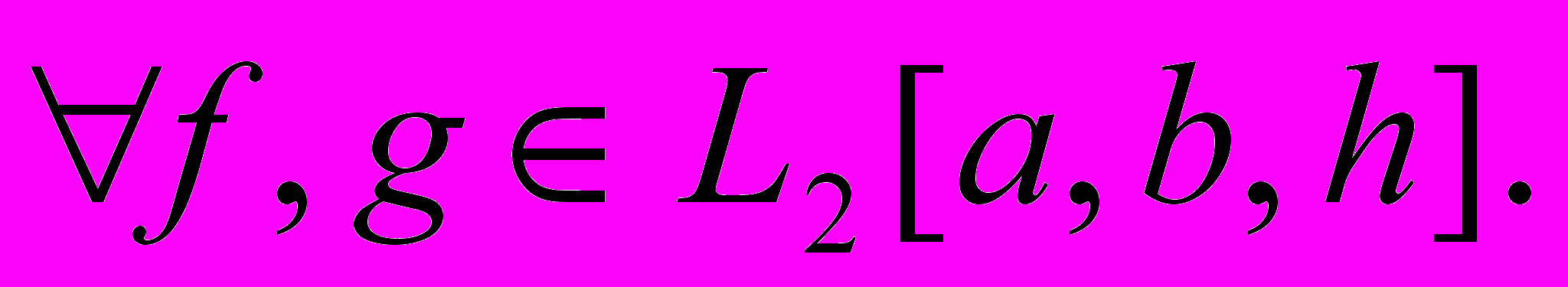
Определение 2.

Расстояние между элементами f и g определяется равенством:

.

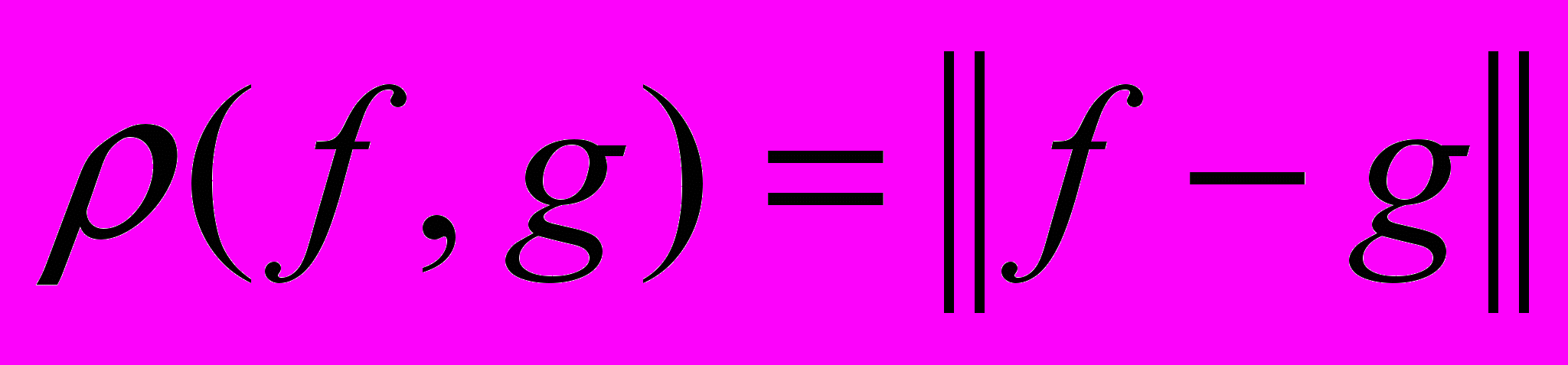Возникает вопрос о том, как понимать нулевой элемент. Если норма 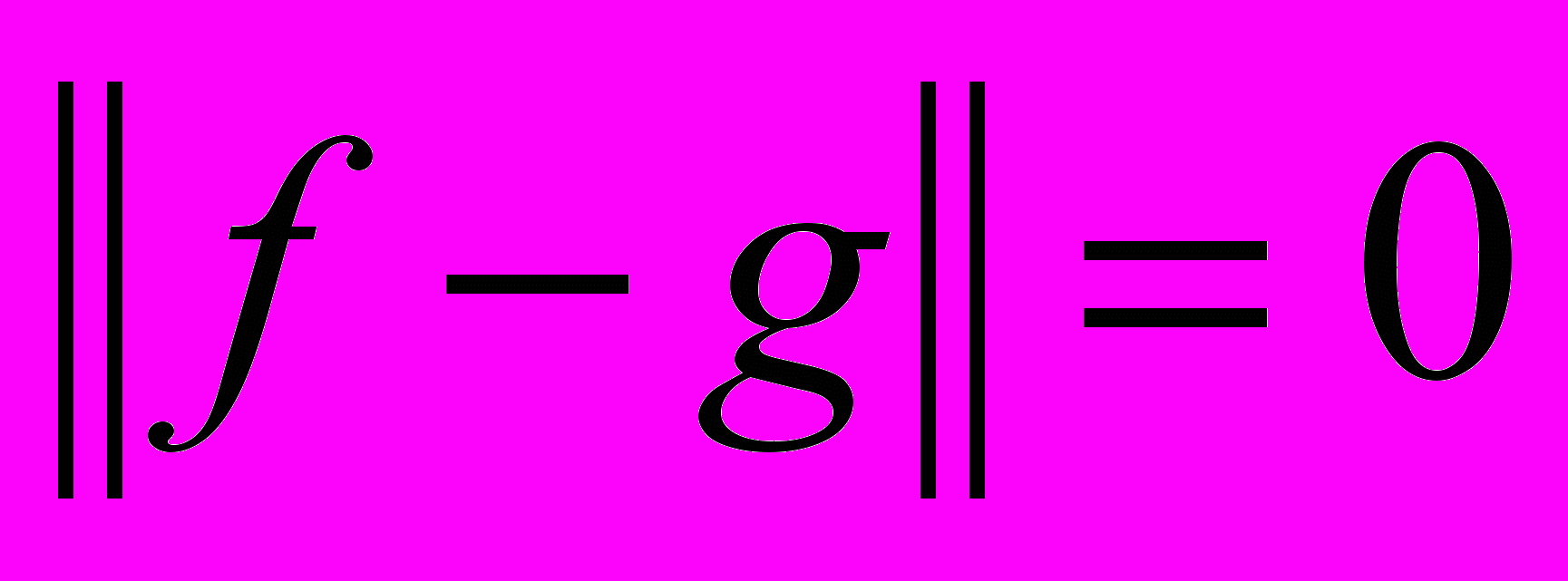, следует ли отсюда, что f=g? Вводится терминология: f=g почти всюду, то есть они могут отличаться в конечном числе точек.


Определение 3.

f и g ортогональны на отрезке [a,b] с весом h(x), если =0 (кратко пишут ).

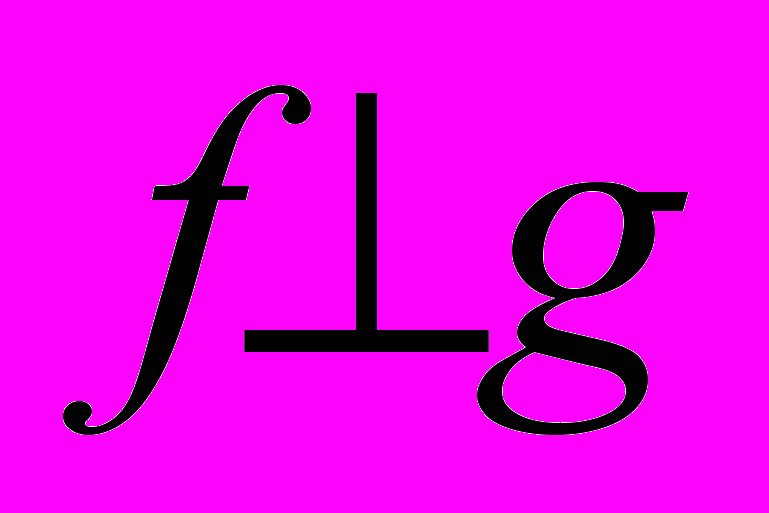Если в гильбертовом пространстве взять любую линейно независимую систему 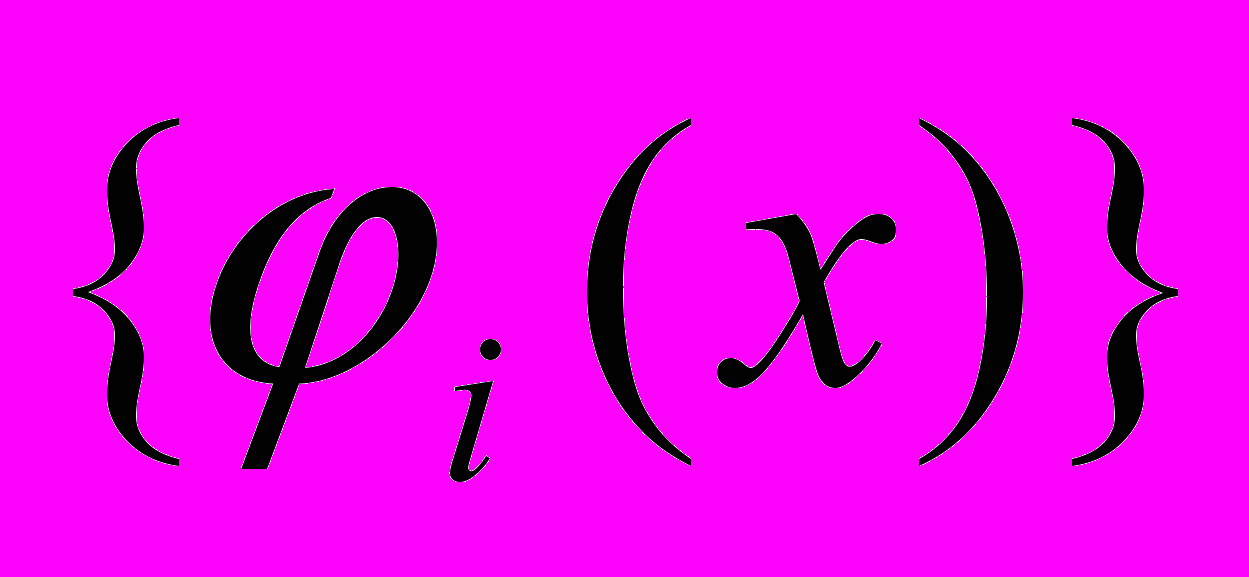, i=0,1,2,…, то ее можно ортогонализировать.


Рассмотрим в качестве примера систему: 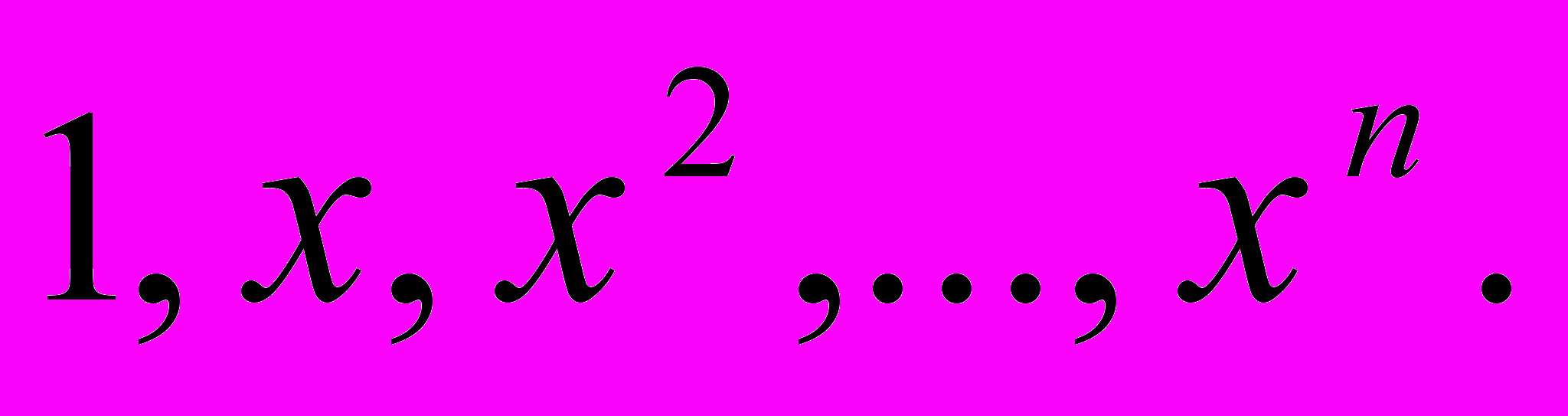При 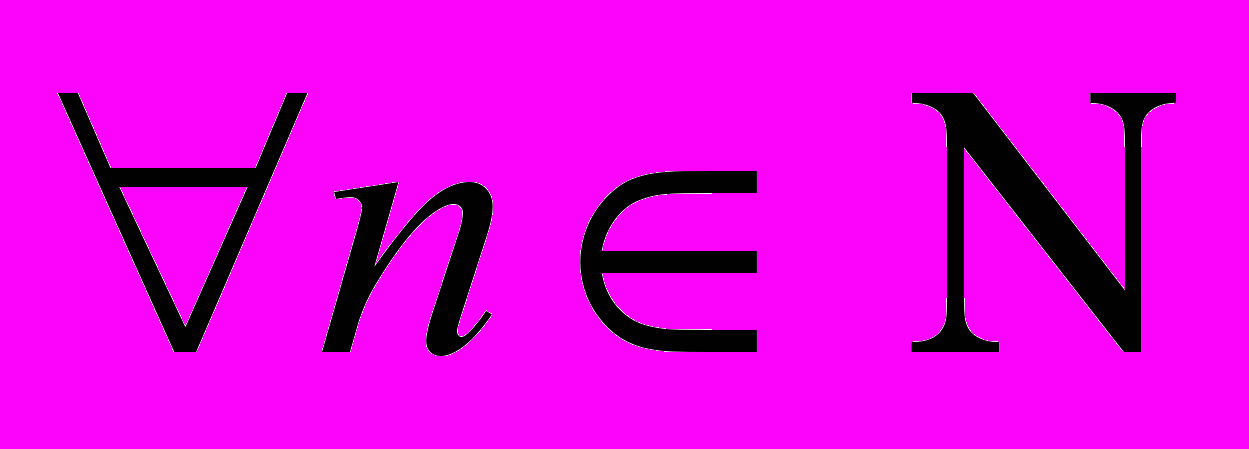конечный набор степенных функций линейно независим, поэтому на базе этой системы можно построить ортогональные полиномы. Известна следующая рекуррентная процедура ортогонализации (процедура Грама - Шмидта):

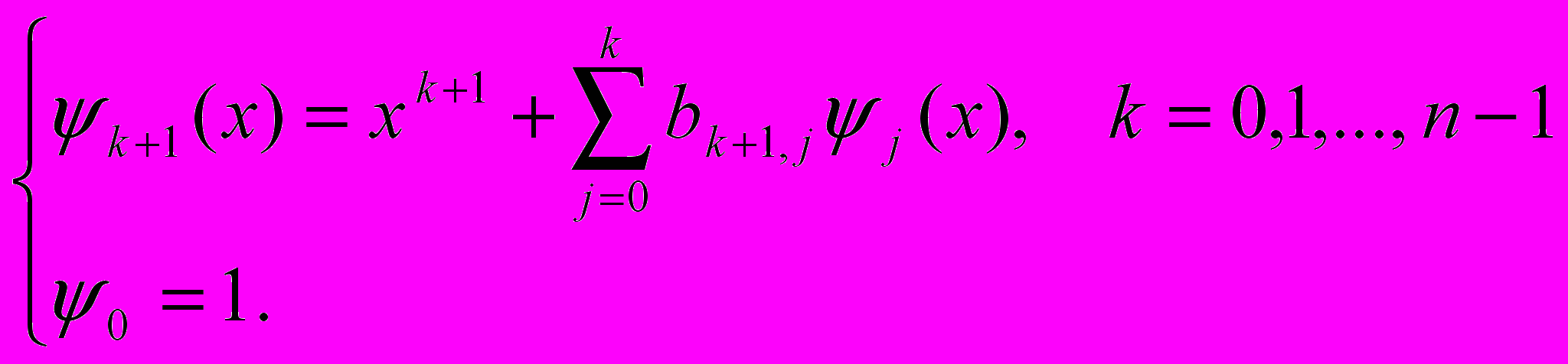(3)

Коэффициенты b_k+1,j определяются из условий ортогональности:



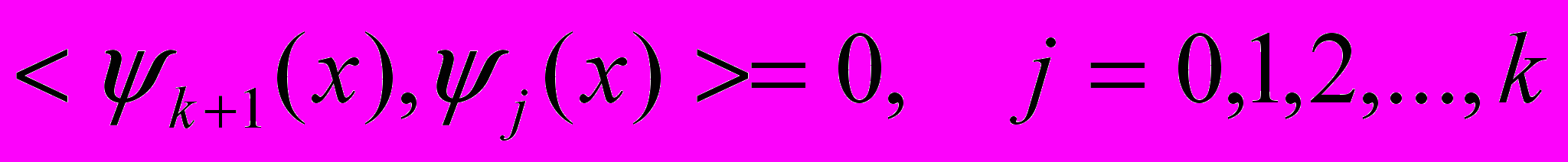
Последовательно умножая (3) на 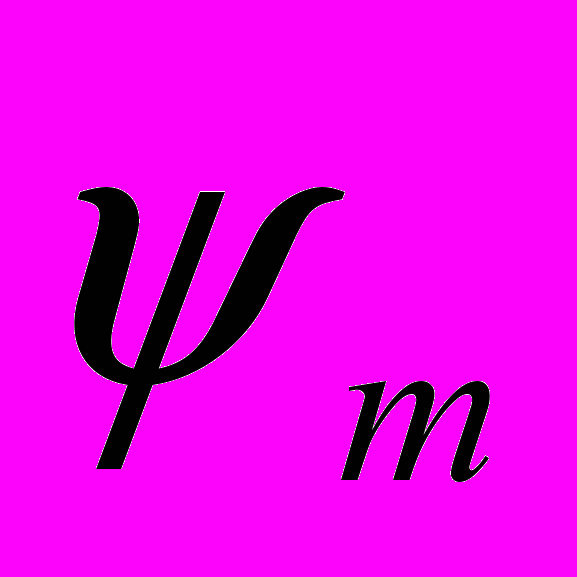получаем

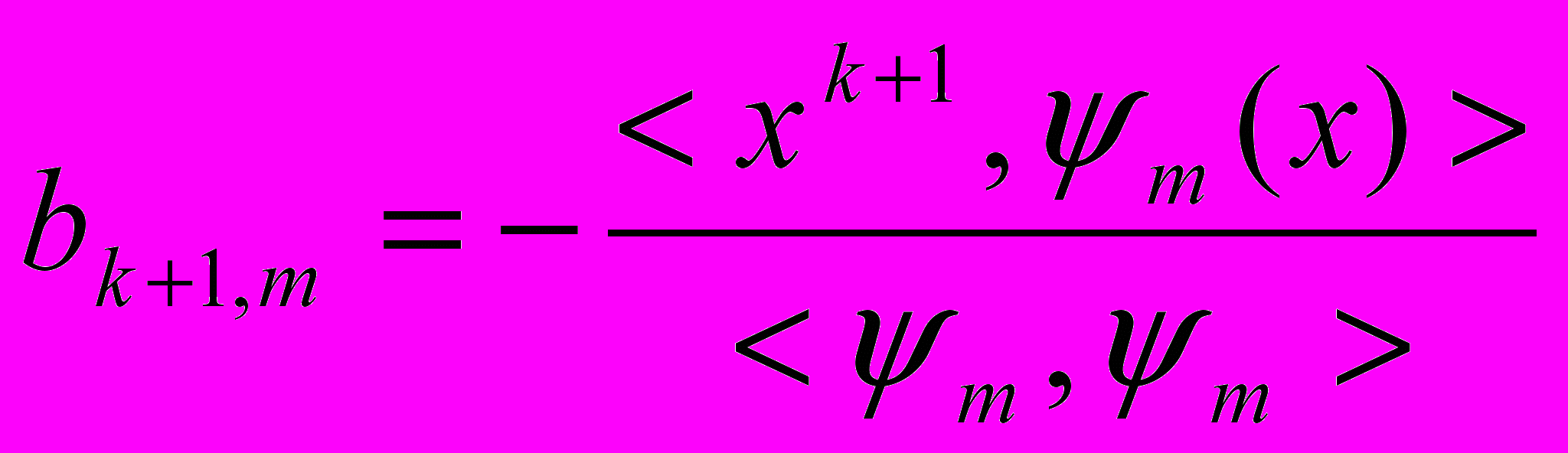(4)

Пример 1.

Пусть h(x)1, [a,b]=[-1,1].

Построить первые три ортогональных полинома по процедуре (3) - (4).

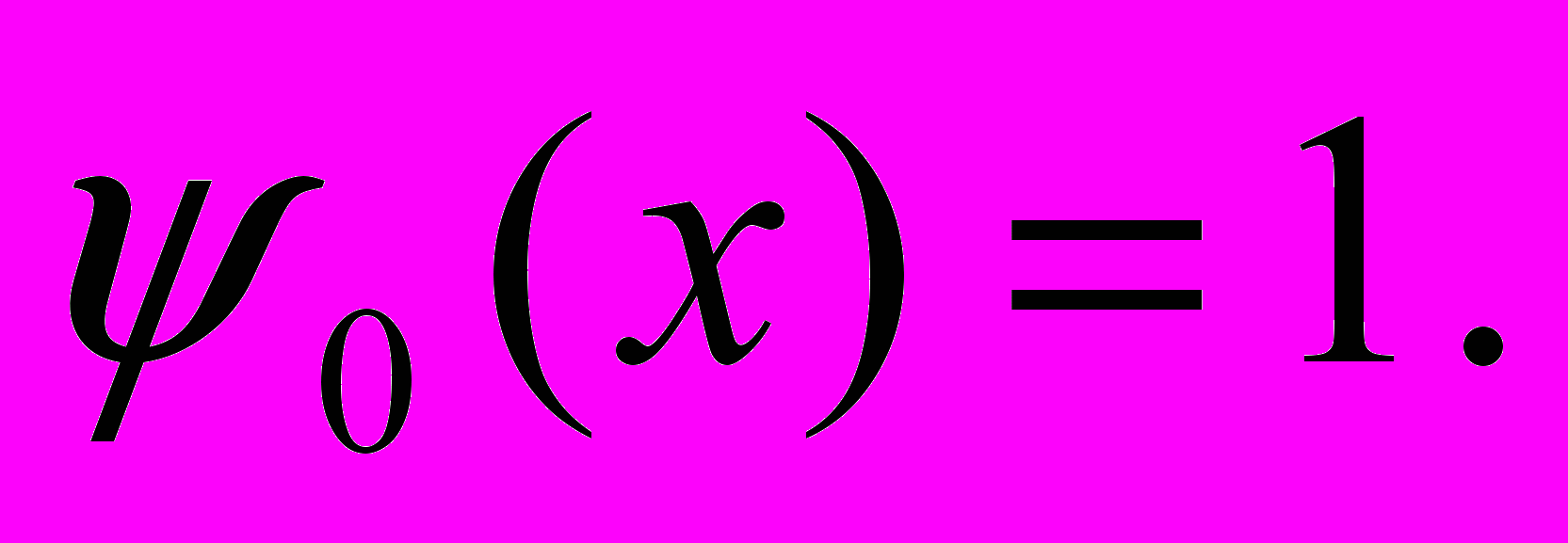Далее имеем:

,

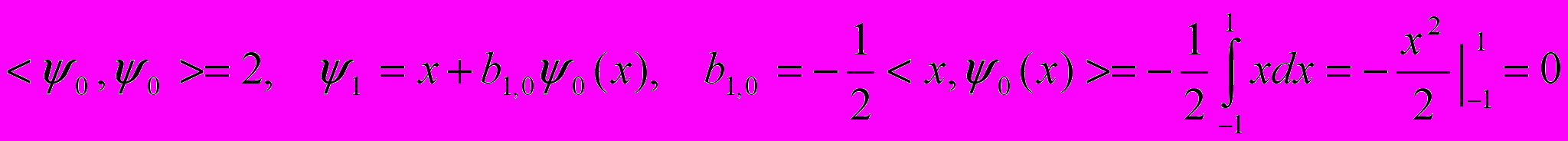следовательно,



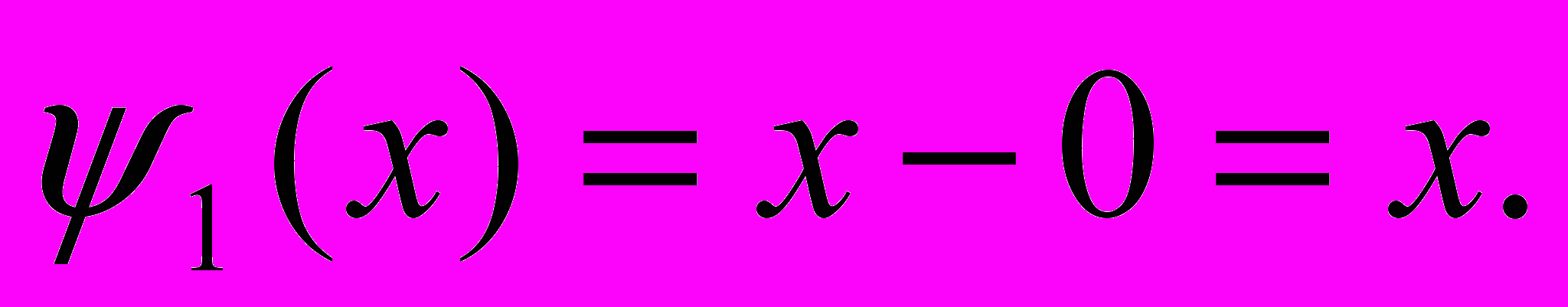
Действуя, аналогично далее, получаем:



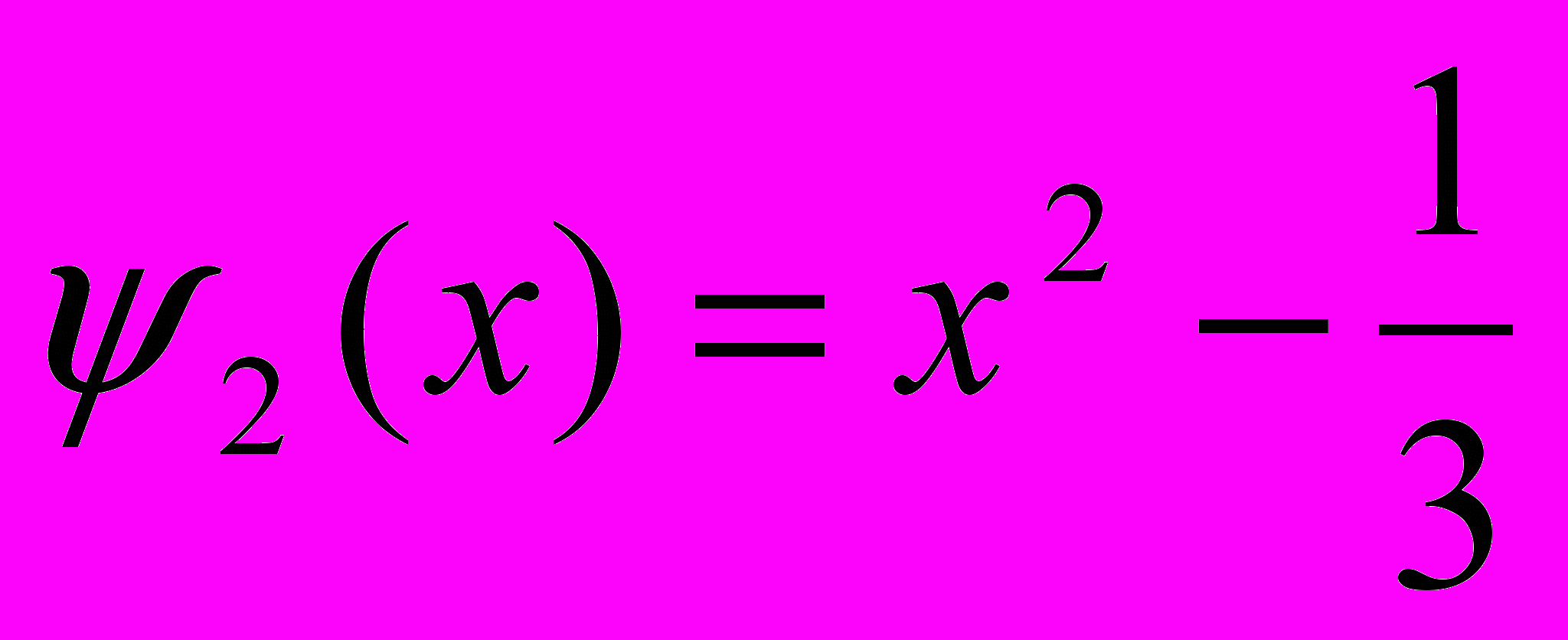
Для системы ортогональных многочленов на отрезке [-1,1] с весом h(x)=1 справедлива формула Родрига:

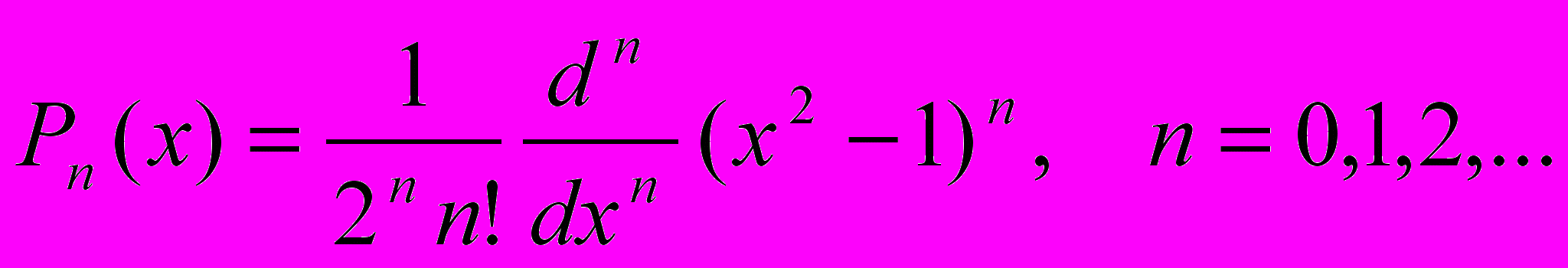(5)

Из (5) последовательно получаем:



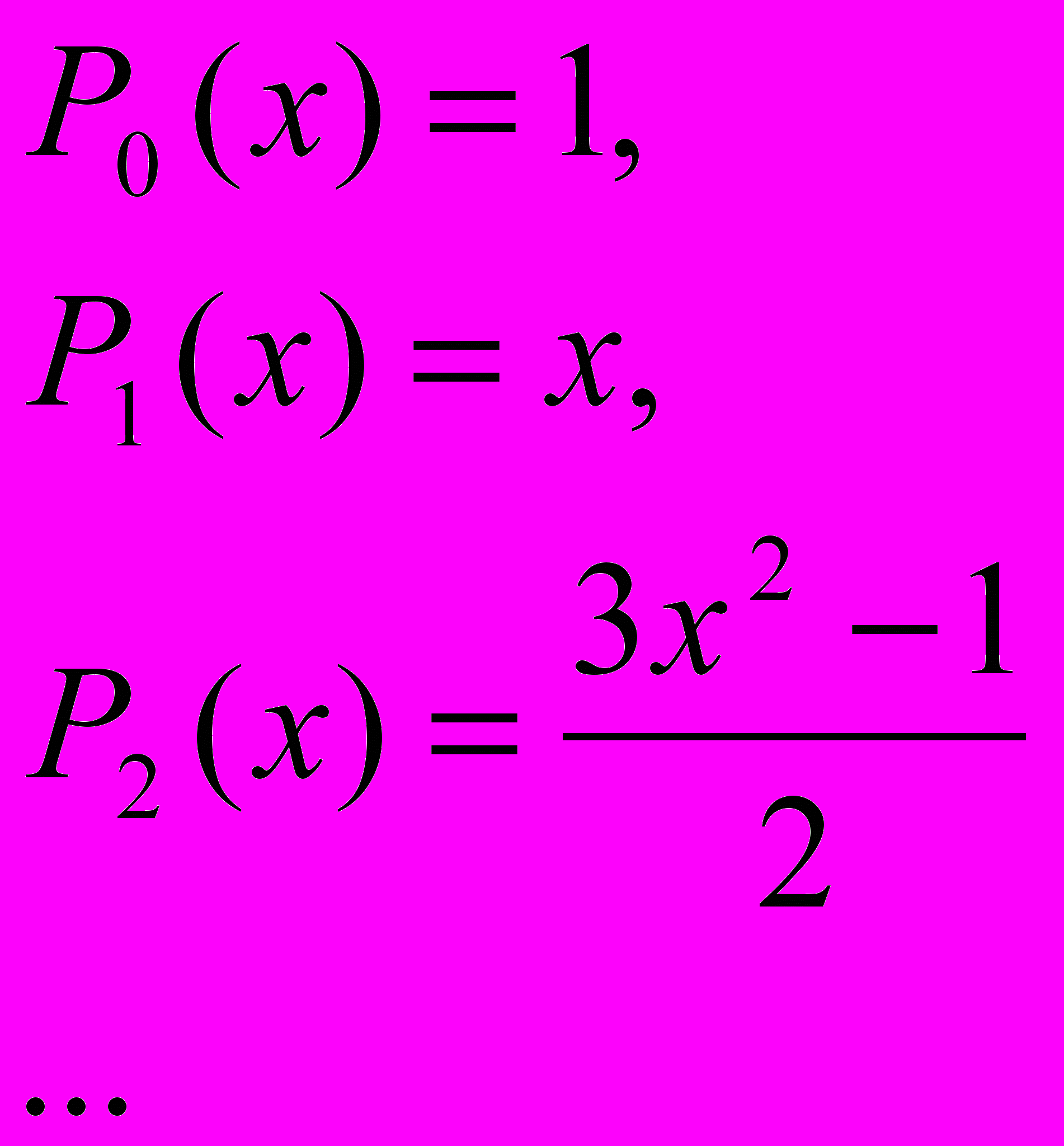
и т.д.

Получаемые таким образом полиномы называются полиномами Лежандра.

Замечание.

Найденные по процедуре (3) – (4) ортогональные многочлены могут лишь множителями отличаться от тех, которые строятся по явной формуле Родрига (5).

Квадрат нормы у этих полиномов равен:

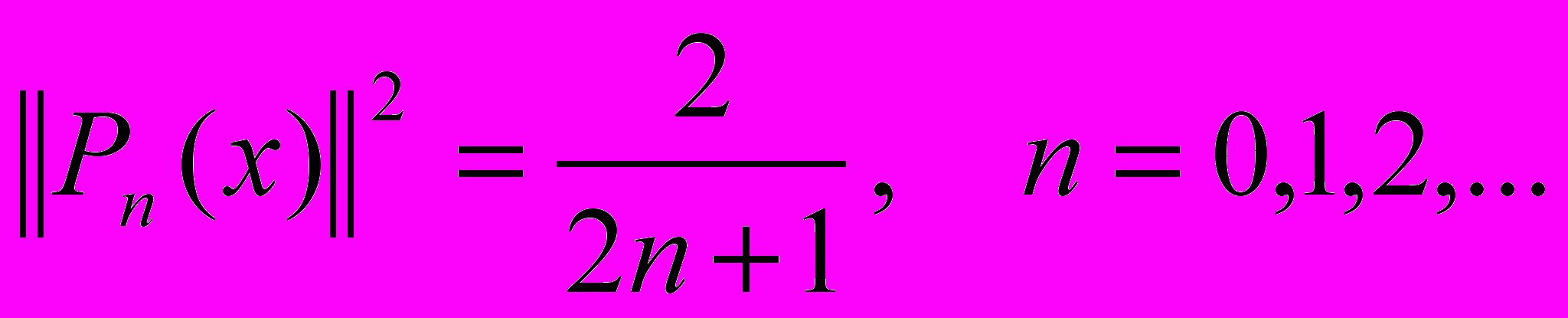
То есть эти многочлены не нормированы, так как

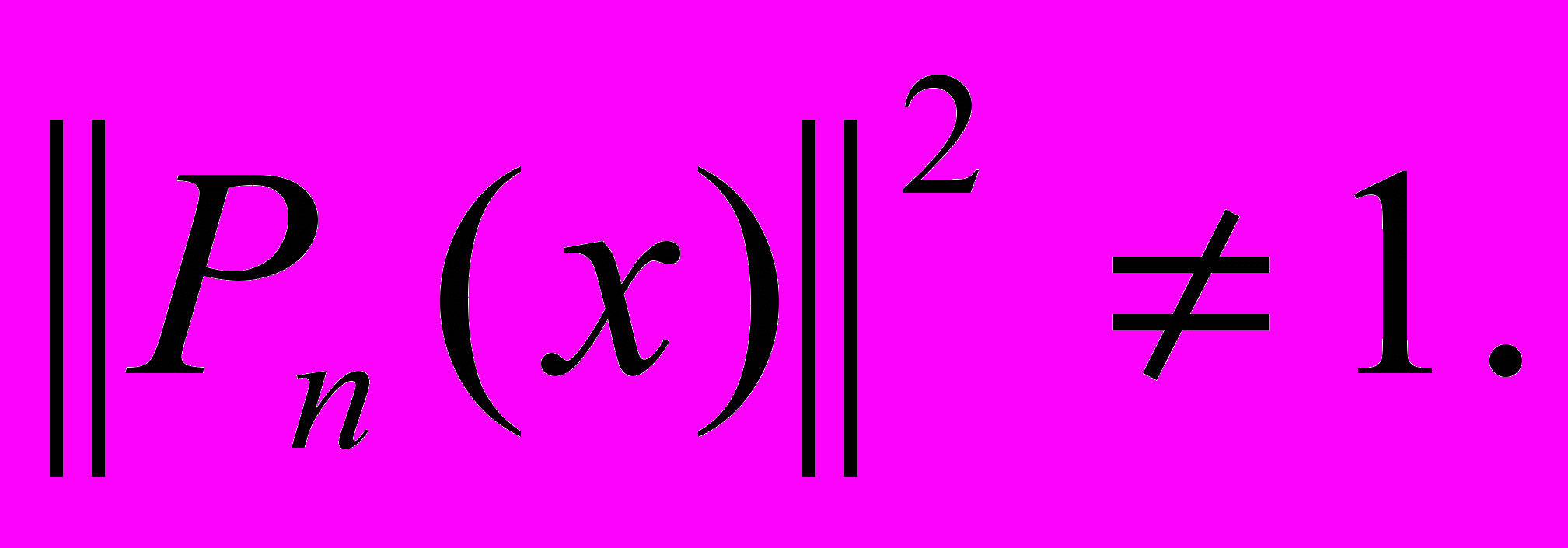
Для всех классических многочленов существует рекуррентная формула. Для полиномов Лежандра она имеет следующий вид:

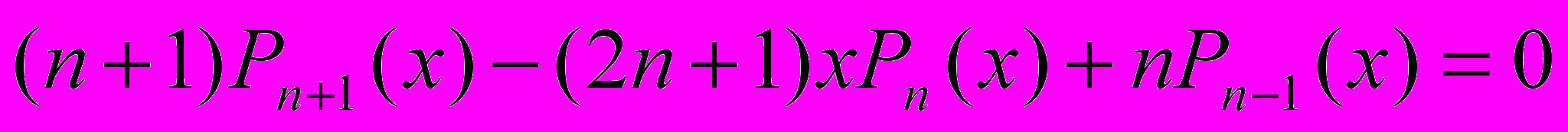(6)

Пусть 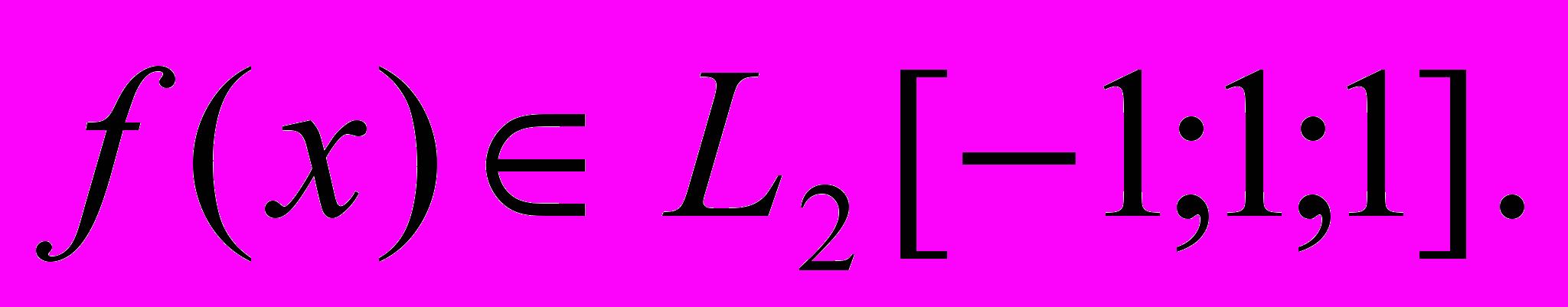Рассмотрим среднеквадратичное приближение: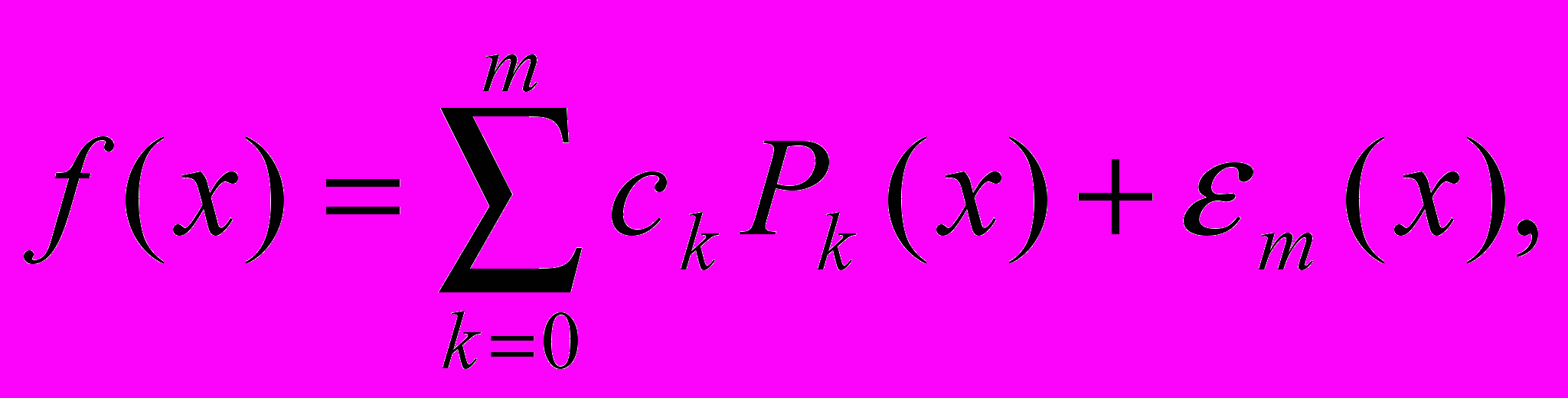



где 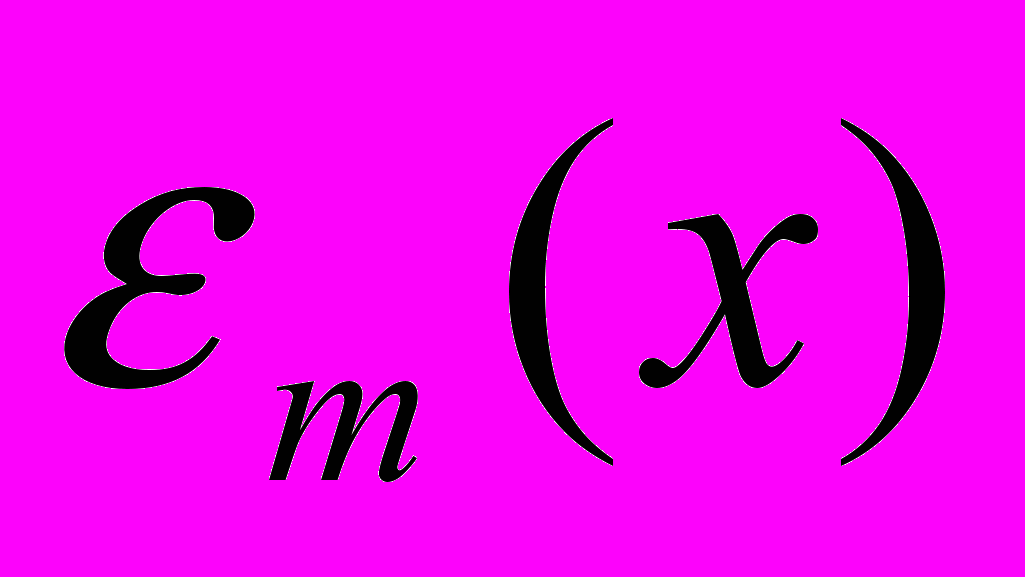- среднеквадратичная ошибка аппроксимации,

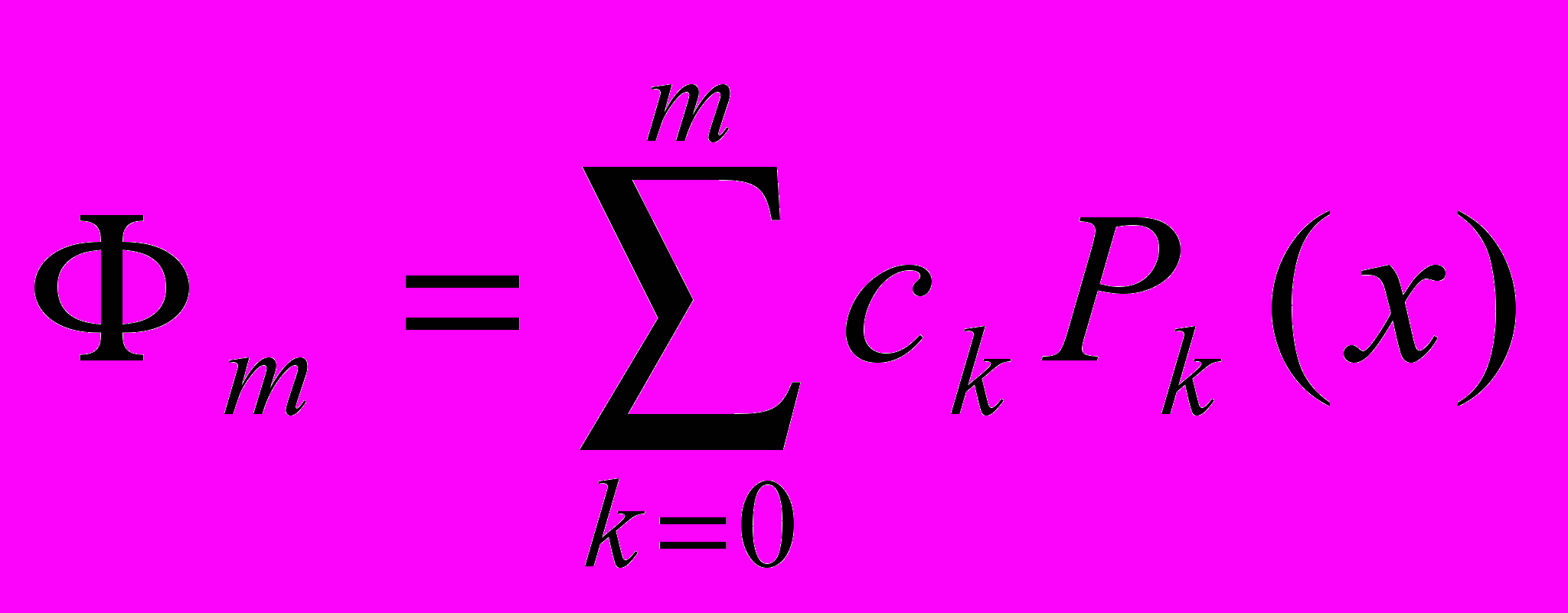- отрезок ряда Фурье для функции f(x) по системе ортогональных многочленов {P_k(x)}.

В силу ортогональности многочленов Лежандра, система нормальных уравнений (2) из §1.5 становится диагональной, и ее решение приводит к следующим выражениям для коэффициентов c_k:

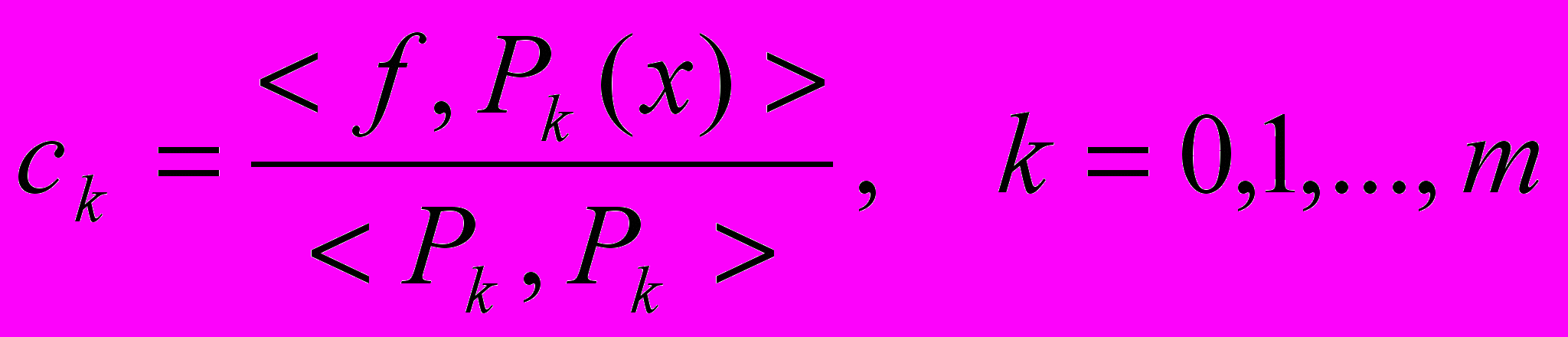(7)

При этом



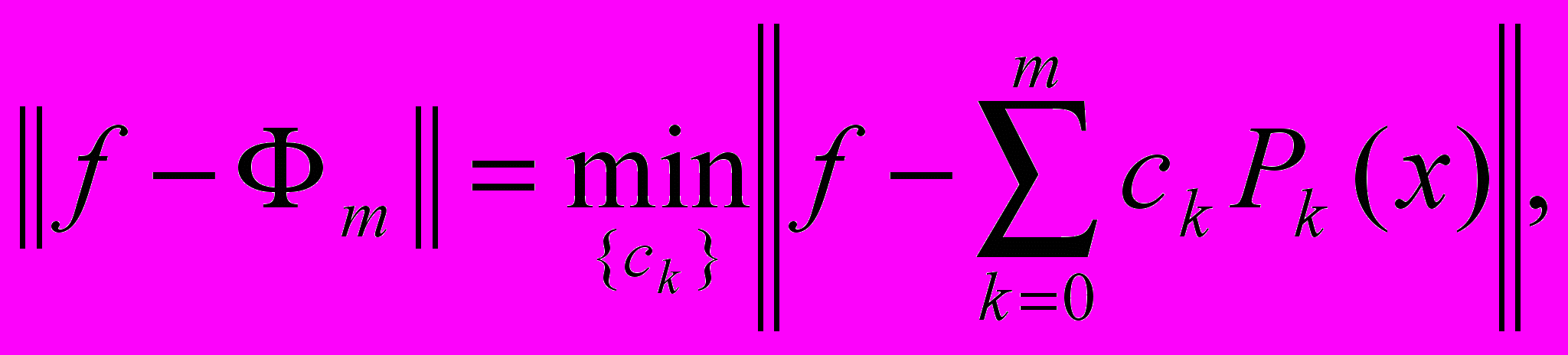
то есть обеспечивается минимум нормы в L₂.

Распишем подробно ошибку аппроксимации

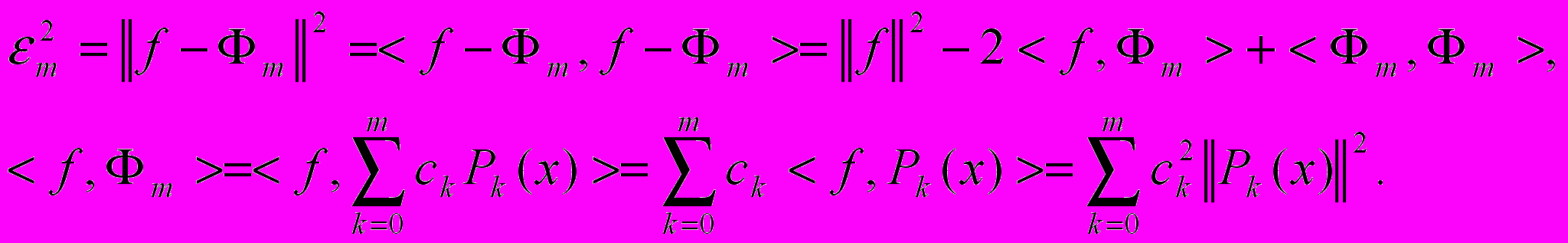(8)

^

С другой стороны

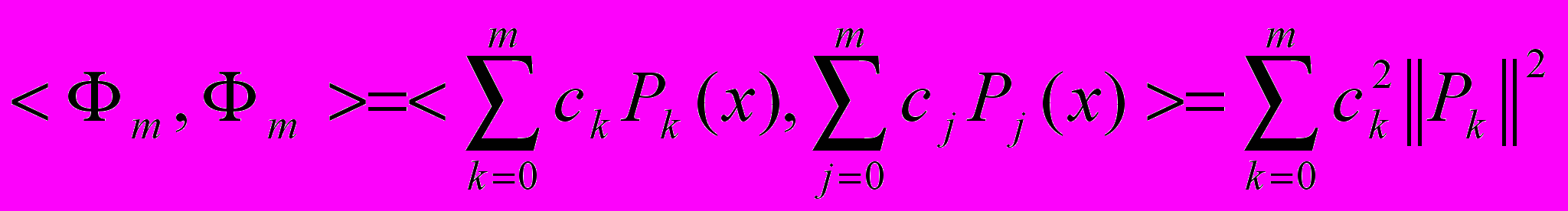
в силу ортогональности.

Подставляя в (8), получим

. (9)

Пример 2.

Пусть f(x)=|x|.

Аппроксимировать f(x) на [-1,1] в среднеквадратичном многочленом второй степени. Вычислить среднеквадратичную ошибку.

Используем ортогональную систему Лежандра:



Коэффициенты c_k находим по формуле (7), учитывая вид полиномов Лежандра:



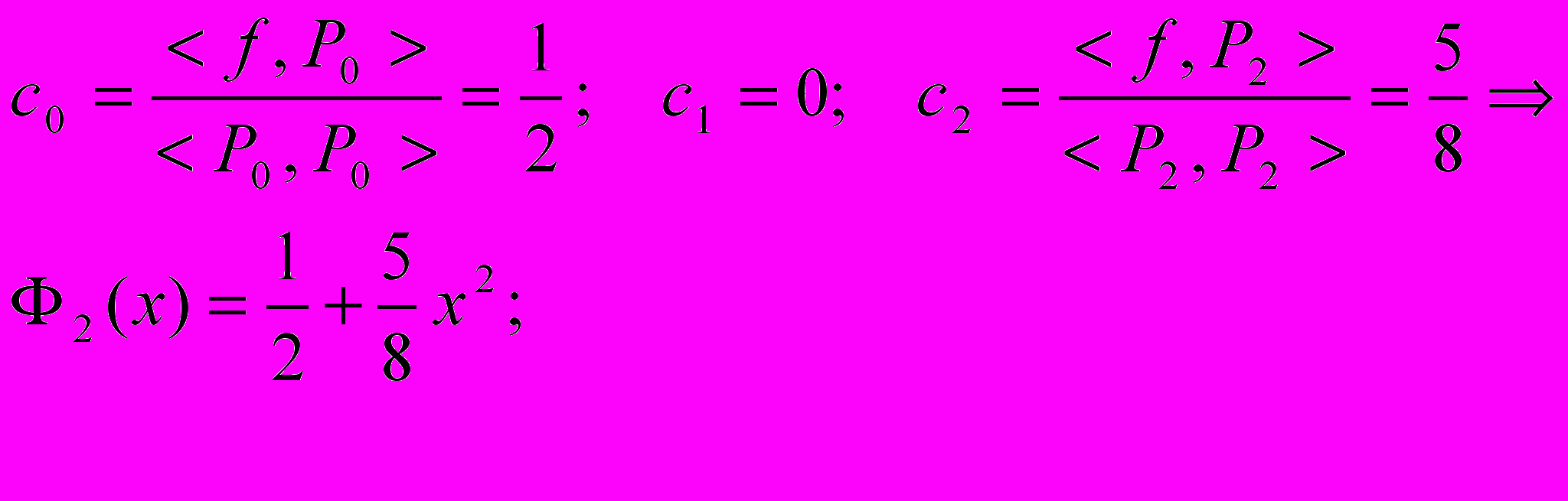
Далее вычисляем среднеквадратичную ошибку по формуле (9):



^

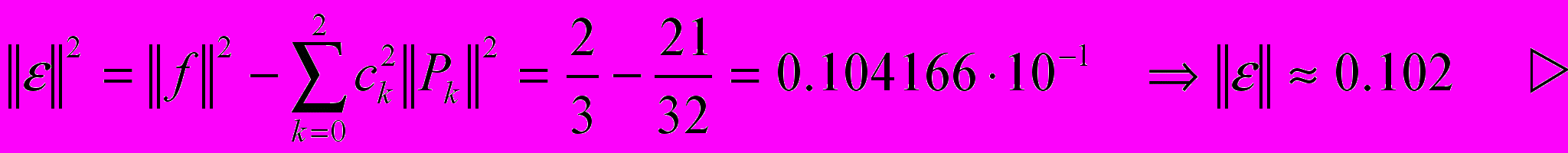
1.7. Некоторые общие свойства ортогональных полиномов.

1. Многочлен P_n(x) ортогонален любому алгебраическому многочлену m-ой степени M_m(x) при m

M_m(x) можно единственным образом представить в виде линейной комбинации многочленов Лежандра: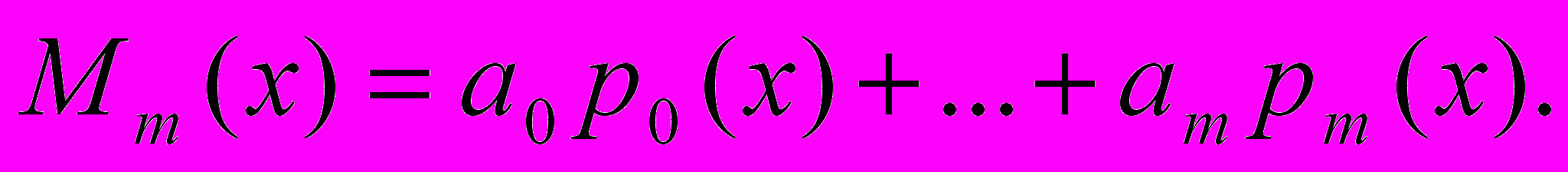

(10)

Равенство (10) тождественное, поэтому коэффициенты a_k единственным образом вычисляются путем приравнивания коэффициентов при старших степенях. Умножая обе части (10) на P_n(x), имеем



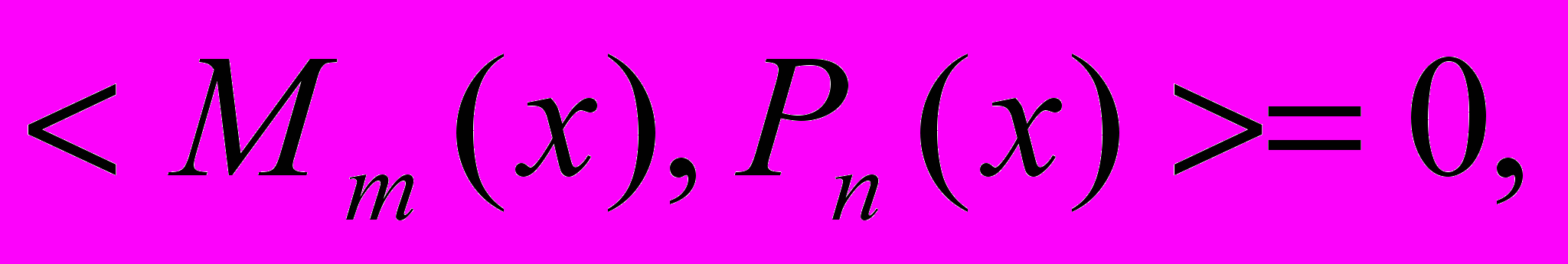
в силу ортогональности системы

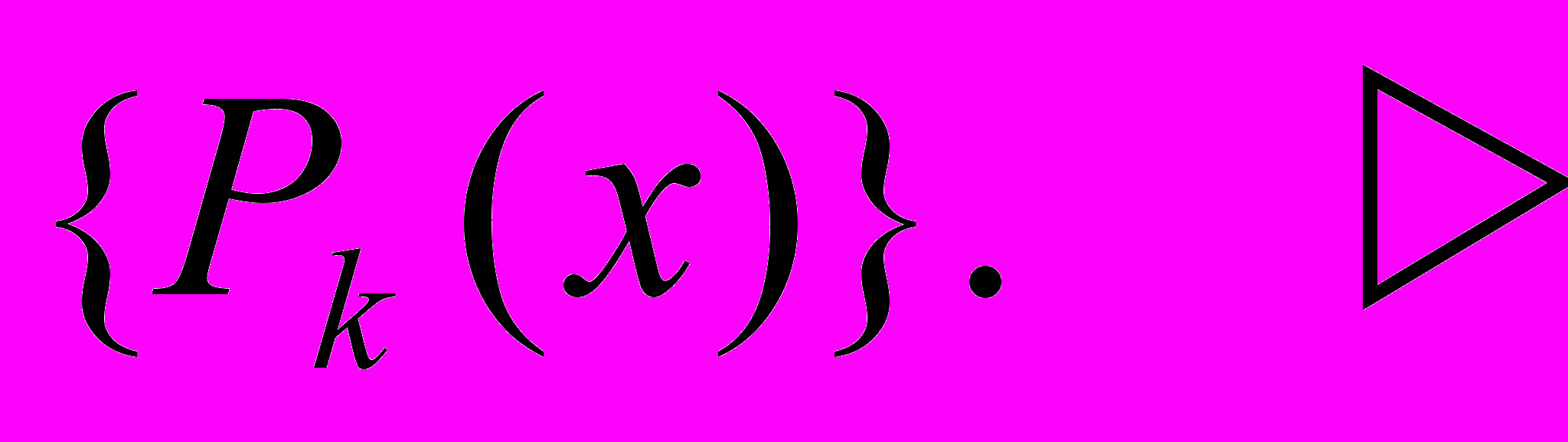
2. Полином P_n(x) имеет на отрезке [-1,1] ровно n действительных и различных корней.
   

Заметим, что в силу теоремы Гаусса многочлен P_n(x) не может иметь более чем n корней (вообще говоря, комплексных). Пусть P_n(x) имеет меньше, чем n простых действительных корней. Обозначим их 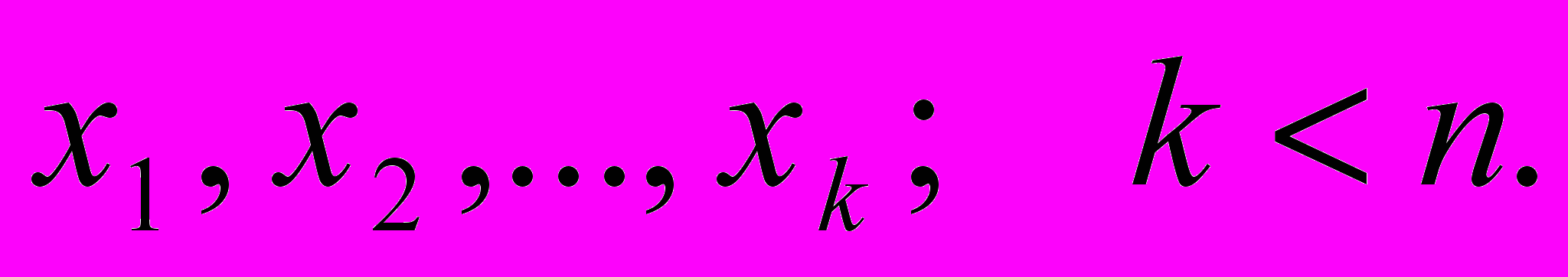По этим точкам построим фундаментальный многочлен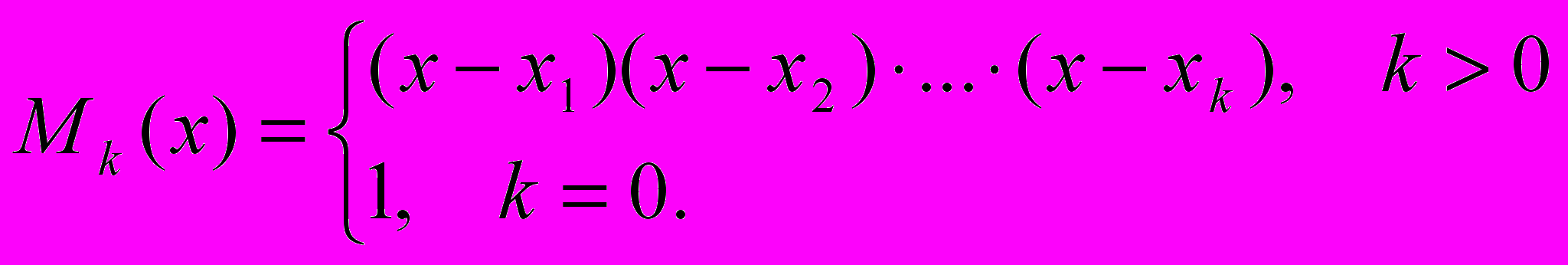



Рассмотрим многочлен: 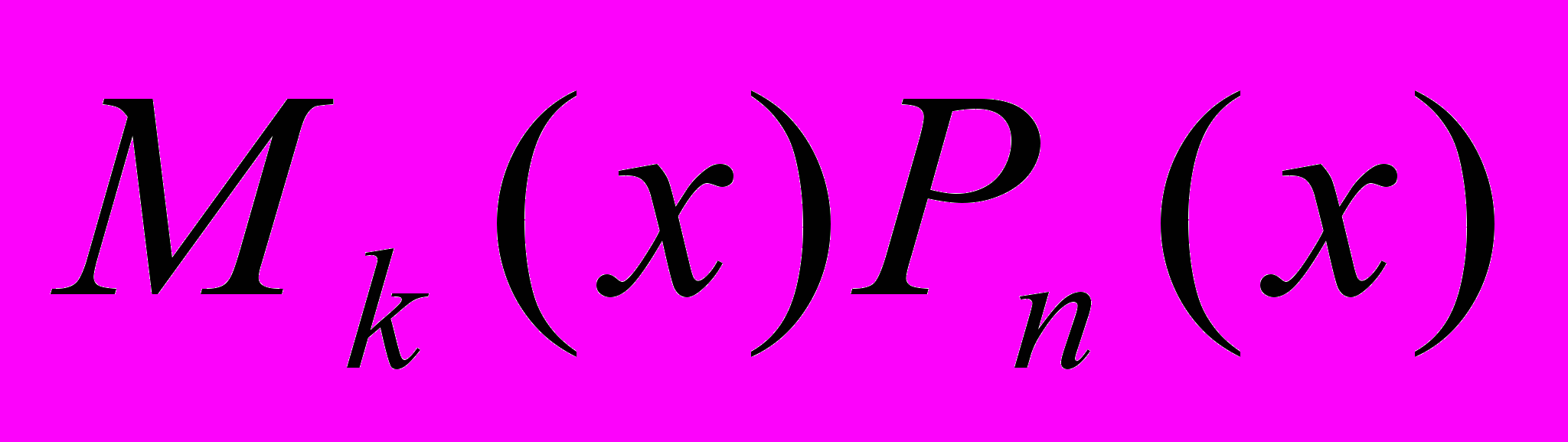- многочлен степени (k+n), который имеет нули 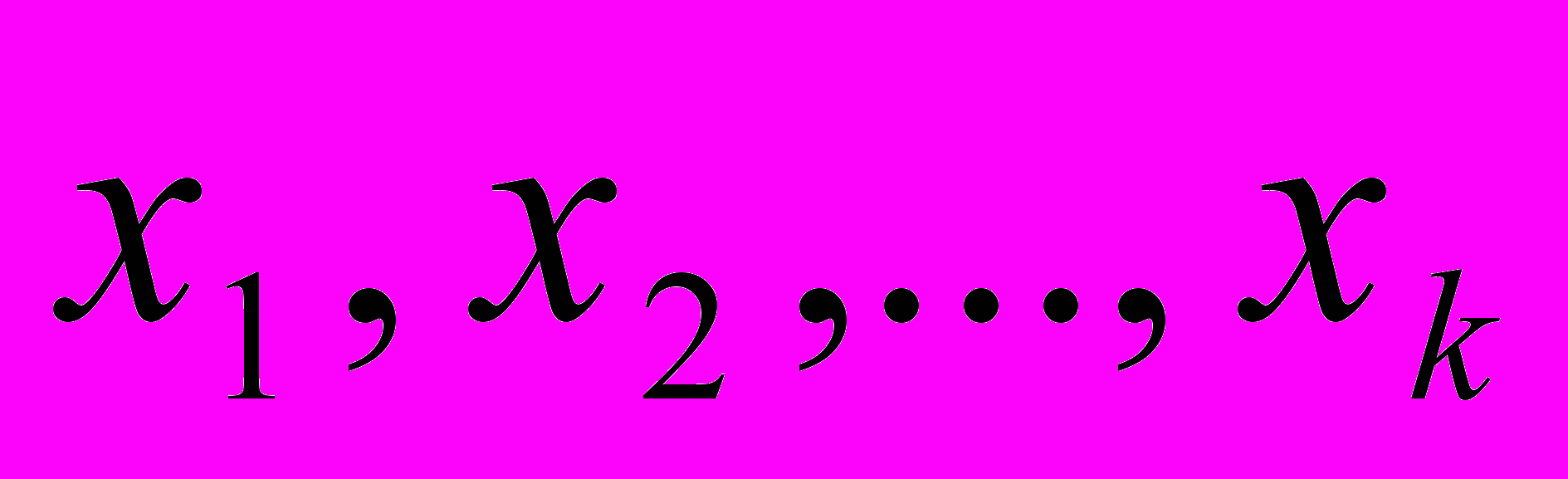четной кратности. Значит, новый многочлен 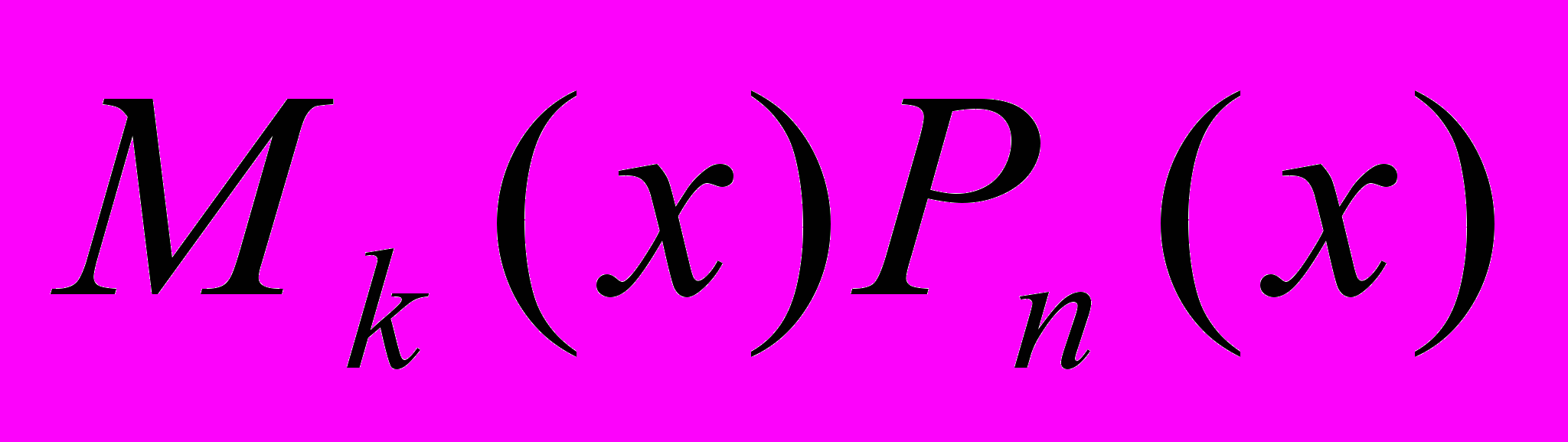сохраняет знак при переходе через эти нули, т.е. сохраняет знак на [-1,1]. Отсюда следует, что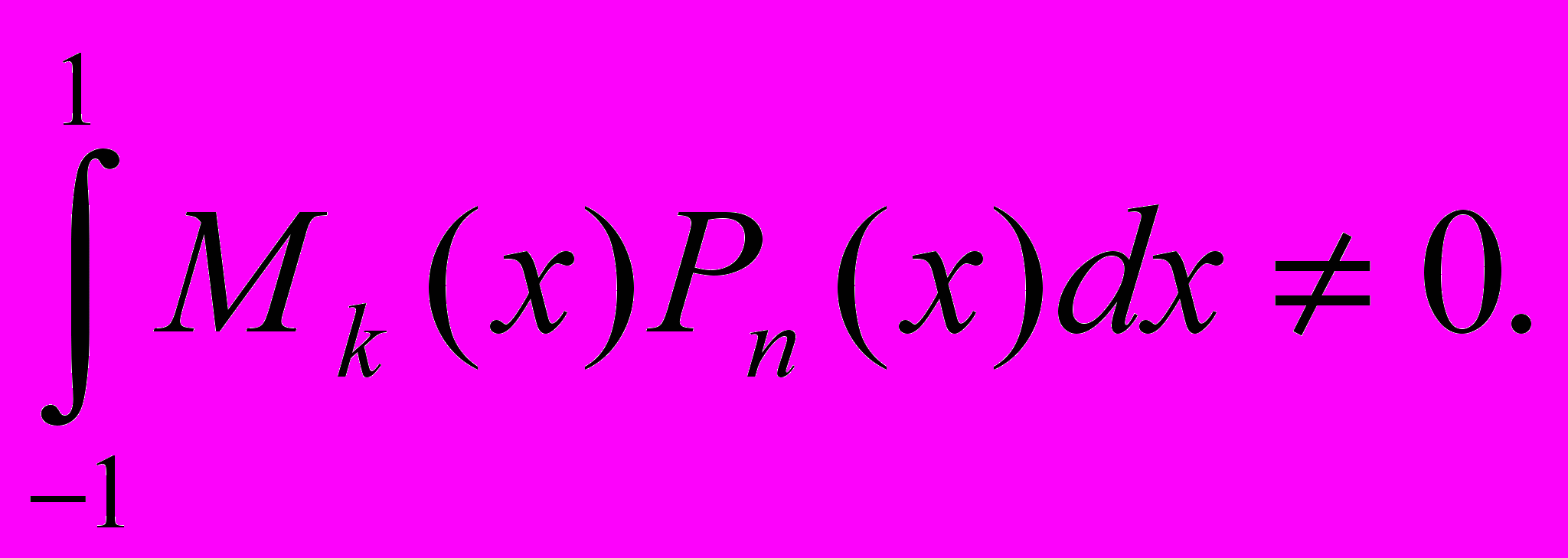



Но это противоречит свойству 1, так как P_n(x) обязательно должен быть ортогонален M_k(x).

3. Между двумя соседними нулями многочлена P_n(x) лежит ровно один нуль многочлена P_n-1(x).
   

Доказывается по индукции с помощью рекуррентного соотношения (6).

4. При n- четном многочлен P_n(x) – четная функция от x, при n- нечетном, P_n(x) – нечетная функция от x.