Домашнее задание: лекция, тест 6 по теме «Линейная функция» (с сайта ), построить графики функций 1)., 2)., 3)
| Вид материала | Лекция |
Содержание5х -10 ≥0 переносим -10 б). 10 – 5х |
- Домашнее задание в период «карантина», 26.76kb.
- Сценарий урока №2 "Решение полных квадратных уравнений", 15.69kb.
- Высшая математика, 34.34kb.
- Итоговый тест по теме «Альдегиды и кетоны» тест взят с сайта, 60.38kb.
- Линейная, квадратичная и дробно-линейная функции, 212.74kb.
- Домашнее задание по дисциплине «Стратегический менеджмент» Домашнее задание может быть, 41.07kb.
- Лекция №3 «Использование функций», 111.17kb.
- Контрольный тест (приложение) Подведение итогов урока Домашнее задание, 95.55kb.
- Домашнее задание №1. Составление эссе по предложенной теме (срок сдачи 6 -ая учебная, 77.56kb.
- Домашнее задание ответа на зачете Алгоритм формирования оценки таков: вес посещаемости, 76.53kb.
Применение свойств и графиков линейной функции при построении графиков функций с модулем.
Очень часто при изучении какой-либо темы по алгебре мы сталкиваемся с вопросом полезности и необходимости данного материала, то есть: « А зачем это нужно?». Думаю, что в этом случае главным аргументом будет практическое применение изученных понятий и свойств для решения более сложных задач. Так мне видится рассмотрение темы «Линейная функция» в 7 классе. В учебнике Ю.Н.Макарычева «Алгебра. 7 класс» после знакомства с основными свойствами, способами построения и взаимным расположением графиков появляется п.17 «Задание функции несколькими формулами», где предлагается всего 7-9 задач на исследование графика «кусочно-заданной» функции. После этого пункта вполне логично и весьма доступно объяснить 7-классникам способы построения графиков функций с модулем по определению модуля, методом интервалов и с помощью преобразований.
Однако, необходимо учесть, что учащиеся 7 класса еще не владеют в полной мере знаниями по теме «Линейные неравенства», но правила настолько просты и перекликаются с теорией решения линейных уравнений, что трудностей в восприятии этих вопросов не возникает. Предлагаю такой вариант изложения этой темы в 7 классах Физико-математического лицея № 38 г. Ульяновска.
(2 урока)
1. Домашнее задание: лекция, тест 6 по теме «Линейная функция» (с сайта www.atw-matem.narod.ru), построить графики функций 1).
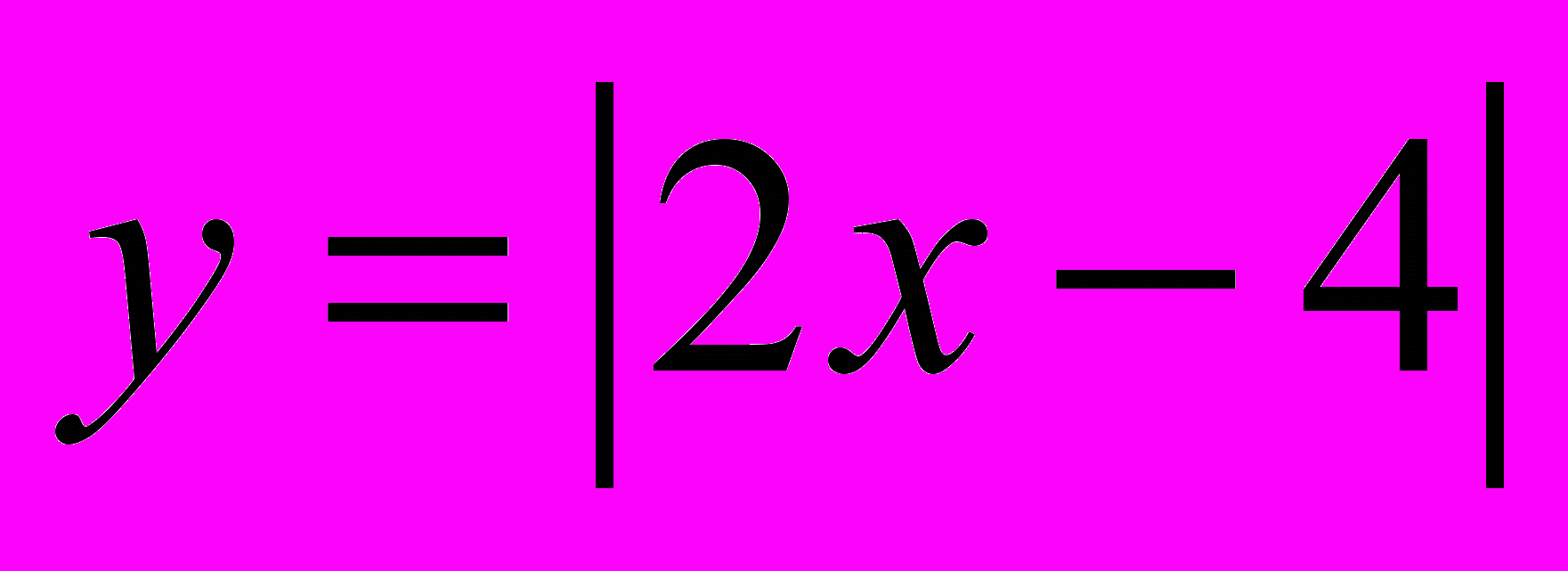 , 2).
, 2). 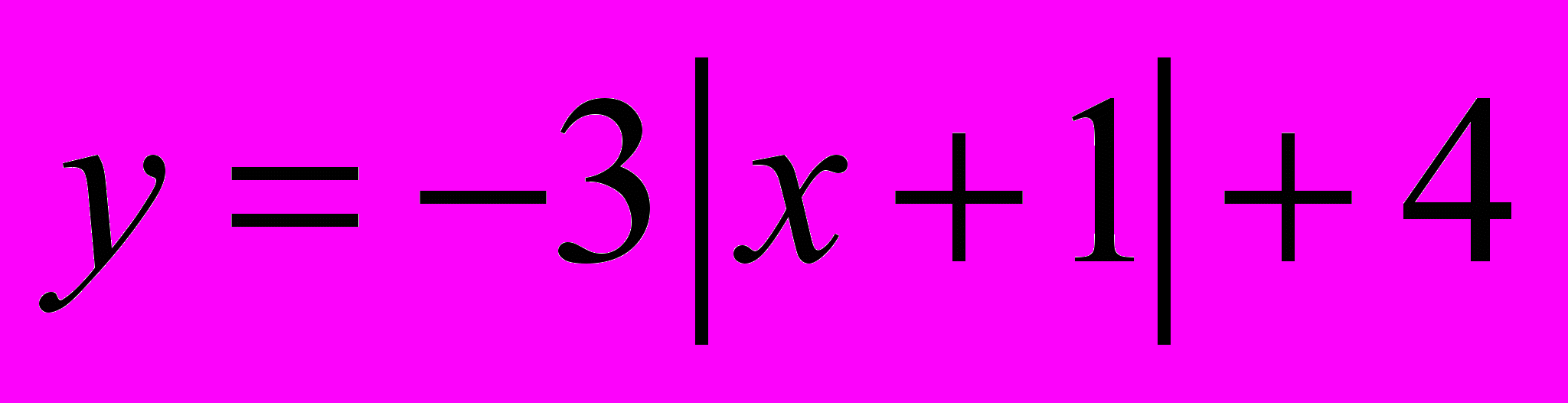 ,
, 3).
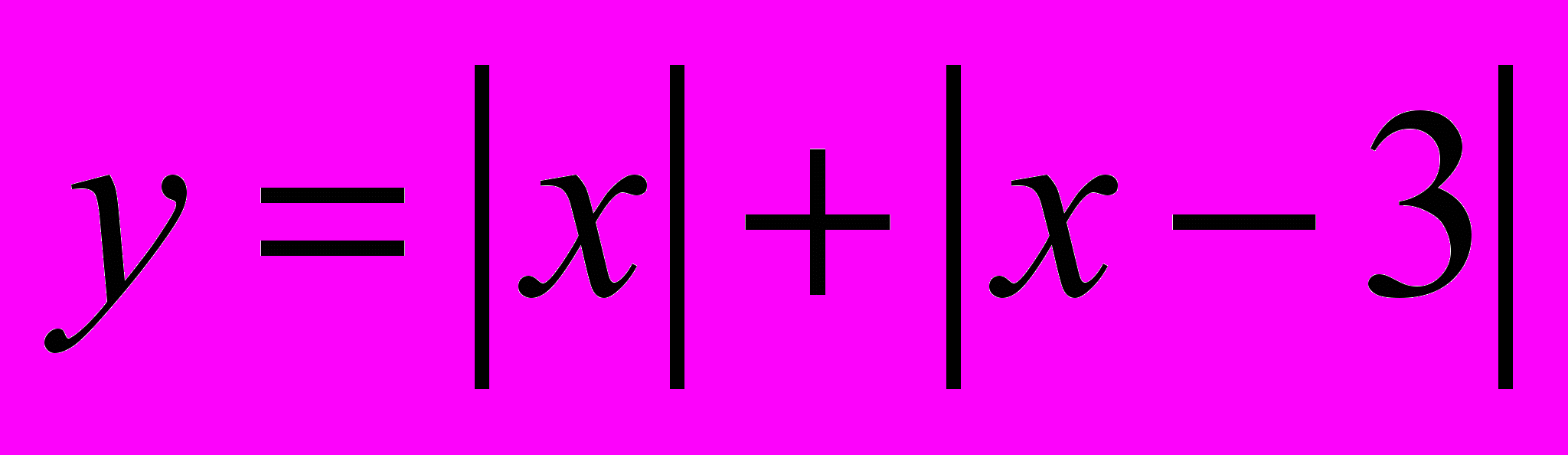
2. Устный счет по теме «Линейная функция». (6 вариантов) Приложение 1.
3. Лекция:
Повторение понятий, изученных в 6 классе:
1. Определение: Модуль – расстояние от нуля до числа, выраженное в единичных отрезках
Обязательно надо отметить «дуализм» модуля, т.е. возможность отложить на луче одинаковое расстояние и влево, и вправо

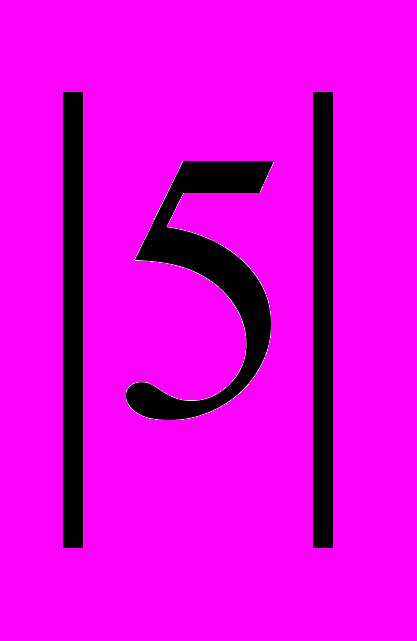 =5,
=5, 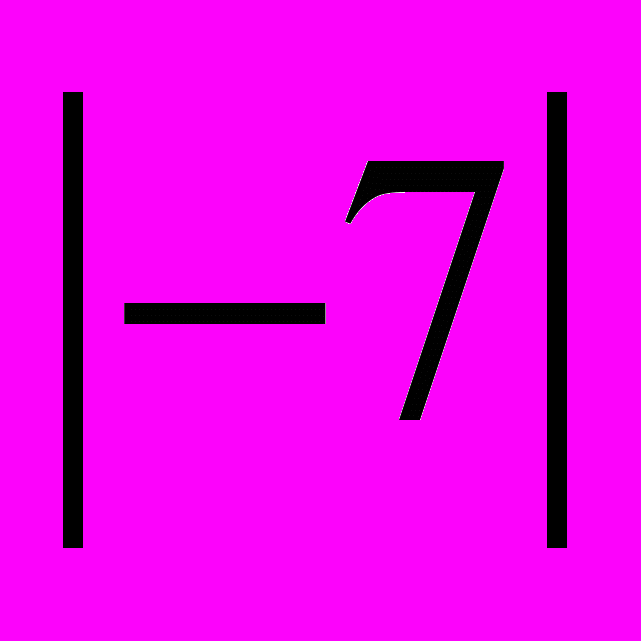 = 7,
= 7, 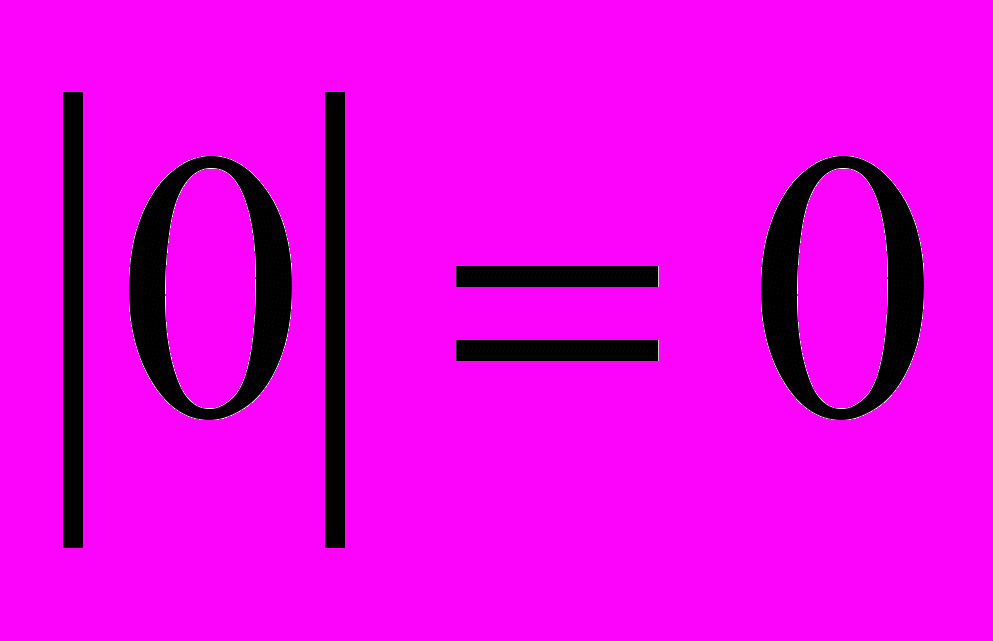
-7 0 5 х
Правило:
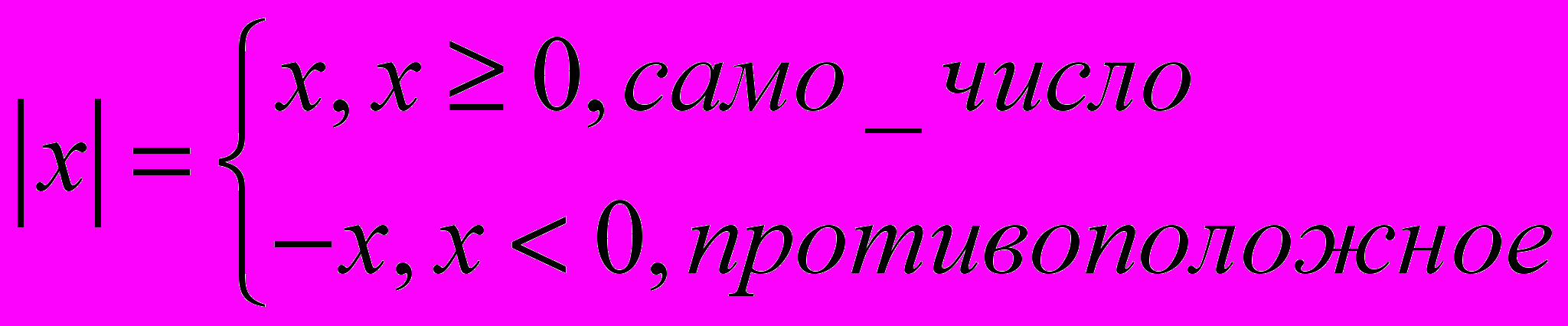
х – подмодульное выражение, любое число
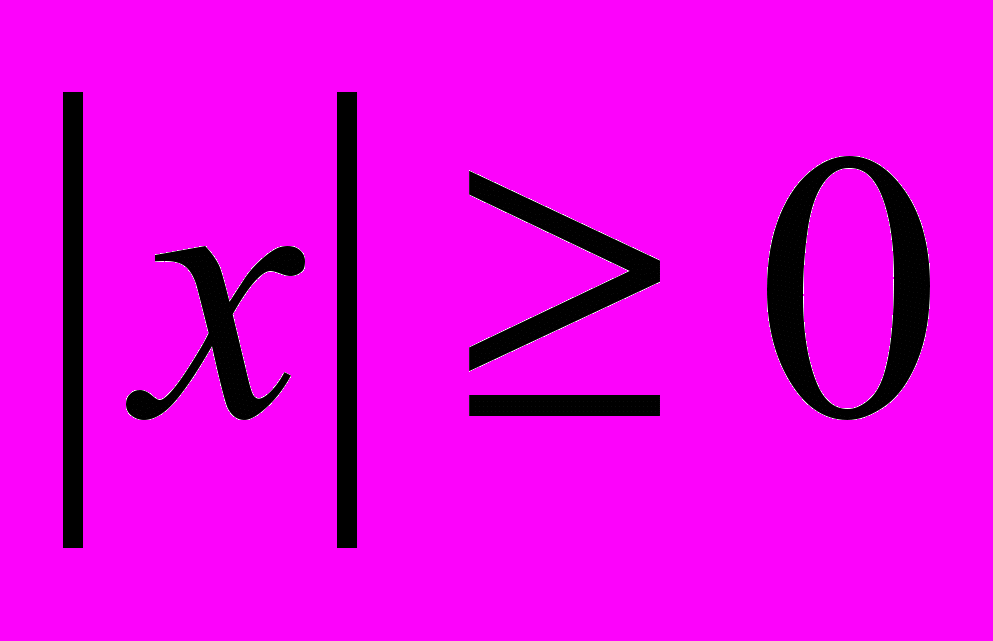 - всегда неотрицательное число!
- всегда неотрицательное число!2. Примеры:
Раскройте модуль:
а).
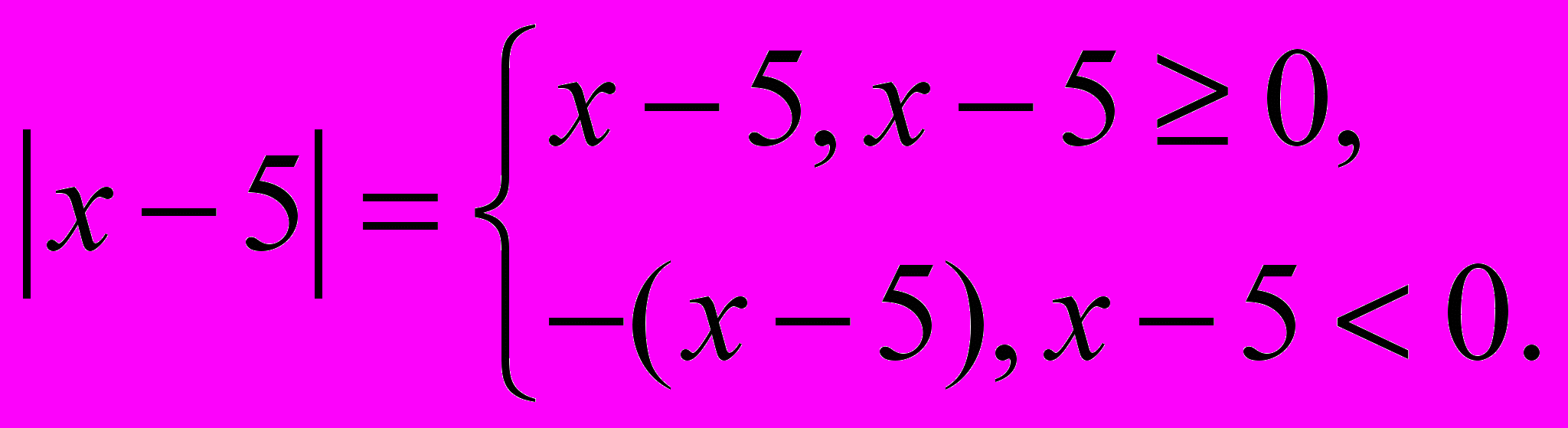 б).
б). 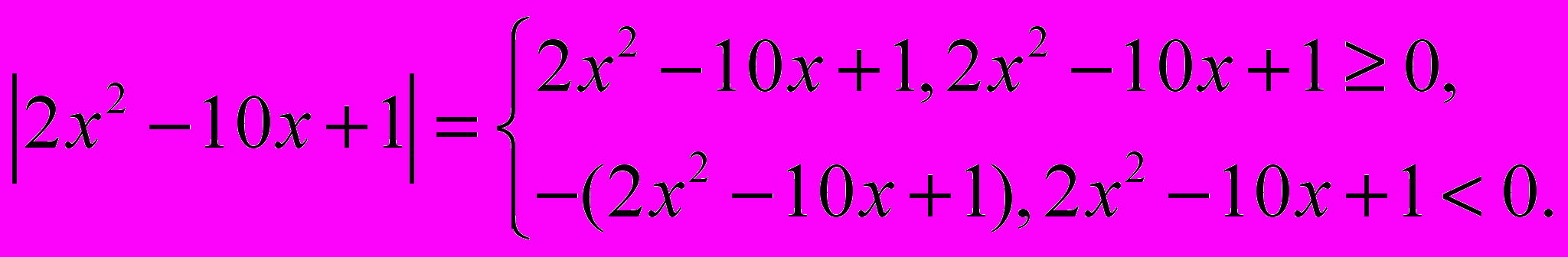
в). Правила раскрытия скобок:
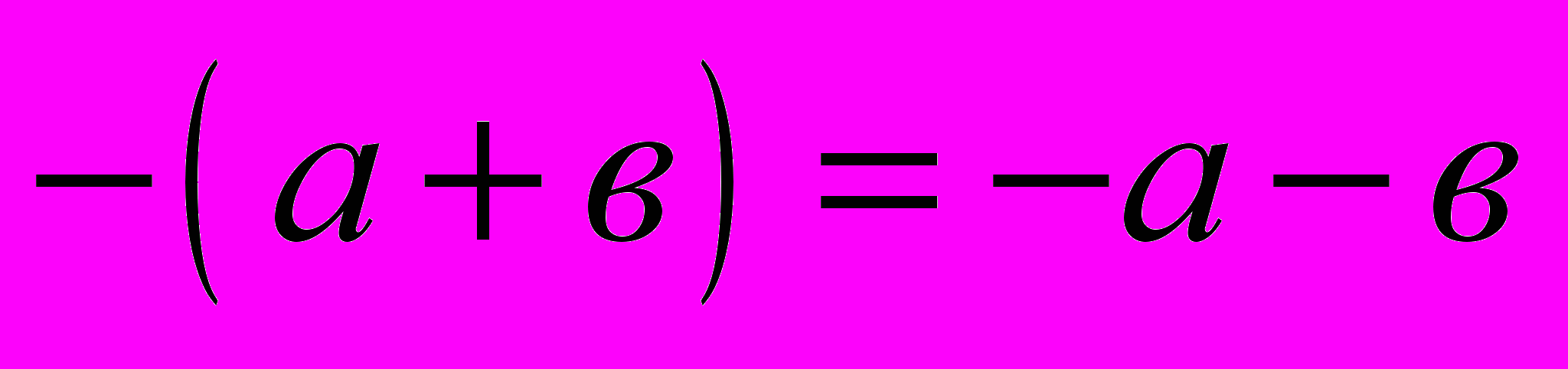
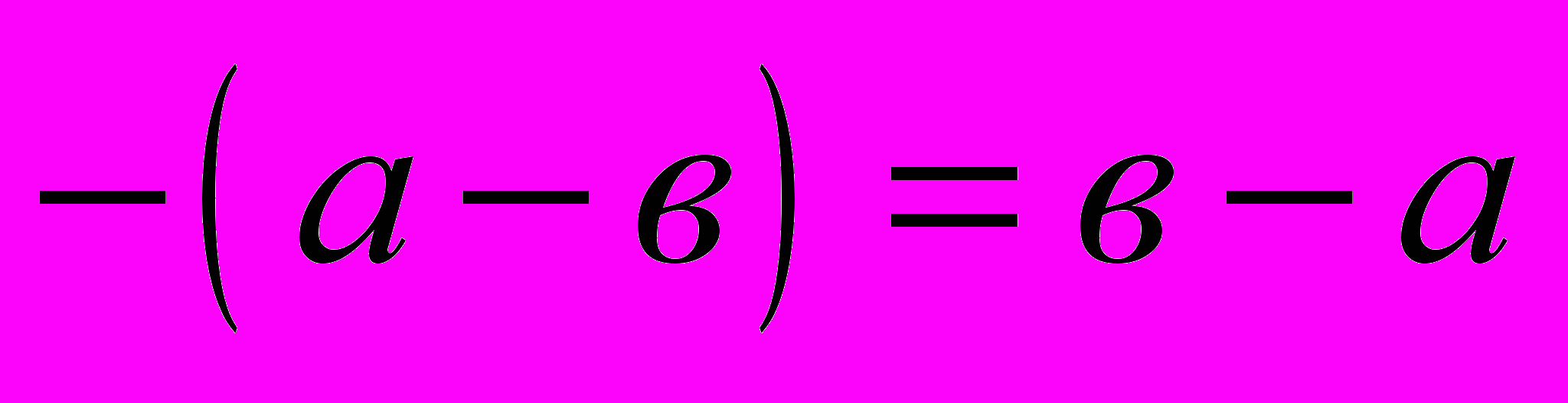
3. Простейшие неравенства:
Чем больше, тем – правее
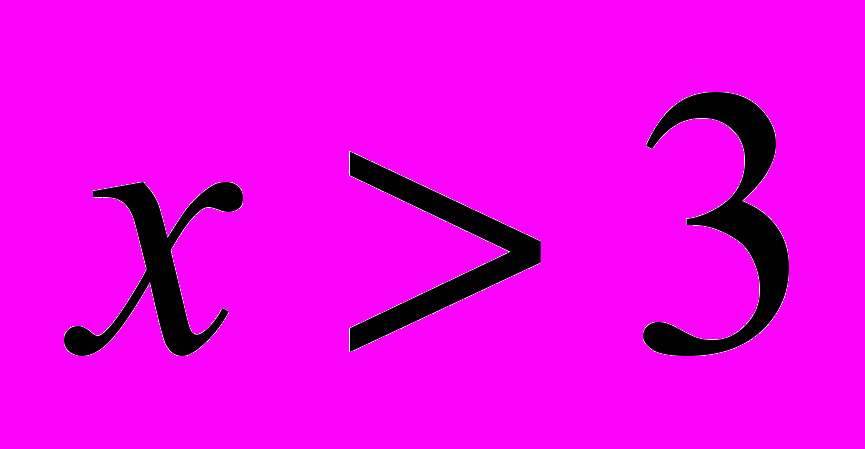 (все числа, правее числа 3)
(все числа, правее числа 3)Чем меньше, тем – левее
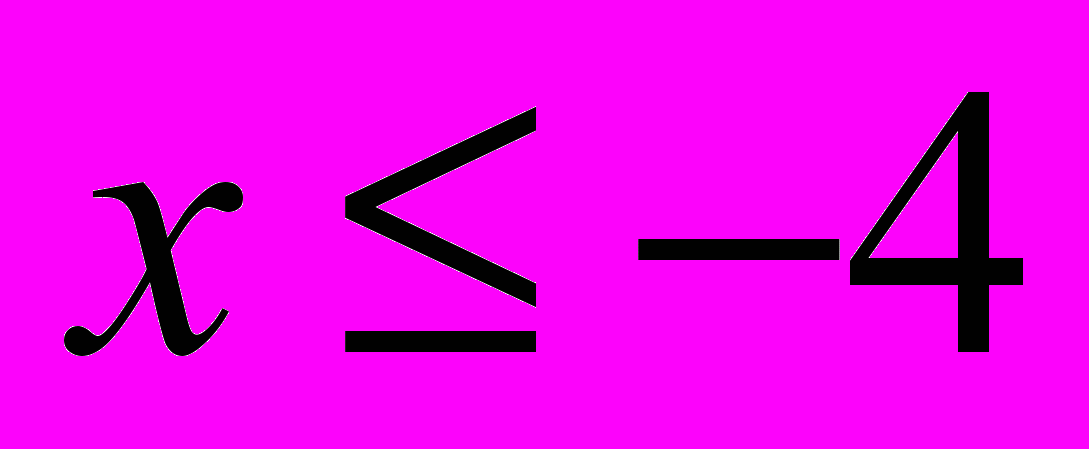 (все числа, левее числа – 4 и само число -4)
(все числа, левее числа – 4 и само число -4)Правила:
1.При переносе слагаемого из одной части неравенства в другую знак неравенства не меняется, а знак слагаемого меняется на противоположный(как в уравнениях).
2. Переносить слагаемые так, чтобы коэффициент при переменной был положительным.
3. При делении обеих частей неравенства на
 число знак неравенства
число знак неравенства 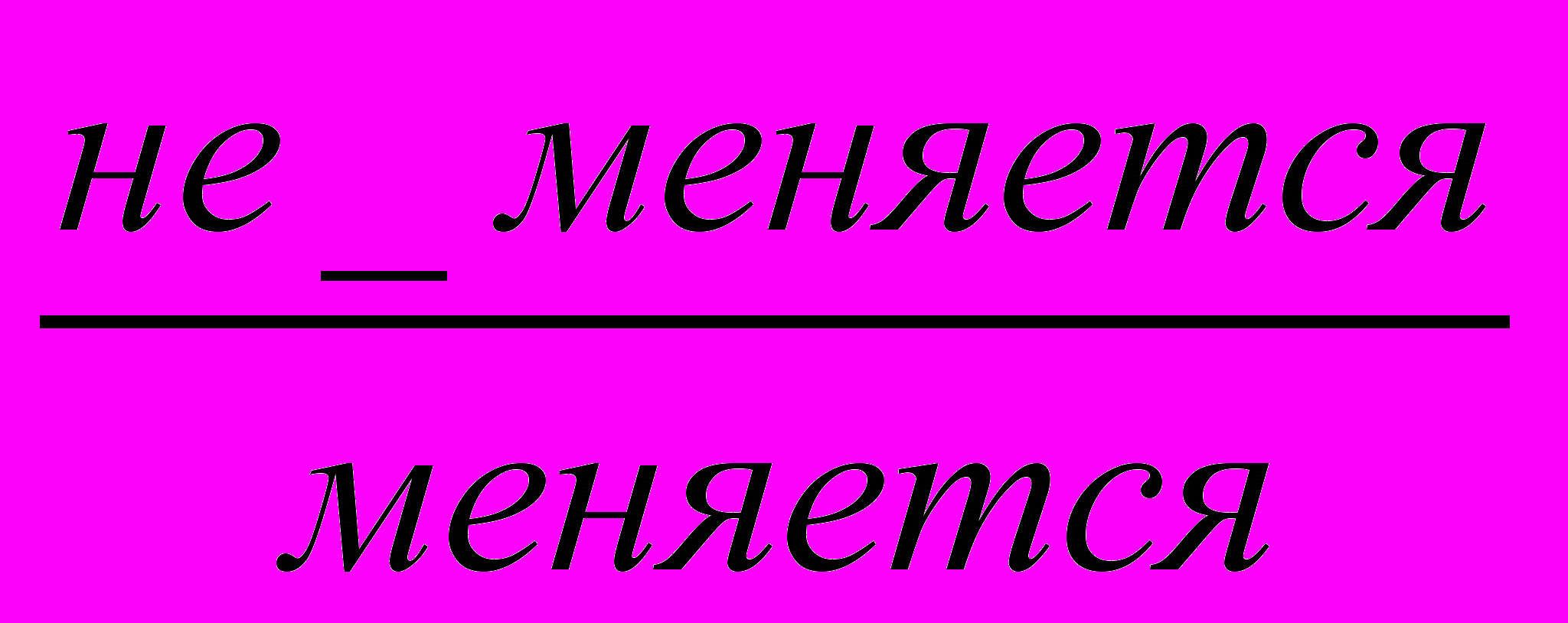 .
.Примеры:
а). ^ 5х -10 ≥0 переносим -10 б). 10 – 5х ≥ 0 переносим -5х
5х ≥ 10 делим обе части на 5 10 ≥ 5х делим обе части на 5
х ≥ 2 2 и все числа, правее 2 2 ≥ х «развернем» неравенство
х ≤ 2 2 и все числа, левее 2
4. Построение графиков.
После такой подготовительной работы можно приступить к построению простейших графиков методом «по определению модуля».
1.
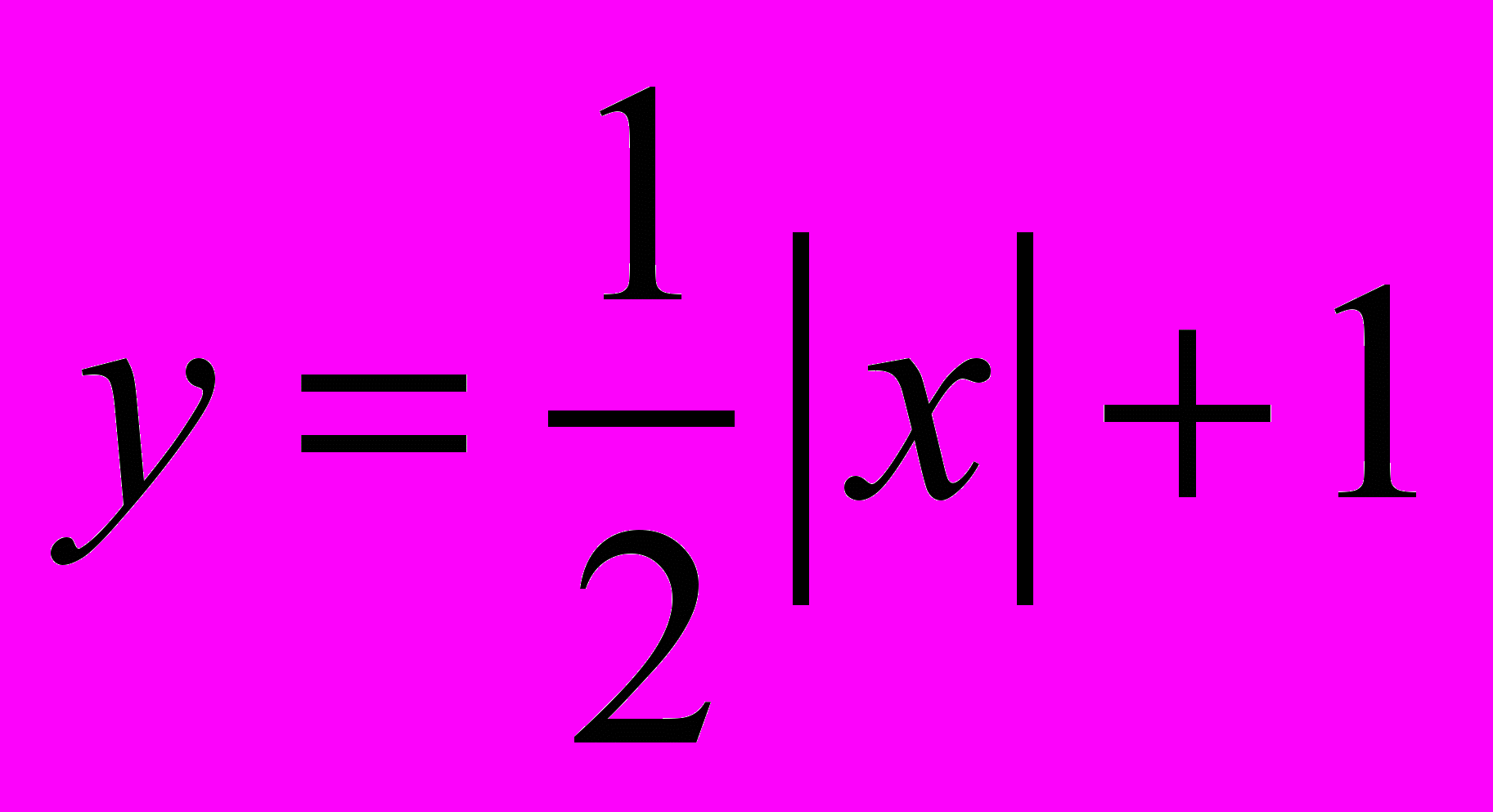 . Выясняем, сколько модулей присутствует в данной формуле какое подмодульное выражение.(х). Обращаемся к определению модуля и рассматриваем 2 ситуации, в зависимости от знака подмодульного выражения.
. Выясняем, сколько модулей присутствует в данной формуле какое подмодульное выражение.(х). Обращаемся к определению модуля и рассматриваем 2 ситуации, в зависимости от знака подмодульного выражения.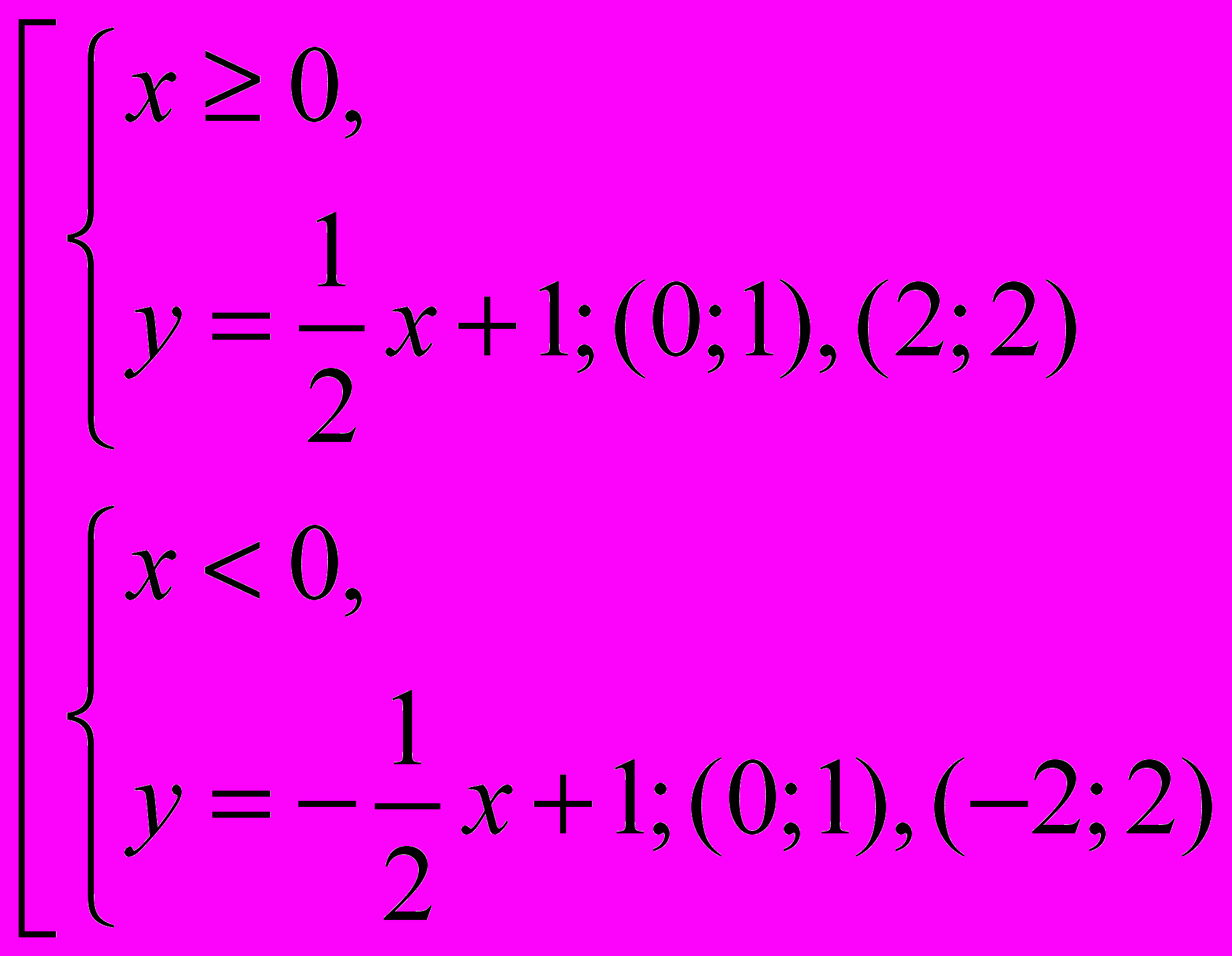
Н
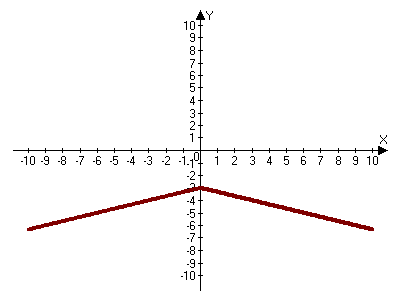 а этом этапе очень важно объяснить учащимся, что значения абсцисс точек для построения обязательно должны соответствовать условиям системы, при этом, первое значение выбираем «концевое». (В данном примере х=0). Фиксируем вспомогательный элемент построения: х = 0 – «разделяющая прямая». С нее и начинаем построение, для того, чтобы отделить зоны расположения графика.
а этом этапе очень важно объяснить учащимся, что значения абсцисс точек для построения обязательно должны соответствовать условиям системы, при этом, первое значение выбираем «концевое». (В данном примере х=0). Фиксируем вспомогательный элемент построения: х = 0 – «разделяющая прямая». С нее и начинаем построение, для того, чтобы отделить зоны расположения графика.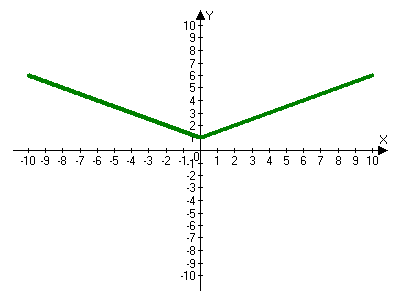
График 1. График 2.
2.
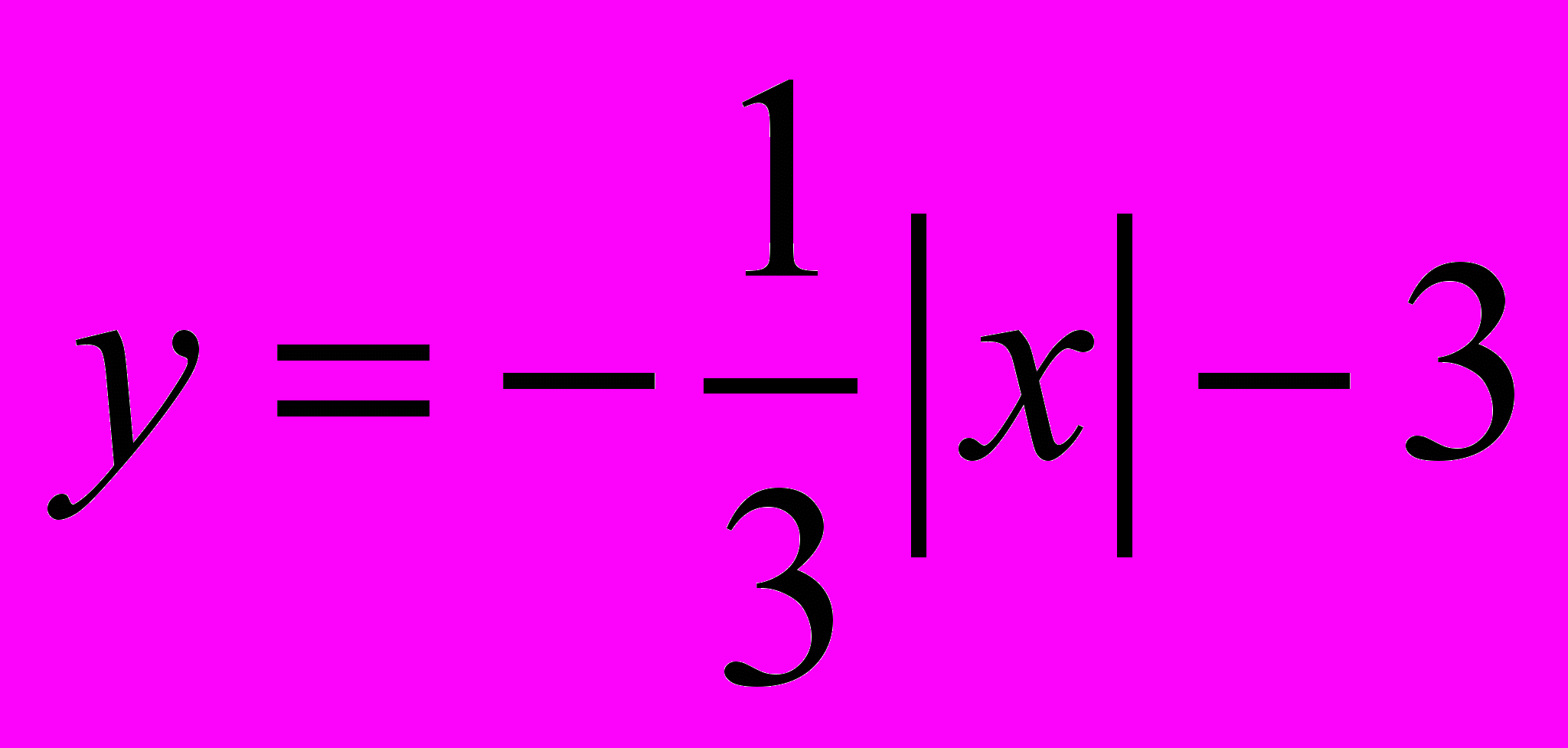 . Все рассуждения строим аналогично, только при подборе опорных точек учитываем, что координаты должны быть целыми числами.
. Все рассуждения строим аналогично, только при подборе опорных точек учитываем, что координаты должны быть целыми числами.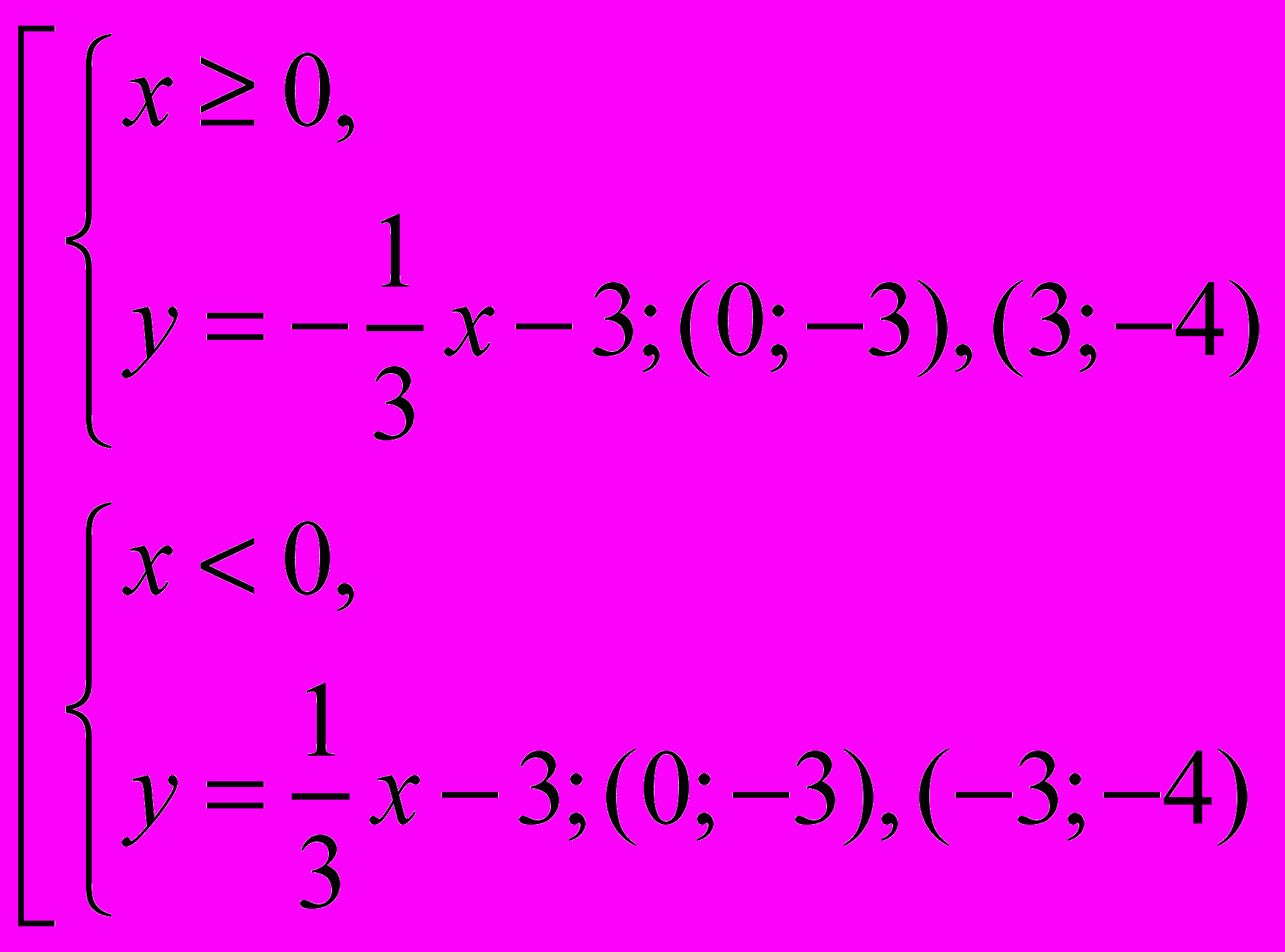
3.
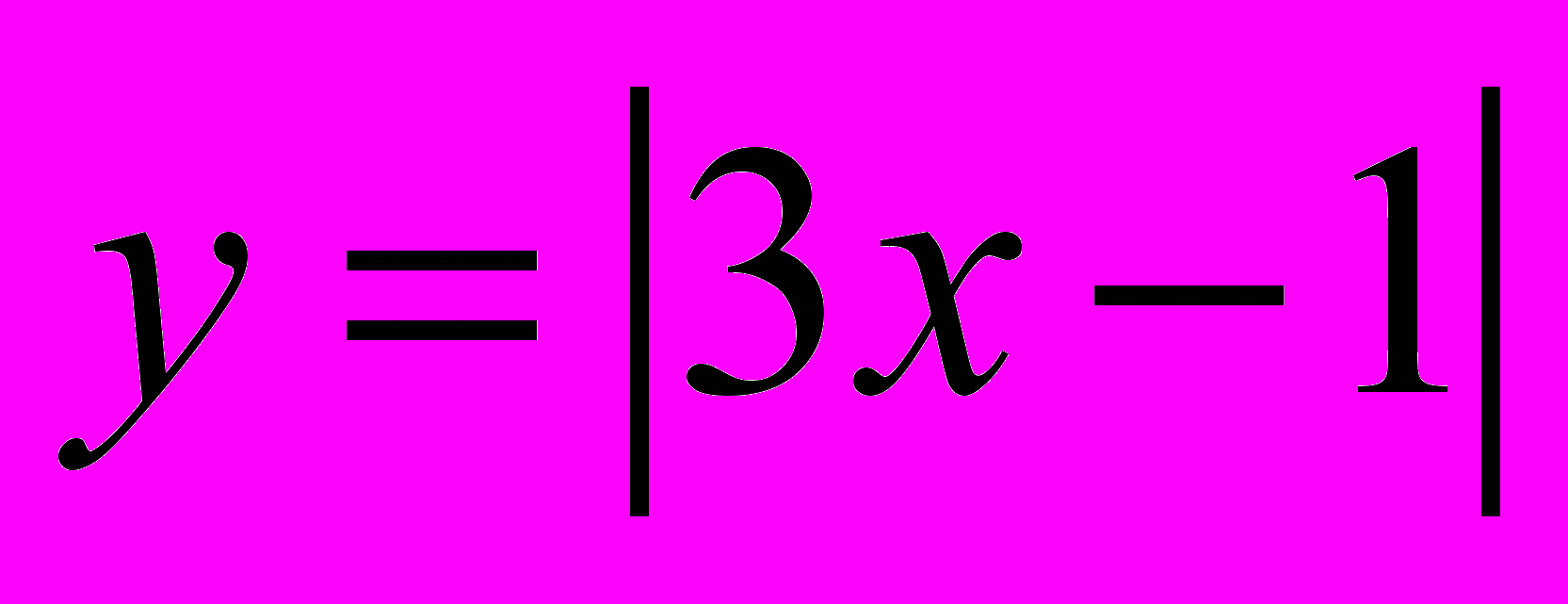 . Применяя определение модуля, обратим внимание учащихся, что подмодульное выражение в этом случае уже не «х», а «3х-1», поэтому раскрытие зависит от знака этого выражения.
. Применяя определение модуля, обратим внимание учащихся, что подмодульное выражение в этом случае уже не «х», а «3х-1», поэтому раскрытие зависит от знака этого выражения.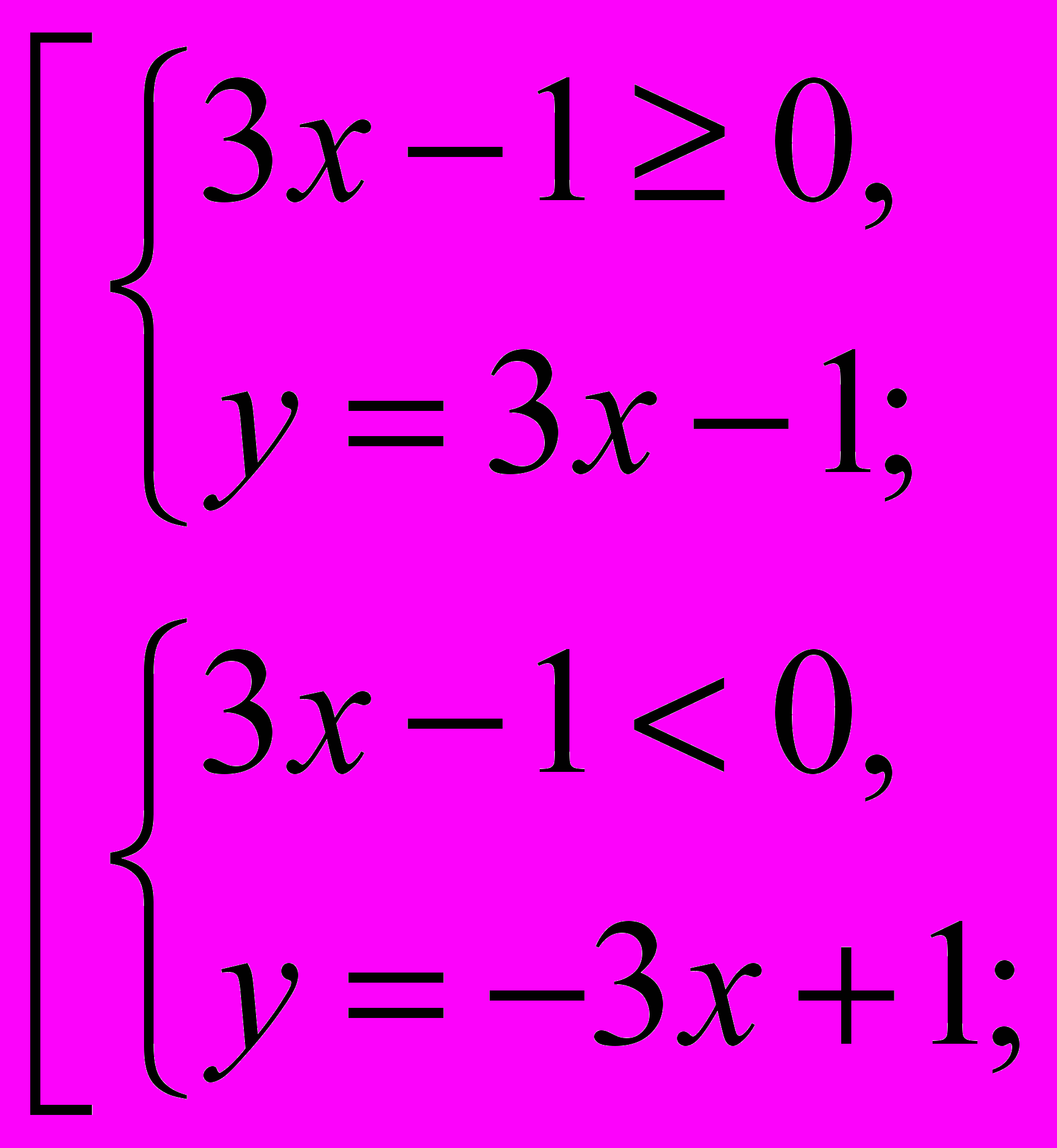 =>
=> 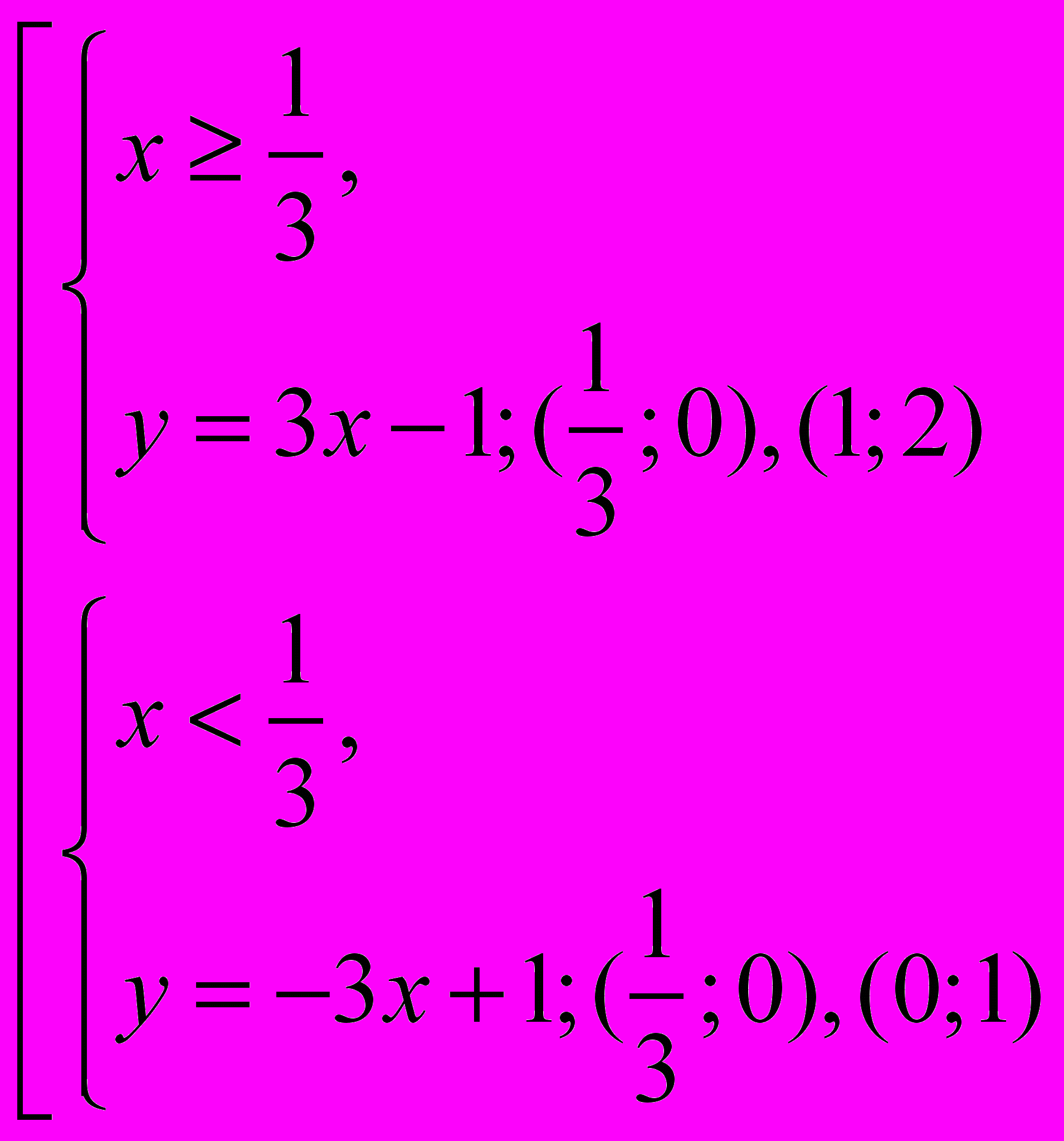 х =
х = 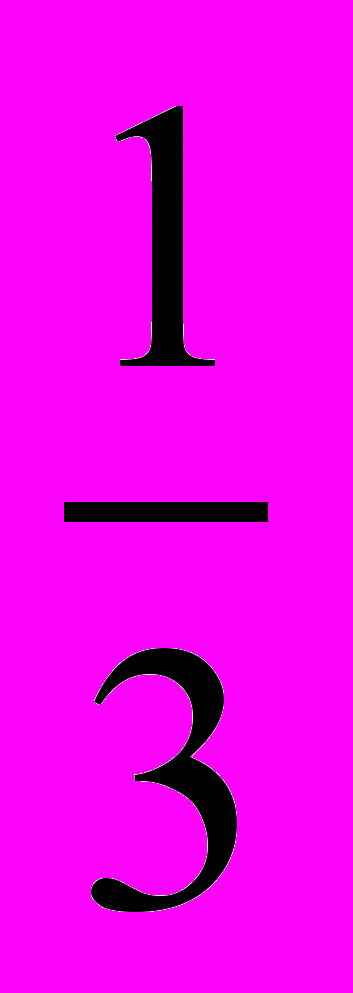 - разделяющая прямая.
- разделяющая прямая.М
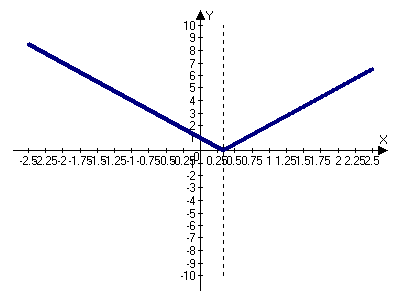
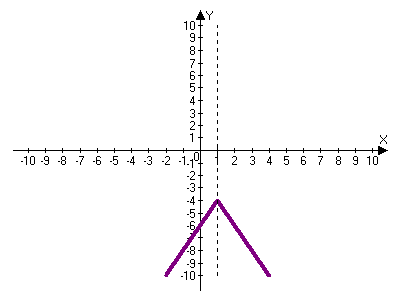 ожно порекомендовать учащимся изменить масштаб по оси Ох для более точного построения графика.
ожно порекомендовать учащимся изменить масштаб по оси Ох для более точного построения графика.График 3. График 4.
4.
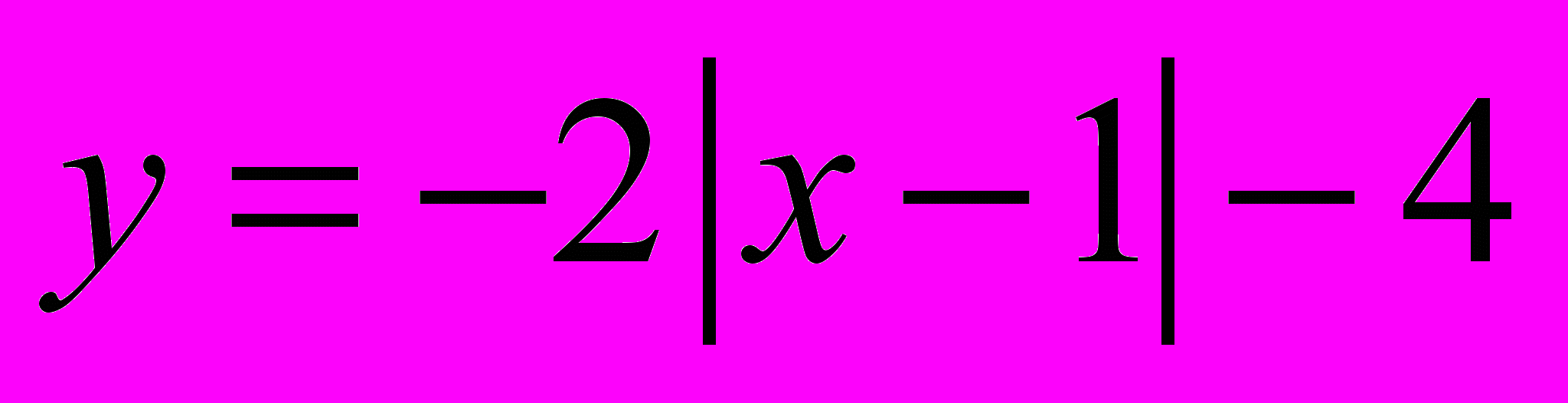 . Подмодульное выражение «х – 1»
. Подмодульное выражение «х – 1»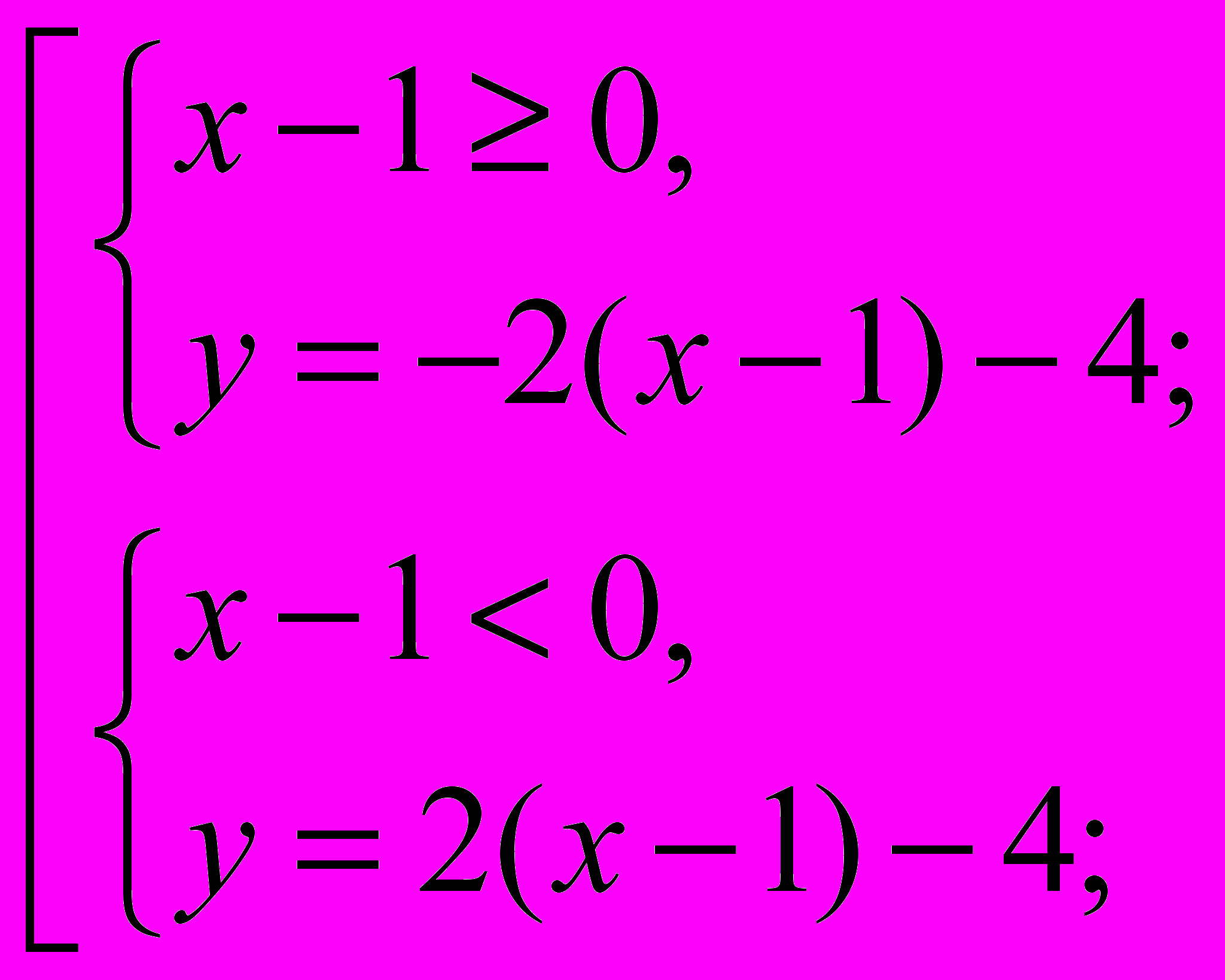 =>
=> 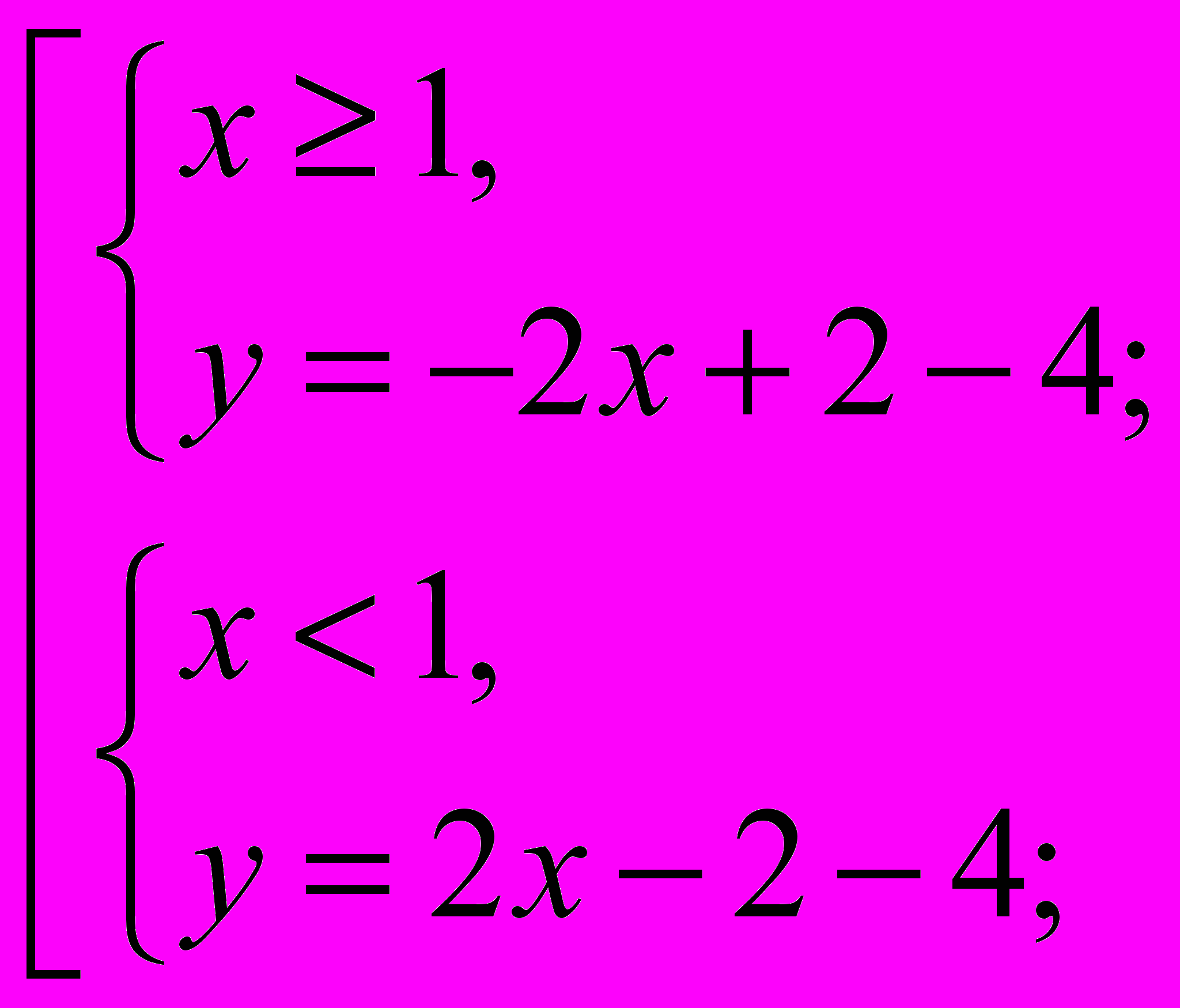 =>
=>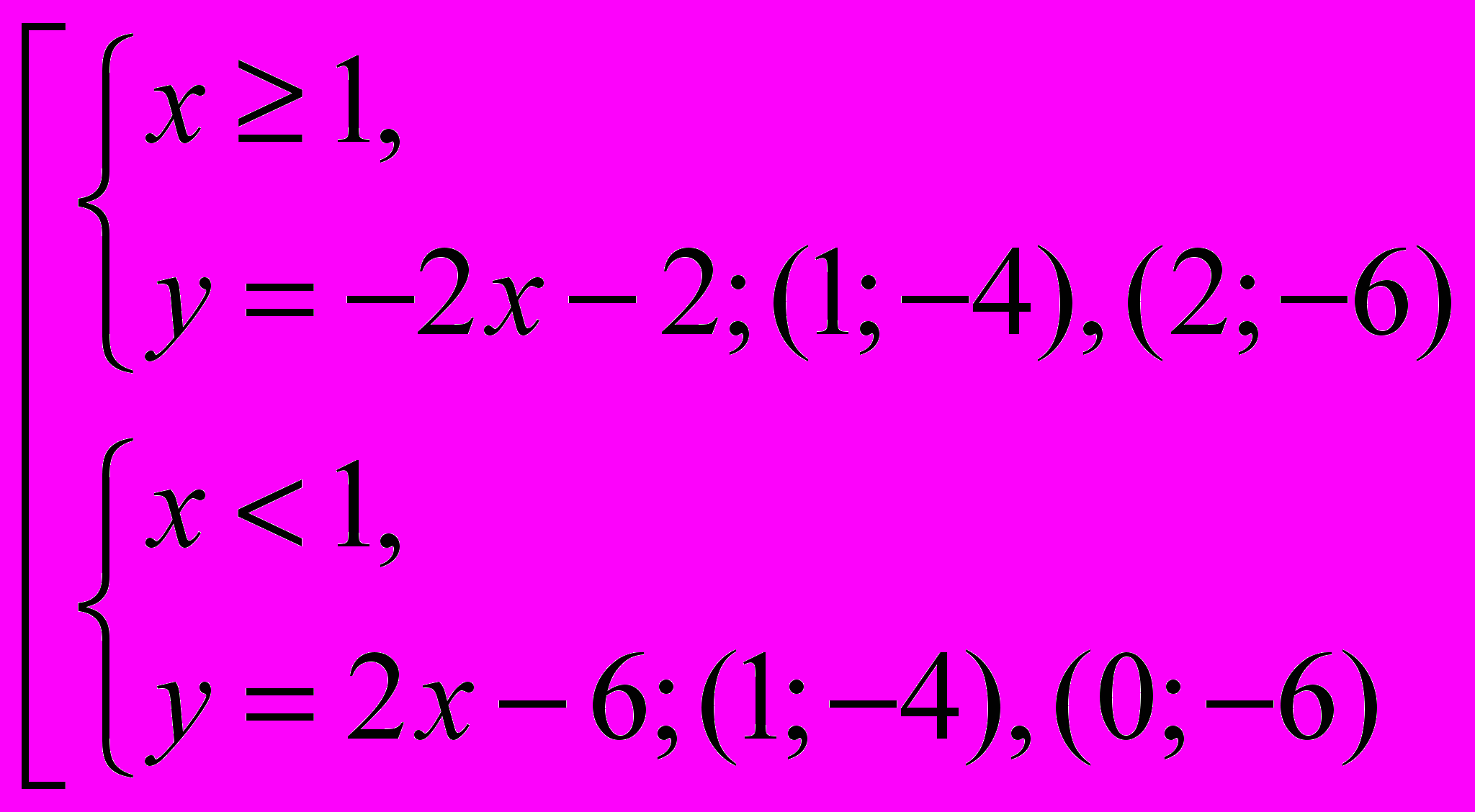
х = 1 – разделяющая прямая.
5. После выполнения этих упражнений можно перейти к самой сложной части темы – к построению графиков «методом интервалов». При объяснении материала необходимо дать четкий алгоритм действий, приводящих к итоговому построению. Также, предварительно, надо повторить свойство возрастающей линейной функции, меняющей свой знак при переходе через «ноль функции».(Достаточно показать на рисунке).
Правило: Возрастающая линейная функция (к>0) при переходе через свой ноль меняет знак с минуса на плюс.
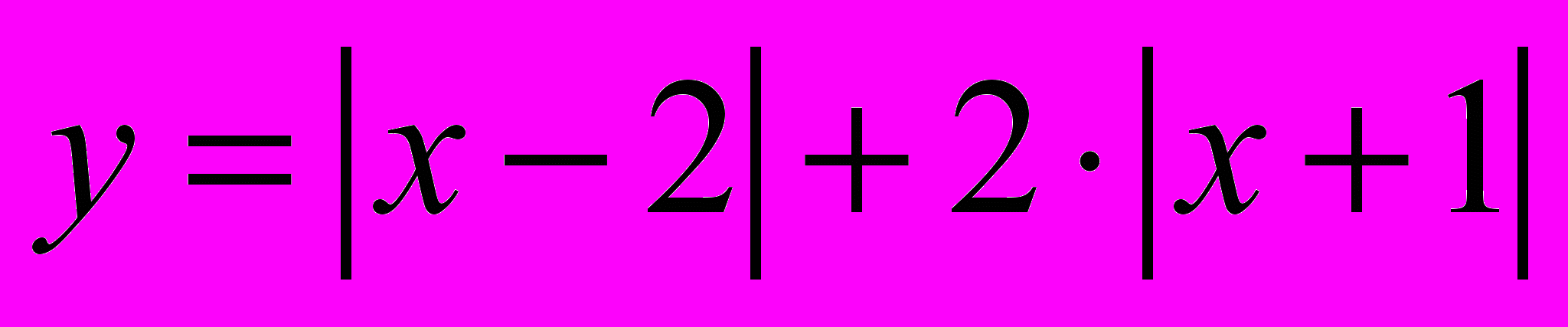 . Обратим внимание учащихся на то, что формула функции содержит 2 модуля, значит, нельзя применить метод «по определению модуля». Тогда начинаем выполнять действия «по шагам»:
. Обратим внимание учащихся на то, что формула функции содержит 2 модуля, значит, нельзя применить метод «по определению модуля». Тогда начинаем выполнять действия «по шагам»:- Найдем нули модулей: х = 2, х = -1.
- Отметим на числовом луче и определим количество зон построения (3)
- Заполним таблицу знаков подмодульных выражений:
- 1 2
| х | 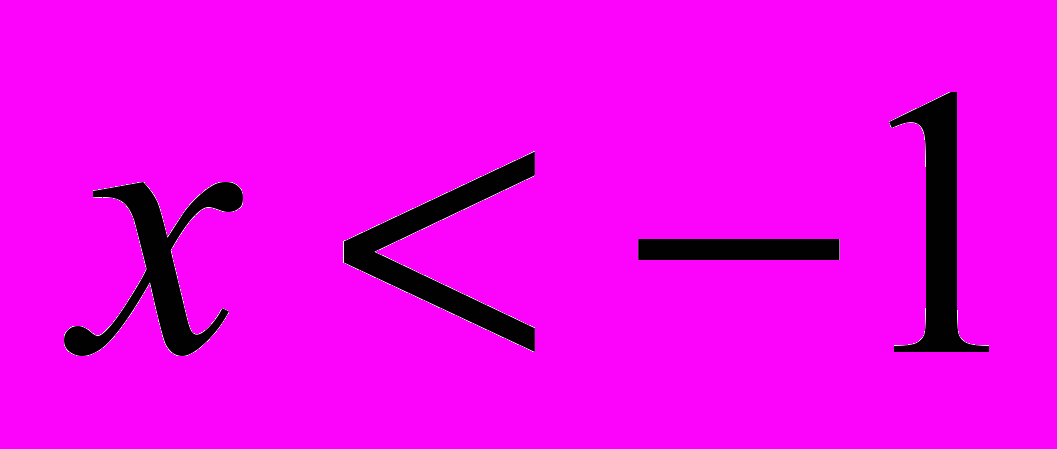 |  | 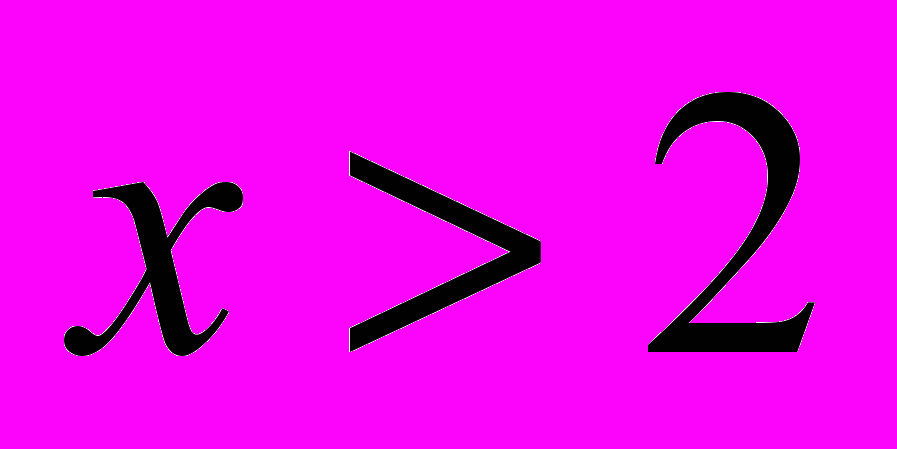 |
| Х - 2 | - | - | + |
| Х + 1 | - | + | + |
4.Раскроем модули по определению на каждом из промежутков, учитывая знаки подмодульных выражений.
1).
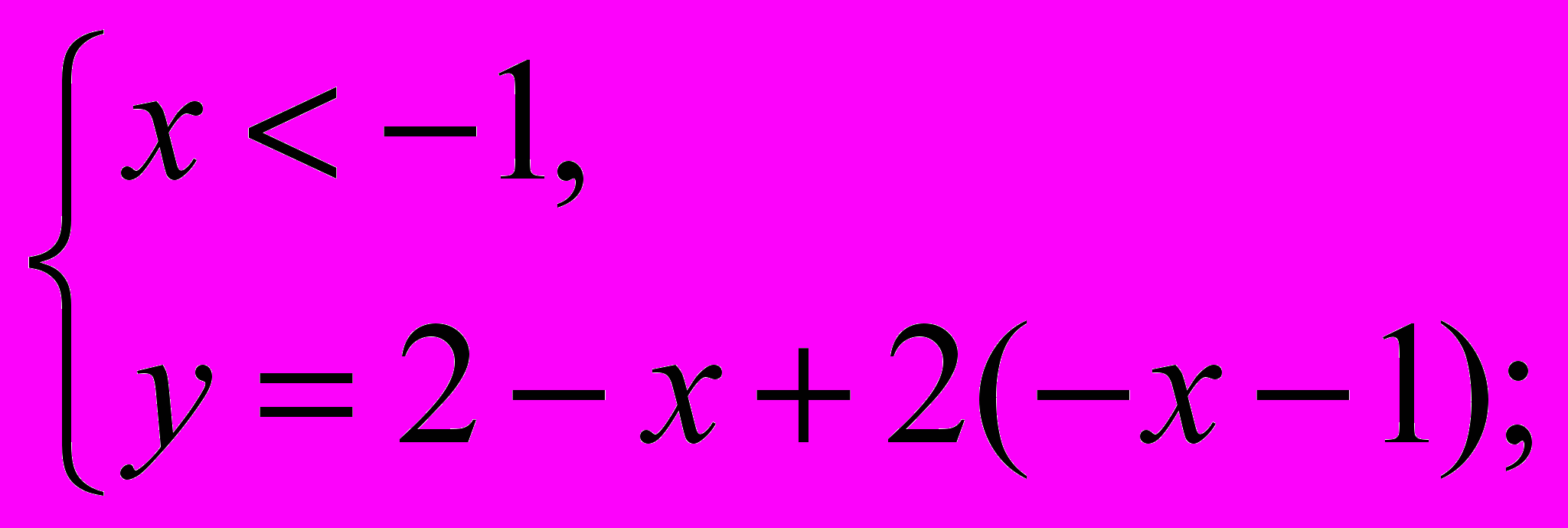 =>
=>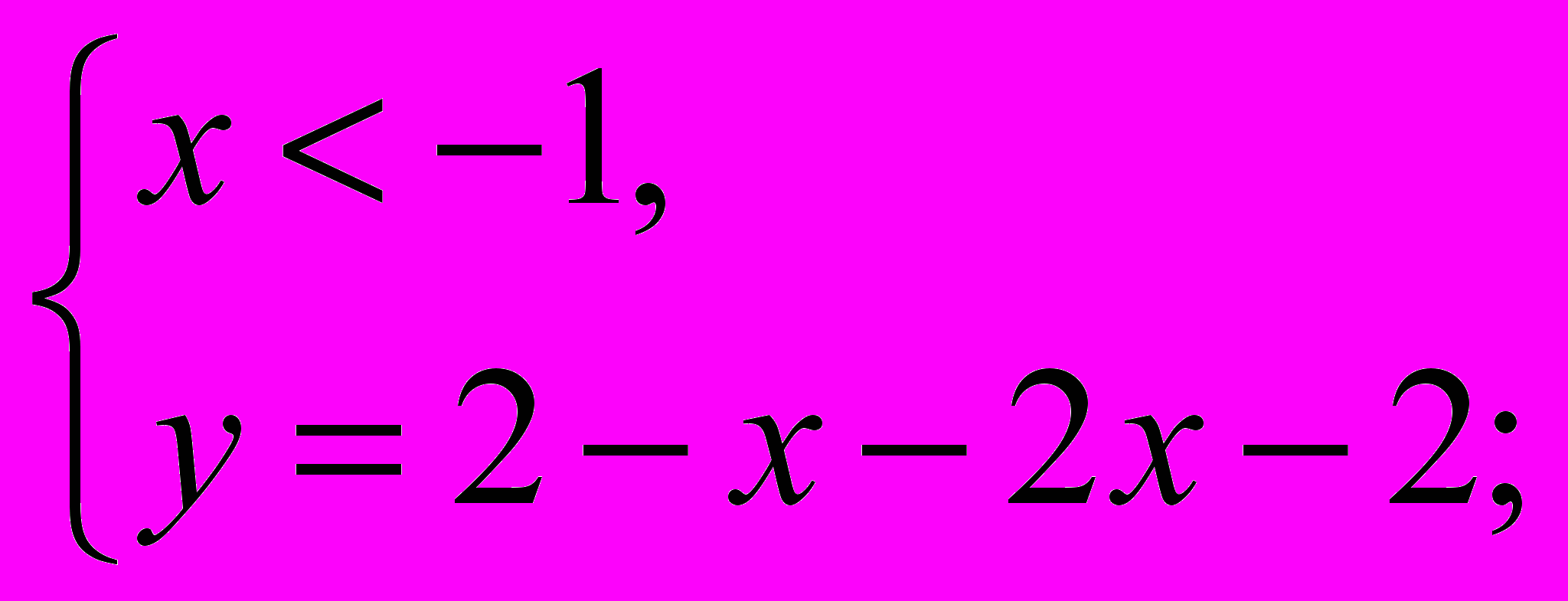 =>
=> 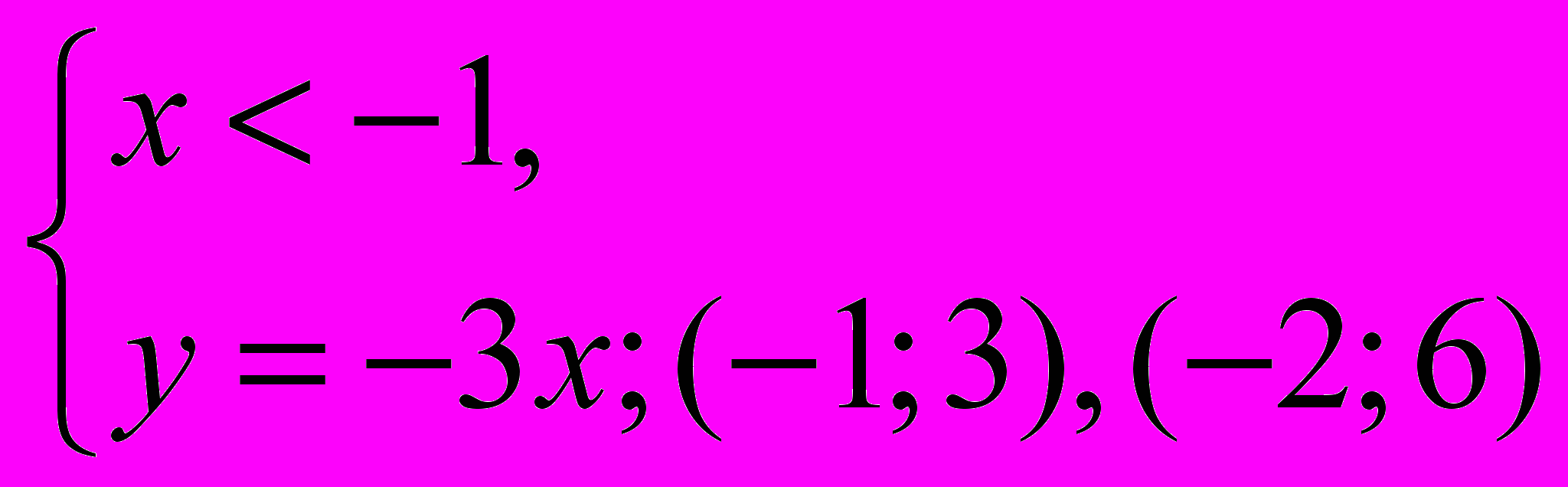
2).
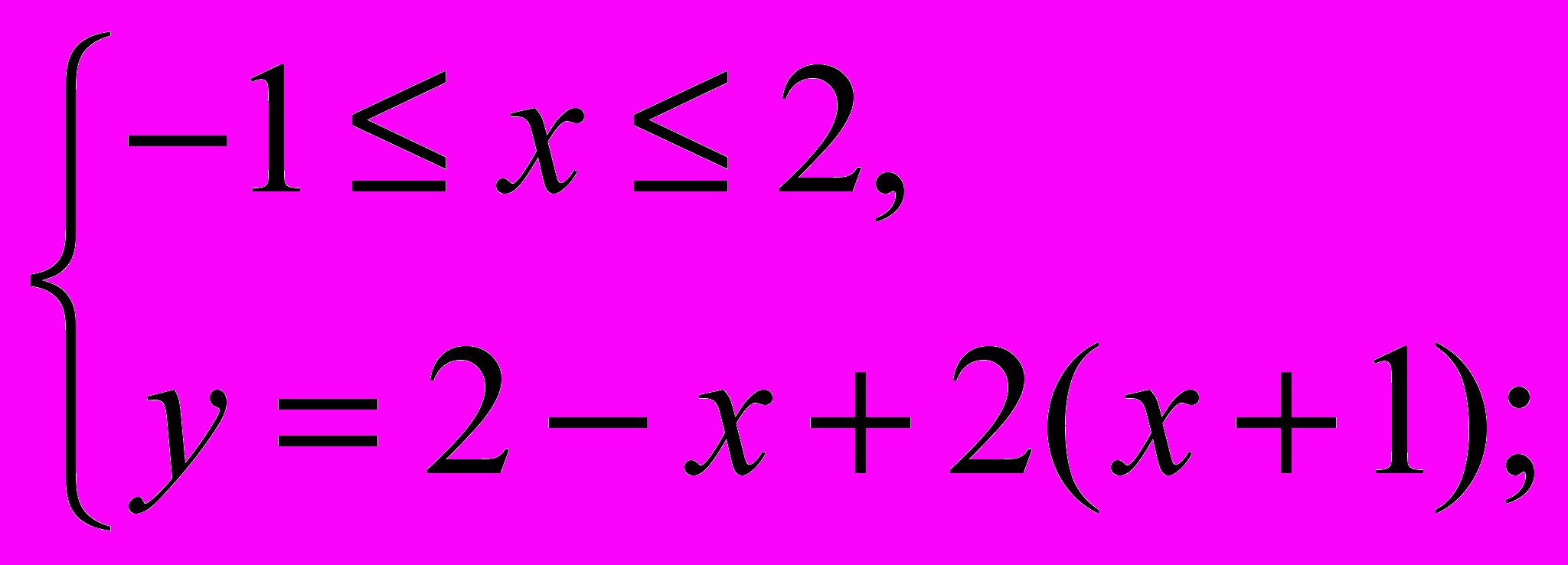 =>
=> 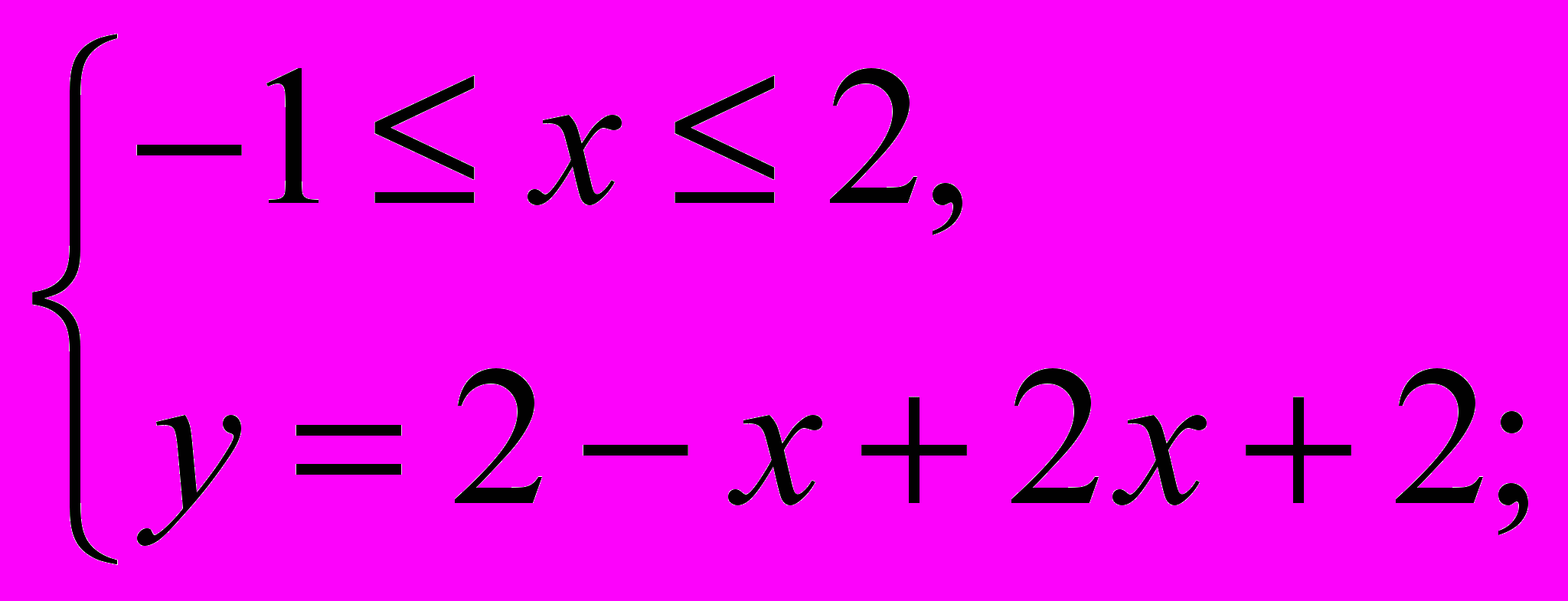 =>
=> 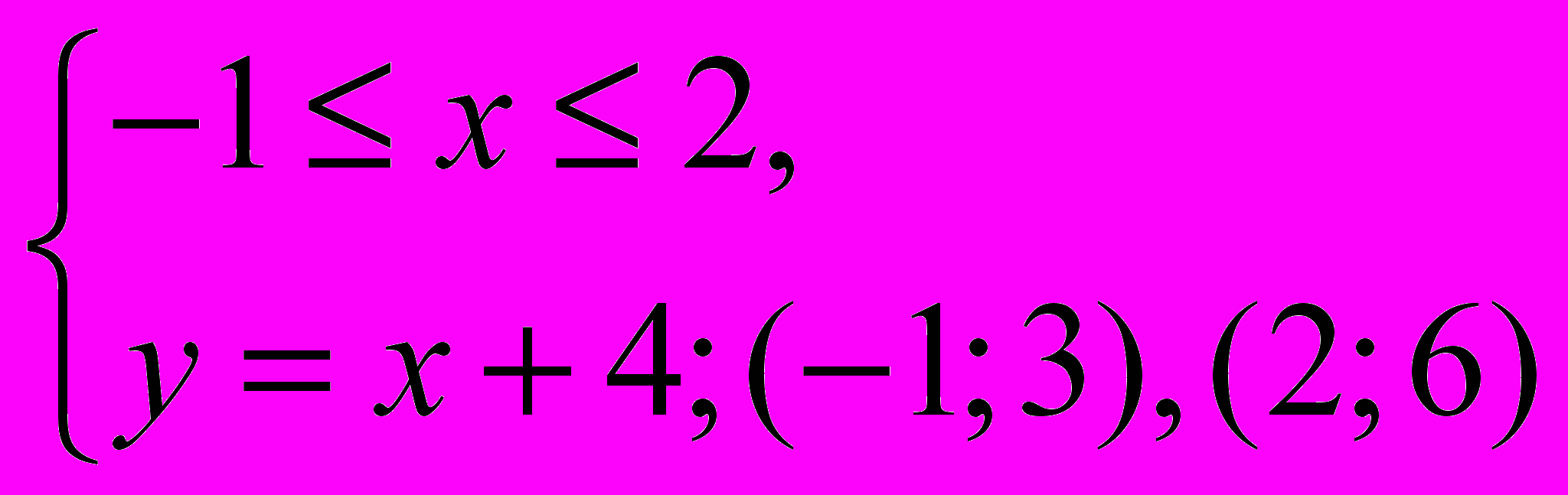
3).
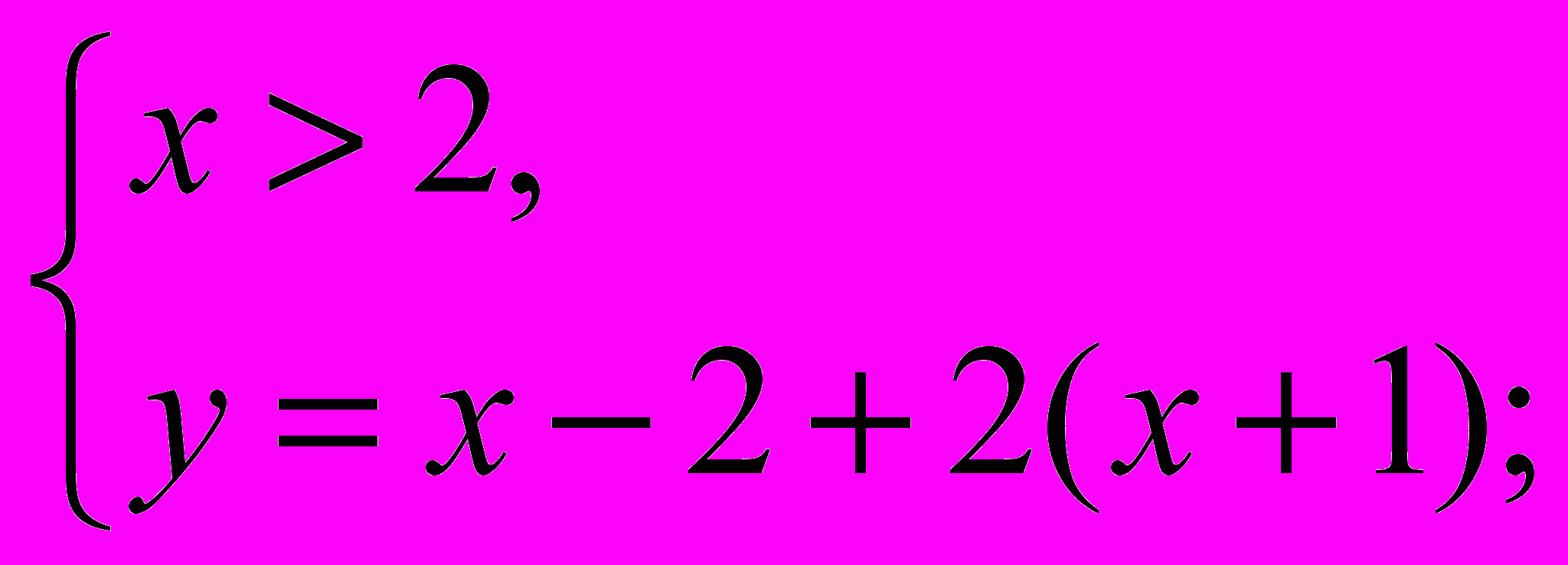 =>
=> 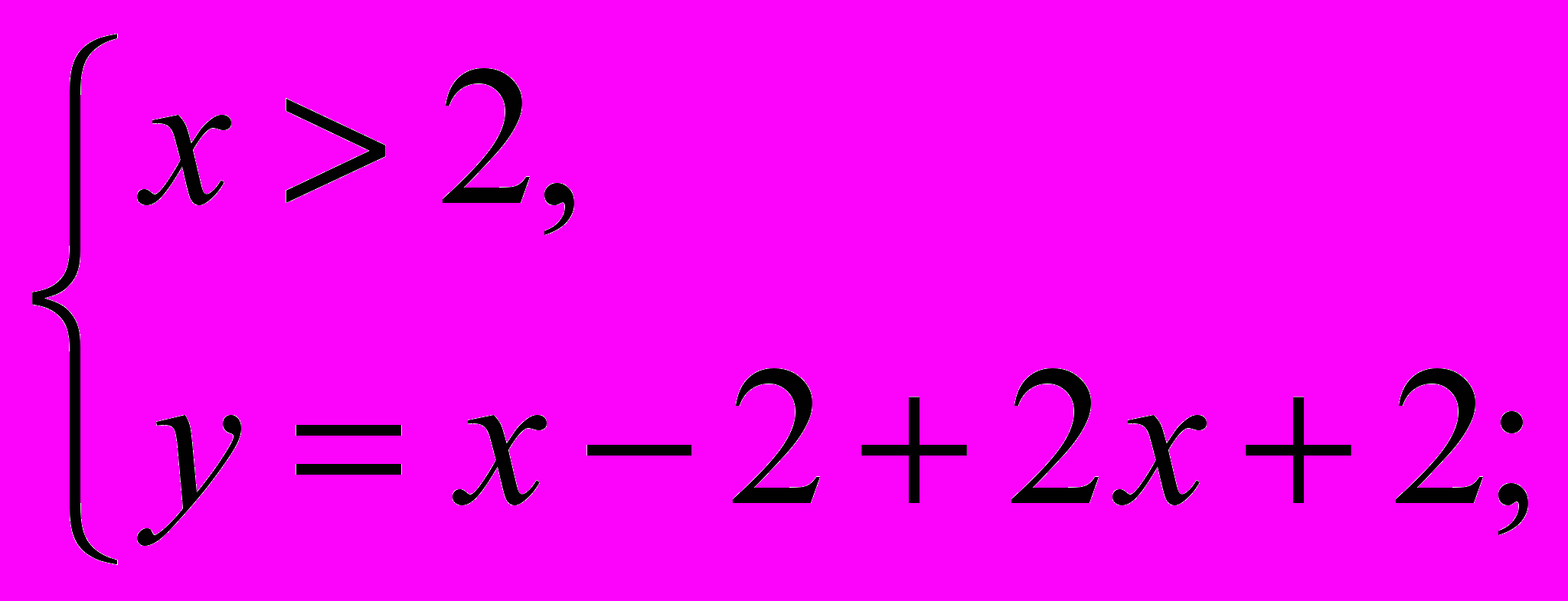 =>
=> 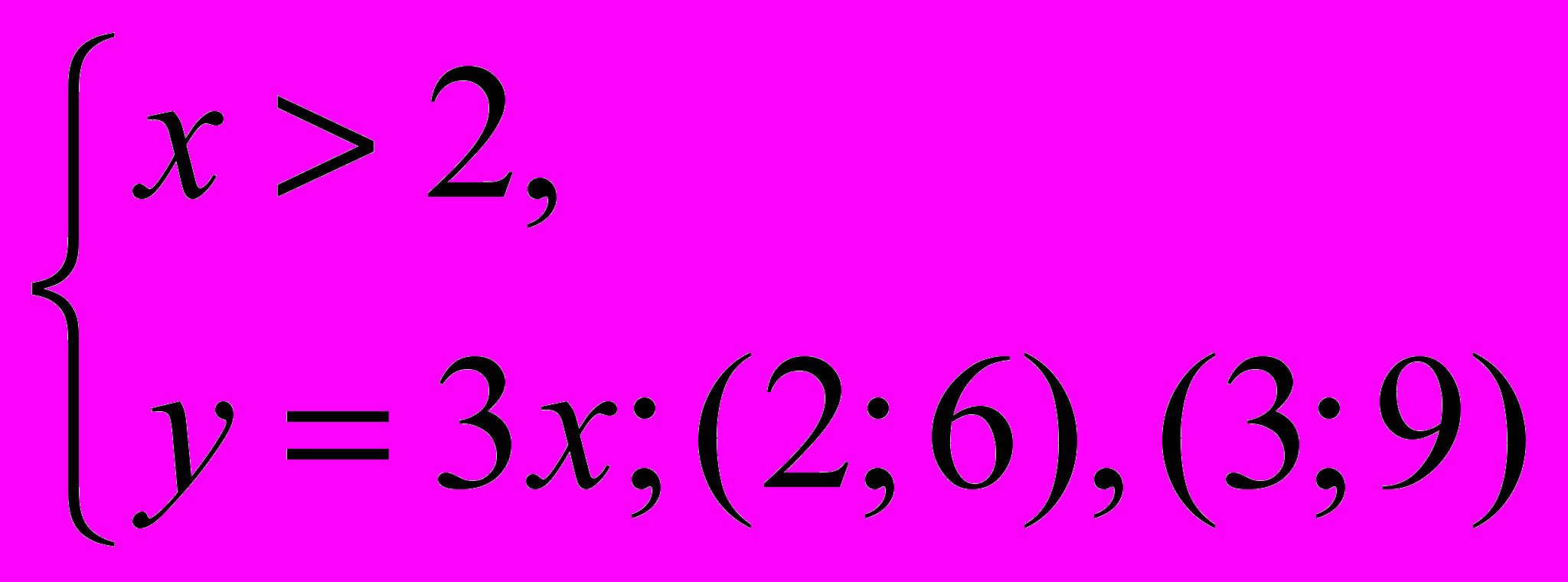
х
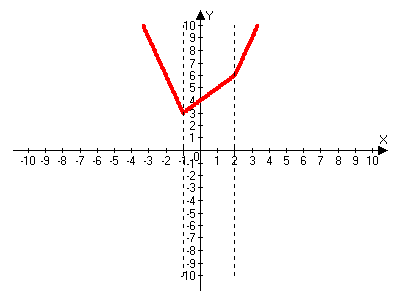 = 2, х = - 1 – разделяющие прямые. График состоит из лучей и отрезков, расположенных в соответствующей полосе. Подбор опорных точек таков, что они попадают на разделяющие прямые, поэтому для построения частей графика достаточно соединить это точки.
= 2, х = - 1 – разделяющие прямые. График состоит из лучей и отрезков, расположенных в соответствующей полосе. Подбор опорных точек таков, что они попадают на разделяющие прямые, поэтому для построения частей графика достаточно соединить это точки.График 5.
После объяснения материала необходимо поработать с графиками и в классе, и дома.
Задания для классной работы:
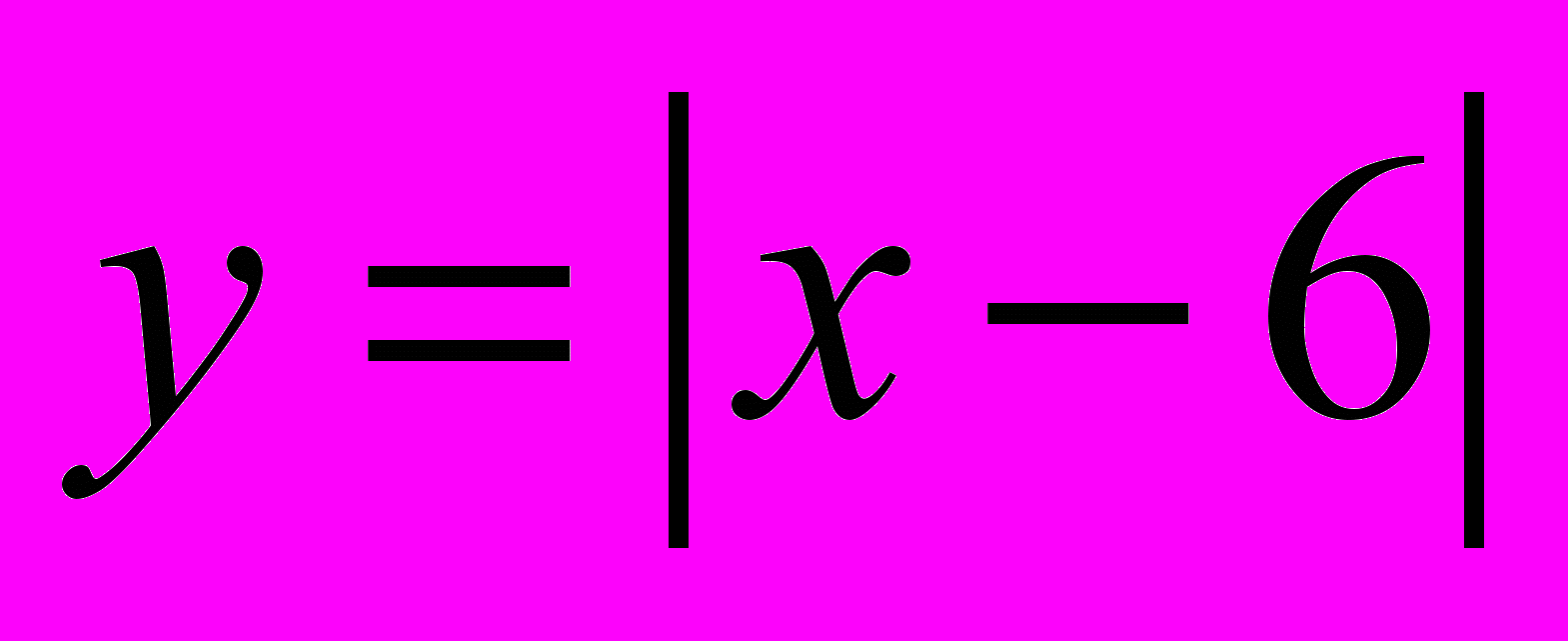
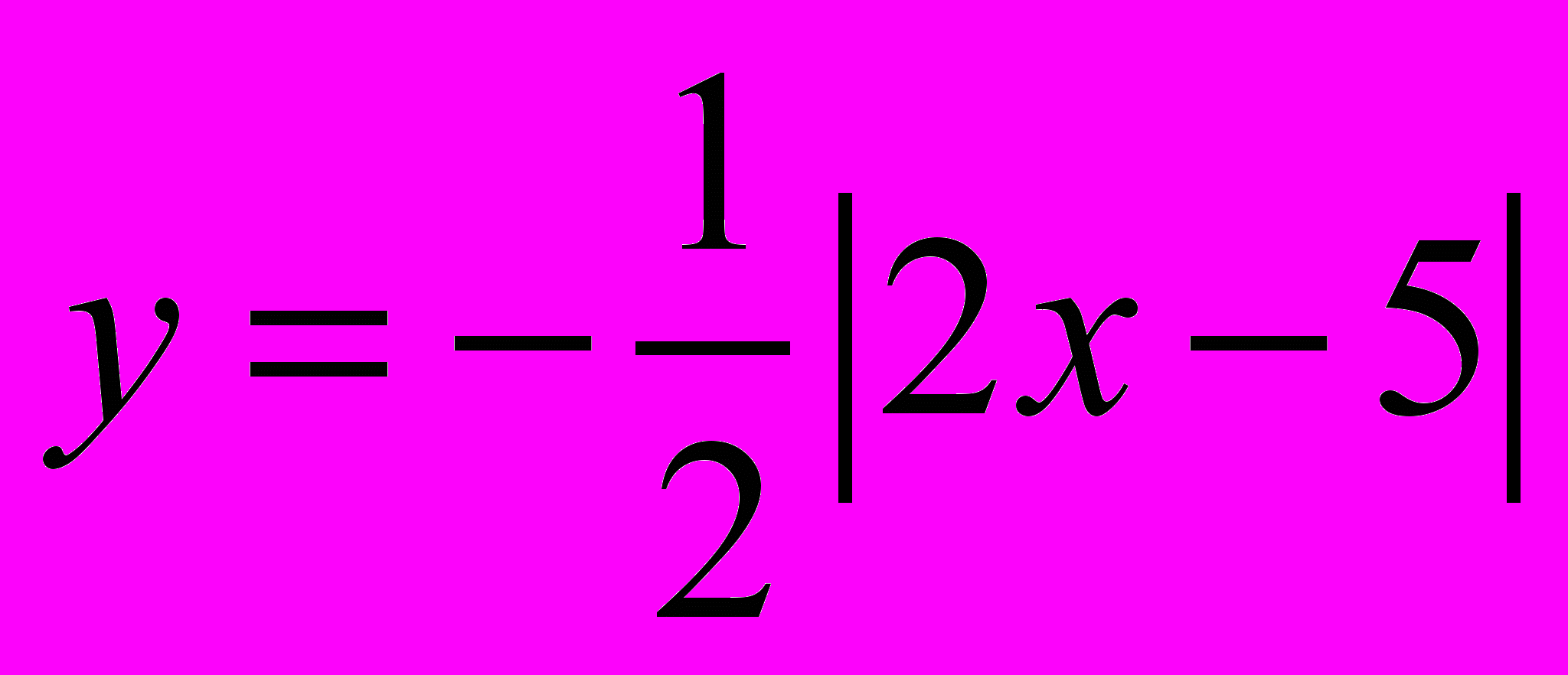
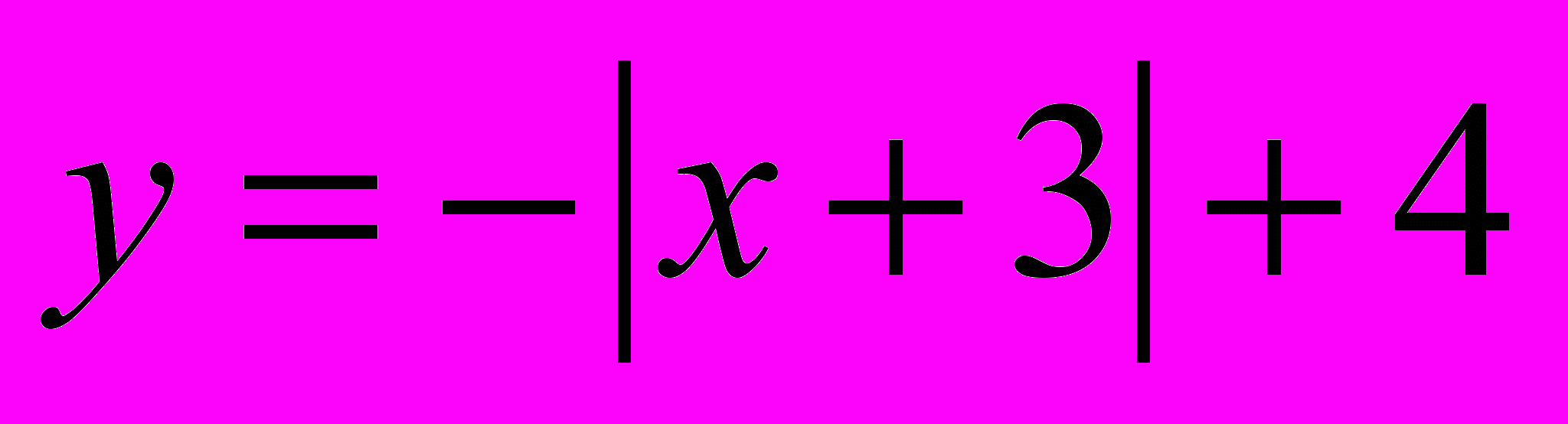
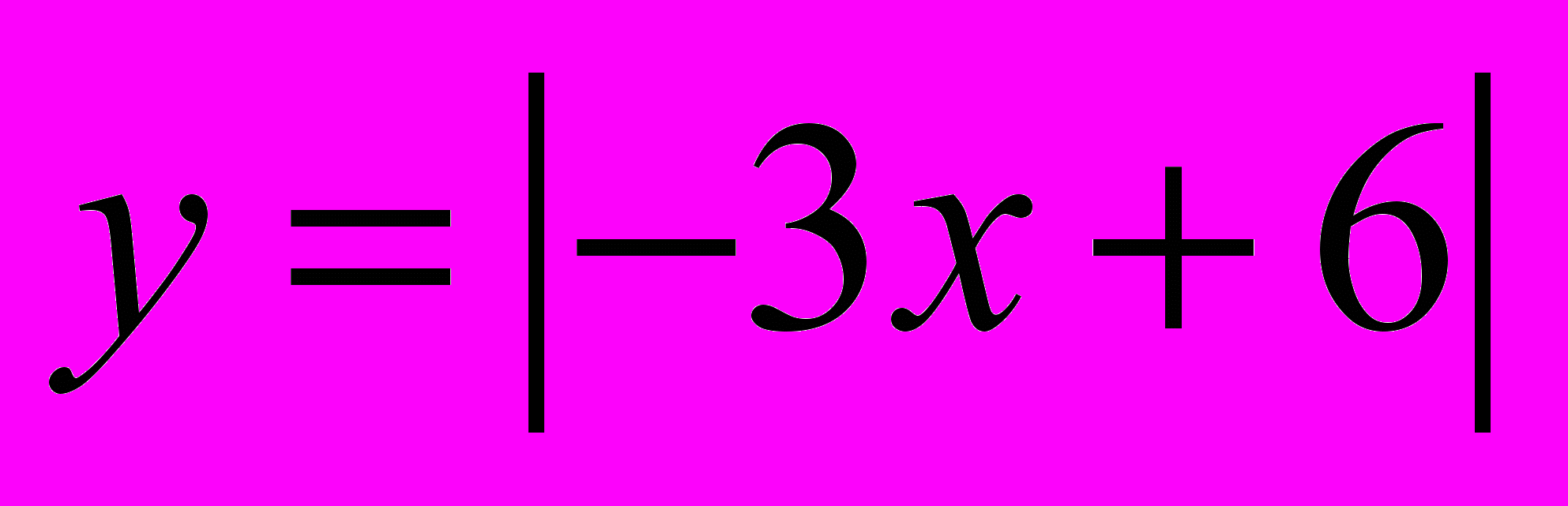
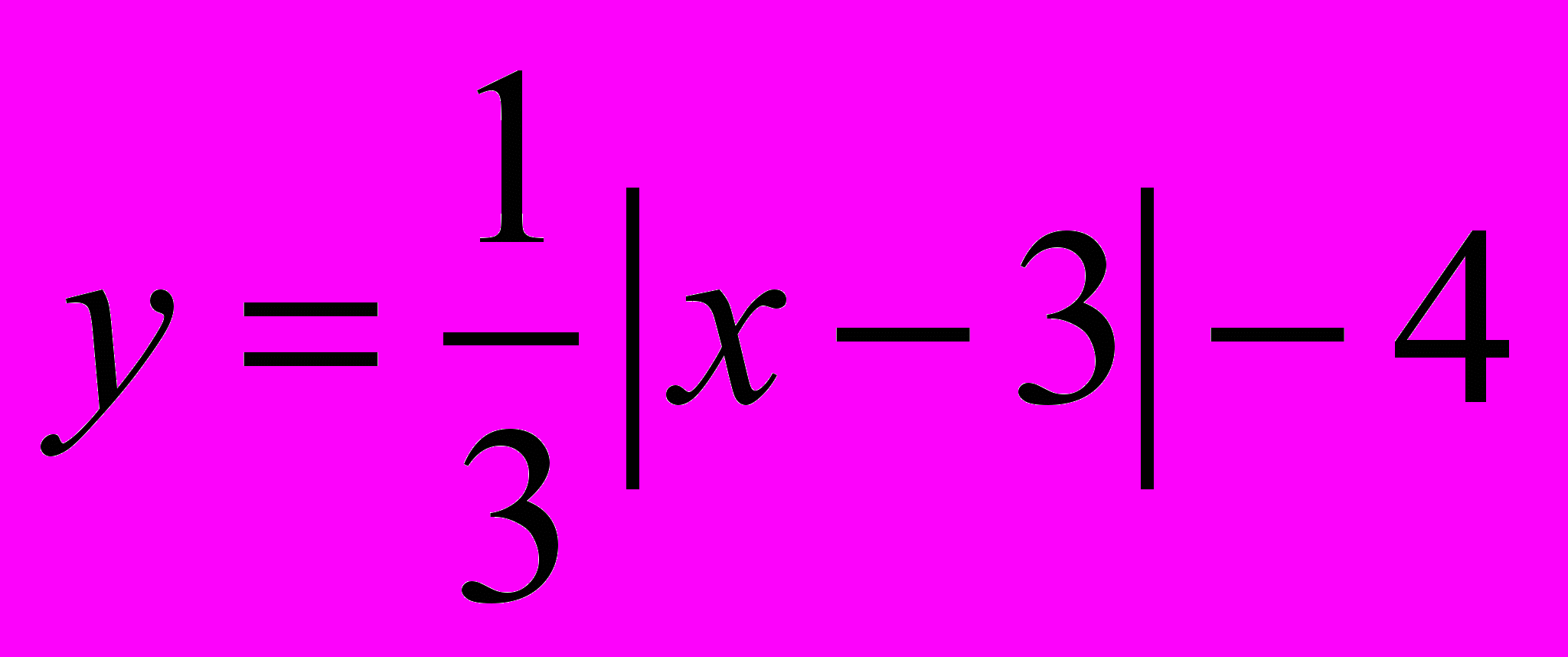
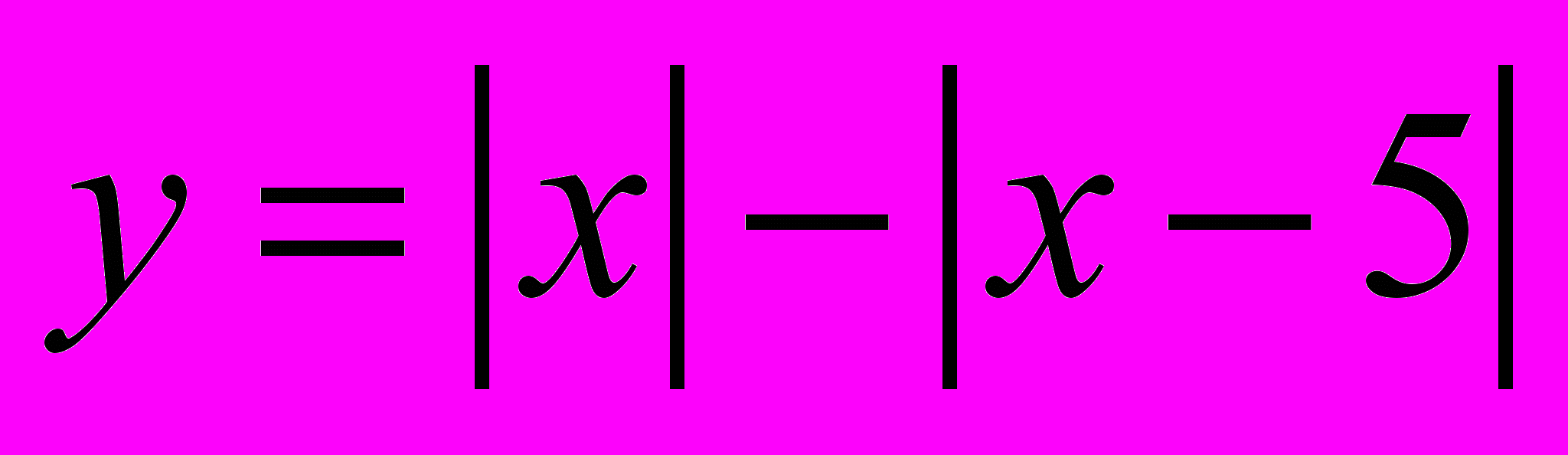
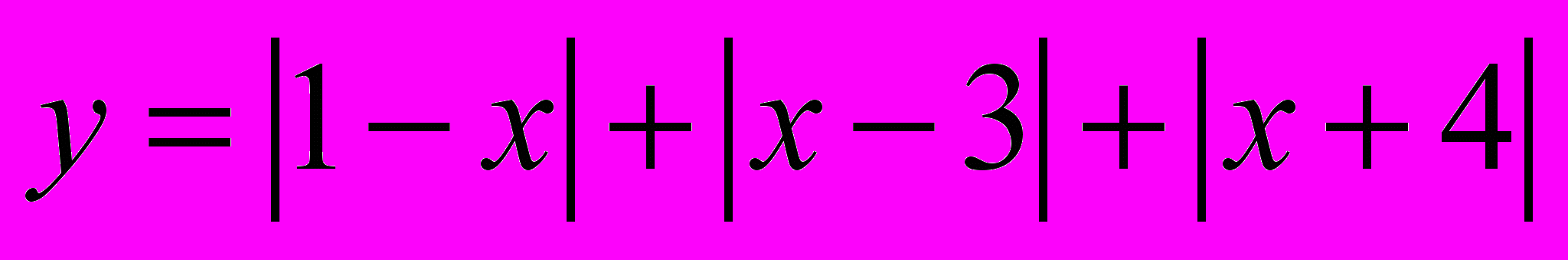
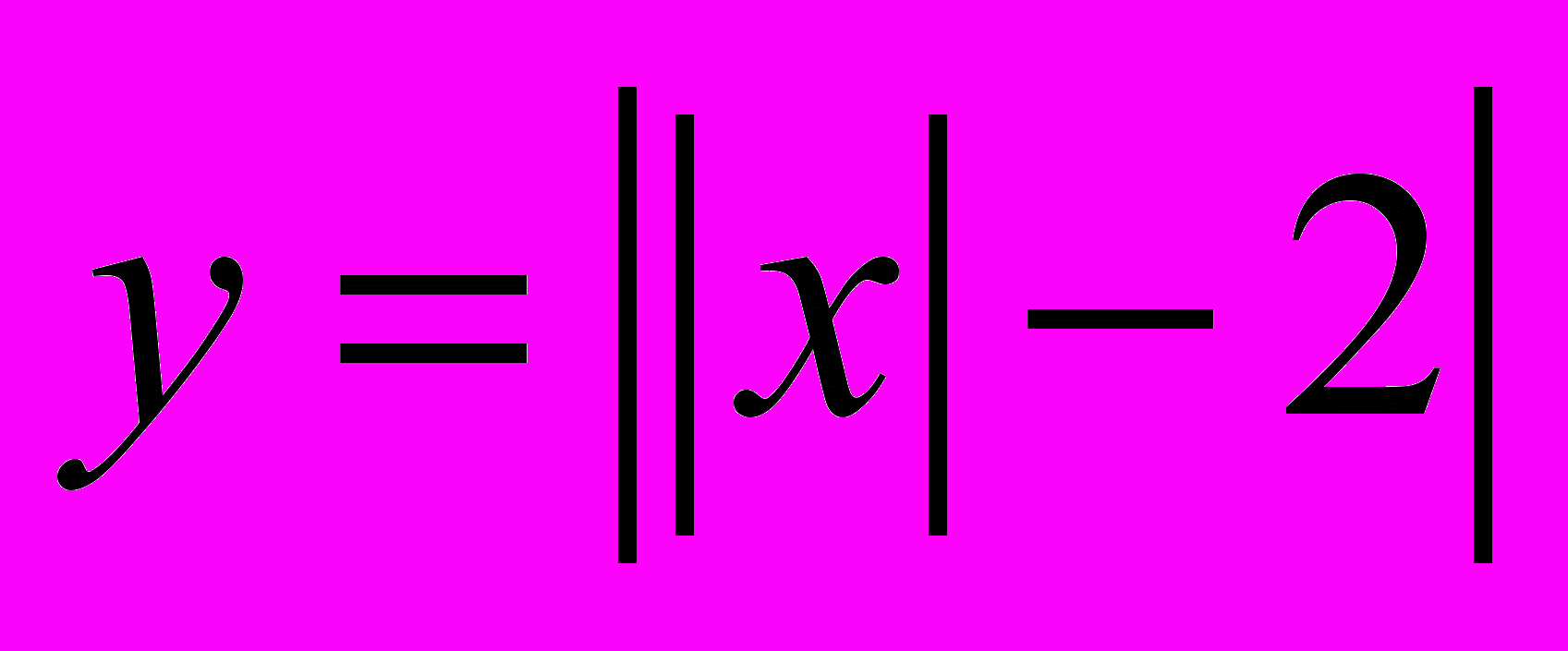
Задания для домашней работы:
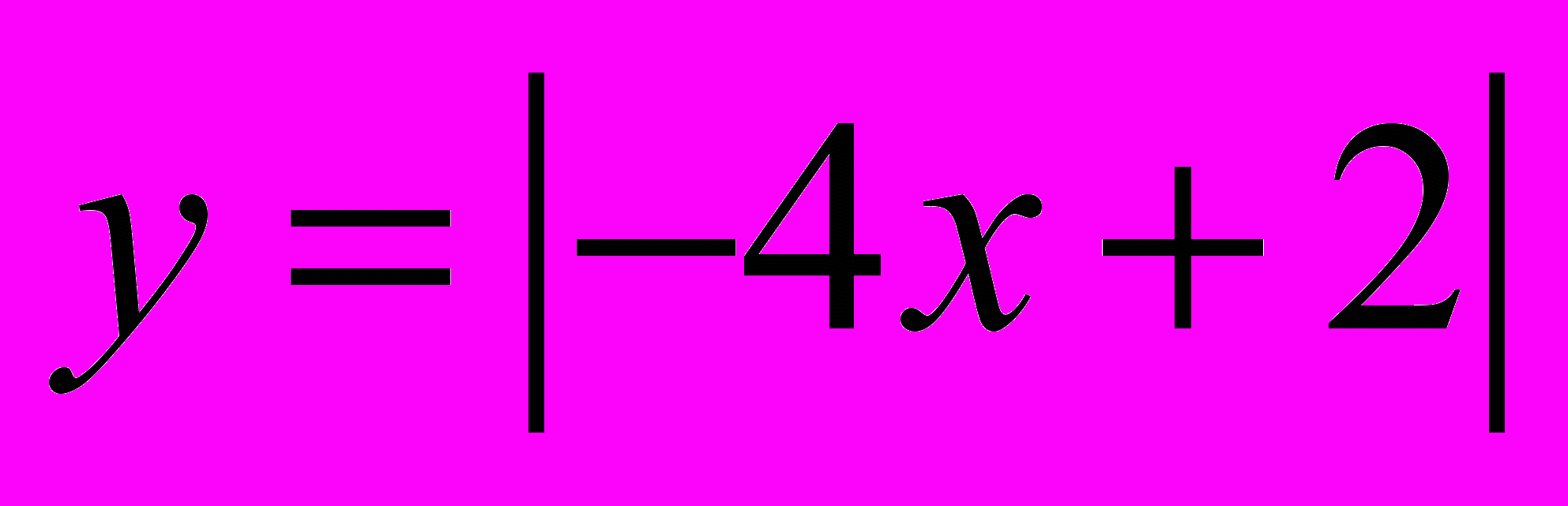
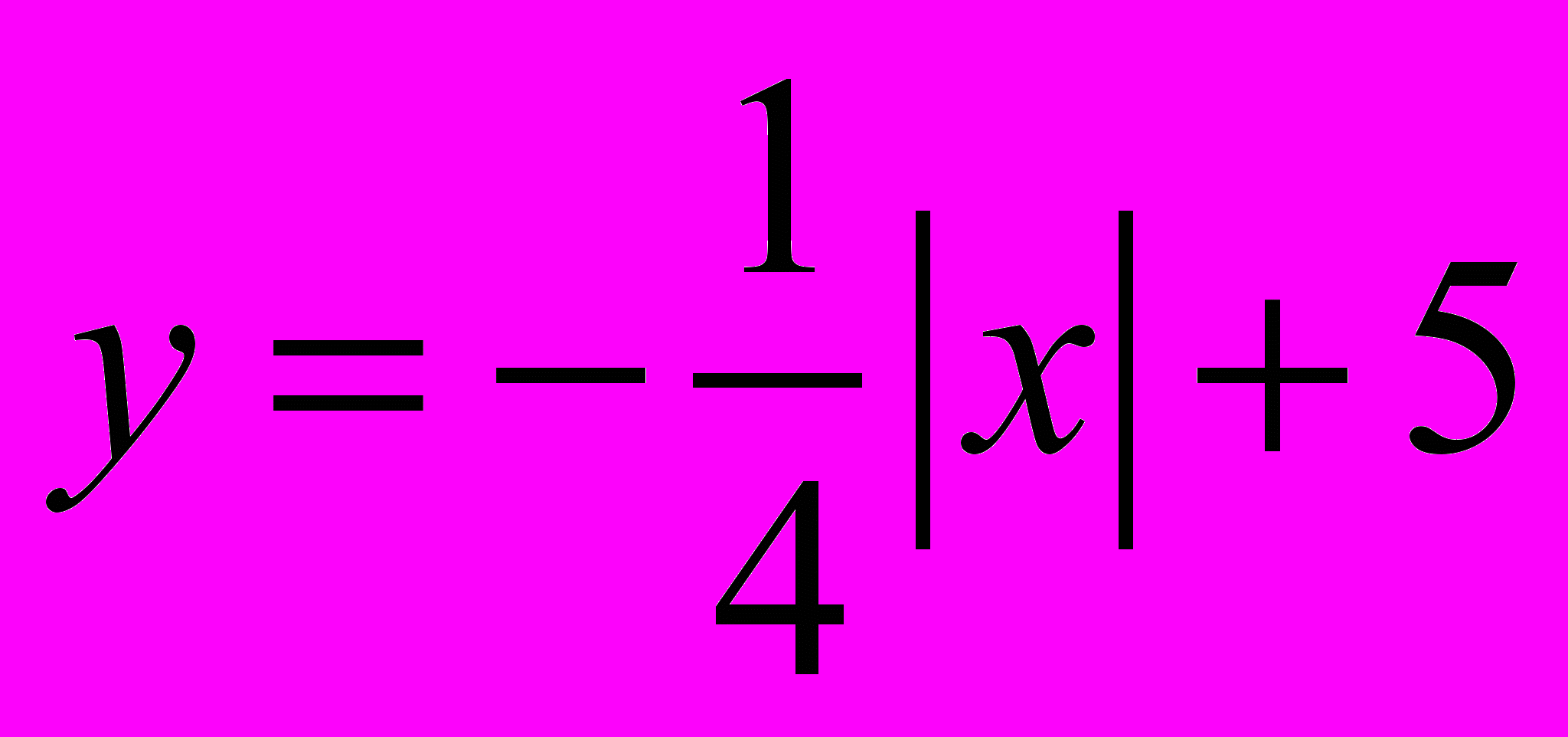
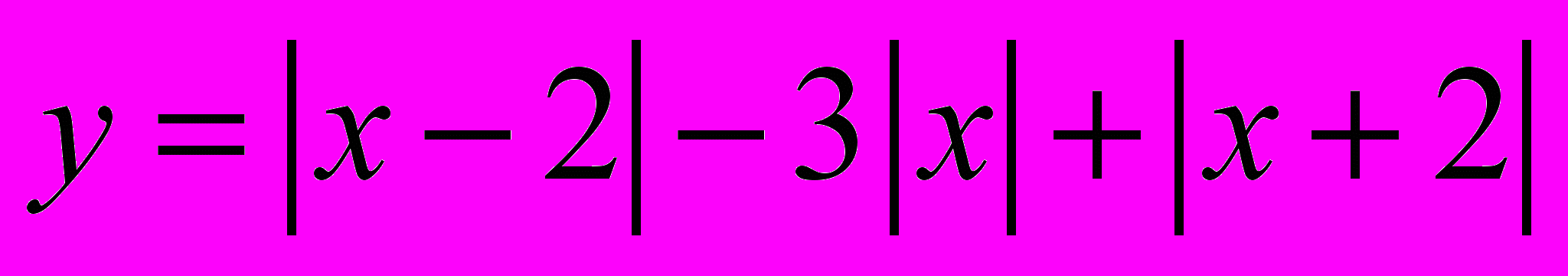
Задания для самостоятельной работы:
| 1 вариант: 1. 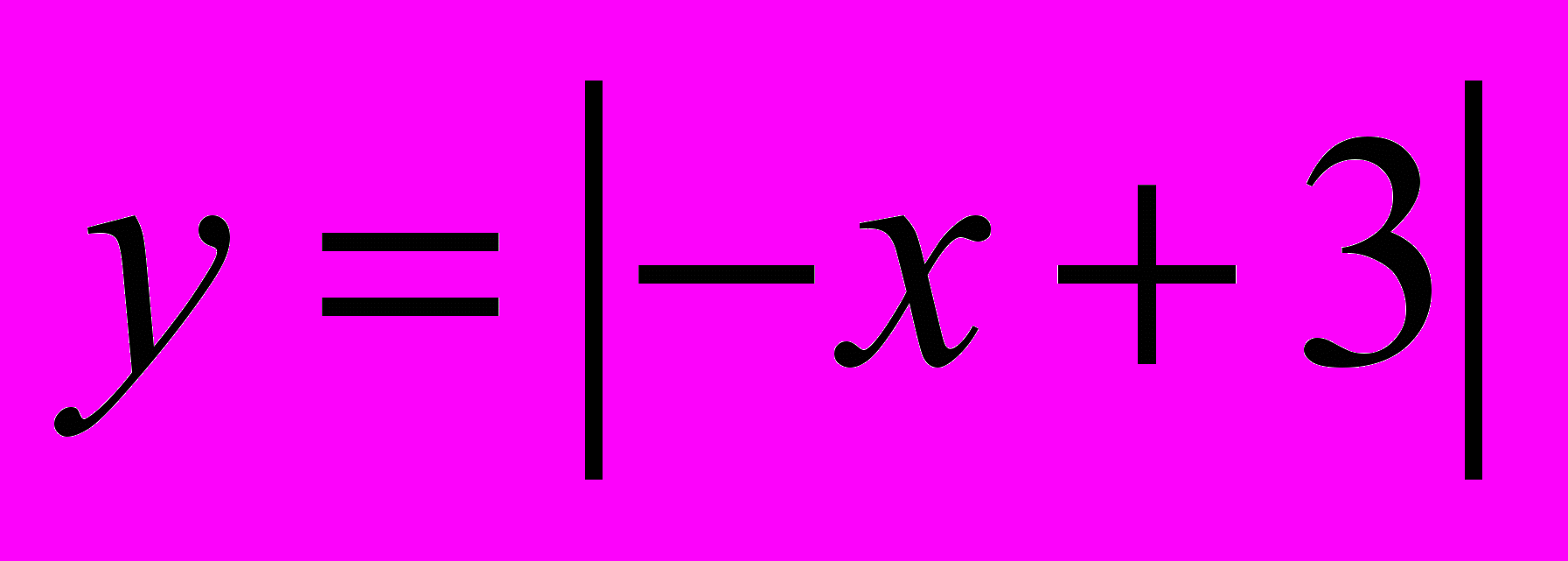 2. 2. 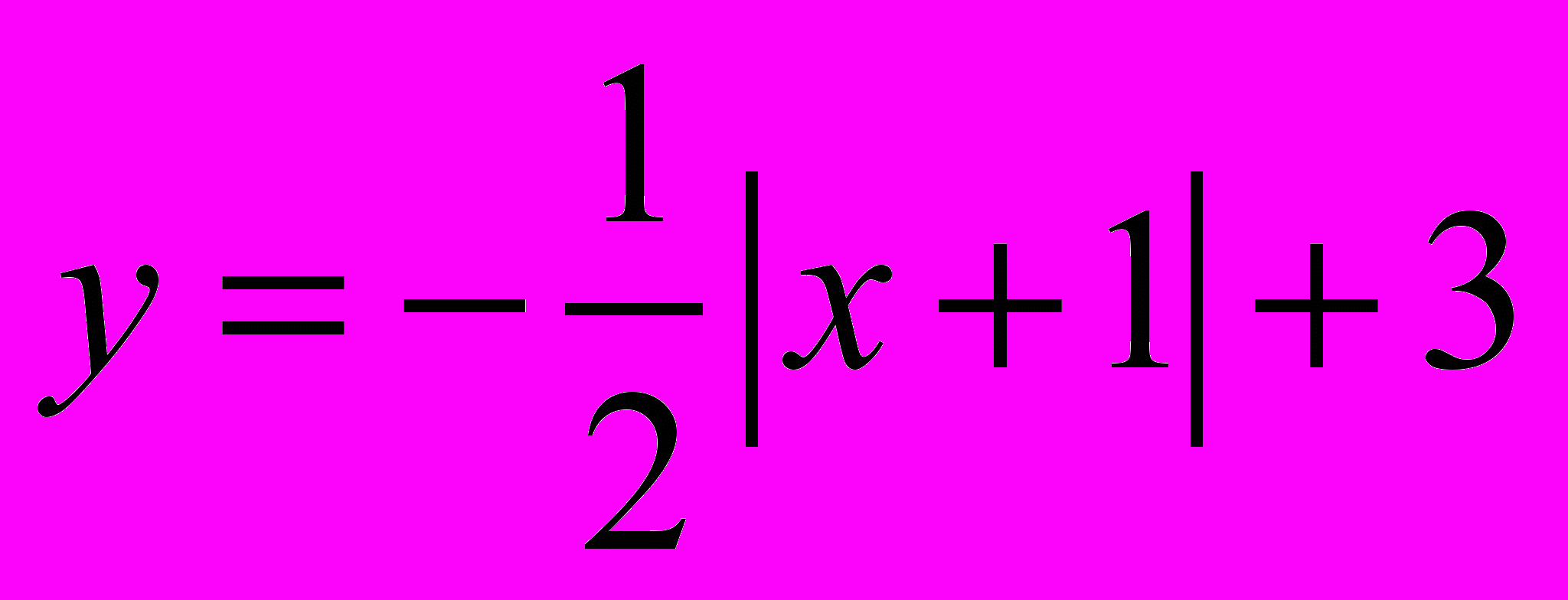 | 2 вариант: 1. 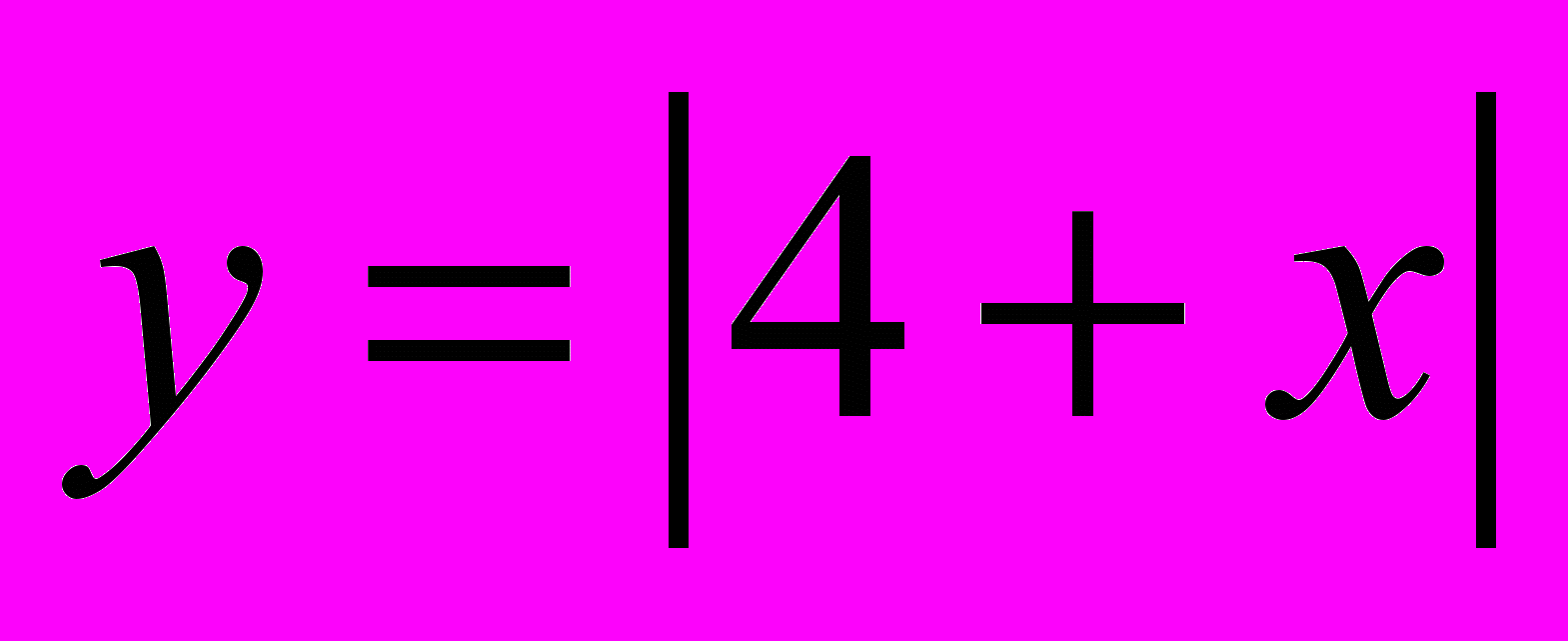 2. 2. 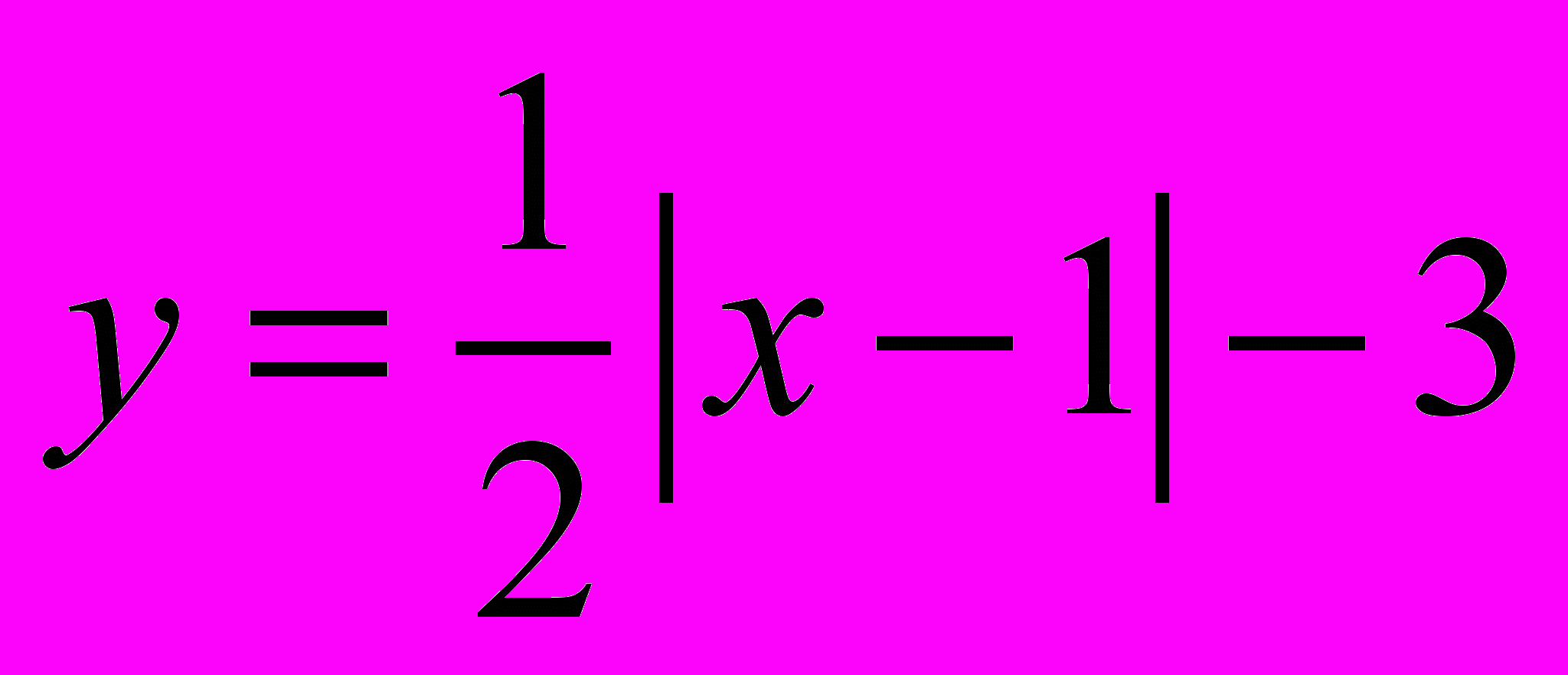 |
Несомненно, данный материал очень трудный для восприятия семиклассников, все задания классной работы надо выполнять под руководством учителя, обязательно проверить со всем классом задания домашней работы и за самостоятельную работу выставить только положительные отметки.
После усвоения этого метода построения графиков вполне логично было познакомить учащихся с преобразованиями графиков функций
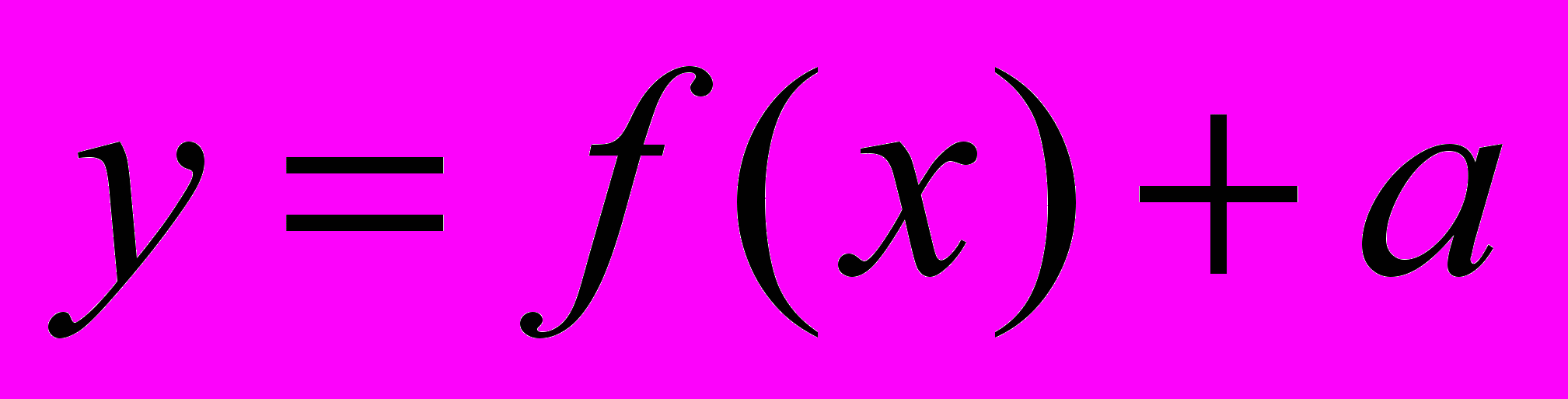 и
и 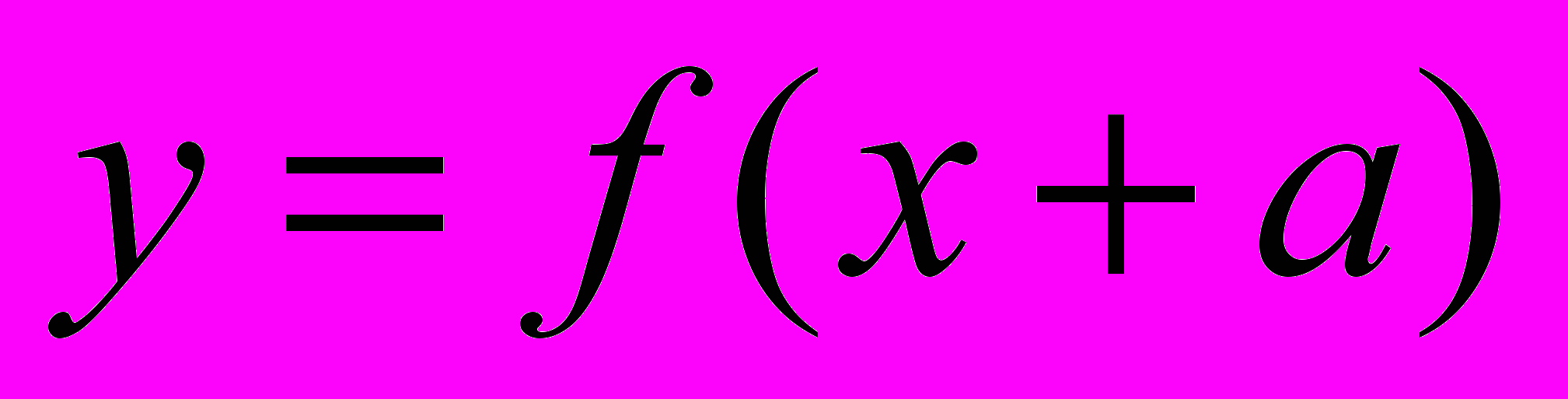 , и показать на примере функции с модулем, как осуществляется движение графика в системе координат. Этот материал учащиеся осваивают легко и быстро, при этом, не забываем о предыдущем методе, т.к. преобразования можно использовать не всегда.
, и показать на примере функции с модулем, как осуществляется движение графика в системе координат. Этот материал учащиеся осваивают легко и быстро, при этом, не забываем о предыдущем методе, т.к. преобразования можно использовать не всегда.Такое прочтение данной темы позволило показать практическое применение знаний учащихся о линейной функции и подготовило к восприятию, в дальнейшем, методов решения уравнений и неравенств с модулем, а также, построения любых графиков с помощью преобразований и по определению модуля.
