Решение выполняется с помощью пакета Mathcad

Вид материала

Решение

Содержание Задание 5. Постройте прямую регрессии Y на X. Решение (6) с помощью пакета MathCAD

Подобный материал:

• «математические пакеты mathcad и mathematica в решении прикладных химических задач», 360.54kb.
• Тематический план введение, 469.57kb.
• «Алгоритмизация и решение физических задач на эвм», 391.8kb.
• Решение задач одно из важных применений Excel. Системы линейных уравнений решаются, 39.61kb.
• Использование Mathcad и Excel при изучении школьного курса физики, 67.71kb.
• MathCad Mathcad, 7.16kb.
• Домашняя работа, 28.4kb.
• С помощью сред Mathcad и Labview, а так же сравнительный анализ двух рассматриваемых, 89.08kb.
• Контрольная работа (типовой расчет) №2 "расчет сложной цепи периодического синусоидального, 29.02kb.
• Учебно-тематический план курса повышения квалификации профессорско-преподавательского, 73.73kb.

ЛЕКЦИЯ 11


Построение прямой регрессии (задача 1 задания № 3 из задачника Л.Н. Пронина)


Совместное дискретное распределение случайных величин задано таблицей

	-3	-1	1	3
-1	0.15	0.04	-	-
1	0.05	0.14	0.07	-
3	-	0.06	0.17	0.06
5	-	0.03	0.03	0.2

Решение выполняется с помощью пакета MathCAD


Ввод данных




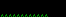
индексация массивов начинается с 1



индекс значения случайной величины





ввод значений случайных величин



матрица вероятностей

Задание 1. Найдите частные законы распределения случайных величин .


Частное распределение случайной величины 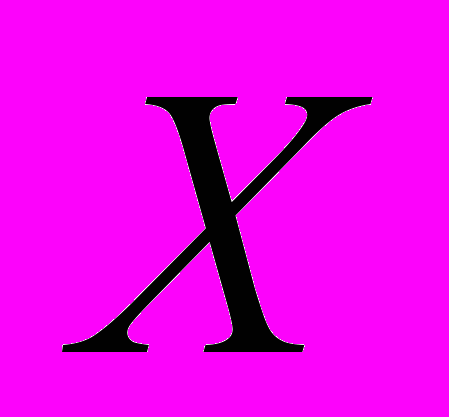найдём по формуле 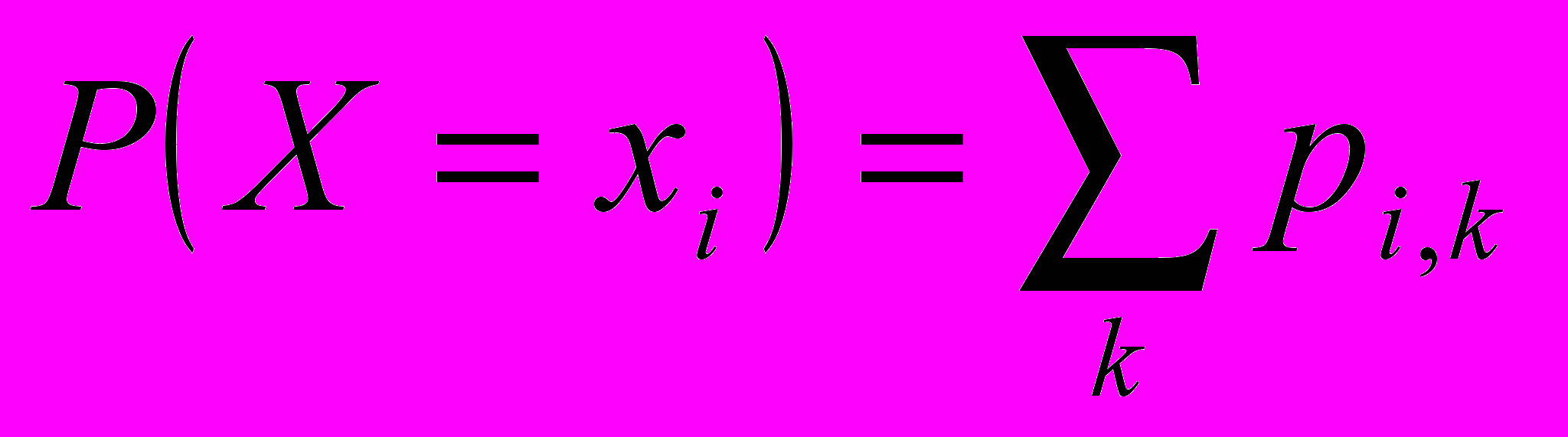, то есть найдём сумму вероятностей

.


Вероятность 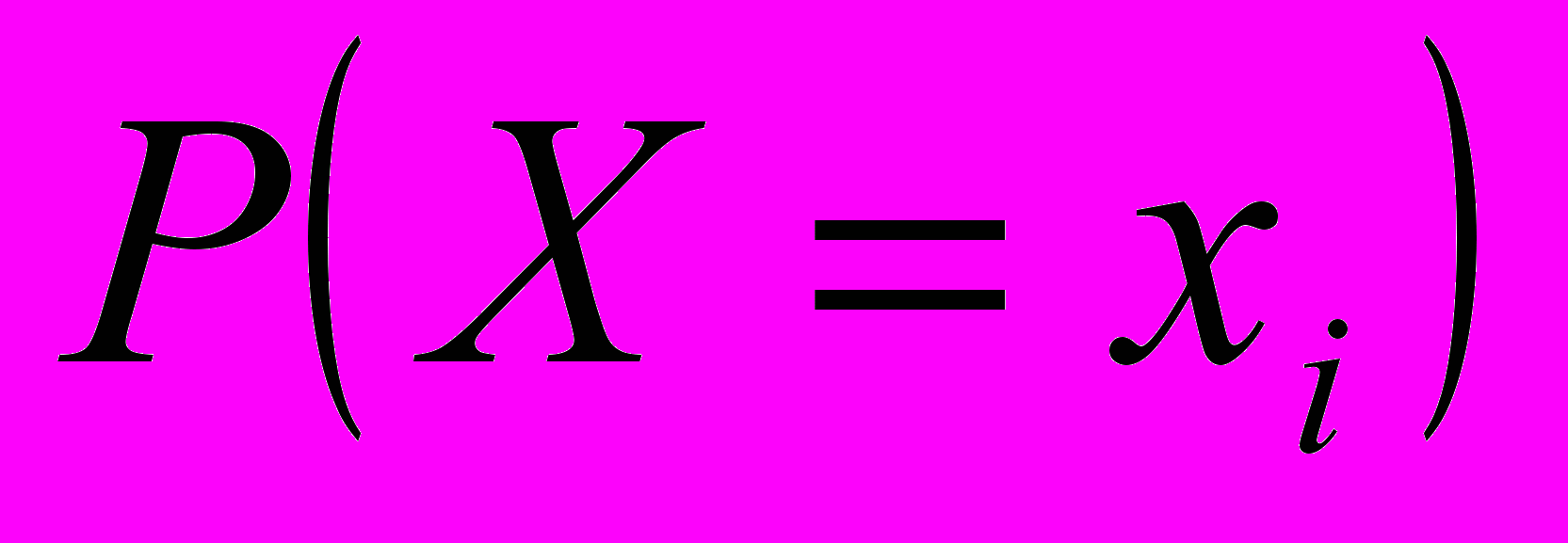обозначим .


Аналогично найдём частное распределение случайной величины 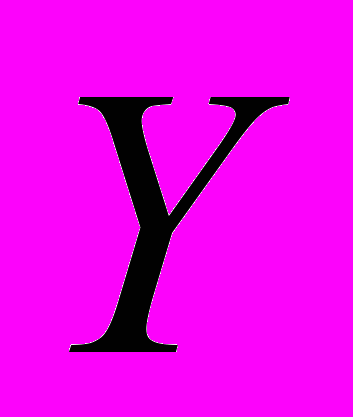. Вероятность 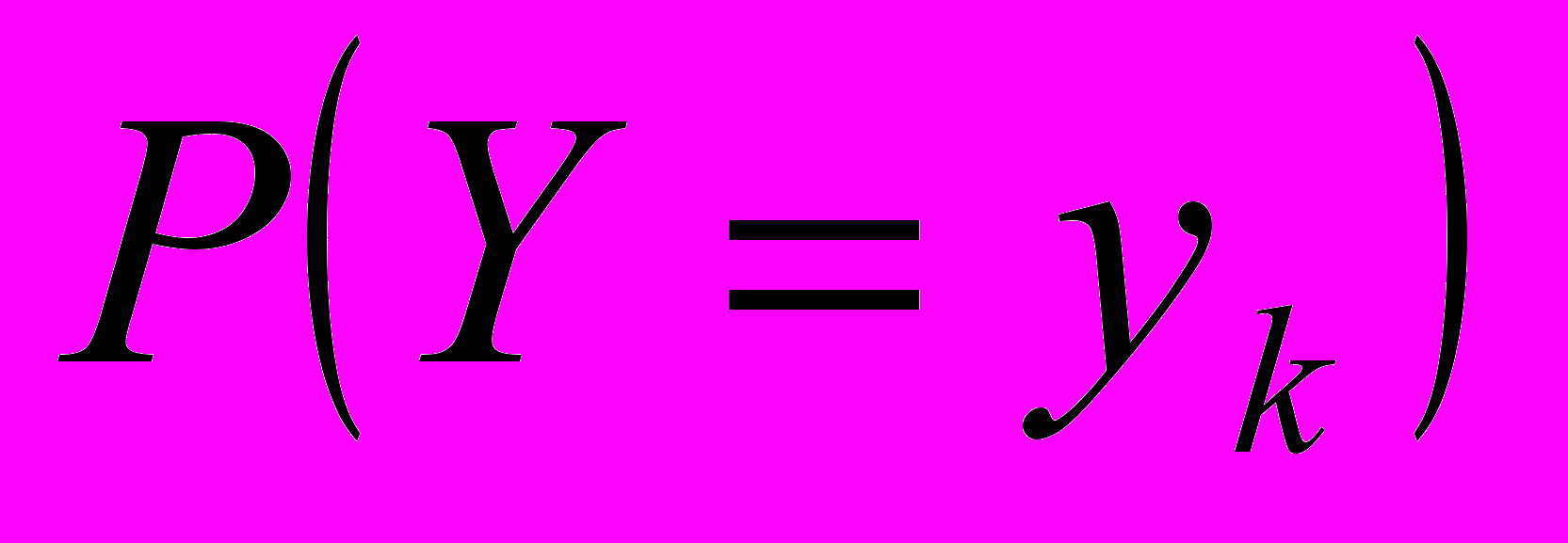обозначим .


Нахождение частных распределений с помощью пакета MathCAD. Обозначим 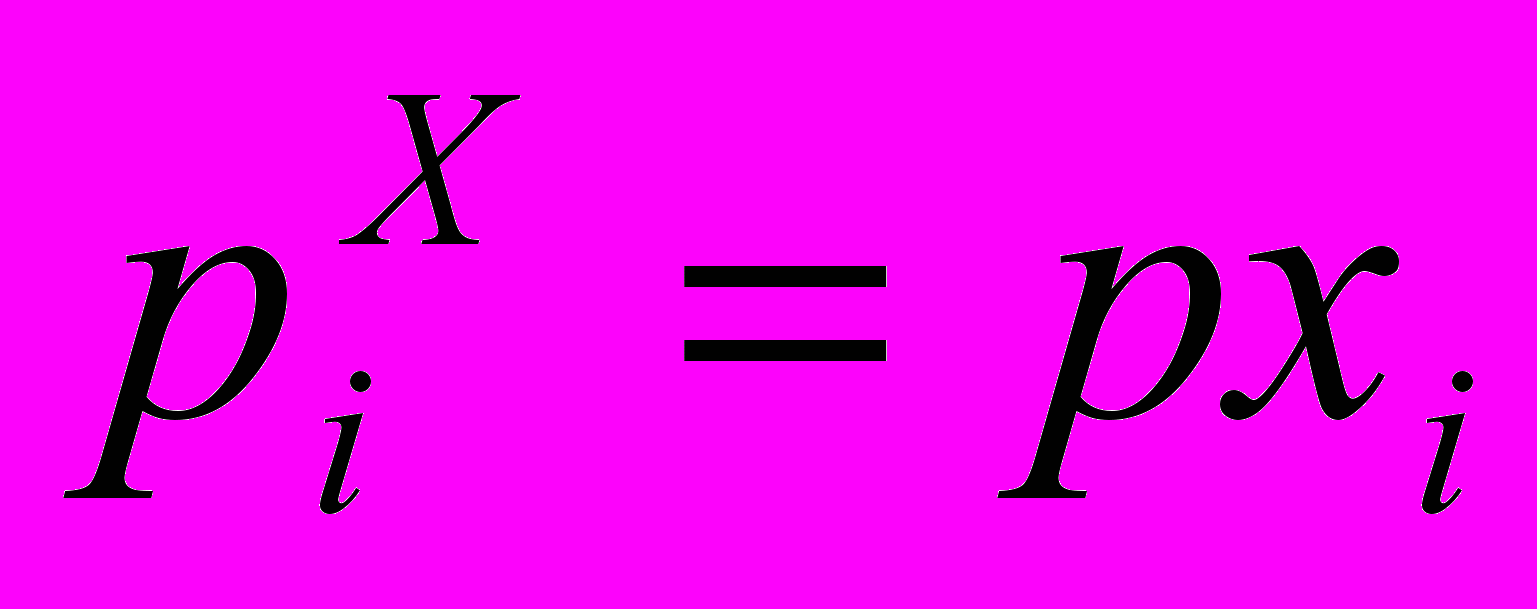и .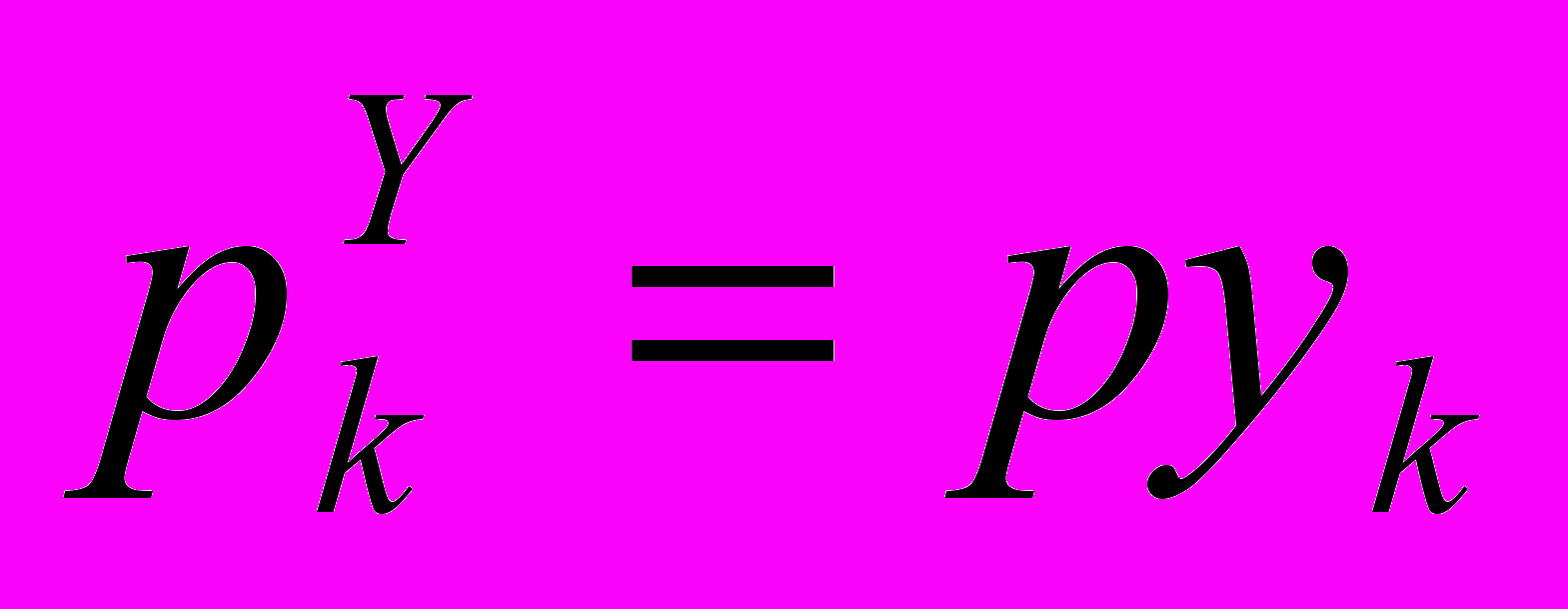



индекс значений случайной величины Y









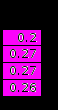
частные распределения

_{Запишем частные распределения в виде таблиц}

X	-1	1	3	5
P	0.19	0.26	0.29	0.26

Y	-3	-1	1	3
P	0.2	0.27	0.27	0.26

Задание 2. Найдите математические ожидания, дисперсии и средние квадратические отклонения частных распределений случайных величин .


Найдём вначале первые два момента , 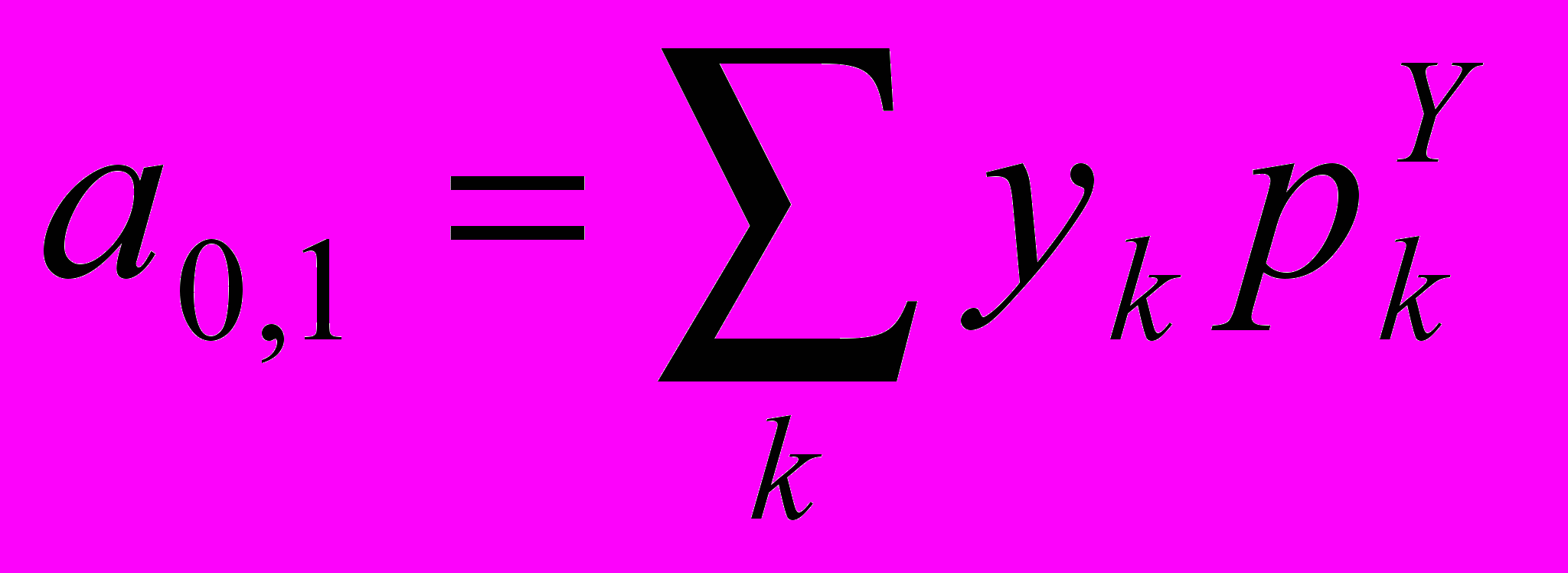и

вторые моменты , .


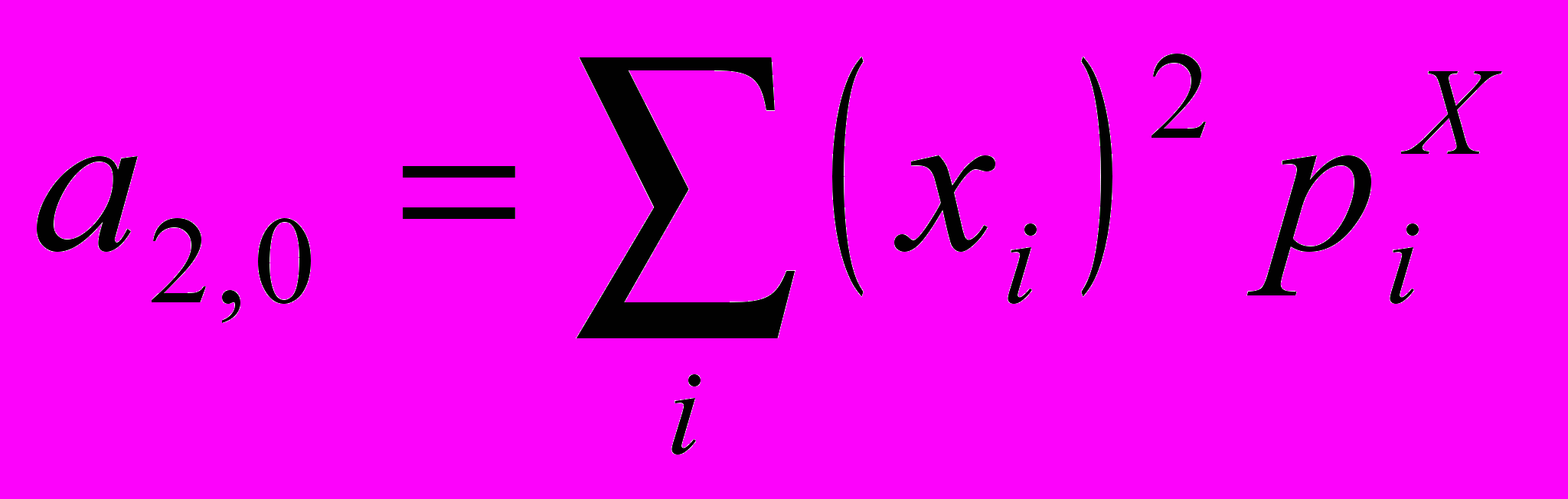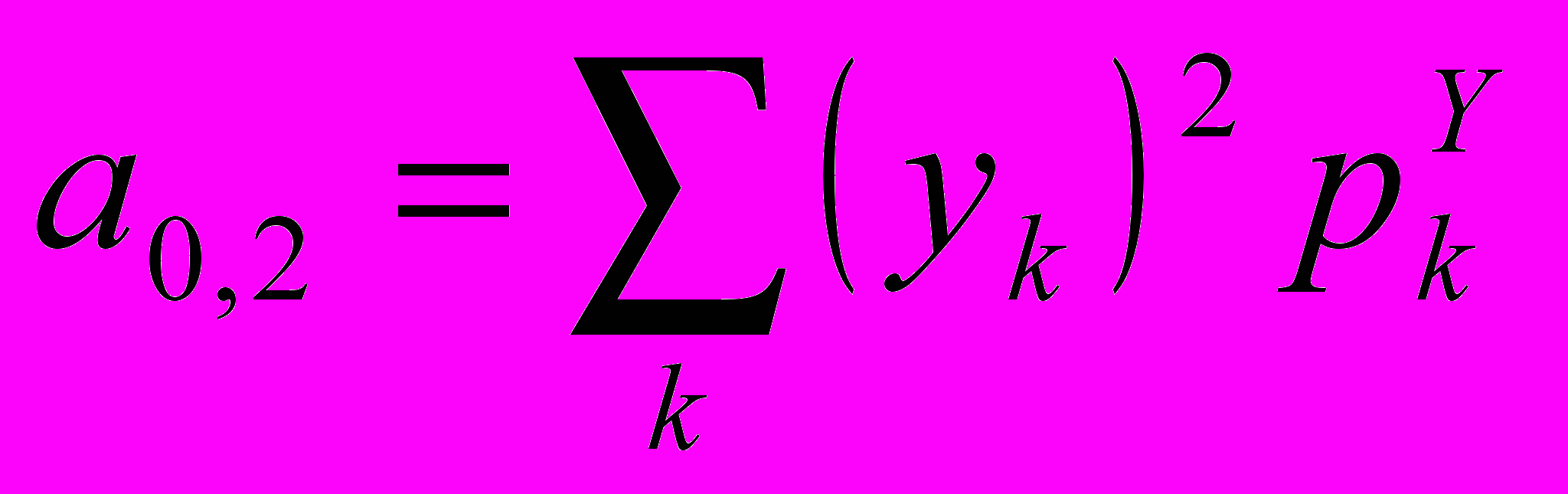Нахождение моментов с помощью пакета MathCAD. Обозначим , ,









первые моменты









вторые моменты

Далее вспомним, что 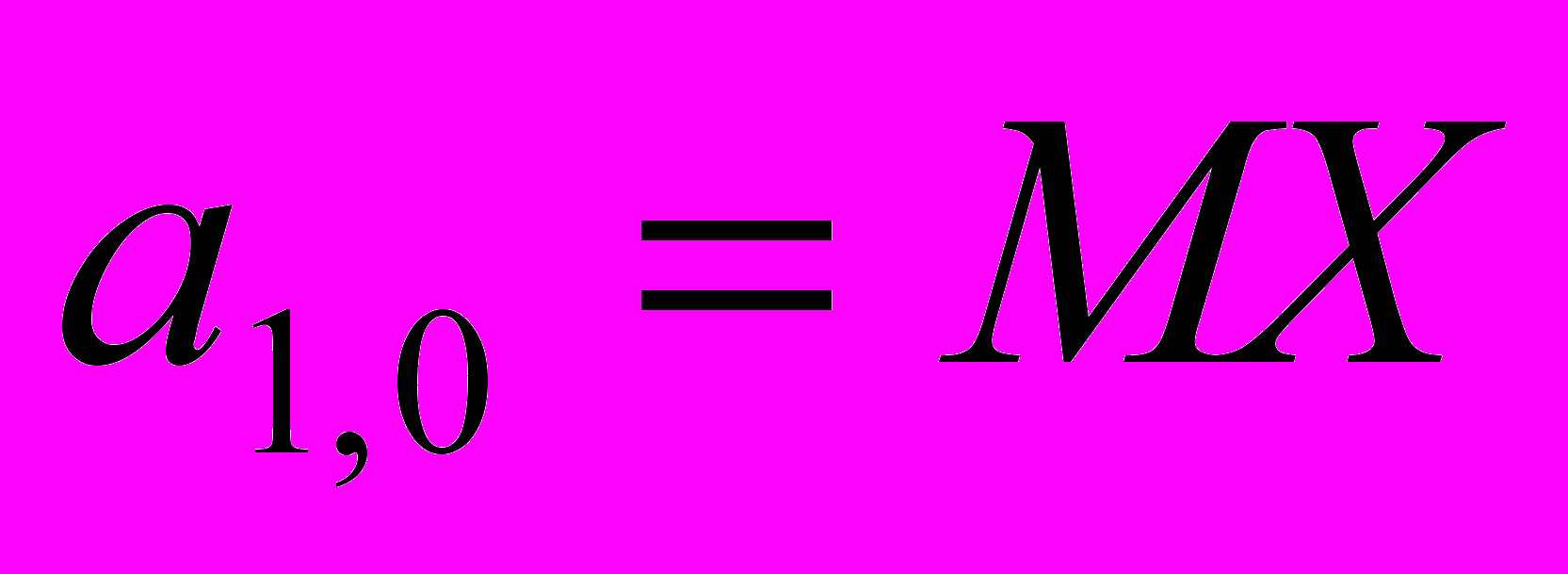, , 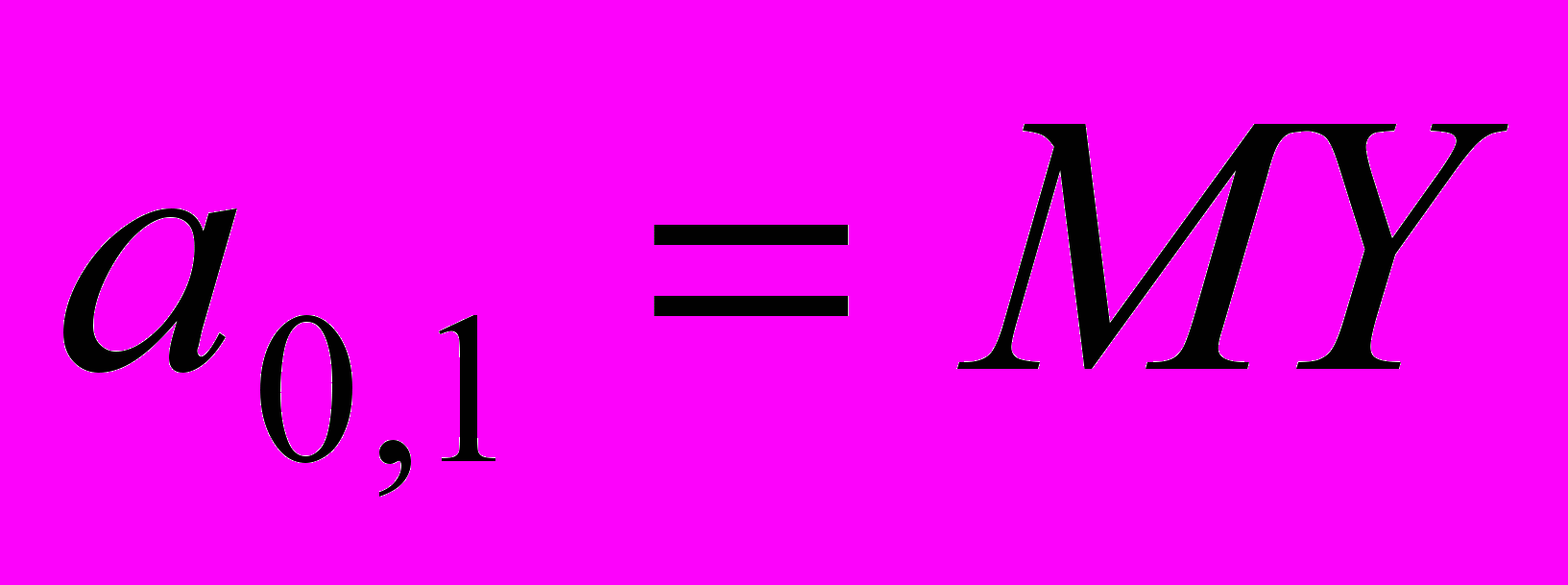, , 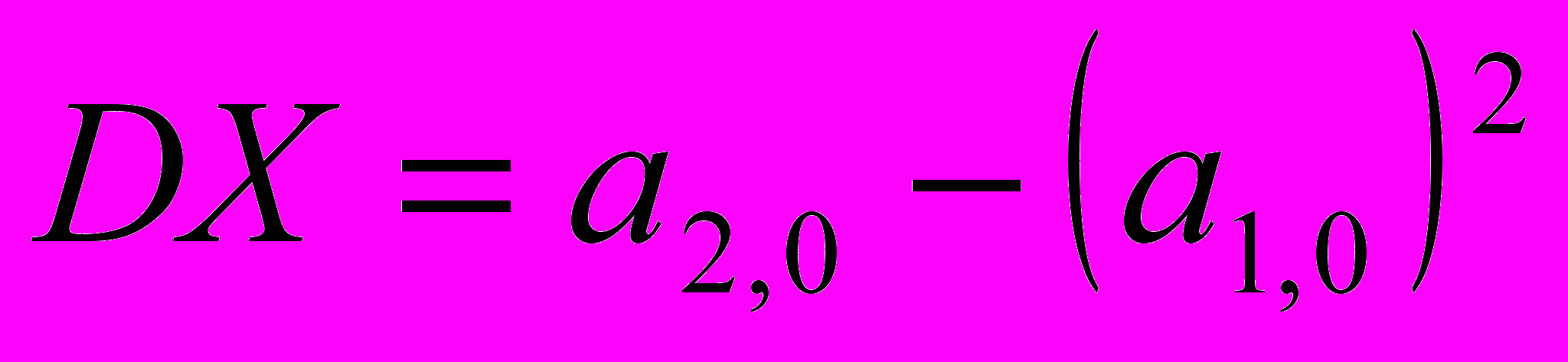, 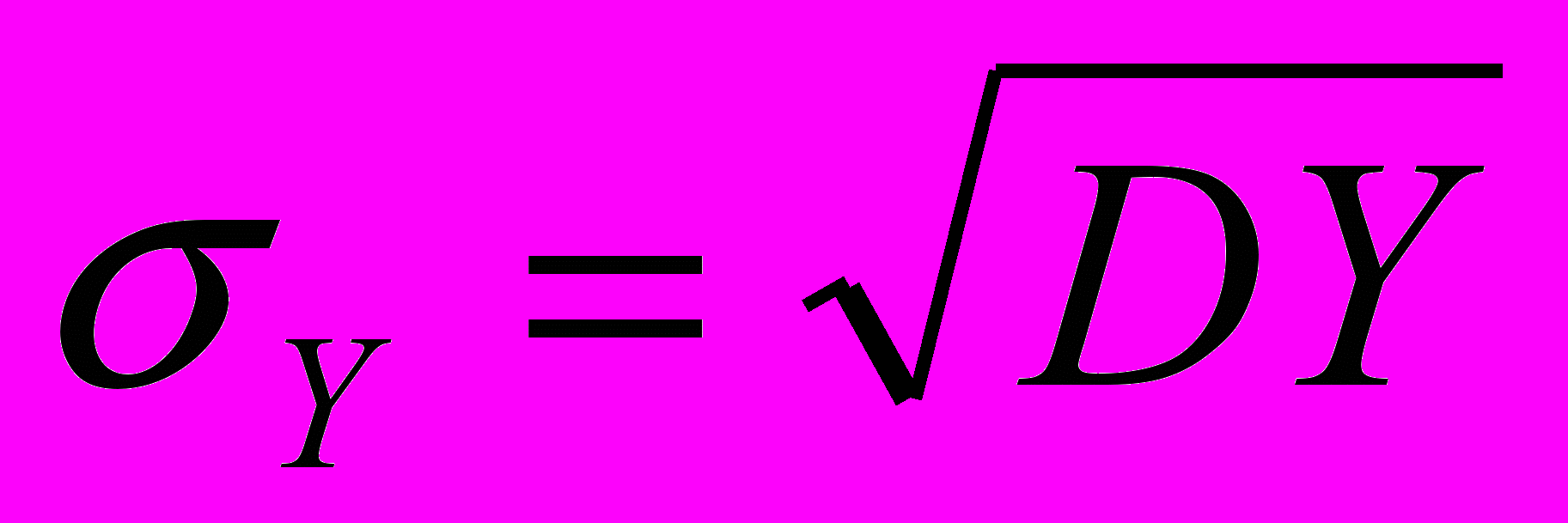. Таким образом, математические ожидания найдены, осталось найти дисперсии и среднее квадратическое отклонение

Нахождение дисперсий и средних квадратических отклонений с помощью пакета MathCAD. Обозначим ,










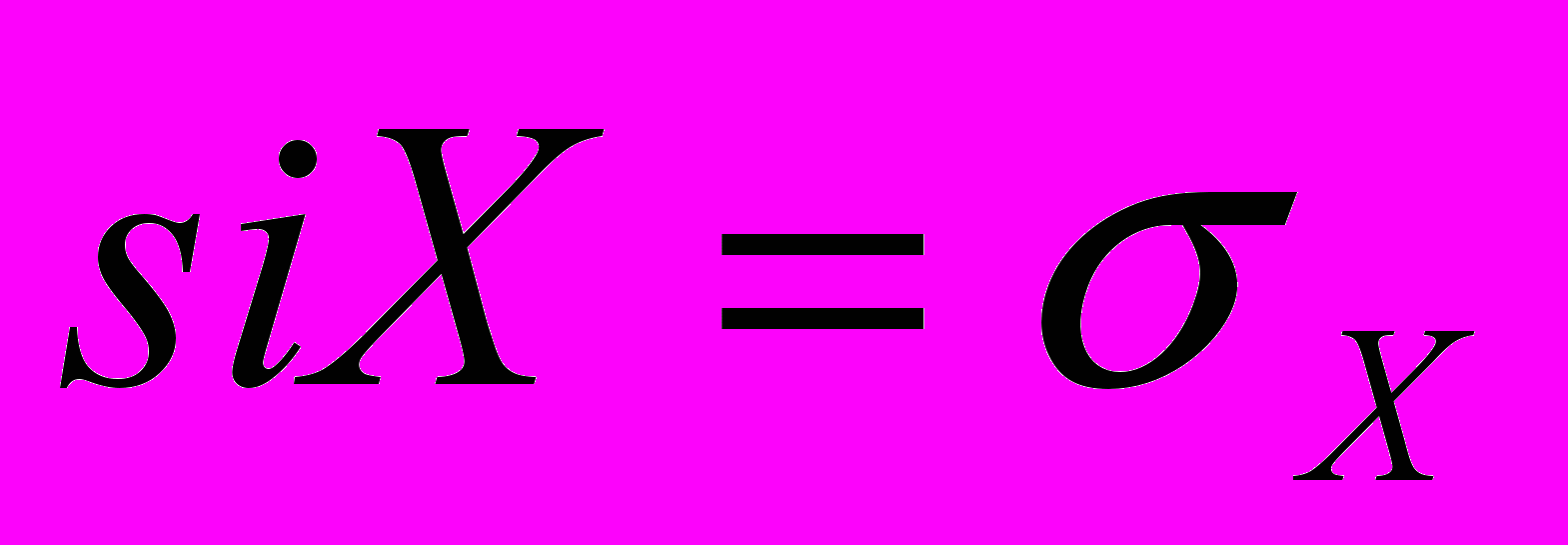дисперсии









cредние квадратические отклонения

Таким образом, получили , , , .




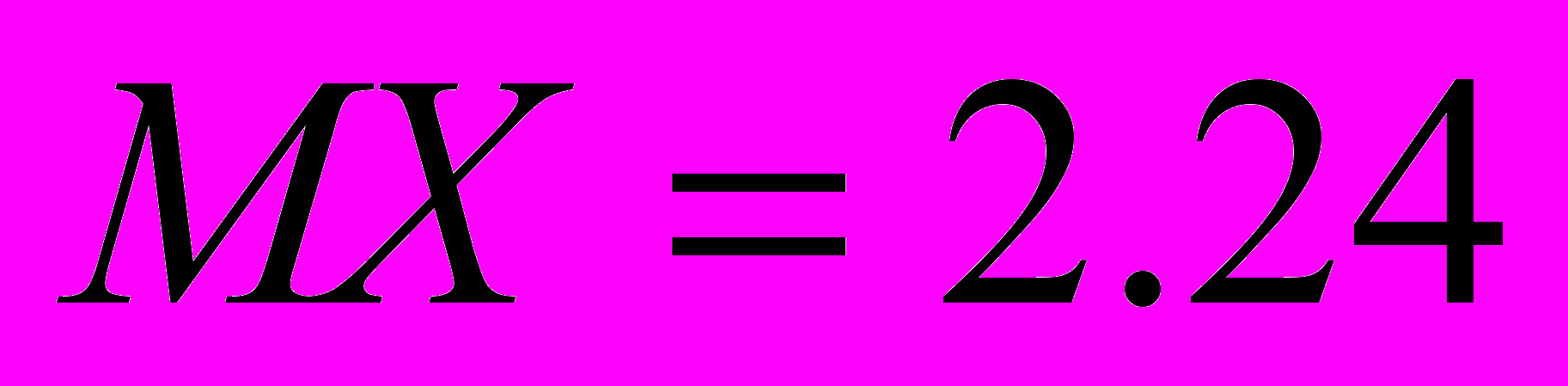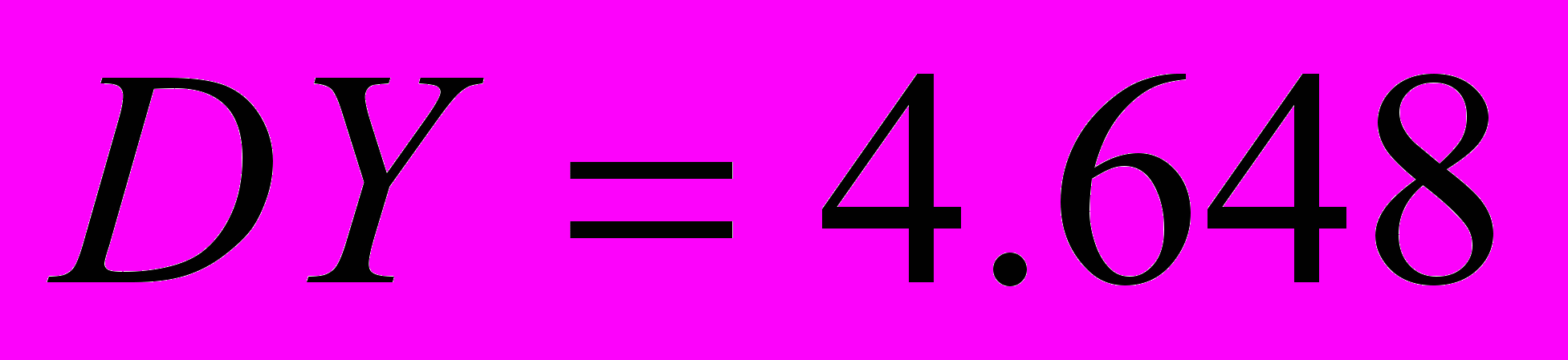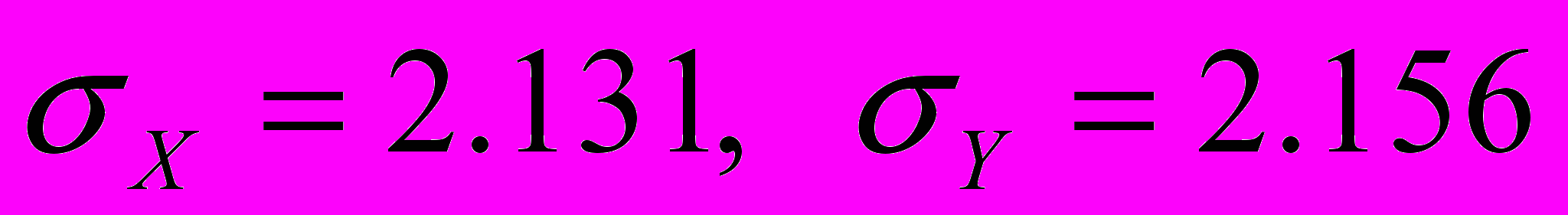Задание 3. Найдите условное распределение случайной величины .


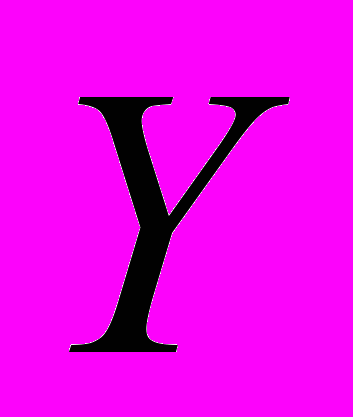Здесь требуется найти


Нахождение условного распределения с помощью пакета MathCAD. Обозначим

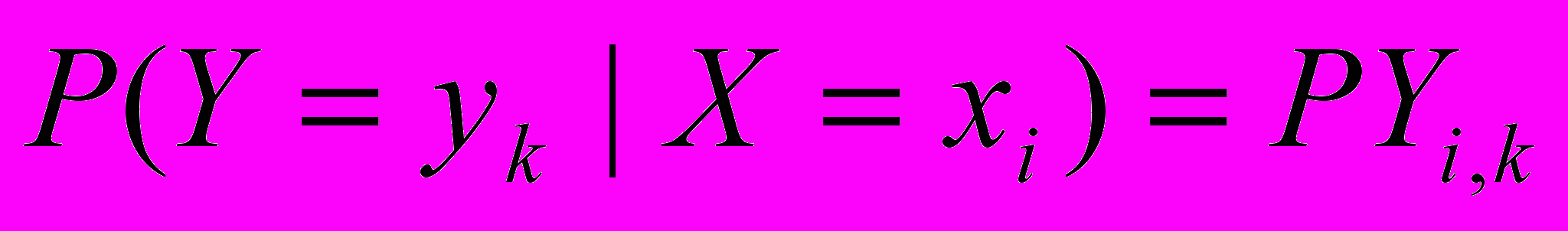и напомним, что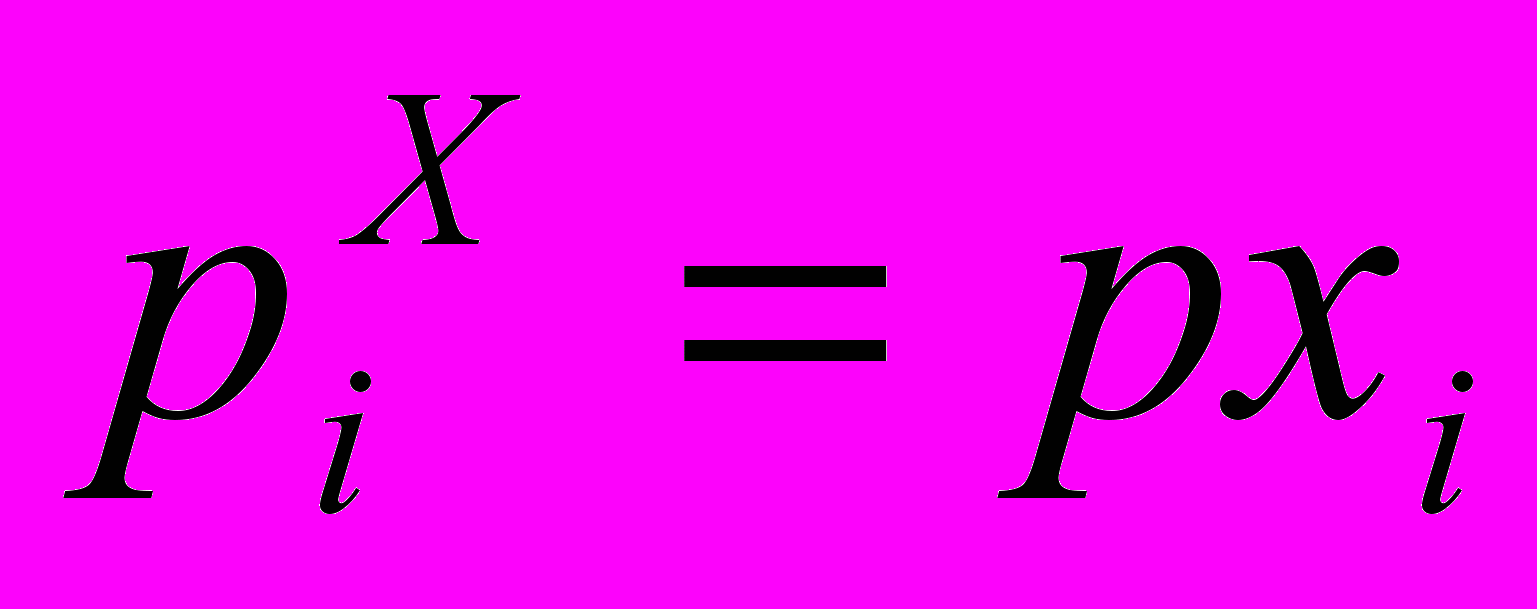

условные вероятности





Представим результат в виде таблицы

X\Y	-3	-1	1	3
-1	0.789	0.211
1	0.192	0.538	0.269
3		0.207	0.586	0.207
5		0.115	0.115	0.769

Здесь в строке стоят распределения величины Y при фиксированной значении X. Поэтому сумма чисел в строке равна 1.


Представим эти данные графически



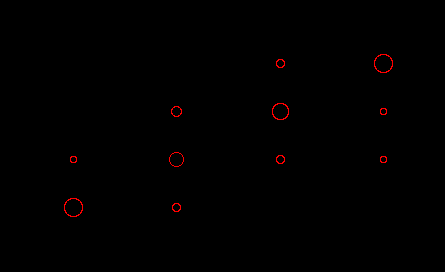
Здесь диаметр точки пропорционален условной вероятности.


Задание 4. Найдите условные математические ожидания случайной величины .


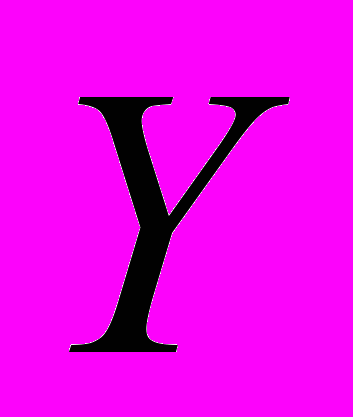Требуется найти 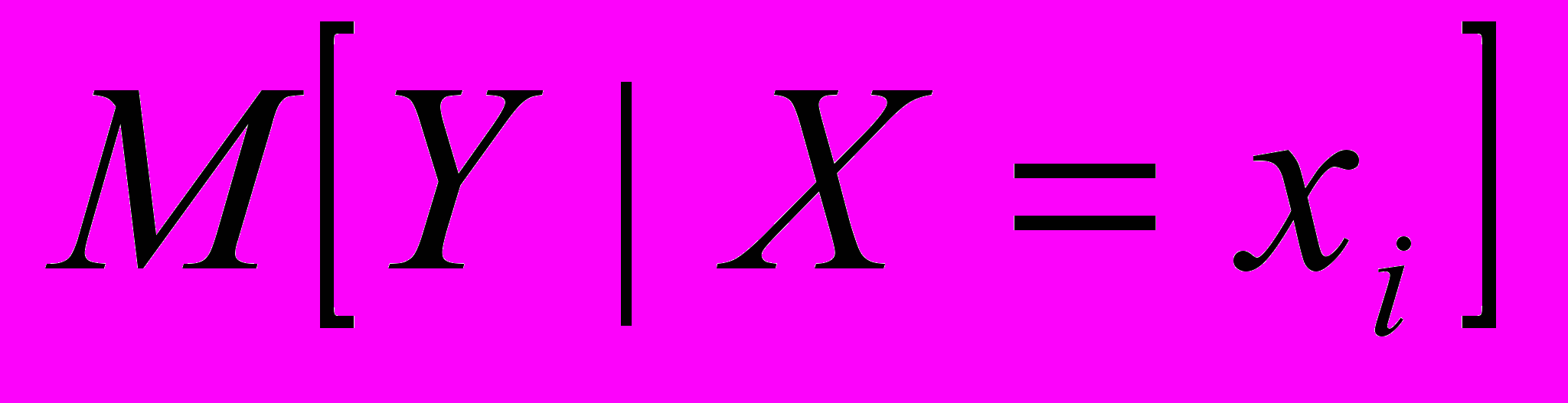. Условное математическое ожидание обладает свойством экстремальности. Поясним это. Будем рассматривать фиксированном случайную величину распределённую с вероятностями 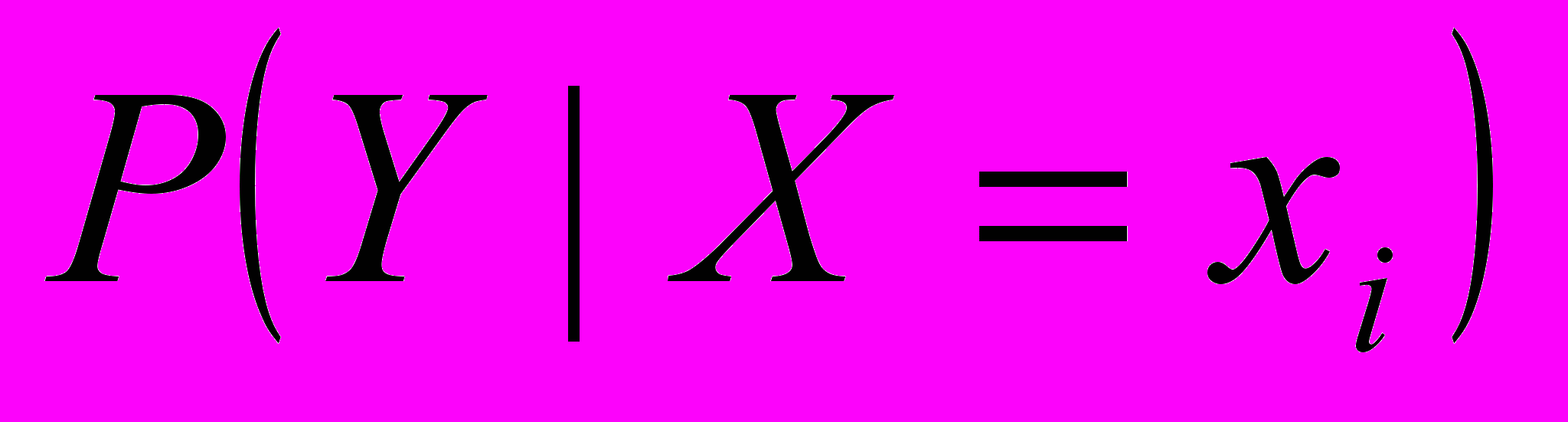. (см.Задание 2 и рис.) . Каждому 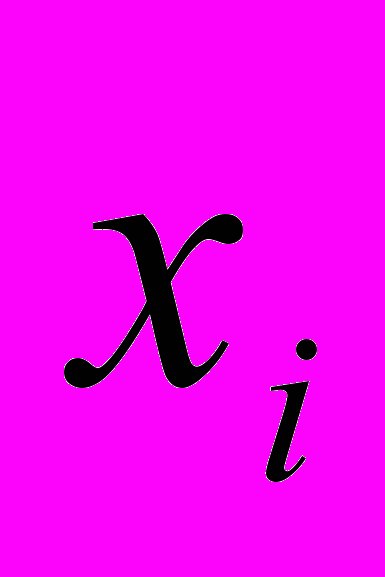можно поставить в соответствие некоторое число 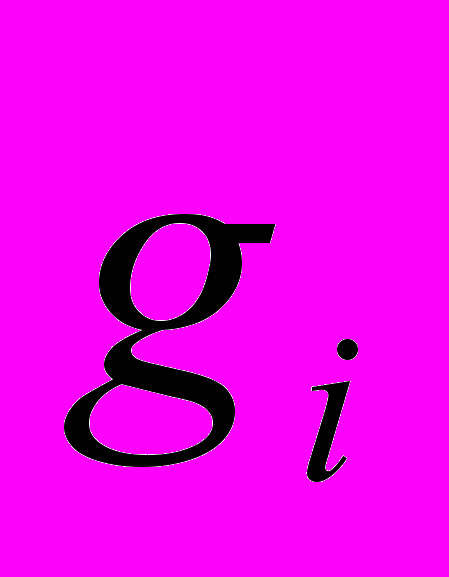и рассмотреть квадраты отклонений значений случайной величины от 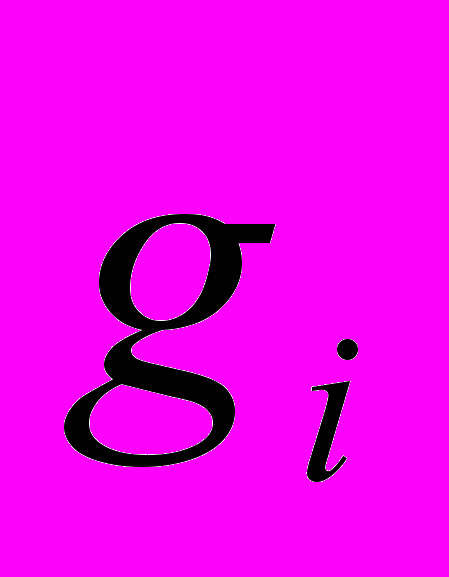, то есть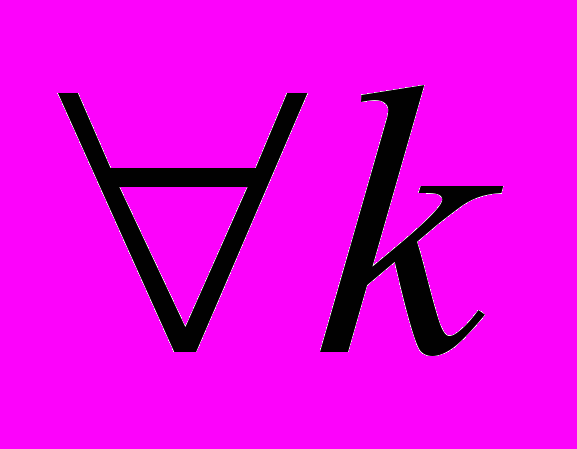 . Это новая случайная величина с вероятностями 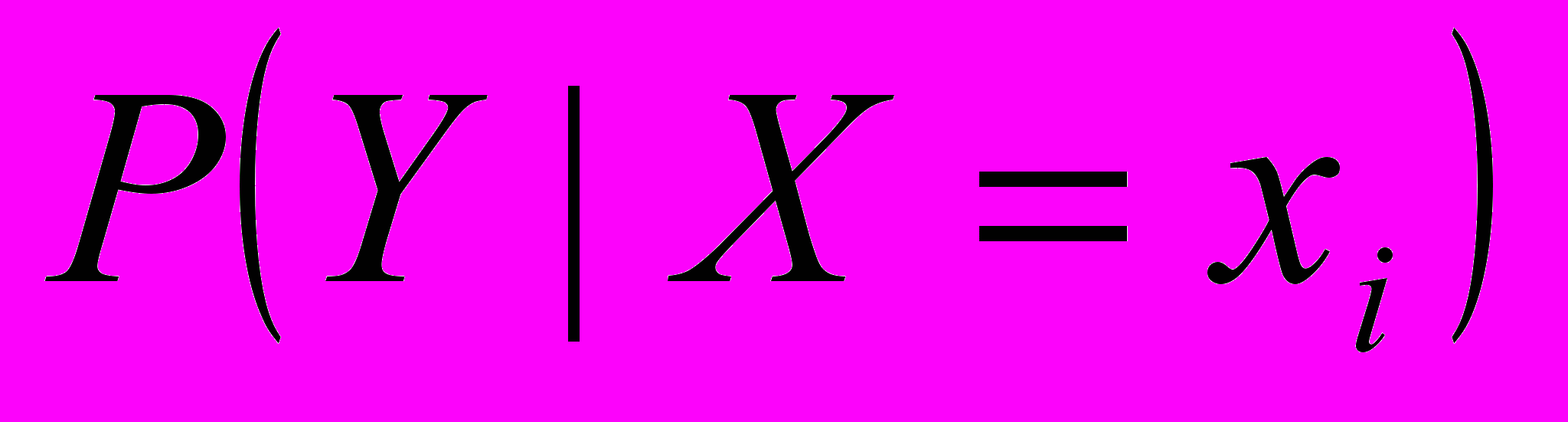. Может быть найдено её среднее, то есть

. (1)

Геометрически это интерпретируется следующим образом – квадрат отклонения берётся с весом равным вероятности и чем больше вероятность, тем весомее вклад отклонения в сумму 1.

Поставим задачу: найти такое число чтобы минимизировать равенство (1), то есть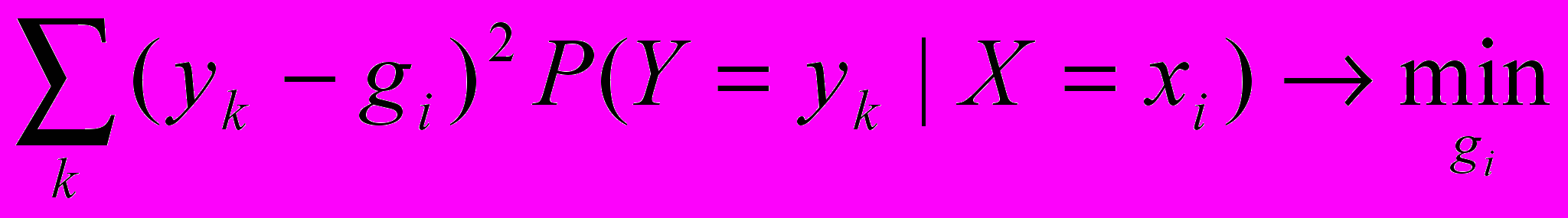

(3)


В теории доказано (Лекция 10), что минимум (3) достигается при 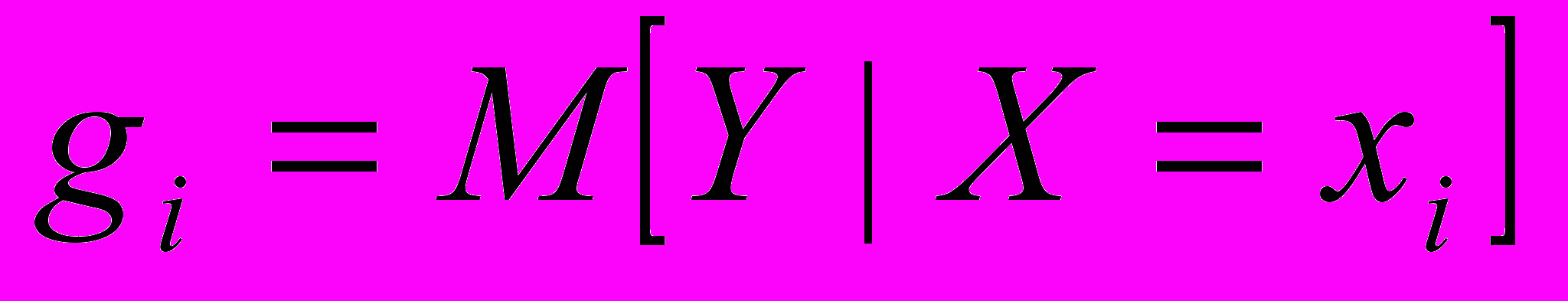и равен минимуму


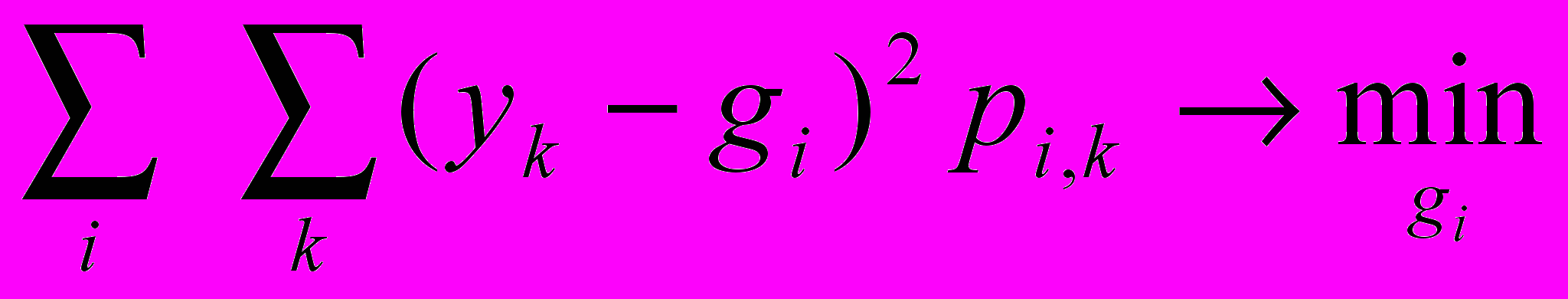(4)

Вычислим .


Нахождение условного математического ожидания с помощью пакета MathCAD. Напомним обозначение 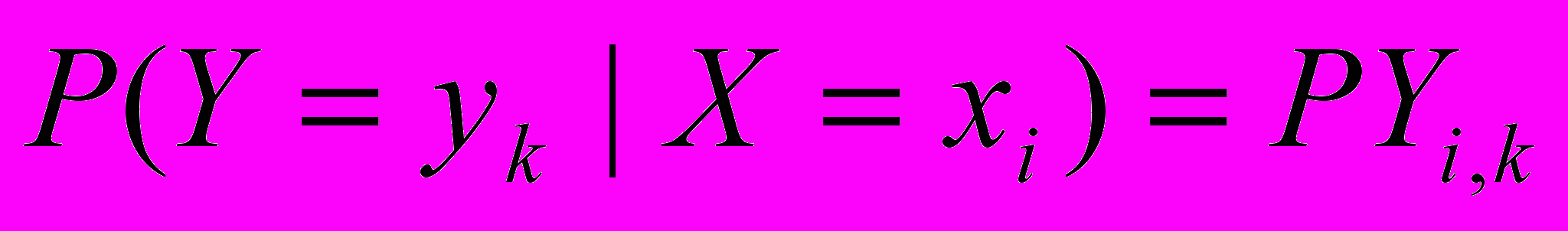. Обозначим






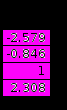
условные математические ожидания

Добавим к рисунку условных распределений условные математические ожидания



^ Задание 5. Постройте прямую регрессии Y на X.


Уравнение прямой регрессии будем искать в виде 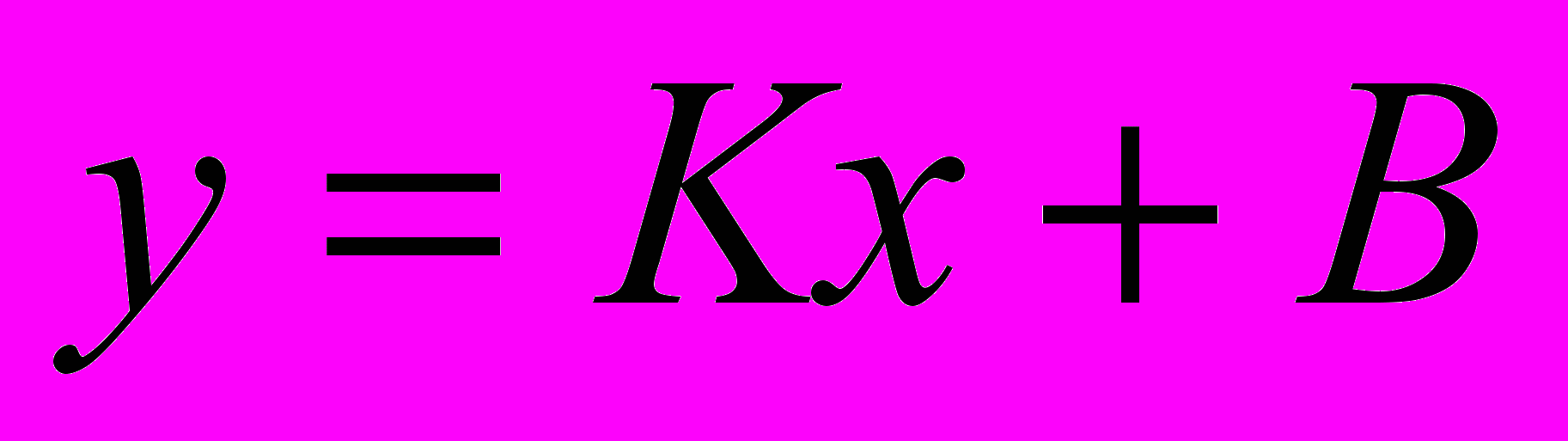. Коэффициенты 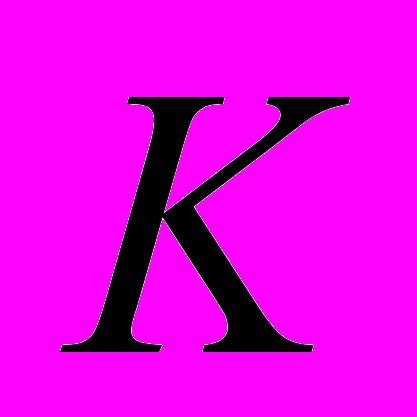и будем искать по аналогии с (4) так, чтобы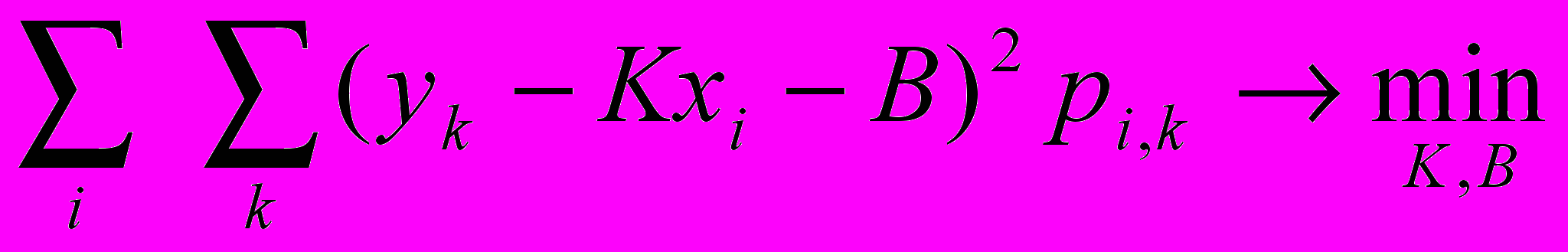


(5)


Минимизируемая функция в (5) – это функция двух переменных 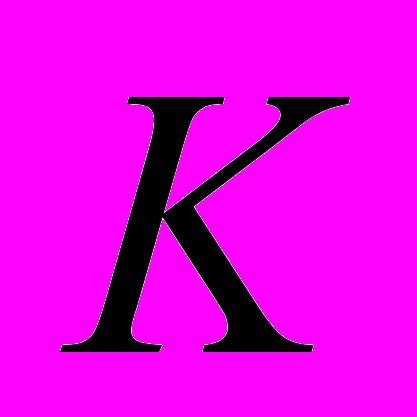и . Найдём градиент этой функции и приравняем к нулю





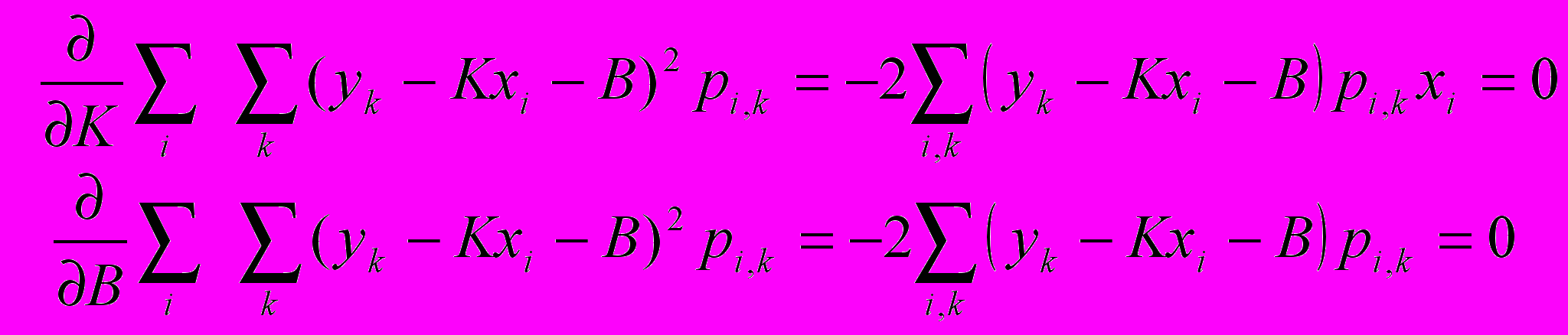
Отсюда имеем систему линейных уравнений относительно переменных 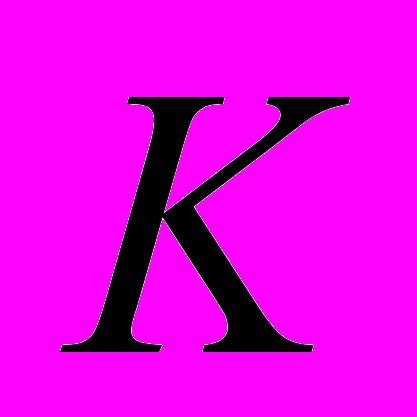и .


(6)


^ Решение (6) с помощью пакета MathCAD









Получили ,


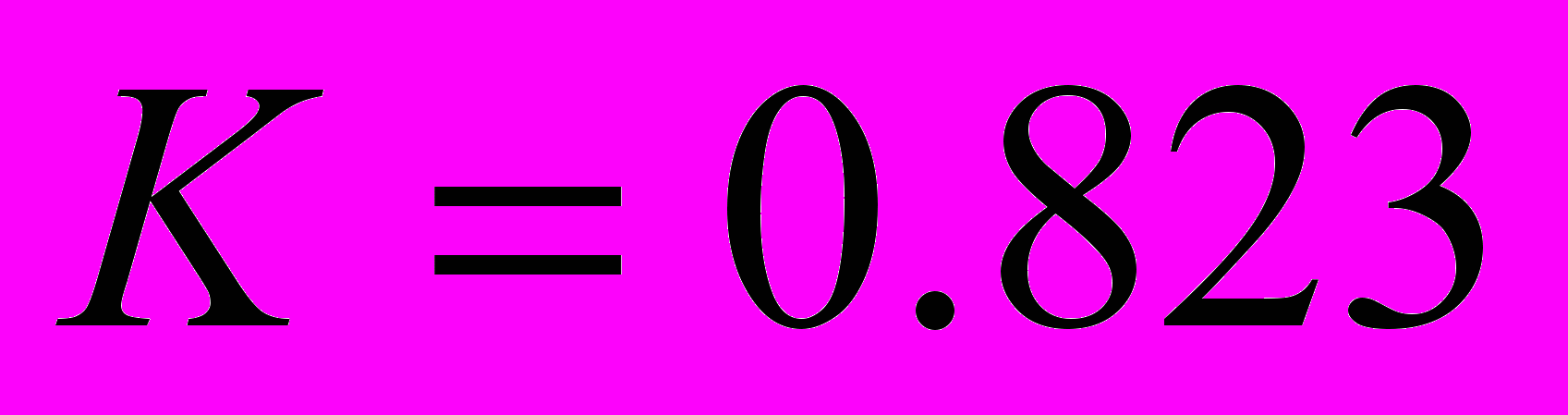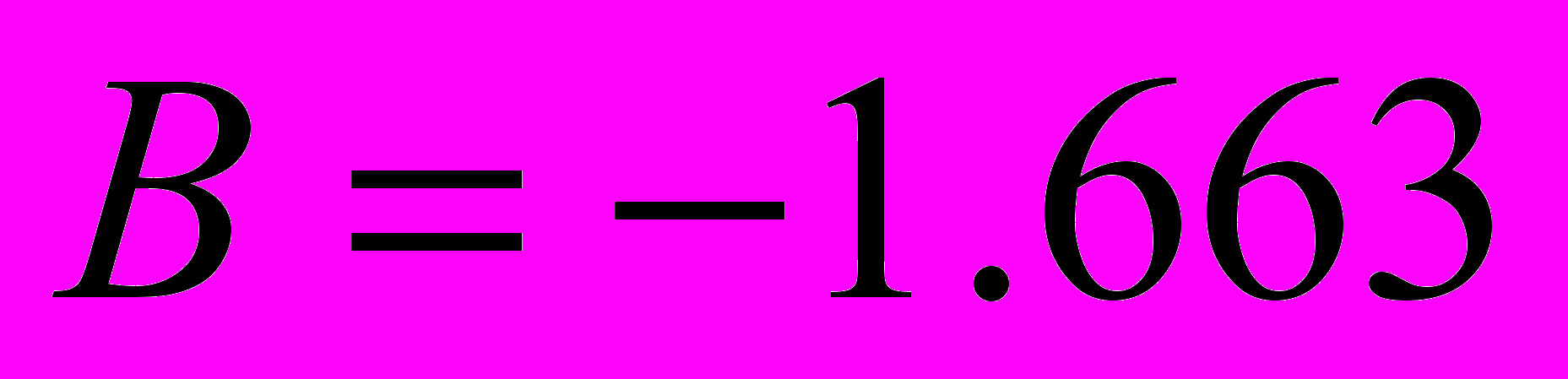
Построение прямой регрессии 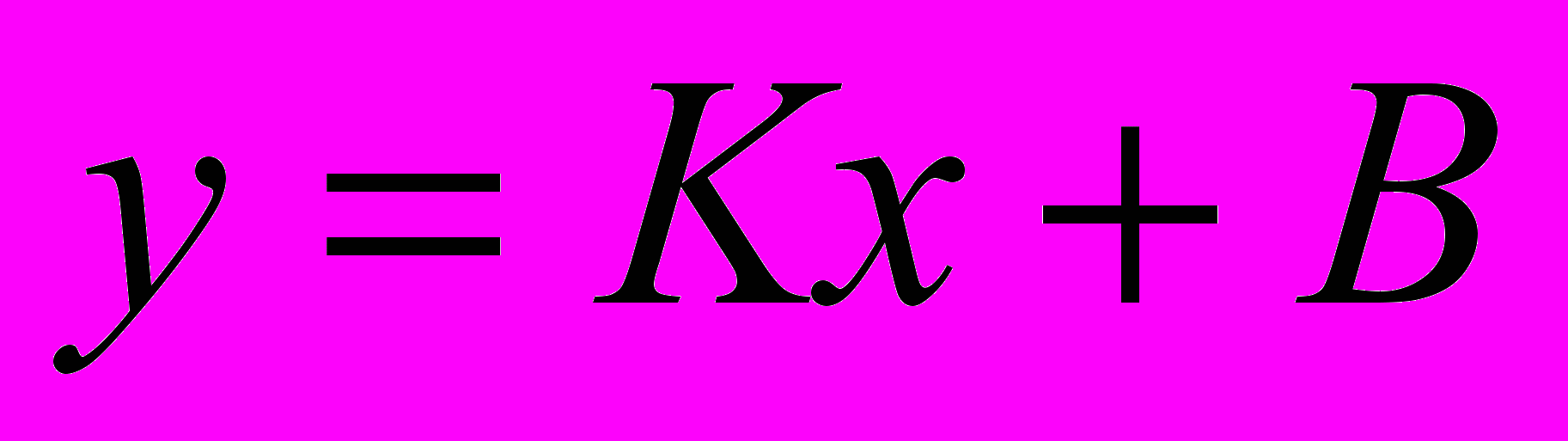с помощью пакета MathCAD.



В теории доказано, что коэффициенты прямой регрессии можно было вычислить по формулам 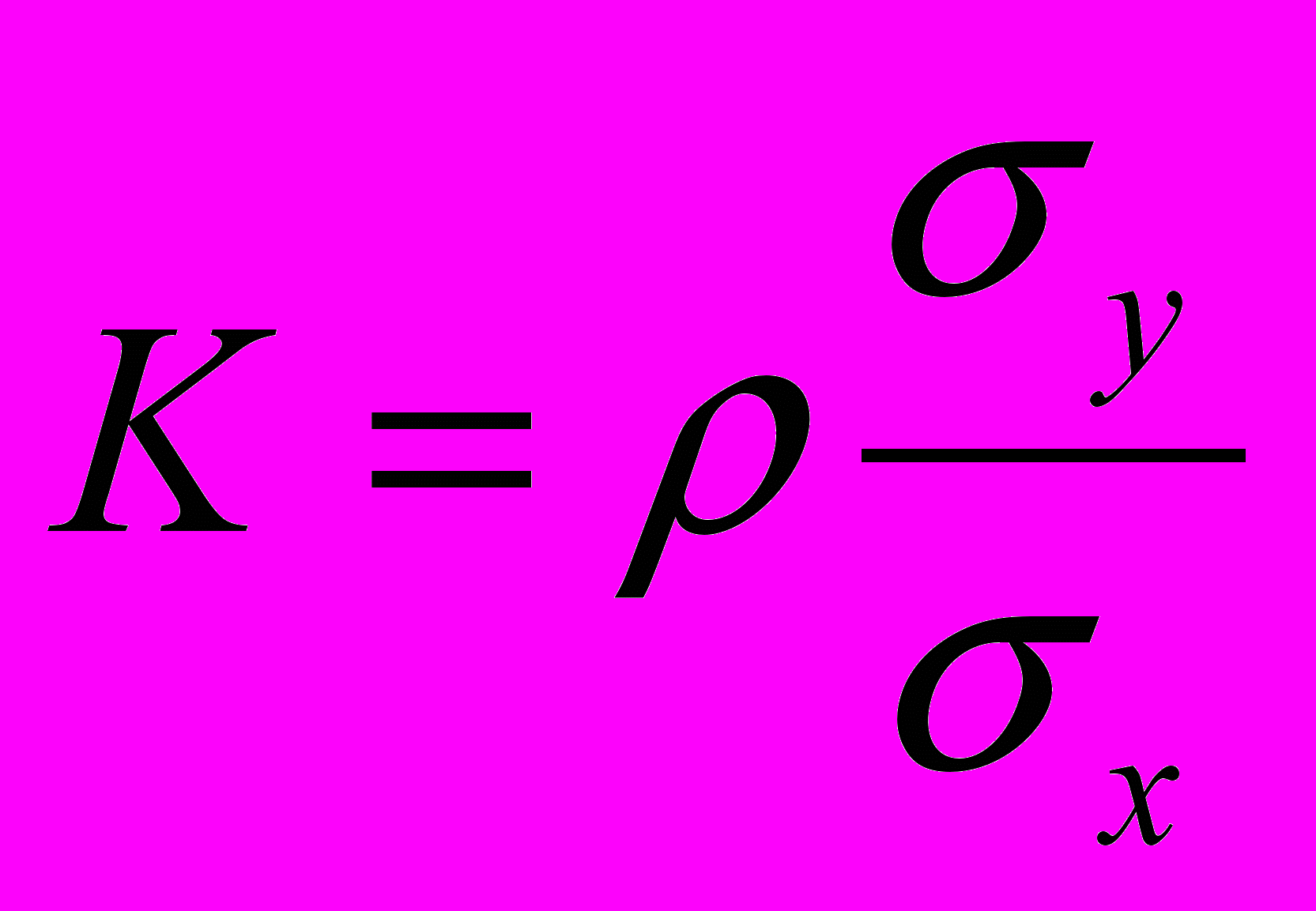, , 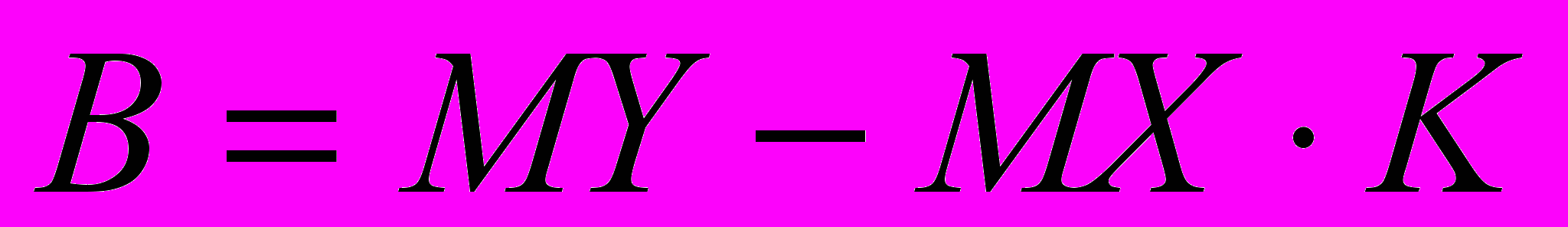где .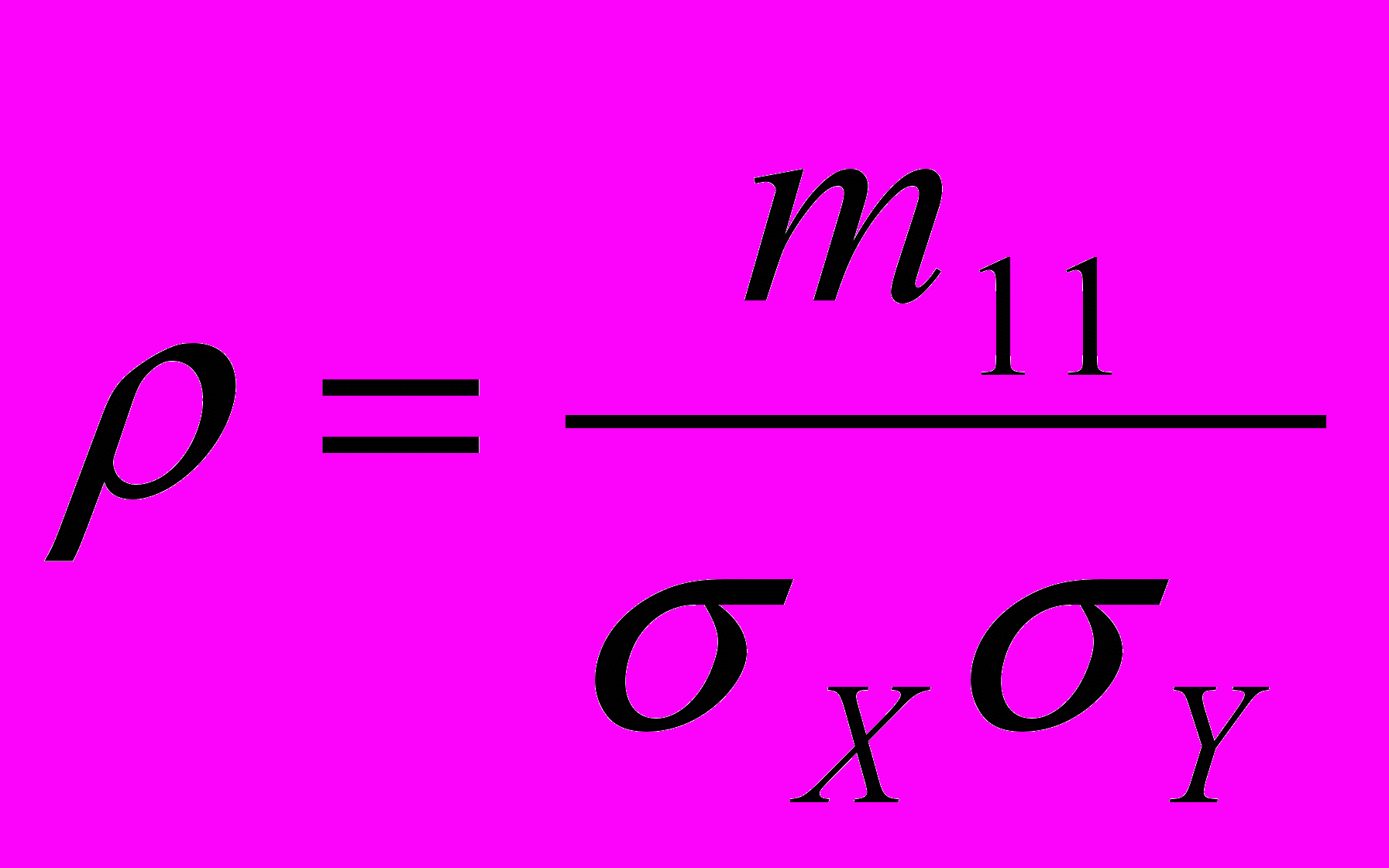


Вычислим коэффициенты прямой регрессии с помощью пакета MathCAD. Обозначим 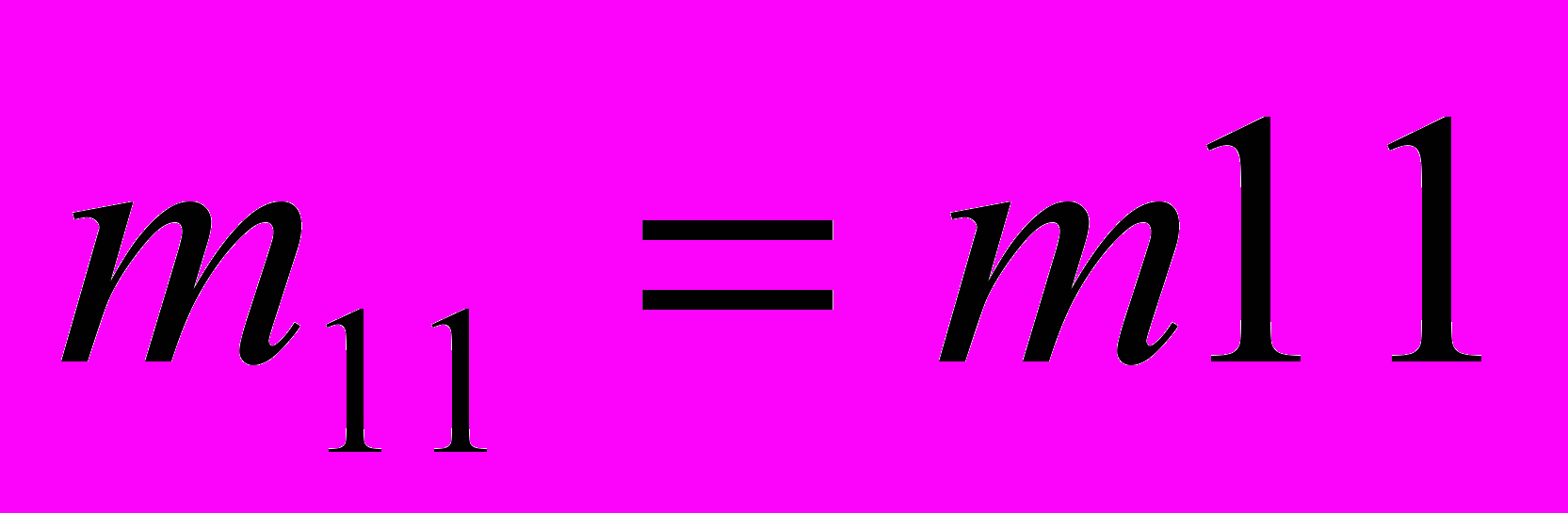. Напомним обозначения , , ,



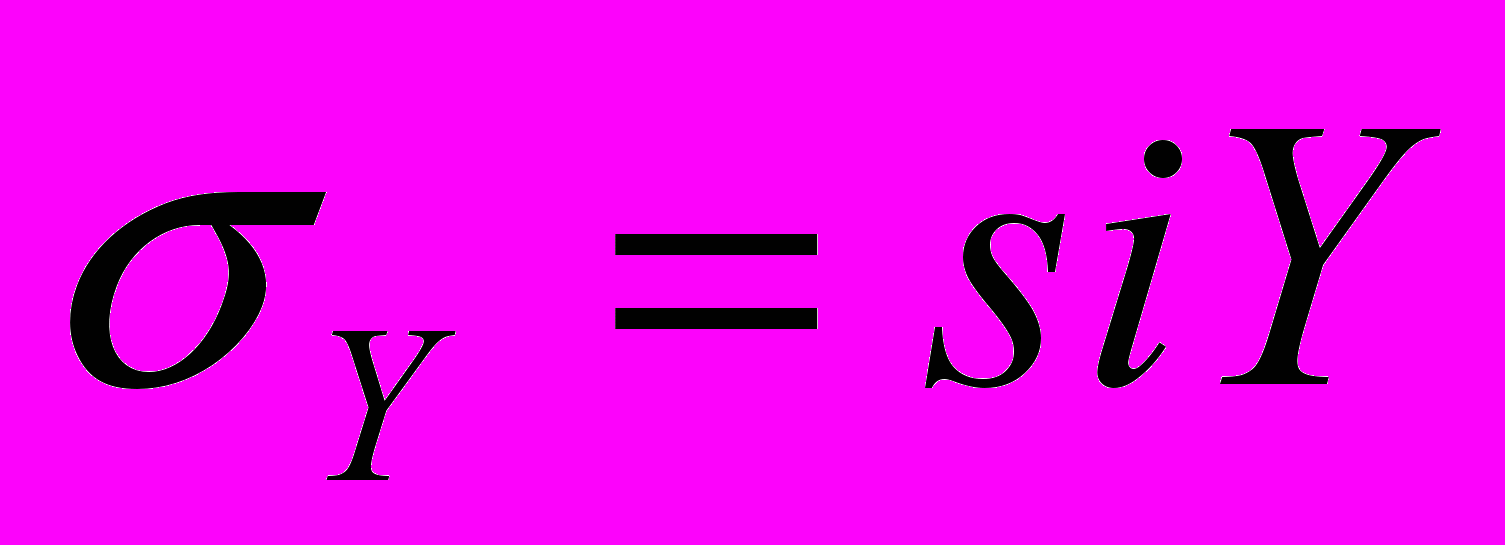смешанный момент