Парные регрессионные модели

Вид материала

Документы

Подобный материал:

• Лекция 5 Аддитивные и полупараметрические регрессионные модели, 3.66kb.
• Тема Введение в эконометрику, 220.73kb.
• Вестник Брянского государственного технического университета. 2010, 281.4kb.
• Тесты на наличие автокорреляции остатков и методы учета автокорреляции. 13. Классификация, 21.05kb.
• 1– анализ отсутствует, 1304.1kb.
• Самостоятельная работа 87 130 Всего часов на дисциплину, 58.84kb.
• Тема 41. Предпосылки модели экономики с экзогенными ценами (кейнсианская модель равновесия, 96.08kb.
• Аудит общественного здания образец аудита, 1221.73kb.
• Материальные и информационные модели, 27.68kb.
• Урок по информатике «Информационные модели», 76.56kb.

Парные регрессионные модели.


Важным этапом регрессионного анализа является определение типа функции, с помощью которой характеризуется зависимость между признаками. Приблизительное представление о линии связи можно получить на основе эмпирической линии зависимости, которая строится по полученным для исследования данным и имеет вид ломаной. Различают линейные (определяются линейной функцией) и нелинейные (определяются нелинейными функциями) модели. Наиболее часто для характеристики связей экономических показателей используют следующие типы функций:

1. линейная ;
   
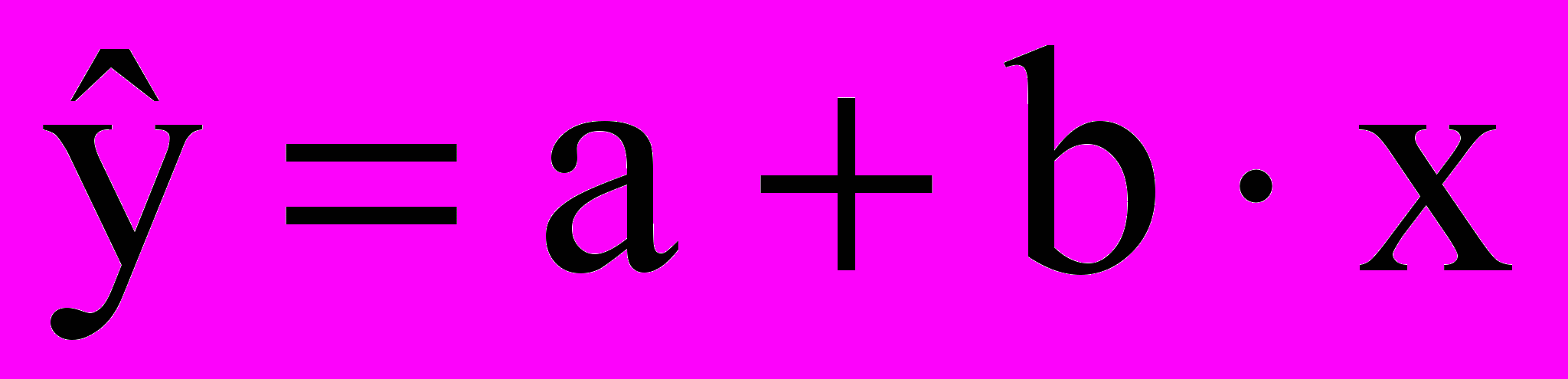2. гиперболическая ;
   
3. параболическая ;
   
4. логарифмическая ;
   
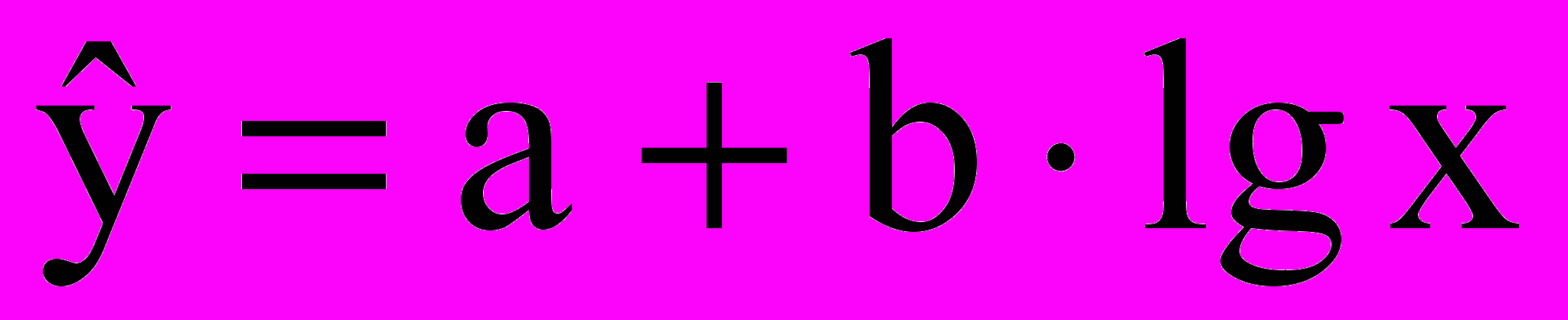5. показательная ;
   
6. степенная .
   

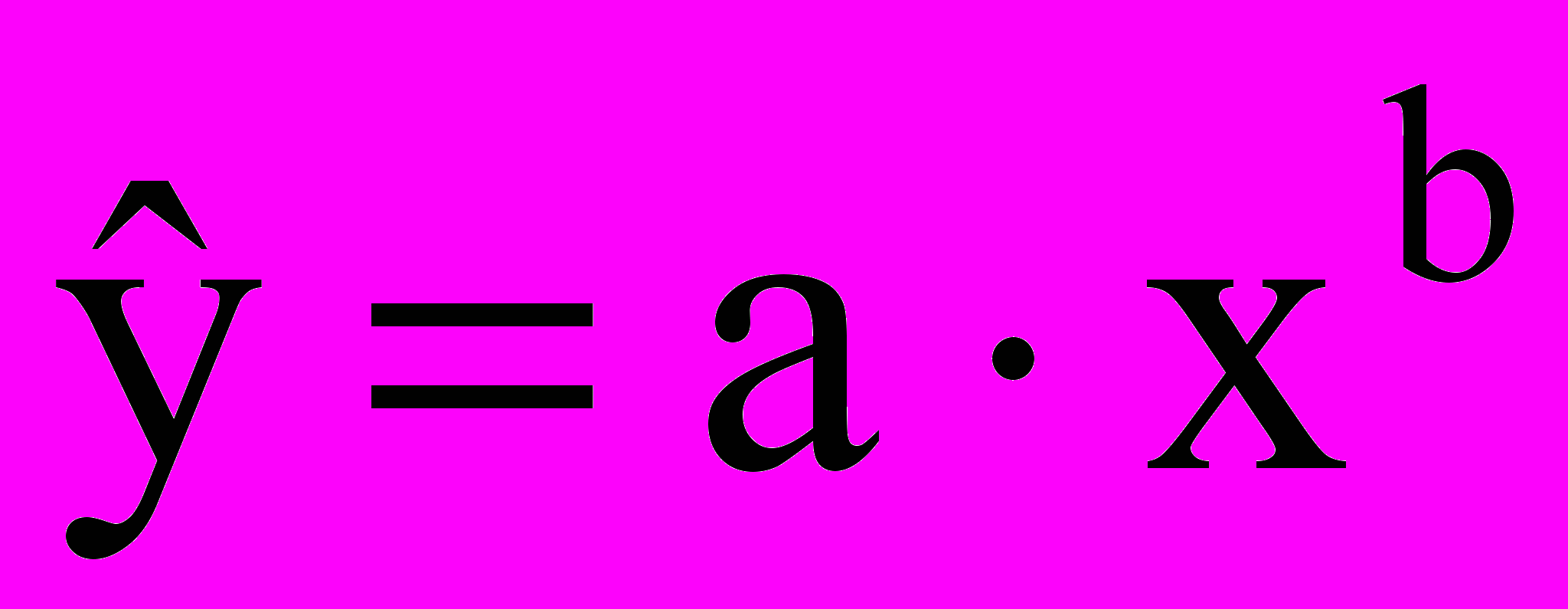Линейная регрессионная модель.


Уравнение линейной регрессионной модели в общем виде представляется равенством

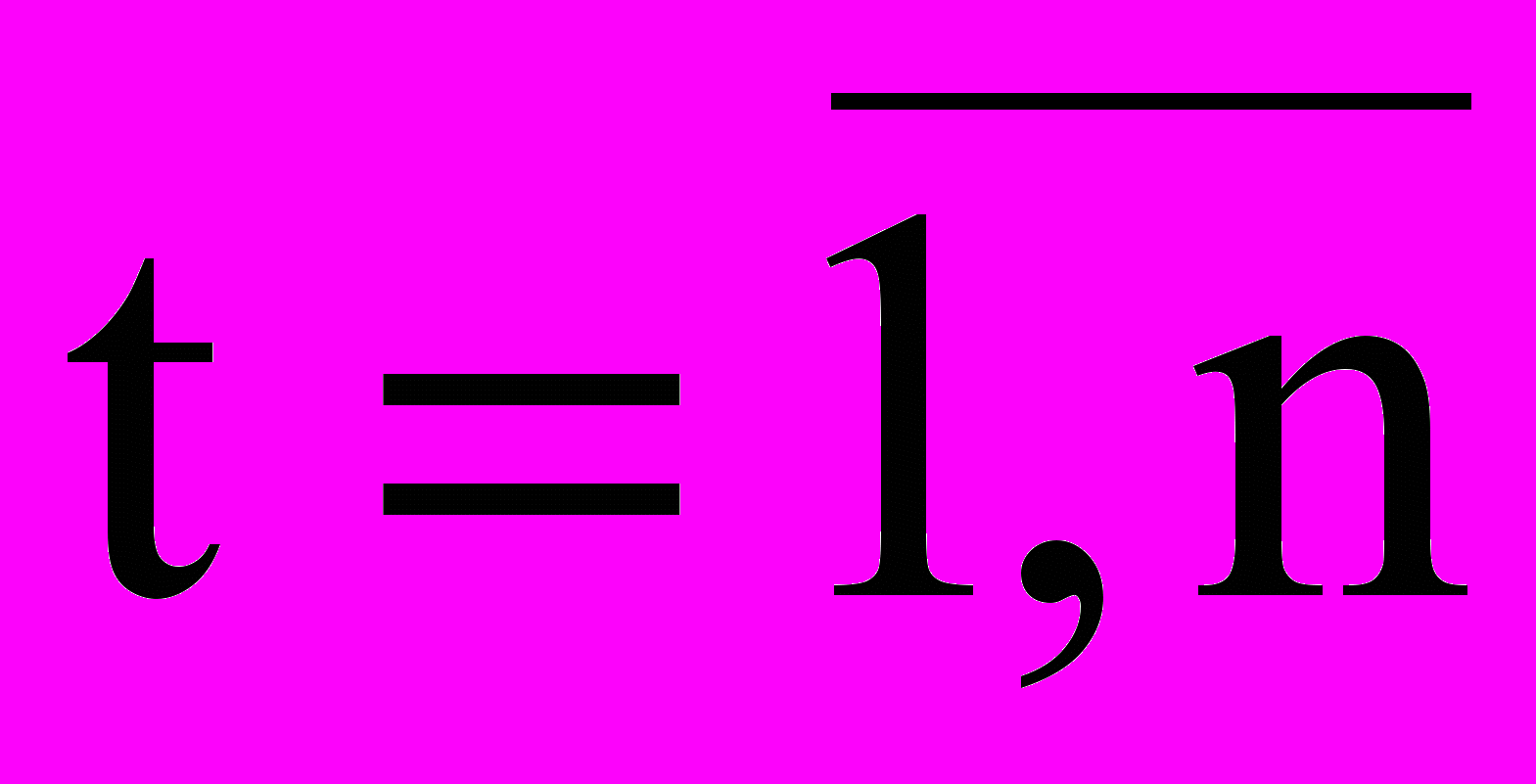, . Где:

• х_t – неслучайная величина, независимая переменная, фактор-признак;
  
• - случайная величина, зависимая переменная, признак-результат;
  
• - случайная величина.
  

К основным причинам случайности можно отнести следующие:

1. Модель является упрощением действительности. На самом деле существуют и другие параметры, от которых результат может зависить. Так зарплата может зависить от уровня образования, стажа работы, пола сотрудника, формы собственности предприятия и многих других факторов.


2. Трудности в измерении данных (т.е. присутствуют ошибки измерений). Так при рассмотрении зависимости расходов на питание от доходов семьи мы можем опираться лишь на данные, составленные членами этой семьи.

Следовательно, - случайная величина с некоторой функцией распределения, которая соответствует функции распределения случайной величины .

В дальнейшем нашей задачей будет задача составления уравнения регрессии линейной модели в виде 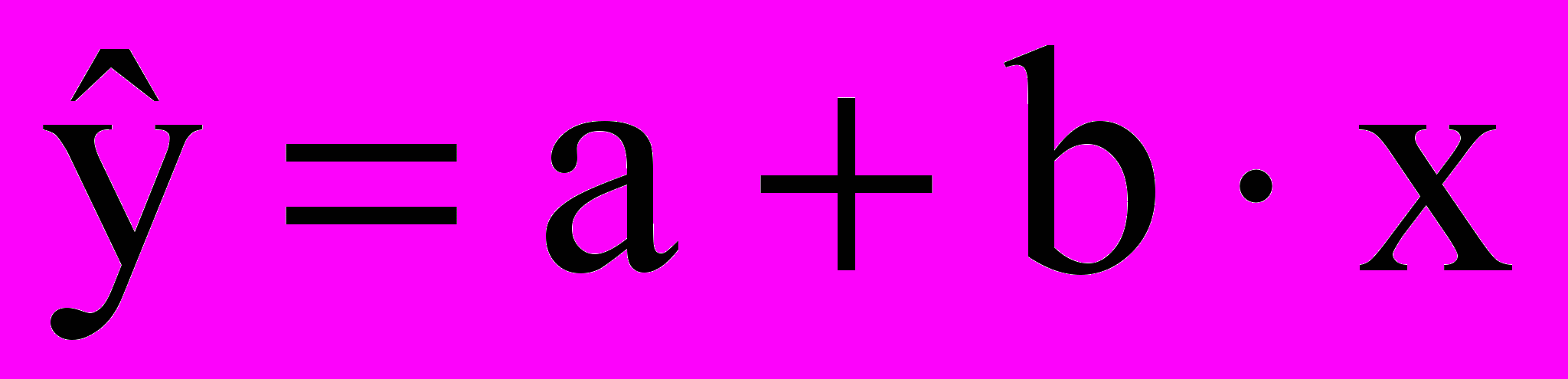, коэффициенты которого можно определить методом наименьших квадратов.


Параметр b называется коэффициентом регрессии. Данный коэффициент показывает среднее изменение результата при изменении фактора на единицу. Коэффициент регрессии является постоянным в рамках одной зависимости. Возможность четкой экономической интерпретации данного коэффициента сделала линейную модель достаточно распространенной в эконометрических исследованиях.

Формально а - значение у при х=0. Если признак-фактор х не имеет и не может иметь нулевого значения, то вышеуказанная трактовка свободного члена а не имеет смысла. Параметр а может не имеет экономического содержания. Интерпретировать можно лишь знак при параметре а. Если а > 0, то относительное изменение результата происходит медленнее, чем изменение фактора. Если же а < 0, то наблюдается опережение изменения результата над изменением фактора.

Коэффициент регрессии применяют для определения коэффициента эластичности Э_i, который показывает, на сколько процентов изменится величина результативного признака у при изменении признака – фактора на один процент.

Понятие эластичности функции дается в математическом анализе. Эластичность функции – это предел отношения относительного приращения функции у к относительному приращению аргумента х при :

.

Исходя из определения, коэффициент эластичности линейной функции определяется формулой . Видно, что это переменный коэффициент, поскольку его значение зависит от значения признака-фактора. В общем виде можно записать .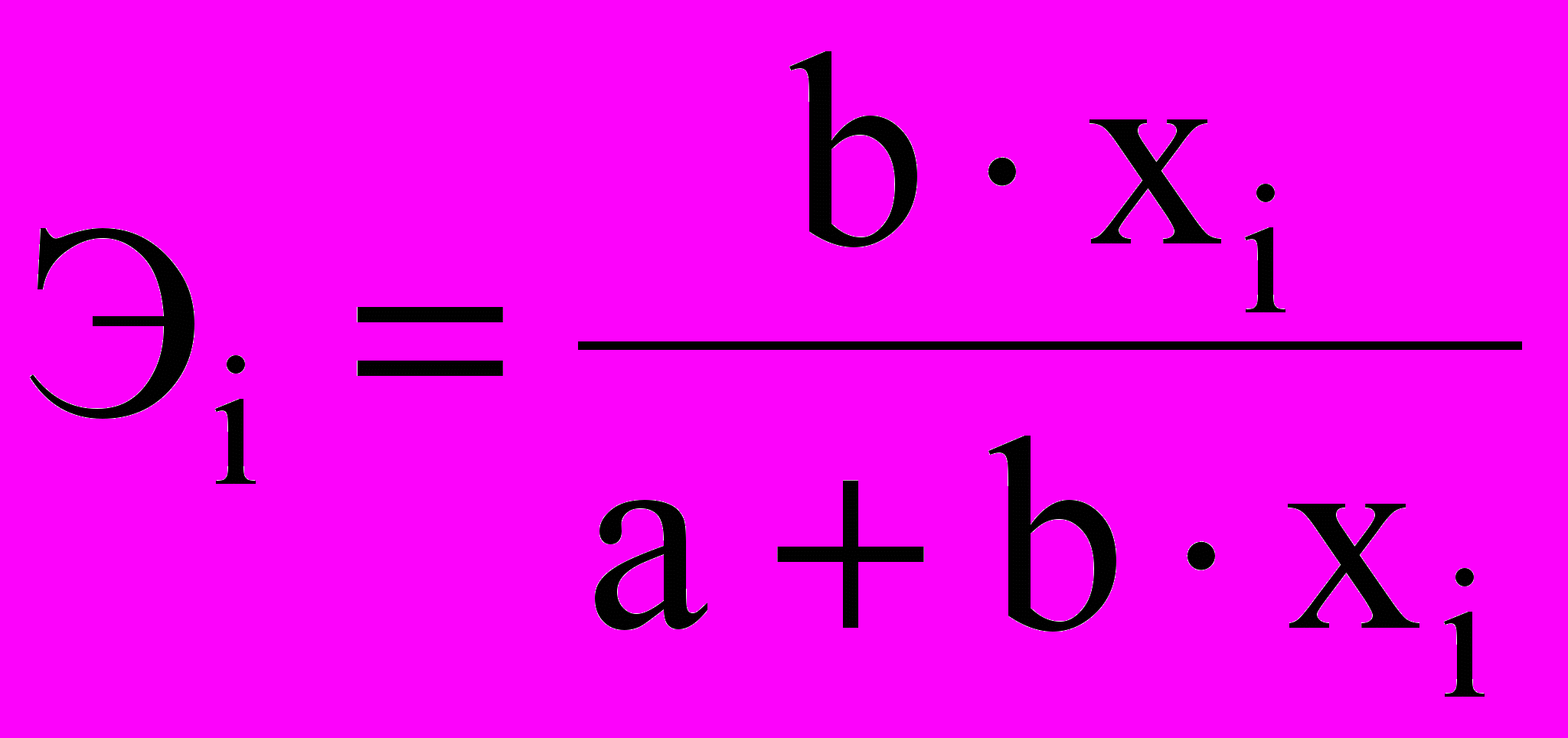

Часто рассчитывается средний показатель эластичности , где - средние значения признаков.


Раннее отмечалось, что показателями степени тесноты корреляционной связи являются коэффициенты корреляции.

К простейшим подобным показателям относят коэффициент Фехнера - коэффициент корреляции знаков. Он основан на сравнении поведения отклонений индивидуальных значений каждого признака от своей средней величины. При этом во внимание принимаются не величины отклонений, а только их знаки. Совпадения знаков отклонений обозначают через d, а несовпадений – с. Коэффициент Фехнера вычисляется по формуле , где

- число совпадений знаков отклонений,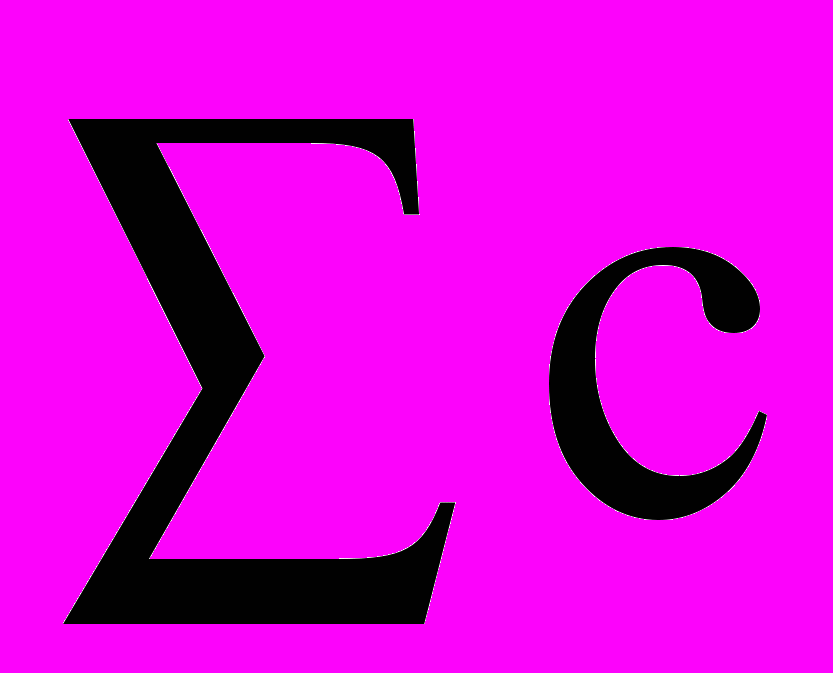

- число несовпадений знаков отклонений.


Коэффициент Фехнера может принимать различные значения в пределах от -1 до +1. Причем, если Н > 0, то между признаками наблюдается прямая связь; при Н < 0 – связь имеет обратное направление.

В силу того, что данный коэффициент учитывает только знаки отклонений, а не их величины, коэффициент Фехнера на практике характеризует в большей мере лишь наличие и направление связи.

Более совершенным показателем степени тесноты связи является линейный коэффициент корреляции, который был предложен английским ученым К. Пирсоном. Данный коэффициент учитывает значения отклонений индивидуальных значений каждого признака от своей средней величины. Вычисление этого коэффициента удобно проводить по формуле


.

Линейный коэффициент корреляции может принимать любые значения в пределах от -1 до +1. Чем ближе коэффициент корреляции по абсолютной величине к 1, тем теснее связь между признаками. Знак при линейном коэффициенте корреляции, так же как и коэффициент Фехнера, указывает на направление связи между признаками. Если , то говорят о наличии функциональной связи. В том случаи, когда r = 0 линейная связь между исследуемыми параметрами отсутствует.

Интерпретируя значение линейного коэффициента корреляции, следует иметь в виду, что он рассчитан для ограниченного числа наблюдений и подвержен случайным колебаниям. Следовательно, как любой выборочный показатель, он содержит случайную ошибку и не всегда однозначно отражает действительно реальную связь между изучаемыми признаками. Оценка значимости линейного коэффициента корреляции основана на сопоставлении абсолютного значения самого коэффициента с его средней квадратической ошибкой . Коэффициент корреляции считается значимым, если его абсолютное значение более чем в три раза превышает свою среднюю квадратическую ошибку: т.е. .

В зависимости от числа наблюдений n различают следующие методы расчета средней квадратической ошибки:

1. если число наблюдений велико (), то ;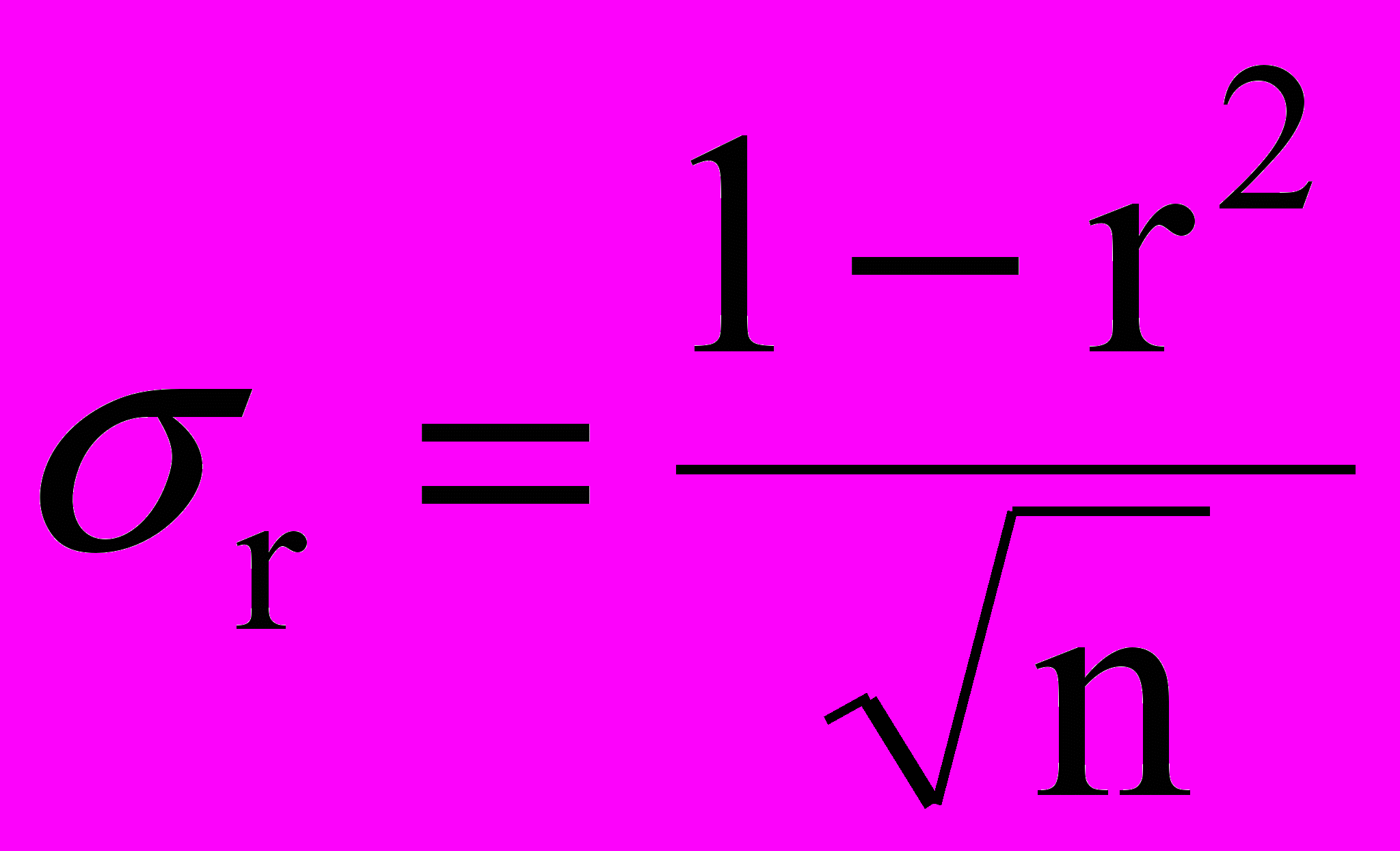

2. при небольшом числе наблюдений ( ) .


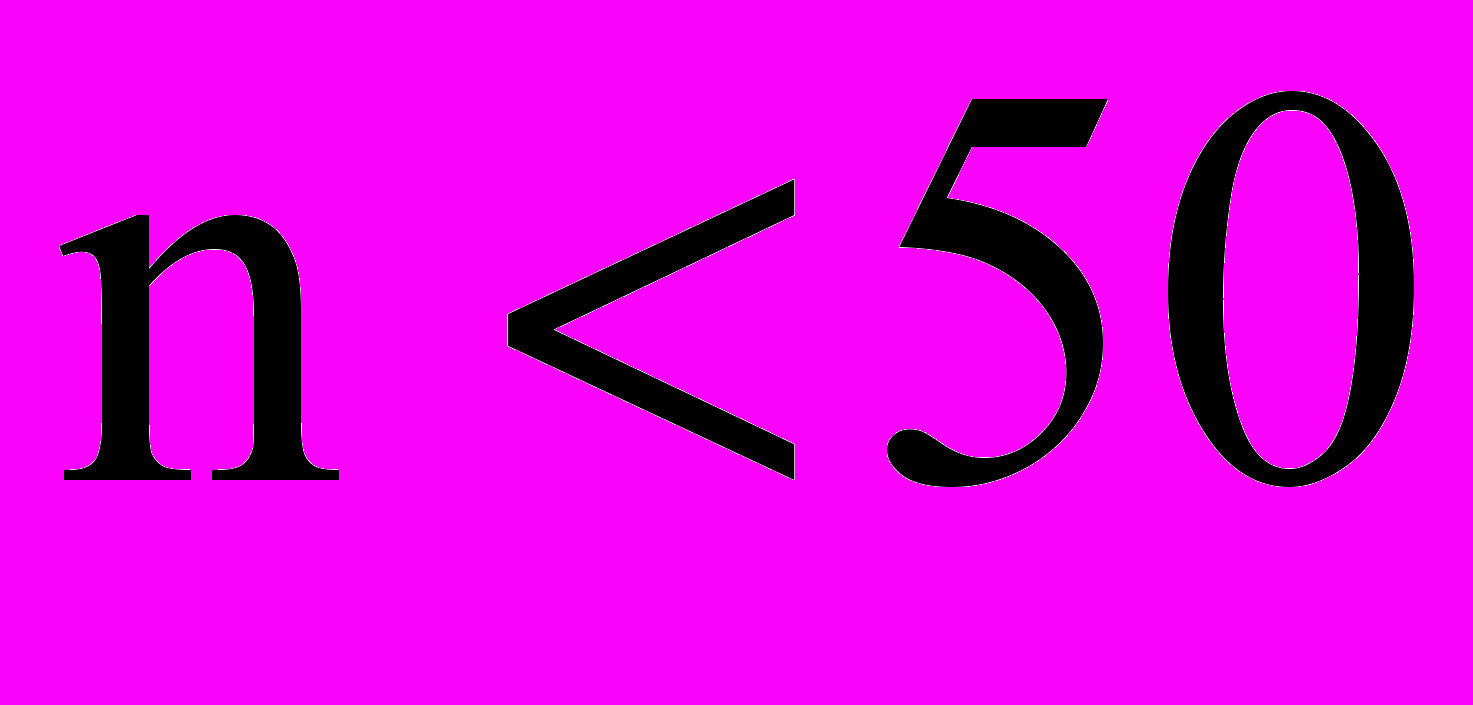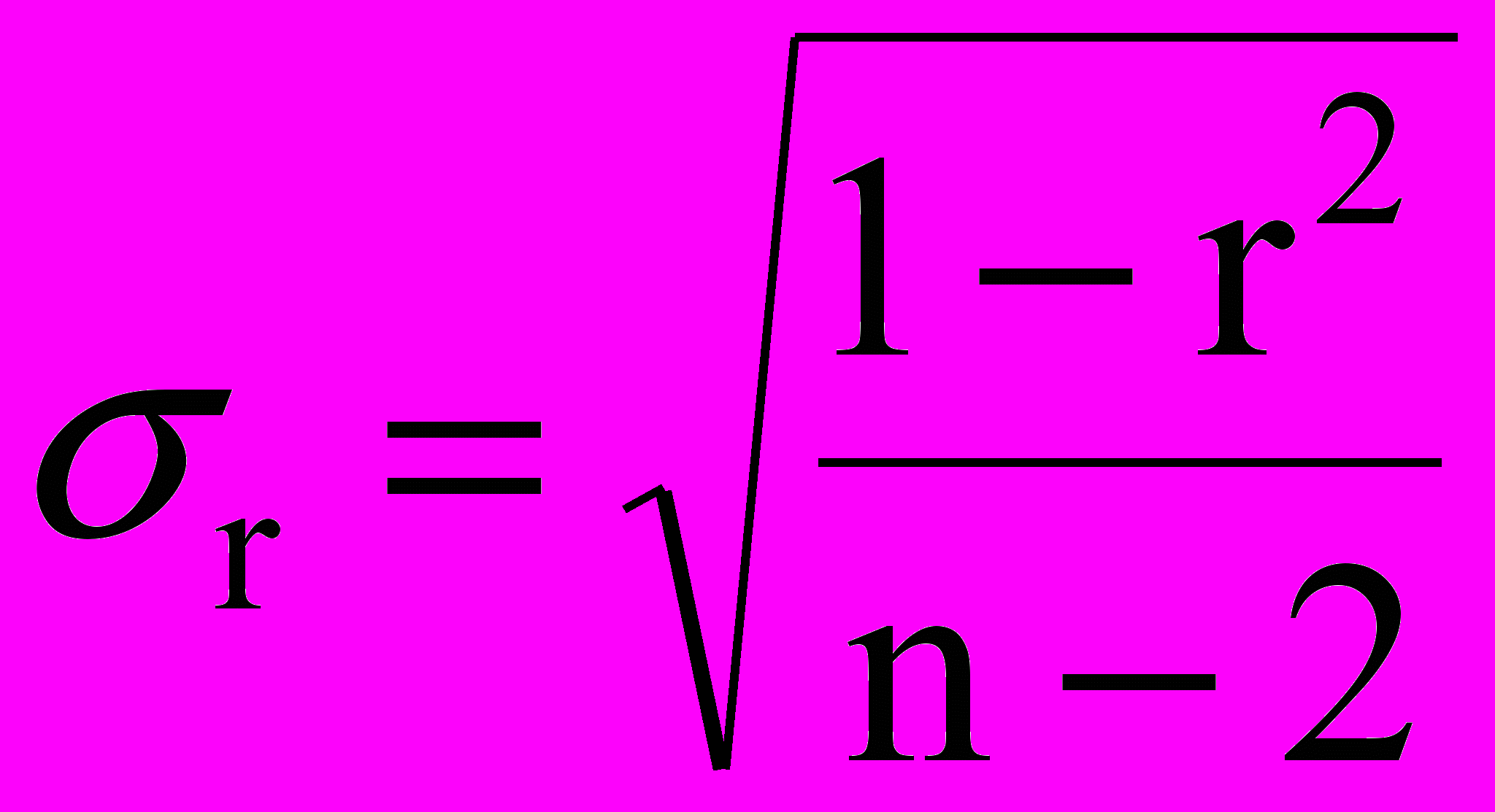Оценка надежности линейной модели.

1. Обоснованность выбора линейной функции в качестве уравнения регрессии.
   

1.Оценка существенности линейного коэффициента корреляции (через распределение Стьюдента).

• Данная оценка дает возможность распространить выводы по результатам выборки на всю генеральную совокупность.
  

✔ Вычисляется показатель , где

r – линейный коэффициент корреляции,

n – длина выборки.

✔ Определить значение t_табл.

• определяется по таблице распределения Стьюдента в зависимости от числа степеней свободы k = n – 2 и уровня значимости α = 5%.
  

✔ Сравнить t_расч. и t_табл.

• если t_расч. > t_табл., то с вероятностью 95 % во всей генеральной совокупности действительно существует линейная зависимость между изучаемыми признаками.
  

2. Оценка обоснованности выбора линейной функции в качестве уравнения регрессии.


✔ Вычислить:

• среднеквадратическую ошибку
  
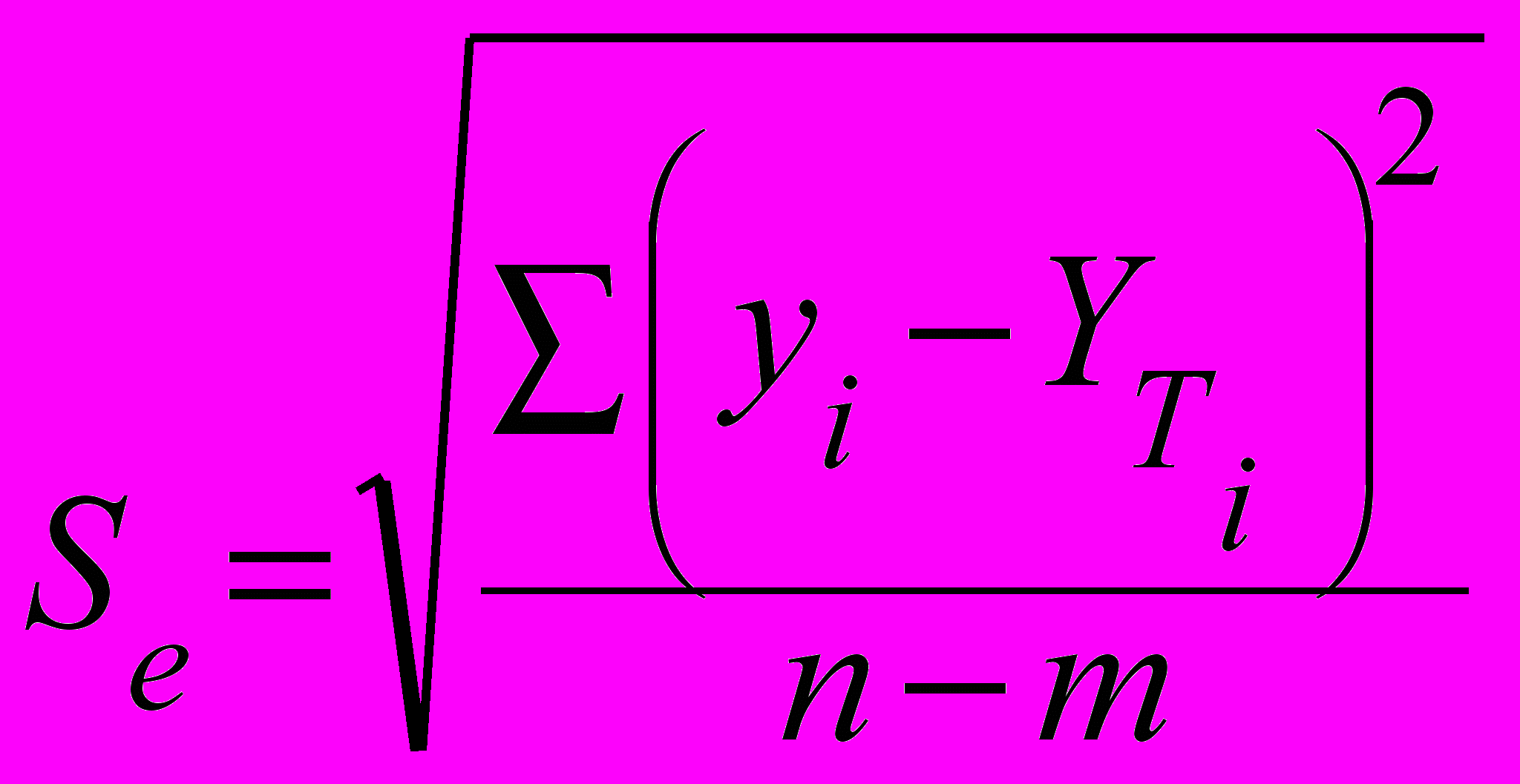
• среднеквадратическое отклонение
  
• индекс корреляции
  

✔ Анализ параметров:




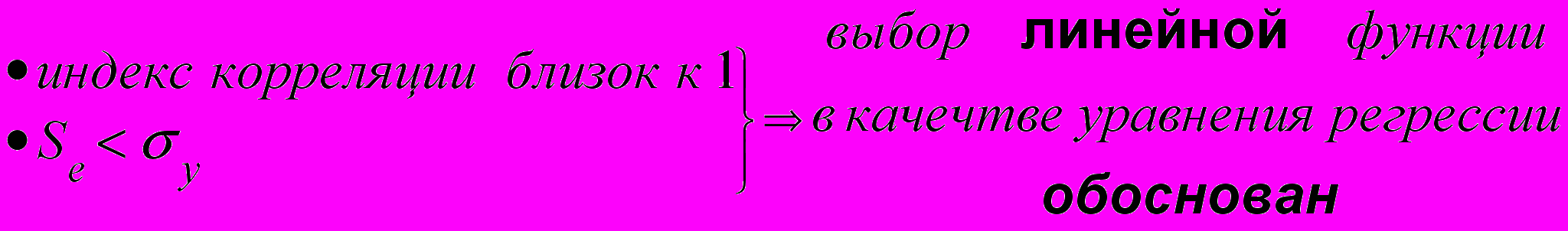
II. Прогноз значений результативного признака по уравнению регрессии.

• Средняя квадратическая ошибка уравнения S_e дает нам возможность в каждом конкретном случае с определённой вероятностью указать, что величина результативного признака расположена в определённом интервале относительно значения, вычисленного по уравнению регрессии. Данный интервал называют доверительным.
  

✔ Определить границы доверительного интервала.

• вычислить дисперсию ;
  
• определить множитель ;
  
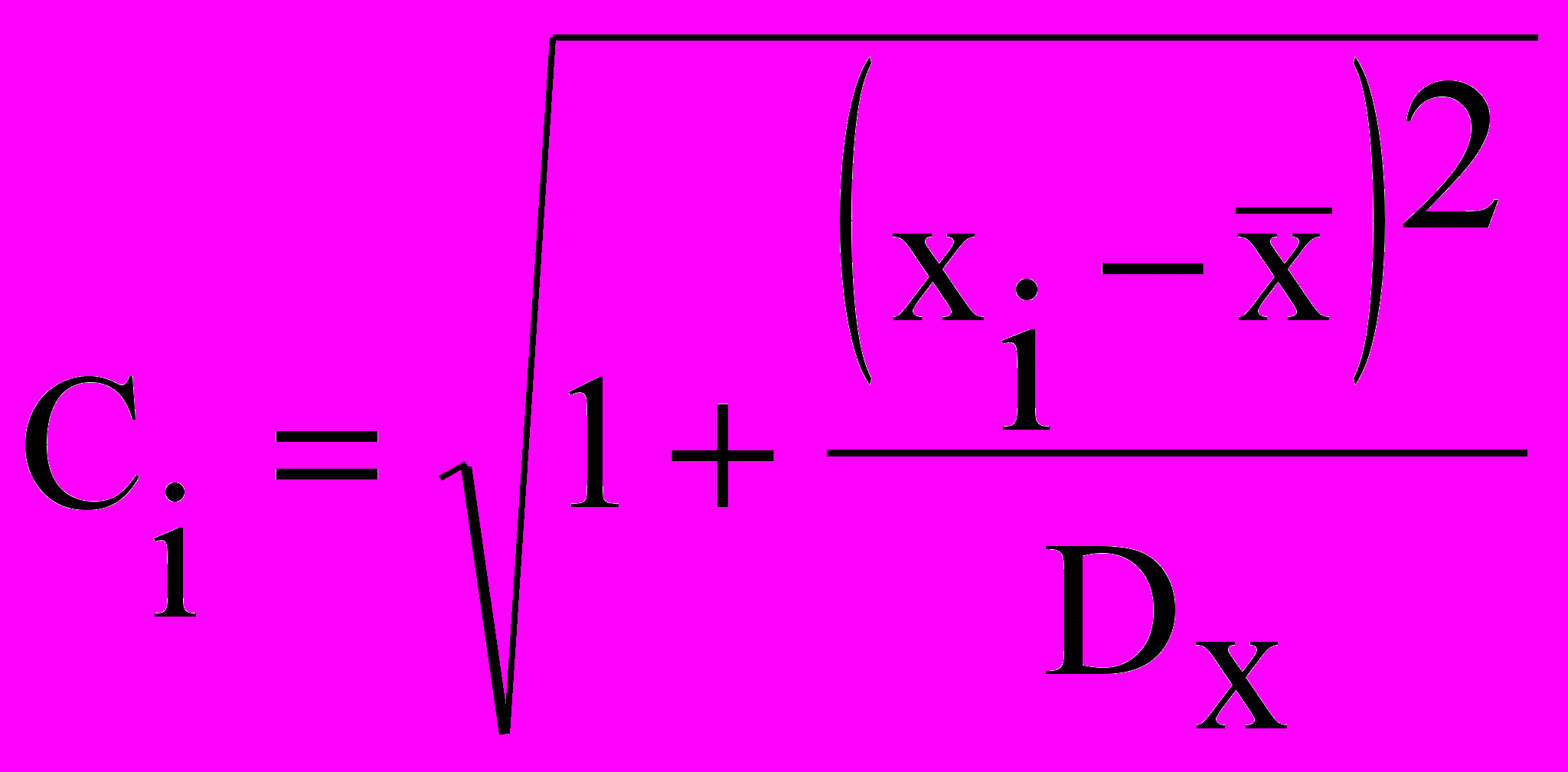• определить значение t_табл. по таблице распределения Стьюдента в зависимости от числа степеней свободы и уровня значимости α = 5%;
  
• рассчитать отклонение ;
  
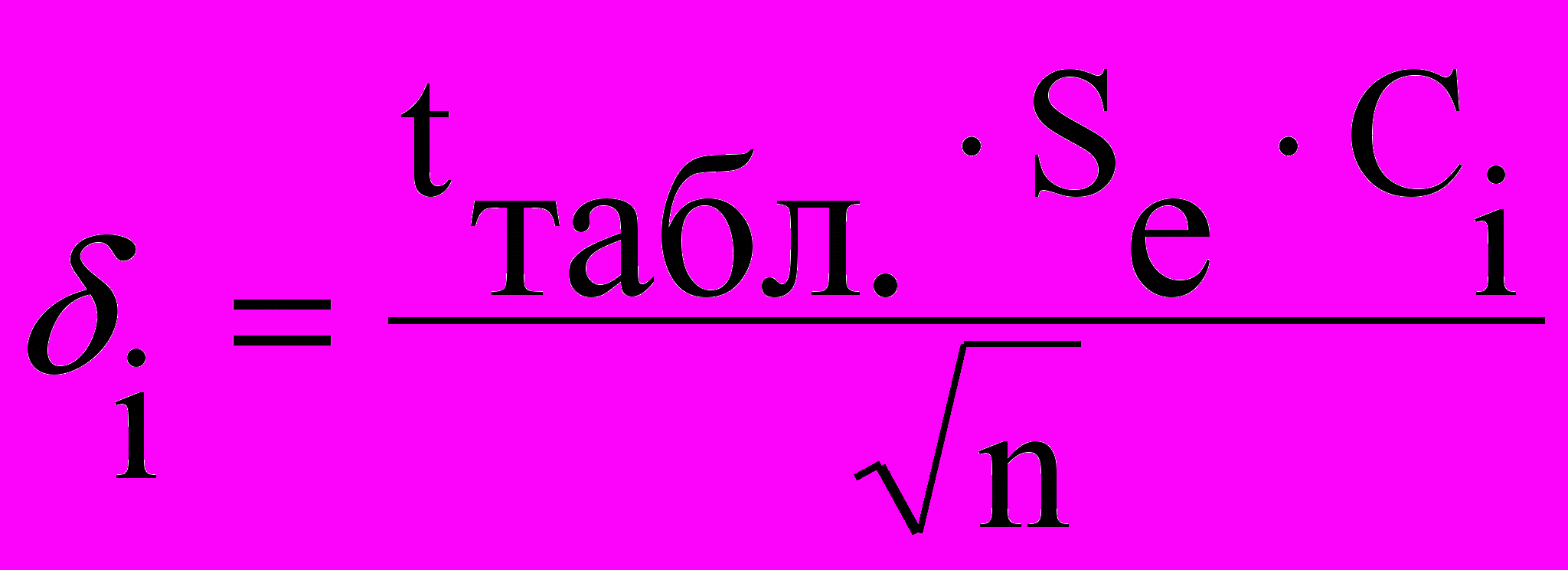• вычислить границы доверительного интервала;
  
• построить диаграммы:
  

1. практическую (эмпирическая линия),
   
2. прогноз (теоретическая линия),
   
3. доверительный интервал:
   
   • нижняя граница
     
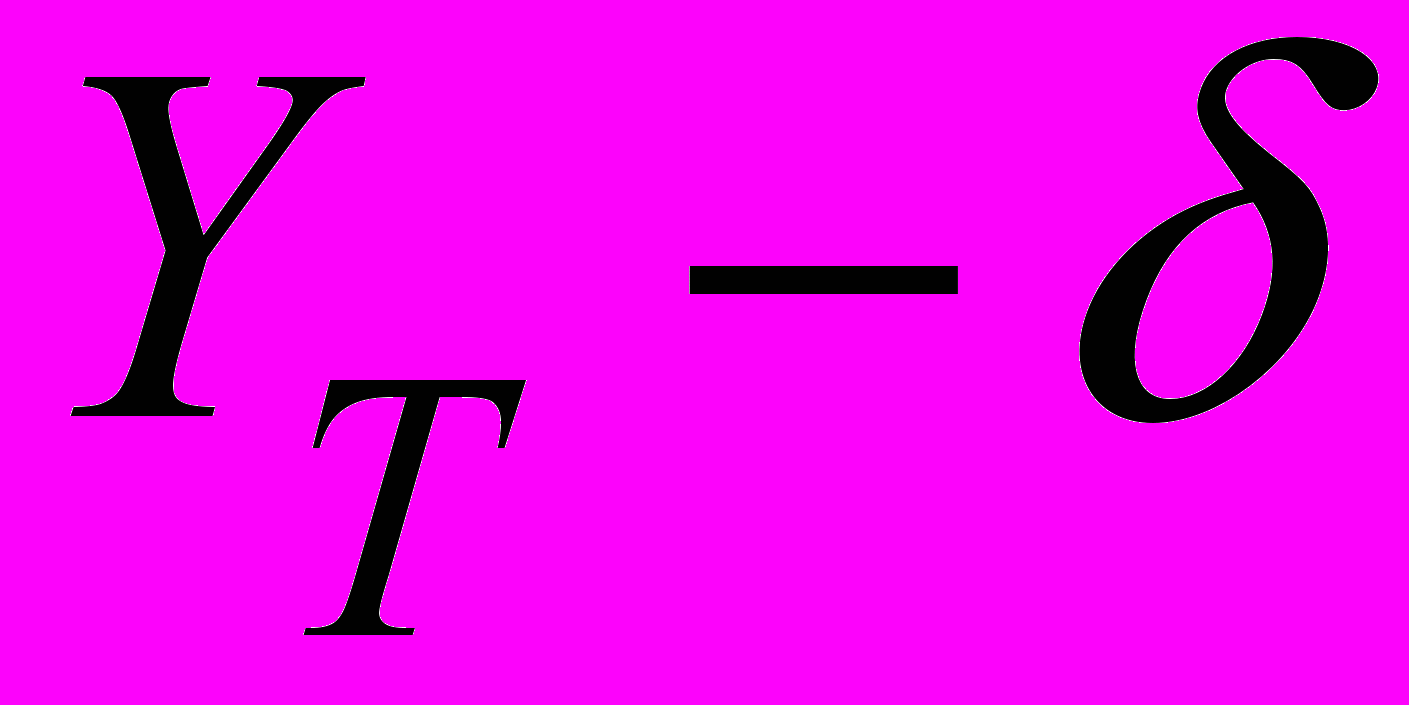
   • верхняя граница
     

Значения t_γ,k – критерия Стьюдента

k	Вероятность γ		k	Вероятность γ		k	Вероятность γ
	0,95	0,99		0,95	0,99		0,95	0,99
1	12,71	63,66	12	2,18	3,05	23	2,07	2,81
2	4,30	9,92	13	2,16	3,01	24	2,06	2,80
3	3,18	5,84	14	2,14	2,98	25	2,06	2,79
4	2,78	4,60	15	2,13	2,95	26	2,06	2,78
5	2,57	4,03	16	2,12	2,92	27	2,05	2,77
6	2,45	3,71	17	2,11	2,90	28	2,05	2,76
7	2,36	3,50	18	2,10	2,88	29	2,04	2,76
8	2,31	3,35	19	2,09	2,86	30	2,04	2,75
9	2,36	3,25	20	2,09	2,84	40	2,02	2,70
10	2,23	3,17	21	2,08	2,83	60	2,00	2,66
11	2,2,	3,11	22	2,07	2,82	120	1,98	2,62

Задачи корреляционно- регрессионного анализа решаются по следующему алгоритму:

1. строится эмпирическая линия по данным наблюдения (по виду этой линии определяется тип регрессионной модели);
   
2. определяется теснота связи между признаками. В качестве показателей тесноты связи между признаками используются коэффициенты корреляции. (определяется значимость указанных коэффициентов);
   
3. составляется уравнение регрессии, коэффициенты которого определяются методом наименьших квадратов;
   
4. рассчитываются коэффициенты эластичности;
   
5. строится теоретическая линия;
   
6. проводится прогноз значений результативного признака;
   
7. делаются выводы.