Методические указания для выполнения курсовой работы по дисциплине «Теория принятия решений» для студентов специальности 230102

Вид материала

Методические указания

Содержание 4. Основные теоретические положения для выполнения задания

Подобный материал:

• Методические указания к выполнению курсовой работы по дисциплине «Теория инноваций», 284.66kb.
• Методические указания для выполнения курсовых работ по дисциплине «Теория организации», 322.88kb.
• Методические указания для выполнения курсовой работы по дисциплине «Макроэкономика», 976.03kb.
• Методические указания по содержанию и организации выполнения курсовой работы по дисциплине, 1445.93kb.
• Методические указания для выполнения курсовой работы по дисциплине «Управление персоналом», 489.37kb.
• Методические указания для выполнения курсовой работы по дисциплине «Управление персоналом», 408.97kb.
• Методические указания по выполнению курсовой работы Для студентов высших учебных заведений, 822.07kb.
• Методические указания для выполнения курсовой работы по дисциплине «Экономика организаций, 379.4kb.
• Методические указания для выполнения курсовой работы по дисциплине: «Метрология, стандартизация, 170.43kb.
• Методические указания для выполнения курсовой работы по дисциплине «Финансы» (для студентов, 506.46kb.

4. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ ДЛЯ

ВЫПОЛНЕНИЯ ЗАДАНИЯ

В основной части работы отражается технология решения конкретной задачи, включающая этапы:

1. анализ ситуации, содержательная постановка задачи управления и принятия решения;
   
2. формализованное описание системы управления;
   
3. выбор и обоснование критериев эффективности;
   
4. построение математической модели задачи принятия решения и поиск наилучшего решения;
   
5. анализ и разработка рекомендаций по практическому использованию результатов.
   

Этап 1. Анализ ситуации, содержательная постановка задачи управления и принятия решения.

На данном этапе отражается [1,2,9] краткая характеристика системы управления (назначение, описание входов и выходов, обобщенные свойства системы), краткая характеристика систем внешней среды, описание взаимодействия элементов исследуемой системы и с элементами среды, формирование требований (ограничений) к исследуемой системе. Анализ ситуации должен дать ответы на такие вопросы:

- какую проблему, и в каких условиях нужно её решать;

- когда её нужно решать;

- какими силами и средствами будет решаться проблема.

Содержательная постановка задачи заключается в выявлении и определении компонентов модели, и предполагает раскрытие вопросов:

- кто принимает решение;

- каковы его (их) цели;

- на какие параметры (управляемые переменные) может влиять лицо, принимающее решение (ЛПР), в каком диапазоне можно изменять значения этих переменных;

- каковы параметры окружающей среды, которые могут влиять на результаты решения задачи (неуправляемые переменные).

Таким образом, для возникновения задачи принятия решений ЛПР должно иметь цель Z, средства воздействия С на систему и должно уметь оценивать результаты этого воздействия Y. Поэтому иногда задачу принятия решений определяют как задачу, которая может быть сформулирована в терминах цели, средств и результата.

При содержательном описании задачи формируется цель. Цели должны определять желаемое состояние системы, формируются в виде текста. Например, «улучшить качество производимой продукции», «улучшить условия труда персонала», «достигнуть европейского уровня организации производства». Цель может быть представлена в одном из следующих видов:

1) стремление к достижению определенного состояния управляемой системы;

2) экстремизация параметров процесса управления.

Такое деление, в общем, является условным, но оно позволяет в какой-то мере формализовать процесс выбора и определения критериев эффективности (целевых функций).

Далее, на основании ответов на эти вопросы, необходимо провести формализованное описание системы управления и задачи принятия решения.

Этап 2. Формализованное описание системы управления.

Формализованное описание задает меры для измерения выше выявленных компонентов модели системы управления. На данном этапе формализованного описания необходимо определить способы и единицы измерения уровня достижения цели, определить единицы измерения параметров задачи, их характер (непрерывный, дискретный), а также формальную запись ограничений на эти параметры. Определяются неуправляемые параметры задачи, влияющие на ее решение. Значения неуправляемых параметров необходимо учесть при формировании ограничений на задачу. Если неуправляемые параметры имеют случайный характер, то можно ввести статистические оценки этих параметров.

Проведя содержательную и формализованную постановку задачи, можно определить состав и структуру входной и выходной информации для задачи. В зависимости от степени формализованного описания решаемой задачи в дальнейшем используются соответствующие методы теории принятия решения в условиях определенности или риска и неопределенности [9].

Этап 3. Выбор и обоснование критериев эффективности.

Сравнение и выбор альтернативных решений возможен, если ввести измеритель степени достижения намеченной цели. Таким измерителем является критерий. Содержанием данного этапа является построение системы критериев, однозначно характеризующих соответствующие цели субъекта управления. Сформированные критерии в дальнейшем должны в некотором смысле заменить цели, стать их подобием, моделью целей. Критерием ценности альтернативы может служить любой ее признак, измеренный на качественном либо количественном уровне. Например, «Минимизировать затраты на производство продукции», «Выпуск продукции увеличить на 75%», «Сократить среднее время обслуживания клиента в 2 раза».

Одним из требований повышения адекватности описания цели является требование многокритериальности. Для описания цели должно быть введено столько критериев, чтобы они достаточно полно характеризовали цель при минимальном их числе. Это требование удовлетворяется, если критерии независимы. Поиск компромисса между полнотой (точностью) описания целей и количеством критериев является более искусством, чем наукой. Определение критериев оценки и выбора решений может быть осуществлено методами экспертных оценок, а также с помощью методов математической статистики.

Процесс выбора и обоснования критериев эффективности невозможно полностью формализовать, является творческим процессом, поэтому могут быть даны лишь общие рекомендации. Для хорошо формализуемых проблем цели первого вида (стремление к достижению определенного состояния управляемой системы) могут быть оценены по критерию минимума «отклонения» или «расстояния» до цели. Если цель относится ко второму виду (экстремизация параметров процесса управления), то минимизируется или максимизируется значение некоторого параметра процесса управления, который зависит от управляемых переменных. Для оценки альтернатив разрешения слабо формализуемых сложных проблем привлекаются эксперты [9].

Этап 4. Построение математической модели задачи принятия решения и поиск наилучшего решения

Качество функционирования системы управления, призванной учитывать многоцелевой характер целей Z, неопределенность исходов Y вследствие влияния среды Е, не может быть оценено без учета мнения ЛПР, без его системы взглядов (предпочтений), сопоставления способов использования ресурсов С. Поэтому для принятия решения ЛПР должно выработать для себя правила оценки альтернатив и их выбора через свою систему предпочтений

,

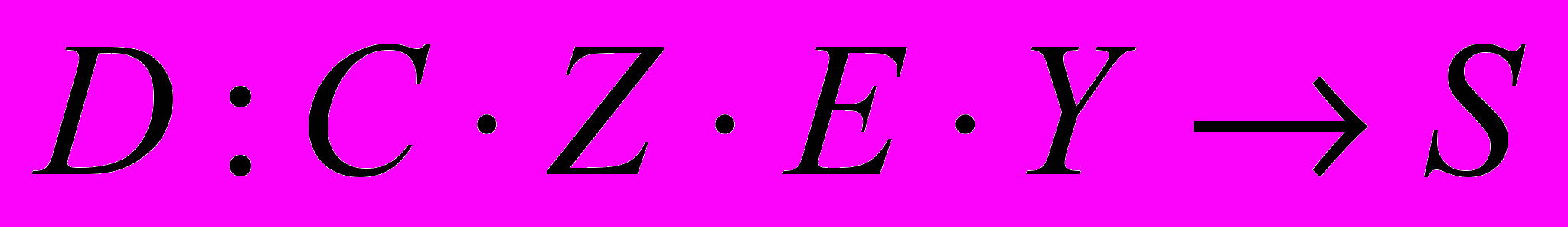где S — система предпочтений ЛПР;

D — решающее правило (модель выбора, принятия решения) для ЛПР, адекватно отображающее систему предпочтений S в выборе лучшей альтернативы .

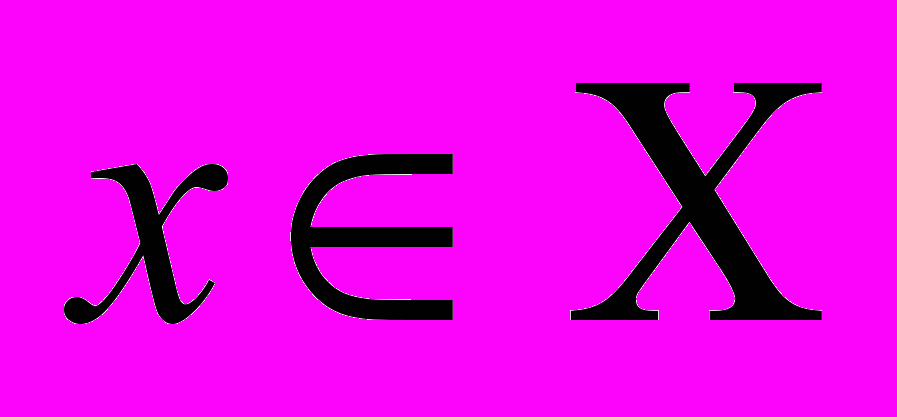Под системой предпочтений S ЛПР здесь понимается совокупность его представлений 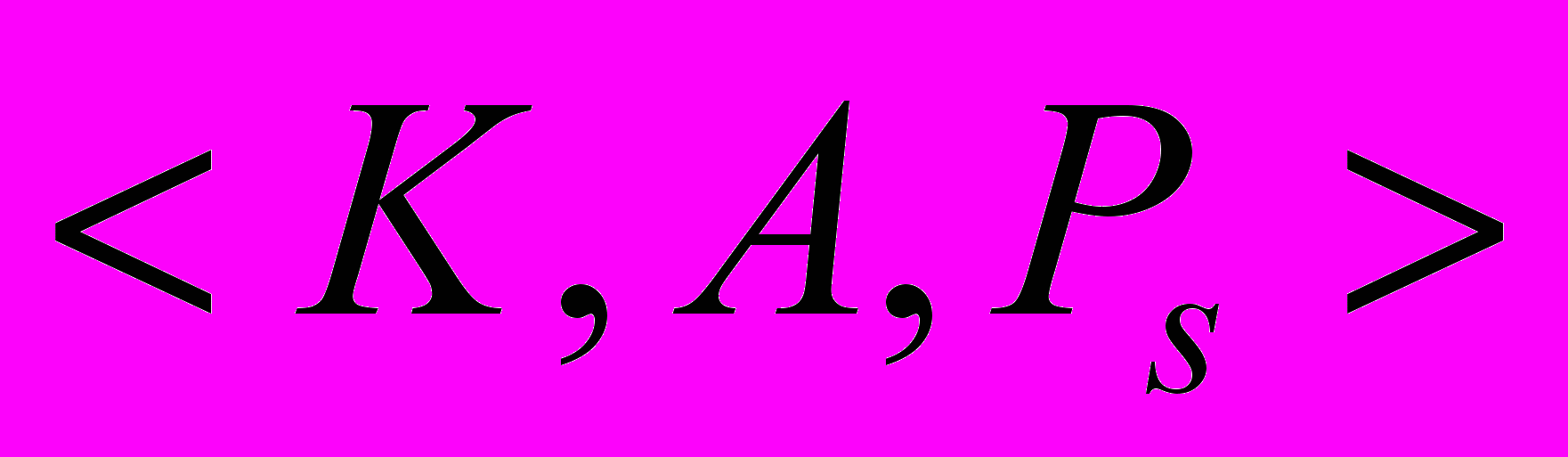, позволяющих оценивать исходы 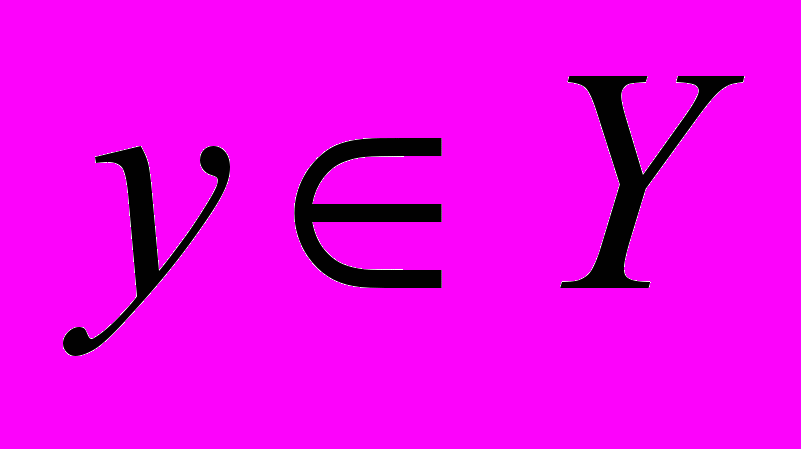и производить целенаправленный выбор альтернатив ,

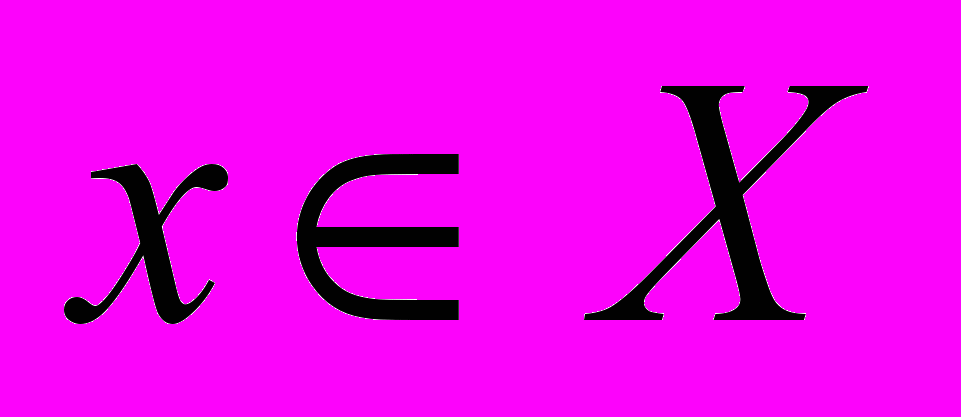где K — множество критериев оценки исходов;

A — множество шкал измерения критериев К;

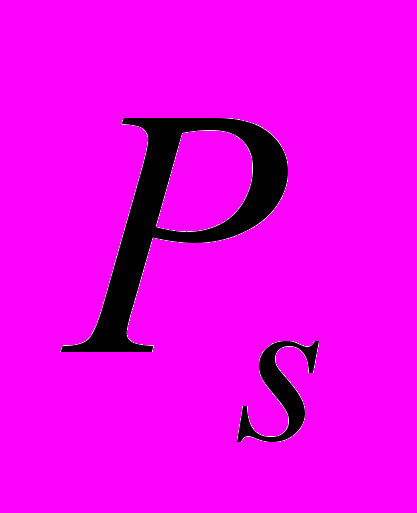— система отношений на множестве элементов процесса принятия решений (например, критериев, альтернатив).

В условиях определенности задачи принятия решений, как правило, хорошо формализуются и описываются в терминах количественных переменных, и для их решения используются оптимизационные модели и аппарат математического программирования. Построение математической модели при таких условиях включает построение целевых функций и ограничений на область изменения переменных. В соответствии с введенными переменными строятся целевые функции. Если в задаче одна целевая функция, то это задача скалярной оптимизации, если две и более функций — задача векторной оптимизации. Ограничения на область изменения переменных (множество допустимых решений, множество альтернативных решений) определяется ограничениями (ресурсными, временными, технологическими и др.), сформулированными при содержательном и формализованном описании задачи.

При выборе переменных, по возможности, следует отдавать предпочтение непрерывным переменным, т.к. алгоритмы для решения задач с непрерывными переменными разработаны лучше, чем для задач с дискретными переменными.

Важным следствием применения методов оптимизации для широкого круга задач явилось выделение небольшого числа классов, к которым сводится большинство из них. Все эти задачи достаточно полно описаны в рекомендуемой литературе. Вследствие их частой повторяемости для них были разработаны методы построения моделей и получения решений на этих моделях.

Независимо от того, какой метод решения задачи используется, всегда отыскивается оптимальное или близкое к нему решение, максимизирующее критерий качества на модели (целевую функцию) при заданных условиях и ограничениях. При решении задач принятия решений по многим критериям (задач многокритериальной оптимизации) возникают трудности определения наилучшего с точки зрения ЛПР компромиссного решения из множества допустимых решений, в том числе и оптимальных решений, полученных по отдельным локальным критериям. К этим трудностям, прежде всего, относят нормализацию критериев, определение принципа (схемы) выбора компромиссного решения (принципа оптимальности), учет приоритета критериев [8].

Для хорошо формализуемых задач принятия решений множество альтернативных решений определяется ограничениями модели на область изменения переменных, и как таковой, этап генерации решений отпадает сам по себе. Зато для задач слабо и неподдающихся формализации этап генерации множества решений, из которого в дальнейшем производится отбор решения, играет важную роль. При формировании вариантов решений следует достаточно полно генерировать варианты для того, чтобы не исключить потенциально оптимальный вариант.

Полученная в процессе подготовки решения информация о множестве целей, критериев их достижения, приоритетов целей и критериев, значений (качественных или количественных оценок) критериев по оцениваемым альтернативам в предполагаемых возможных ситуациях их реализации уменьшает неопределенность задачи и обеспечивает условия для выбора оптимального решения [9].

Оценка альтернатив 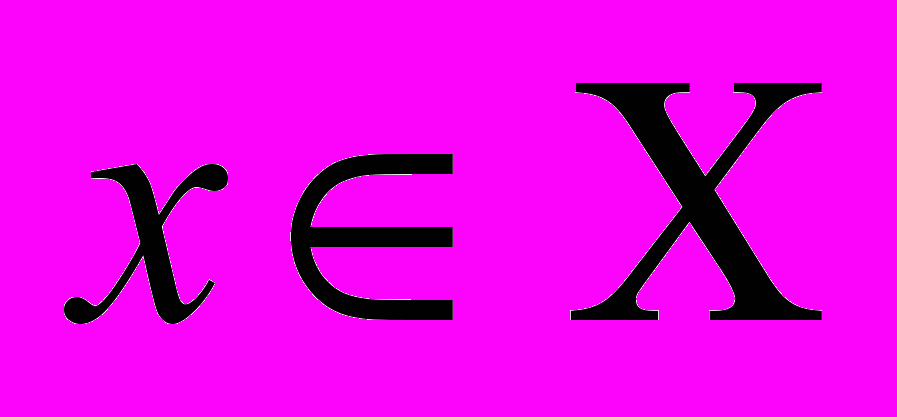производится на базе возможной информации о критериях 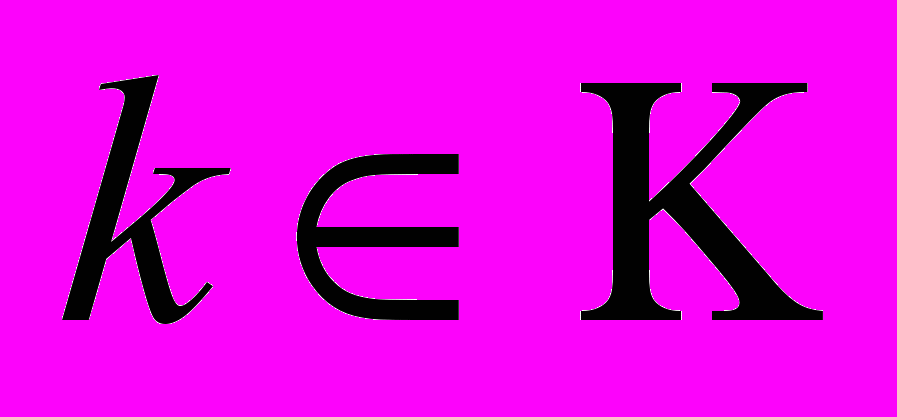и предполагаемых состояниях внешней среды 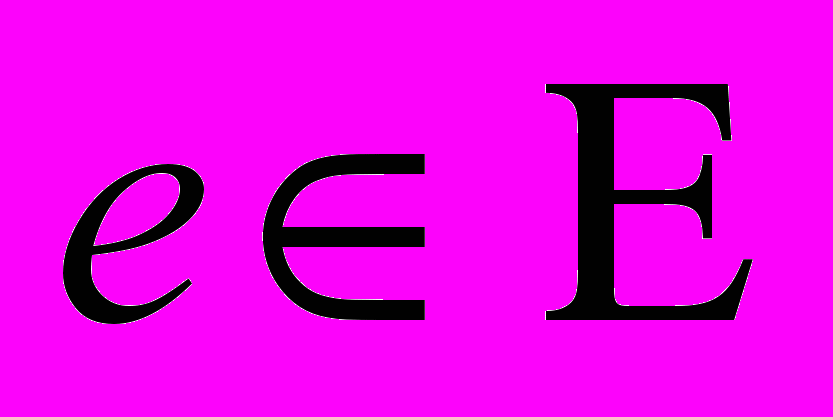при реализации этих альтернатив (табл. 1).


Таблица 1 - Информация для оценки альтернатив

Критерии		Состояния
Мощность	Шкала измерения	Мощность	Описание
Один критерий	Качественная (ранговая)	Одно состояние	Определенность
Много критериев	Количественная	Много состояний	Риск Неопределенность

Наличие и отсутствие той или иной информации позволяет выделить характерные типы индивидуальных задач принятия решений [9].

1. Один критерий k, качественные и (или) количественные оценки измерения альтернатив, одно состояние внешней среды e.

Д
Таблица 2- Тривиальная ЗПР

Альтернатива	Исход
. . .	. . .
. . .	. . .

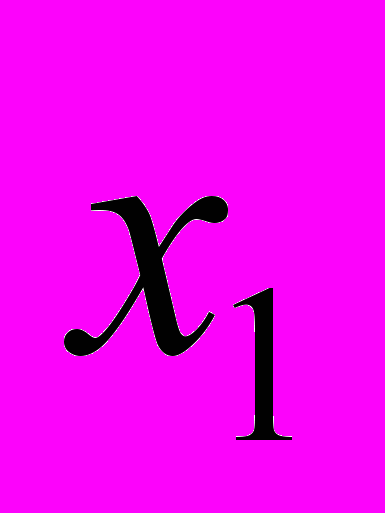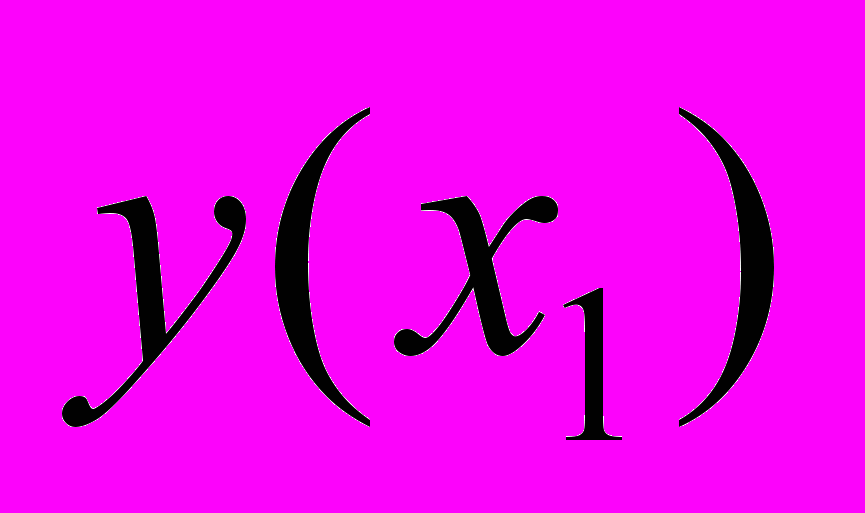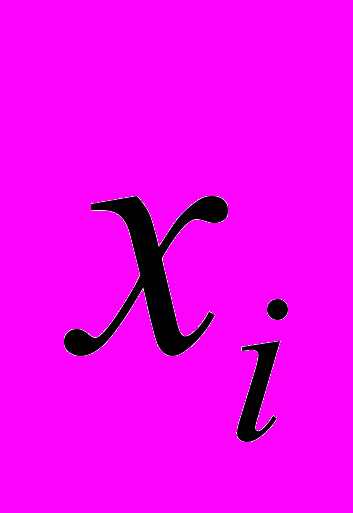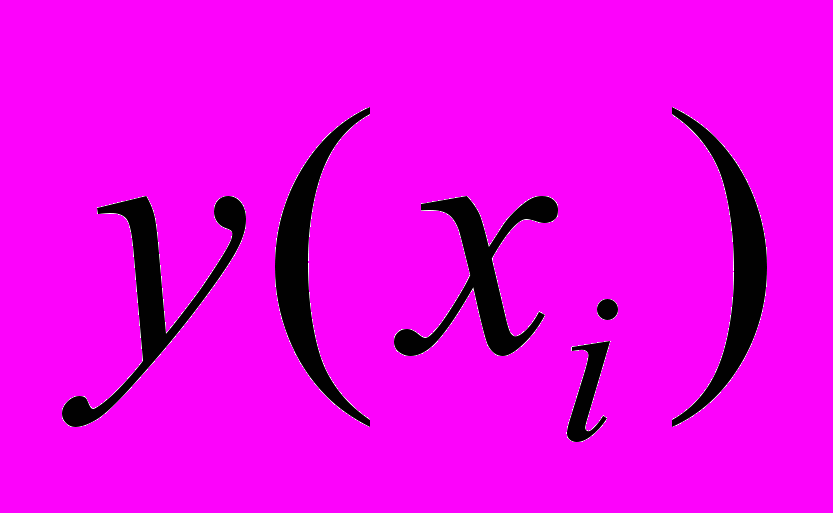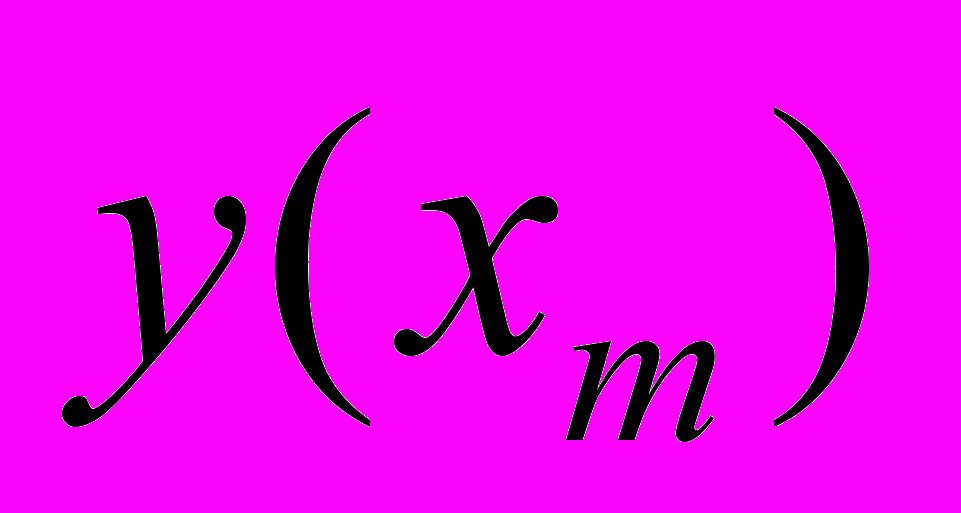ля таких задач принятия решений в условиях определенности каждой альтернативе 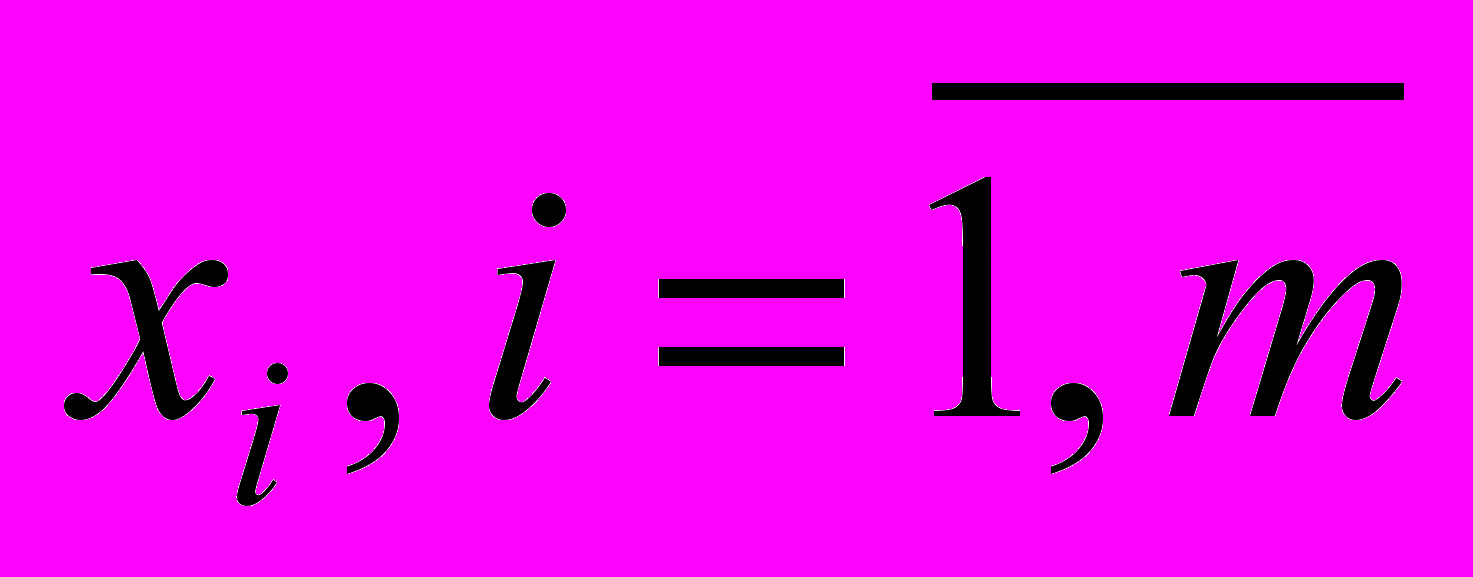соответствует однозначно исход 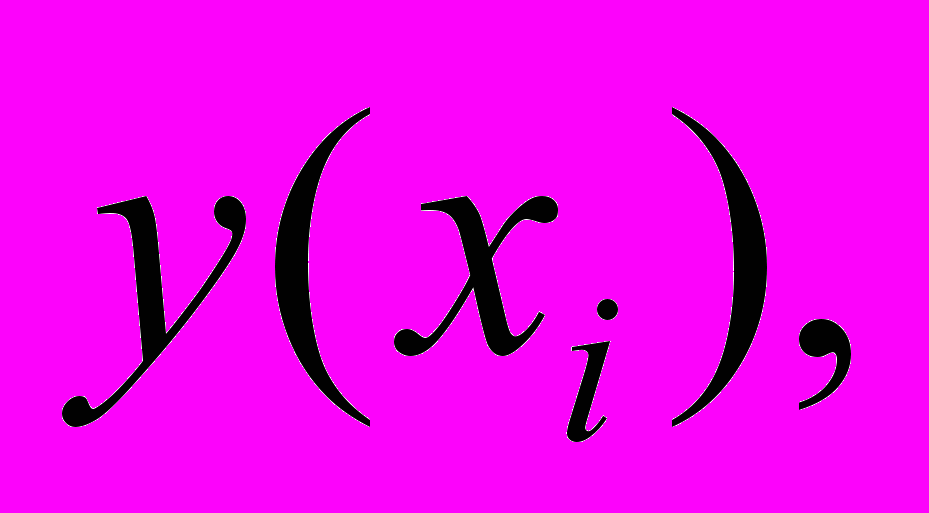измеренный по критерию k, (табл. 2).


Наилучшей альтернативой будет считаться альтернатива 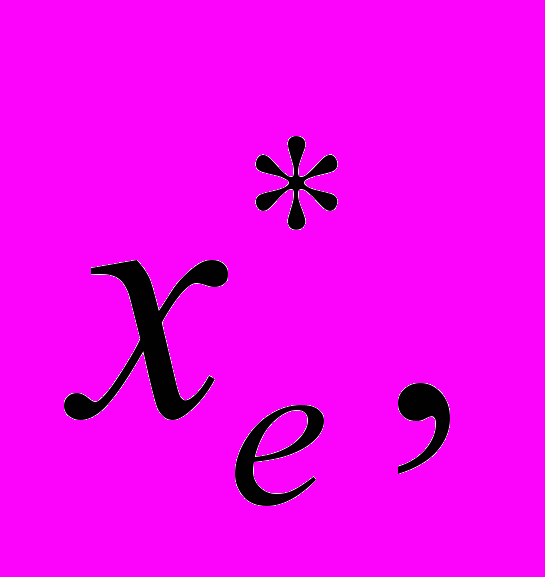у которой исход 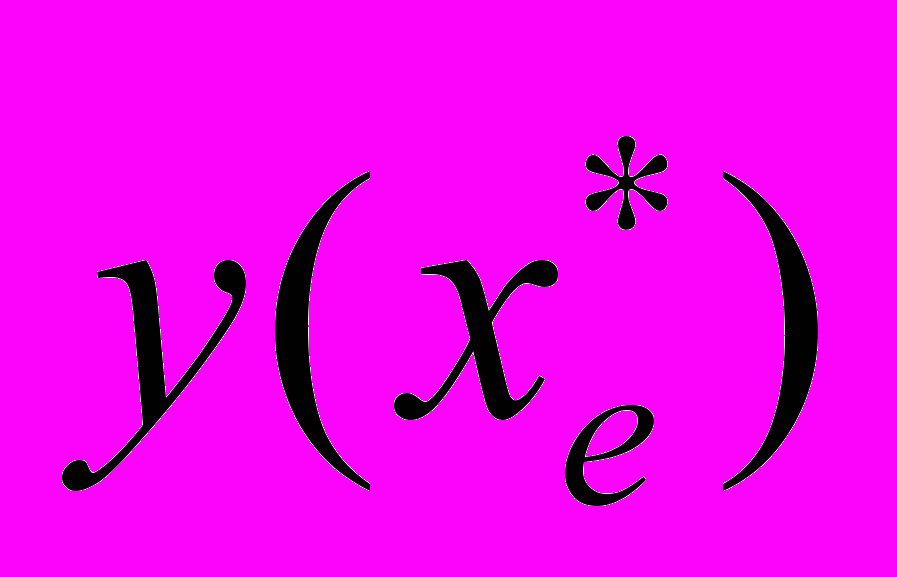будет принимать экстремальное значение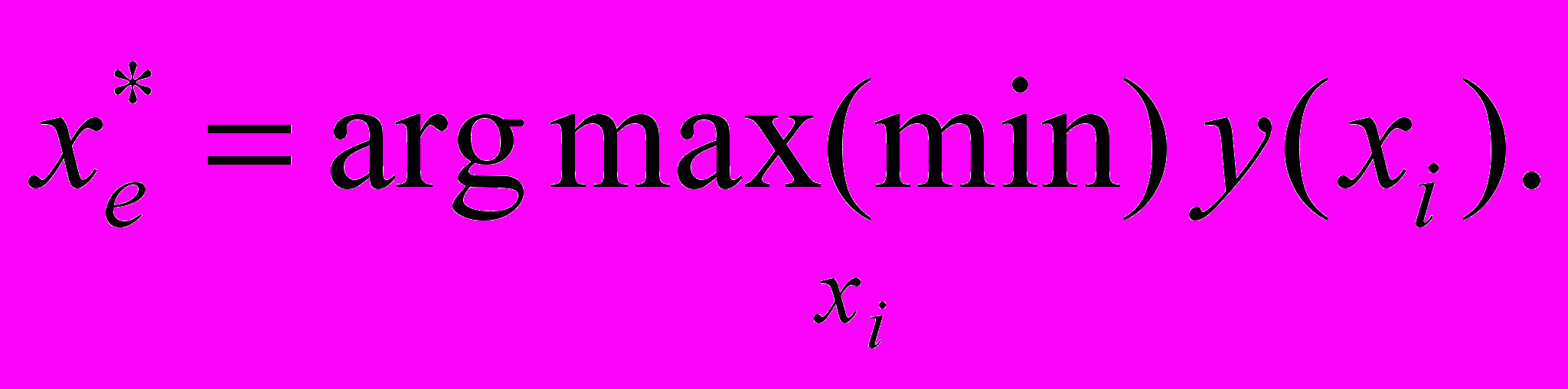



2. Много критериев 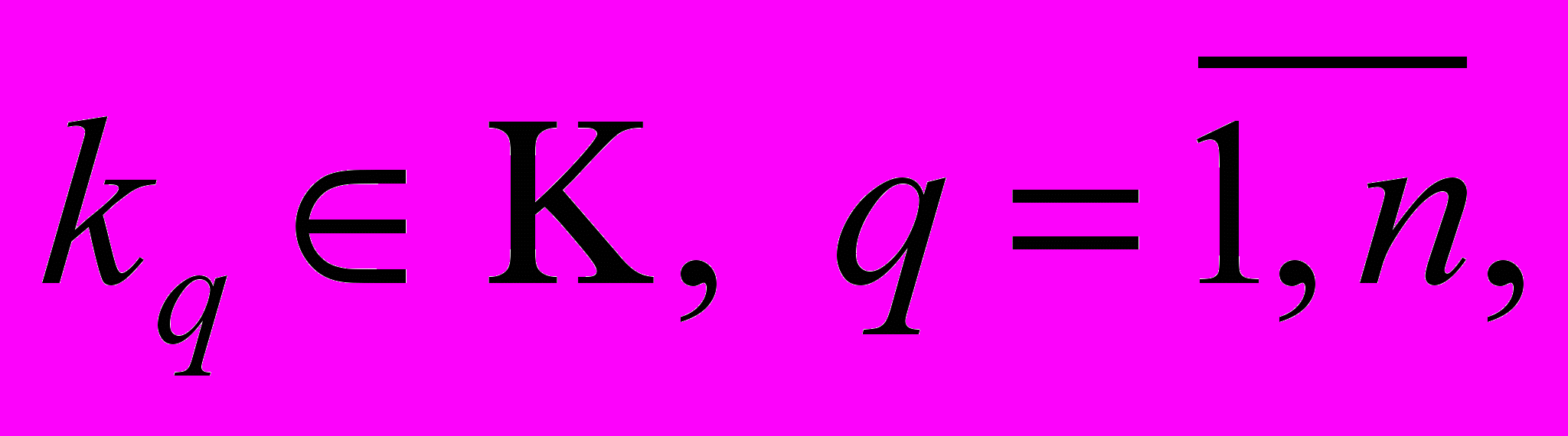качественная и (или) количественная шкала измерения критериев, одно состояние внешней среды e.

Для таких многокритериальных ЗПР в условиях определенности исход альтернативы 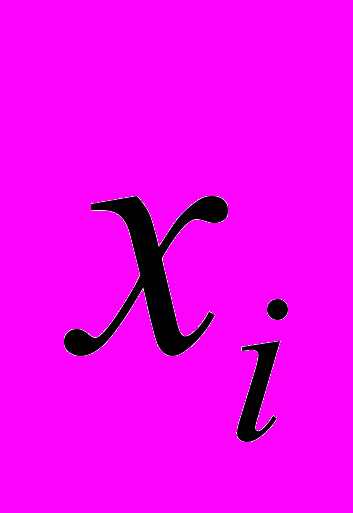оценивается через критериальные оценки (табл. 3).

Таблица 3 - Задача векторной оптимизации

Альтернатива	Исход
		…		…
		…		…
. . .	. . .	…	. . .	…	. . .
		…		…
. . .	. . .	…	. . .	…	. . .
		…		…

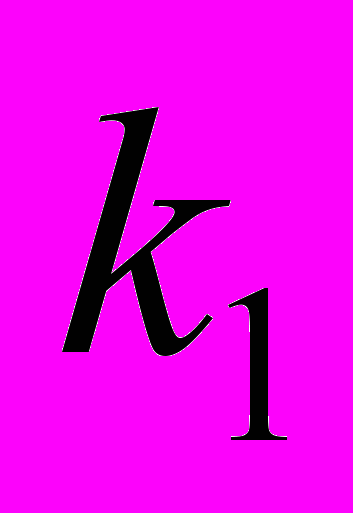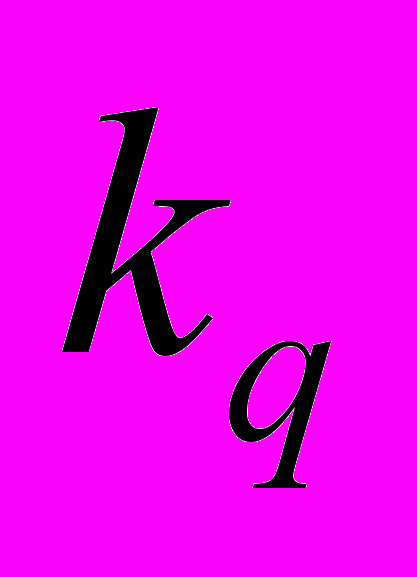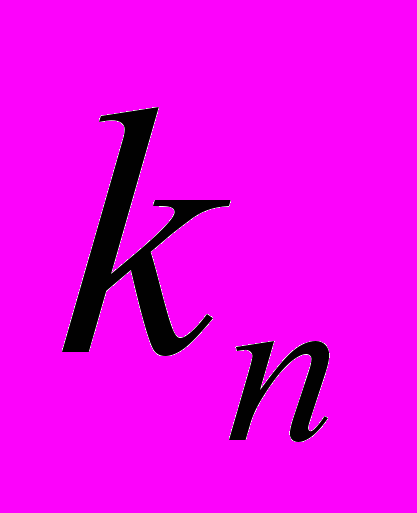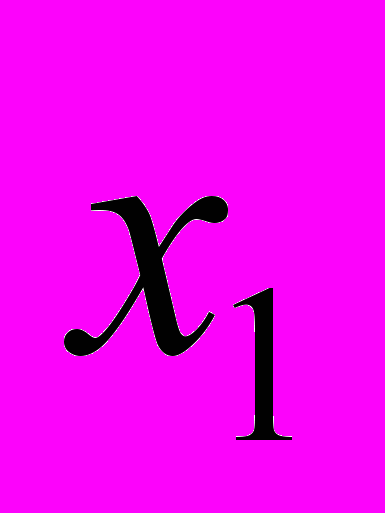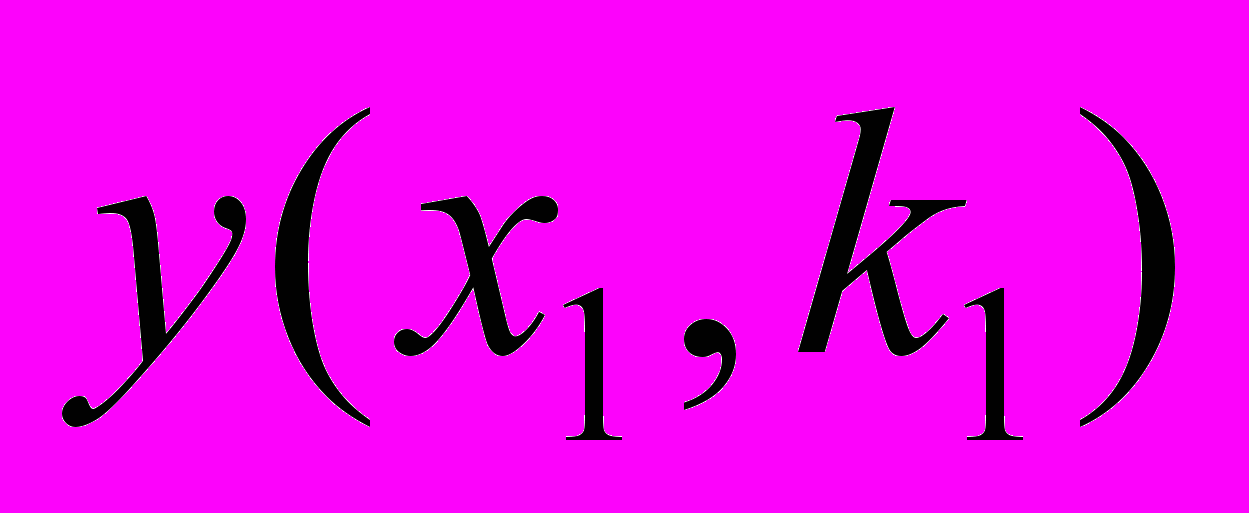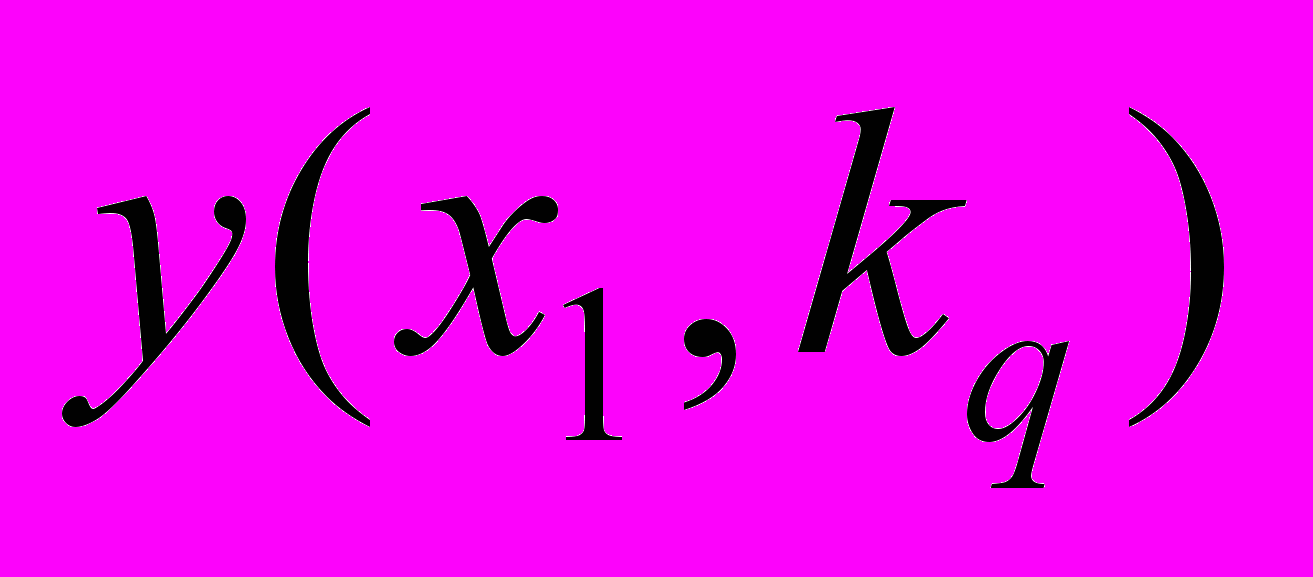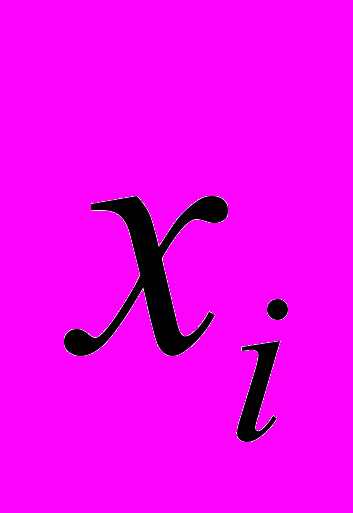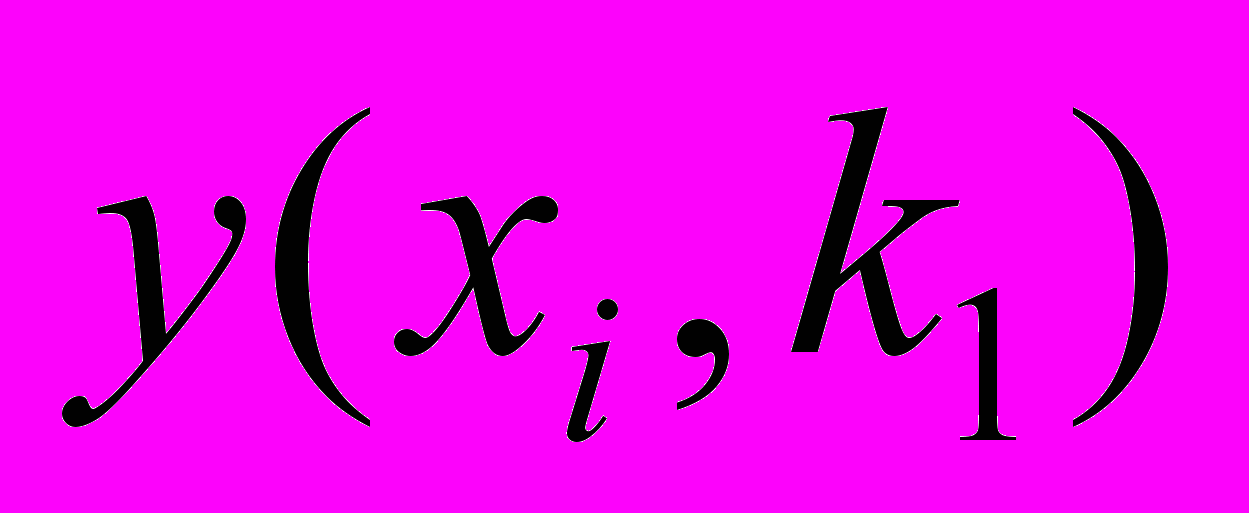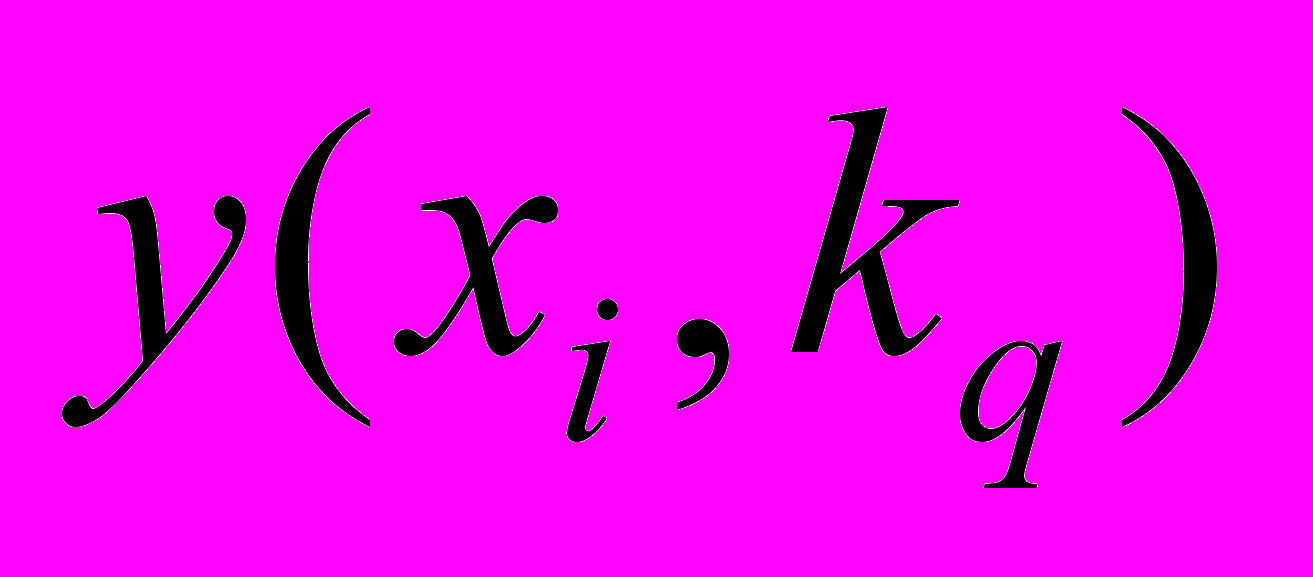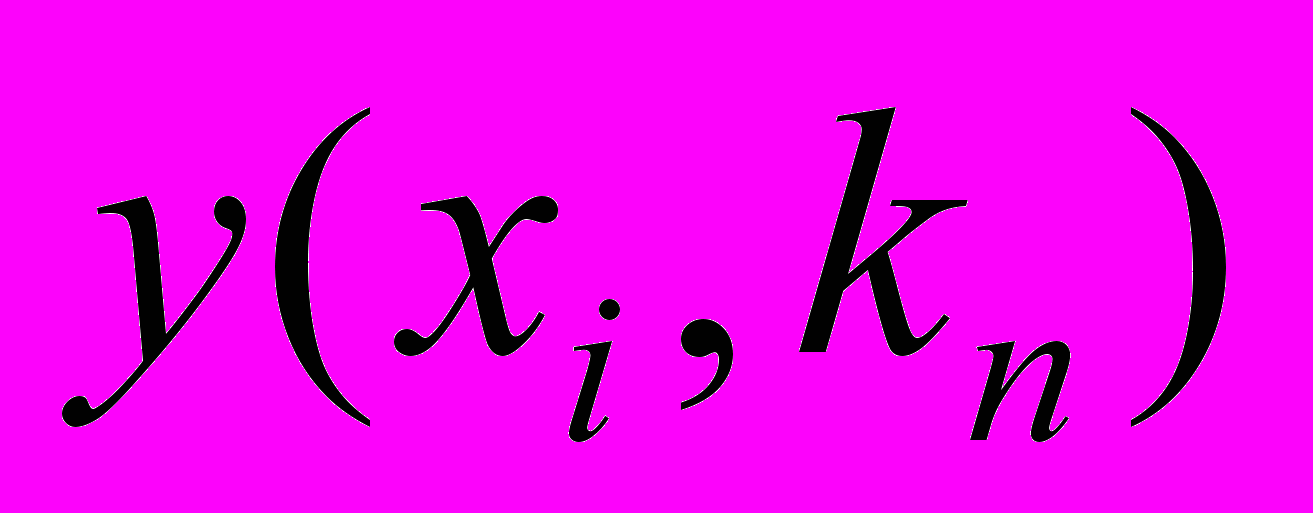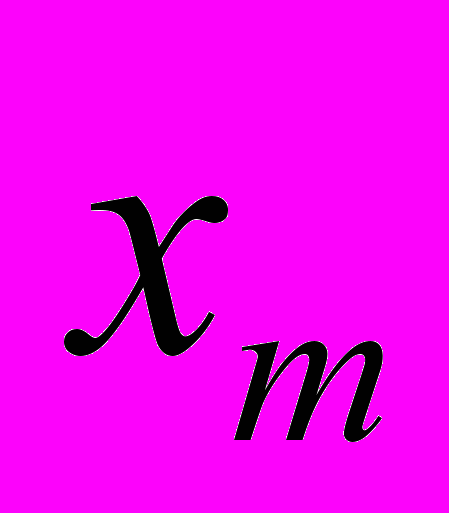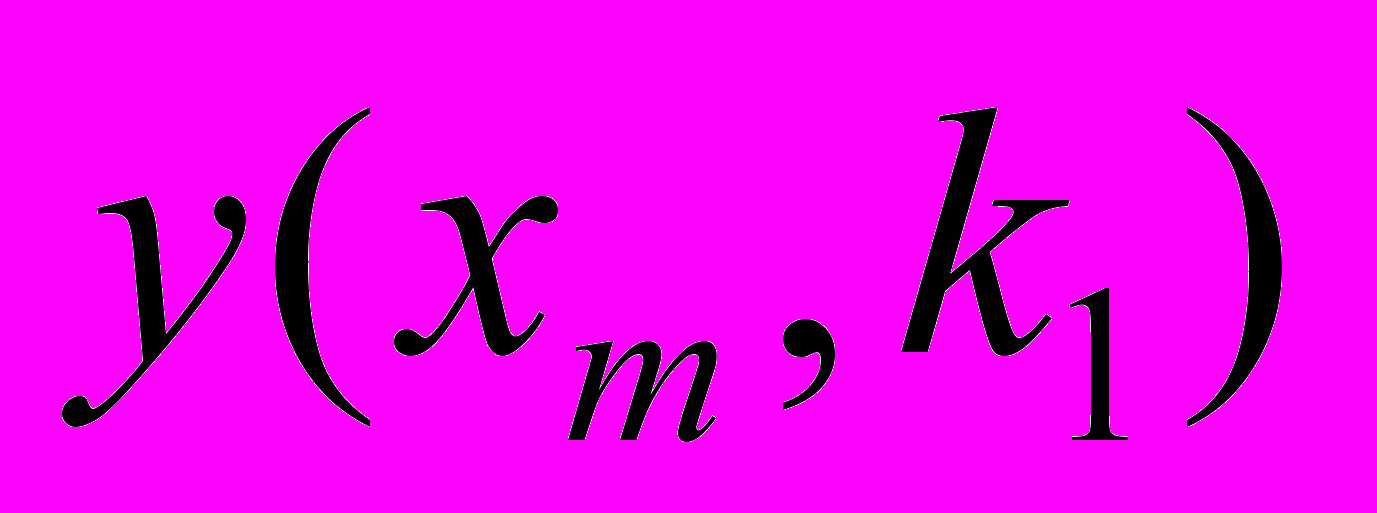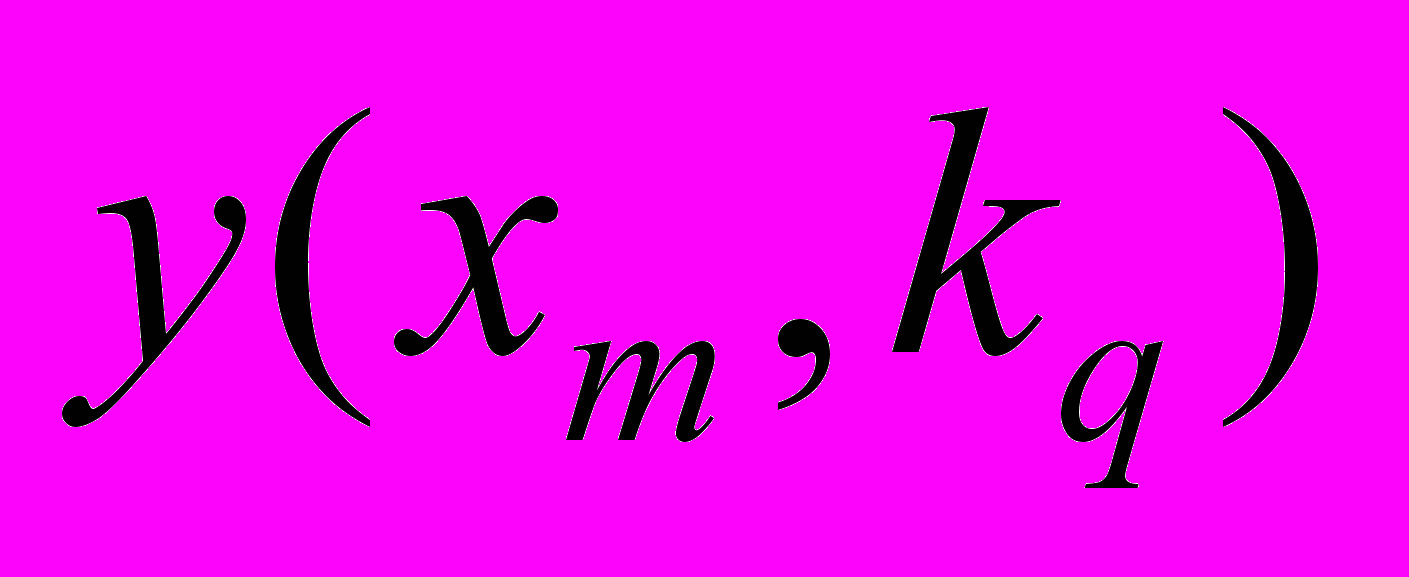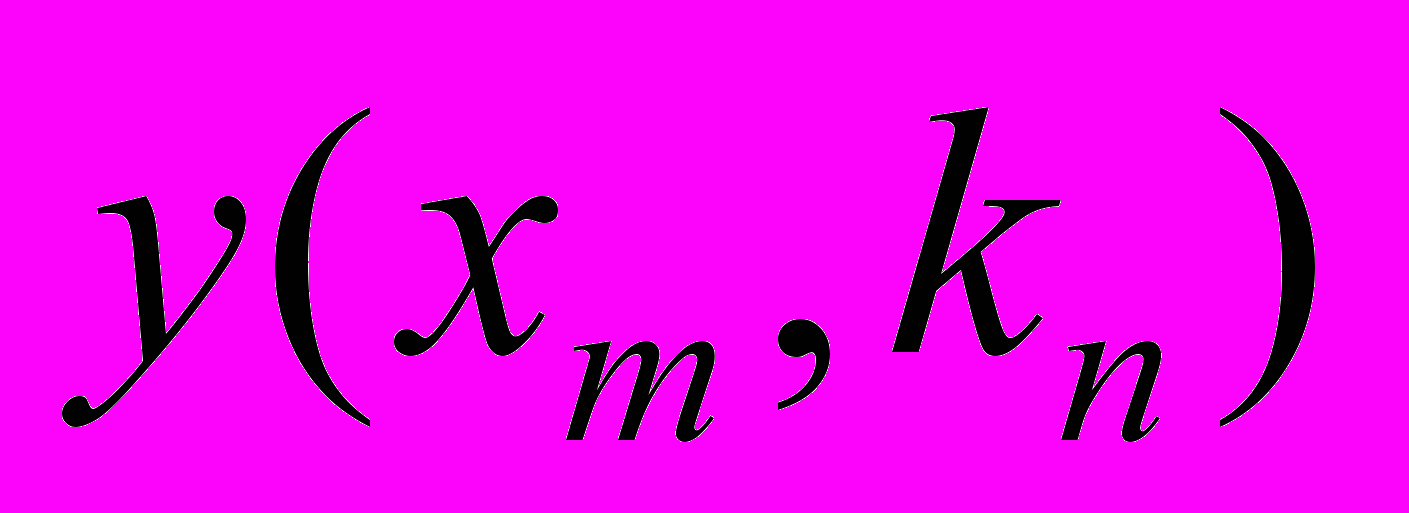Для определения наилучшей альтернативы следует перейти к одной (ранговой либо качественной) шкале измерения критериев, а далее свернуть критерии в один и перейти к тривиальной задаче, рассмотренной выше, либо применить известные схемы поиска компромиссных решений задач векторной оптимизации, либо применить известные методы решения многокритериальных ЗПР на основе четкого и нечеткого отношения предпочтения альтернатив (например, методы порогов несравнимости «Электра»), нечетких бинарных отношений [10, 11, 12, 13, 14].

3. Один критерий k, качественная или количественная шкала измерения, много состояний внешней среды

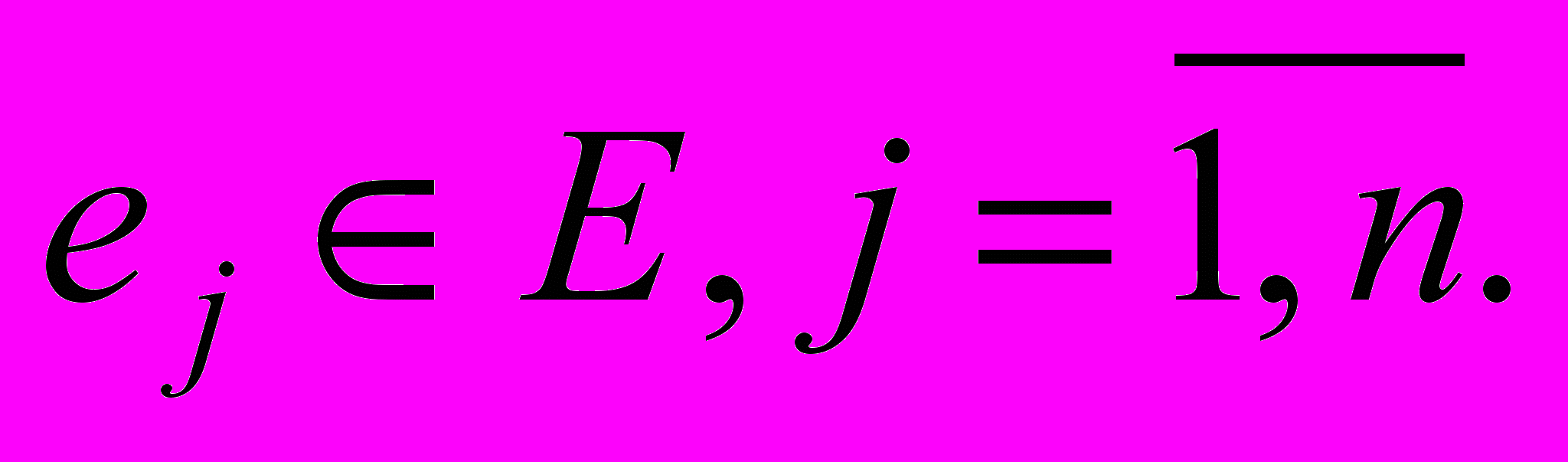
Реализация альтернативы 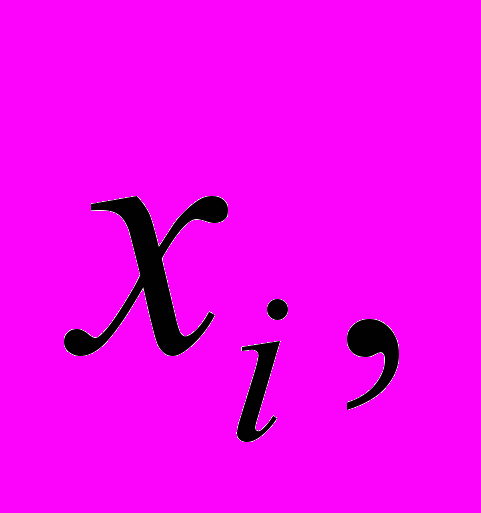оцениваемой по критерию k в зависимости от ситуации может привести к исходу 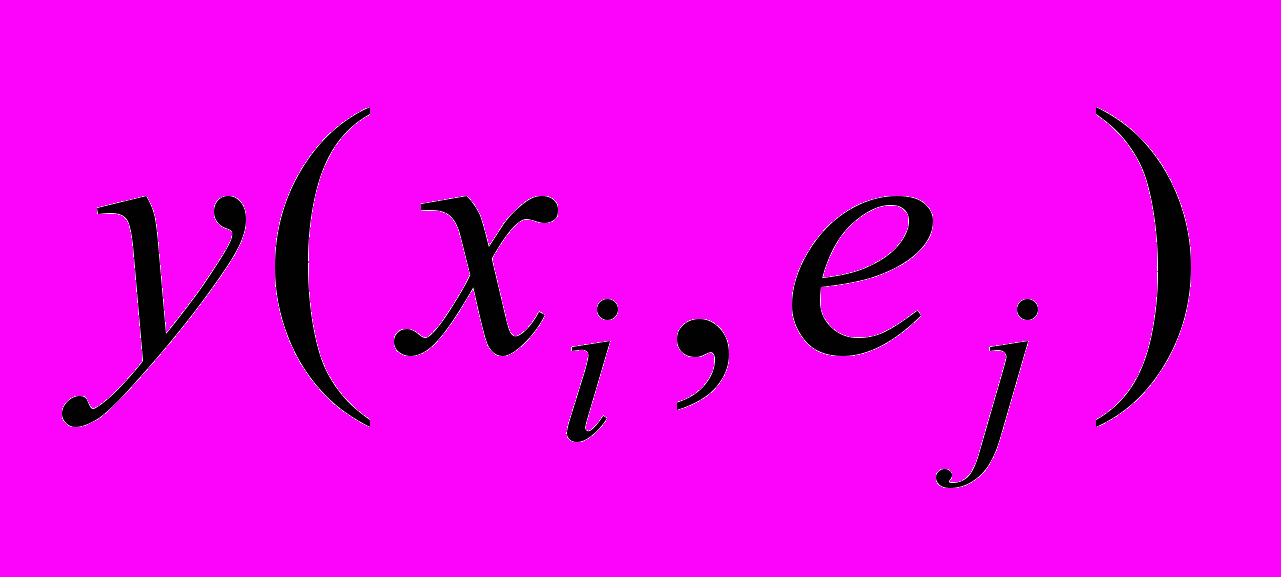(табл. 4).

Оценку исходов приводят к одной шкале измерения. Если известны вероятности 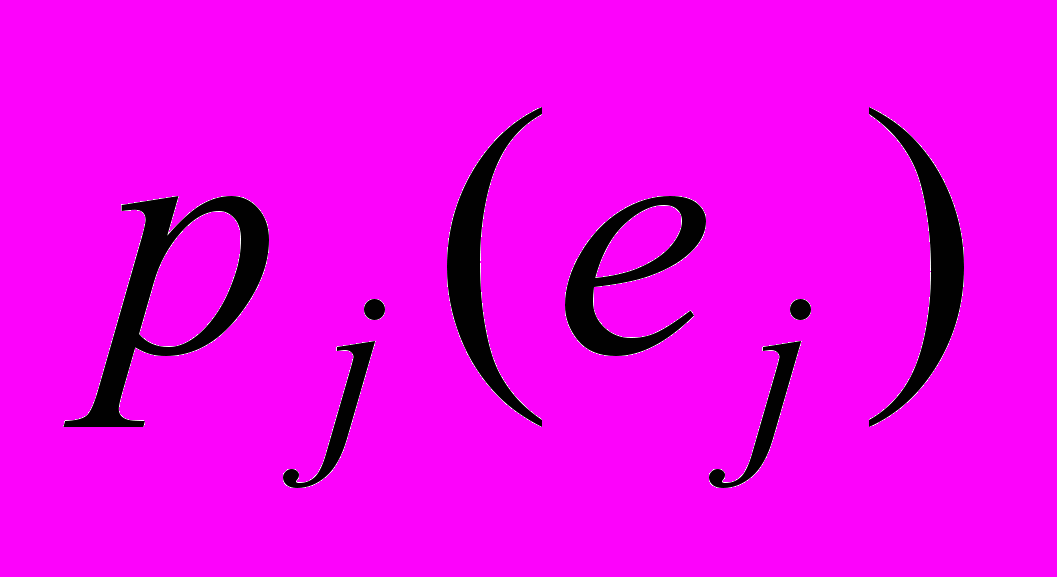наступления ситуаций 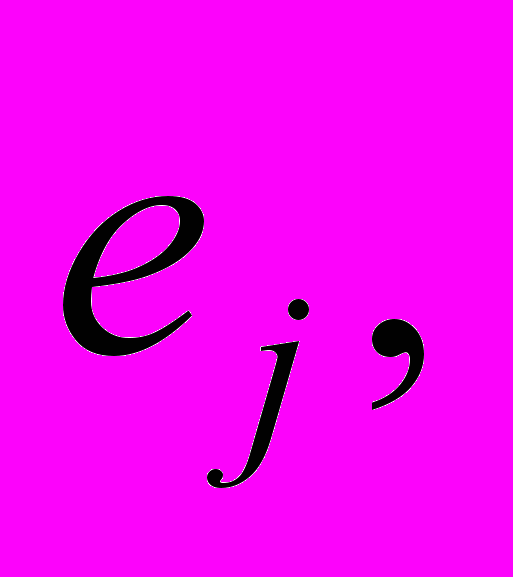то определение наилучшей альтернативы может быть произведено через критерии выбора решений в условиях риска (например, по критерию Байеса). При отсутствии информации о вероятностях 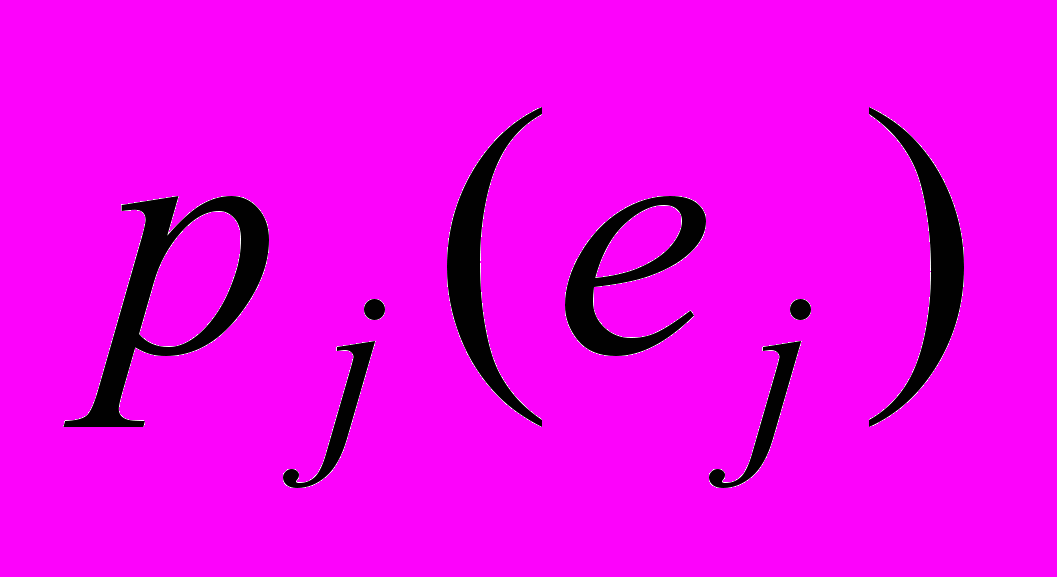в зависимости от наличия

или отсутствия дополнительной информации о предпочтениях наступления ситуаций, от активности поведения (противодействия) элементов внешней среды применяют соответствующие способы выбора альтернатив. Эти способы описаны в [9, 15, 16, 17, 18].


Таблица 4 - Задача ПР в условиях риска и неопределенности

Альтернатива	Исход
		…		…
		…		…
. . .	. . .	…	. . .	…	. . .
		…		…
. . .	. . .	…	. . .	…	. . .
		…		…

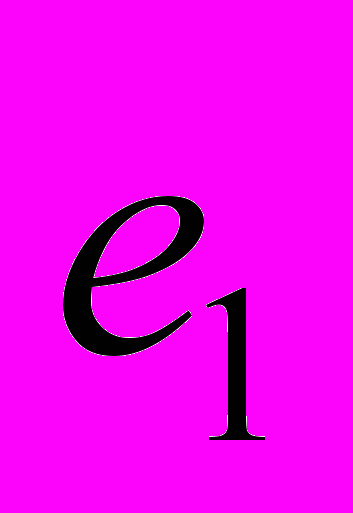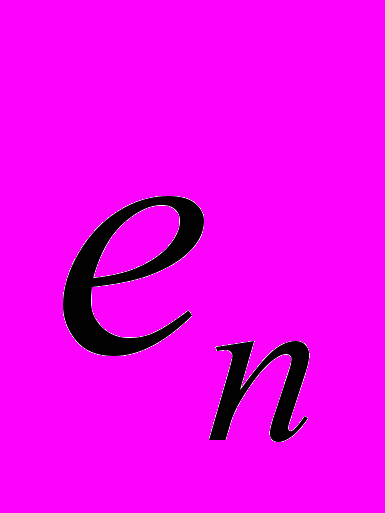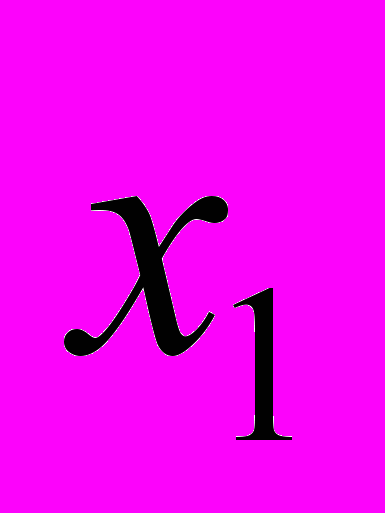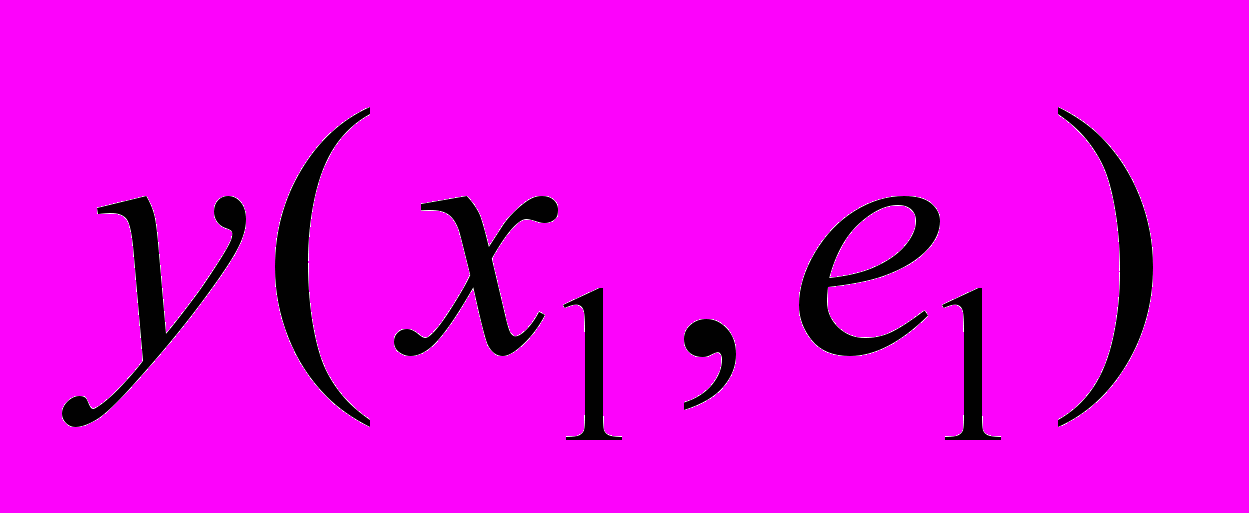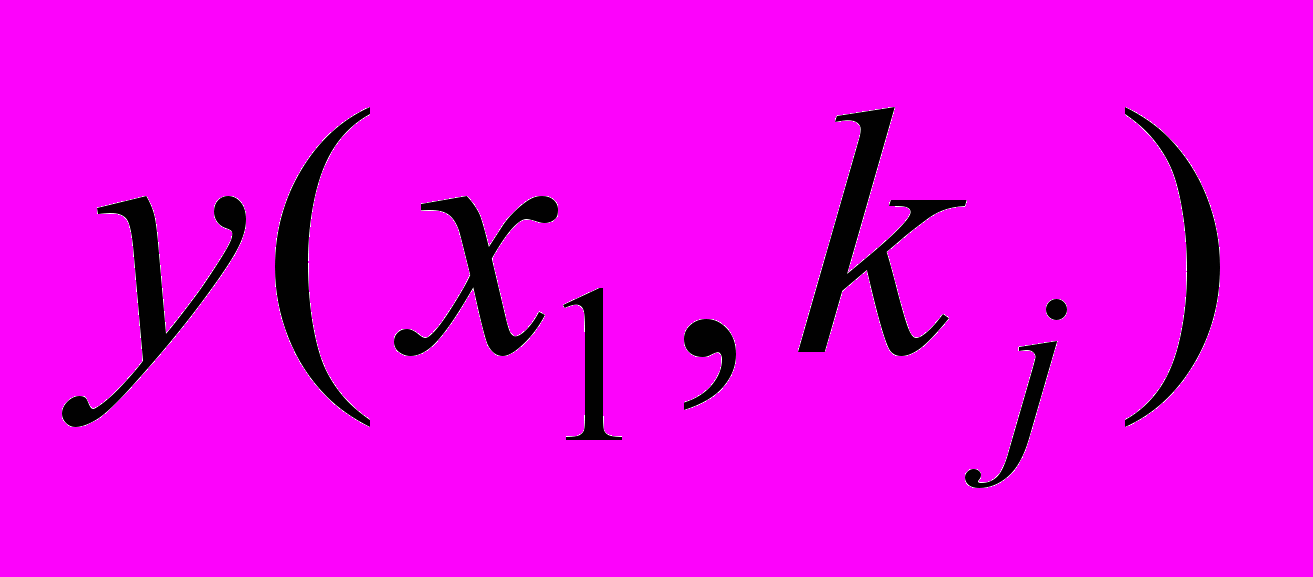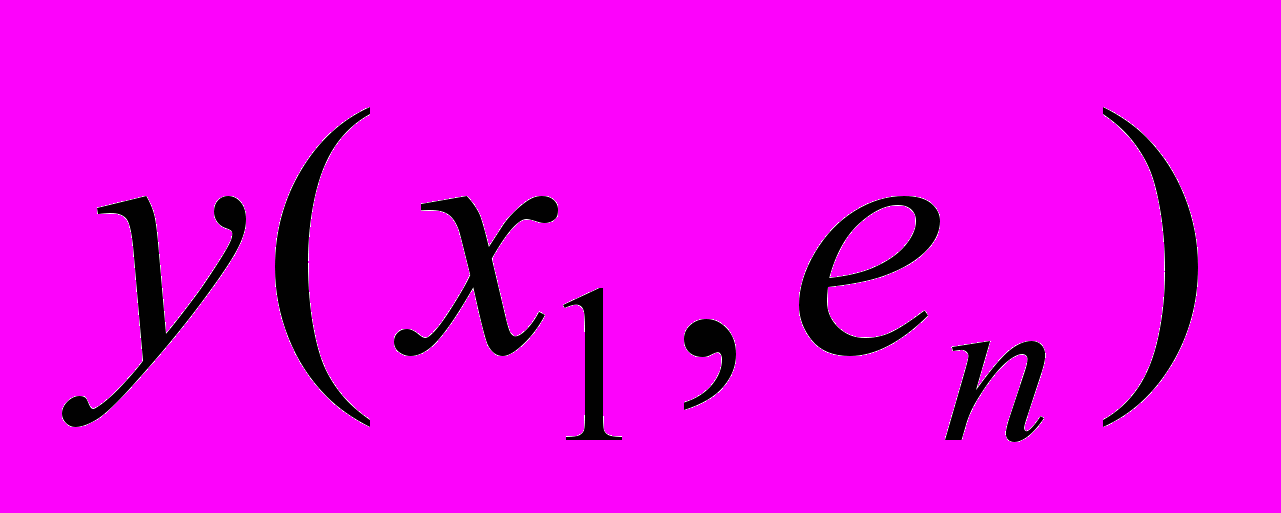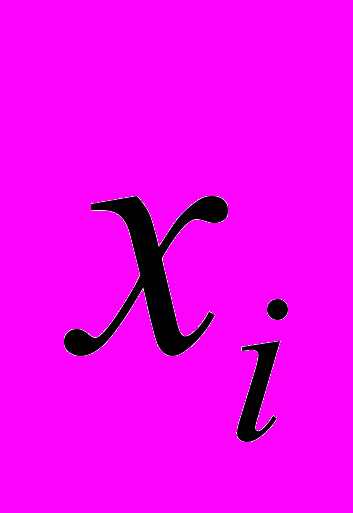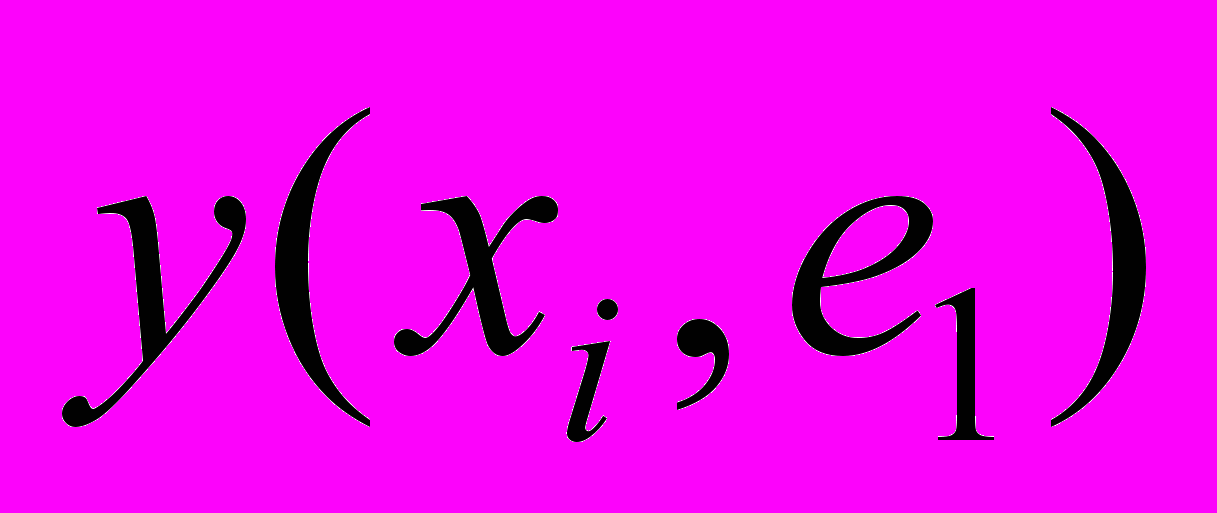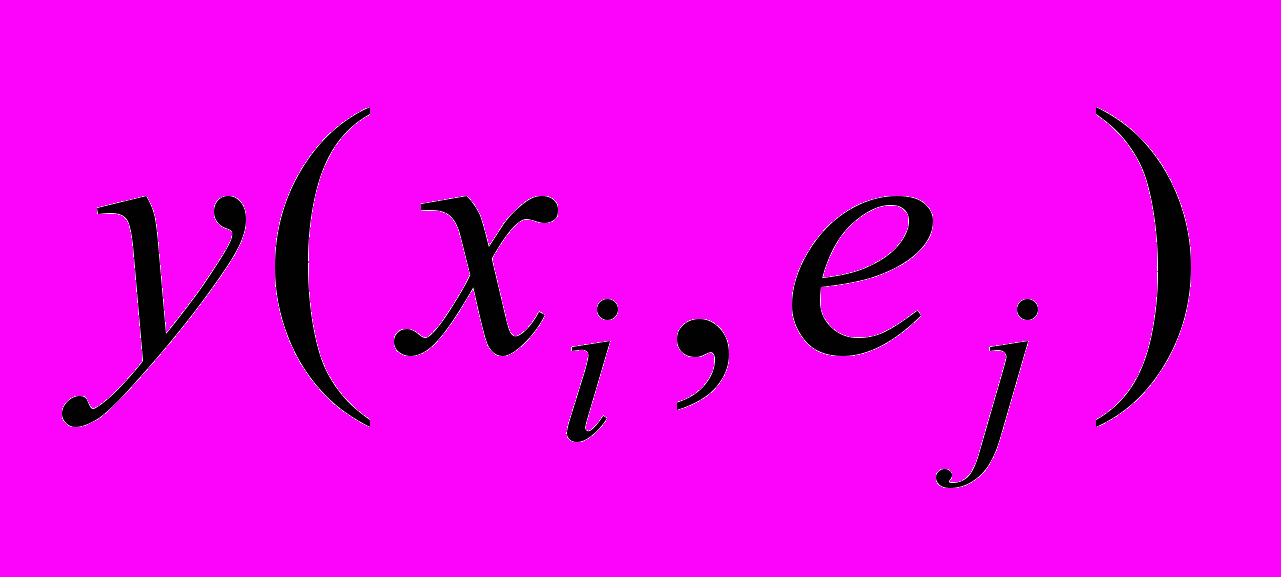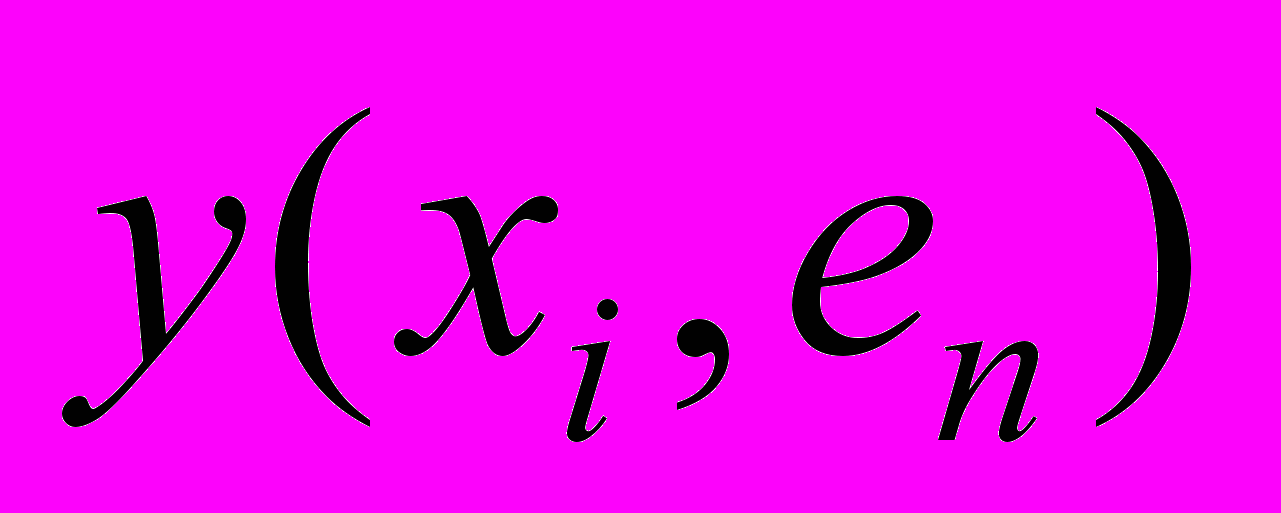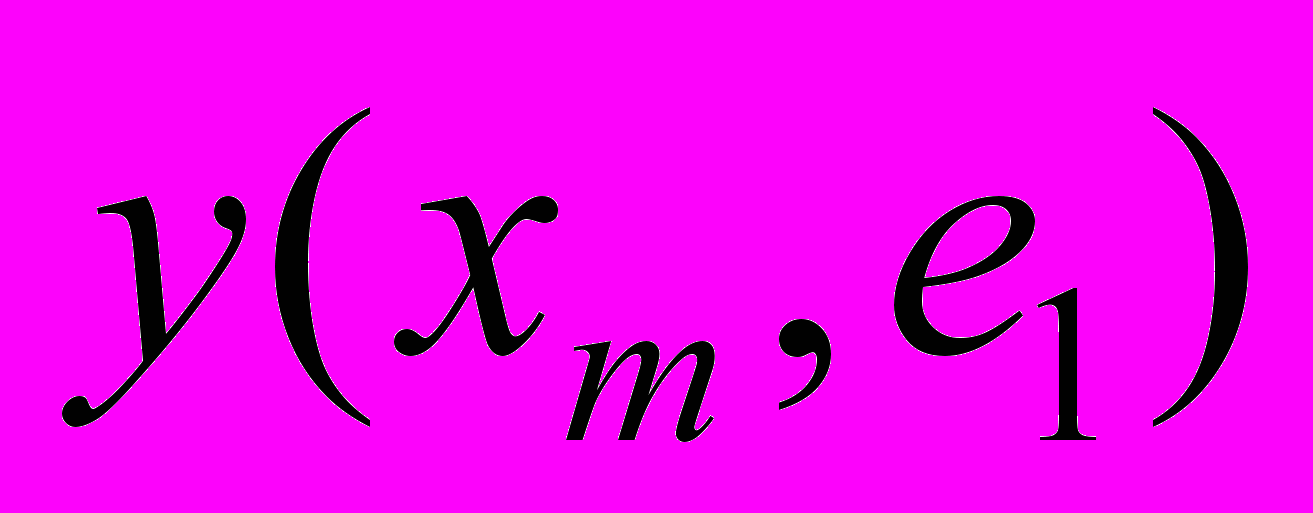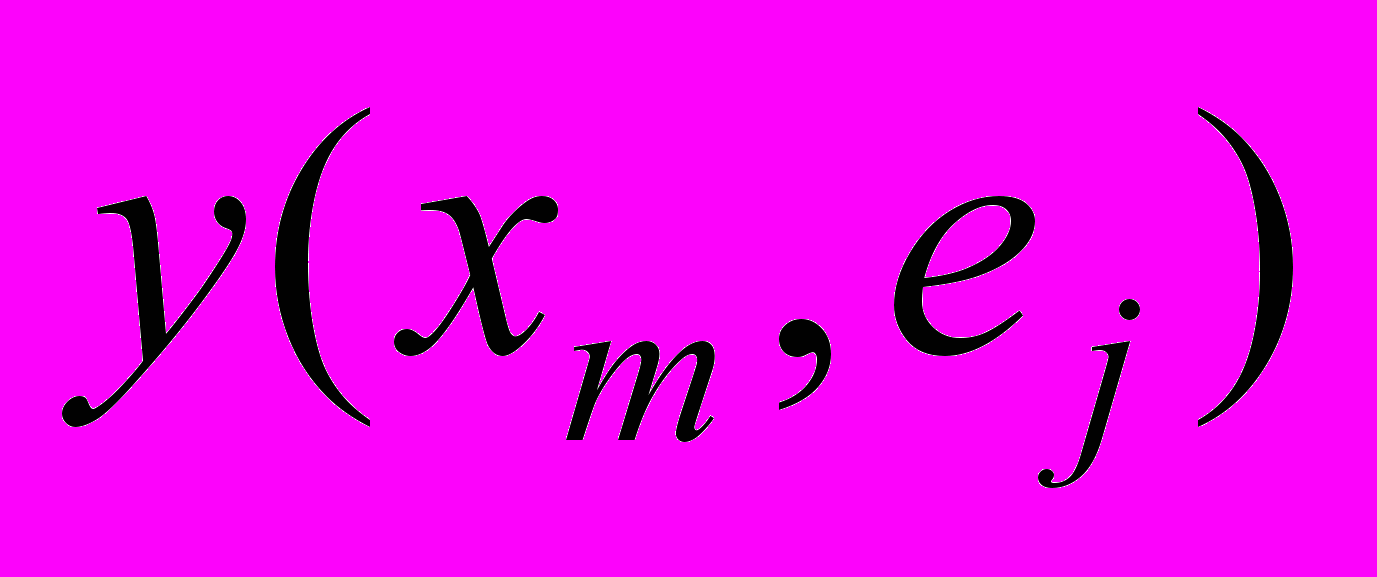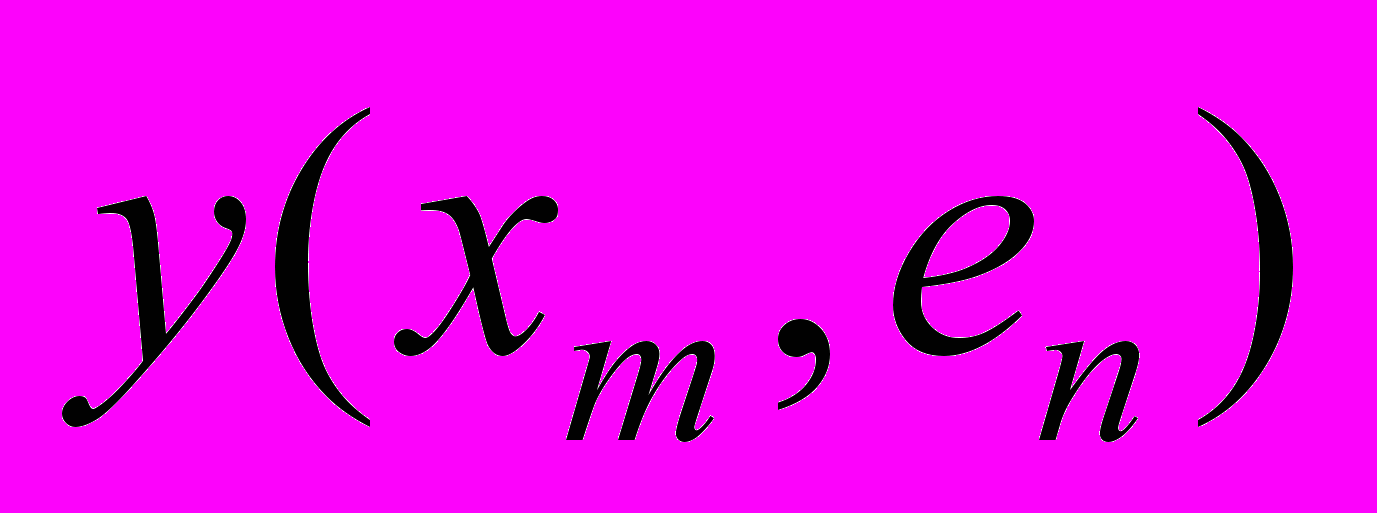4. Много критериев 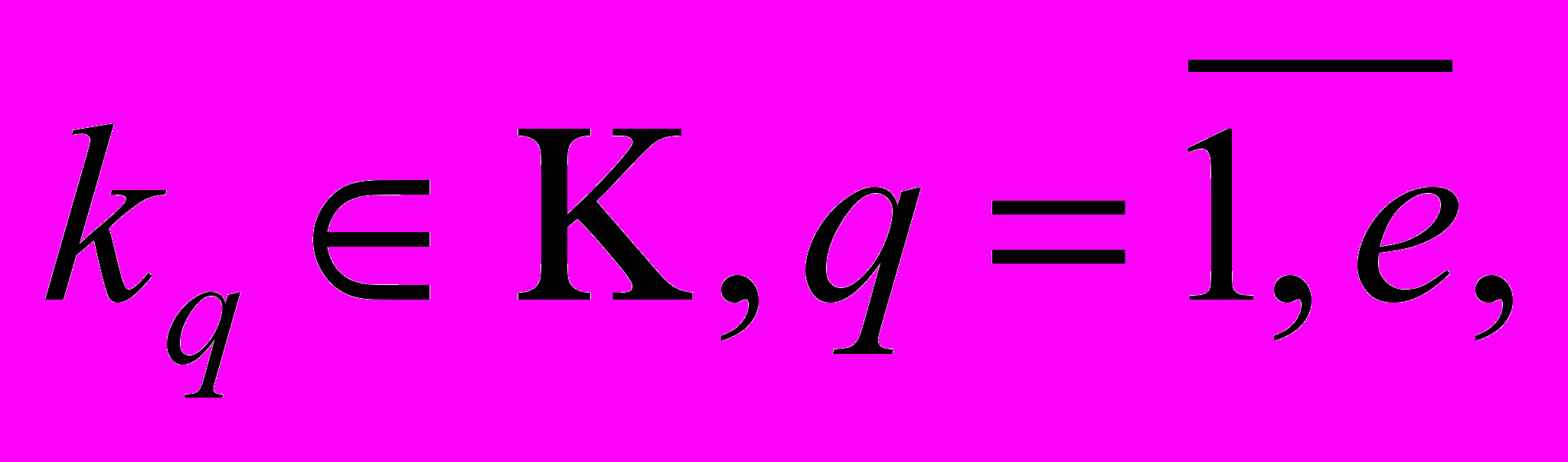качественная и (или) количественная шкала измерения критериев, много состояний внешней среды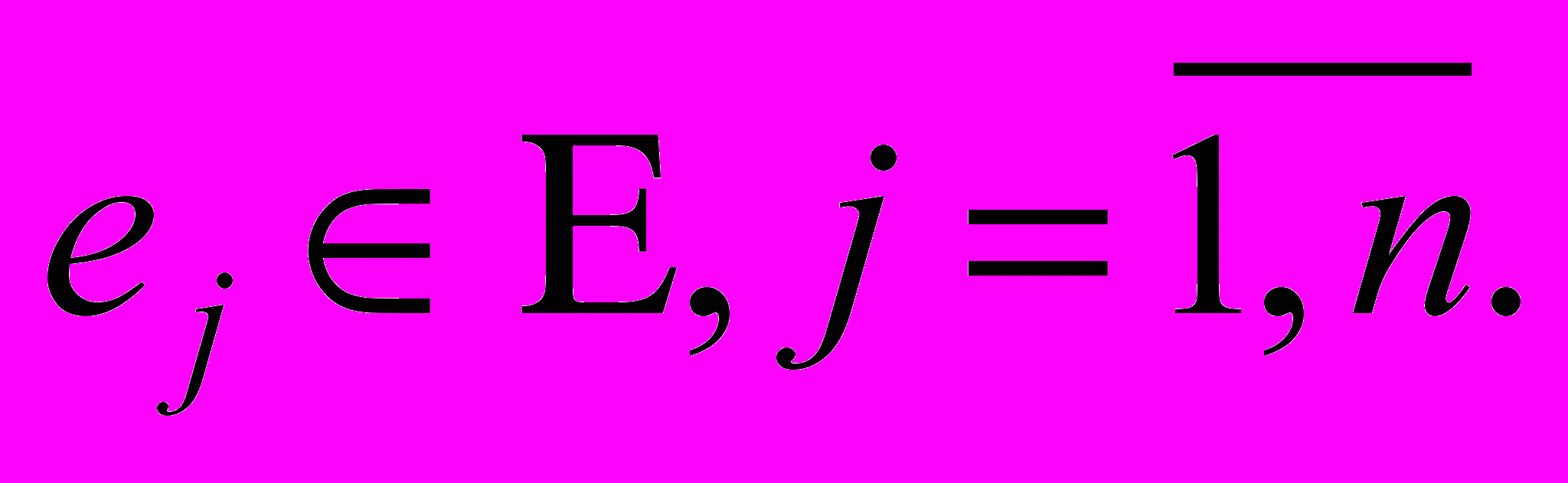

Реализация альтернативы 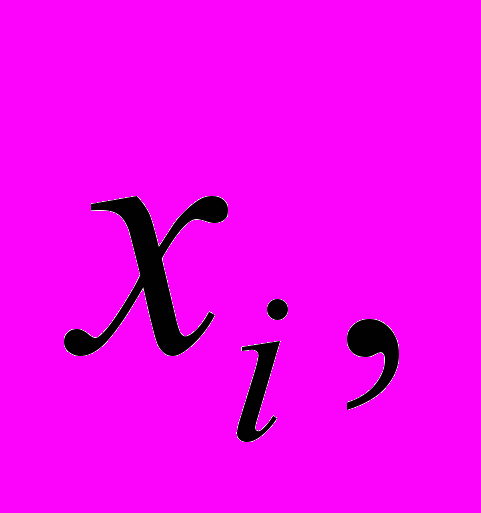оцениваемой по критериям 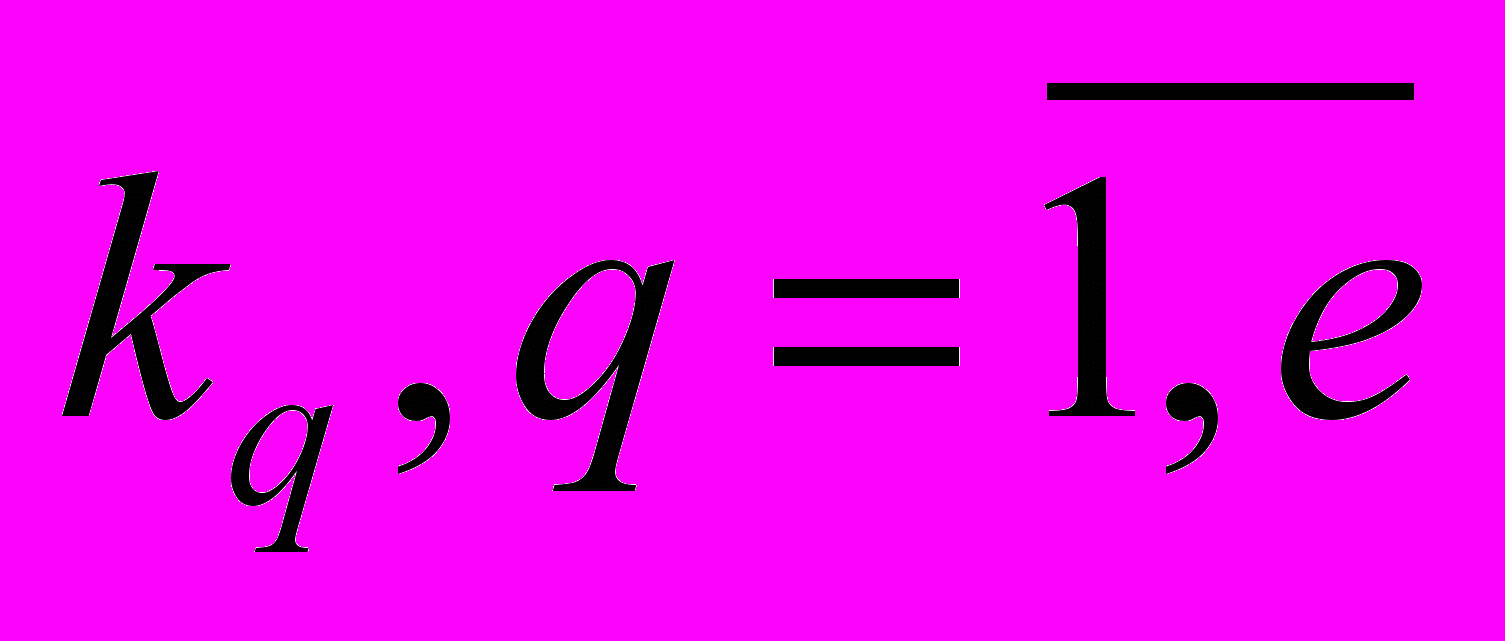в ситуации 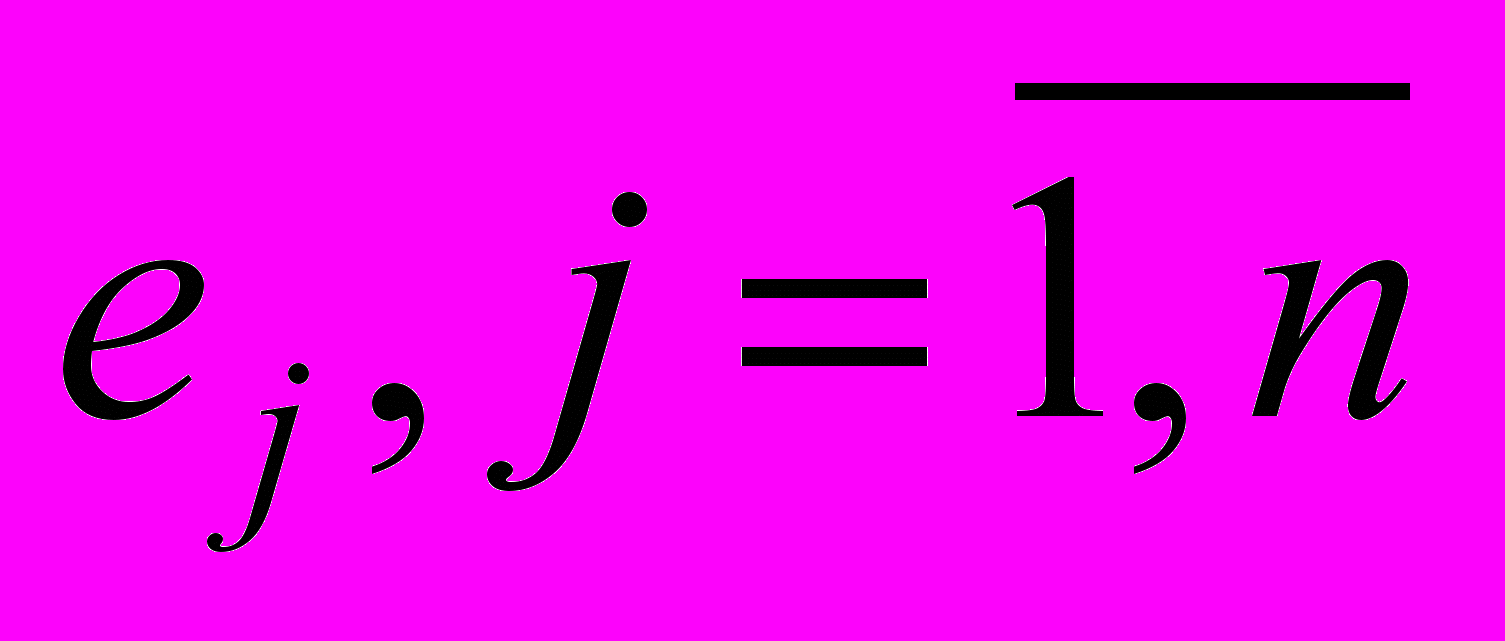может привести к исходу 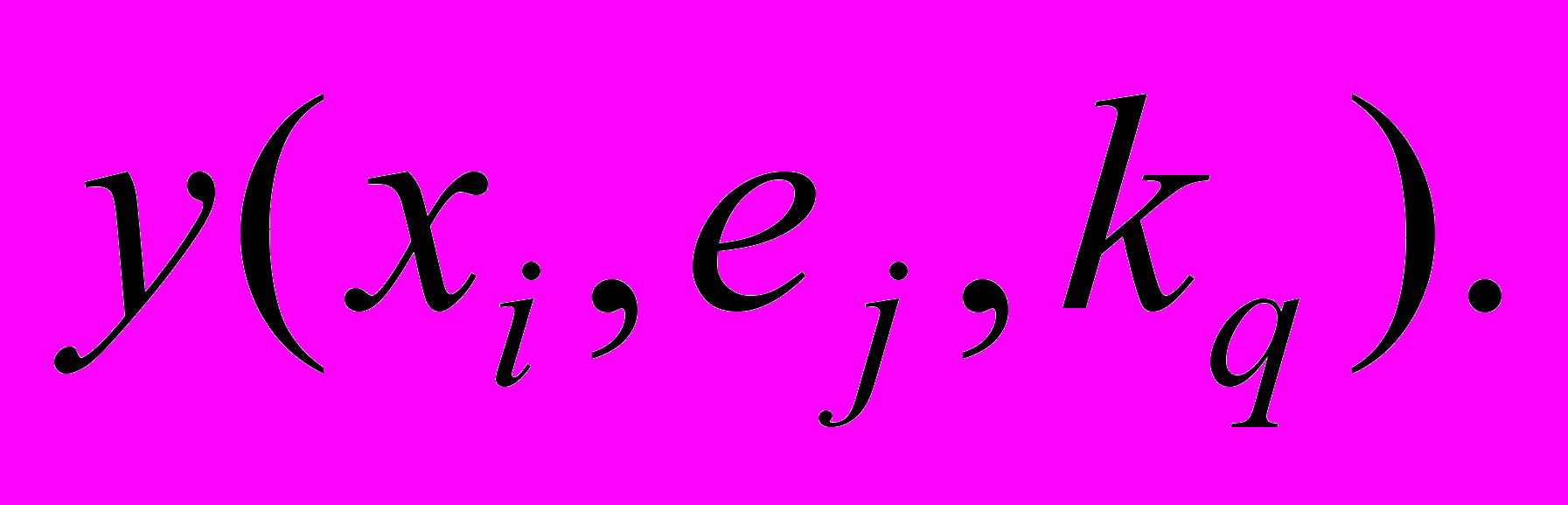Для определения наилучшей альтернативы в зависимости от конкретной постановки ЗПР реализуют один из подходов:

1) по каждой альтернативе 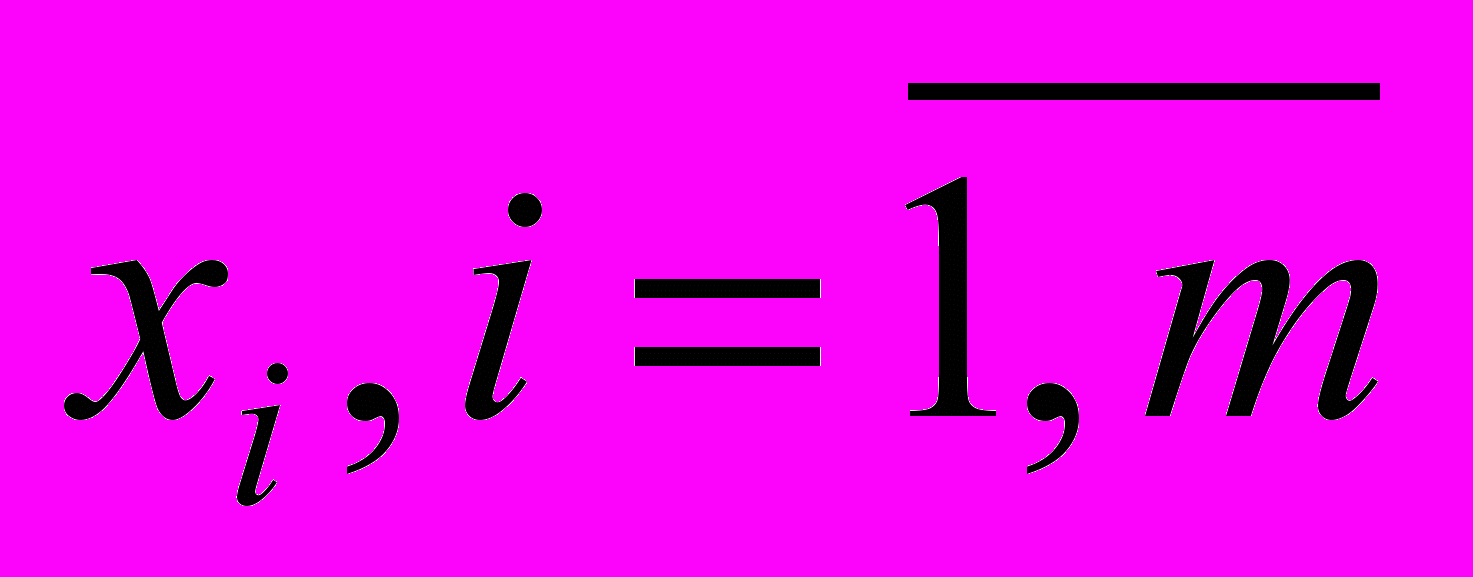и по каждой ситуации 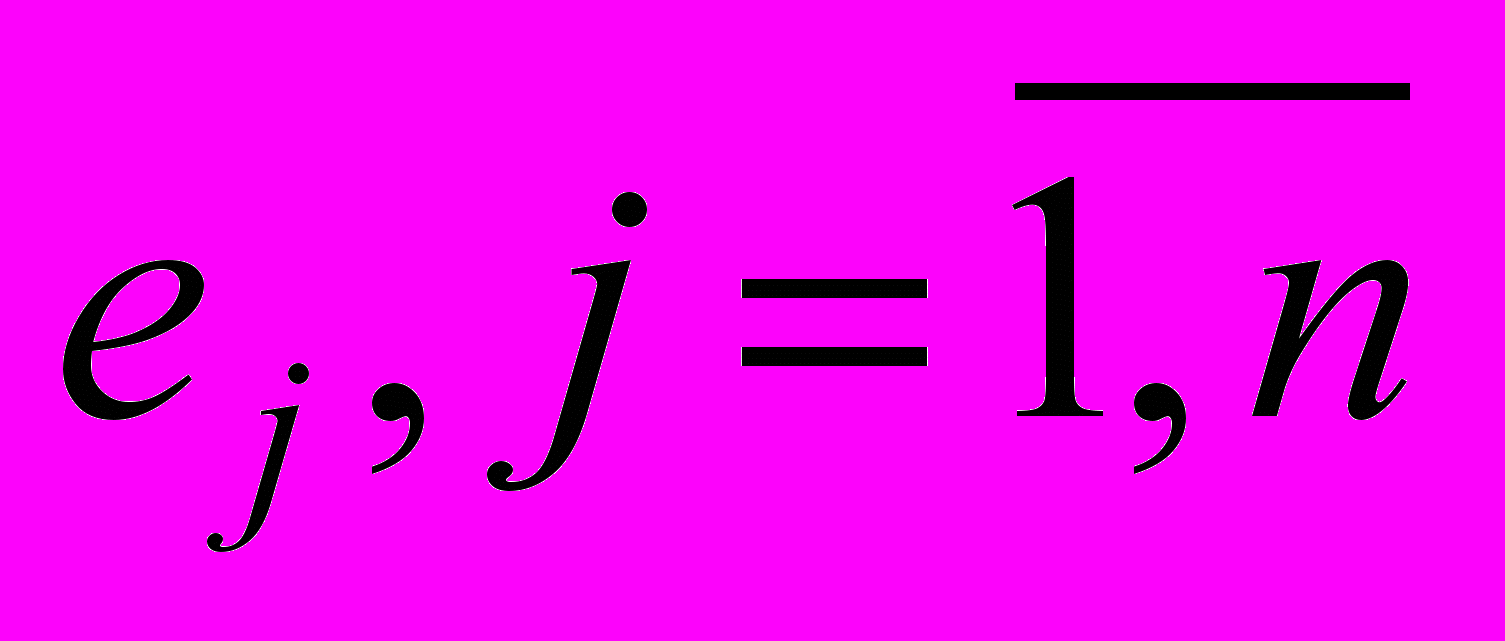получают методом свертки критериев критериальную оценку 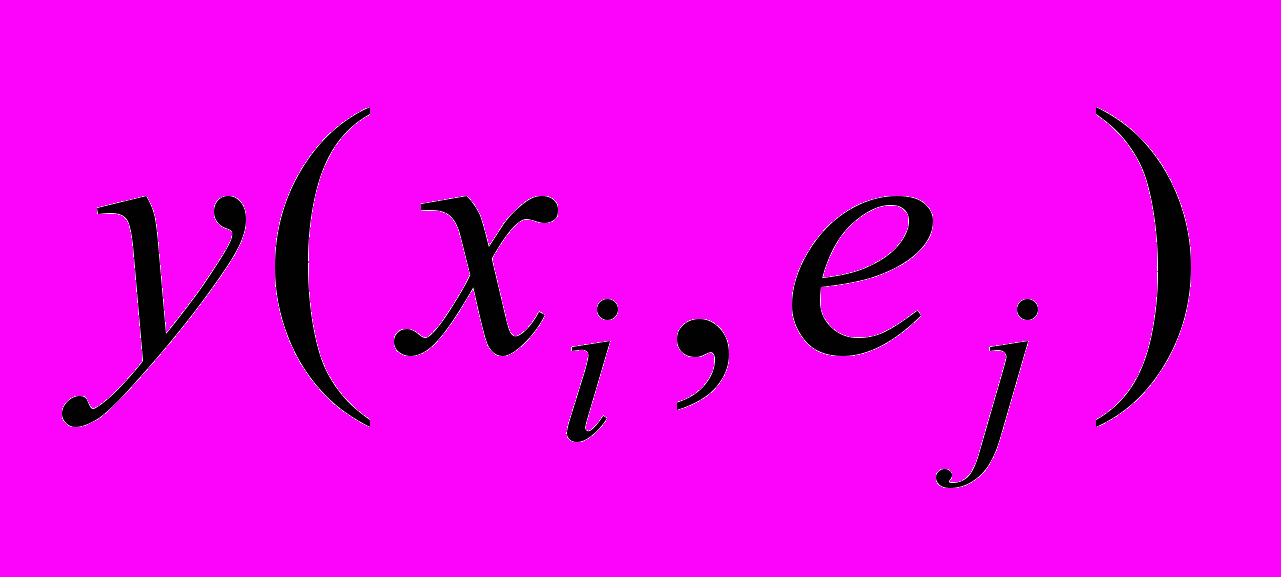и переходят к рассмотренной выше типовой задаче 3;

2) по каждой альтернативе 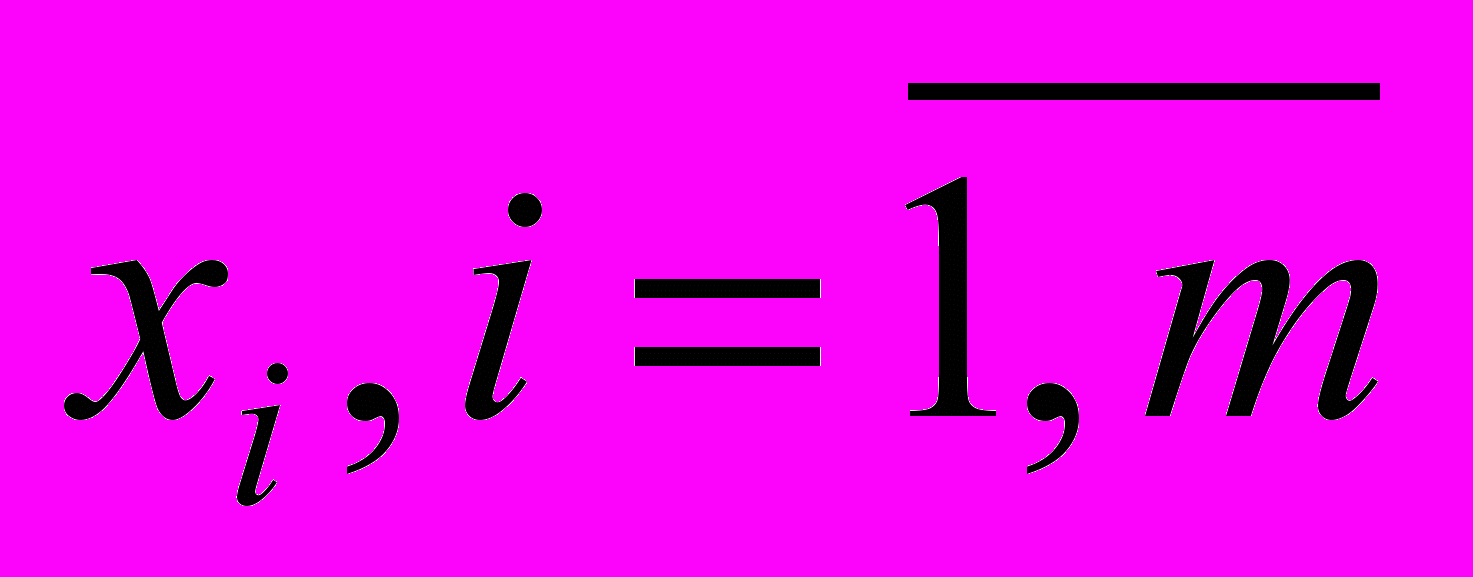и по каждому критерию 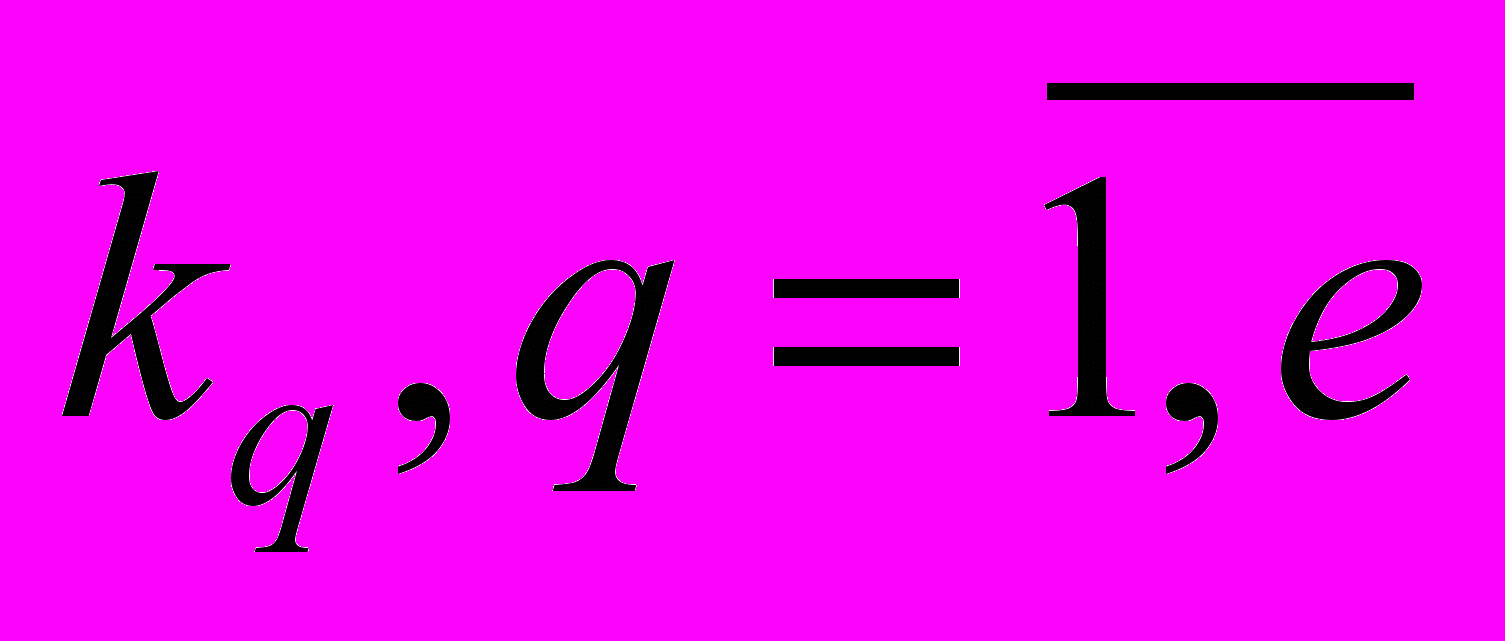получают среднестатистическую оценку исхода 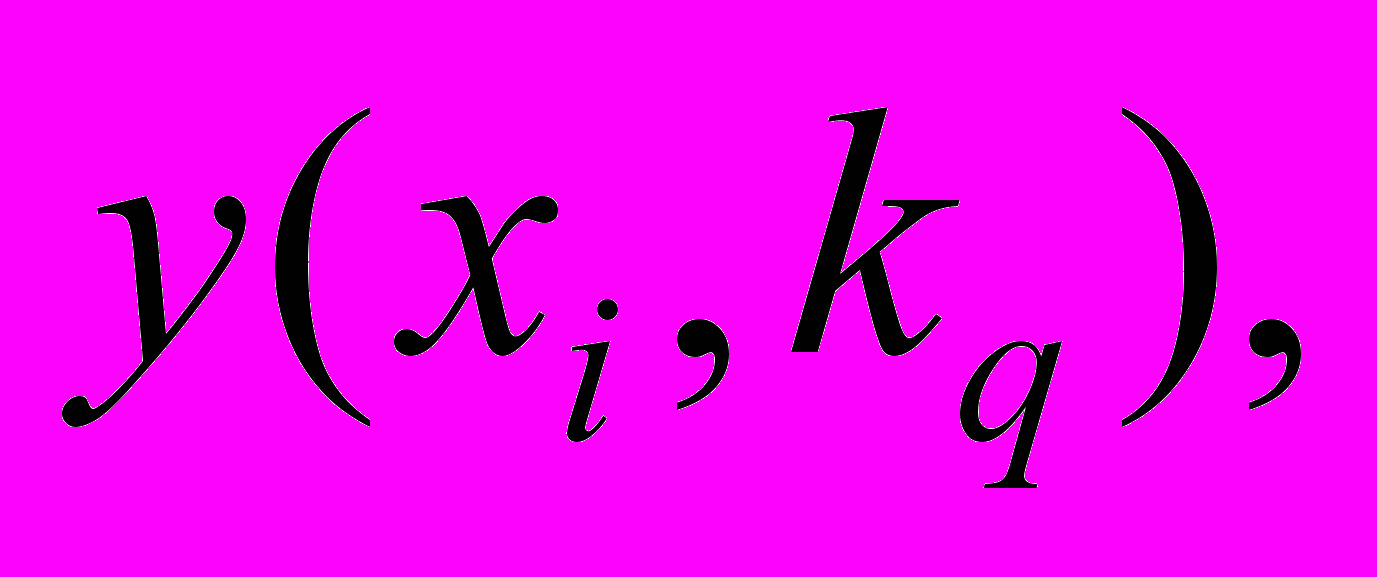затем переходят к рассмотренной выше типовой задаче 2.


Этап 5. Анализ и разработка рекомендаций по практическому использованию результатов

Оценка эффективности решения складывается из оценки качества самого решения и оценки качества исполнения. Поскольку управленческие решения влияют на социальную среду, производственную и финансовую деятельность, то для всесторонней оценки эффективности решений необходимо производить социологический, производственный, финансовый анализ последствий этих решений.

Следует отметить, что приведенная последовательность этапов разработки управленческих решений отражает, в основном, рациональную последовательность действий ЛПР. В действительности процесс разработки решений является более сложным и не всегда строится по приведенной схеме. Реальный процесс допускает определенную параллельность выполнения этапов и процедур, кроме того, при выполнении той или иной процедуры по мере получения новой и дополнительной информации возникает необходимость корректировки предшествующих процедур.

Из приведенных рекомендаций разработки управленческих решений следует, что все этапы процесса принятия сложных решений допускают использование строгих математических методов в сочетании с субъективными предпочтениями ЛПР и экспертов. Таким образом, вопросы автоматизации процесса разработки решений становятся все более актуальными, требующими широкого применения компьютерных систем поддержки решений в практике управления [10, 23, 24].