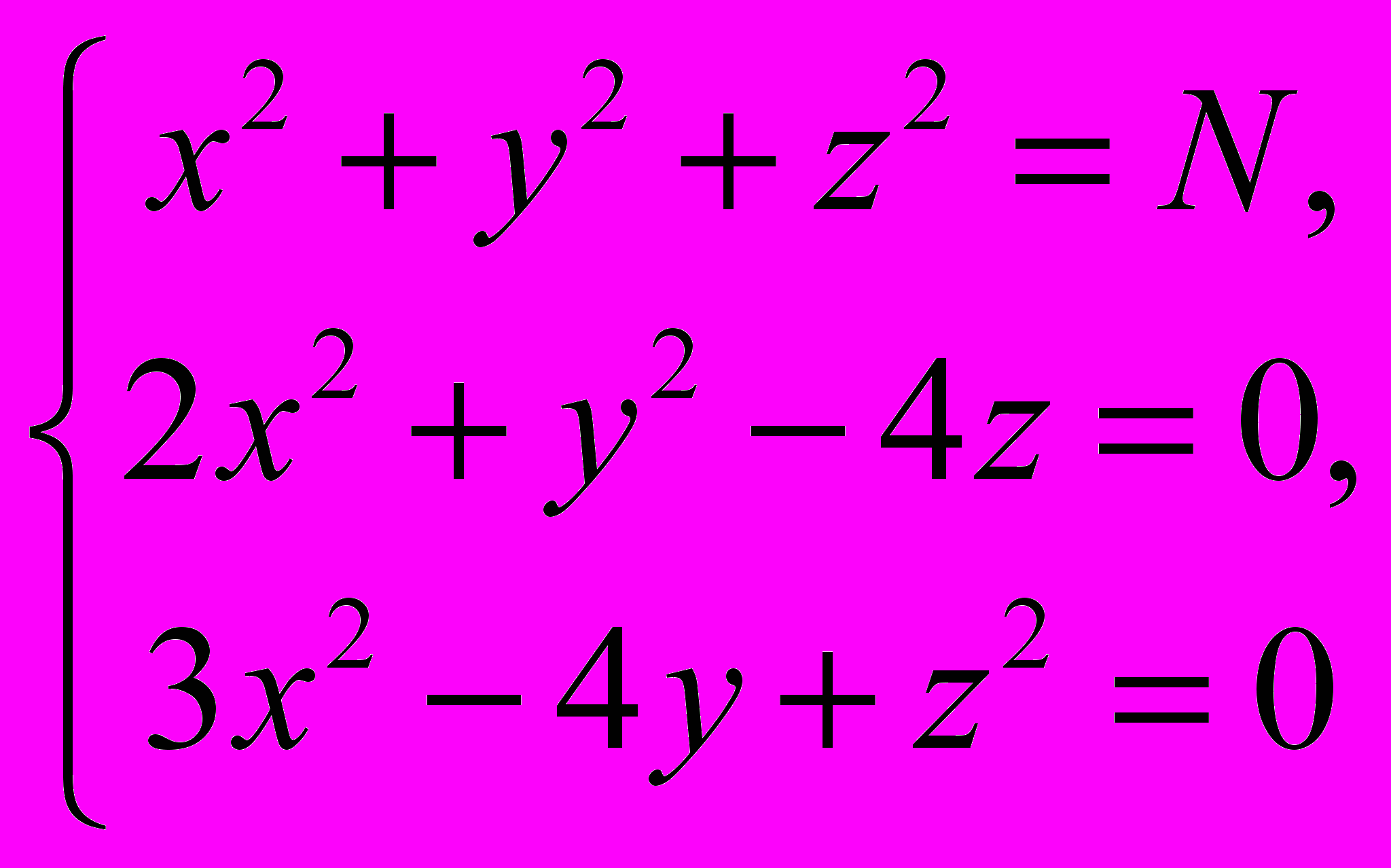Решение систем нелинейных алгебраических уравнений
| Вид материала | Решение |
СодержаниеВыполнить проверку решения. |
- Решение систем нелинейных уравнений, 119.58kb.
- Метод касательных гиперплоскостей для решения систем нелинейных алгебраических уравнений, 25.48kb.
- Решение алгебраических уравнений высоких степеней. Решение нелинейных уравнений методом, 9.13kb.
- В. Н. Страхов новая теория регуляризации систем линейных алгебраических уравнений, 25.89kb.
- Практических: 0 Лабораторных:, 21.53kb.
- Й в виде прямоугольной таблицы элементов кольца или поля, которая представляет собой, 71.89kb.
- Вопросы к экзамену по курсу «Высшая математика часть, 14.58kb.
- Программа элективного курса «решение алгебраических уравнений высоких степеней», 84.18kb.
- Нахождение первых интегралов нелинейных дифференциальных уравнений является одной, 31.75kb.
- Лекция № Тема 1: Системы линейных алгебраических уравнений. Метод Гаусса решения систем, 50.61kb.
Решение систем нелинейных алгебраических уравнений
Системы нелинейных уравнений
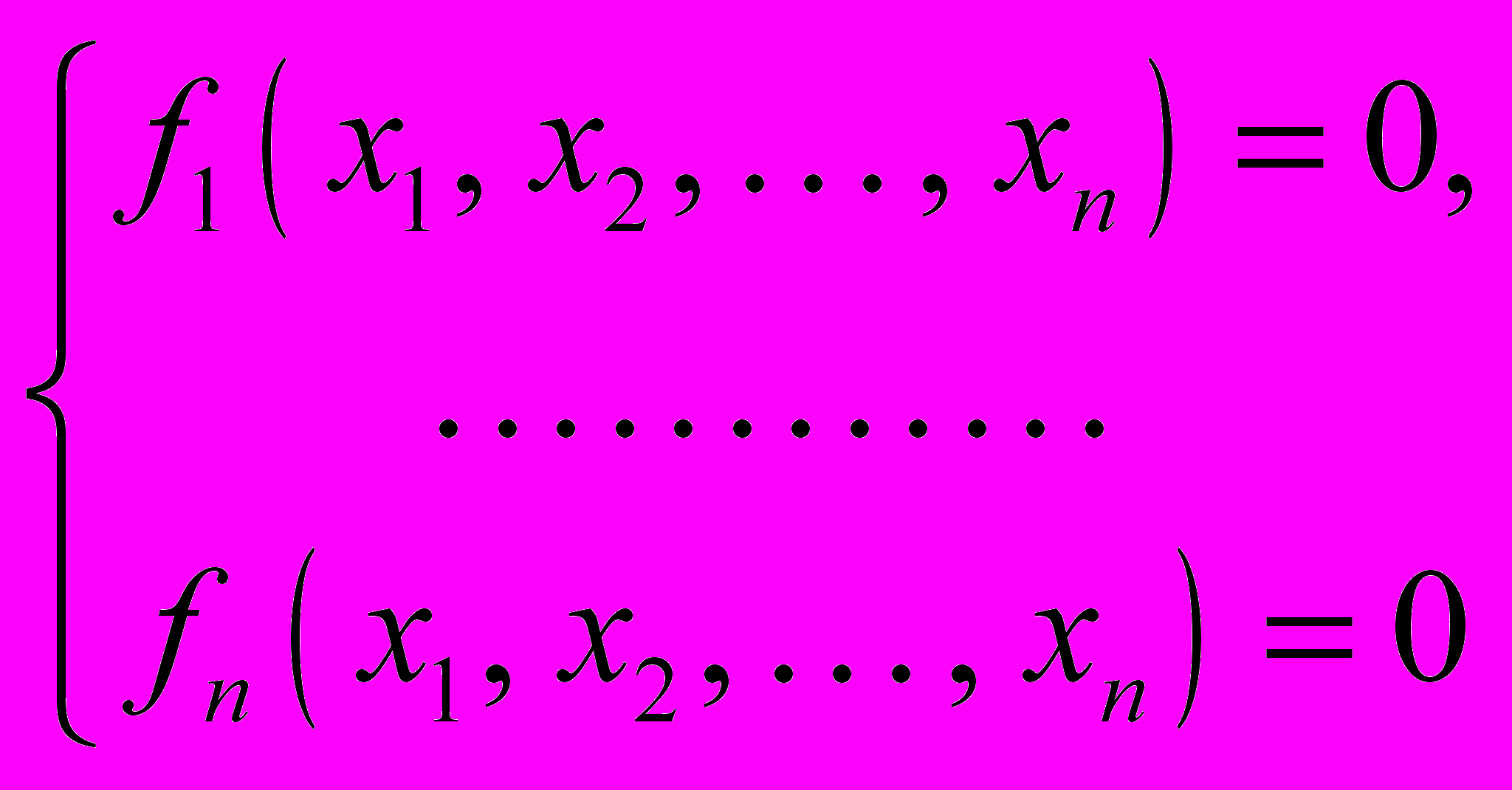
решают практически только итерационными методами: пусть известно некоторое приближение
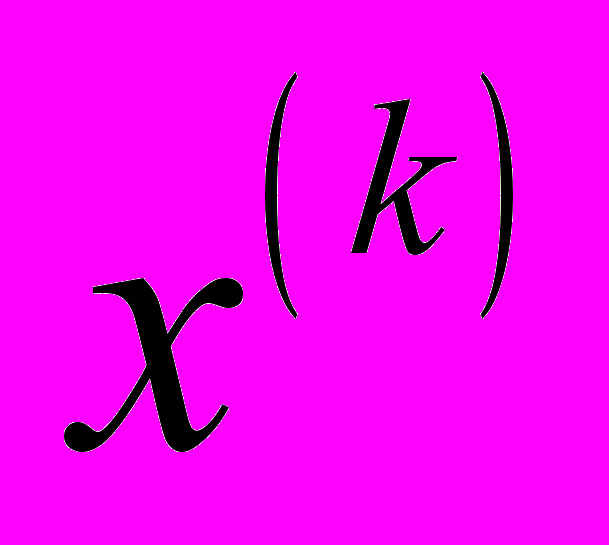к корню 
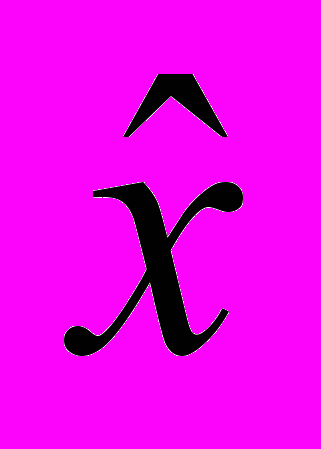, тогда следующее приближение находят по формуле 
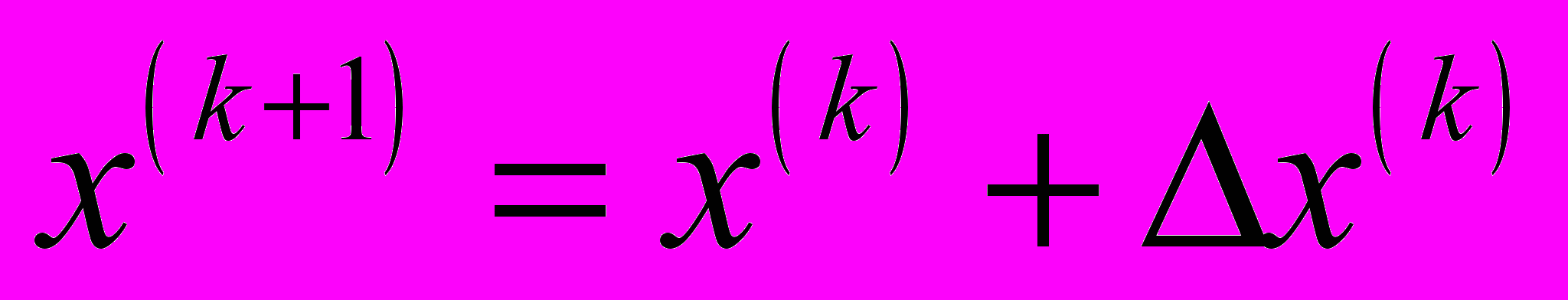, где
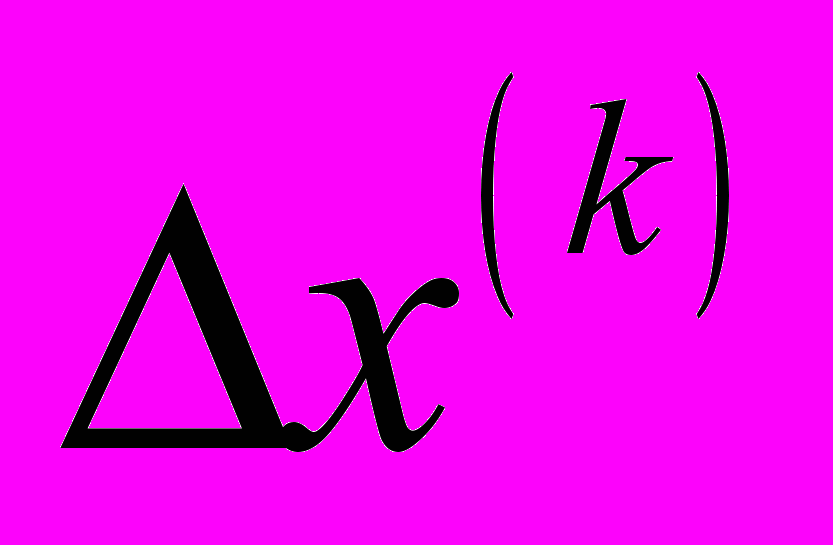– решение системы линейных уравнений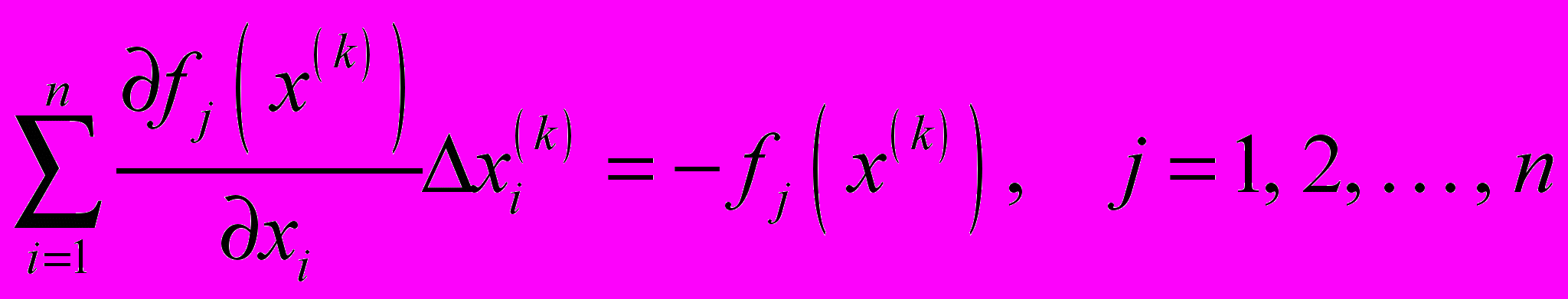 
Данный метод решения системы нелинейных уравнений называется методом Ньютона. Итерации методом Ньютона продолжают до тех пор, пока выполняется
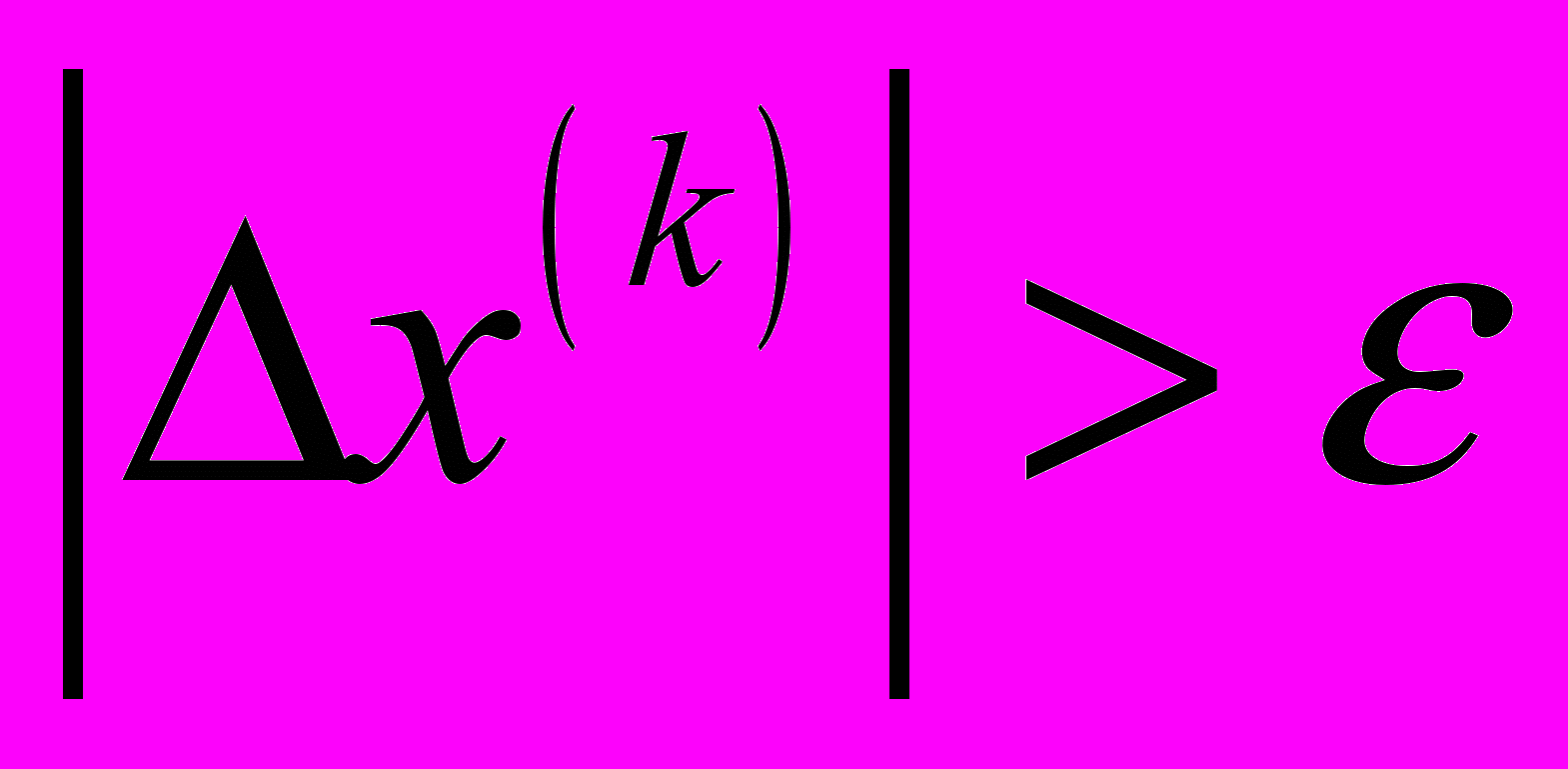, где 
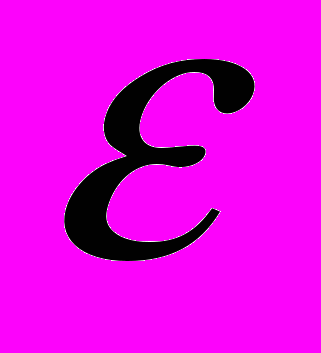– заданная точность решения.Нулевое приближение
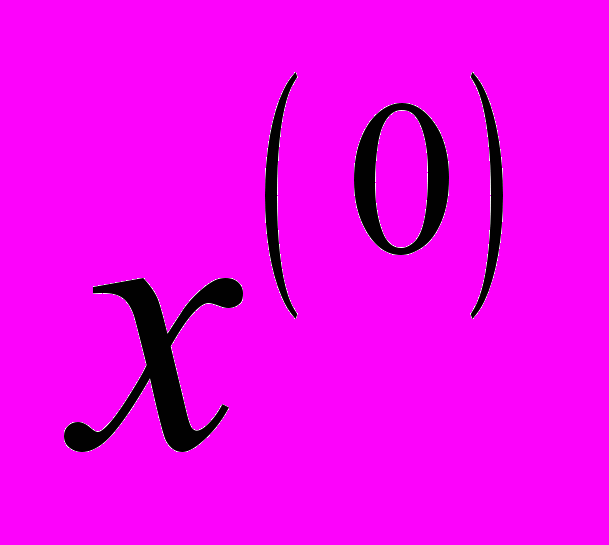в случае двух переменных можно найти графически: построить на плоскости кривые 
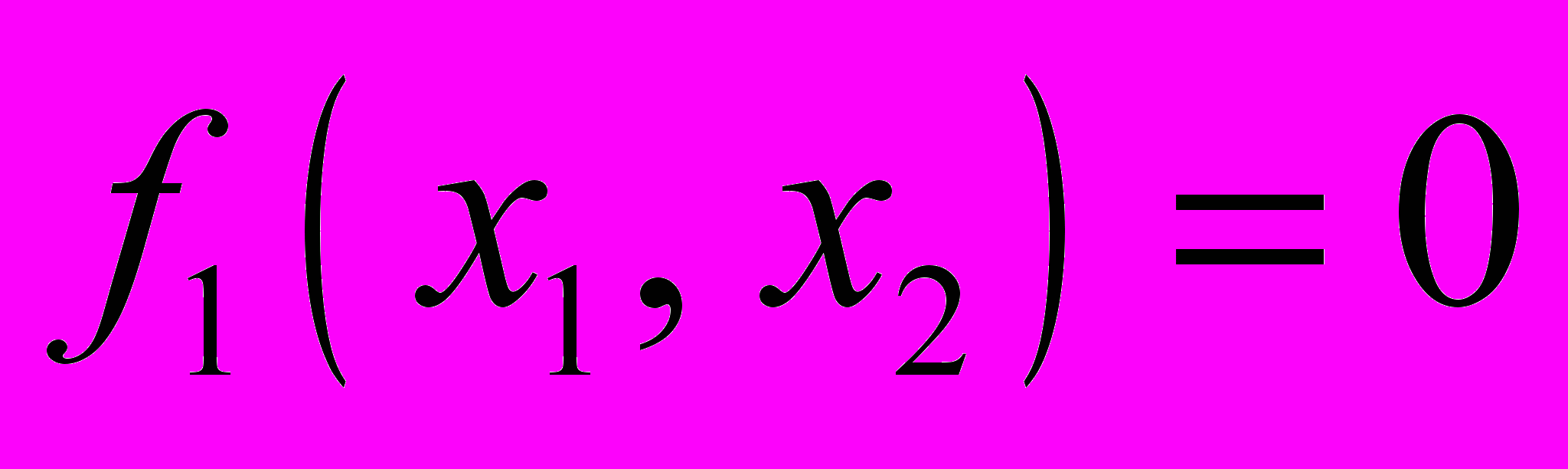и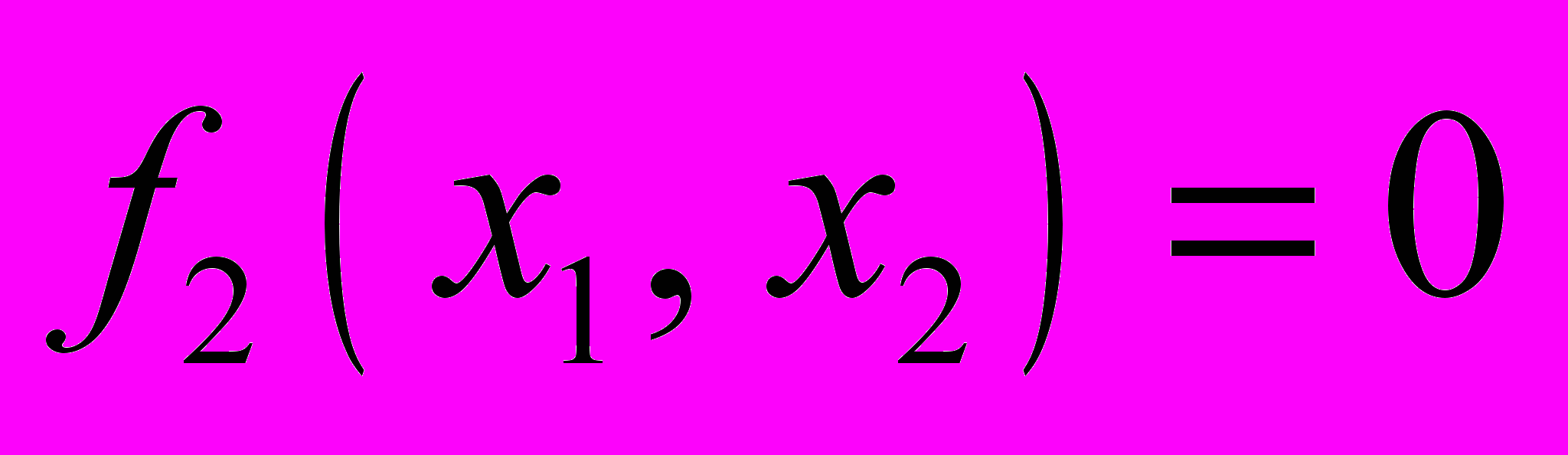 
и найти точки их пересечения. Для трёх и более переменных удовлетворительных способов подбора нулевых приближений нет.Задача 32 . Решить методом Ньютона с точностью
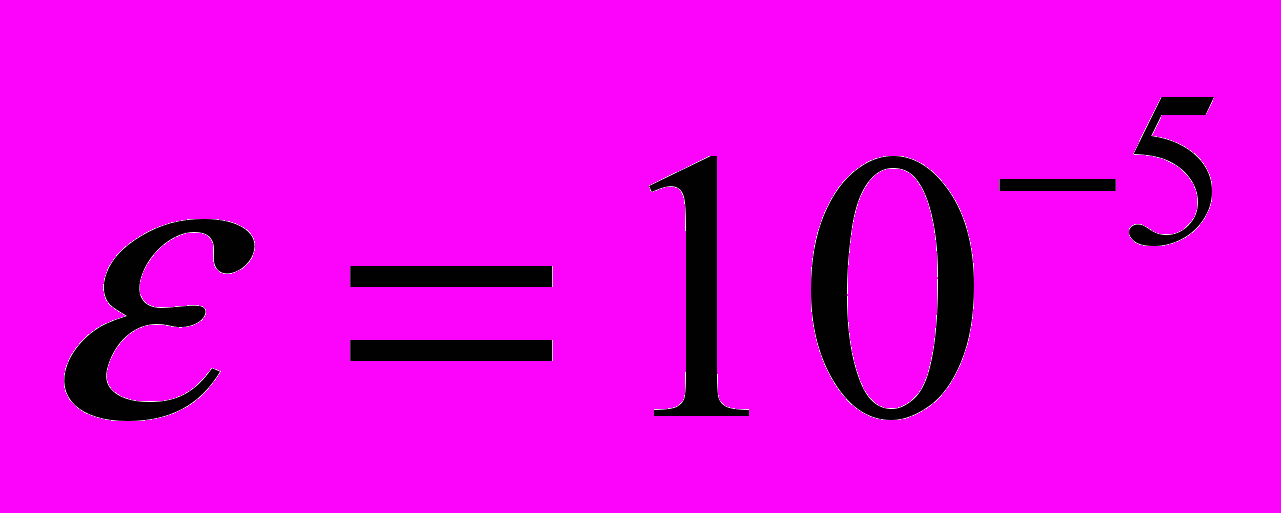систему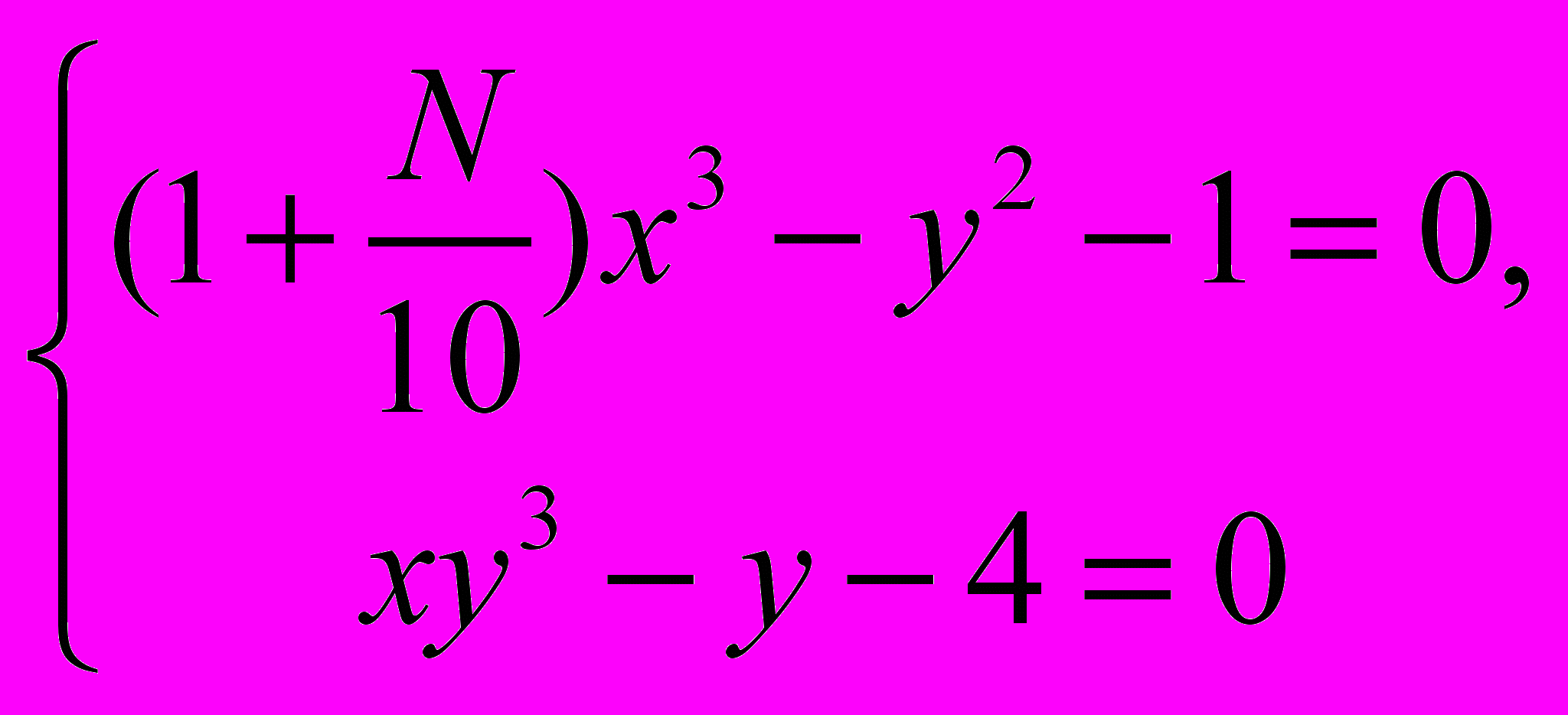 
Выполнить проверку решения.
Меню программы решения этой задачи должно иметь кнопку для определения начального приближения графическим методом, кнопку вызова программы решения и кнопку проверки решения. Программа решения должна выдавать запрос на ввод начального приближения.
В MATLAB систему нелинейных уравнений решает функция
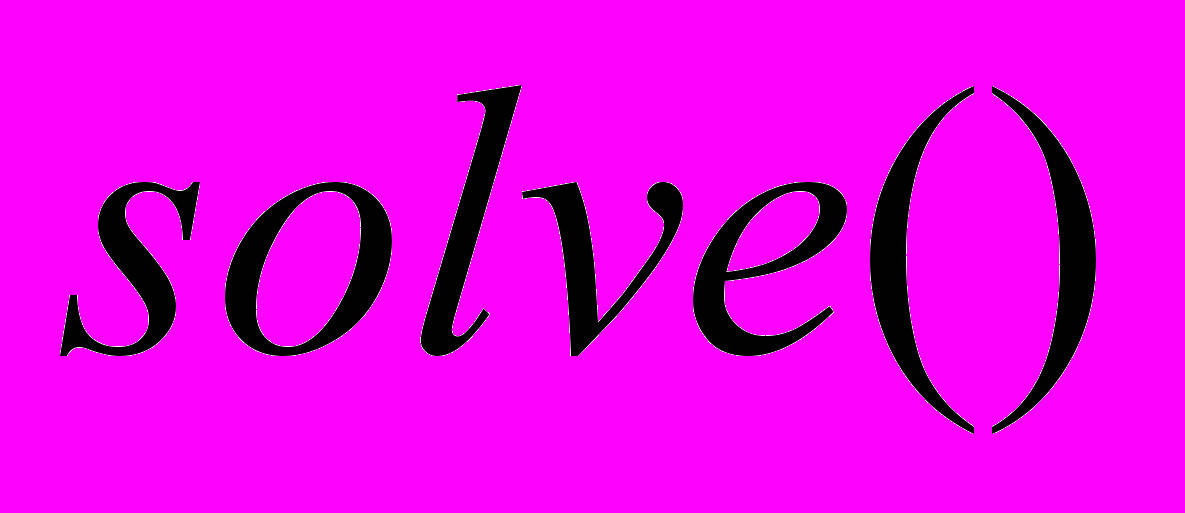. Пример. Используем эту функцию для решения системы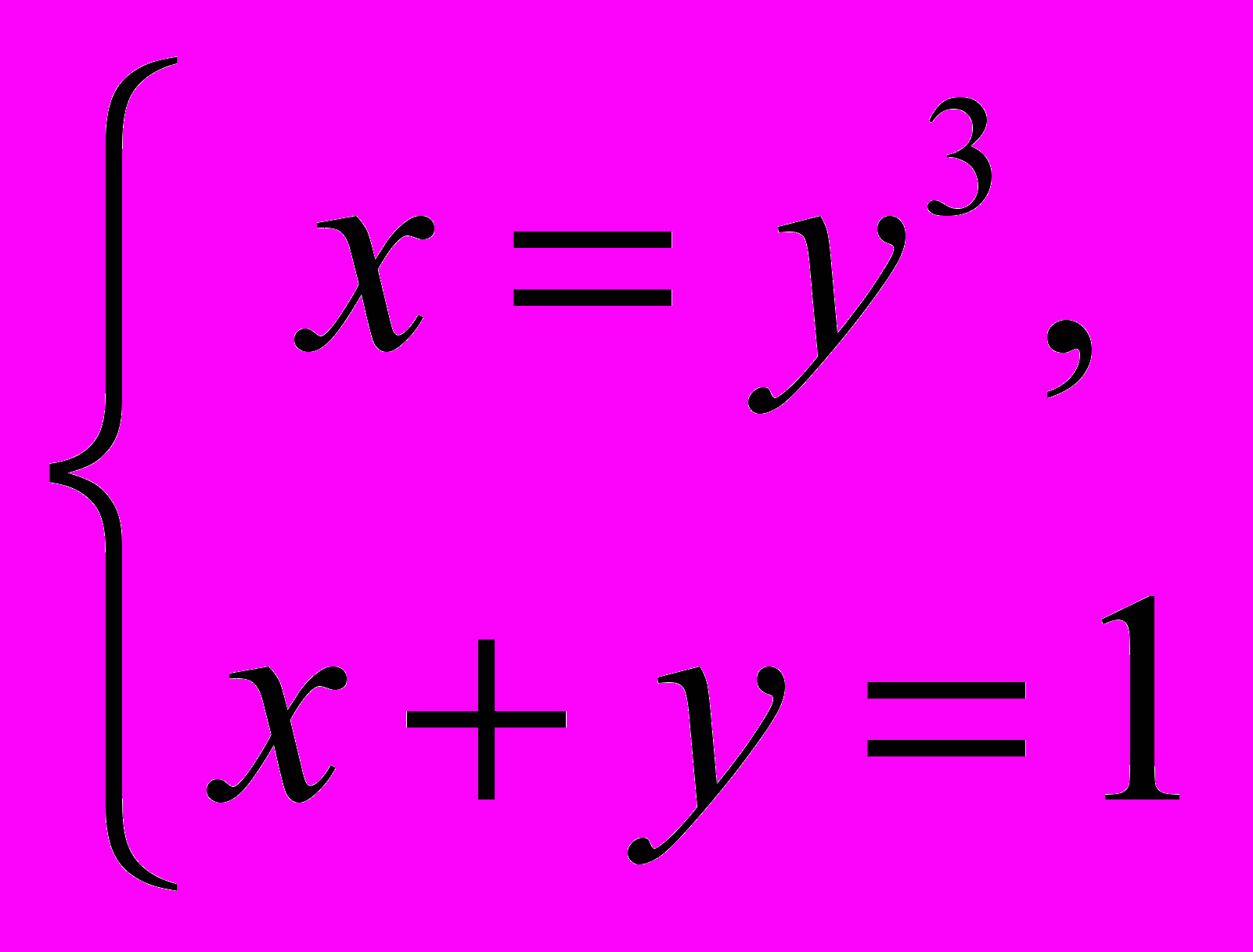
>>s= solve('x=y3','x+y=1')
ans =
x: [3x1 sym]
y: [3x1 sym]
Функция
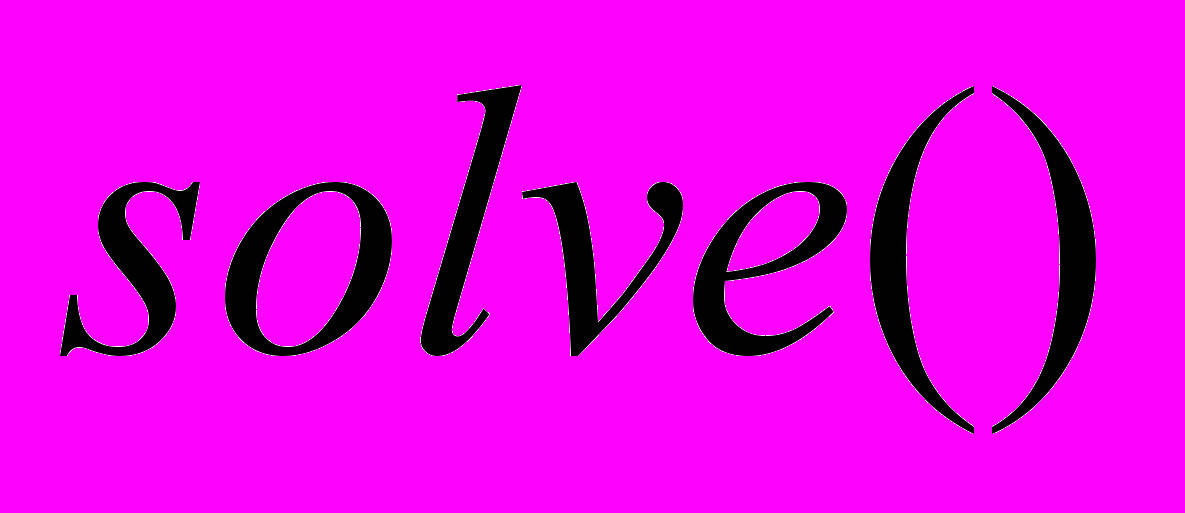находит аналитическое решение и для хранения результата создаётся структура с полями, соответствующими именам неизвестных. В этом примере имя структуры s , в поле x хранятся значения неизвестной x, в поле y − значения неизвестной y. Эти значения можно вывести:>> s.x
ans =
[ 1/6*(108+12*93(1/2))(1/3)+2/(108+12*93(1/2))(1/3)+1]
[ 1/12*(108+12*93(1/2))(1/3)-1/(108+12*93(1/2))(1/3)-1/2*i*3(1/2)*(1/6*(108+12*93(1/2))(1/3)+2/(108+12*93(1/2))(1/3))+1]
[ 1/12*(108+12*93(1/2))(1/3)-1/(108+12*93(1/2))(1/3)+1/2*i*3(1/2)*(1/6*(108+12*93(1/2))(1/3)+2/(108+12*93(1/2))(1/3))+1]
Можно вывести и отдельные значения полей, например, выведем первое значение поля x:
>> s.x(1)
ans =
-1/6*(108+12*93(1/2))(1/3)+2/(108+12*93(1/2))(1/3)+1
Аналитические выражения корней громоздки. Чтобы преобразовать результат вычисления корней в числовой вид, используют функцию subexpr() :
>> [r, q]=subexpr(s. x); r
r =
0.3177
1.3412 - 1.1615i
1.3412 + 1.1615i
>> [r, q]=subexpr(s. y); r
r =
0.6823
-0.3412 + 1.1615i
-0.3412 - 1.1615i
Массив r содержит корни, а массив q вспомогательный, его можно не выводить.
Задача 33. Решить функцией
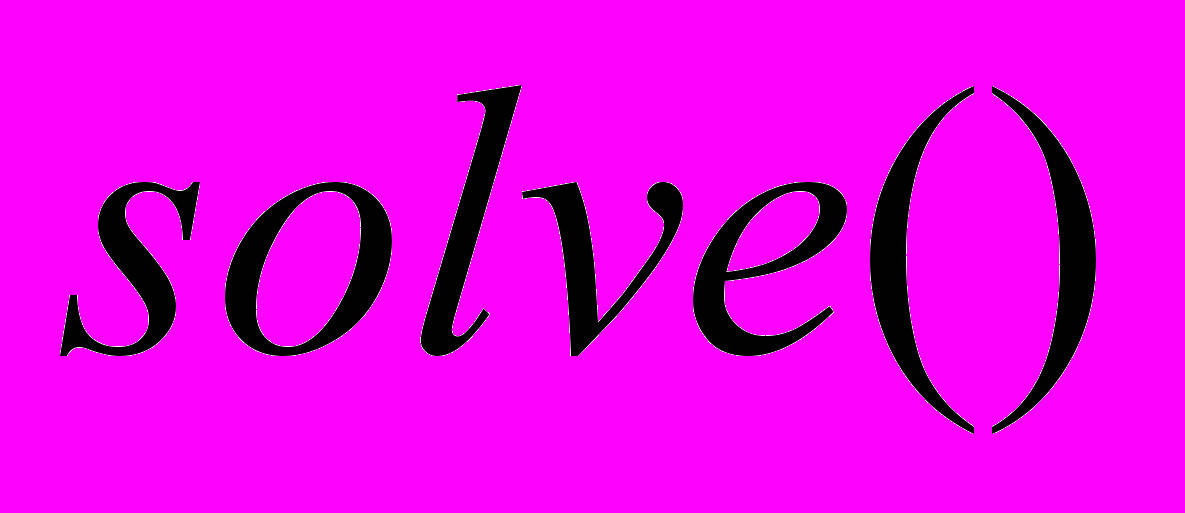систему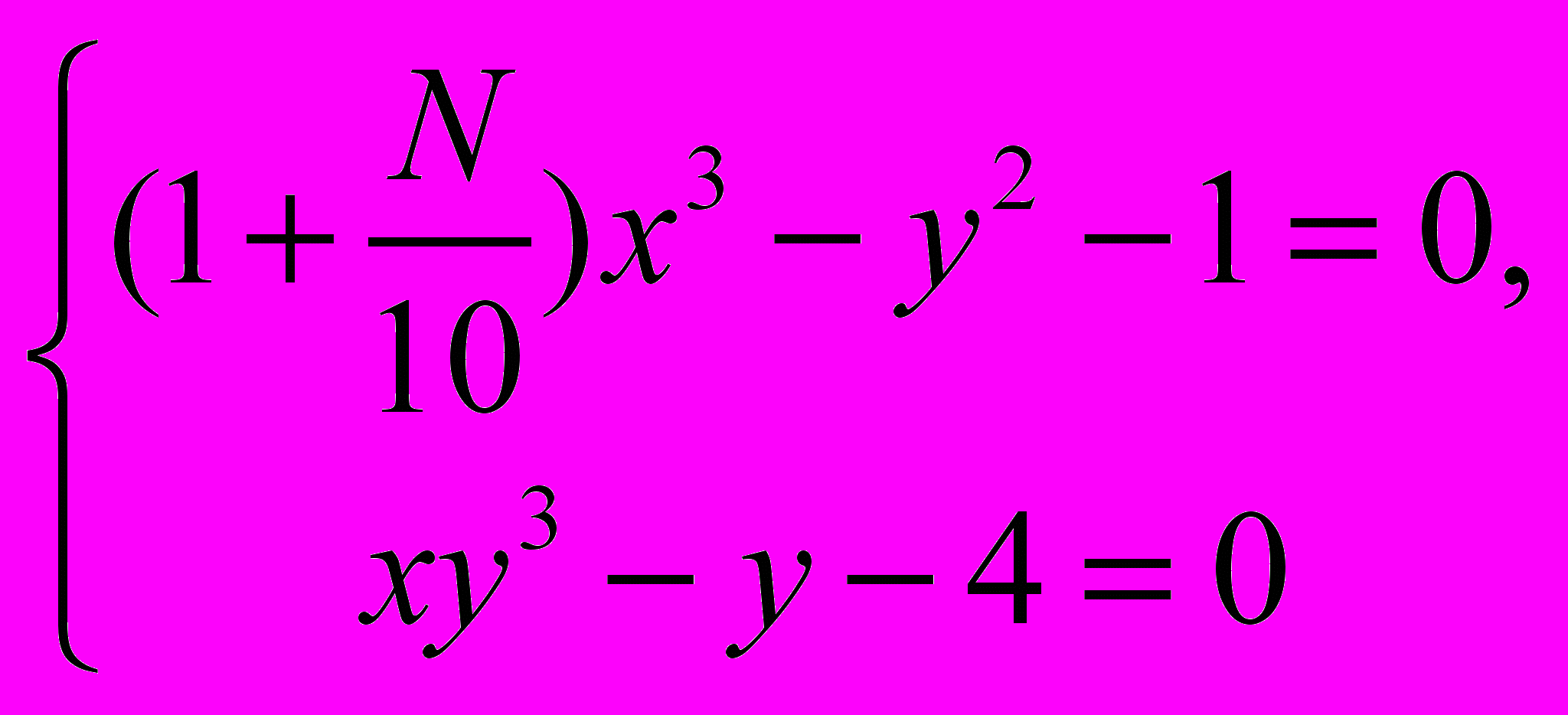 Проверить корни.
Задача 34. Решить систему
