4 Универсальное уравнение состояния идеального газа

Вид материала

Лекция

Содержание Поэтому окончательно формулу для давления газа представим в виде Р=nkT 4.3. Температура 4.4.1. Изотермический процесс (T = const) Изотермическим процессо Рис.Семейство изотерм на плоскости (p, V). T Зависимость между плотностью газа и его давле­нием 4.4.2.Изохорный процесс (V = const)  2 / 1 = T2 / T1 Закон Шарля с точки зрения молекулярной теории 4.4.3. Изобарный процесс (p = const) Изобарным процессом

Подобный материал:

• Л. Н. Гумилева Физико-технический факультет Экзаменационные билеты, 42.99kb.
• Вопросы вступительного экзамена по физике для специальности «6N0604-физика», 33.91kb.
• Программа вступительных экзаменов в магистратуру по специальности 6М011000 Физика Кинематика, 52.46kb.
• Романов Сергей Викторович программа, 206.22kb.
• Элективный курс «Решение задач» Тема: «Молекулярно-кинетическая теория идеального газа», 63.54kb.
• Контрольная работа №5 10 класс По теме: «Молекулярно-кинетическая теория. Свойства, 99.75kb.
• Темы к экзаменам Семестр, 52.51kb.
• План-конспект урока Урок открытие с элементами исследования. Уравнение состояния идеального, 137.15kb.
• Новая гипотеза о внутреннем строении звезд Юровицкий, 101.12kb.
• Контрольная работа "Молекулярно-кинетическая теория идеального газа. Газовые законы., 9.92kb.

Лекция 4.


4.1. Универсальное уравнение состояния идеального газа.


Идеальным газом называется такой газ, у которого отсутствуют силы взаимного притяжения и отталкивания между молекулами и пренебрегают размерами молекул. Все реальные газы при высоких температурах и малых давлениях можно практически считать как идеальные газы. Уравнение состояния как для идеальных, как и для реальных газов описываются тремя параметрами по уравнению (1.7). Уравнение состояния идеального газа можно вывести из молекулярно-кинетической теории или из совместного рассмотрения законов Бойля-Мариотта и Гей-Люссака.

После того, как было установлено экспериментально, что 1 моль любого газа при нормальных условиях (Р = 1 атм = 1,013^.10⁵ Па; t =0 °С или Т= 273 К) занимает объем 22,4 л, объединенный газовый закон для одного моля любого газа стали записывать так:

Р V = R Т,             (1)

где R - универсальная газовая постоянная.

Действительно, объединенный газовый закон для любой постоянной массы газа (а значит, и для одного моля газа) имеет вид:

P ₁ V ₁ / T ₁ = P ₂ V ₂ / T ₂ ,

или

PV / T = const ,

но и для одного моля газа const имеет одно и то же значение для всех реальных газов при таких условиях, при которых они ведут себя как идеальный газ. Обозначив эту постоянную R , получим уравнение (1).

Газовая постоянная равна работе расширения 1 моля идеального газа при нагревании на 1 К при постоянном давлении.

Чтобы найти численное значение R , необходимо знать, какой объем занимает газ при каких-либо определенных значениях Р и Т. Проще всего считать условия нормальными, тогда

R = PV / T = P ₀ V ₀ / T ₀

и в системе СИ R = 8,3144 Дж/(моль • К).

Левая часть уравнения (1) увеличивается в v раз, так как v молей займут в v раз больший объем, а правая часть не изменится ( R - постоянная величина, а T не зависит от числа молей). Чтобы уравнение (1) было справедливо для v молей, надо умножить правую часть на v :

PV = vRT , (2)

где v = m / M ; число молей равно общей массе газа, деленной на молярную массу. Подставляя это значение в уравнение (2), получим

PV = m / M ^. RT (3)

Уравнение идеального газа в форме (2) и (3) называется уравнением Клапейрона-Менделеева, оно выражает взаимосвязь между всеми величинами, характеризующими газ, а поэтому является наиболее общим в приближении модели идеального газа.

Из уравнения Клапейрона-Менделеева можно вывести ряд простых, но важных следствий.

1) Многие газовые реакции происходят при постоянных температуре и давлении. При этих условиях

V = (R Т / Р ) • v = const•v.             (4)

Уравнение (4) есть не что иное как закон Авогадро, который утверждает, что в равных объемах газов при постоянных температуре и давлении содержится одинаковое число молекул.

2) Другое интересное следствие касается плотности газов. Из  уравнения (3) следует, что

ρ = т/ V = (Р/ R Т) • М = const • М            (5)

при постоянных давлении и температуре. Это означает, что при этих условиях плотность газа определяется только его молярной массой. Такой результат позволяет ввести понятие относительной плотности одного газа по другому:

D ₁ = ρ ₁ / ρ ₂ = M ₁ / M ₂            (6)

Эта величина показывает, во сколько раз первый газ тяжелее второго при одинаковых условиях.

3) Если реакция происходит в замкнутом сосуде ( V = const ) при постоянной температуре, то

P = ( RT / V ) • v = const • v .               (7)

Это соотношение означает, что в замкнутом сосуде при заданных условиях давление зависит только от общего числа молекул газов.


4.2. Давление

Давление определяется силой, с которой газ давит на единицу площади стенки сосуда. Давление газа на стенки сосуда является результатом многочисленных ударов молекул. При каждом ударе стенка получает силовой импульс, величина которого зависит от скорости молекул и, следовательно, от энергии их движения. При огромном числе ударов создается постоянное давление газа на стенку. Число ударов зависит от концентрации молекул n. Таким образом, можно ожидать, что давление газа связано с концентрацией молекул и с энергией их движения. Чтобы найти давление газа, нужно найти, какой импульс передает газ единице площади стенки сосуда (6.9)

Поэтому окончательно формулу для давления газа представим в виде:

(6.10)

Итак, давление идеального газа в состоянии равновесия pавно двум третям произведения средней кинетической энергии поступательного движения молекулы газа на число молекул в единице объема газа.

Таким образом, давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

Р=nkT

4.3. Температура

Одним из наиболее важных параметров, характеризующих равновесные свойства макроскопической системы, является температура. Введем этот параметр, для чего рассмотрим два тела, которые могут взаимодействовать и обмениваться энергией. Этот тип взаимодействия, который называется тепловым, приводит к тому, что в результате столкновений молекул в области контакта двух тел происходит передача энергии от быстрых молекул к медленным. Это означает, что энергия движения атомов в одном теле уменьшается, в другом – увеличивается. Тело, которое теряет энергию, называют более нагретым, а тело, к которому энергия переходит – менее нагретым. Такой переход энергии продолжается до тех пор, пока не установится состояние теплового равновесия. В состоянии теплового равновесия степени нагретости тел одинаковы. Для характеристики степени нагретости тела вводят параметр, называемый температурой.

Из опыта известно, что при изменении температуры изменяются размеры тел, электрическое сопротивление и другие свойства. Таким образом, температуру можно определить по изменению какого-либо удобного для измерения физического свойства данного вещества.

Чаще всего для измерения температур используют свойство жидкости изменять объем при нагревании и охлаждении. Прибор, с помощью которого измеряется температура, называется термометром.

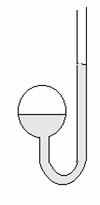
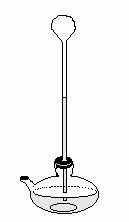
Измерение теплового состояния тел начал Галилео Галилей. В 1597 году он демонстрировал на своих лекциях первый термометр, или, как его называли, термоскоп. Он представлял собой стеклянную трубку с расширением в верхней части, опущенную в сосуд с жидкостью (Рис. ) Нагревание или охлаждение трубки вызывало изменение высоты столба жидкости. Это устройство (комбинация термометра с барометром) фиксировало только изменение температуры, но не могло измерить ни температуру, ни давление.

В 1702 году Гийом Амонтон усовершенствовал термометр Галилея: U - образная трубка наполнялась ртутью, один конец трубки был открыт, другой соединялся с баллоном, содержащим воздух (Рис. ). Это был первый газовый термометр. Температура измерялась по высоте столбика ртути.

Были и другие термометры. В частности, одним из первых конструкторов был итальянский врач Санторио, который применял свой прибор для измерения температуры у больных. Это было, вероятно, первое практическое применение термометра.

Несмотря на успехи в конструировании термометров, эти приборы были весьма несовершенны: не было установлено общей температурной шкалы, каждый конструктор устанавливал ее по-своему, поэтому термометры показывали при одних и тех же условиях разные температуры.

Впервые пригодные для практических целей термометры стал изготавливать мастер - стеклодув из Голландии Фаренгейт в начале 18 века. К этому времени физики уже знали, что некоторые физические процессы протекают всегда при одной и той же степени нагретости тела. Так было замечено, что один и тот же термометр всегда дает одно и то же показание, если его опускать в смесь воды и льда, или в кипящую воду. Поэтому ученые предположили, что процессы плавления льда и кипения жидкости протекают всегда при одной и той же температуре.

Ртутные и спиртовые термометры Фаренгейта имели ту же форму, что и современные. Для построения своей шкалы он использовал следующие основные температурные точки: первая температурная точка - температура смеси нашатырного спирта, льда и поваренной соли - 0⁰F (полагая, что это самая низкая температура, которую можно получить искусственно, Фаренгейт принял ее за ноль); вторая температурная точка - температура смеси льда и воды, т.е. температура таяния льда, - 32⁰ F.

Температура тела по шкале Фаренгейта получилась равной 96⁰F. Эту температуру Фаренгейт считал третьей основной точкой своей шкалы. Температуру кипения воды он не брал в качестве основной температурной точки. Будучи измерена по его шкале, она получилась равной 212⁰F.

Шкала Фаренгейта применяется в некоторых странах (Англия, США) до сих пор. После Фаренгейта были предложены многие другие шкалы и конструкции термометров. Из всех шкал до нашего времени дошли только две. Первая шкала: 0⁰ - температура смеси льда и воды, и 80⁰ - температура кипения воды - была предложена французским ученым Р. Реомюром в 1730 году и носит его имя. Вторая шкала не совсем правильно носит имя шведского физика и астронома Цельсия. Цельсий использовал ртутный термометр, у которого промежуток между точками таяния льда и кипения воды был разделен на 100⁰. Чтобы избежать отрицательных температур, при измерении низких температур, он принял точку замерзания воды за 100⁰, а точку кипения за 0⁰. Однако более удобной оказалась "перевернутая" шкала, на которой температура таяния льда 0⁰С, а температура кипения воды 100⁰С. Именно таким прибором впервые пользовались шведский ботаник Линней и астроном Штремер. Эта шкала получила широкое распространение и, применяется до сих пор, нося имя Цельсия..

Покажем, как перевести показания температуры по Фаренгейту в привычные нам градусы по Цельсию. Между точками замерзания и кипения воды размещено 180 градусов по Фаренгейту и только 100⁰ Цельсия. Это значит, что один градус Фаренгейта соответствует 100/180, или 5/9 градуса Цельсия. Наоборот, градус Цельсия соответствует 9/5 градуса Фаренгейта. Отметим так же, что и нулевые точки на этих двух шкалах не совпадают.

С учетом всего вышесказанного можно вывести формулу для перевода:

, (8)

где С- температура по шкале Цельсия, а - по шкале Фаренгейта. Попробуйте решить это уравнение относительно .

Обыкновенный жидкостной термометр состоит из небольшого стеклянного резервуара, к которому присоединена стеклянная трубка с узким внутренним каналом. Резервуар и часть трубки наполнены ртутью или другой жидкостью. Температуру среды, в которую погружен термометр, определяют по положению верхнего уровня ртути в трубке. Деления на шкале условились наносить следующим образом. Цифру 0 ставят в том месте шкалы, где устанавливается уровень столбика жидкости, когда термометр опущен в тающий снег, цифру 100 – в том месте, где устанавливается уровень столбика жидкости, когда термометр погружен в пары воды, кипящей при нормальном давлении (10⁵ Па). Расстояние между этими метками делят на 100 равных частей, называемых градусами. Такая температурная шкала создана Цельсием. Градус по шкале Цельсия обозначают °С.

Существует и дpугой способ измеpения темпеpатуpы: с помощью теpмопаpы. Теpмопаpой называется электpическая цепь с включенным в нее гальванометpом, имеющая два спая pазноpодных металлов (напpимеp, меди и константана) (pис. 6.2) Один спай помещен в сpеду с фиксиpованной темпеpатуpой, напpимеp в тающий лед, а дpугой - в сpеду, темпеpатуpу котоpой нужно опpеделить.



Из пpиведенных пpимеpов видно, что введенное понятие темпеpатуpы (основанное на законах теплового pавновесия) действительно неоднозначно. Оно существенно зависит от способа измеpения темпеpатуpы. Такая темпеpатуpа называется эмпиpической. Нуль шкалы эмпиpической темпеpатуpы всегда выбиpается пpоизвольно. По опpеделению эмпиpической темпеpатуpы физический смысл имеет только pазность темпеpатуp, ее изменение, а не ее абсолютное значение.

Во всех рассмотренных ранее температурных шкалах нуль был выбран произвольно. Такой выбор нуля температур существенно усложняет теоретический вывод ряда зависимостей, приводит к громоздким формулам и ненужным вычислениям.

Исходя из этих соображений, У. Томсон (получивший за научные заслуги титул лорда Кельвина) предложил в 1848 г. ввести новую шкалу температур, которая называется либо абсолютной, либо термодинамической шкалой температур. Температура, измеренная по этой шкале, называется абсолютной температурой (или термодинамической температурой).

 Мы знаем, что температура определяется средней кинетической энергией беспорядочного (теплового) движения частиц вещества. В газах это движение молекул или атомов. Введем новую шкалу температур так, чтобы абсолютная температура была пропорциональна средней кинетической энергии беспорядочного движения молекул. 

Вспомним, что от средней кинетической энергии молекул зависит давление газа: чем больше кинетическая энергия молекул, тем с большей скоростью и чаще они соударяются со стенками сосуда. Поэтому при неизменном объеме газа и неизменном числе молекул в нем давление газа будет прямо пропорционально его абсолютной температуре.

Нам осталось ввести единицу абсолютной температуры и установить нулевой уровень термодинамической шкалы. За единицу абсолютной температуры принят кельвин (1 К); он равен одному градусу Цельсия.

Абсолютный ноль температуры определен экспериментально и равен —273,15 °С. Отсюда следует: температура плавления льда по абсолютной шкале температур равна 273,15 К. Соответственно температура кипения воды равна 373,15 К.

При очень низких температурах наблюдаются необычные явления, в частности сверхтекучесть гелия и сверхпроводимость некоторых металлов. В 1978 г. советский физик П. Л. Капица за исследования в области низких температур был удостоен Нобелевской премии.

При сверхнизких температурах в последние годы получены новые необычные состояния вещества.

4.4. Изопроцессы

Следует отметить, что задолго до того, как уравнение состояния идеального газа было теоретически получено на основе молекулярно-кинетической модели, закономерности поведения газов в различных условиях были хорошо изучены экспериментально. Поэтому уравнение (*) можно рассматривать как обобщение опытных фактов, которые находят объяснение в молекулярно-кинетической теории.

Газ может участвовать в различных тепловых процессах, при которых могут изменяться все параметры, описывающие его состояние (p, V и T). Процессы могут быть изображены на диаграмме состояний (например, в координатах p, V) в виде некоторой траектории, каждая точка которой представляет равновесное состояние.

Интерес представляют процессы, в которых один из параметров (p, V или T) остается неизменным. Такие процессы называются изопроцессами.


4.4.1. Изотермический процесс (T = const)


Произведем такой опыт. В закрытую с одного конца тол­стостенную трубку из прозрачного материала поместим ватку, слегка смоченную эфиром, и этим создадим внутри трубки смесь паров эфира с воздухом, взрывающуюся при нагревании. Затем быстро вдвинем в трубку плотно входящий поршень. Мы увидим, что внутри трубки произойдет маленький взрыв. Это зна­чит, что при сжатии смеси паров эфира с воздухом темпера­тура смеси резко повысилась. Это явление вполне понятно. Сжимая газ внешней силой, мы производим работу, в ре­зультате которой внутренняяэнергия газа должна была увеличиться; это и произошло—газ нагрелся.

Теперь предоставим газу расширяться и производить при этом работу против сил внешнего давления. Это можно осуществить. Пусть в большой бу­тыли находится сжатый воздух, имеющий комнатную тем­пературу. Сообщив бутыль с внешним воздухом, дадим воздуху в бутыли возможность расширяться, выходя из не­большого. отверстия наружу, и поместим в струе расширяю­щегося воздуха термометр. Термометр покажет тем­пературу, заметно более низкую, чем комнатная, а что будет указывать на понижение темпера­туры воздуха в струе.

Итак, сжатие газа внешней силой вызывает его нагрева­ние, а расширение газа сопровождается его охлаждением.

Изотермическим процессом называют процесс, протекающий при постоянной температуре T. Если, перемещая поршень, изменять объем газа в сосуде то, температура газа тоже будет изменяться, однако можно охлаждая сосуд при сжатии газа и нагревая при расширении можно достичь того, что температура будет постоянной при изменениях объема и давления, такой процесс называется изотермическим (Т=const).

Из уравнения (*) состояния идеального газа следует, что при постоянной температуре T и неизменном количестве вещества ν в сосуде произведение давления p газа на его объем V должно оставаться постоянным:

pV = const.

 

Н
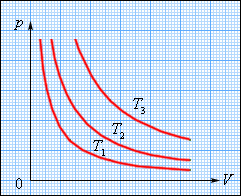
а плоскости (p, V) изотермические процессы изображаются при различных значениях температуры T семейством гипербол p ~ 1 / V, которые называются изотермами. Так как коэффициент пропорциональности в этом соотношении увеличивается с ростом температуры,

Рис.Семейство изотерм на плоскости (p, V). T₃ > T₂ > T₁.


изотермы, соответствующие более высоким значениям температуры, располагаются на графике выше изотерм, соответствующих меньшим значениям температуры (рис. 3.3.1). Уравнение изотермического процесса было получено из эксперимента английским физиком Р. Бойлем (1662 г.) и независимо французским физиком Э. Мариоттом (1676 г.). Поэтому это уравнение называют законом Бойля–Мариотта.


P₁ / P₂ =  ₂ /  ₁

Однако, закон Бойля — Ма­риотта перестает оправдываться, если перейти к большим давлениям. И это обстоятельство может быть прояснено, как считал еще М. В. Ломоносов, на основании молекулярных представлений.


  Зависимость между плотностью газа и его давле­нием

Вспомним, что плотностью вещества называется масса, заключенная в единице объема. Если мы как-нибудь изменим объем данной массы газа, то изменится и плот­ность газа. Если, например, мы уменьшим объем газа в пять раз, то плотность газа увеличится в пять раз. При этом увеличится и давление газа; если температура не изме­нилась, то, как показывает закон Бойля — Мариотта, давление увеличится тоже в пять раз. Из этого примера видно, что при изотермическом процессе давление газа изме­няется прямо пропорционально его плотности.

Обозначив плотности газа при давлениях  и  буквами  и , можем написать:

    (3)

Этот важный результат можно считать другим и более существенным выражением закона Бойля — Мариотта. Дело в том, что вместо объема газа, который зависит от случай­ного обстоятельства — оттого, какая выбрана масса газа,— в формулу (3) входит плотность газа, которая, также как и давление, характеризует состояние газа и вовсе не зависит от случайного выбора его массы.


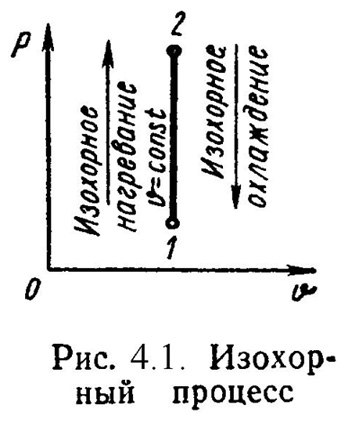
4.4.2.Изохорный процесс (V = const)


Изохорный процесс – это процесс нагревания или охлаждения газа при постоянном объеме V и при условии, что количество вещества ν в сосуде остается неизменным.

Если поршень зафиксирован и объем не меняется, то произойдет повышение давления в сосуде. Такой процесс называется изохорным (v=const), идущий при постоянном объеме;

Как следует из уравнения (*) состояния идеального газа, при этих условиях давление газа p изменяется прямо пропорционально его абсолютной температуре: p ~ T или

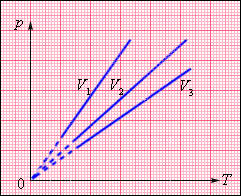
На плоскости (p, T) изохорные процессы для заданного количества вещества ν при различных значениях объема V изображаются семейством прямых линий, которые называются изохорами. Большим значениям объема соответствуют изохоры с меньшим наклоном по отношению к оси температур (рис. 3.3.2).

2

Рисунок 3.3.2. Семейство изохор на плоскости (p, T). V3 > V2 > V1.

Экспериментально зависимость давления газа от температуры исследовал французский физик Ж. Шарль (1787 г.). Поэтому уравнение изохорного процесса называется законом Шарля.

 ₂ / ₁ = T₂ / T₁

Закон Шарля с точки зрения молекулярной теории

Что происходит в микромире молекул, когда темпера­тура газа меняется, например когда температура газа повы­шается и давление его увеличивается? С точки зрения моле­кулярной теории возможны две причины увеличения давле­ния, данного газа: во-первых, могло увеличиться число ударов молекул на 1 см² в течение 1 сек; во-вторых, могло увеличиться количество движения, передаваемое при ударе в стенку одной молекулой. И та и другая причина требует увеличения скорости молекул. Отсюда становится ясным, что повышение температуры газа (в макромире) есть увеличение средней скорости беспорядочного движения молекул (в микромире). Опыты по определению скоростей газовых молекул, о которых буду говорить немного далее, подтверждают этот вывод.

Когда мы имеем дело не с газом, а с твердым иди жидким телом, в нашем распоряжении нет таких непосредственных методов определения скорости молекул тела. Однако и в этих случаях несомненно, что с повышением температуры ско­рость движения молекул возрастает.


Уравнение изохорного процесса может быть записано в виде:

где p₀ – давление газа при T = T₀ = 273,15 К (то есть при температуре 0 °С). Коэффициент α, равный 1/273,15 К^–1, называют температурным коэффициентом давления. 




4.4.3. Изобарный процесс (p = const)


Теперь установим, как ведет себя газ, если меняются его температура и объем, а давление остается постоянным.

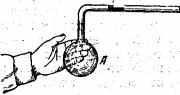Рассмотрим такой опыт. Коснемся Ладонью сосуда, изо­браженного на рис., в котором горизонтальный столбик ртути запирает .некоторую массу воздуха. Газ в сосуде нагреется, его давление повысится, и ртутный столбик нач­нет перемещаться вправо. Движение столбика пре­кратится, когда благодаря увеличению объема возду­ха в сосуде давление его сделается равным наруж­ному. Таким образом, в конечном результате этого опыта объем воздуха при нагревании увеличился а давление осталось неизменным.

Изобарным процессом называют процесс, протекающий при неизменным давлении p.

Если поршень свободен, то нагреваемый газ будет расширяться, при постоянном давлении такой процесс называется изобарическим (P=const), идущим при постоянном давлении

Уравнение изобарного процесса для некоторого неизменного количества вещества ν имеет вид:

где V₀ – объем газа при температуре 0 °С. Коэффициент α равен 1/273,15 К^–1. Его называют температурным коэффициентом объемного расширения газов. 

На плоскости (V, T) изобарные процессы при разных значениях давления p изображаются семейством прямых линий (рис. 3.3.3), которые называются изобарами.

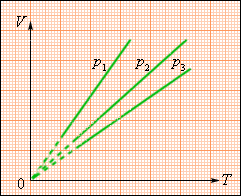3

Рисунок 3.3.3. Семейство изобар на плоскости (V, T). p3 > p2 > p1.

Зависимость объема газа от температуры при неизменном давлении была экспериментально исследована французским физиком Ж. Гей-Люссаком (1862 г.). Поэтому уравнение изобарного процесса называют законом Гей-Люссака.

Опыты показали, что увеличение объема газа пропорционально приращению температуры. Поэтому тепловое расширение газа можно, так же как и для других тел, охарактеризовать при помощи коэффициента объемного расширения b. Оказалось, что для газов этот закон соблюдается гораздо лучше, чем для твердых и жидких тел, так что коэффициент объемного расширения газов есть величина, практически постоянная даже при очень значительных повышениях Температуры, тогда как для жидких и твердых тел это; постоянство соблюдается лишь приблизительно.

Отсюда найдем:

  (4)

Опыты Гей-Люссака и других обнаружили замечательный результат. Оказалось, что коэффициент объемного расширения у всех газов одинаков (точнее, почти одинаков)   и равняется  = 0,00366 .

Таким образом,  при нагревании при постоянном давлении на 1° объем некоторой массы газа увеличивается на того объема, который эта масса газа занимала при 0°С (закон Гей-Люссака).

Коэффициент β называют температурным коэффициентом объемного расширения. Этот коэффициент у жидкостей в десятки раз больше, чем у твердых тел. У воды, например, при температуре 20 °С β_в ≈ 2·10^–4 К^–1, у стали β_ст ≈ 3,6·10^–5 К^–1, у кварцевого стекла β_кв ≈ 9·10^–6 К^–1.

Тепловое расширение воды имеет интересную и важную для жизни на Земле аномалию. При температуре ниже 4 °С вода расширяется при понижении температуры (β < 0). Максимум плотности ρ_в = 10³ кг/м³ вода имеет при температуре 4 °С.

При замерзании вода расширяется, поэтому лед остается плавать на поверхности замерзающего водоема. Температура замерзающей воды подо льдом равна 0 °С. В более плотных слоях воды у дна водоема температура оказывается порядка 4 °С. Благодаря этому может существовать жизнь в воде замерзающих водоемов.

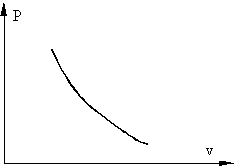
Процесс, при котором отсутствует теплообмен между системой и окружающей средой, называется адиабатным, при этом количество теплоты в системе остается постоянными (Q=const). В реальной жизни адиабатных процессов не существует поскольку полностью изолировать систему от окружающей среды не возможно. Однако часто происходят процессы, при которых теплообменном с окружающей средой очень мал, например, быстрое сжатие газа в сосуде поршнем, когда тепло не успевает отводиться за счет нагрева поршня и сосуда.

Примерный график адиабатного процесса в P - v координатах