Исследование интегрирующих и дифференцирующих цепей

Вид материала

Исследование

Содержание P = U i = L i di/dt Цель анализа 2. Гармонические колебания и их представление 3. Прохождение гармонического сигнала Для резистора Для емкости Интегрирующие и дифференцирующие цепи Анализируемая цепь описывается переходной характеристикой, равной реакции цепи на единичный скачек воздействия. Схема цепи изобр Частотные характеристики RC – и CR – цепей Список рекомендуемой литературы

Подобный материал:

• Государственный технический университет, 28.59kb.
• И. В. Мельникова основы теории цепей схемные функции и частотные характеристики линейных, 21.18kb.
• Задачи работы: описать кратко историю мировых гостиничных цепей; рассмотреть основные, 34.72kb.
• Полная техническая и качественная характеристика, 212.49kb.
• Центре внимания которых поиски общих и дифференцирующих принципов построения языковых, 22.54kb.
• Аннотация дисциплины, 34.98kb.
• Программа курса «Основы радиоэлектроники», 15.36kb.
• Дополнительные разделы теории цепей, 12.7kb.
• Лекция n 10, 69.36kb.
• Теория электрических цепей (часть, 63kb.

ИССЛЕДОВАНИЕ ИНТЕГРИРУЮЩИХ

И ДИФФЕРЕНЦИРУЮЩИХ ЦЕПЕЙ

Цель работы: Изучение процесса прохождения сигналов через простейшие RC-цепи. Измерение и вычисление основных параметров, частотных и фазовых характеристик RC-цепей. Освоение вопросов синтеза и анализа радиоэлектронных схем с помощью ЭВМ.

Введение. Теоретическая часть

Основные понятия радиоэлектронных цепей

Радиоэлектронное устройство независимо от конструкции и технологии его изготовления представляет собой некоторое соединение элементов – резисторов, конденсаторов, диодов, источ­ников электрической энергии и др. Совокупность соединенных опре­деленным образом элементов устройства называется радиоэлектронной цепью.

Элементы цепи подразделяются на активные и пассивные. Основной признак активного элемента - это его способность отдавать электрическую энергию. К пассивным элементам относятся потребители и накопители электрической энергии.

В теории цепей рассматриваются идеализированные элементы, обладающие каким-нибудь одним свойством, - это, например, сопротивление, емкость, индуктивность, источники тока и напряжения.

Сопротивление – идеализированный элемент, в котором электри­ческая энергия преобразуется в тепловую, механическую или световую. Сила тока в сопротивлении связана с напряжением на нем законом Ома: U = R i. Величину 1/R = G - называют прово­димостью. Форма тока, проходящего через сопротивление, всегда совпадает с формой приложенного к нему напряжения, поэтому всегда положительна мгновенная мощность Р = U i = R i² = G U².

Емкость – идеализированный элемент, обладающий свойством за­пасать энергию электрического поля. Ток в емкости и напряжение на ее зажимах связаны соотношением i = C dU/dt.

Мгновенная мощность Р = U i = UC dU/dt может быть как положительной (когда знаки напряжения и его производной одинаковы), так и отрицательной. Если мощность положительна, то емкость накапливает энергию, а заряд q = CU на нем увеличивается. Если же мощность отрицательна, то емкость разряжается и отдает энергию. Накопленная за промежуток времени t₂ – t₁ энергия


W (t₁, t₂) = C ∫ U dU/dt dt = С∫UdU = ½ CU² (t₂) – ½ CU² (t₁).

^{t t}

Индуктивность – идеализированный элемент, обладающий способностью запасать энергию магнитного поля. Ток в индуктивности с напряжением на её зажимах связаны соотношением U = L di/dt. Мгновенная мощность на индуктивности

P = U i = L i di/dt, как и для ёмкости может быть положительной и отрицательной.

Каждый элемент к цепи подключается двумя выводами – полюсами, поэтому простейшая электрическая цепь является двухполюсником.

Цепь, в которой выделены вход и выход и, таким образом имеет четыре полюса, называется четырёхполюсником. Цепи, размеры которых значительно меньше длины волны электрических сигналов, считают цепями с сосредоточенными параметрами. В таких цепях сопротивления, ёмкости и индуктивности сосредоточены в отдельных элементах.

Цепи, размеры которых соизмеримы с длинной волны электрических сигналов или больше её, относятся к цепям с распределенными параметрами. Каждый элемент конструкции такой цепи обладает сопротивлением, емкостью, индуктивностью.

По признаку зависимости параметров элементов цепи от приложенных напряжений и протекающих токов различаются линейные и нелинейные цепи.

Радиоэлектронная цепь считается линейной, если параметры ее элементов не зависят от токов и напряжений. Примером линейной цепи может быть цепь, состоящая из идеализированных элементов ни один из которых не зависит от протекающих токов и напряжений.

Цепь считается нелинейной, если параметры ее элементов зависят от токов и напряжений. Такими являются цепи, содержащие элементы сопротивления с нелинейными вольтамперными характеристиками, а также цепи с диодами, транзисторами и конденсаторами в виде p-n – перехода.

Цепи, параметры элементов которых меняются во времени по заданному закону, считаются параметрическими. Такие цепи чаще всего создаются из нелинейных элементов, параметры которых изменяются с помощью управляющих сигналов.

По признаку наличия или отсутствия источников электрической энергии внутри цепи различают активные или пассивные цепи. Активная – это цепь, содержащая внутренние источники энергии, например усилитель. Пассивная - это цепь, не содержащая внутренних источников энергии, например цепь, состоящая только из пассивных элементов – резисторов, конденсаторов, катушек индуктивности.

Задачи теории цепей делятся на две группы: задачи анализа и задачи синтеза. Цель анализа – исследование процессов в цепи с заданной структурой и заданными характеристиками всех элементов цепи, например расчёт реакции заданной цепи на известные воздействия. Цель синтеза – отыскание структуры цепи и параметров её элементов, при которых электрический процесс будет удовлетворять заданным требованиям. Синтез цепей основывается на общих свойствах электрических цепей. Эти свойства выясняются в процессе анализа, поэтому синтезу должен предшествовать анализ.

Задача синтеза значительно более сложная и трудоемкая по сравнению с задачей анализа, поэтому в инженерной практике часто используют нестрогий синтез, заключающийся в выборе нужной цепи из множества подробно исследованных.


2. Гармонические колебания и их представление


Электрическое колебание, которое описывается гармоническими (sin и cos) функциями времени, называется гармоническим. Такое колебание можно записать S (t) = A_m cos (ωt – φ).

Здесь A_m – амплитуда, ωt – φ = θ(t) – фаза. Величину ω = 2πf = 2π/T называют угловой частотой. Гармонические колебания в радиоэлектронике занимают исключительное место благодаря:

• простоте технической реализации генератора;
  
• неизменности формы гармонических колебаний при прохождении через линейную цепь с постоянными параметрами (меняется только амплитуда и фаза).
  

Гармоническое колебание полностью характеризуется двумя величинами: амплитудой A_m и фазой θ. Как известно, аналогичными величинами определяется положение вектора на плоскости. Используя эту аналогию, гармоническое колебание можно условно изображать вектором на плоскости.

Наряду с векторным представлением гармонические колебания можно представлять комплексными числами. Как известно, комплексное число

a + jb = A_m e^jα = A_mcos(α) + jA_msin(α)

полностью характеризуется модулем A_m и аргументом α, аналогичными амплитуде и фазе гармонического колебания. Комплексное число Á_m = A_me^­jφ называют комплексной амплитудой гармонического колебания.

Метод расчета цепей, базирующихся на понятии комплексной амплитуды, называют методом комплексных амплитуд. Метод комплексных амплитуд в электротехнике впервые в 1883 году применил немецкий ученый Ч.Штейнмец. В России этот метод широко использовал академик В.Ф. Миткевич.

Переход от временной функции к комплексной амплитуде обратим: S(t) = A_mcos(ωt – φ)  . Очевидно, что при всех математических преобразованиях, где вещественная и мнимая части комплексного числа преобразуются независимо одна от другой, этот метод может быть использован без каких-либо ограничений. Примерами таких математических операций, называемых линейными, являются сложение, вычитание, умножение на постоянную величину, дифференцирование и интегрирование.

Операции умножения и деления являются нелинейными. Для получения правильного результата приходится использовать искусственный прием: один из переменных множителей брать комплексно сопряженным. Примером может служить нахождение мощности переменного тока по формуле P=IUcos(φ)=Re. Практически важным случаем нелинейной операции является введение комплексных изображений для сопротивлений. Учитывая закон Ома 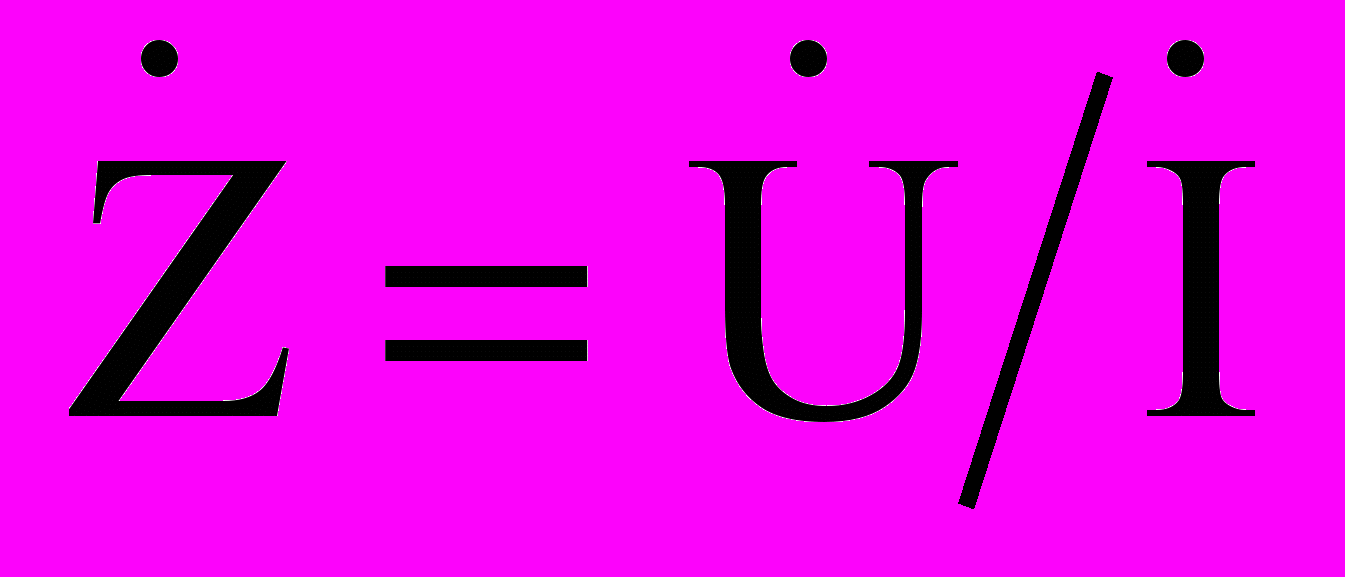, найдем символические изображения для простых случаев чисто активного, чисто емкостного и чисто индуктивного сопротивлений.

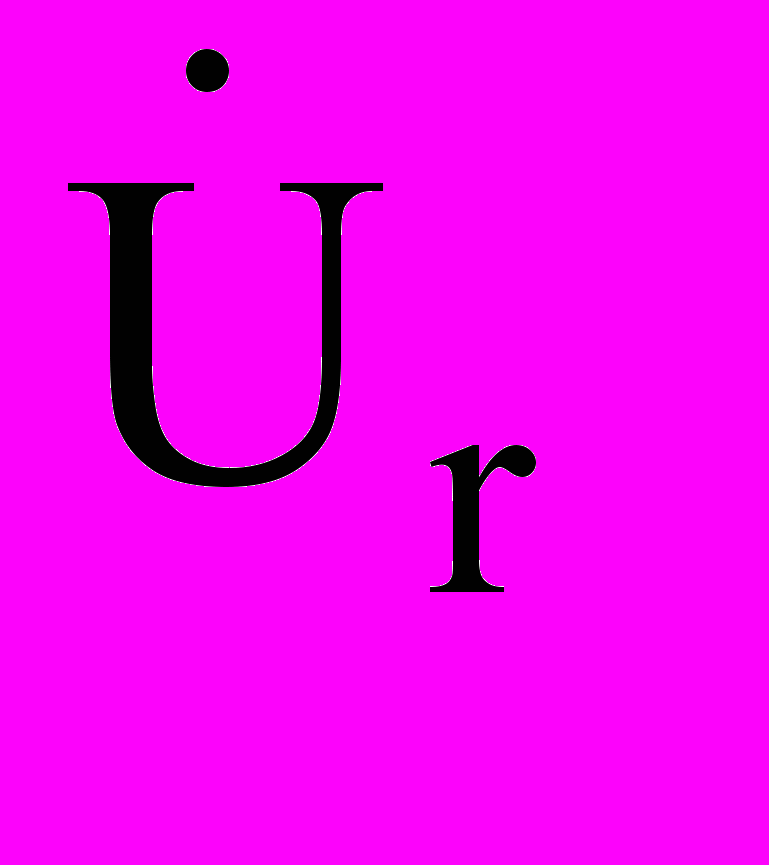= R.

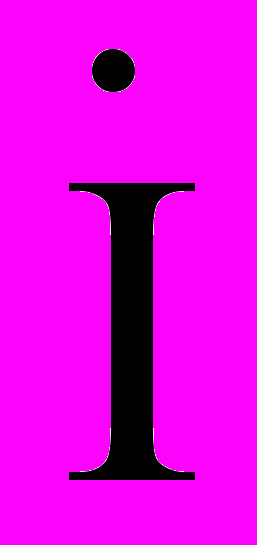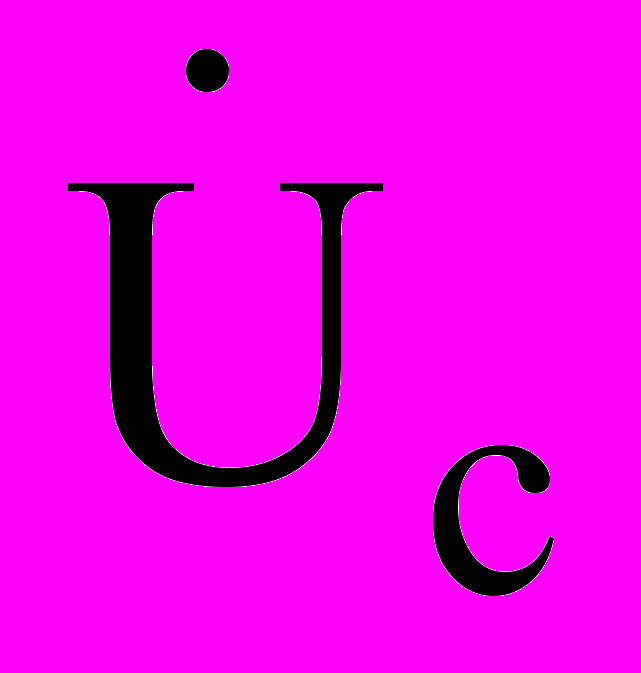= 1/C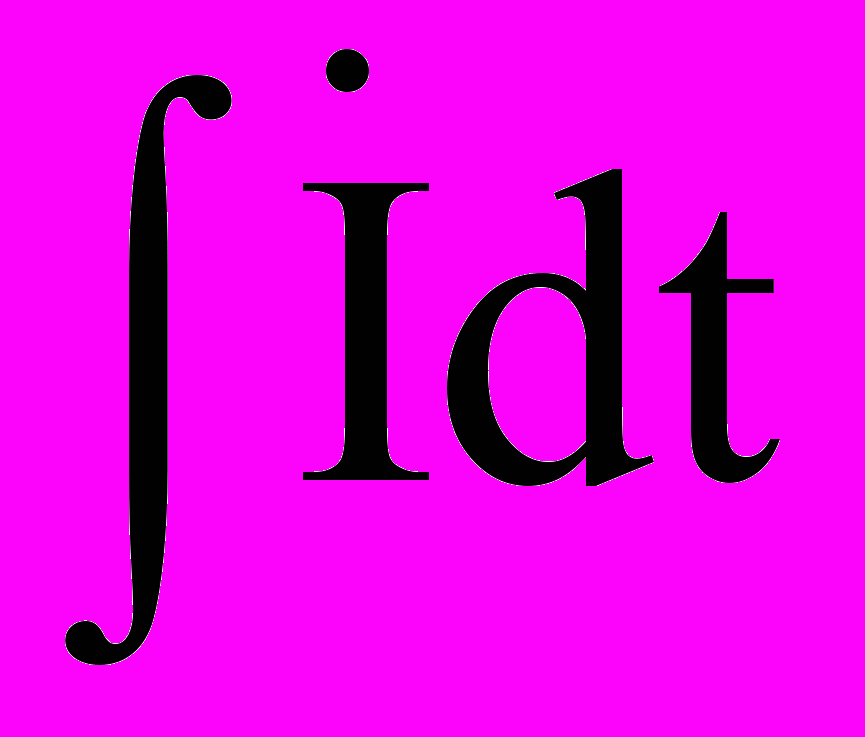= (1/jωC) · i_me^jωt = (1/jωС)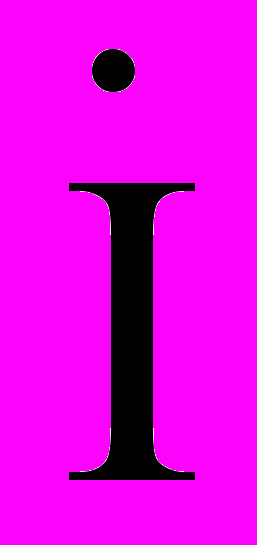

= L di/dt = L d(i_me^jωt)/dt = jωLi_me^jωt = jωL.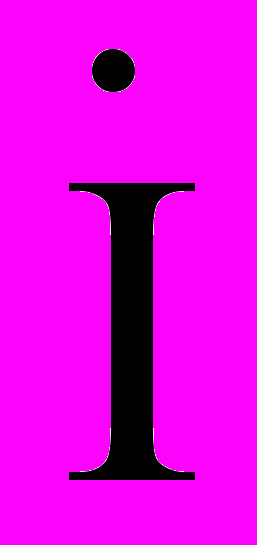

Из этих соотношений непосредственно следуют выражения для



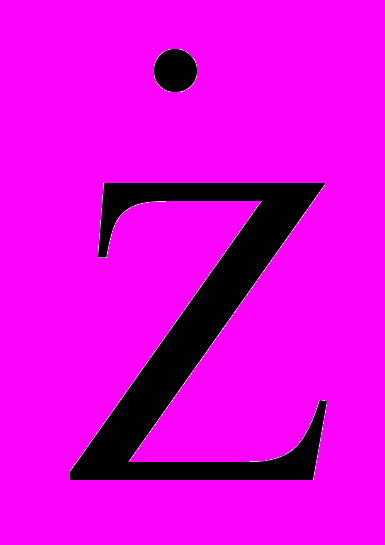
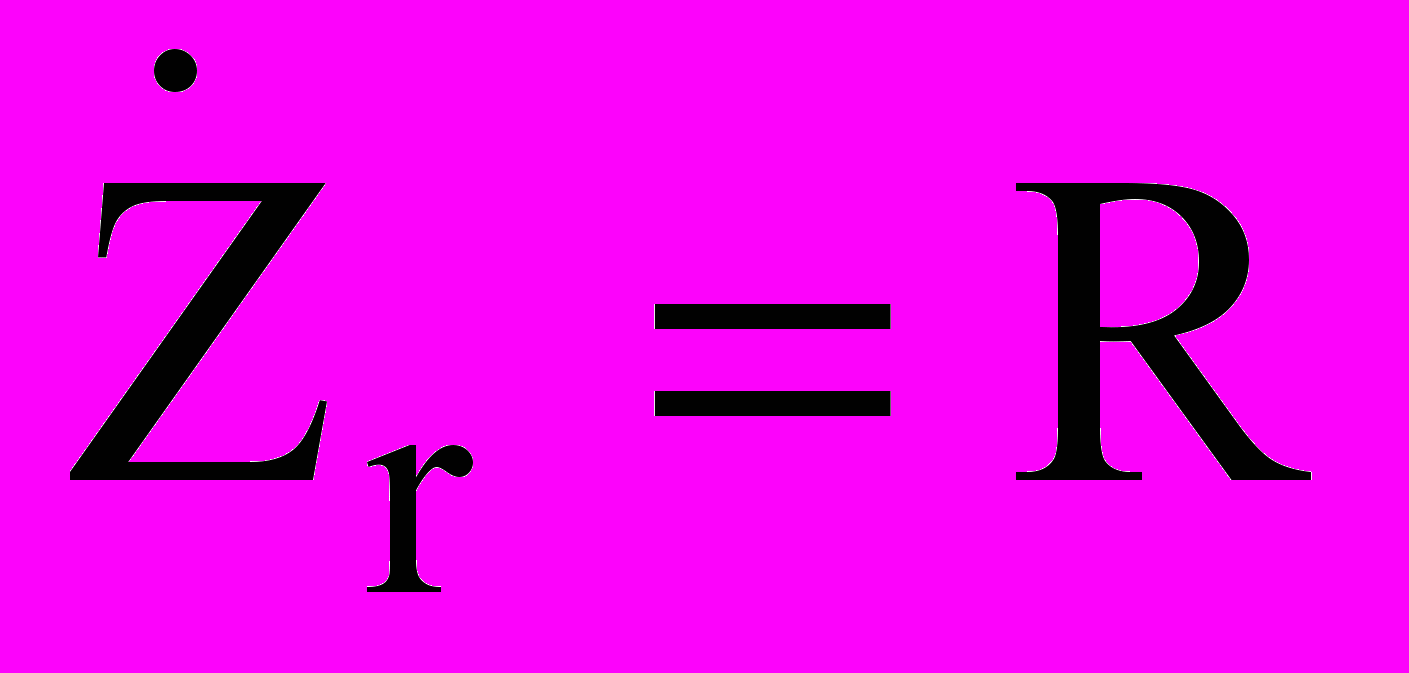
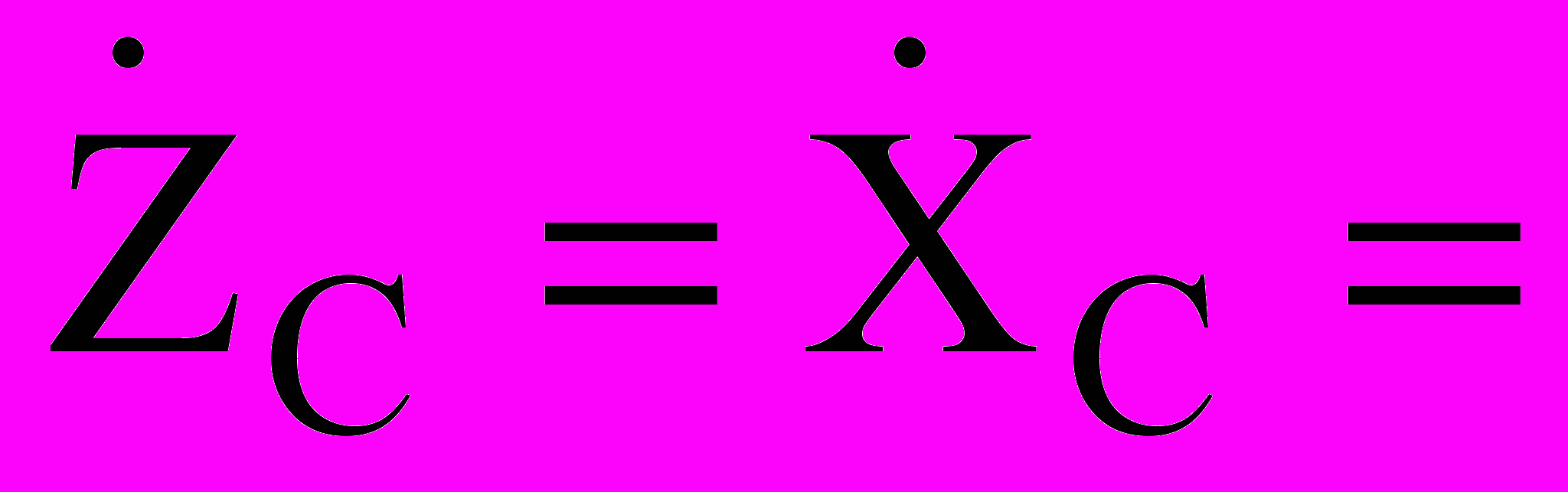1/jωС = (1/j) X_C

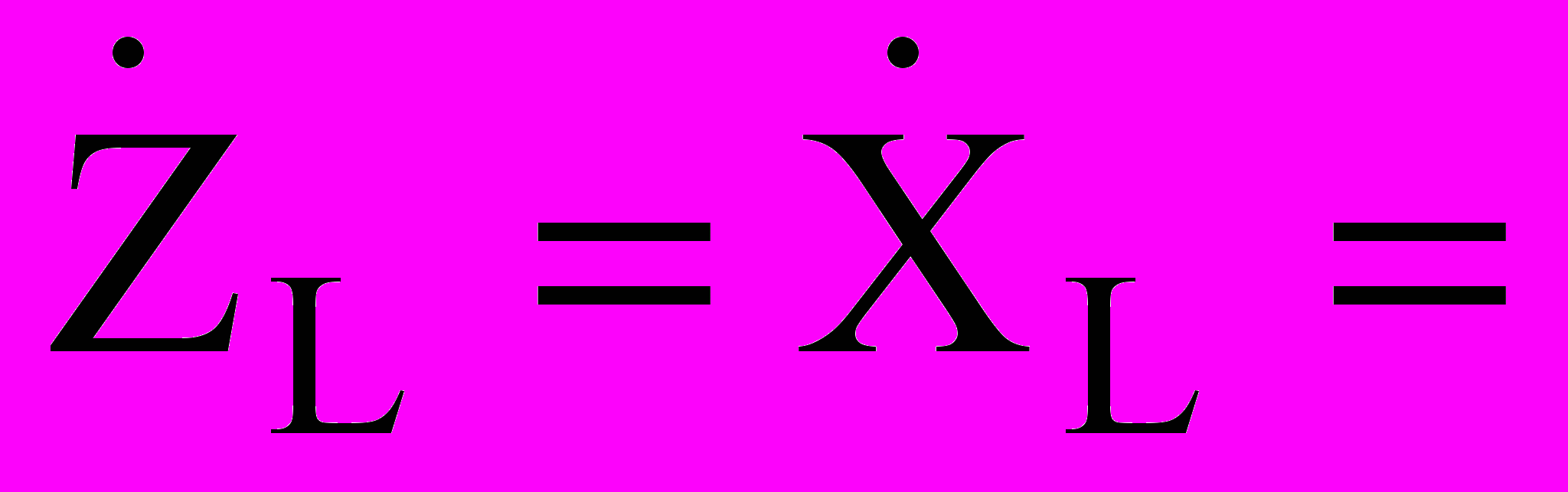jωL = jX_L .

Следует особо подчеркнуть, определение комплексных изображений для сопротивлений включает в себя нелинейную операцию 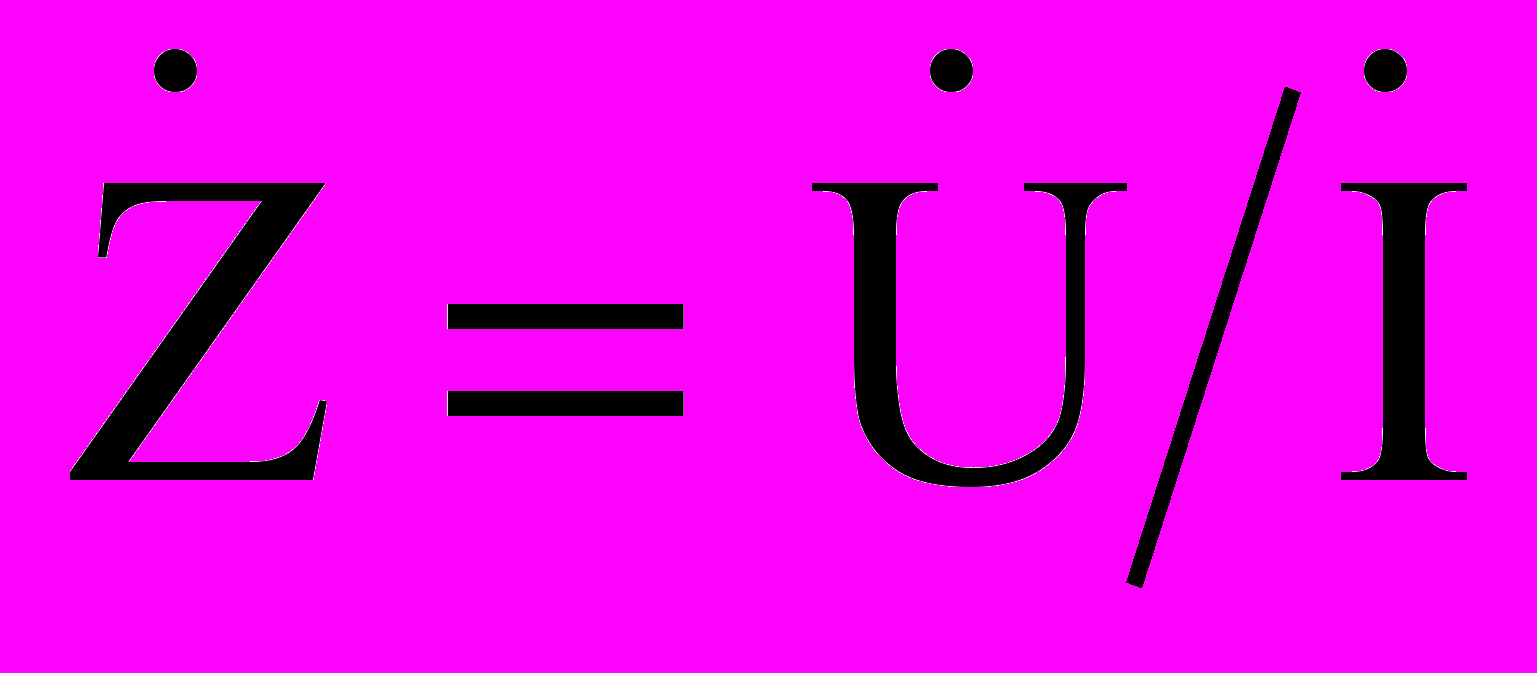. Поэтому соотношение между сопротивлением и его комплексным изображением имеет другой характер, чем в случае тока и напряжений. Сопротивление равно не вещественной или мнимой части, а модулю своего символического изображения.


3. Прохождение гармонического сигнала

по элементам электрической цепи

Рассмотрим явления при прохождении гармонического тока по элементам электрической цепи.

Для резистора

R

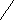
I_r I_r U_r

U_r

U_r = U_m sin(ωt), I_r = U_m/R sin(ωt).

Ток и напряжение в цепи активного элемента – сопротивления совпадают по фазе.

Для емкости

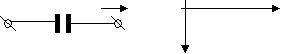С I_c

I_c


U_c U_c

U_c = U_m sin(ωt)

I_c = C d (U_m sinωt)/dt = C ω U_m cos(ωt) или

I_c = U_m/(1/ωC) sin(ωt + π/2),

где X_c = 1/ωC – реактивное емкостное сопротивление.

Из приведенных соотношений видно, что ток в цепи конденсатора опережает падение напряжение на нем на π/2.

Для индуктивности


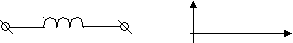
L U_L

I_L I_L

U_L

U_L = U_msinωt, I_L = (- 1/L) · U_m ∫ sinωt dt = (- 1/ωL) · U_m cosωt,

I_L = (U_m/ωL) · sin(ωt – π/2),

где X_L = ωL – реактивное индуктивное сопротивление. Ток в цепи катушки индуктивности отстает от падения напряжения на ней на π/2.

4. Интегрирующие и дифференцирующие цепи
   

CR – цепь.



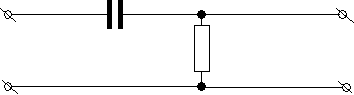
U₁ C R U₂


Напряжение на резисторе U_r = U₂ = IR, где I=C dU_c/dt, тогда

U₂ = CR dU_c/dt.

Зная, что U_c = U₁ – U₂, получим для U₂ =CR dU₁/dt – CR dU₂/dt.

При малых частотах и постоянных токах U_r – величина малая, тогда

U₂=CR dU/dt,

т.е. напряжение на выходе цепи пропорционально дифференциалу U₁, поэтому ее называют дифференцирующей.

RC – цепь.

R




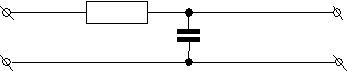
U₁ C U₂


Ток в цепи конденсатора I = C dU_c/dt, а напряжение U_c = 1/C ∫ Idt, где I =U_r/R, тогда 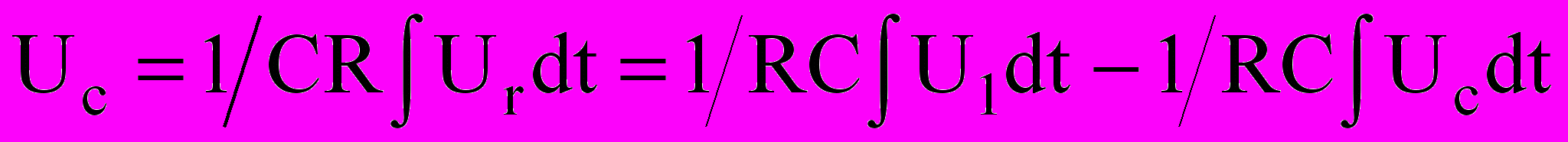. При R » 1/ωC, 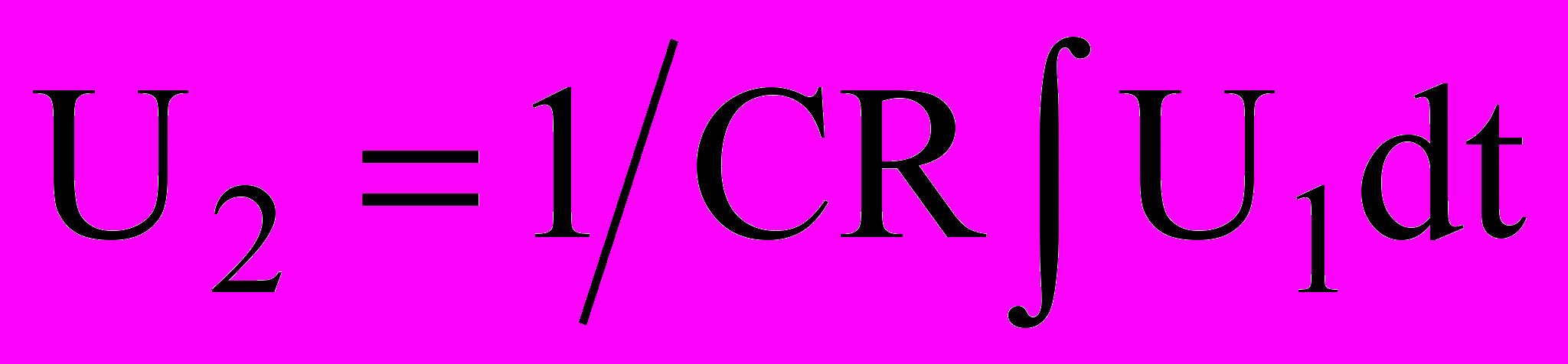, т.е. напряжение на выходе RC – цепи пропорционально интегралу от входного напряжения. Такая RC – цепь именуется интегрирующей.


5. Переходные характеристики CR - и RC – цепей

Анализируемая цепь описывается переходной характеристикой, равной реакции цепи на единичный скачек воздействия. Схема цепи изображена на рис.1

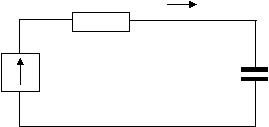U_r I


R

e (t)

C U_c

Рис. 1

Воздействие e(t) – скачек напряжения в момент времени t = 0 на величину Е. Согласно закону Кирхгофа запишем уравнение U_r + U_c = e(t). Так как U_r = iR, a i = CdU_c/dt, то уравнение примет вид RC dU_c/dt + U_c = e(t). При e(t) = 0 решение однородного уравнения цепи U_c(t) = Аe ^–t/RC.

Частное решение неоднородного уравнения описывает стационарный режим. В рассматриваемом примере с течением времени емкость зарядится до стационарного значения U_c= E. Константу А можно найти из начального условия: U_c = 0 при t = 0. Поэтому А = - Е. Окончательное выражение для напряжения U_c(t) = E [1 – exp(-t/RC)], t ≥ 0. Переходная характеристика RC – цепи h_c(t) = 1 – exp( - t/RC ), t ≥ 0.

График зависимости напряжения U_c(t) от времени представлен на рис. 2.

U_c



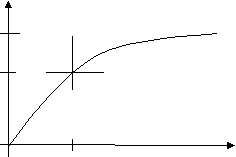
Е

0,63E


τ t

Рис. 2


τ = RC – называется постоянной времени, которая означает время, в течение которого напряжение на конденсаторе изменится в e раз. Например: за время τ напряжение U_c возрастает до 63% от Е, а за время 3τ до 95%.

Форму сигнала, как отклик системы на импульсное воздействие можно исследовать с помощью преобразования Фурье. Применим его для импульсного сигнала, U₁ = e(t) = E при 0 ≤ t ≤ t₁, U₁ = e(t) = 0 при t < 0, t > t₁,

подаваемого на цепь, приведенной на рис. 3.





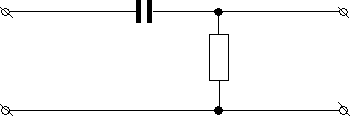
С

U₁ R U₂


Рис. 3


Введем понятие коэффициента передачи рассматриваемой цепи:

.

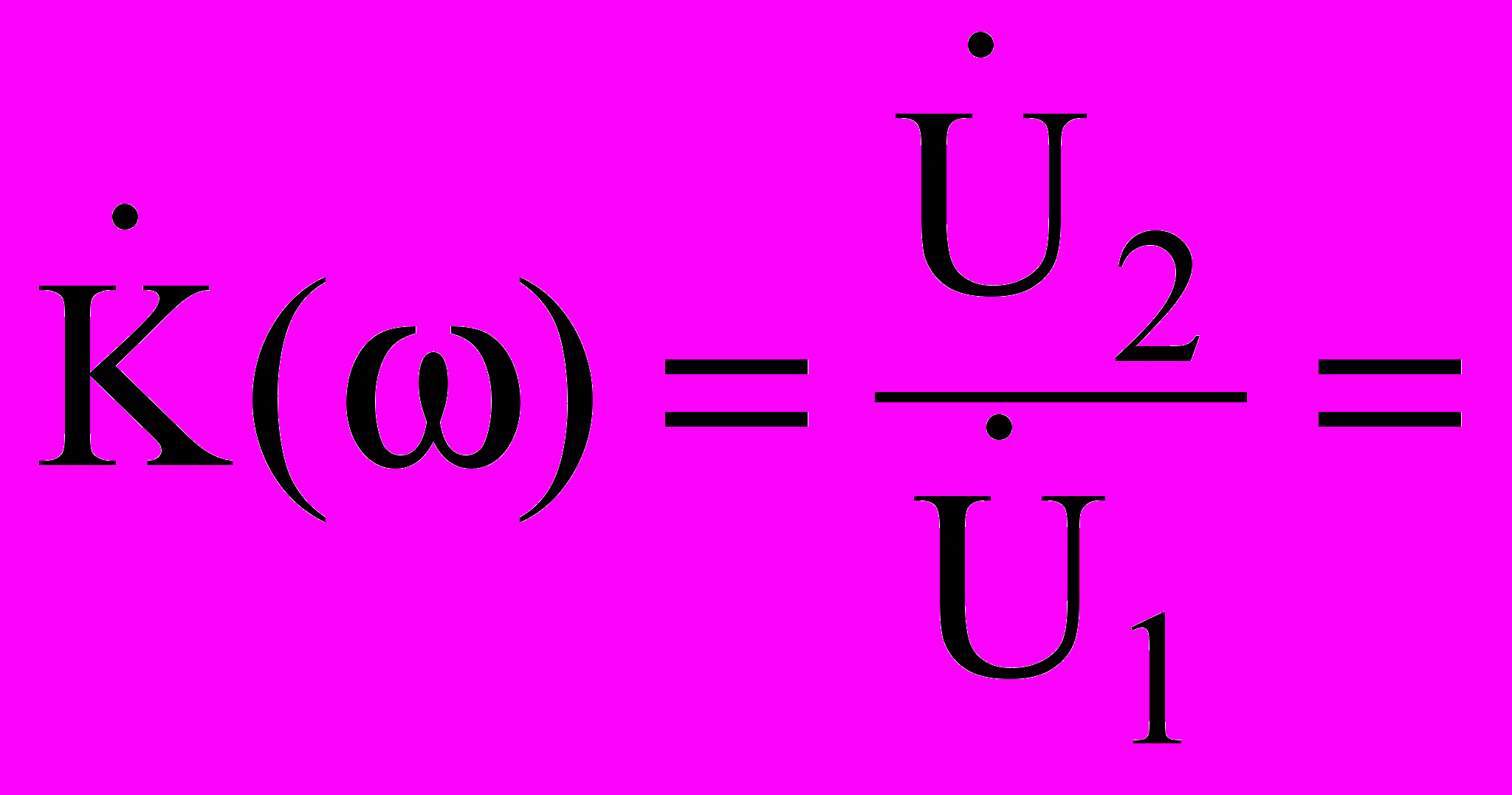
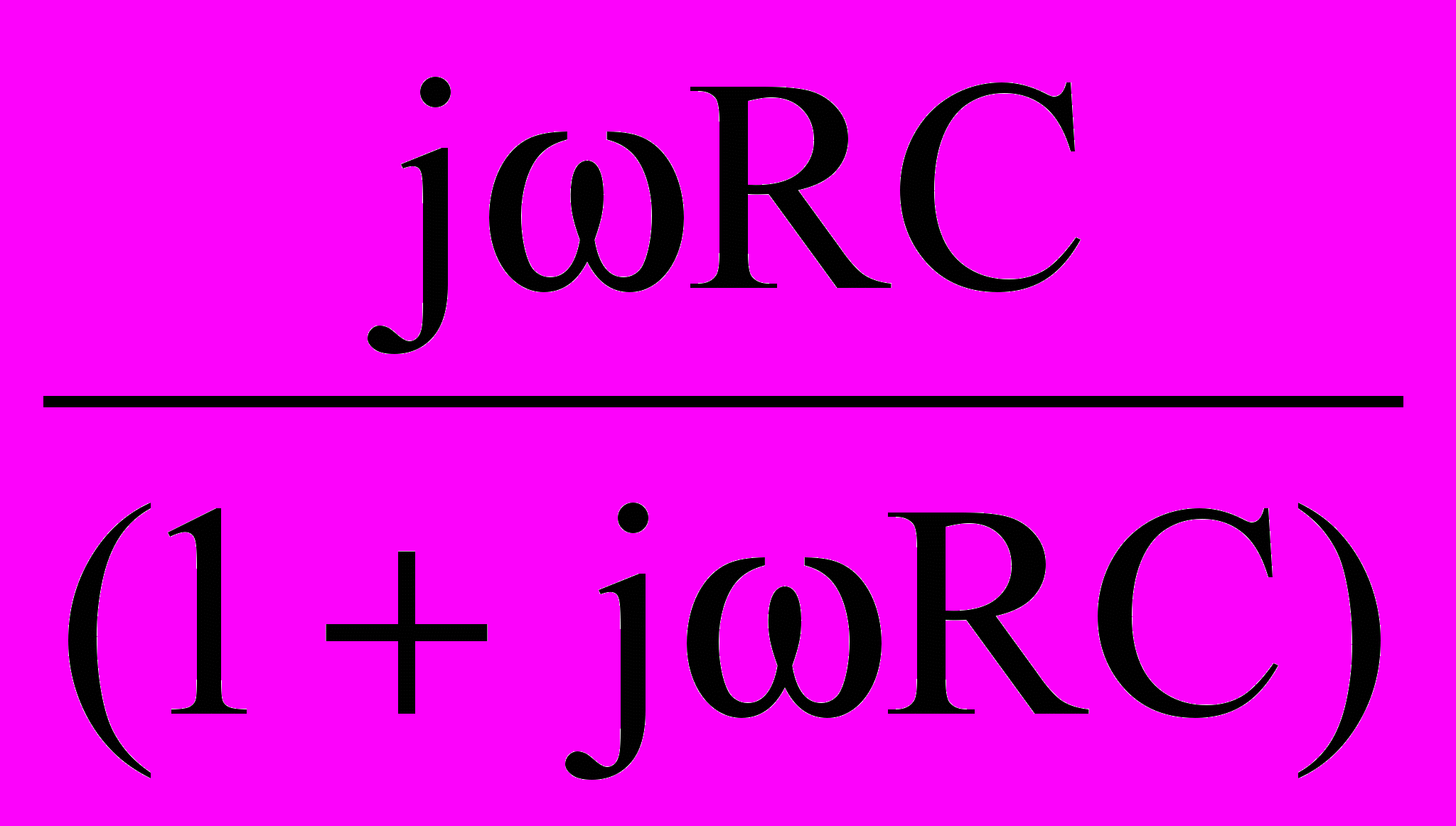1. Находим спектральную функцию сигнала:
   

.

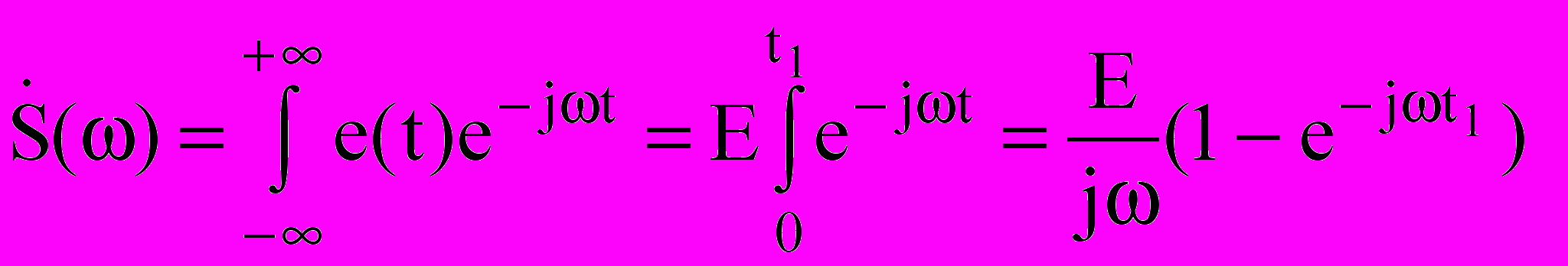2. Определим измененную спектральную функцию сигнала после прохождения через цепь:
   

.

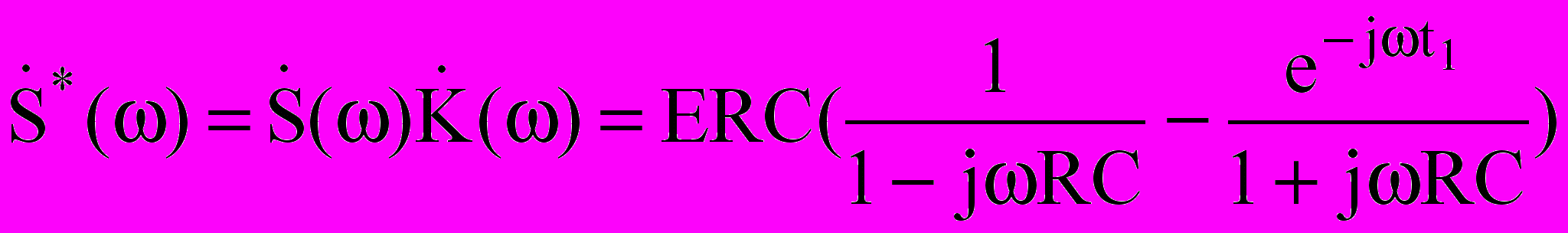3. По измененной спектральной функции сигнала находим сигнал на выходе цепи:
   

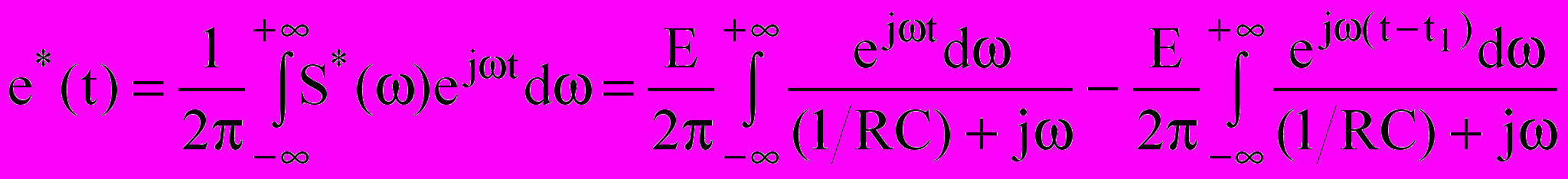
После интегрирования получаем:

U₂ = e^*(t) = Ee ^–t/RC при t < t₁

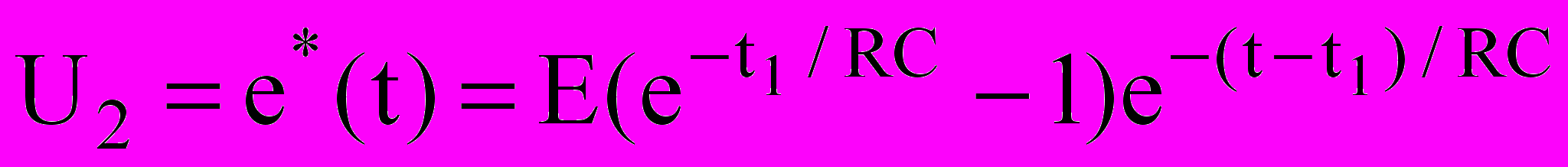при t > t₁.


1.0 U₁/E 1.0 U₂/E


t = t₁

t = 0 t = t₁ t t = 0 t

Рис. 4

Первая часть решения, при 0 ≤ t ≤t₁, соответствует переходному процессу в цепи при включении Е; вторая часть, при t > t₁, при выключении Е. На рис.4 представлены входной сигнал прямоугольной формы и форма сигнала на выходе СR-цепи при различных τ.

1. Частотные характеристики RC – и CR – цепей
   

RC – цепь. Комплексная функция входного сопротивления:

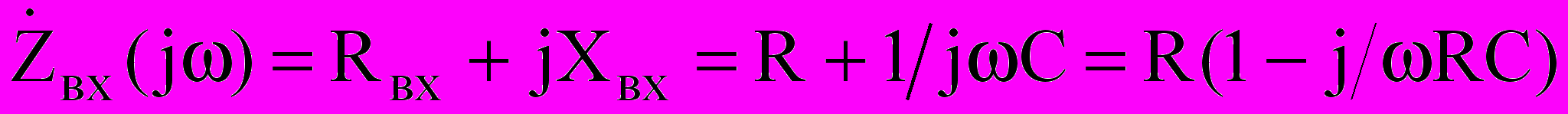. Комплексная передаточная функция напряжения:

.

Амплитудно-частотная и фазово-частотная характеристики примут вид:

.

.

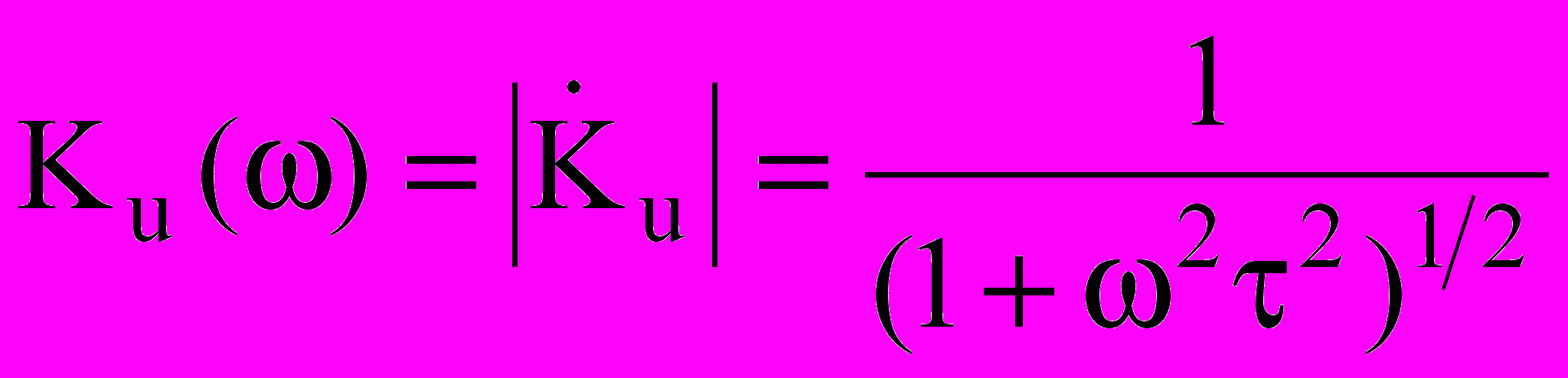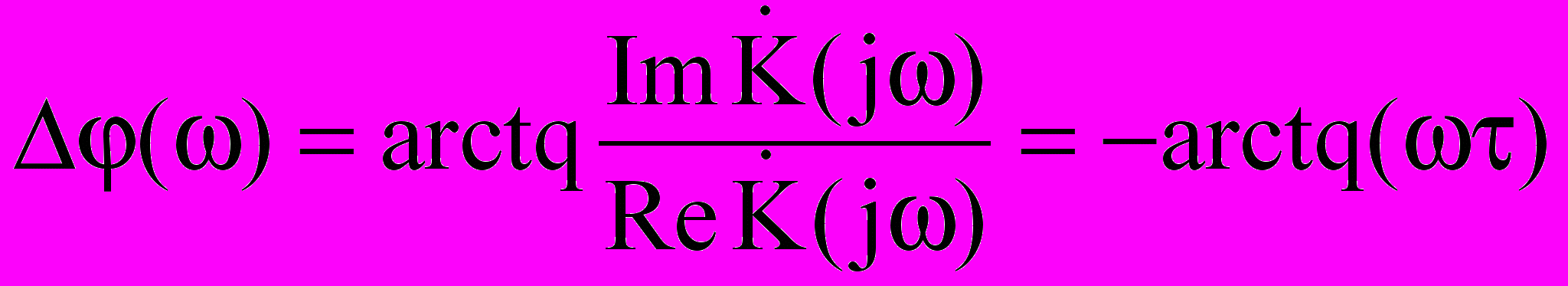Графики амплитудно-частотной и фазово-частотной характеристик показаны на рис.5.

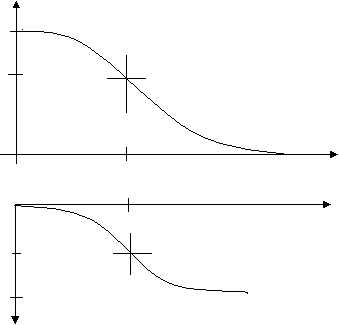K_u


1


1/


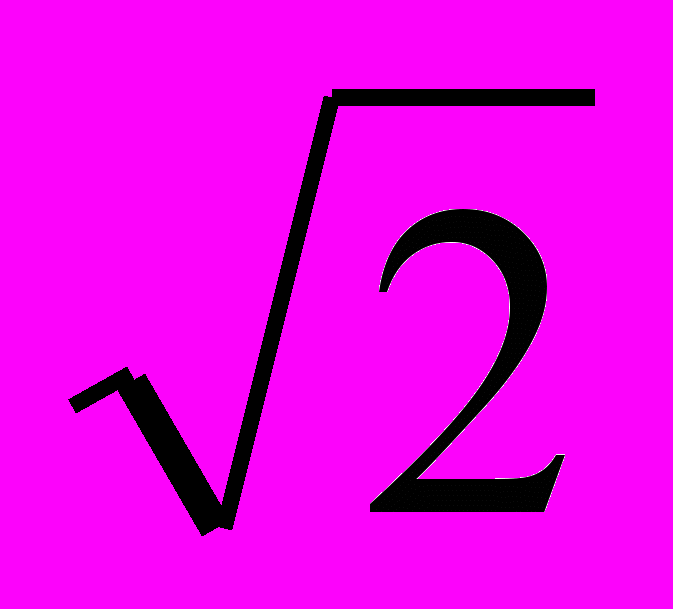
0 ω_c ω


0 ω


- π/4


- π/2




Рис. 5


Из графиков видно, что RC – цепь пропускает низкочастотные колебания, и не пропускает высокочастотные. На частоте среза полосы пропускания ω_с получаем

.

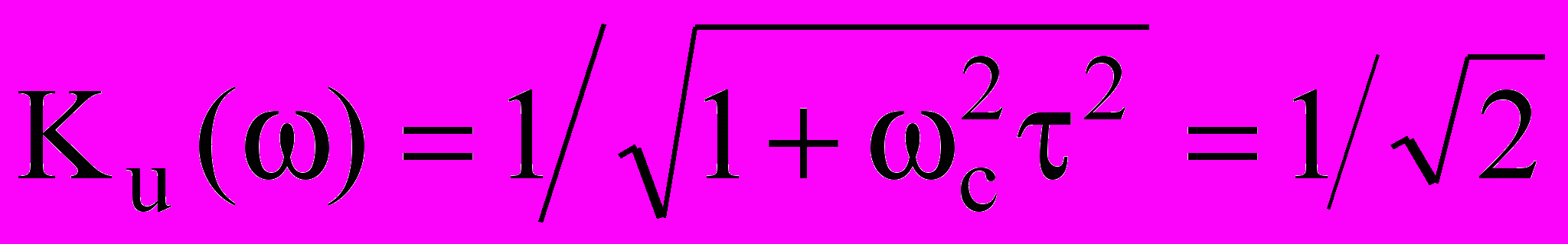Отсюда, частота среза ω_с = 1/ τ. Ширина полосы пропускания RC – цепи равна частоте среза. Рассмотренная RC – цепь может быть использована как фильтр низких частот.


СR – цепь


Входное сопротивление CR – цепи такое же, как и RC – цепи. Комплексная передаточная функция напряжения:


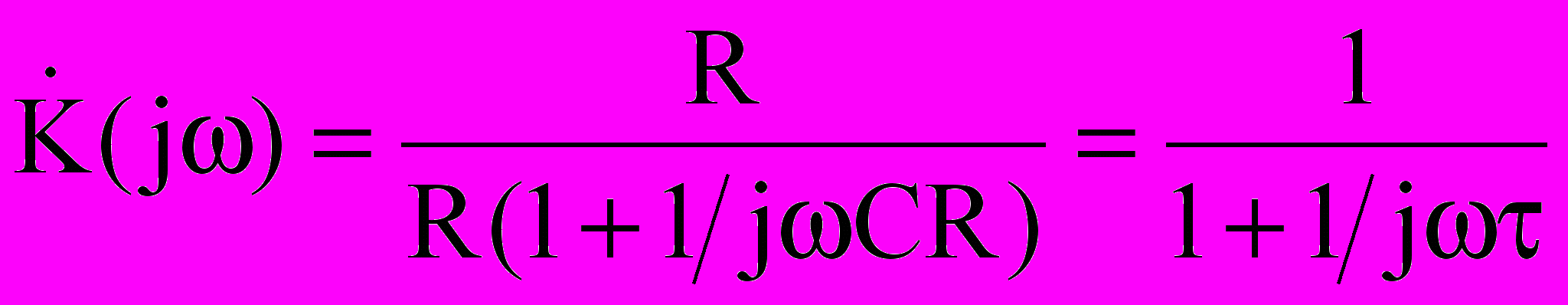
Амплитудно-частотная и фазово-частотная характеристики:

; .

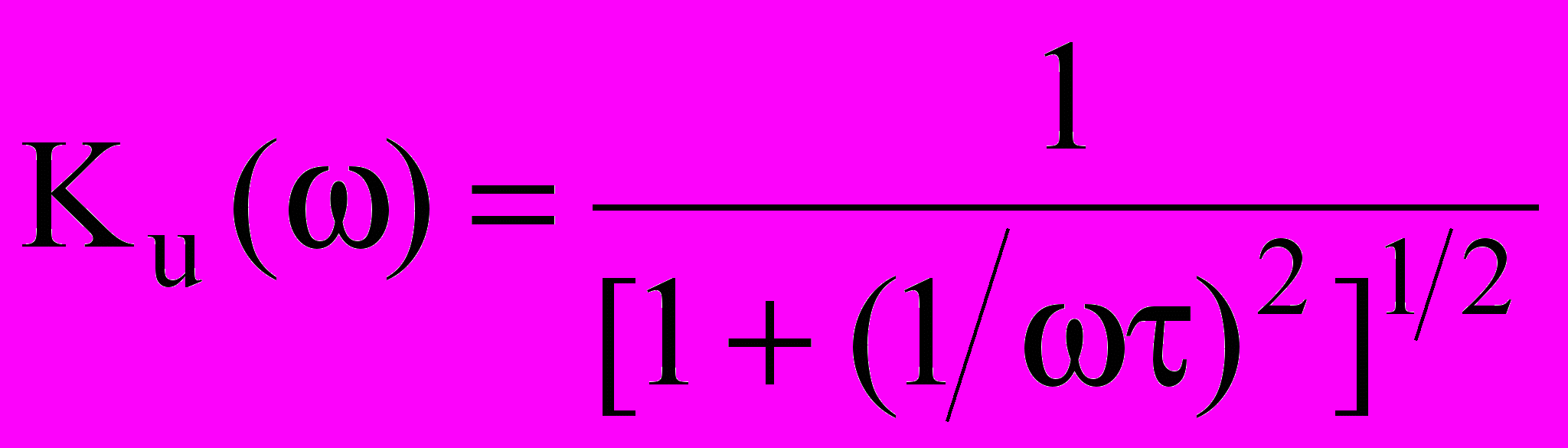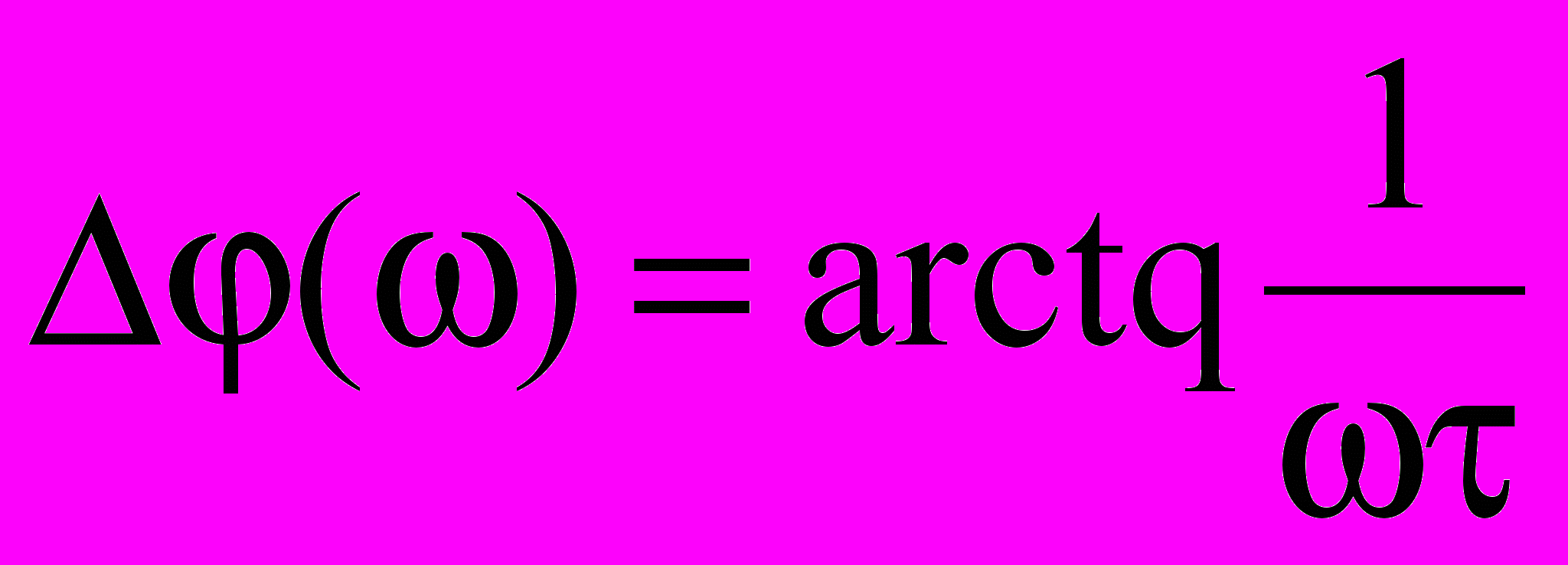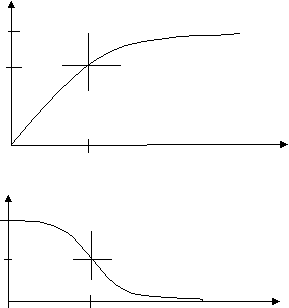K_u

1

1/


0 1/ ω

φ

π/2


π/4


0 1/ τ ω

Рис. 6.


CR – цепь пропускает колебания с частотами выше частоты среза ω_гр = 1/ τ. Сверху полоса пропускания не ограничена. CR – цепь часто используют в качестве фильтра высоких частот. На рис.6 приведены графики амплитудно-частотной и фазово-частотной характеристик пассивного фильтра высоких частот.


П. Экспериментальная часть


Для исследования простейших радиоэлектронных цепей используется лабораторный стенд, который включает в себя три основных устройства:

• источник стабилизированного напряжения (+10В).
  
• релаксационный генератор на операционном усилителе К140 УД608 с двумя фиксированными частотами 500 Гц и 2 кГц и регулируемой скважностью.
  
• дифференцирующие и интегрирующие цепочки с фиксированными параметрами R и С. (R=20 кОм, 10 кОм, 5 кОм. С= 100 нФ, 10 нФ, 1 нФ.)
  

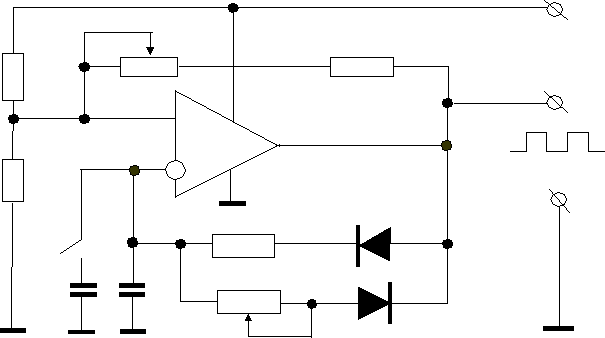
На рис.7 приведена схема релаксационного генератора.



U_n

R₁ 10k R₅ 37k +10B

R₃ 20k


R₄ 20k


11k D₁

K


C C D₂


R₂ 11k


Рис. 7. Принципиальная схема релаксационного генератора.

Тумблер К₁ переключает частоту генерации, резисторы R₁ и R₂ регулируют

скважность выходного сигнала.


Устройство работает следующим образом. При включении питания на выходе операционного усилителя устанавливается напряжение близкое к напряжению питания +10 В. Через резистор 11кОм и диод Д₁ начинается зарядка конденсатора С_2. При достижении на нем напряжения U’_пор. операционный усилитель переключается и на выходе устанавливается U_вых.= 0. Конденсатор разряжается через резистор R₂ и диод Д₂. При достижении на нем U”_пор. происходит обратное переключение операционного усилителя с установкой на выходе напряжения близкого к напряжению питания, что приводит к новой зарядке конденсатора. Эти процессы повторяются пока подано напряжение питания. Частота колебательного процесса определяется из соотношения:


.


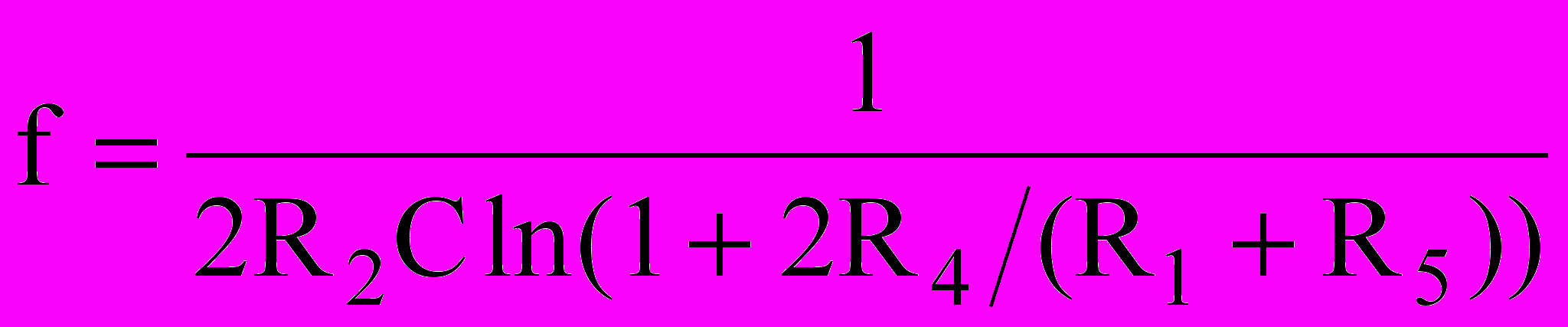Уменьшение времени разрядки конденсатора С₂ резистором R₂ изменяет скважность выходного сигнала.

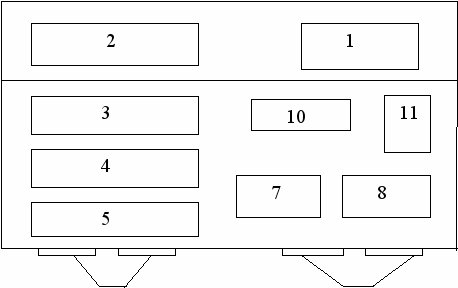
На рис. 8 приведена схема расположения основных блоков, управляющих элементов и выводов для подключения измерительных приборов лабораторного стенда.





6 9

Рис. 8.

1. Сетевой трансформатор блока питания.
   
2. Стабилизатор напряжения +10 В.
   
3. Плата релаксационного генератора и переключатель частоты генерации прямоугольных импульсов.
   
4. Переключатель выхода (6) на работу от внутреннего или от внешнего генераторов.
   
5. Резистор регулировки скважности выходного сигнала.
   
6. Клеммы выхода внутреннего генератора и подключения внешнего.
   
7. Плата конденсаторов с переключателем номиналов конденсаторов RC и CR – цепей.
   
8. Плата резисторов с переключателем номиналов резисторов RC и CR- цепей.
   
9. Клеммы для выходного сигнала с RC и CR – цепей.
   
10. Тумблер переключения дифференцирующей и интегрирующей цепей.
    
11. Тумблер и сигнальный светодиод питания.
    

Ш. Порядок выполнения работы


Задание1. Исследование переходных характеристик дифференцирующих и интегрирующих цепей

1. Выходные клеммы “Общий”, “Вых. генер.” подключить, соблюдая полярность, коаксиальным кабелем к входу первого канала осциллографа С1 – 118А.
   
2. Выходные клеммы “Общий”, “Выход” подключить, соблюдая полярность, коаксиальным кабелем к входу второго канала осциллографа.
   
3. Тумблер 4 (рис.8) поставить в положение “Внутренний генератор”.
   
4. Тумблер 3 (рис.8) поставить в положение 2 кГц.
   
5. Тумблер 10 (рис.8) поставить в положение “Диф. цепь”.
   
6. Установить минимальную чувствительность по входам первого и второго каналов осциллографа.
   
7. Включить сетевое питание лабораторного стенда и осциллографа.
   

8. Ручками управления осциллографа установить рациональные по длительности и амплитуде осциллограммы входного и выходного сигналов.
   
9. Переключая номиналы R и С (7 и 8) (рис.8), пронаблюдать и зарисовывать входной сигнал и девять видов осциллограмм выходного сигнала.
   
10. Измерить по осциллограммам постоянную времени “τ” для четырех комбинаций номиналов R и С. При затруднении измерения больших “τ” перейти на меньшую частоту следования импульсов – 500 Гц и меньшую длительность импульсов (ручка “Скважность”). Сравнить измеренные значения постоянной времени с расчетными.
    
11. Переключить тумблер 10 (рис.8) в положение “Интегр. цепь”. Повторить аналогичные наблюдения и измерения.
    
12. Проанализировать полученные результаты и сделать соответствующие выводы.
    

Задание 2. Исследование частотных и фазовых характеристик

RC – и CR – цепей

1. Переключить тумблер 4 (рис.8) в положение "Внешний генератор".
   
2. Коаксиальным кабелем соединить вход генератора ГЗ-112 со входом 6 лабораторного стенда, с первым каналом осциллографа С1-118А и первым входом фазометра.
   
3. Вход 9 лабораторного стенда соединить со вторыми каналами осциллографа и фазометра, а также вольтметром В7-35.
   
4. Поставить ручки переключателей 7 и 8 в положение R=10kOм, C=10нФ, а тумблер 10 в положение "Интегр. цепь".
   
5. Установив частоту 20 Гц и полагая, что для интегрирующей цепи коэффициент передачи при малых частотах равен "единице", подстроить амплитуду выходного сигнала U_вых.= 2В.
   
6. Изменяя частоту входного сигнала, измерять вольтметром В7-35 U_вых., а фазометром разность фаз  между входным и выходным сигналами. Наблюдать на экране осциллографа форму входного и выходного сигналов.
   

7. Повторить измерения при С = 1нФ и R = 20кОм. Данные занести в таблицу 1.

8. По результатам эксперимента построить графики К(f) – АЧХ и (f) – ФЧХ в логарифмическом масштабе. По графикам измерить частоту среза f_ср. и сравнить её с расчетной.
   

Таблица 1




С = 10 нФ, R = 10 кОм С = 1 нФ, R = 20 кОм


№ U₁, В f, Гц U₂, В U₂/U₁ Δφ № U₁, В f, Гц U₂, В U₂/U₁ Δφ

1 1

2 2

… …

n n

8. Повторить аналогичные измерения, построения и расчеты для дифференцирующей цепи. Учесть, что коэффициент передачи для дифференцирующей цепи равен "единице" при высоких частотах.
   
9. Проанализировать полученные результаты и сделать выводы.
   

Задание 3. Компьютерное проектирование RC- и CR-цепей

и анализ их работы.

1. Используя программное обеспечение, предлагаемое преподавателем (Electronics Workbench 3.0E или CircutMaker v.5.0), построить на экране компьютера интегрирующую цепь.
   

2. Подключить к этой цепи генератор, осциллограф и измеритель АЧХ.
   
3. Задавая параметры R и С соответствующие тем, что использовались в эксперименте, наблюдать переходные характеристики и сравнить их с экспериментальными.
   
4. Используя возможности компьютерного измерителя АЧХ и ФЧХ, наблюдать амплитудно-частотные и фазово-частотные характеристики при R =10 кОм, С=10 нФ и R=20 кОм, С=1 нФ. Измерить частоты среза и сравнить с экспериментом и расчетами.
   

5. Провести аналогичный компьютерный анализ для дифференцирующей цепи.

6. Графический материал распечатать на принтере и приложить к отчету.


СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. Каяцкас А.А. Основы радиоэлектроники: Учебное пособие для студентов вузов. М.: Высш.шк., 1988. 464с.; ил.
   
2. Молчанов А.П., Занадворов П.Н. Курс электротехники и радиотехники. М.: Наука, 1976.
   
3. Основы радиоэлектроники: Учебное пособие / Ю.Н. Волощенко, Ю.Ю. Мартюшев и др. М.: Изд-во МАИ, 1993. 416с.; ил.
   
4. Радиотехника: Учебное пособие для вузов / Е.М. Гершензон, Г.Д. Полянина, Н.В. Соина. М.: Просвещение, 1986. 319с.; ил.
   
5. Сингхал К., Влах И. Машинные методы анализа и проектирования электронных схем. М.: Радио и связь, 1988.