Методические указания для выполнения лабораторной работы по учебной дисциплине «Метрология, стандартизация и сертификация» для студентов очной и заочной формы обучения. Направления 150400 Технологические машины и оборудование
| Вид материала | Методические указания |
- Методические указания для выполнения курсовой работы по дисциплине: «Метрология, стандартизация, 170.43kb.
- Учебно-методический комплекс дисциплина опд. Ф. 06 «Метрология, стандартизация и сертификация», 433.68kb.
- Методические указания рассмотрены и рекомендованы к изданию методическим семинаром, 405.03kb.
- Методические указания и контрольные задания для студентов заочников Специальности 230101, 135.39kb.
- Методические указания к дисциплине и темы рефератов для студентов заочной формы обучения, 102.72kb.
- Методические указания «Выполнение практических заданий по дисциплине «Метрология, стандартизация, 636.89kb.
- Методические указания по написанию курсовой работы для студентов очной, заочной и очно-заочной, 318.34kb.
- Методические указания по выполнению курсовой работы по учебной дисциплине, 70.97kb.
- Методические указания для выполнения курсовых работ по дисциплине «Финансы» для студентов, 348.35kb.
- Методические указания к выполнению лабораторной работы №12 для студентов очной и заочной, 222.24kb.
Основные СВЕДЕНИЯ пО ВЗАИМОЗАМЕНЯЕМОСТИ
В процессе изготовления и контроля размеров деталей и узлов используются следующие понятия.
Номинальный размер – основной размер, определяемый исходя из функционального назначения детали или узла. Он проставляется на чертеже и служит началом отсчета отклонений: для отверстия -D, для вала - d.
Действительный размер – размер установленный измерением: для отверстия - Dr, для вала - dr.
Два предельно допускаемых размера, между которыми должен находиться действительный размер годной детали, называются предельными размерами. Больший из двух предельных размеров называется наибольшим предельным размером: для отверстия - Dmax, для вала - dmax, а меньший – наименьшим предельным размером: для отверстия - Dmin, для вала - dmin (рис. 1).
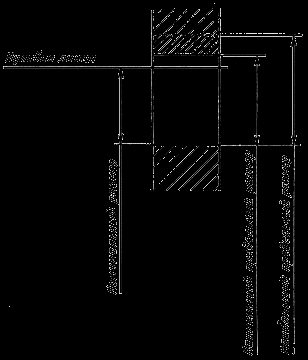
Рисунок 1 - Номинальный и предельные размеры отверстия
Разность между наибольшим и наименьшим предельными размерами называется допуском, Т. Для отверстия ТD = Dmax – Dmin, для вала Тd = dmax – dmin.
Допуск является мерой точности размера: чем меньше допуск, тем выше требуемая точность детали, тем меньше допускается колебание действительного размера. И наоборот низкая точность характеризуется большим допуском. Допуск может принимать только положительные отличные от нуля значения.
Различают действительные и предельные отклонения размера.
Действительным отклонением называется алгебраическая разность между действительным и номинальным размерами. Для отверстия Er = Dr – D, для вала er = dr – d.
Предельным отклонением называется алгебраическая разность предельным и номинальным размерами. Различают верхнее и нижнее предельные отклонения.
Верхнее предельное отклонение – алгебраическая разность между наибольшим предельным и номинальным размером:
ES = Dmax – D,
es = dmax – d,
где ES, es – верхние предельные отклонения для отверстия и вала
соответственно.
Нижнее предельное отклонение – алгебраическая разность между наименьшим предельным и номинальным размером:
EI = Dmin – D,
ei = dmin – d,
где EI, ei – нижние предельные отклонения для отверстия и вала
соответственно.
По номинальному размеру и отклонению можно определить соответствующие предельные размеры:
для отверстия: Dmax = D + ES; Dmin = D + EI;
для вала: dmax = d + es; dmin = d + ei.
Понятие о номинальном размере и отклонениях упрощает графическое изображение допусков и посадок в виде схем расположения полей допусков. На схеме в определенном масштабе откладывают предельные отклонения от нулевой линии соответствующей номинальному размеру (рис.2). Вверх от нулевой линии откладываются положительные значения отклонений, вниз – отрицательные. Зона, заключенная между двумя линиями, соответствующими верхнему и нижнему отклонениям называется полем допуска.
Детали изготавливают с разной точностью. Для нормирования требуемых уровней точности установлены квалитеты.
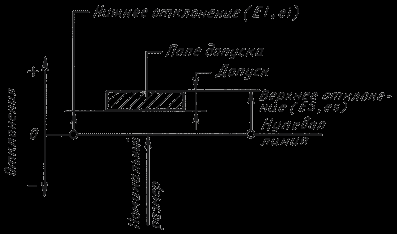
Рисунок 2 - Схема расположения поля допуска
Квалитет – совокупность допусков, характеризуемых постоянной относительной точностью для всех номинальных размеров.
Величина допуска в пределах одного квалитета зависит только от номинального размера. ГОСТ 25346-89 устанавливает 20 квалитетов, которые обозначаются цифрами: 01,0,1,2,…16,17,18.
Таблица 1 - Области применения деталей, изготовленных с разными квалитетами
| Квалитет | |||||||||||||||||||
| 01 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Особо точные изделия концевые меры длины, детали прецизионных приборов, оптические детали.... | Сопрягаемые поверхности деталей, подшипники, направляющие поверхности... | Несопрягаемые поверхности деталей машин | |||||||||||||||||
| Детали станков, авиастроение, двигатели... | Менее ответственные машины... | ||||||||||||||||||
 | |||||||||||||||||||
Для обеспечения равных возможностей образования полей допусков валов и отверстий в единой системе допусков и посадок (ЕСДП) предусмотрены наборы расположения полей допусков относительно номинального размера (рис.3).
Определенный уровень расположения поля допуска относительно номинального размера обозначается буквой или двумя буквами латинского алфавита: для отверстий – А, В, С, СD и тд., для валов – a, b, c, cd, d и тд.
Поле допуска обозначается сочетанием буквы (букв) и номера квалитета, например: g6, H7.
Обозначение поля допуска указывается после номинального размера элемента: Ø40 g6, Ø100 Н7.
SHAPE \* MERGEFORMAT
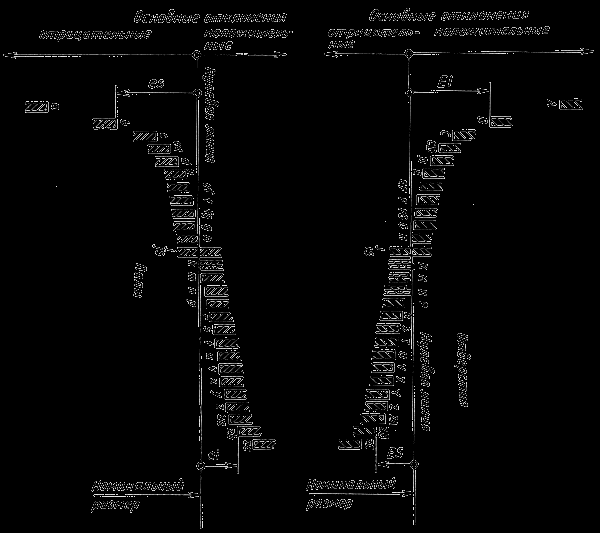
Рисунок 3 - Схема расположения полей допусков валов и отверстий для гладких цилиндрических поверхностей (ГОСТ 25346-89)
Основные СВЕДЕНИЯ ПО МЕТРОЛОГИИ
Физическая величина – свойство физического объекта, общее в качественном отношении для многих физических объектов, но в количественном отношении индивидуальное для каждого из них.
Для того чтобы у каждого объекта можно было установить различия в количественном содержании свойства, отображаемого физической величиной, в метрологии введены понятия ее размера и значения.
Размер физической величины – количественная определенность физической величины, присущая конкретному материальному объекту, системе, явлению или процессу.
Значение физической величины – выражение размера физической величины в виде некоторого конкретного числа принятых для нее единиц.
Единица измерения физической величины – физическая величина фиксированного размера, которой условно присвоено числовое значение, равное единице, и которая применяется для количественного выражения однородных с ней физических величин.
Истинным значением физической величины называется значение физической величины, которое идеальным образом характеризует в качественном и количественном отношениях соответствующую физическую величину. Истинное значение физической величины может быть получено только в результате бесконечного процесса измерений с бесконечным совершенствованием методов и средств измерений.
Измерения физической величины – совокупность операций по применению технического средства измерения, хранящего единицу физической величины, которая обеспечивает нахождение соотношения измеряемой величины с ее единицей.
Средство измерения - техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и (или) хранящее единицу величины, размер которой принимается неизменным (в пределах установленной погрешности) в течение известного интервала времени.
Измерения, как экспериментальные процедуры, весьма разнообразны и классифицируются по разным признакам. Классификация измерений приведена на рис. 4.
По способу получения информации измерения бывают четырех типов: прямые, косвенные, совокупные, совместные.
Наиболее распространены прямые и косвенные.
Прямым называют измерение, при котором значение физической величины получают путем непосредственного сравнения ее с мерой (взвешивание, измерение длины и т.д.).
 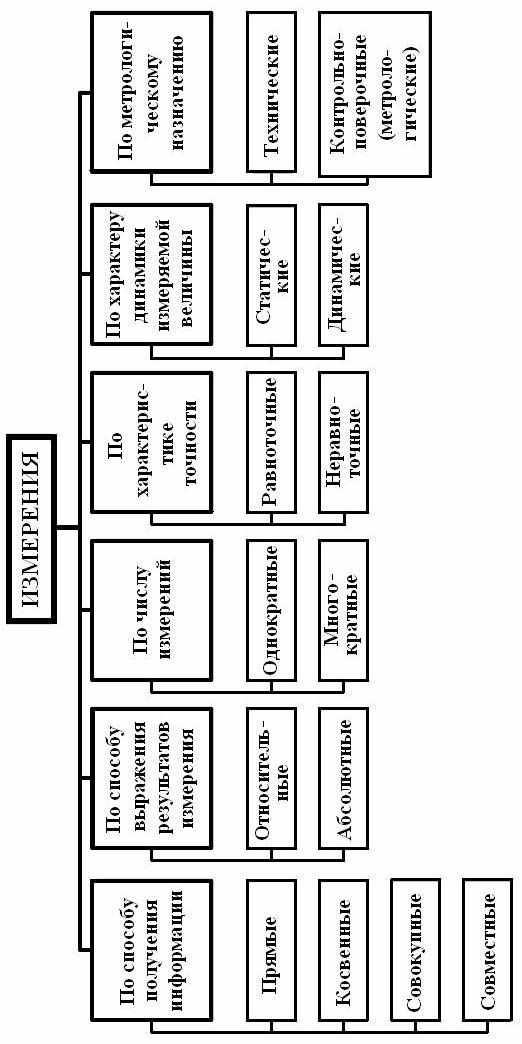 | Рисунок 4- Классификация видов измерений по различным признакам |
Косвенным называют измерение, при котором результат определяют на основании прямых измерений величин, связанных с определяемой величиной известной зависимостью (определение сопротивления по закону Ома, если измерены сила тока и напряжение).
Совокупные измерения связаны с определением значения величины, являющейся результатом решения системы уравнений, составляемых по итогам одновременных измерений нескольких однородных величин.
Совместные измерения представляют собой измерения двух и более неоднородных физических величин для определения зависимости между ними.
По способу выражения результатов измерения разделяют на абсолютные и относительные.
При абсолютных измерениях используют прямое измерение основной величины и физическую константу (например, скорость света, ускорение свободного падения и др.).
При относительных измерениях устанавливают отношение измеряемой величины к однородной, используемой в качестве единицы.
По количеству замеров величин различают однократные и многократные измерения.
Однократные измерения предполагают соответствие числа измерений числу измеряемых физических величин.
Многократные измерения предполагают большее число измерений, чем количество измеряемых величин.
По характеру точности измерения разделяют на равноточные и неравноточные.
Равноточные измерения - ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений в одних и тех же условиях с одинаковой тщательностью.
Неравноточные измерения - ряд измерений какой-либо величины, выполненных различающимися по точности средствами измерений (или) в разных условиях. Результаты неравноточных измерений обрабатываются с учетом веса отдельных измерений, входящих в ряд. Вес результатов измерений - это положительное число, служащее оценкой доверия к тому или иному отдельному результату измерения, входящему в ряд неравноточных измерений, а результат обработки неравноточных измерений - среднее взвешенное или среднее весовое значение
Различия по характеру динамики измеряемой величины обусловили существование двух разновидностей измерений статических и динамических.
Статические измерения проводятся при измерении практически постоянной величины.
Динамические измерения проводят при измерении величин, изменяющихся в процессе измерений.
По метрологическому назначению выделяют технические и контрольно-поверочные измерения.
Технические измерения проводятся рабочими средствами измерения, где принимается наперед заданная погрешность, достаточная для решения данной практической задачи. Технические измерения проводят для определения значения физической величины.
Контрольно-поверочные (метрологические) измерения выполняются при помощи эталонов с целью воспроизведения единиц физических величин для передач их размера рабочим средствам измерения.
Любое измерение можно считать законченным, если найден не только результат измерения, но и оценена его погрешность.
Погрешность результата измерений - отклонение результата измерения от истинного (действительного) значения измеряемой величины.
Погрешность средства измерения – это разность между показанием средства измерения и истинным (действительным) значением измеряемой величины.
Эти два понятия: погрешность результата измерений и погрешность средства измерения во многом близки друг к другу. Погрешность результата каждого конкретного измерения складывается из многих составляющих, обязанных своим происхождением различным факторам и источникам. Традиционный аналитический подход к оцениванию погрешностей результата состоит в выделении этих составляющих, изучении их по отдельности и последующем суммировании.
Погрешности результатов измерений и средств измерения классифицируются по одинаковым признакам: по характеру проявления; по способу выражения; по отношению к условиям применения. В настоящее время принята следующая классификация погрешностей (рис. 5).
По характеру проявления во времени бывают погрешности случайные, систематические и промахи.
Случайная погрешность измерения (Δ0) - составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку, значению) при повторных измерениях одной и той же физической величины, проведенных с одинаковой тщательностью, одной и той же физической величины. В проявлениях таких погрешностей не наблюдается какой-либо закономерности, они обнаруживаются при повторных измерениях одной и той же величины в виде некоторого разброса результатов. Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результате измерения. Описание случайных погрешностей возможно только на основе теории случайных процессов и математической статистики. Случайные погрешности уменьшаются с увеличением количества измерений.
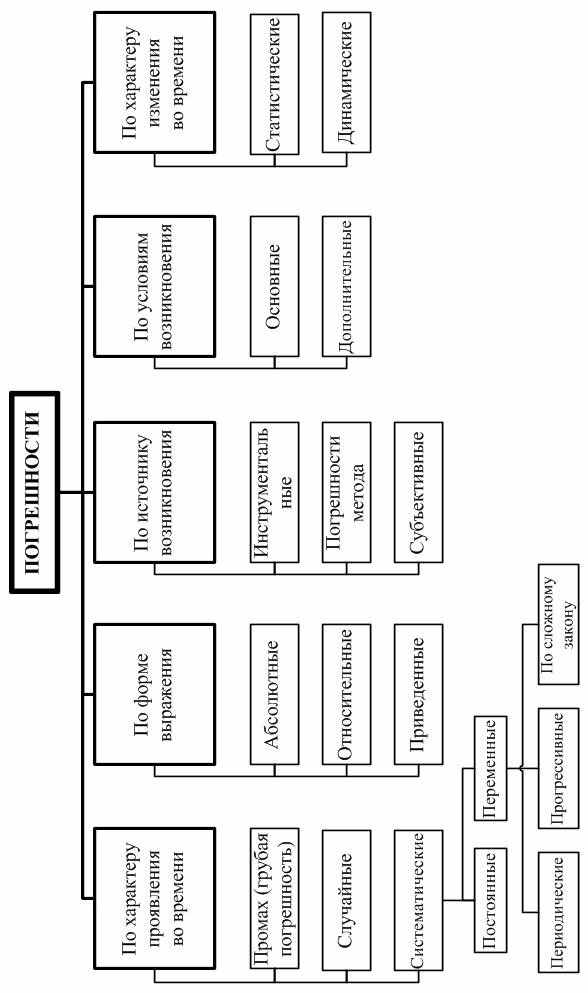
Систематическая погрешность измерения (Δ0) - составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. В зависимости от характера изменения систематические погрешности подразделяют на постоянные и переменные, которые в свою очередь могут быть прогрессивные, периодические или изменяющиеся по сложному закону. Погрешности, изменяющиеся по сложному закону, происходят вследствие совместного действия нескольких систематических погрешностей. Такие погрешности выявляют детальным анализом их возможных источников (например, неточное нанесение отметок на шкалу или деформация стрелки) и уменьшают введением соответствующей поправки, применением более точных средств измерений, калибровкой средств измерений.
Грубая погрешность (промах) - погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. В случае однократного измерения обнаружить промах нельзя. При многократных измерениях грубые погрешности выявляют и исключают в процессе обработки результатов измерений.
По форме выражения погрешности разделяют на абсолютную, относительную и приведенную.
Абсолютная погрешность измерения (Δ) - погрешность измерения, выраженная в единицах измерения.
Абсолютная погрешность определяется по формуле:
Δ = Xi – X0 ,
где Δ – погрешность измерения;
Хi – значение измеряемой физической величины, найденное с помощью средства измерений;
Х0 – действительное значение измеряемой величины.
Разновидностью абсолютной погрешности является предельная погрешность – максимальная погрешность, допускаемая для данной измерительной задачи. Абсолютная погрешность не может в полной мере служить показателем точности. Например, при измерении величин 10 мм и 100 мм получена одинаковая абсолютная погрешность Δ = 0,5 мм, но качество измерения будет различно. Для сравнения качества измерения используют относительную погрешность.
Относительная погрешность (δ) – погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины.
Относительная погрешность определяется по формуле:
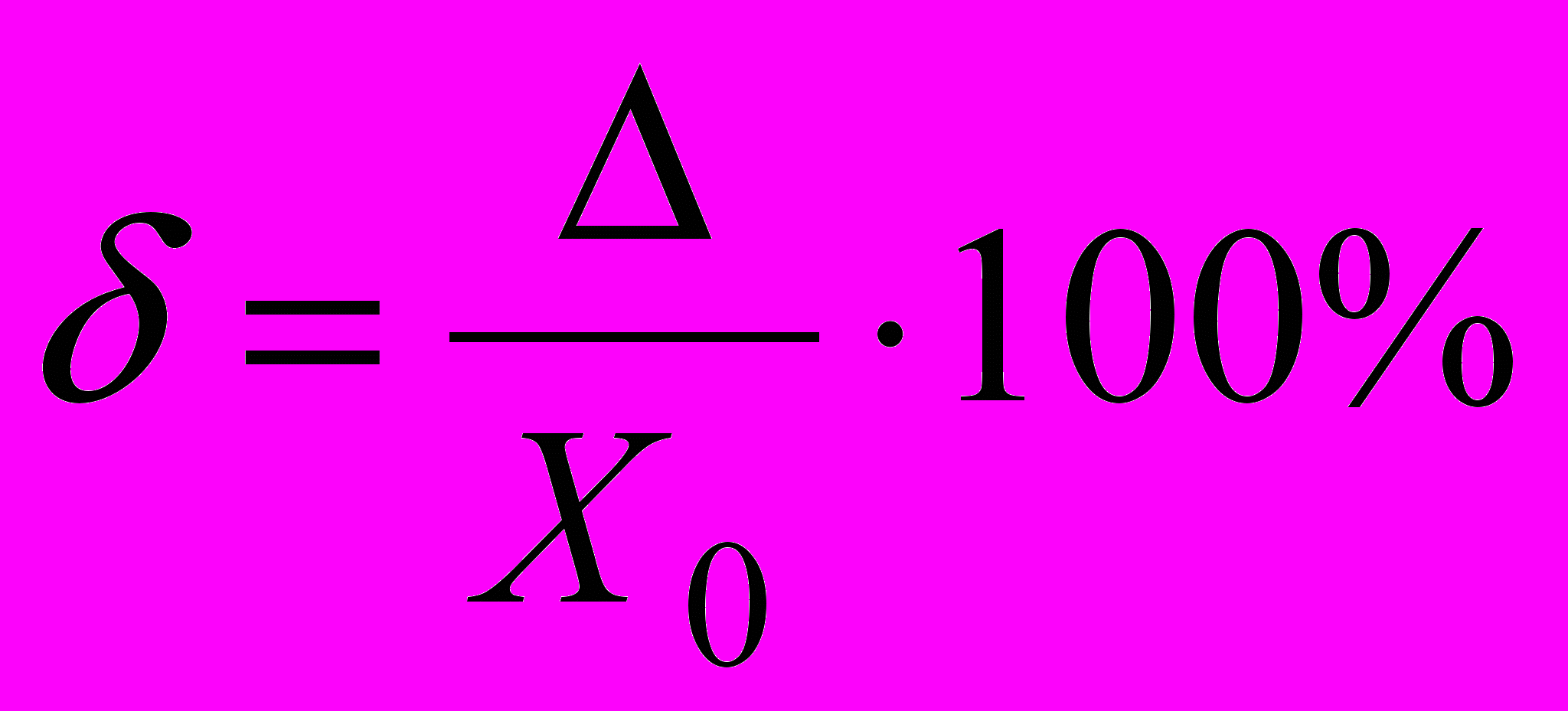
где δ – относительная погрешность, выраженная в процентах.
Приведенная погрешность средства измерения (γ) – относительная погрешность, выраженная отношением абсолютной погрешности средства измерения к условно принятому значению величины. Условно принятое значение называют нормирующим значением и часто за такое условно принятое значение принимают верхний предел измерений. Приведенную погрешность обычно выражают в процентах:
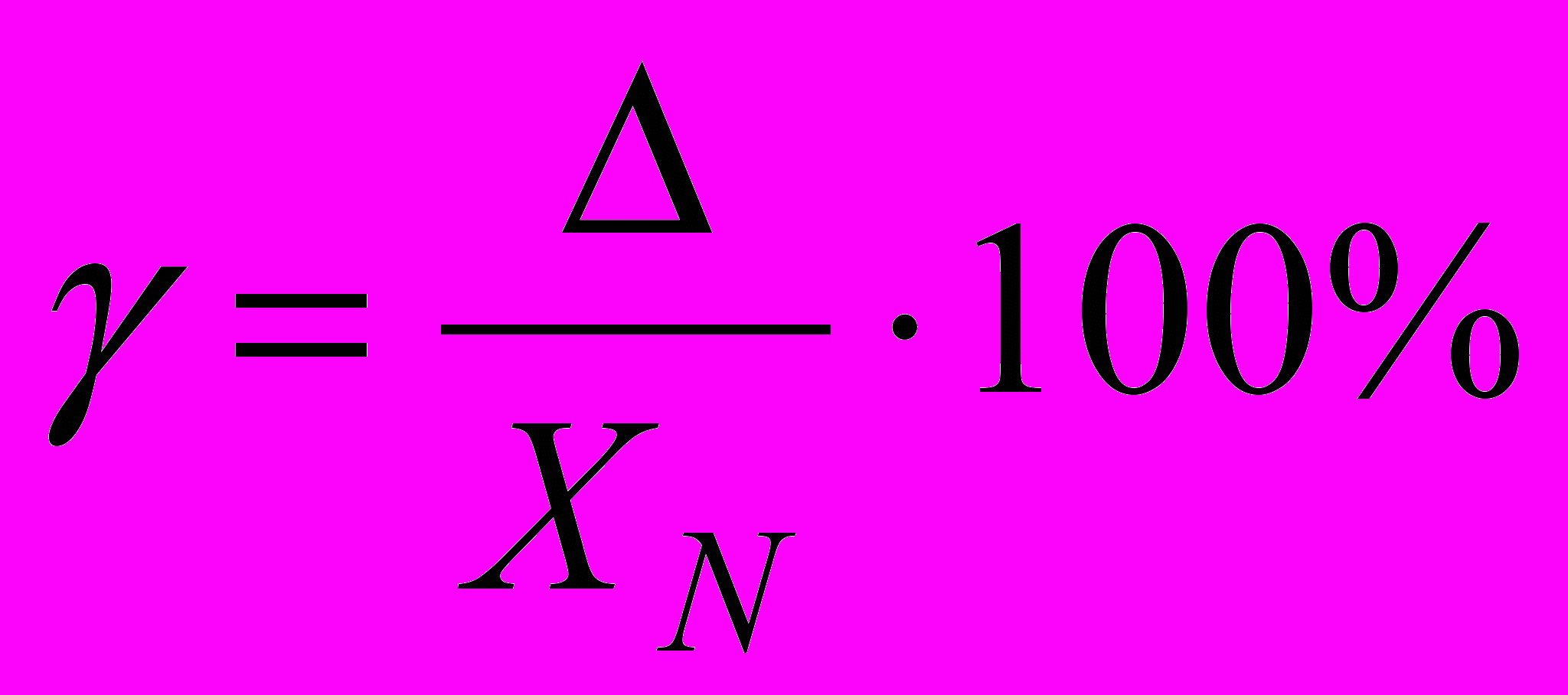
где γ – приведенная погрешность, выраженная в процентах;
XN – нормирующее значение.
По источнику возникновения (или по причине возникновения) может быть инструментальная погрешность, погрешность метода измерений и погрешность субъективная.
Погрешность результата каждого конкретного измерения складывается из составляющих, обязанных своим происхождением различным факторам и источникам. Обязательными компонентами любого измерения являются средство измерения, в котором реализован определенный метод измерения, а также оператор (человек), проводящий измерения. Несовершенство каждого из этих компонентов приводит к появлению своей составляющей погрешности результата. При этом различают следующие погрешности:
Инструментальная погрешность – составляющая, обусловленная погрешностью применяемого средства измерений. Очевидно, что каждому из приборов, использованных при измерении, присущи определенные погрешности, причем в общей погрешности прибора может присутствовать и систематическая и случайная составляющая, которые окажут свое влияние на результат измерения.
Погрешность метода измерений – составляющая систематической погрешности измерений, обусловленная несовершенством реализованного метода измерения. Вследствие упрощений, принятых в уравнениях для измерений, нередко возникают существенные погрешности, для компенсации которых следует вводить поправки. Погрешность метода иногда называют теоретической погрешностью. При некоторых обстоятельствах погрешность метода измерения может проявляться как случайная;
Субъективная погрешность измерения – составляющая систематической погрешности, обусловленная индивидуальными особенностями оператора. Встречаются операторы, которые систематически опаздывают (или опережают) снимать отсчеты показаний средств измерений. Иногда субъективную погрешность называют личной погрешностью. В результате отсутствия правильных навыков работы с приборами экспериментатор может внести в результат измерения личную составляющую погрешности из-за неточности отсчета доли деления по шкале, невнимательности и др.
По условиям возникновения погрешность может быть основной и дополнительной.
Как уже неоднократно повторялось, на результат измерения влияют условия измерения. Нормальные условия измерений - это условия, характеризуемые совокупностью значений или областей значений влияющих величин, при которых изменением результата измерений пренебрегают вследствие малости. Нормальные условия измерений устанавливаются в нормативных документах на средства измерений конкретного типа и они характеризуются номинальными значениями влияющих величин. Некоторые номинальные значения нормальных условий измерения для ряда влияющих величин приведены в табл. 2.
Таблица 2 - Некоторые номинальные значения влияющих величин при нормальных условиях
| Влияющая величина | Значение |
| Температура для всех видов измерений, °С (К) | 20 (293) |
| Давление окружающего воздуха для линейных, угловых измерений, измерений массы, силы света и в других областях кроме указанных выше, кПА (мм. рт.ст.) | 101,3 (760) |
| Относительная влажность воздуха для линейных, угловых измерений, измерений массы, % | 58 |
Для данных номинальных значений выделяют нормальную область значений влияющих величин, рабочую область и предельные условия измерений, которые устанавливают возможные колебания указанных номинальных значений, когда в результате измерения присутствует только основная погрешность средства измерения.
Основная погрешность средства измерения – погрешность средства измерения, применяемого при нормальных условиях, при которых величины, влияющие на погрешность данного средства измерения, находятся в области нормальных значений.
Дополнительная погрешность средства измерения – составляющая погрешности средства измерения, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального ее значения или нормальной области значений. Для оценивания дополнительных погрешностей в документации на средство измерений обычно указывают нормы изменения показаний при выходе условий измерения за пределы нормальных.
По характеру изменения измеряемой величины различают статическую и динамическую погрешности средства измерения.
Статическая погрешность – погрешность средства измерения, применяемого при измерении физической величины, принимаемой за неизменную.
Динамическая погрешность – погрешность средства измерений, возникающая при измерении изменяющейся физической величины.
В основе современных подходов к оцениванию погрешностей лежат принципы, обеспечивающие выполнение требований единства измерений.
Единство измерений – состояние измерений, характеризующееся тем, что их результаты выражаются в узаконенных единицах, а погрешности результатов известны и с заданной вероятностью не выходят за установленные пределы измерений.
Для исследования и оценивания погрешность описывается с помощью определенной модели (систематическая, случайная, методическая, инструментальная и др.). На выбранной модели определяют характеристики, пригодные для количественного выражения тех или иных свойств. Выбор модели погрешности обусловлен сведениями об ее источниках как априорных, так и полученными в ходе измерительного эксперимента.
Оценить результат измерения – это значит приписать ему погрешность с заданной доверительной вероятностью.
В основе модели случайных погрешностей лежит теория вероятностей и методы математической статистики. Из этого следует, что погрешности можно только оценить с некоторой вероятностью. Оценку случайной погрешности и определение интервала, внутри которого с заданной вероятностью лежит истинное значение физической величины, проводят по результатам ее многократных измерений.
Наиболее близким к истинному значению измеряемой величины является среднее арифметическое ряда отдельных измерений:
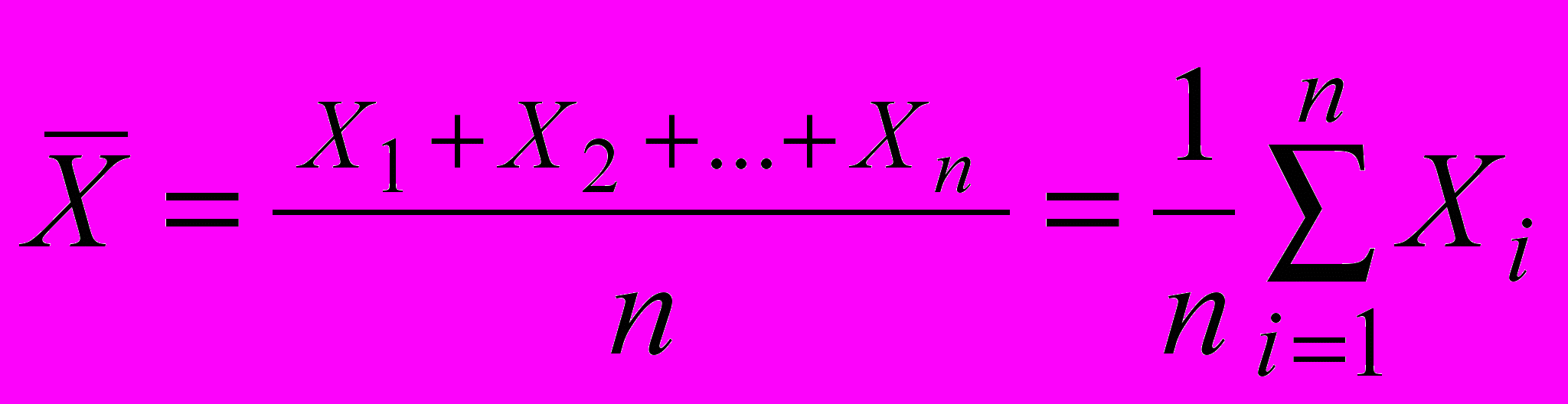
где n – количество измерений;
Xi – результат i–го измерения.
