Задача А. Однорукий программист Ограничение по времени: 2 секунды
| Вид материала | Задача |
- Основные звездные характеристики, 140.57kb.
- Основные звездные характеристики, 143.28kb.
- Институт Кафедра Реферат, 152.6kb.
- Школа «Интеграйия 21 век» Реферат, 150.07kb.
- Классификация: нестандартный, структурированный (сложный) тип. Имя определяет программист, 158.26kb.
- План: Определение предпринимательской деятельности. Понятие предпринимателя, ограничение, 270.8kb.
- Общая характеристика квалификационной программы направления 010500 «прикладная математика, 168.02kb.
- Общая характеристика квалификационной программы направления 010300 «Математика. Компьютерные, 171.34kb.
- Общая характеристика квалификационной программы направления 100500 «прикладная математика, 168.53kb.
- Общая характеристика квалификационной программы направления 100300 «Математика. Компьютерные, 171.77kb.
Университетская олимпиада по программированию
среди студентов 1-3 курсов
Оренбург 2003г.
Задача А. Однорукий программист
Ограничение по времени: 2 секунды.
Один опытный программист Нео уже давно освоил десятипальцевый метод печати. По этому методу каждую клавишу нажимает всегда один и тот же палец. Например, буквы Q, A и Z нажимаются мизинцем левой руки. А буквы Y, U, H, J, N, M указательным пальцем правой руки.
Беда в том, что Нео очень любит пирожки. Когда он их ест, то часть пальцев его рук становится испачкана. Как всякий опытный программист, он немного ленив, чтобы сразу после еды помыть руки, но все же очень щепетильно относится к чистоте своей клавиатуры. Таким образом, при печати слов Нео не может использовать часть пальцев. Помогите ему определить слова, которые он может напечатать, не испачкав клавиатуры.
ВВОД
Входной файл содержит набор строк. В первой строке указано число пальцев F (0≤F≤10) и число слов W (0≤W≤10 000). Во второй строке через пробел перечислены номера пальцев, которые не испачканы. 1 соответствует мизинцу левой руки (буквы Q, A и Z), 2 безымянному (буквы W, S и X) и т.д. Мизинец правой руки имеет номер 10 (буква P). 5 и 6 - это большие пальцы рук, нажимают пробел.
Далее в каждой новой строке содержится слово. Слова могут содержать только буквы латинского алфавита в верхнем регистре. Длина слов не превышает 50 символов.
В таблице ниже приведены номера пальцев и буквы, которые печатаются этими пальцами.
-
Номер пальца
Печатаемые буквы
1
Q, A, Z
2
W, S, X
3
E, D, C
4
R, F, V, T, G, B
5, 6
Пробел
7
Y, H, N, U, J, M
8
I, K
9
O, L
10
P
ВЫВОД
Выходной файл должен содержать количество слов, которые Нео может напечатать, не испачкав клавиатуры и сами слова. Каждое слово находится на новой строке. Слова выводятся в том же порядке, в котором они указаны во входном файле.
Примечание: вам гарантируется, что выходной файл не будет содержать более 1000 слов.
| ПРИМЕР ВХОДНОГО ФАЙЛА (input.txt) | ПРИМЕР ВЫХОДНОГО ФАЙЛА (output.txt) |
| 6 7 1 3 5 7 8 9 HELLO WORLD THIS IS A CONTEST ZOO | 3 HELLO A ZOO |
Задача B. Протекающая крыша
Ограничение по времени: 5 секунд.
Нео живет в квартире на последнем этаже. И у него есть одна проблема – в дождь и по весне крыша начинает протекать. Так получилось, что крыша протекает почти только в одном месте, вдоль одной стены. На этой стене прибиты книжные полки. Книги с полки он уже давно переложил к себе под кровать, но проблема, тем не менее, не решена.
Нео, как любой программист, очень ленив. У него никогда нет времени ни на то чтобы залатать крышу, ни на то чтобы нормально заняться полками. Поэтому и полки у него весят все криво, и вода, стекая по ним, продолжает течь к соседям. Чтобы устранить последние, Нео не придумал ничего лучше чем ставить ведро там, где течет. Помогите ему определить эти места.
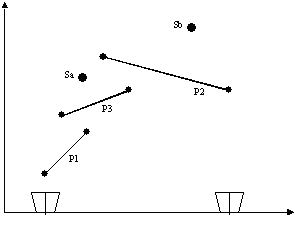
ВВОД
Входной файл состоит из двух секций.
Сначала идет число полок N (0≤N≤1000), каждая из которых задана координатами x1, y1, x2 и y2 в следующих N строках. Все четыре координаты полки находятся на отдельной строке, и разделены одним пробелом между собой.
Примечание: полки между собой не пересекаются (не имеют общих точек), не примыкают друг другу, нет ни вертикальных (x1 всегда не равно x2), ни горизонтальных полок (y1 всегда не равно y2).
Во второй части входного файла указаны точки на стене, в которых начинает течь вода. Сначала идет число точек M (0≤M≤500). Далее в M строках указаны координаты точек x и y, разделенные одним пробелом между собой.
Все указанные во входном файле координаты целого типа и не отрицательны.
В случае, когда вода попадает точно на верхнюю точку полки, считается, что она не падает вниз, а течет по полке.
ВЫВОД
Для каждой точки протечки в выходной файл нужно выдать одно число – координату x, где вода закончит свой путь, пройдя все полки.
| ПРИМЕР ВХОДНОГО ФАЙЛА (input.txt) | ПРИМЕР ВЫХОДНОГО ФАЙЛА (output.txt) |
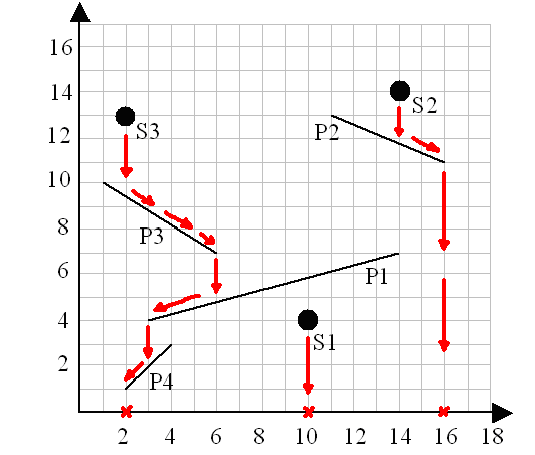
| 4 14 7 3 4 11 13 16 11 1 10 6 7 2 1 4 3 3 10 4 14 14 2 13 | 10 16 2 |
ПРИМЕЧАНИЕ
Рисунок, приведенный ниже, объясняет пример.
Задача C. Неправильный сумматор
Ограничение по времени: 2 секунды.
Однажды Нео делал программную эмуляцию двоичного сумматора. Сумматор – это устройство для сложения двух чисел. Эмуляция у него получилась, числа складывались, но только не совсем правильно. Результат получался неправильным, из-за того, как выяснил Нео позже, что его сумматор не учитывал перенос от сложения двух предыдущих битов. Так если сложить 789 и 123 сумматором Нео, то получится 878:
(789) 1100010101
+
(123) 0001111011
=
(878) 1101101110
ВВОД
Входной файл содержит набор строк. В каждой строке записано два числа a и b разделенных пробелом. Входной файл заканчивается двумя нулями. Во входном файле не более 1000 строк.
ВЫВОД
Для каждой строки входного файла нужно выдать найденное значение K. Значение K есть разница между реальной суммой чисел a и b, и суммой полученной сумматором Нео.
| ПРИМЕР ВХОДНОГО ФАЙЛА (input.txt) | ПРИМЕР ВЫХОДНОГО ФАЙЛА (output.txt) |
| 789 123 89745 45 34580 6883 666 777 0 0 | 34 2 1024 1040 |
Задача D. Вычисление формул
Ограничение по времени: 4 секунды.
У Нео есть племянник, который учится в школе. И он очень часто просит своего дядю помочь ему с домашней работой, так как он не силен в математике. Но Нео не любит делать простые вещи, и поэтому быстро написал программу, которая сама вычисляет формулы. Ведь формулы очень простые, все, что в них используется, так это операции сложения, вычитания и подстановка констант.
Нео написал программу буквально за пять минут, но у него появилось сомнение в правильности ее работы. Напишите программу, проверяющую вычисления программы Нео.
ВВОД
Входной файл состоит из двух секций: в первой задаются константы, во второй записываются выражения, которые надо проверить.
Константы задаются следующим образом: в первой строке записано количество констант N (0≤N≤26), далее следует N строк с заданием значений константам. Константы именуются одной латинской буквой в верхнем регистре. Далее, через один пробел, следует значение константы.
В первой строке секции описания формул записано количество формул M (0≤M≤1000). Затем в M строках записаны формулы. До знака равно записывается сама формула, после – ответ, который выдала программа Нео. В строке с формулой не содержится никаких символов кроме +, -, =, цифр и латинских букв в верхнем регистре. Все выражения записаны корректно. Длина выражения не длиннее 250 символов.
ВЫВОД
Для каждой формулы в выходной файл нужно записать YES, если программа Нео выдала правильный результат, и NO, в противном случае.
| ПРИМЕР ВХОДНОГО ФАЙЛА (input.txt) | ПРИМЕР ВЫХОДНОГО ФАЙЛА (output.txt) |
| 4 A 6 B 78 D 90 X -5 3 1+2+3=6 A+B+D+X=66 D-B-12+X=-5 | YES NO YES |
Задача E. Светофоры
Ограничение по времени: 5 секунд.
Очень часто работа находиться далеко от дома. Вот и Нео в таком положении. Каждый день ему приходиться добираться до работы на машине. Очень часто, добираясь на работу, он останавливается на перекрестках на красный свет.
Вот так, в очередной раз, застряв, он начал размышлять и искать закономерности. Он заметил, что все светофоры имеют цикл длиной несколько секунд. Половину этого цикла горит красный, 5 секунд желтый и оставшееся время зеленый. Ему стало интересно, могут ли все светофоры вдоль улицы, по которой он едет, одновременно загореться зеленым светом, хотя бы на секунду, если знать длительность цикла каждого светофора. Помогите Нео разобраться.
ВВОД
Входной файл содержит набор строк. В каждой строке задан список длительности циклов для каждого светофора вдоль улицы. Каждый список заканчивается нулем. В списке всегда не менее двух и не более 100 значений. Длительность циклов задается целым числом. Например, число 25 означает, что 20 секунд горит зеленый, 5 секунд - желтый и 25 – красный.
Следует учесть, что после красного следует зеленый свет, а не желтый. Длительность цикла не может быть менее 10 и превышать 90 секунд. Входной файл заканчивается тремя нулями.
ВЫВОД
Для каждой строки входного файла в выходной нужно записать время, через которое все светофоры будут гореть зеленым светом. Известно, что в первый момент времени все светофоры горят зеленым. Другими словами, в выходной файл нужно выдать время, через которое светофоры вновь загорятся зеленым. Формат времени можно увидеть в примере.
Если через 5 часов светофоры так и не загорятся зеленым светом, нужно выдать надпись – « No solution in 5 hours» (без кавычек).
| ПРИМЕР ВХОДНОГО ФАЙЛА (input.txt) | ПРИМЕР ВЫХОДНОГО ФАЙЛА (output.txt) |
| 19 20 0 30 25 35 0 0 0 0 | 00:00:40 00:05:00 |
Задача F. Кофейные пятна
Ограничение по времени: 2 секунды.
Как многие программисты, Нео во время своей работы любит пить кофе. Случается, что он капает, оставляет разводы от кружки, да и просто разливает кофе прям на свои исходники.
Однажды к нему пришел его друг Морфеус и поразился состоянию исходных текстов программ Нео. «Сколько же ты вылил на них кофе?!» - поразился он.
А Нео после этого задался вопросом, а и в правду сколько? Упрощая себе задачу, он стал просто считать пятна на листах. О состоянии текстов его программ вы можете сделать вывод сами, посчитав пятна самостоятельно.
ВВОД
Входной файл содержит несколько строк. В первой содержится размер страницы, на которой считаются пятна. Размер представлен двумя числами: N количество строк (0<N≤50) и M количество столбцов (0<M≤50). Далее следуют N строк длиной M символов. Чистые участки листа представлены символом “.”, испачканные кофе – “#”.
ВЫВОД
Выходной файл должен содержать всего одно число – количество пятен.
Примечание: Пятна могут состоять из одного и более испачканных участков. Если испачканные участки примыкают друг к другу по вертикали или горизонтали, они относятся к одному тому же пятну.
| ПРИМЕР ВХОДНОГО ФАЙЛА (input.txt) | ПРИМЕР ВЫХОДНОГО ФАЙЛА (output.txt) |
| 7 8 ......## .##.##.# .#.#.... .#...##. .#..#### .##.#..# ..#.#### | 5 |
Задача G. Большие числа
Ограничение по времени: 3 секунды.
Как-то раз Нео написал неплохую программу шифрования. Для того чтобы расшифровать (или зашифровать) данные нужен ключ. Ключ в свою очередь является обыкновенной суммой двух чисел. Чтобы избежать элементарного взлома и исключить перебор, Нео для ключей использовал длинные числа до 250 знаков. Он утверждает, что может сложить два таких длинный числа в уме. Напишите программу, которая проверит Нео.
ВВОД
Входной файл содержит набор строк. Количество строк кратно трем. В первой строке записано первое слагаемое, во второй – второе, в третьей ответ который дал Нео. Далее все повторяется. Входной файл заканчивается концом файла. Во входном файле не более 3000 строк.
ВЫВОД
Для каждых трех чисел в отдельной строке выдать CORRECT, если Нео верно сложил числа, и правильный ответ в противном случае.
| ПРИМЕР ВХОДНОГО ФАЙЛА (input.txt) | ПРИМЕР ВЫХОДНОГО ФАЙЛА (output.txt) |
| 2 2 4 812347602347075893475023479 28347987523465876234934 234897234652634823487 45683450982387623 3475683846583465230409834578345763847 3475683846583465230455518029328151470 679234568230 470 45743628340987537489570 | CORRECT 812375950334599359351258413 CORRECT 679234568700 |
Задача H. Простые суммы
Ограничение по времени: 7 секунд.
Изучая математику, программист Нео наткнулся в литературе на очень интересную гипотезу Гольдбаха-Эйлера, которая гласит, что любое натуральное четное число можно представить в виде суммы двух простых чисел. Например: 4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5, 10 = 5 + 5, 100 = 47 + 53, 21000 = 17 + 20983, и так далее.
Эта гипотеза не доказана и до сих пор, лишь проверена для очень больших чисел на ЭВМ. Однако, Нео очень заинтересовал вопрос сколькими различными способами можно представить данное четное число в виде суммы двух простых чисел. Например, 10 = 5 + 5 и 10 = 3 + 7. Таким образом, число 10 представимо в виде суммы двух простых чисел двумя способами. Число различных способов, означает, что 10 = 3 + 7 и 10 = 7 + 3 считаются одинаковыми разложениями. Помогите ему решить эту проблему.
ВВОД
Входной файл содержит не более 1000 строк. В каждой строке дано четное число N (4≤N≤50000). Ввод заканчивается строкой содержащей ноль. Это число не следует обрабатывать.
ВЫВОД
Для каждого числа N в выходной файл выдать число различных способов, которыми можно представить число N в виде суммы двух простых чисел.
| ПРИМЕР ВХОДНОГО ФАЙЛА (input.txt) | ПРИМЕР ВЫХОДНОГО ФАЙЛА (output.txt) |
| 6 12 26 72 734 0 | 1 1 3 6 15 |
Задача I. Числа Колатца
Ограничение по времени: 7 секунд.
Функция Колатца обладает свойством, что длина последовательности чисел порождаемой функцией не может быть непосредственно вычислено от аргумента. Функция Колатца определенная для целых чисел имеет вид:
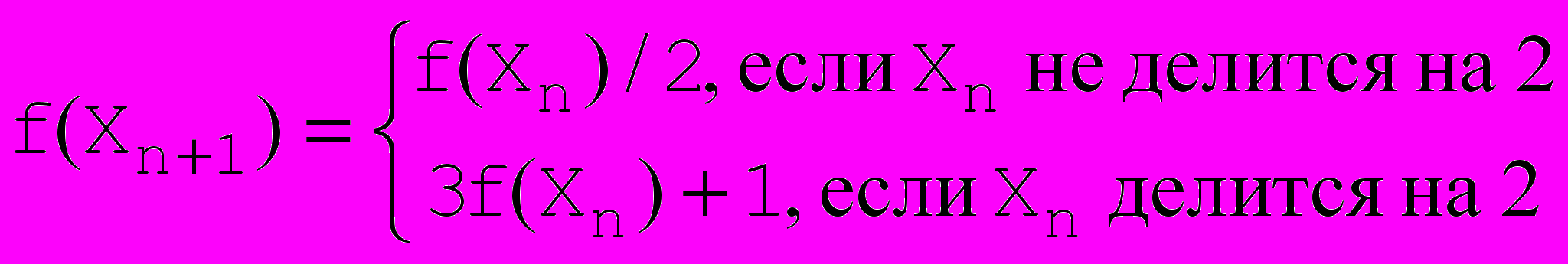
Данная функция определяет одну из известных нерешенных задач в математике. Задача состоит в доказательстве, что для любого целого начального значения Xn≥1, эта функция порождает последовательность, которая сходится к значению 1. Ниже приведено несколько примеров. В квадратных скобках указано начальное значение Xn, далее приведена порождаемая последовательность, в фигурных скобках приведена длина порождаемой последовательности.
[10] 5 16 8 4 2 1 {6}
[13] 40 20 10 5 16 8 4 2 1 {9}
[14] 7 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1 {17}
[19] 58 29 88 44 22 ... 2 1 {20}
[32] 16 8 4 2 1 {5}
[1] 4 2 1 {3}
Ваша программа должна считать из входного файла два числа L и H. Требуется найти какое начальное значение Xn, в промежутке [L, H], которое порождает самую длинную последовательность. Если два и более числа из промежутка порождают наидлиннейшую последовательность, то вывести меньшее число.
ВВОД
Во входном файле через пробел находятся два целых положительных числа L и H.
(1≤L, H≤100000, L ≤ H)
ВЫВОД
В выходной файл вывести на одной строке через пробел числа V и S, где V – минимальное число из промежутка [L, H], порождающее самую длинную последовательность, S – количество чисел в полученной последовательности.
| ПРИМЕР ВХОДНОГО ФАЙЛА (input.txt) | ПРИМЕР ВЫХОДНОГО ФАЙЛА (output.txt) |
| 1 20 | 18 20 |
