Защита изображений на основе решения систем диофантовых уравнений и неравенств
| Вид материала | Документы |
- М. В. Корытова научный руководитель Р. Т. Файзуллин, д т. н., профессор Омский государственный, 26.14kb.
- Общий метод решения сюжетных задач состоит в моделировании их в виде уравнений или, 467.25kb.
- Методические рекомендации к проведению урока: «Методы решения уравнений и неравенств., 15.21kb.
- Удаленного решения линейных диофантовых уравнений в неотрицательных целых числах, 165.6kb.
- Задачи курса : расширить представления обучающихся о приемах и методах решения уравнений, 223.2kb.
- Программа профильного курса «Алгебра плюс», 214.93kb.
- Элективный курс по математике, 37.2kb.
- Реферат по математике. На тему: «основные методы решения систем уравнений с двумя переменными», 140.92kb.
- Тема: «Рациональные и иррациональные уравнения, неравенства и системы», 199.57kb.
- Урок по теме: "Показательные функции, уравнения, неравенства", 69.08kb.
Защита изображений на основе решения систем диофантовых уравнений и неравенств
М.В. Корытова, Р.Т. Файзуллин
Омский государственный университет
Развитие мультимедийных средств сопровождается большим количеством хранимой и передаваемой графической информации. Следовательно, встает важный вопрос о ее защите. В работе предлагается метод преобразования, защиты и передачи изображений, основанный на алгоритме решения системы диофантовых уравнений и неравенств.
Рассмотрим следующее преобразование:
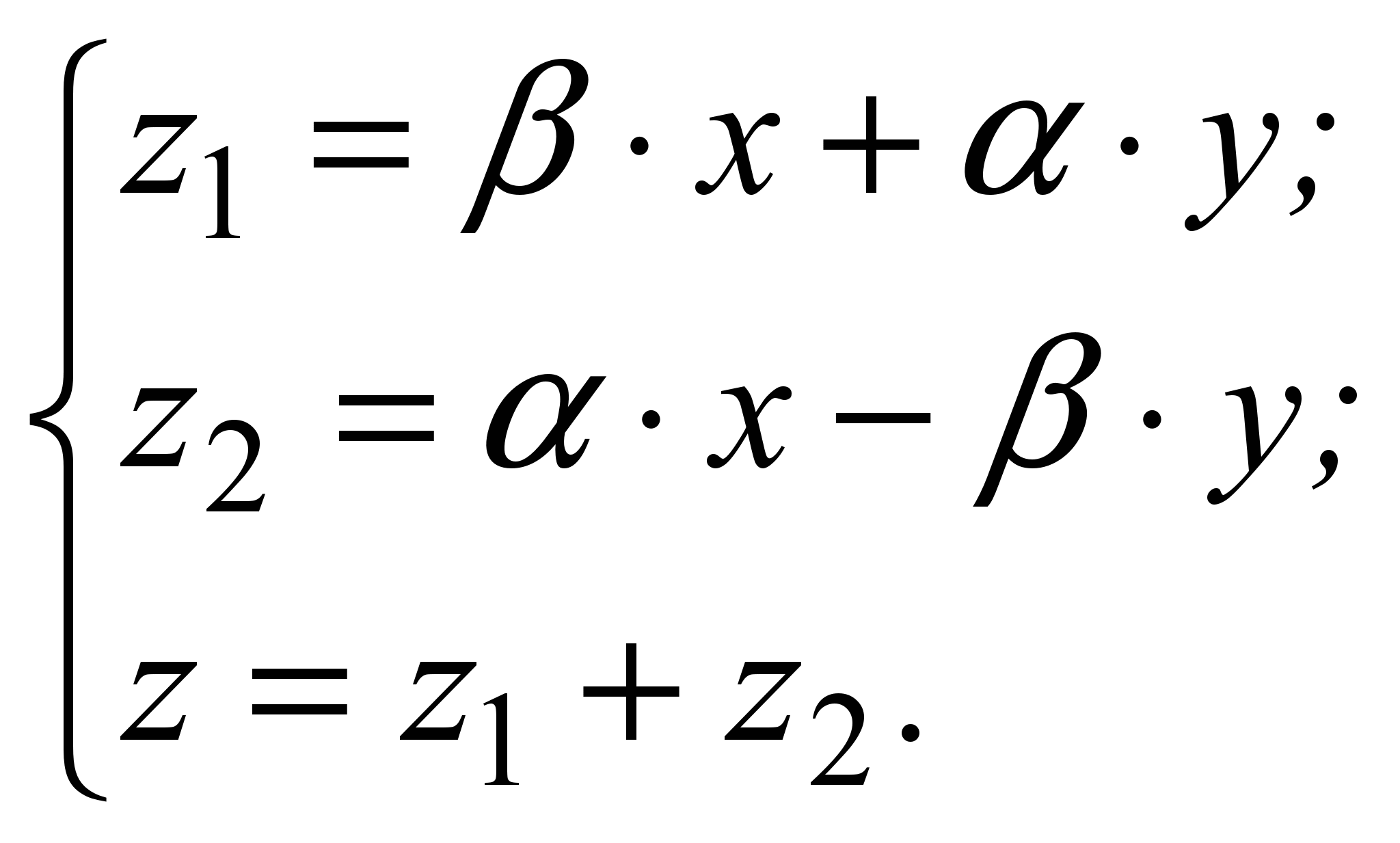
(1)Без потери общности предположим, что рассматривается два 24-битовых изображения – «экрана». Каждая точка – это комбинация трех основных цветов – красного, зеленого и синего, которые занимают каждый по одному байту, следовательно, три на точку. Применим преобразование (1) по отдельности к составляющим цвета точки, причем будем считать, что значение x отвечает первому изображению, а y второму. Таким образом, для каждой пары точек получится три результата для красной, зеленой и синей составляющей цвета. Если на параметры преобразования (1) наложить ограничения (
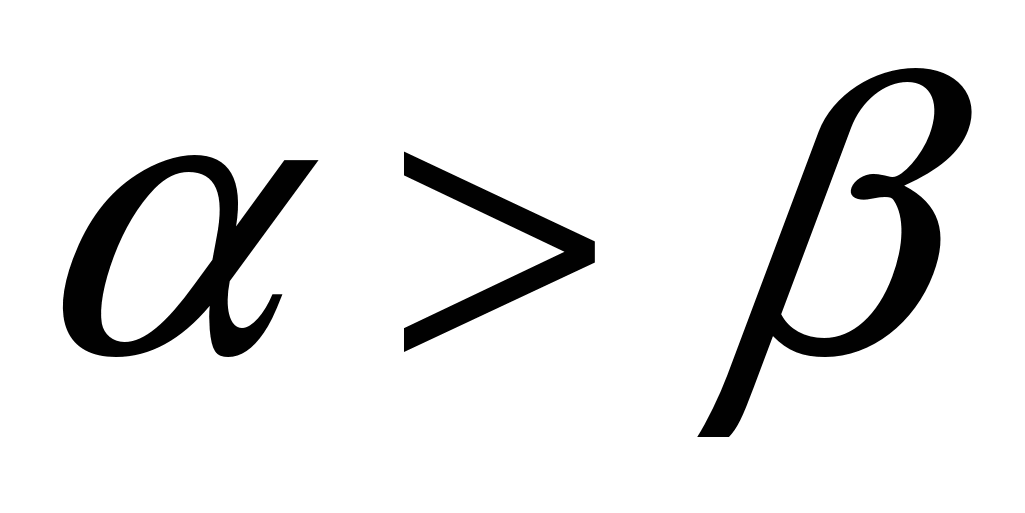и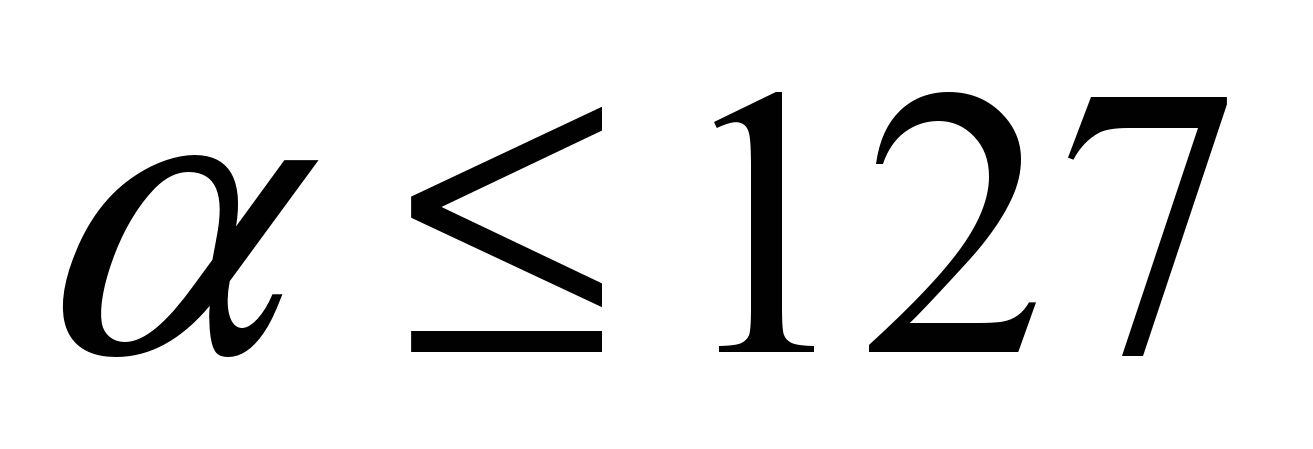 
), то полученные числа можно интерпретировать как составляющие цвета новых двух точек, выбрав для представления первой точки первую половину записи числа z, а для второй вторую половину записи z (имеется в виду запись числа в некоторой системе счисления). Если затем из этих точек составлять новое изображение, то оно будет содержать информацию об исходных рисунках. Поясним сказанное на примере. Пусть имеются две точки изображения (255,0,50) и (100,250,20), в качестве параметров преобразования выбраны
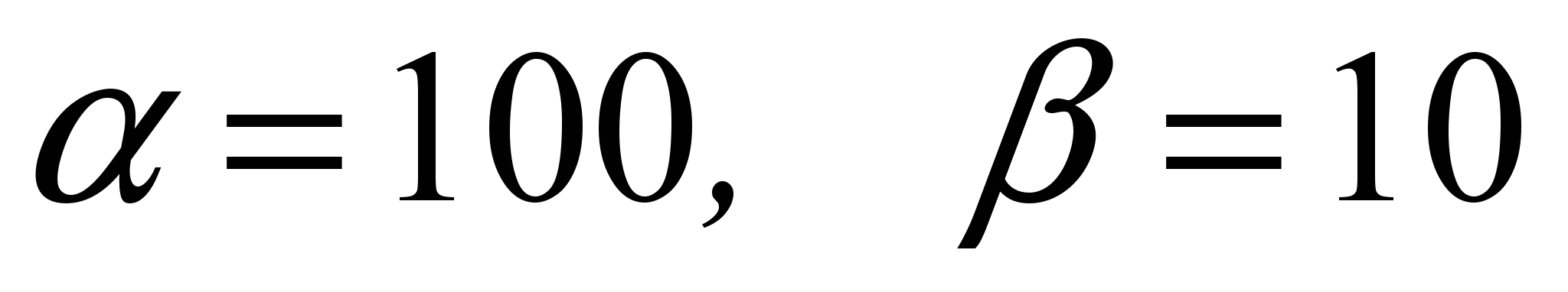. Для красной составляющей, т. е. для чисел 255 и 100 получаем значение 
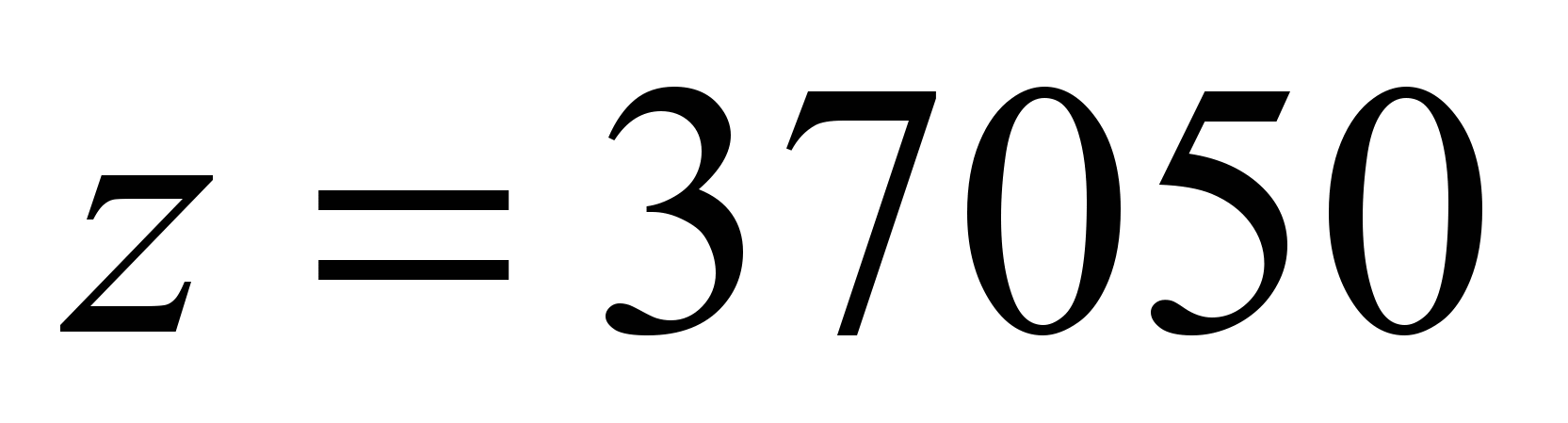. В шестнадцатеричной системе это 90BA, далее разделяем z на две части, 90 и BA, и, таким образом, для красной составляющей двух новых точек получаются следующие значения в десятеричной системе 144 и 186. Аналогично для синей составляющей 
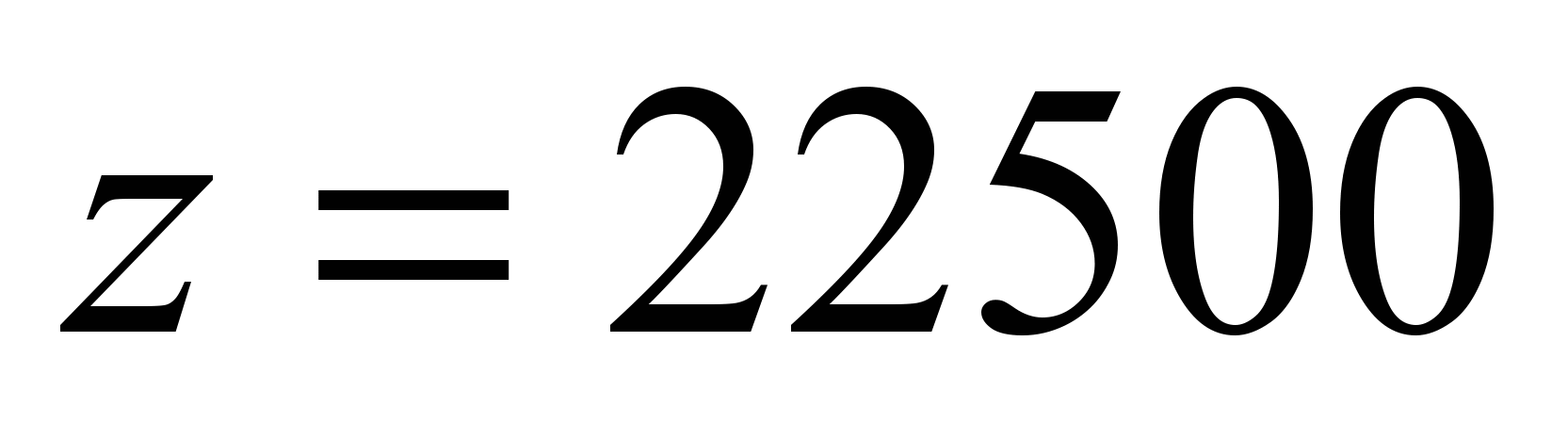, или 57E4, получаем 87 и 228. И для зеленой 
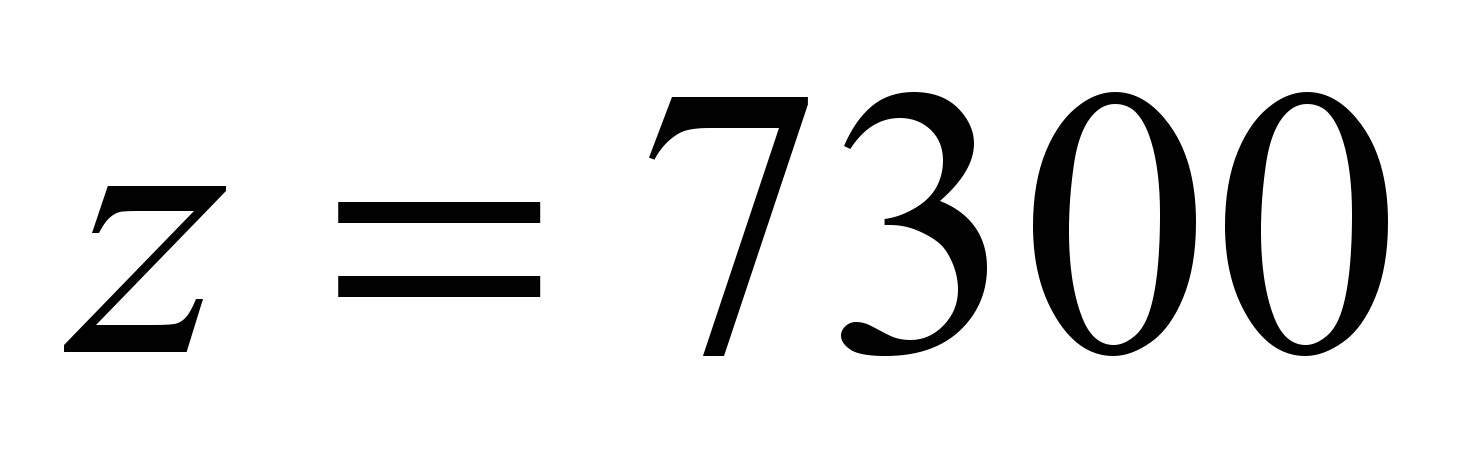, здесь имеем 28 и 132. В итоге мы получим две новые точки (144,87,28) и (186,228,132).Очевидно, что для корректной организации протокола передачи данных необходимо выбирать параметры преобразования таким образом, чтобы число решений системы диофантовых уравнений и неравенств было минимальным.
Анализируя систему, можно сделать вывод о том, что при
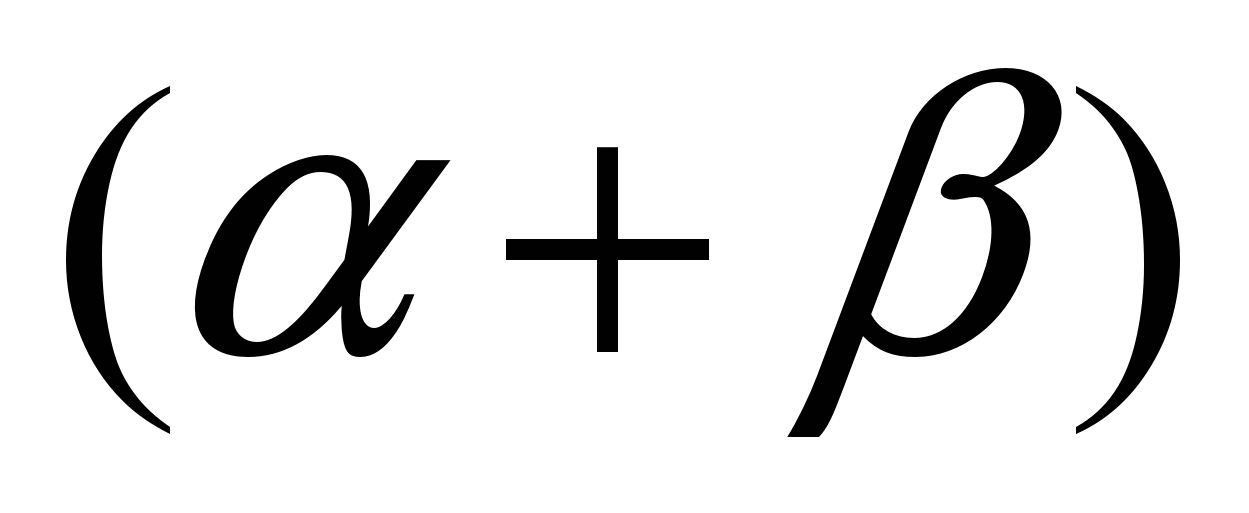>127 будет не больше двух решений, есл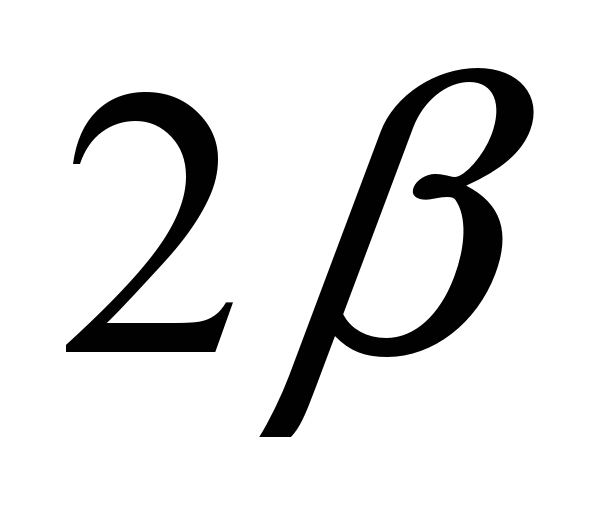и 
и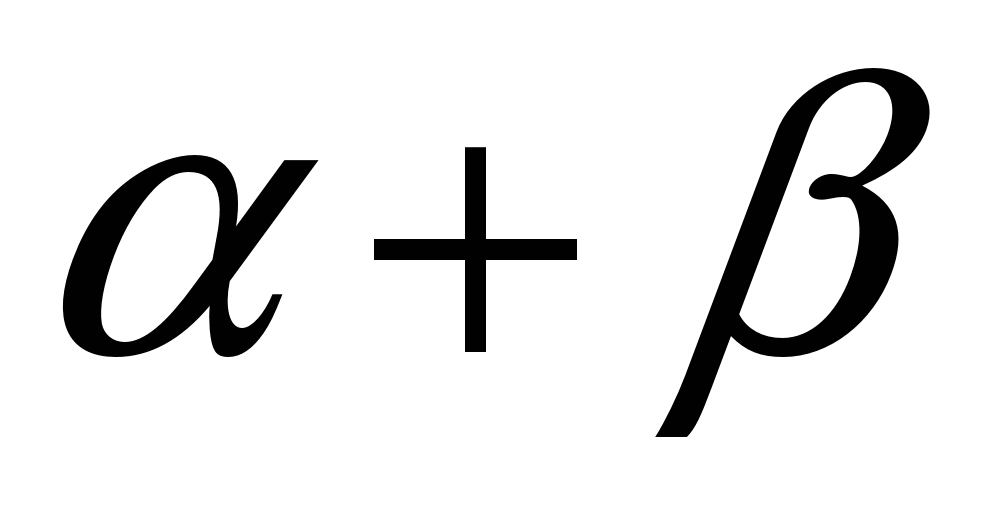 
взаимно простые числа. При этом если одно из возможных решений x будет четным, то другое, «паразитное», обязательно будет нечетным, и наоборот, то же самое можно сказать и относительно y. Таким образом, при приведенных ограничениях даже в худшем случае надо будет выбирать всего из двух вариантов и для однозначности выбора можно передавать дополнительную информацию о четности x. Альтернативный подход, не требующий передачи дополнительной информации, – это восстановление гладкого селектора, например, с помощью нейронной сети [1].
Ниже приведены примеры, иллюстрирующие представленный алгоритм. Так, например, рассмотрим следующие два изображения (рис. 1 и 2).
Рис. 1 Рис. 2
Параметры преобразования могут быть выбраны следующими:
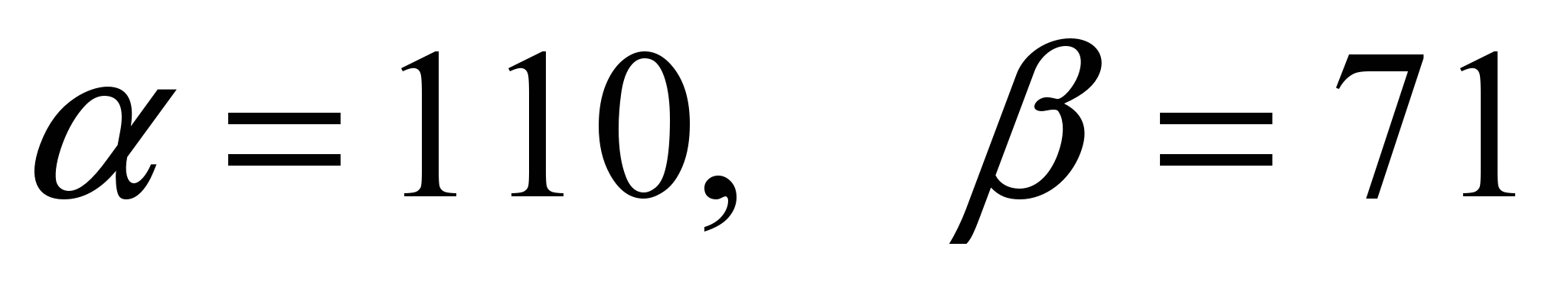. В результате преобразования мы получим изображение, приведенное на рис. 3.
Рис. 3
После восстановления получим рис. 4 и 5.
Рис. 4 Рис. 5
Отметим, что данный метод передачи информации можно использовать и в качестве алгоритма шифрования данных, организовав каскадное сложение «подэкранов».
Заметим, что если над «суммой» изображений провести специальное преобразование, сжать вдвое, то первое изображение может быть получено. Оно будет весьма удовлетворительного, но не исходного качества, главным образом будет нарушена цветопередача. Этот факт можно использовать, например, для защиты авторских прав, предоставляя потребителю «сумму» для ознакомления.
В отличие от стандартного стеганографического метода сокрытия информации [2], когда модифицируются младшие биты изображения, в предложенном алгоритме не происходит потери информации, и изображения восстанавливаются точно. Данное обстоятельство, например, можно использовать для градации степеней защиты частей изображения. Но в этом случае требуется специальный подбор первого, «ведущего» изображения. С другой стороны, выбор (генерация) «ключевых» картин, с которыми складываются части передаваемых изображений, позволяет естественным образом построить алгоритм шифрования.
___________________
1. Осовский С. Нейронные сети для обработки информации. М.: Финансы и статистика, 2002.
2. Грибунин В.Г., Оков И.Н., Туринцев И.В. Цифровая стеганография. М.: Солон-Пресс, 2002.