Моделирование адиабатических потенциалов циклических и полициклических соединений 05. 13. 18 Математическое моделирование, численные методы и комплексы программ

Вид материала

Автореферат

Содержание Общая характеристика работы Цель работы Научная новизна результатов Практическая значимость Достоверность полученных результатов и выводов Основные положения и результаты, выносимые на защиту Апробация работы Личный вклад соискателя Структура и объем диссертации Содержание работы В первой главе Во второй главе В четвертой главе В пятой главе В шестой главе Основные результаты и выводы По теме диссертации опубликованы работы

Подобный материал:

• Математическое моделирование управляемого движения космических аппаратов, 213.72kb.
• Математическое моделирование многомерных квазистационарных электромагнитных полей, 380.28kb.
• Математическое моделирование термомеханических процессов в системах армированных стержней, 259.01kb.
• Программа кандидатского экзамена по научной специальности 05. 13. 18 «Математическое, 83.4kb.
• Численное моделирование и разработка комплекса программ исследования теплообмена, 466.89kb.
• Моделирование нештатных ситуаций военно-технического характера в реальном времени, 336.75kb.
• Математическое моделирование процессов самоорганизации в широкополосных системах 05., 181.86kb.
• Математическое моделирование течения высоковязких жидкостей с маловязким пристенным, 225.73kb.
• Математическое и компьютерное моделирование динамического состояния систем передачи, 388.39kb.
• Математическое моделирование негауссовых случайных процессов на основе моментных функций, 321.55kb.

На правах рукописи


Джалмухамбетова Елена Азатуллаевна


МОДЕЛИРОВАНИЕ АДИАБАТИЧЕСКИХ ПОТЕНЦИАЛОВ

ЦИКЛИЧЕСКИХ И ПОЛИЦИКЛИЧЕСКИХ СОЕДИНЕНИЙ


05.13.18 – Математическое моделирование,
численные методы и комплексы программ


АВТОРЕФЕРАТ

диссертации на соискание ученой степени

кандидата физико-математических наук


Астрахань – 2008


Работа выполнена на кафедре технической физики и информационных
технологий Саратовского государственного технического университета


Научный руководитель: доктор физико-математических наук,

профессор Элькин Михаил Давыдович


Официальные оппоненты: доктор физико-математических наук,

профессор Уманский Игорь Маркович


доктор химических наук,

профессор Алыков Нариман Мирзаевич


Ведущая организация: Саратовский государственный университет,
г. Саратов


Защита диссертации состоится ___________ 2008 г. в ___ часов ___ минут
на заседании диссертационного совета ДМ 212.009.06 при Астраханском государственном университете по адресу: 414056, г. Астрахань, ул. Татищева, 20 а.


С диссертацией можно ознакомиться в библиотеке Астраханского государственного университета.


Автореферат разослан «___» _____________ 2008 г.


Ученый секретарь диссертационного

совета ДМ 212.009.06

кандидат физико-математических наук, доцент Смирнов В.В.


ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ


Актуальность темы

Все физико-химические свойства молекулярной системы, как квантового объекта, определяет адиабатический потенциал, отражающий строение электронной оболочки молекулы в рассматриваемом электронном состоянии.

Получить явный вид адиабатического потенциала, как решение уравнения Шредингера для электронной подсистемы молекулы при заданной конфигурации ядер, удается лишь для двухатомных молекул. Для многоатомных молекул квантовые уравнения решаются численно, что позволяет оценить коэффициенты разложения (силовые постоянные) адиабатического потенциала в ряд по координатам атомов. Система силовых постоянных определяет положение полос колебательных спектров соединений.

В оценке параметров адиабатического потенциала имеют место два подхода. Первый подход базируется на решении обратных задач – оценки силовых постоянных по экспериментальным данным в спектрах исследуемых объектов и их изотопозамещенных аналогов. При этом исходные параметры адиабатического потенциала заимствуют из родственных по электронной структуре соединений, а затем подвергают варьированию. Решение обратных задач ограничивается, как правило, рамками гармонического приближения теории молекулярных колебаний. Несоответствие расчетных и экспериментальных данных принято объяснять наличием резонансов Ферми. Методика учета этих резонансов позволяет оценить лишь отдельные кубические и квартичные силовые постоянные.

Многолетние исследования, проведенные отечественными научными школами по спектроскопии, позволили создать банк данных по гармоническим силовым полям соединений различных классов, который внес заметный вклад в становление и развитие нового научного направления – молекулярного моделирования.

Второй подход базируется на оценке параметров адиабатического потенциала из неэмпирических (ab initio) расчетов электронной структуры молекул. В основе модельного квантового уравнения лежит физически обоснованное понятие молекулярной орбитали (метод Хартри-Фока), как линейной комбинации атомных орбит (метод Хартри-Фока-Рутаана). Расчеты с использованием данного метода позволили выработать рекомендации для выбора базиса электронных функций при построении молекулярных орбиталей. Однако результаты анализа колебательных состояний сложных молекулярных систем носили качественный характер и не позволяли осуществлять предсказательные расчеты параметров адиабатических потенциалов. Основная причина – отсутствие учета корреляционных эффектов в ансамбле электронов.

Добиться более точных результатов позволило развитие теории функционала плотности, где главную роль играет не многоэлектронная волновая функция, а распределение электронной плотности молекулы. Появилась возможность исследовать параметры адиабатического потенциала сложных молекулярных структур с точностью, достаточной для их спектральной идентификации.

Современные неэмпирические квантовые методы расчета электронной структуры молекул, в совокупности с теоретическими методами анализа их колебательных спектров, позволяют осуществлять предсказательные расчеты колебательных состояний сложных молекулярных систем, для которых объем экспериментальных данных ограничен, а практические потребности связаны с идентификацией соединений по их колебательным спектрам. Поэтому разработка и апробирование методик моделирования и расчета колебательных состояний многоатомных молекул в ангармоническом приближении с использованием прямых квантовых методов является актуальной и практически важной задачей.

Выбранные для исследования молекулярные объекты можно разделить на две группы. Первую составляют спутники современных промышленных производств, вызывающие загрязнение окружающей среды токсичными органическими соединениями, такими как полихлорированные диоксины, арсин- и фосфинзамещенные дифенила, дибензогетероциклические соединения. Экологический мониторинг всех этих соединений использует методы оптической физики, в частности, колебательную спектроскопию. Во вторую группу входят биологически активные молекулярные соединения. Это азотистые основания, урацил и пурин, составляющие основу нуклеиновых кислот, обеспечивающих хранение и передачу наследственной информации в живых организмах. Различные таутомерные производные пурина являются основой целого класса противоопухолевых лекарственных препаратов, а также играют определяющую роль в мутагенных процессах белковых образований.

Структура и физико-химические свойства рассматриваемых соединений проявляются в оптических спектрах, и, следовательно, могут быть исследованы квантовыми методами. Установление связи между структурой и спектрами, как самих исследуемых соединений, так и их отдельных молекулярных фрагментов, сопоставление параметров структурно-динамических моделей считается одной из важных задач конформационного анализа сложных молекулярных соединений.


Цель работы

Основной целью диссертационной работы является исследование возможностей математических и вычислительных методов квантовой механики в предсказательных расчетах адиабатических потенциалов молекул ряда пятичленных и шестичленных циклических и полициклических соединений.

Конкретная реализация намеченной цели включала в себя решение комплекса задач:

- разработку методики анализа адиабатического потенциала и колебательных состояний соединений в ангармоническом приближении с использованием системы естественных колебательных координат;

- разработку алгоритма численного решения прямых и обратных механических задач для изотопозамещенных соединений в произвольной системе естественных колебательных координат;

- проведение квантовых расчетов геометрической структуры и колебательных состояний молекул различных классов в рамках ангармонического приближения с целью интерпретации имеющихся экспериментальных данных и выбора молекулярных параметров в задачах идентификации соединений методами оптической физики.


Научная новизна результатов

Для пятичленных, шестичленных циклических и полициклических соединений предложен неэмпирический квантовый метод расчета адиабатических потенциалов, позволяющий интерпретировать колебательные спектры соединений по частотам колебаний и интенсивностям в колебательных спектрах.

Предложены численные алгоритмы описания молекулярной динамики в ангармоническом приближении теории молекулярных колебаний с использованием произвольной системы естественных колебательных координат (энергии состояний, формы колебаний, резонансные взаимодействия состояний).

Осуществлена компьютерная реализация задачи интерпретации инфракрасных спектров (ИК) и спектров комбинационного рассеяния (КР) молекул, анализа колебательно-вращательного взаимодействия, учета ангармонических резонансов.

Осуществлена полная интерпретация фундаментальных колебаний исследуемых соединений с целью выявления характеристических полос для идентификации молекулярных фрагментов.


Практическая значимость

Практическая значимость работы определяется совокупностью результатов, полученных применительно к исследованным соединениям различных классов (силовые поля в гармоническом и ангармоническом приближении, электрооптические параметры, константы ангармоничности, интерпретация колебательных состояний, геометрия молекул), что составляет фундамент для исследования строения и спектральных свойств соединений более сложной структуры.

Предложенная методика анализа колебательных спектров, на основе квантово-механических расчетов в ангармоническом приближении, в сочетании с разработанным программным обеспечением может быть
использована в предсказательных расчетах оптических и структурных параметров широкого класса соединений.

Данные по геометрической структуре урацила и пурина, анализ механизма межмолекулярного взаимодействия соединений в различных фазовых состояниях могут быть использованы в спектральных и биофизических исследованиях нуклеиновых кислот, что актуально для фармакологии и генной инженерии.

Для полициклических соединений указаны полосы в колебательных спектрах, которые позволяют осуществлять идентификацию соединений, в том числе и таких промышленных экотоксикантов, как диоксин и его производные. Результаты, полученные на основе высокоточных ab initio расчетов, дают возможность надежно интерпретировать сложную структуру экспериментальных спектров.

Методы расчета структуры и колебательных спектров сложных молекул, рассматриваемые в диссертации, используются в учебном процессе на кафедре общей физики Астраханского государственного университета, в курсе «Вычислительная физика».


Достоверность полученных результатов и выводов

Достоверность полученных результатов и выводов обеспечивается адекватностью используемых в исследовании физических моделей и квантовых вычислительных методов поставленной задаче, корректностью используемых приближений, а также количественным и качественным соответствием полученных в работе теоретических результатов экспериментальным данным.


Основные положения и результаты, выносимые на защиту:

1. Методика и алгоритмы расчета параметров кинематической ангармоничности, анализ резонансных эффектов на основе рассчитанных ангармонических силовых постоянных, которые реализованы в едином программном комплексе для решения прямых и обратных спектральных задач на основе квантовых методов.
   
2. Квантовые расчеты параметров адиабатического потенциала и констант ангармоничности методом функционала плотности, которые позволяют в хорошем согласии с экспериментальными данными дать теоретическую интерпретацию колебательных состояний изученных соединений.
   
3. Результаты неэмпирических расчетов кубических и квартичных силовых постоянных исследуемых соединений. Построение и обоснование их структурно-динамических моделей в ангармоническом приближении.
   

Апробация работы

Основные результаты диссертационной работы докладывались на следующих конференциях:

• 9-ая Международная молодежная научная школа по оптике, лазерной физике и биофизике (Саратов, 2005);
  
• Юбилейная 5-ая международная научно-практическая конференция «Международные и отечественные технологии освоения природных и минеральных ресурсов и глобальной энергии» (Астрахань, 2006);
  
• 10-ая Международная молодежная научная школа по оптике, лазерной физике и биофизике (Саратов, 2006);
  
• 11-ая Международная молодежная научная школа по оптике, лазерной физике и биофизике (Саратов, 2007).
  

Публикации

По материалам диссертации опубликовано 18 печатных работ. Из них шесть в изданиях, рекомендованных ВАК, и три статьи в реферируемых журналах.

Личный вклад соискателя

Все основные результаты, на которых базируется диссертация, получены лично автором. В работах с соавторами соискателю принадлежит участие в выборе направлений исследований, постановке задач, разработке алгоритмов и методов их решения, интерпретации результатов.

Структура и объем диссертации

Диссертация состоит из введения, шести глав, общего заключения, списка литературы и двух приложений. Она содержит 127 страниц основного текста, включает 29 таблиц и 8 рисунков. Список используемых литературных источников содержит 186 наименований. Общий объем работы с приложениями составляет 161 страницу.


СОДЕРЖАНИЕ РАБОТЫ

Во введении обоснована актуальность темы диссертационной работы, ее новизна и практическая значимость, сформулированы цели и задачи исследования, обозначены объекты исследования.

В первой главе рассматривается выбранная ангармоническая колебательная модель многоатомной молекулы, обосновывается выбор криволинейной системы координат для описания молекулярных колебаний. В качестве таковой используется система естественных колебательных координат, определяемых как изменение длин связей и валентных углов в молекуле по сравнению с опорными их значениями, как правило, равновесными. Рассматривается связь (метрика) между естественными колебательными координатами, в которых осуществляется интерпретация колебаний, и декартовыми координатами, в которых производятся квантовые расчеты геометрической и электронной структуры молекул в программном комплексе «Gaussian 03».

Решение уравнения Шредингера осуществляется в адиабатическом приближении. В этом случае для ядерной подсистемы в n-ом электронном состоянии уравнение принимает вид:

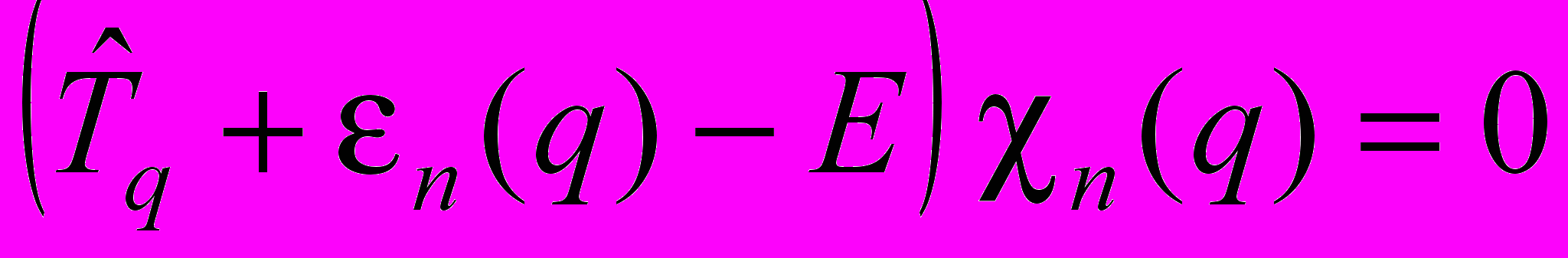. (1)

Здесь – оператор кинетической энергии ядер; 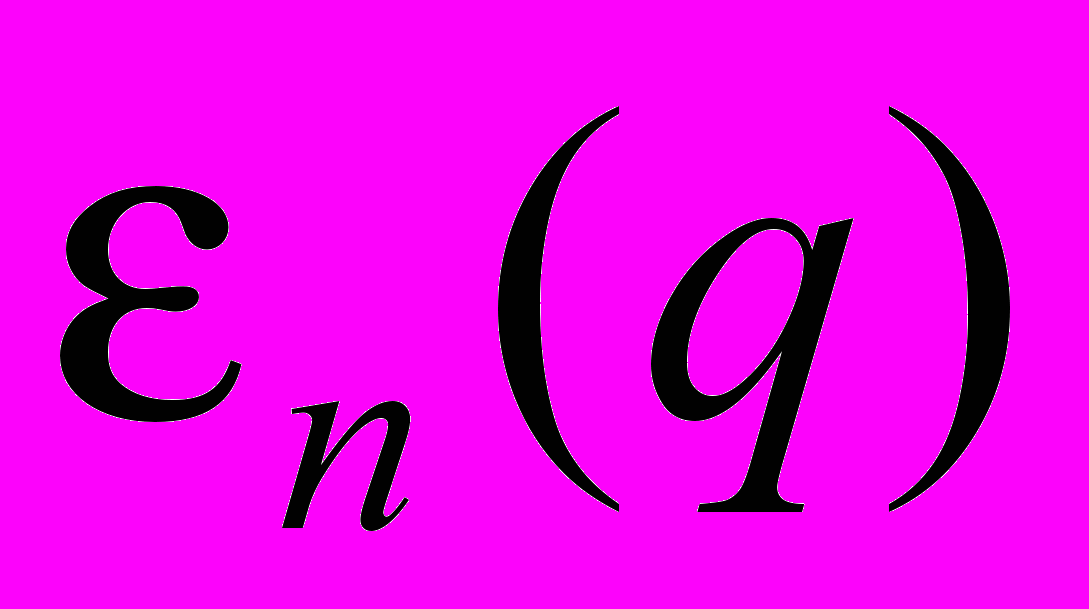– адиабатический потенциал n-го электронного состояния; _n(q) – колебательная функция ядер; E – энергии состояний молекулы.

Представление адиабатического потенциала в виде ряда Тейлора по ядерным координатам q^a относительно положения равновесия ядерной конфигурации

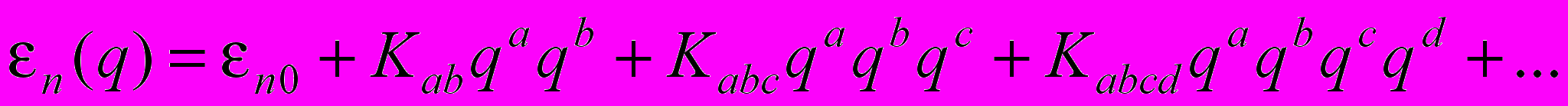(2)

приводит к понятию квадратичных, кубических, квартичных силовых постоянных 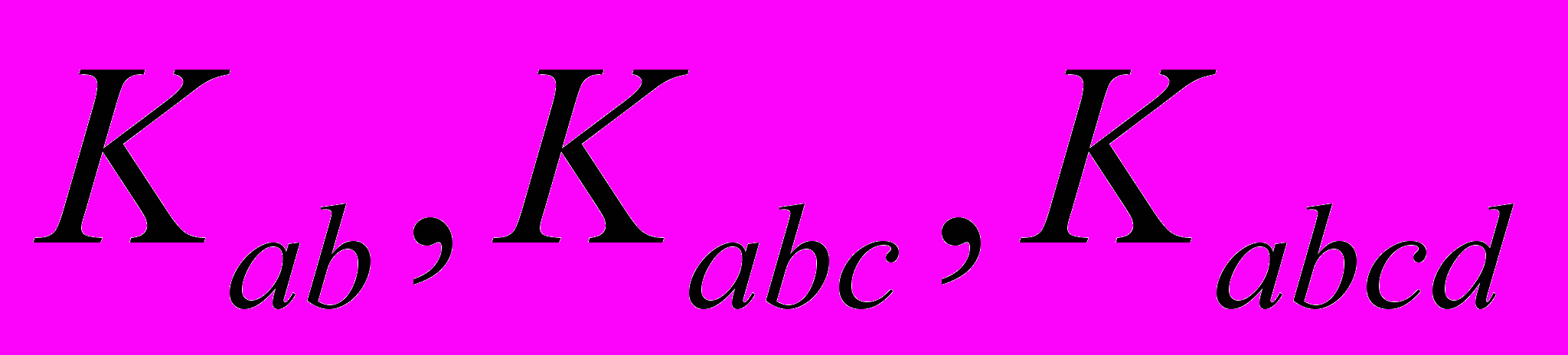и позволяет осуществить решение уравнения (1) в соответствующем порядке теории возмущения. Современные расчетные квантово-механические методы, в том числе и ab initio, позволяют анализировать параметры адиабатического потенциала, определяющего свойства молекулярной системы.

Для получения метрических соотношений между декартовыми координатами и естественными колебательными координатами предложены два определяющих соотношения, связывающих длину S_ij химической связи i-го и j-го атомов, величину валентного угла β c декартовыми координатами атомов R^iα и единичными векторами связей :

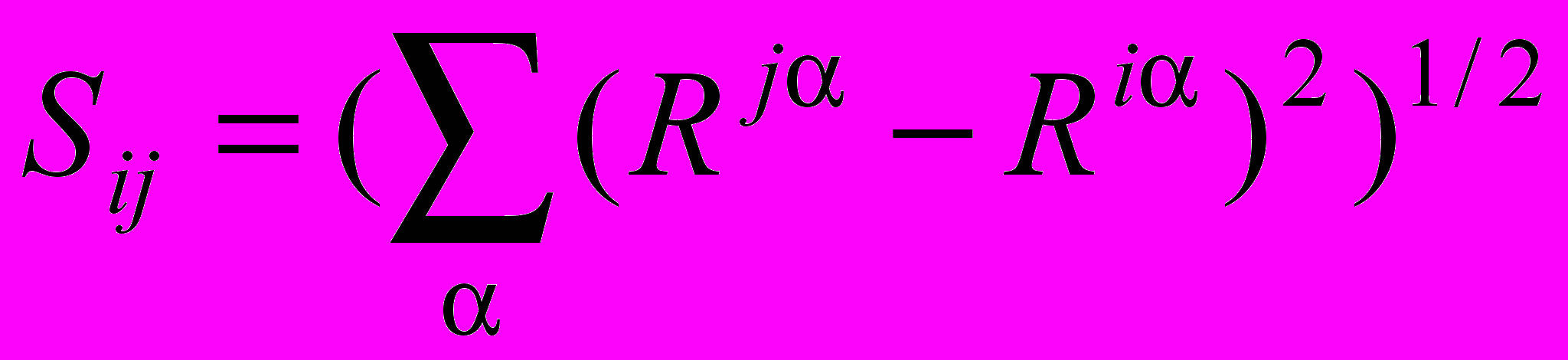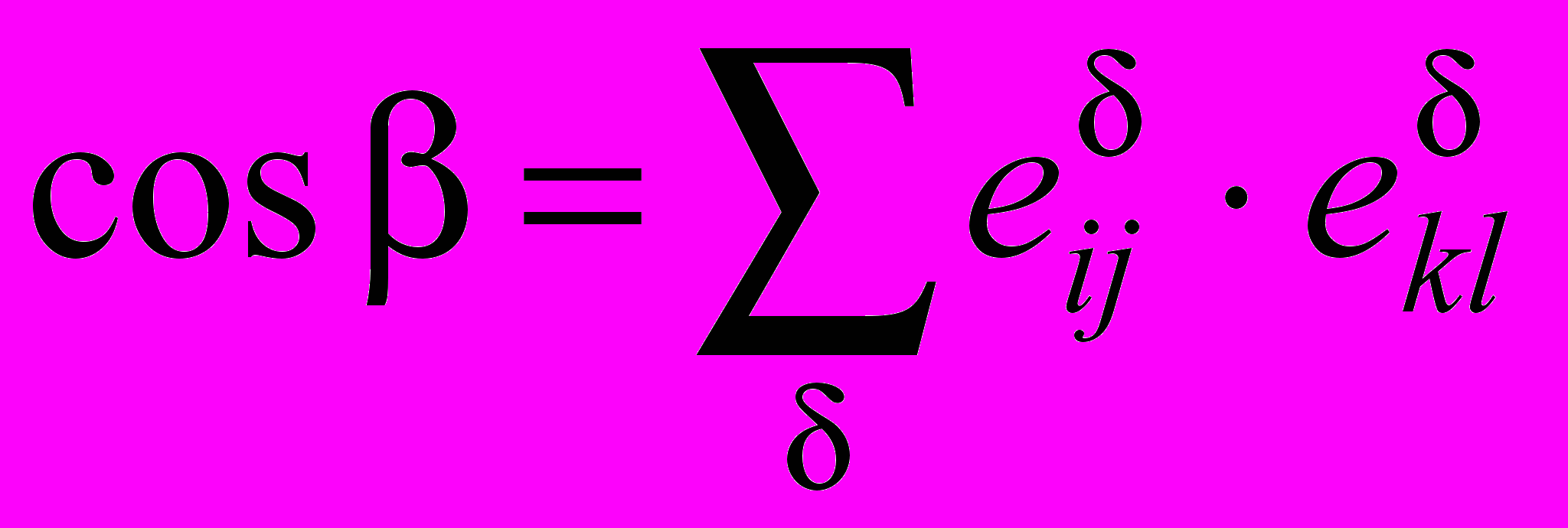; , (,  = x, y, z). (3)

Для неплоских координат единичные векторы связей заменяются направляющими векторами молекулярных фрагментов. Дифференцирование выражений (3) позволяет получить искомые метрические соотношения и записать уравнения в виде удобном для компьютерной реализации.


Во второй главе рассмотрены особенности современных квантовомеханических методов исследования колебательной динамики молекул. Обоснован выбор программного комплекса, с помощью которого проводился расчет основных параметров исследуемых молекул.

Решение уравнения Шредингера или эквивалентной вариационной задачи для электронной подсистемы многоатомной молекулы в рамках различных квантовохимических методов позволяет оценить форму адиабатического потенциала. Однако выбор самого квантового метода и соответствующего ему базиса не очевиден и требует проведения численного эксперимента. Используемые в расчетах адиабатического потенциала программные продукты общеизвестны, однако лишь с начала текущего столетия стали возможными расчеты ангармонических параметров адиабатического потенциала.

В данной работе использовался известный программный пакет «Gaussian 03». Именно эта версия программного комплекса позволяет осуществлять вычисления кубических и квартичных параметров разложения адиабатического потенциала.

Анализ имеющихся литературных данных по результатам расчета адиабатических потенциалов соединений различных классов, прямо указывает на предпочтительность метода функционала плотности (DFT – метода). Он обеспечивает высокую точность результатов и при этом более экономичен, т.к. требует меньших затрат времени и ресурсов, чем классические методы, учитывающие электронную корреляцию. Его применение является наиболее эффективным в исследовании структуры и спектров многоатомных молекул.


Объектом исследования в третей главе является урацил, замещенные урацила, димеры урацила.

И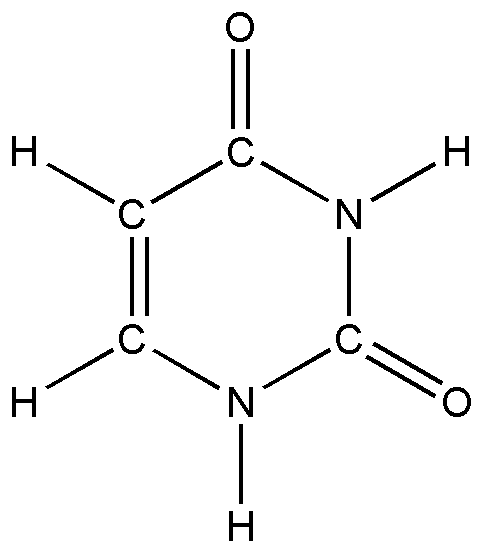сследование ангармонических колебательных со стояний базовой молекулы – урацила проводилось прямыми квантовыми методами с помощью пакета программ «Gaussian-03». На основе проведенного анализа литературы было выяснено, что для молекул рассматриваемого класса надежными предсказательными возможностями обладает квантовый метод DFT/B3LYP/6-31G(d,p).

Рис. 1. Молекула урацила

Результаты проведенного численного эксперимента и его сравнение с экспериментальными данными по структуре и спектрам урацила позволили сделать ряд выводов. Изменение геометрических параметров шестичленного кольца при замещении несущественно. Имеет место зависимость частот плоских деформационных колебаний от положения и числа заместителей. Частоты валентных колебаний связей метильной группы, как заместителя, определяются их числом и местоположением в кольце. Интервал их разброса достигает ~ 70 см^–1.

Хорошее совпадение опытных и вычисленных частот валентных колебаний связей достигаются лишь при решении колебательной задачи в ангармоническом приближении. Можно говорить о характеристичности интенсивностей валентных колебаний связей N-H. Она существенно выше таковой для связей C-H. Учет ангармонизма колебаний приводит к лучшему согласию с экспериментальными данными и для плоских деформационных колебаний. Исключение составляют частоты валентных колебаний молекулярных связей С-О.

Влияние ангармоничности на отнесение фундаментальных неплоских частот колебаний урацила и его замещенных не существенно. Их поведение определяется взаимным расположением заместителей относительно атомов кислорода. Для неплоских колебаний смена атома заместителя в заданном положении приводит к изменению частоты колебания, относящейся к выходу из плоскости связи C-X (X = CH₃, Cl). Колебание является характеристичным по форме, его интенсивность определяется электроотрицательностью атома заместителя. Крутильное колебание метильной группы воспроизводится в случае, если плоскость кольца является плоскостью симметрии метилурацилов. Структура метильного фрагмента такова: длина связи С-Н имеет значение 1.09 Å, отступление углов от тетраэдричности находится в границах 106.5º – 111.3º.

Частоты валентных колебаний метильной группы метилзамещенных урацилов практически не отличаются от таковых в алкилзамещенных бензола и легко интерпретируются. Для деформационных колебаний это отличие существенно, определяется типом замещения, а по форме сильно перепутываются с близкими по частоте колебаниями азациклического кольца. Для надежной их интерпретации необходимо было сопоставить соответствующие спектры галоидозамещенных урацила.

В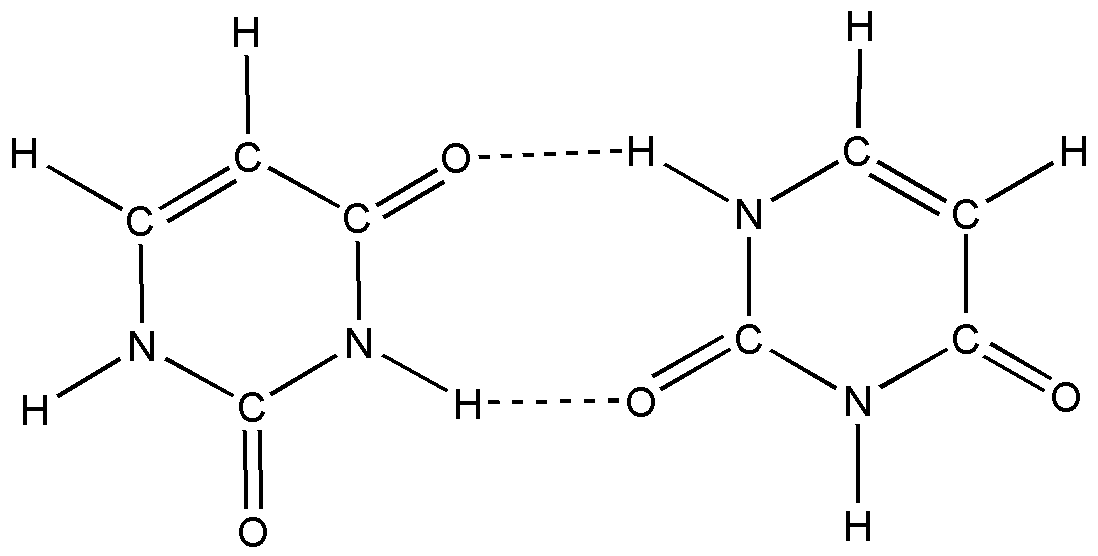о втором параграфе данной главы приведены результаты моделирования колебательных спектров возможных димеров урацила. При проведении модельных расчетов предполагалось наличие одной водородной связи между атомом кислорода одного мономера и водорода другого.

Рис. 2. Молекула димера урацила

Исходное значение длины водородной связи О---Н полагалось равным 1.9 Ǻ, углы между водородной и валентными связями СН и NH – 178º. Расчеты осуществлены как для плоской конформации димера, так и для случая, когда плоскости мономеров взаимно перпендикулярны.

Квантовые расчеты оптимизированной геометрической структуры указали на восемь возможных плоских моделей димеров урацила, в которых присутствуют две водородные связи O_i---H_j(штрихованная нумерация атомов относится ко второму мономеру). Для этих моделей были вычисленные значения геометрических параметров.

Различие в длинах водородной связи в зависимости от принадлежности атома водорода валентной связи NH (1.79 – 1.89 Ǻ) или СН
(2.21 – 2.24 Ǻ). Существенно изменяются углы СO---H(N) (122.9 – 129.6º) и СO---H(C) (119.4 – 129.3º) по сравнению с исходным его значением 178º. Уменьшаются по сравнению с исходными и значения углов NH---O (до 172.3º) и СH---O (до 160.2º).

Представленные данные расчета показывают, что изменению подвержены частоты валентных и деформационных колебаний связей урациловых фрагментов, примыкающих к водородной связи. Это касается валентных колебаний связей NH, частоты которых уменьшаются ~ 200 см^–1. Смещение частот неплоских колебаний этих связей существенно (~ 350 см^–1). Резко изменяется интенсивность полос. Такое поведение полос колебаний характерно для водородной связи. Для поликристаллического состояния урацила имеет место хорошее совпадение экспериментальных и расчетных данных. Таким образом, в поликристаллическом состоянии урацила имеет место межмолекулярное взаимодействие типа водородной связи между атомами кислорода одного фрагмента и водорода другого, образующего валентную связь с атомом азота.

Интересным представляется изменение частот неплоских колебаний связей NH в димерах. Наличие водородной связи приводит к повышению частоты указанных колебаний до 860 – 940 см^–1 в зависимости от модели димера. Этот факт можно использовать в задачах идентификации димера урацила в различных фазовых состояниях.


В четвертой главе рассматривается адиабатические потенциалы таутомерных формы пурина, исследуется механизм межмолекулярного взаимодействие при образовании димеров пурина.




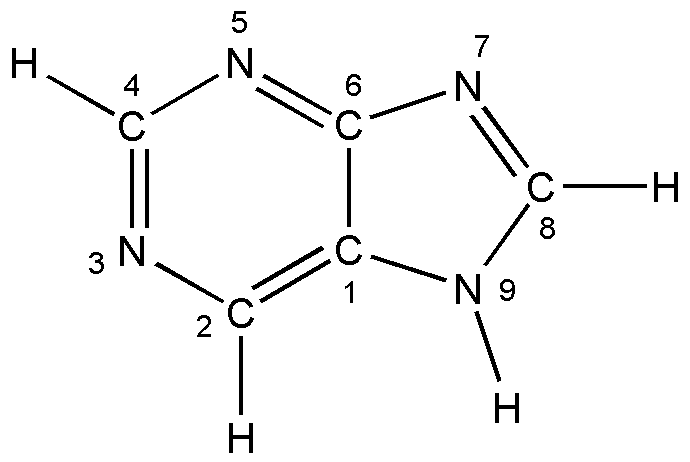
а б

Рис. 3. Таутомерные формы пурина: а) N₇H; б) N₉H.


Исходная модель молекулы пурина предполагалась плоской. Она состоит из примыкающих друг к другу шестичленного (пиримидинового) и пятичленного (имидазольного) колец. Таутомерные формы N₇H и N₉H определяются наличием или отсутствием связи NH в соответствующих положениях пятичленного фрагмента.

Результаты оптимизации геометрической структуры таутомеров пурина показывают, что таутометрия заметно сказывается лишь на величине валентного угла NCH (~ 4º) пятичленного (имидазольного) цикла. Изменения остальных углов не превышают 1º. Влиянием ангармоничности на геометрические параметры можно пренебречь.

Частоты указанных колебаний в свободных таутомерах практически не различаются, и по ним нельзя судить о доминирующем присутствии того или иного таутомера в изолирующей матрице. Влияние ангармонизма на плоские фундаментальные колебания шести- и пятичленного кольца в обоих таутомерах составляет приблизительно 40 см^–1, что соответствует разбросу частот плоских фундаментальных колебаний в экспериментальных данных для пурина.

Исследование межмолекулярного взаимодействия проведено для четырех моделей димеров пурина N₇H–N₇H, N₇H–N₉H, N₉H–N₉H, N₉H–N₇H. В этих димерах, имеет место водородная связь (~ 1.93 – 2.01 Å) между атомами азота одного мономера и атомом водорода связи NH другого в имидазольных циклах. Исследуемые конформации каждой из перечисленных моделей димера пурина различаются значением двугранного угла между плоскостями мономеров (пять конформаций с шагом π/4).

Согласно проведенным квантовым расчетам, для моделей N₇H–N₇H, N₉H–N₉H, N₉H–N₇H оба мономера лежат в одной плоскости. Они различаются положением имидазольных колец мономеров относительно друг друга и углами между водородной и примыкающей валентной связью N-H. Для модели N₇H–N₉H оптимизация энергии достигается для всех пяти конформеров. Однако для плоских конформеров этой модели не воспроизводятся частоты крутильных колебаний мономеров вокруг предполагаемой водородной связи.

Конформация димера относительно водородной связи несущественно сказывается на частотах колебаний шести- и пятичленного циклов мономера. За исключением деформационного колебания связей С-Н имидазольного кольца (диапазон 1034 – 1085 см^–1), смещение остальных фундаментальных частот не превышает 20 см^–1, что подтверждает общую закономерность изменения фундаментальных частот колебаний при переходе от мономеров к димеру с водородной связью.

Наличие водородной связи в димерах пурина практически не сказывается на геометрических параметрах соответствующих мономеров. Длины связей С-N шестичленного цикла попадают в интервал 1.33 – 1.35 Å, связей С-С в интервал 1.39 – 1.41 Å. В имидазольном кольце длины связей C-N укладываются в интервал 1.38 – 1.39 Å, за исключением связей С₈-N₇ в модели N₉H и С₈-N₉ в модели N₇H (1.31 Å).

Наличие димера может определяться по частоте валентного колебания связи N-H, соседствующей с водородной связью. Понижение указанной частоты на ~ 200 см^–1 согласуется с эффектом водородной связи. Заметно увеличивается частота неплоского колебания связи С-H, примыкающей к водородной связи. Для различных таутомеров это колебание смещается на ~ 60 см^–1. Идентификацию димера можно осуществить по частоте неплоского колебания связи N-H, участвующей в образовании водородной связи.

Необходимость учета ангармонизма колебаний связана с наличием значительного числа атомов водорода в соединениях, что подтверждается представленными расчетами колебательных спектров в соответствующем приближении. Получаемые при этом данные об ангармонических постоянных дают возможность анализировать обертонные состояния.


В пятой главе рассматривается построение структурно динамических моделей пятичленных полициклических соединений и их кольцевых производных. Установление связи между структурой и спектрами, как самих базовых молекул, так и соответствующих им фрагментов в исследуемых сложных соединениях, сопоставление параметров структурно-динамических моделей считается одной из важных задач конформационного анализа сложных молекулярных соединений.





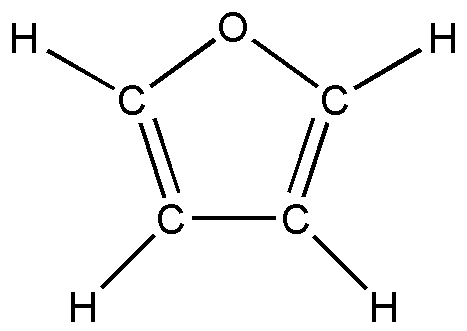
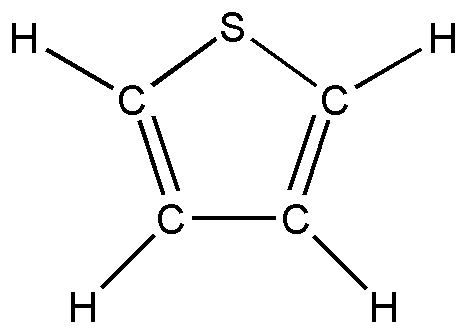
а б в


Рис.4. Пятичленные циклические молекулы: а) фуран; б) тиофен; в) селенофен.


В первом параграфе выполнен анализ колебательных спектров пятичленных циклических молекул – фурана, тиофена, селенофена, в ангармоническом приближении теории молекулярных колебаний. Уточнено отнесение частот, выяснено, что учет ангармонических слагаемых в адиабатическом потенциале молекулы приводит к улучшению соответствия расчетных и экспериментальных спектров.

Основная тема данной главы – теоретический анализ колебательных спектров дибензоциклических гетероциклов: флуорена, дибензофурана, дибензотиофена и карбазола.

В качестве неэмпирического расчетного метода использовался метод функционала плотности DFT/B3LYP/6-31G*(**), позволяющий осуществлять анализ адиабатического потенциала в ангармоническом приближении. В этом случае появляется возможность интерпретировать обертонные колебательные состояния.

При проведении численного эксперимента предполагалась плоская структура трехкольцевого фрагмента. Результаты оптимизации геометрии показали, что существенно различаются длины связей и валентные углы пятичленного фрагмента, что определяется свойствами гетероатома (N, O, S, С) этого фрагмента.





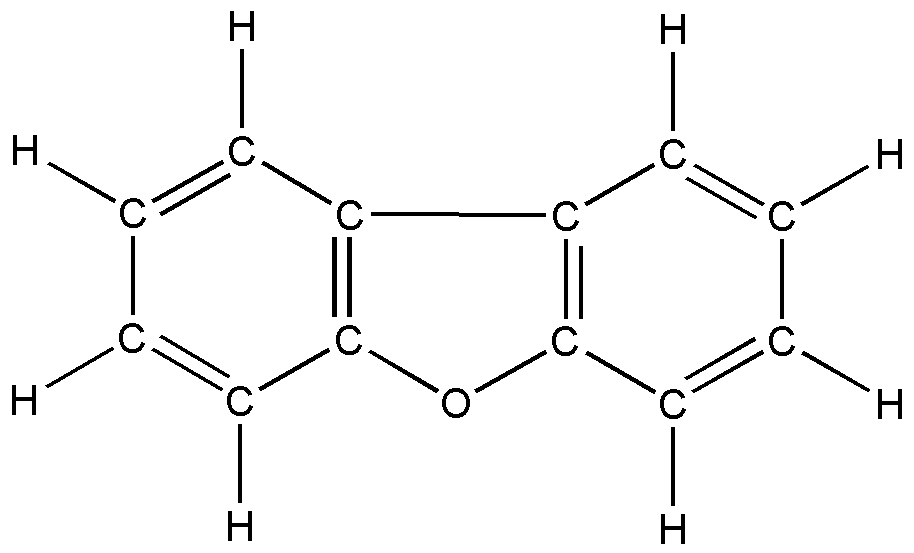
а б





в г


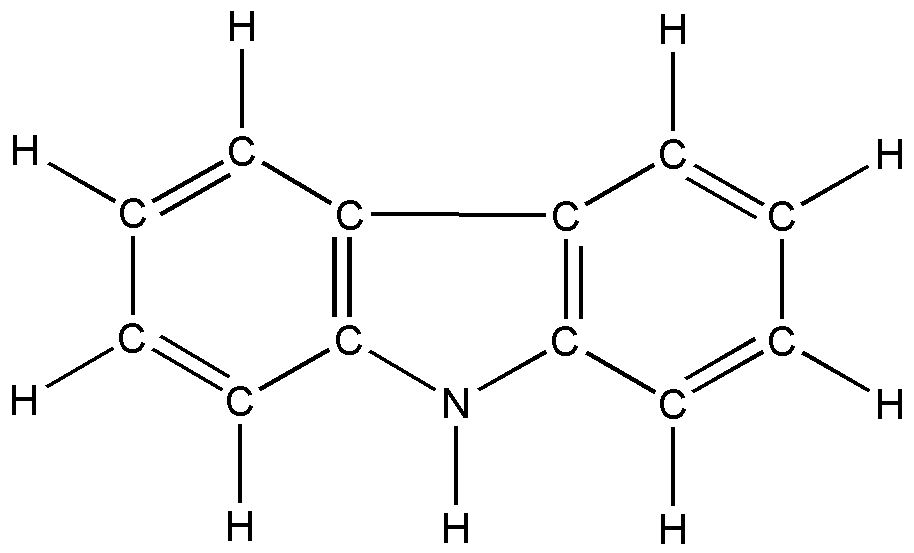
Рис. 5. Дибензогетероциклические соединения:
а) дибензофуран; б) дибензотиофен; в) карбазол; г) флуорен


Разброс в значениях геометрических параметров бензольных фрагментов заметного кинематического влияния не оказывает. Значения валентных связей и валентных углов этих фрагментов находятся в границах, характерных для различных замещенных бензола. Показано, что влияние гетероатома пятичленного цикла на гармоническое силовое поле носит локальный характер. Дана полная интерпретация спектра фундаментальных колебаний соединений.


В шестой главе представлен анализ структурно-динамических моделей шестичленных полициклических соединений, представляющих значительный теоретический и практический интерес.

Замена атома углерода центрального кольца на атом азота или кислорода в корне меняет биологическое проявление свойств многоатомных молекул данного класса соединений. Так базовое соединение класса – антрацен (С₁₄Н₁₀) в плане биологической активности ничем не выделяется. При замене атомов X_i центрального шестичленного цикла (X₁C₂C₃X₄C₅C₆, X = C, O, N) на кислород или азот приходится иметь дело с известными биологически активными соединениями – диоксином (С₁₂Н₈O₂), акридоном (С₁₃Н₉ON) и антрахиноном (С₁₄H₈O₂). Первое из них обладает канцерогенными свойствами, а его хлорзамещенные соединения высоко токсичны. Акридон, как и антрахинон, проявляет цитостатические свойства. Лекарственные препараты на их основе обладают противовирусной активностью.




а б





в г


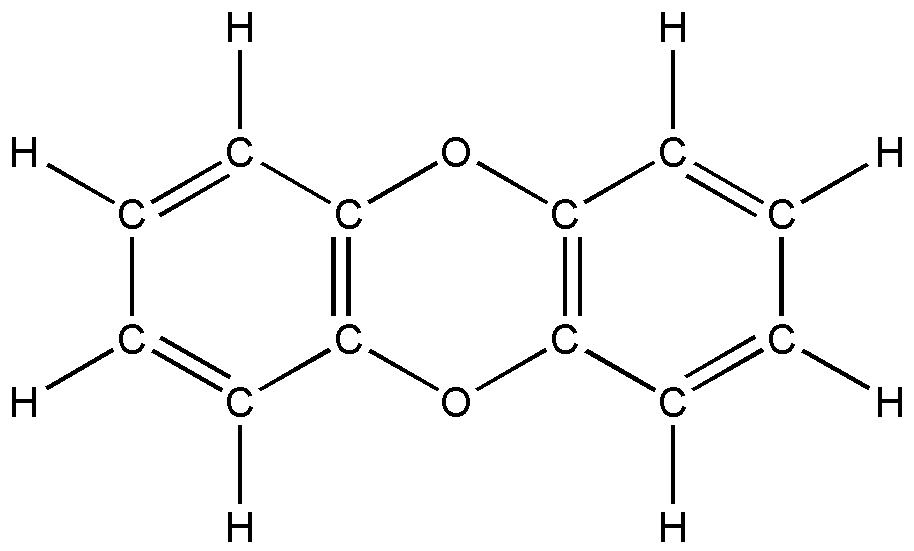
Рис. 6. Шестичленные полициклические соединения:
а) антрацен; б) акридон; в) антрахинон; г) дибензо-n-диоксин.


Для анализа поверхности адиабатического потенциала молекулярных соединений использовались прямые (ab initio) квантовые методы расчета геометрии и электронной структуры. Расчетным был выбран метод DFT/B3LYP/6-31G(d). Построение структурно-динамических моделей исследуемых соединений осуществлялось в предположении плоской конфигурации молекул.

Квантовые расчеты геометрической структуры исследуемых соединений и сравнение с имеющимися экспериментальными данными показали, что влияние ангармонизма колебаний сказывается на третьем знаке мантиссы для длин валентных связей и на втором для валентных углов. Галоидозамещение сказывается аналогичным образом. Существенное изменение геометрии центрального цикла связано с заменой карбонильной группы в акридоне на фрагмент С-Н.

Результаты проведенного теоретического анализа колебательных состояний 9,10-антрахинона, акридона дибензо-n-диоксина сопоставлены с результатами оптического эксперимента, что позволяет сделать следующие выводы. Изменение электронной структуры центрального фрагмента для базовых молекул несущественно сказывается на колебательных состояниях. Имеющееся различие частот кольцевых колебаний связано с кинематическими свойствами центрального кольца. Однако электрооптические свойства центрального фрагмента от соединения к соединению меняются так, что могут служить ориентиром при идентификации соединений.

Ангармонические эффекты в данных соединениях существенной роли не играют, хотя их учет при теоретическом анализе колебательных спектров данного класса соединений приводит к лучшему согласию экспериментальных и расчетных данных для частот фундаментальных колебаний. Ангармоничность существенно сказывается на валентных и деформационных колебаниях связей С-Н и N-H.

Согласно проведенным расчетам связи С-О в акридоне для всех типов хлорзамещенных акридона (от монохлорзамещенных до октохлорзамещенных) по частоте (~ 1660 см^–1), форме колебаний и интенсивностям в спектрах инфракрасного поглощения (ИК ~ 229.5 км/моль) и комбинационного рассеяния (КР ~ 224.2 Ǻ⁴/а.е.м.) это колебание является характеристичным. Идентифицировать акридон и его замещенные удобнее всего именно по данному колебанию и частоте валентного колебания cвязи N-H, которое на 300 – 350 см^–1 выше частот валентных колебаний связей С-Н.

Второй группой исследуемых соединений в данной главе были выбраны молекулы дифениларсина, дифенилдихлорарсина, дифенилфосфина дифенилдихлорфосфина (C₁₂H₉XY₂; X = As, P; Y = H, Cl).

Литературные данные по колебательным спектрам указанных соединений весьма ограничены. Естественным этапом решения колебательной задачи для молекул C₁₂H₉AsH₂, C₁₂H₉PCH₂, C₁₂H₉AsCl₂ и C₁₂H₉PCl₂ является построение структурно-динамической модели для базовой молекулы, каковой является молекула дифенила C₁₂H₁₀.





а б


Рис. 7. а) Молекула дифенила; б) молекула замещенного дифенила.


Квантовый расчет электронной структуры, геометрии и колебательных спектров молекулы дифенила осуществлялся для трех геометрических моделей: плоская; с разворотом бензольных колец на угол π/2; угол между кольцами в интервале [0, π/2]. По результатам можно сделать следующие выводы.

Описать крутильное колебание бензольных колец относительно связи С-С удается только для третьей модели при значении угла π/4. Именно эта модель определяет равновесную конфигурацию дифенила. Межкольцевое взаимодействие значительно уступает взаимодействию внутри бензольных колец. Взаимное расположение колец при этом не оказывает
существенного влияния. Интенсивности в спектрах ИК для различных конформеров различаются существенно, что связано с их симметрией.

Поведение колебаний каждого фенильного кольца характерно для монозамещенных бензола (для дифенила в качестве заместителя выступает второй бензольный фрагмент). Тем самым подтверждается предположение о локальном характере влияния замещения на силовое поле ароматического кольца при монозамещении.

Взаимное расположение колец существенно влияет на частоты деформационных колебаний углов, образованных связью С-С. По этим частотам можно идентифицировать структуру соединения.

Завышение расчетных значений фундаментальных частот колебаний полученных в гармоническом приближении по отношению к экспериментальным частотам можно устранить учетом ангармоничности колебаний. Больше всего ангармонизм сказывается на высокочастотных колебаниях, особенно колебания валентных связей С-Н.

Значения соответствующих длин валентных связей и валентных углов для различных конформеров различаются незначительно (разброс составляет ~ 0,01 Ǻ для связей и ~ 2˚ для углов). В этих же пределах искажаются значения геометрических параметров самого бензольного кольца.

Квантовые расчеты электронной структуры, частот фундаментальных колебаний, геометрических параметров дифенилдихлорфосфина (C₁₂H₉PCl₂) и дифенилдихлорарсина (C₁₂H₉AsCl₂) проведены только в предположении третьей модели, при которой угол между плоскостями шестичленных колец составляет π/4 и двух положений фрагментов PCl₂ и AsCl₂ относительно фенильного кольца.


ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ


Методом DFT/B3LYP/6-31G(*) проведен анализ параметров адиабатических потенциалов и выполнены расчеты структуры и колебательных состояний урацила и его замещенных, пятичленных циклических молекул – фурана, тиофена, селенофена, шестичленных полициклических соединений – полихлорированных дибензоциклов (дибензо-n-диоксина, антрацена, акридона, антрахинона), а также арсин- и фосфинзамещенных дифенила. Для соединений, экспериментальные данные по колебательным состояниям которых являются неполными, осуществлены предсказательные расчеты. Обоснованием их достоверности служат надежность используемых квантовых методов и эффективность применяемой методики расчета для родственных по электронной структуре соединений.

На основании неэмпирических квантовых расчетов методом DFT/B3LYP/6-31G*(**) дана интерпретация колебательных спектров флуорена, дибензофурана, дибензотиофена и карбазола в ангармоническом приближении теории молекулярных колебаний. Показано, что влияние гетероатома пятичленного цикла на гармоническое силовое поле носит
локальный характер, что позволяет считать достоверным предложенное отнесение фундаментальных колебаний для флуорена и карбазола, для которых отсутствуют полные имеющиеся экспериментальные данные по колебательным спектрам.

Проведено моделирование колебательных спектров возможных димеров урацила. Выяснен механизм межмолекулярного взаимодействия на основании квантовых расчетов геометрических параметров и адиабатического потенциала в рамках метода DET/B3LYP/6-31G(**). Установлено, что в поликристаллическом состоянии урацила, имеет место межмолекулярное взаимодействие типа водородной связи между атомами кислорода одного фрагмента и водорода другого, образующего валентную связь с атомом азота. Выявленное изменение спектра фундаментальных колебаний касается именно связей N-H урацила. По ним можно идентифицировать фазовое состояние исследуемого образца.

Использование метода функционала плотности DFT/B3LYP/6-31G(d)* позволило оценить параметры структурно-динамических моделей мономеров и димеров пурина, дать надежную интерпретацию колебательных спектров соединений, выяснить механизм межмолекулярного взаимодействия. Показана необходимость учета ангармонизма колебаний, связанная с наличием значительного числа атомов водорода в соединениях, что подтверждается сравнением с представленными расчетами колебательных спектров полученных в гармоническом и ангармоническом приближении, с экспериментальными.

Проанализированы гармонические и ангармонические силовые постоянные и коэффициенты ангармоничности в исследуемых соединениях. Показано, что в доминирующем числе расчетов колебательных спектров учет ангармонических эффектов приводит к лучшему согласию с экспериментом и позволяет устранить имеющиеся разногласия в интерпретации колебательных состояний исследуемых соединений.


По теме диссертации опубликованы работы

1. Элькин П.М. Структурно-динамические модели и ангармонический анализ колебательных спектров замещенных урацила. / П.М. Элькин, В.Ф. Пулин, Е.А. Джалмухамбетова // Вестник СГТУ.– 2005.– № 4(9). – С. 36-44.
   
2. Элькин П.М. Ангармонический анализ колебательных спектров дибензо-n-диоксина. / П.М. Элькин, В.Ф. Пулин, Е.А. Джалмухамбетова // Вестник СГТУ. – 2006. – №1(11), Выпуск 2. – С. 52-59.
   
3. Джалмухамбетова Е.А. Структурно-динамические модели и колебательные спектры дибензогетероциклов (флуорен, дибензофуран, дибензотиофен, карбазол) / Е.А. Джалмухамбетова, Л.М. Элькин // Вестник СГТУ. – 2007. – №2(25), Выпуск 2. – С. 7-11.
   
4. Элькин П.М. Ангармонический анализ колебательных состояний пятичленных гетероциклических соединений. / П.М. Элькин, О.В. Пулин, Е.А. Джалмухамбетова // Журнал прикладной спектроскопии. – 2007.– Т.74, №2. – С. 153-156.
   
5. Элькин П.М. Теоретический анализ колебательных спектров таутомерных форм пурина / П.М. Элькин, О.В. Пулин, Е.А. Джалмухамбетова // Журнал прикладной спектроскопии. – 2008. – Т.75, №1. – С. 23-27.
   
6. Элькин П.М. Колебательные спектры и структурно-динамические модели арсин- и фосфинзамещенных дифенила / П.М. Элькин, В.Ф. Пулин, Е.А. Джалмухамбетова // Журнал прикладной спектроскопии.– 2008. – Т.75, №4. – С. 463-469.
   
7. Элькин П.М. Колебательные спектры и структурно-динамические модели арсин- и фосфинзамещенных дифенила. / П.М. Элькин, В.Ф. Пулин, Е.А. Джалмухамбетова // Проблемы оптической физики. Материалы 9-ой Международной молодежной научной школы по оптике, лазерной физике и биофизике, 27-30 сентября 2005 г. Саратов (2006). С. 204-212.
   
8. Джалмухамбетова Е.А. Структурно-динамические модели и ангармонический анализ колебательных состояний тиофена, фурана, селенофена и их 2,5-N и 3,4-N производных. / Е.А. Джалмухамбетова, Э.К. Костерина, М.Д. Элькин // Проблемы оптической физики. Материалы 9-ой Международной молодежной научной школы по оптике, лазерной физике и биофизике, 27-30 сентября 2005 г. Саратов (2006). С. 224-232.
   
9. Элькин П.М. Структурно-динамические модели и ангармонический анализ колебательных состояний замещенных урацила. / П.М. Элькин, М.А. Эрман, Е.А. Джалмухамбетова // Южно-российский вестник геологии, географии и глобальной энергии, №2(15), 2006, с. 3-11.
   
10. Джалмухамбетова Е.А. Оптические спектры и фотофизические свойства полихлорированных дибензоциклов. / Е.А. Джалмухамбетова, А.Б. Осин, Л.М. Элькин // Южно-российский вестник геологии, географии и глобальной энергии, №5 (18), 2006, с. 118-120.
    
11. Элькин Л.М. Колебательные спектры и фото-физические свойства полихлорированных дибензоциклов (дибензо-n-диоксина, антрацена, акридона, антрахинона. / Л.М. Элькин, А.Б. Осин, Е.А. Джалмухамбетова // Проблемы оптической физики. Материалы 10-ой Международной молодежной научной школы по оптике, лазерной физике и биофизике, 26-29 сентября 2006 г. Саратов (2007). С. 214-220.
    
12. Джалмухамбетова Е.А. Анализ колебательных состояний дибензогетероциклов / Е.А. Джалмухамбетова, Л.Е. Лежень, П.М.Элькин // Известия Саратовского университета. Новая серия , 2007, Т.7, №2, с.64-67.
    
13. Элькин Л.М. Анализ колебательных состояний арсин- и фосфинзамещенных дифенила в ангармоническом приближении. / Л.М. Элькин, Е.А. Джалмухамбетова // Южно-российский вестник геологии, географии и глобальной энергии, №7(20), 2006, с. 16-23.
    
14. Джалмухамбетова Е.А. Анализ колебательных состояний полихлорзамещенных дибензо-n-диоксина. / Е.А. Джалмухамбетова, В.Ф. Пулин // Южно-российский вестник геологии, географии и глобальной энергии, №7(20), 2006, с. 32-38.
    
15. Джалмухамбетова Е.А. Структурно-динамические модели и колебательные спектры тризамещенных боразина. / Е.А. Джалмухамбетова, А.Б. Осин // Южно-российский вестник геологии, географии и глобальной энергии, №7(20), 2006, с. 60-67.
    
16. Джалмухамбетова Е.А. Моделирование геометрической структуры и спектров димеров с водородной связью. / Е.А. Джалмухамбетова, В.И. Коломин, М.Д. Элькин // Южно-российский вестник геологии, географии и глобальной энергии, №7(20), 2006, с. 117-124.
    
17. Джалмухамбетова Е.А. Анализ межмолекулярного взаимодействия в димерах урацила. / Е.А. Джалмухамбетова, С.С. Куриленко, Л.М. Элькин // Проблемы оптической физики. Материалы 11-ой Международной молодежной научной школы по оптике, лазерной физике и биофизике, 25-28 сентября 2007 г. Саратов (2008), с. 156-159.
    
18. Элькин М.Д. Квантовый анализ колебательных спектров таутомерных форм пурина. / М.Д. Элькин, О.В. Пулин, Е.А. Джалмухамбетова // Проблемы оптической физики. Материалы 11-ой Международной молодежной научной школы по оптике, лазерной физике и биофизике, 25-28 сентября 2007 г. Саратов (2008), с. 172-175.