Бакуна Виталия Викторовича Руководители: доцент Клебанович Николай Васильевич ассистент Шешко Сергей Михайлович Минск 2009 Оглавление Перечень условных обозначений 4 реферат

Вид материала

Содержание

Глава 3. Методика построения цифровой модели рельефа УГС «Западния Березина»
3.1.1. Метод сплайновой интерполяции
3.1.2. Метод обратно взвешенных расстояний
3.2. Построение геометрической сети постоянных потоков
3.3. Представление гипсометрических поверхностей в виде модели Topogrid
3.4. Представление гипсометрических поверхностей в виде модели TIN

Подобный материал:

1 2 3 4 5

Глава 3. Методика построения цифровой модели рельефа УГС «Западния Березина»

3.1. Представление гипсометрических

поверхностей в виде грид-моделей

Грид – это прямоугольный массив ячеек одного размера, которые в совокупности представляют тематические, спектральные или фотографические данные. Грид-модели могут изображать все, что характеризует земную поверхность, от высоты или растительности до космических изображений, сканированных карт и фотографий. Формат грид-данных очень прост, но поддерживает богатое разнообразие типов данных.

Значения ячеек грида могут представлять измеренную величину, например, высоту, концентрацию загрязнения или количество осадков. Значение от одной ячейки к другой постепенно меняется, и все вместе, эти значения могут моделировать некоторый тип поверхности. Значения ячеек для пространственно непрерывных данных представляют собой величины, относящиеся к центрам ячеек.

Значения для ячеек грида могут представлять категорию или классификацию данных, например, тип владения землями или тип растительности. Чаще всего, значение от одной ячейки к другой одинаково или резко меняется. Этот тип данных предстает в виде набора зональных областей с общими значениями, как, например, на картах землепользования или лесных участков. Значения ячеек для пространственно дискретных данных представляют собой классификацию, которая относится ко всей области ячейки.

Гриды представляют рельеф поверхности в виде регулярной сетки равномерно распределенных ячеек со значениями координаты Z. Разрешающая способность сетки – ширина и высота ячеек – определяет точность грид-модели.

Гриды образованы ячейками. Ячейка – это однородный элемент, который представляет собой определенный участок земли. Высота и ширина каждой ячейки фиксированы и одинаковы.

Каждая ячейка грида имеет значение, которое соответствует спектральному коэффициенту отражения или другой характеристике данного места, например, типу почв, данным переписи или классу растительности. Дополнительные значения ячейки могут записываться в таблице атрибута.

Размер, выбираемый для ячейки грида исследуемой области, зависит от той разрешающей способности данных, которая потребуется для наиболее детального анализа. Ячейка должна быть достаточно мала, чтобы улавливать требуемые детали, но и достаточно велика, чтобы эффективно хранить и анализировать данные на компьютере. Чем однороднее область в отношении критических переменных, например топографии и использования земель, тем крупнее может быть размер ячейки, используемый с необходимой точностью.

Между значениями ячейки грида (или ее кодами) и числом ячеек, которым назначен код, обычно существуют отношения "один ко многим". То есть, на гриде землепользования может быть 400 ячеек со значением четыре (жилой участок с одним семейством) и 150 ячеек, связанных со значением пять (коммерческая зона).

Значение кода многократно встречается в гриде, но только однажды в таблице атрибута, которая сохраняет дополнительные атрибуты для кода. Такая схема бережет память и упрощает обновление. Единственное изменение в атрибуте может применяться к нескольким сотням экземпляров этого значения.

Гриды поддерживают богатый набор видов пространственного анализа, например, пространственного совпадения, близости, дисперсии и наименьших потерь пути, и которые можно быстро выполнить. Недостатки грид-представления состоят в том, что разрывы непрерывности, типа гребней, изображаются плохо, и точные местоположения таких, например, предметов как вершины, теряются при дискретизации грида [9].

Интерполяция рассчитывает значения ячеек грида на основании ограниченного числа точек измерений. Ее можно использовать для вычисления неизвестных значений любых географических точечных данных: высоты над уровнем моря, уровня осадков, концентрации химических веществ, уровня шума и т.д.

Измерить высоту, величину или концентрацию какого-либо свойства в каждой точке исследуемой области обычно трудно или дорого. Вместо этого можно выбрать набор распределенных по некой схеме точек замеров и по ним рассчитать значения в остальных точках. Исходные точки, содержащие значения высоты, величины или концентрации свойства, могут быть распределены равномерно или случайным образом. Предположение, позволяющее проводить интерполяцию, состоит в том, что пространственно распределенные объекты пространственно связаны; другими словами, близкие объекты обладают близкими характеристиками. Например, если дождь идет на одной стороне улицы, то можно с большой уверенностью предположить, что он идет также и на другой стороне. С помощью этой аналогии легко понять, что значения точек, расположенных ближе к ячейке, скорее будут похожи на рассчитываемое значение ячейки, чем значения дальних точек. Это основа интерполяции. Часто интерполяция используется для создания поверхности рельефа по замерам высоты. Каждый объект слоя точек – это место, где проводилось измерение. С помощью интерполяции рассчитываются значения между точками измерений.

В модуль Spatial Analyst ГИС ArcGIS 9 включены следующие методы интерполяции: интерполяция значений с весом, обратно пропорциональным расстоянию, сплайн, кригинг и Topogrid. Каждый из них опирается на определенные предположения о том, как точнее вычислить значения ячеек. Для наилучшего соответствия расчетных значений реальным в разных случаях следует использовать разные способы интерполяции, в зависимости от того, какое явление отражают значения и как распределены точки замеров. Однако при любом методе интерполяции качество результата прямо пропорционально количеству исходных точек.

Благодаря интерполяции можно получить новую информацию, создав новый набор данных, который выявляет определенные закономерности в исходном наборе данных. Могут быть выявлены закономерности, которые не заметны на изображении исходного набора, например, изолинии, углы уклона, экспозиция склона, отмывка рельефа и видимость, а также изменение рельефа (насыпи/выемки) [4].

3.1.1. Метод сплайновой интерполяции

Метод Сплайн (Spline) рассчитывает значения ячеек грида на основе математической функции, минимизирующей кривизну поверхности, вычисляя наиболее ровную поверхность, точно проходящую через все точки измерений. Идея аналогична растягиванию резиновой пленки, так чтобы она проходила через все точки, при минимизации кривизны поверхности. Она располагается в соответствии с математической функцией от заданного числа ближайших точек при условии прохода через все точки замеров. Этот метод наиболее удобен для медленно меняющихся поверхностей, таких, как высота земной поверхности, уровень грунтовых вод или концентрация вредных веществ.

Существует два метода сплайна: регуляризация (Regularized) и натяжение (Tension).

Метод регуляризации создает гладкую, постепенно меняющуюся поверхность, значения в которой могут выходить за пределы диапазона значений замеров.

Метод натяжения меняет жесткость поверхности в зависимости от характера моделируемого явления. Он создает менее гладкую поверхность, значения в которой ближе к рамкам диапазонов значений замеров.

В сплайновой интерполяции используется опция Вес (Weight). Для метода Регуляризации вес определяет вес третьей производной от поверхности в выражении минимизации кривизны. Чем больше вес, тем более гладкой будет поверхность. Значения, заданные для этого параметра, должны быть больше или равны нулю, например: 0, 0.001, 0.01, 0.1 и 0.5. Для метода Натяжения вес определяет вес натяжения. Чем больше вес, тем грубее поверхность. Значения должны быть больше или равны нулю, например: 0, 1, 5, и 10.

Число точек (Number of points) определяет количество точек, на котором должны быть основаны вычисления, то есть количество точек для вычисления каждого интерполируемого значения ячейки. Чем больше точек задается, тем большее влияние будут иметь удаленные точки, и тем более гладкой будет поверхность [8].

Построение интерполяционного грида с помощью метода Сплайн по данным гипсометрии учебных топографических планов производилось из точечного класса объектов, содержащего в себе все отметки высот топографических планов и отметки точечной темы, полученной при конвертации линейного слоя «горизонтали» в точечный класс объектов, содержащий в себе все вершины данного линейного слоя. Интерполяция производилось по полю Н, содержащему значения высот точек, с величиной выходной ячейки 1×1 метр. Параметр вес был выбран равным 0,1, количество точек, участвующих в создании значения ячейки – 12 (рис. 3.1).

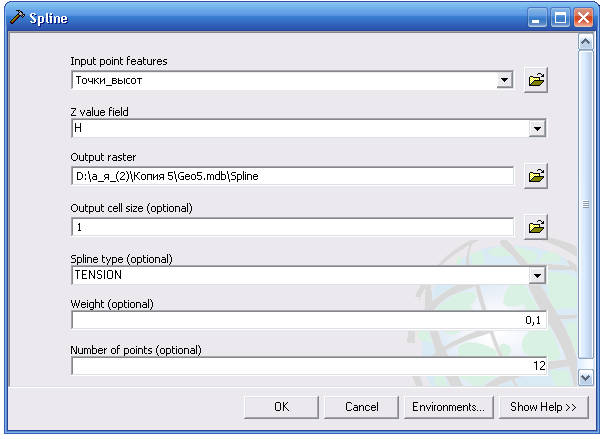
Рис. 3.1. Параметры интерполяции методом Spline

При построении цифровой модели рельефа УГС «Западная Березина» сплайновой интерполяцией были опробованы оба метода: метод регуляризации и метод натяжения. Следует отметить, что наиболее корректный результат был достигнут при использовании метода натяжения, так как при методе регуляризации поверхность растра имеет большее количество ошибок. В целом, оба метода не показали реалистичных результатов. Так, максимальная и минимальная высота на исследуемой местности составляет 209 м и 104 м соответственно, полученные же в интерполяционных гридах максимальная и минимальная высота для метода натяжения составляет 210,0 м и 96,5 м, а для метода регуляризации – 211,2 м и 72,9 м соответственно. Таким образом, расхождения от истинной высоты в некоторых местах доходят до 30%.

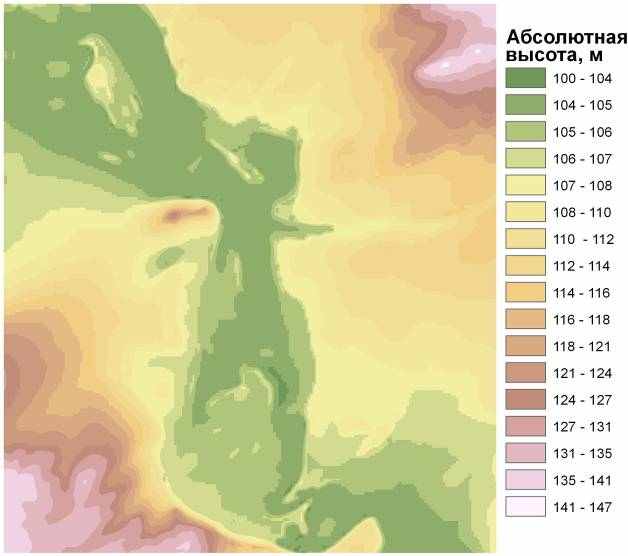
Рис. 3.2. Грид, интерполированный методом Spline

3.1.2. Метод обратно взвешенных расстояний

Метод обратно взвешенных расстояний (ОВР) – Inverse Distance Weighted (IDW) – вычисляет значения ячеек по среднему от суммы значений точек замеров, находящихся вблизи каждой ячейки. Чем ближе точка к центру оцениваемой ячейки, тем больший вес, или влияние, имеет ее значение в процессе вычисления среднего. В интерполировании растра участвует только точечный класс объектов со значениями интерполируемой величины. Этот метод предполагает, что влияние значения измеренной переменной убывает по мере увеличения расстояния от точки замера. Например, при интерполяции поверхности покупательной способности клиентов для анализа продаж магазинов покупательная способность в более удаленной точке будет иметь меньшее значение, поскольку люди предпочитают совершать покупки ближе к дому.

Благодаря опции Степень (Power) в ОВР можно контролировать влияние точек замеров на вычисление на основании их расстояния от ячейки. При задании большого значения степени влияние ближних точек будет более значительным, поверхность получится более детальной и менее гладкой. Задание меньшего значения степени увеличит влияние дальних точек, и поверхность получится более гладкой. Обычно используется значение степени 2, оно же установлено по умолчанию.

Характеристиками интерполируемой поверхности управляет также выбор радиуса поиска (Search radius) (фиксированного или переменного), который ограничивает количество исходных точек, участвующих в интерполяции значения ячейки.

Фиксированный радиус поиска (Fixed) определяется расстоянием и минимальным количеством точек. Расстояние определяет радиус окрестности (в единицах измерения карты). Величина радиуса постоянна, поэтому, для всех интерполируемых ячеек круговая окрестность поиска точек одинакова. Параметр минимального числа точек определяет минимальное количество измеренных точек, которое необходимо найти в заданной окрестности. При вычислении значения ячейки будут использованы все точки замеров, попавшие в заданную окрестность. Если точек в окрестности меньше заданного минимума, радиус поиска будет расширен, пока не удастся найти требуемое количество точек. Заданный фиксированный радиус поиска будет применен к каждой интерполируемой ячейке (центру ячейки) в исследуемой области. Таким образом, если точки замеров распределены неравномерно (а они редко бывают распределены равномерно), вероятно, в заданной окрестности для разных ячеек окажется разное количество точек замеров.

При использовании переменного радиуса поиска (Variable) задается количество точек, участвующих в вычислении значения интерполируемой ячейки, поэтому радиус поиска для каждой ячейки индивидуален и зависит от того, как далеко от каждой ячейки удается найти заданное число точек. Таким образом, одни окрестности будут маленькими, а другие большими, в зависимости от частоты точек замеров в районе интерполируемой ячейки. Можно задать максимальное расстояние (в единицах измерения карты), которое поиск не должен превышать. Если радиус определенной окрестности достигает максимального расстояния, вычисление значения этой ячейки будет выполнено на основе того количества точек, которое оказалось в окрестности максимального радиуса.

Также в методе обратно взвешенных расстояний доступна опция Барьер (Input barrier polyline features). Барьер – это полилиния, используемая для установки границы поиска точек измерений. Полилиния может представлять обрыв, горный хребет или другой разрыв в ландшафте. При вычислении значения ячейки будут учитываться только точки, расположенные по ту же сторону барьера, что и ячейка [9].

Построение интерполяционного грида рельефа территории УГС «Западная Березина» с помощью метода ОВР производилось из точечного класса объектов, содержащего всю гипсометрическую информацию используемых топографических планов – отметки высот, урезы воды и горизонтали, которые были получены при конвертации линейного слоя «горизонтали». Интерполирование производилось по полю Н, содержащему значения высот точек, с величиной выходной ячейки 1×1 метр. Значение опции Степень было выбрано по умолчанию – 2, так как небольшие значения данного показателя содействуют большей гладкости интерполированной поверхности. В качестве барьера был использован линейный класс объектов, содержащий гидрографию. Радиус поиска использовался как фиксированный, так и переменный.

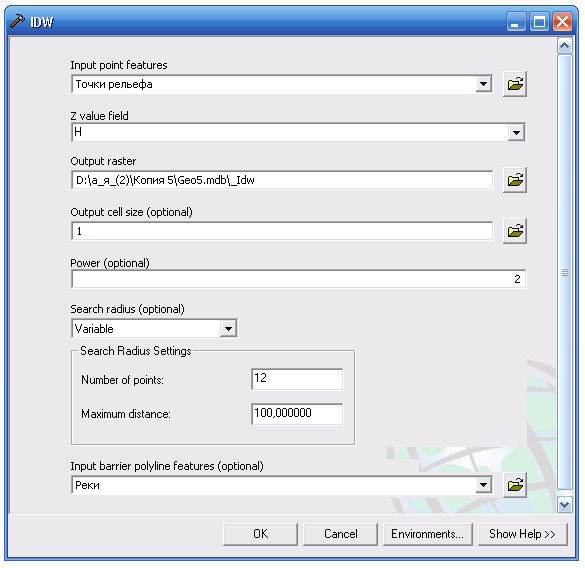
Рис. 3.3. Параметры интерполяции методом IDW

Метод ОВР произвел достаточно корректную цифровую модель рельефа территории УГС «Западная Березина». Минимальная и максимальная точки рельефа и в фиксированном, и в переменном радиусе точно совпали в значении высоты с теми, что есть в действительности на исследуемой местности. Однако применение при использовании данного метода переменного радиуса показало более корректный результат. Таким образом, при интерполяции методом обратно взвешенных расстояний лучше использовать фиксированный радиус поиска, если входных точек много и они равномерно распределены. При неравномерном же или редком расположении точек более корректный результат будет получен при использовании переменного радиуса поиска. Стоит отметить, что большим недостатком данного способа является значительная по сравнению с другими методами продолжительность интерполяции, что вызвано большим количеством точек и объемом математических расчетов по используемой формуле.

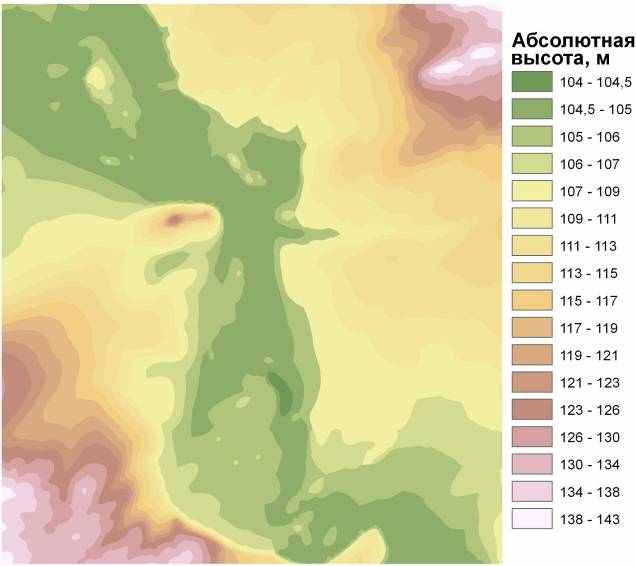
Рис. 3.4. Грид, интерполированный методом IDW

Из двух предложенных методов интерполяции лучший результат был получен при использовании метода обратно взвешенных расстояний. Результат метода сплайн значительно уступает и в визуальном восприятии и в корректности модели. Однако стоит отметить, что сплайн, являясь более простым и быстрым методом, может также успешно применяться при решении более простых задач, например, при составлении картограмм распределения непрерывных явлений. Метод обратно взвешенных расстояний может применяться для более сложных задач, где важна математическая корректность и точность модели.

3.2. Построение геометрической сети постоянных потоков

При создании геометрической сети постоянных водных потоков для целей использования в построении цифровой модели рельефа по методу Topo to Grid важным является то, имеет ли слой гидрографии данные о направлении течения рек. В базе геоданных ArcGIS данный вопрос решается путем создания геометрической сети.

Геометрическая сеть – это математическая модель различных сетевых структур. Концепция геометрической сети позволяет создавать такие сети для моделирования сетей потоков, трубопроводов или проводов, состоящие из ребер и соединений, которые представляют, например, трубы и задвижки в системе водопровода, или провода и переключатели в электросети. Геометрическая сеть дает возможность отслеживать связность сети и проводить анализ потока в сети, а также обеспечивает специальную функциональность редактирования сетей. Главная особенность – это возможность определить правила связности, которые будут характеризовать соединения различных компонентов сети, а также задавать, в каких случаях сетевые объекты, например провода, будут физически разбиваться в местах присоединения к ним других объектов. Таким образом, с помощью геометрической сети можно создать иерархическую систему объектов гидрографии, которая будет содержать данные о направлении течения рек.

Геометрическая сеть представляет собой другой тип топологических отношений между классами пространственных объектов в наборе классов. Геометрическая сеть строится внутри набора классов объектов базы геоданных, а классы пространственных объектов, входящие в данный набор классов, являются источниками данных для геометрической сети. Связность основана на геометрическом совпадении объектов в классах объектов, являющихся источниками для сети [9].

Геометрическая сеть состоит из двух элементов: Edges (ребра) и Junctions (соединения). Edges – ребра – объекты, имеющие длину и по которым осуществляется перемещение потока. Создаются ребра из линейных объектов-источников. Edges подразделяются на простые и комплексные: первые могут касаться только двух соединений, вторые – двух и более. Junctions – соединения – объекты, позволяющие двум или более ребрам касаться друг друга и способствуют перемещению потока по ребрам в сети. Создаются из точечных объектов – источников.

Edges и Junctions топологически соединены друг с другом, ребра касаются друг друга только в соединениях. Поток по ребрам в сети осуществляется через соединения. Так описывается геометрия объектов сети.

Одновременно с геометрической сетью автоматически создается и логическая сеть для описания связности всех объектов. Логическая сеть представляет собой набор таблиц, в которых задается то, как объекты, вовлеченные в геометрическую сеть, соединяются друг с другом. Связность объектов устанавливается в процессе редактирования. Правила связности сети ограничивают типы сетевых предметов, которые могут быть связаны друг с другом, а также число предметов любого конкретного типа, которое может быть связано с предметами другого типа. Правила связности позволяют легко поддерживать целостность сетевых предметов в геометрической сети.

Логическая сеть – это схема, согласно которой функционирует геометрическая сеть. Логическая сеть не имеет реальной геометрии. Ее структура данных позволяет хранить связность геометрической сети и обеспечивает ее быстрое воссоздание. Преимущество логической сети заключается в том, что в ней хранятся реальные связи, которые обеспечивает корректность моделирования сети.

Возможности логической сети позволяют задействовать или нет то или иное ребро или соединение сети, задать вес объекта. Все это дает большие возможности для работы над проектированием и функционированием инженерных систем [7].

Направление потока в геометрической сети задается при помощи набора источников (sourses) и приемников (sinks). В роли источников и приемников выступают соединения junctions, в режиме редактирования необходимо указать его тип (none, sink или sourse).

Все операции, проведенные при создании геометрической сети постоянных водных потоков территории УГС «Западная Березина» можно подразделить на несколько этапов:

Создание необходимых классов объектов;
Создание геометрической сети;
Задание правил связности;
Определение направления течения рек.

На первом этапе создания геометрической сети была произведена оцифровка непосредственно самих рек в линейном классе объектов, а также в точечном классе объектов – начала рек и выход за рамки карты (необходимо для последующего задания направления).

Затем на втором этапе в ArcCatalog производилось построение геометрической сети из уже существующих классов объектов с использованием Мастера создания геометрической сети. В построении сети участвовало два класса объектов, созданных на первом этапе. В опциях Мастера указано, что геометрическая сеть не будет содержать сложные ребра, настроены параметры замыкания, в качестве источников и приемников выступил слой с точками начала рек и их выхода за рамки карты. Вес объектов не задавался, так как при построении цифровой модели рельефа необходимо только направление.

На третьем этапе были заданы правила связности объектов геометрической сети. Приемники и источники были связаны с реками, реки соответственно с приемниками и источниками и соединениями Junctions.

На последнем этапе в режиме редактирования задавалось направление течения рек. В атрибутивной таблице точечного класса объектов с источниками и приемниками, где при создании геометрической сети были автоматически созданы дополнительные поля (Enabled и AncillaryRole), вручную были указаны соответствующие значения (sink или source). Затем с помощью панелей инструментов Geometric Network Editing и Utility Network Analyst в ArcMap было произведено редактирование и отображение направления течения рек.

Рис. 3.5. Параметры Мастера построения геометрической сети

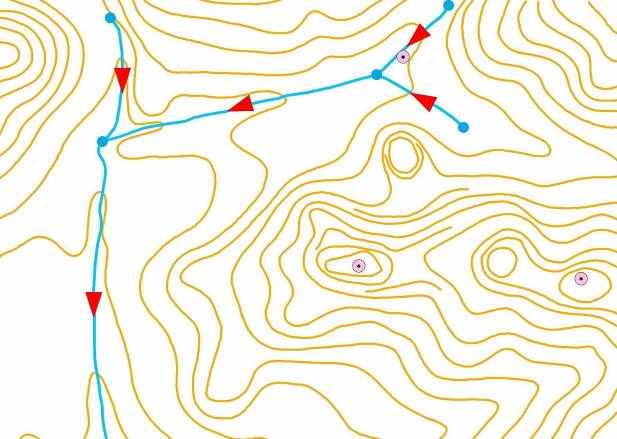
Рис. 3.6. Геометрическая сеть с заданными направлениями течения рек

3.3. Представление гипсометрических поверхностей

в виде модели Topogrid

Практика показывает, что получаемые по картам цифровые модели рельефа зачастую являются некорректными, то есть неправильно воспроизводят рельеф местности в некоторых зонах. К таким зонам можно отнести русла рек с крутыми и обрывистыми берегами. Повышению качества цифровых моделей рельефа должно способствовать максимальное использование присутствующей на карте неявной информации о рельефе. Такую информацию несут в себе элементы карты, описывающие гидрографию: моря, озера, водохранилища, пруды имеют береговую линию одинаковой высоты; линейные реки имеют переменную по высоте береговую линию, монотонно убывающую или возрастающую в зависимости от направления.

Для построения корректной цифровой модели рельефа способом интерполяции в ArcGIS существует функция Topogrid, позволяющая рассчитывать модель рельефа, качество которой многократно превышает качество моделей, получаемых обычными методами интерполяции. В данной функции учитывается не только пространственное положение изолиний рельефа и отметок высот, но и расположение речной сети, закрытых водоемов (озер), локальных понижений рельефа. Есть еще ряд дополнительных опций Topogrid, позволяющих получить хорошо скорректированную гипсометрическую поверхность, пригодную для гидрологического моделирования и учитывающую все особенности рельефа изучаемого региона. Учет гидрографической сети позволяет говорить о гидрологической корректности модели, а использование границ помогает избежать нежелательных краевых эффектов. Особое внимание следует обратить на то, что все реки должны быть оцифрованы с учетом направления течения, что также дает дополнительные возможности для построения цифровой модели рельефа [3, 4].

Необходимые для этого способа интерполяции инструменты входят в Topo to raster модуля 3D Analyst. Инструмент Topo To Raster, который реализует алгоритм Topogrid, представляет собой специализированный инструмент интерполяции для моделирования корректных с точки зрения гидрологии поверхностей, анализировать которые можно с помощью инструментов гидрологии, содержащихся в блоке инструментов Hydrology модуля Spatial Analyst.

Алгоритм интерполяции разработан специально для комплексного использования как данных о рельефе, так и других имеющихся данных. Он сочетает в себе вычислительную эффективность метода обратно взвешенных расстояний и минимизацию кривизны поверхности метода сплайн.

Вода, являясь главной эрозионной силой, определяет форму поверхности большинства ландшафтов. Таким образом, ландшафты представляют собой связанную сеть из локальных понижений (минимумов) и повышений (максимумов), причем замкнутые локальные понижения встречаются в природе довольно редко. Алгоритм Topo to Raster использует данный принцип и накладывает ограничения на интерполяционный процесс, сохраняя целостность гидрографической сети и корректно отображая орографию и гидрографию.

Концепция глобальной гидрографической сети практически исключает в созданной поверхности мелкие бессточные области. Целью моделирования стока в алгоритме Topogrid является удаление неидентифицированных локальных депрессий. Алгоритм удаляет эти понижения, выводя линии стока через низшую точку седловины окружающей области. Следует отметить, что программа действует умеренно при удалении небольших депрессий и не навязывает условия стока в областях, противоречащих имеющимся данным топографии, согласно установленным параметрам допуска. Эти области, как правило, записываются в файлы диагностики, которые можно затем использовать для исправления ошибок. Моделирование стока может быть дополнено линейными данными о водных потоках.

Метод интерполяции Topogrid – единственный метод интерполяции ArcGIS, позволяющий работать с контурами (горизонталями). Горизонтали изначально являются наиболее распространенным способом отображения информации о рельефе. Однако большинство методов интерполяции не могут использовать данный вид представления информации, причем сложности возникают из-за отсутствия информации между горизонталями, что особенно неприемлемо на территориях с низменным рельефом.

Для создания цифровой модели рельефа территории УГС «Западная Березина» при помощи инструмента Topo to raster были использованы оцифрованные слои с горизонталями, отметками рельефа, озерами, границей участка, а также геометрическая сеть с объектами гидрографии, имеющими направление. Для каждого слоя определяется его тип из перечня возможных:

POINTELEVATION – точечный класс объектов, содержащий в себе отметки высот точек. В данном классе объектов отображены отметки высот точек, урезы воды и пункты геодезических сетей. В столбце Field указывается поле со значениями высот, в данном случае поле Н;
CONTOUR – линейный класс объектов, представляет собой изолинии рельефа – горизонтали. В столбце Field также указывается поле со значениями высот горизонталей – Н;
STREAM – линейный класс объектов, который содержит в себе данные по гидрографии. Все дуги для правильности построения модели рельефа должны быть сориентированы вниз по течению;
SINK – точечный класс объектов, который представляет собой набор топографических депрессий – ям, выемок, углублений, понижений и т. д. Инструмент Topo to raster не исключает из анализа поверхности при построении такие мелкие элементы. Также в поле Field можно указать наличие (имя поля с данными) или отсутствие (NONE) данных о высоте или глубине таких элементов рельефа;
BOUNDARY – полигональный класс объектов, содержащий в себе один полигон, который будет служить границей выходного растра. За границами данного объекта интерполяция проводиться не будет. Очень важная опция, так как позволяет строить сложные по форме модели для конкретных районов (административный район, бассейн реки и т. д.);
LAKE – полигональный класс объектов, содержащий в себе информацию о расположении водных объектов (озер, водохранилищ, прудов). Это необходимая опция для гидрологической правильности построения рельефа. В пределах береговой линии водного объекта интерполяция не проводится, а ячейки выходного растра внутри озера приобретают значения высоты ячеек, лежащих снаружи вдоль береговой линии объекта. Таким образом, поверхность водного объекта остается плоской, а высоты – одинаковые по всей поверхности озера.

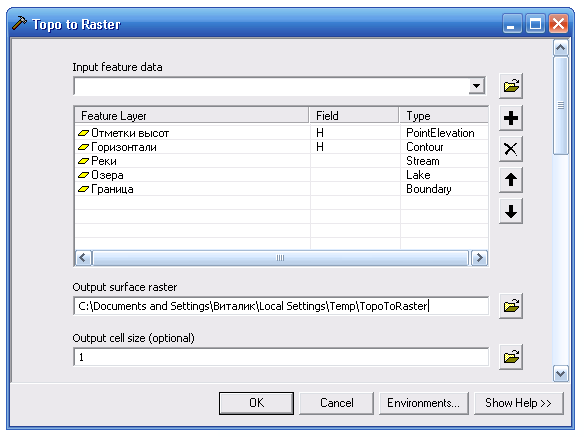
Рис. 3.7. Исходные данные для построения модели Topogrid

Также инструмент Topo to raster имеет большой набор дополнительных параметров интерполяции: размер выходной ячейки (output cell size), выходной экстент(output extent), margin in cells (края ячеек), минимальное и максимальное значение координаты Z, используемое при интерполяции (smallest (largest) z value to be used in interpolation, дренажное давление (drainage enforcement), первичный тип входных данных (primary type of input data), фактор ошибки разделения (maximum number of iterations roughness penalty discretisation error factor), vertical standard error и др. Все параметры, используемые при интерполяции, были определены опытным путем [7].

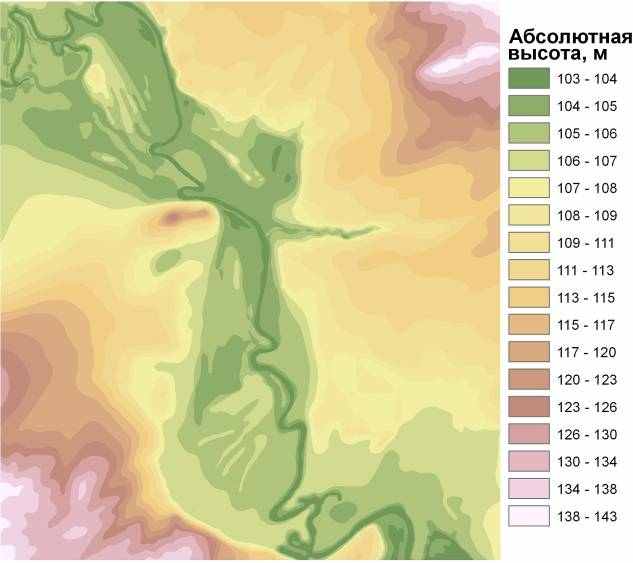
Рис. 3.8. Грид, интерполированный методом Topogrid

В результате интерполяции бала построена цифровая модель рельефа территории УГС «Западная Березина» с учетом гидрографической сети. Гидрологическая согласованность позволяет широко использовать данную модель для всевозможных автоматизированных расчетов, связанных с гидрологией, геоморфологией, агрохимией и другими науками. Однако необходимо отметить, что гидрологическая согласованность достигается все же за счет некоторых отступлений от имеющихся данных, поэтому применять данный способ интерполяции необходимо в зависимости от конкретных задач.

3.4. Представление гипсометрических поверхностей

в виде модели TIN

Термин нерегулярная триангуляционная сеть (triangulated irregular network) точно описывает свойства TIN. Треугольники построены по трем точкам, которые нерегулярно распределены. Представление TIN моделирует поверхность на наборе точек, по которым разбиты треугольники, или иными словами, по которым выполнена триангуляция. Каждый треугольник содержит топологическую информацию о соседних треугольниках, образуя, таким образом, сеть.

«Нерегулярная» определяет ключевое преимущество TIN в моделировании поверхности – точки могут быть взяты с переменной плотностью для моделирования участков, где рельеф поверхности резко меняется.

«Триангуляционная» указывает на способ построения оптимизированного набора треугольников по набору точек. Треугольники хорошо интерпретируют локальную часть поверхности, так как три точки со значениями координаты Z однозначно определяют плоскость в трехмерном пространстве.

«Сеть» отражает топологическую структуру, которая присуща TIN. Каждый треугольник содержит топологическую информацию о соседних треугольниках, образуя, таким образом, сеть. Такая структура делает возможным сложный анализ поверхности и, кроме того, компактное представление поверхности.

TIN является представлением поверхности с единственными z-значениями для каждой точки. Интересное свойство представления данных TIN состоит в том, что оно изображает точки в трехмерном пространстве, но топологическая сеть граней ограничивается двумя измерениями. По этой причине, иногда говорят, что представление данных TIN моделирует пространство размерности "два с половиной". Это описание не совсем точно, но оно фокусирует внимание на том, что поверхности имеют точки, измеренные в трех измерениях, при этом каждая точка может обладать только одним z-значением. Следовательно, в TIN в каждой точке может интерполироваться только одно z-значение. Поэтому некоторый недостаток TIN состоит в том, что нет возможности моделировать достаточно редкие случаи с отрицательными углами, типа нависающих утесов, пещер, гротов и других полостей.

TIN строится по массовым точкам, то есть, точкам с высотами, полученными из разнообразных источников. По набору исходных точек выполняется триангуляция. TIN обычно составляют с помощью фотограмметрических инструментов, измеряя высоты по стереопарам аэрофотоснимков, точно совмещенных в стереомодели. TIN также создают по данным геодезических съемок, по оцифрованным изогипсам, растрам со значениями координаты Z, наборам точек в файлах или базах данных, или оперируя другими TIN.

Модель TIN состоит из узлов, ребер, треугольников, полигонов и топологии. В TIN треугольники называют гранями (faces), точки становятся узлами (nodes) граней, а линии граней называют ребрами (edges).

Узел – node – это фундаментальная строительная единица TIN. Они формируются из точек и вершин линий, содержащихся в исходных данных. Каждый узел соединен в единую сеть треугольников и должен иметь Z-значение.

Каждый узел соединен со своими ближайшими соседями посредством ребер – edges – для формирования треугольников согласно критериям Делоне. Каждое ребро имеет два узла, но узел при этом может иметь два и более ребер. Так как все узлы имеют Z-значение, то можно рассчитать уклон ребра.

Грань – face – показывает положение участка поверхности TIN. Каждая грань TIN является частью плоскости в трехмерном пространстве. Все грани в TIN точно сходятся со своими соседями в каждом узле и вдоль каждой грани. Грани не могут пересекать друг друга. X, Y и Z значения узлов могут быть использованы для расчета данных о грани – ее площади, уклоне. Так как грани формируют поверхность TIN, то очень важной является правильность выбора вершин треугольника.

TIN – топологическая структура данных, управляющая информацией об узлах, которые входят в каждый треугольник, и соседях каждого треугольника. Треугольники всегда имеют три узла и обычно имеют три соседних треугольника. Треугольники на внешней границе TIN могут иметь одного или двух соседей. Для каждого треугольника TIN сохраняет следующую информацию: номер треугольника; номера пограничных треугольников; номера трех узлов; X и Y координаты каждого узла; значение координаты Z для каждого узла; тип каждого ребра (жесткий или мягкий). Также TIN содержит список всех узлов каркаса модели и информацию о проекции и единицах измерения.

При заданном наборе точек, можно построить много вариантов разбиения на треугольники. В ArcGIS, чтобы поверхность оптимально моделировалась треугольниками, применяется алгоритм, известный как триангуляция Делоне. Определение триангуляции Делоне указывает, что любая окружность, проведенная через три узла в треугольнике, не будет включать никакого другого узла. Триангуляция Делоне обладает наибольшей суммой минимальных углов всех своих треугольников, а также наименьшей суммой радиусов описанных вокруг треугольников окружностей среди всех возможных сеток на той же системе точек. Иными словами, основной принцип этого алгоритма заключается в том, чтобы построить треугольники, которые все вместе будут по возможности близкими к равносторонним фигурам. Тогда, в большей близости к известным исходным точкам будет выполняться интерполяция высот в новые точки.

Моделирование объектов поверхности в TIN происходит с помощью таких классов объектов, как элементы топографии, точки с высотами, вершины, водотоки и гребни. Точки с высотами образуют основные вводные данные в TIN и задают общую форму поверхности. При необходимости, их можно снять с горизонталей, но лучше использовать точки, измеренные фотограмметрическим способом, так как оператор может лучше визуально выбрать именно те точки, которые лучше отражают пластику рельефа. Затем добавляют водотоки, гребни и прочие подобные объекты, чтобы уточнить модель поверхности и выделить структурные черты рельефа. Эти объекты сохраняются в TIN и повышают точность модели.

TIN создают по объектам поверхности, которые можно классифицировать по форме и размерности: точки, линии и области. Эти объекты поверхности называют массовыми точками, линиями перегиба и полигонами, и они могут быть введены из самых разных источников данных. Далее они станут топологической сетью узлов, ребер и граней. При формировании TIN массовые точки, линии перегиба и полигоны последовательно добавляются для создания и усовершенствования поверхности модели. В любой момент можно добавить дополнительные элементы, чтобы улучшить модель.

Массовые точки (masspoints) представляют точки, в которых измерено значение Z. Линии перегиба (breaklines) – линейные объекты, которые соответствуют естественным объектам – водотокам и гребням, или искусственным объектам, например автомагистрали. Жесткие линии перегиба (hard breaklines) отражают разрыв в уклоне поверхности, например, линию водотока. Мягкие линии перегиба (soft breaklines) позволяют прибавить ребра, чтобы показать линейные объекты, не влияющие на изменение уклона. Например, можно прибавить на модель поверхности след дороги, которая слабо сказывается на локальной крутизне склона, или границу изучаемой территории. Полигоны представляют площадные объекты с постоянной высотой (озера, океаны) и используются, чтобы разграничить проектную границу, отсечь или стереть части триангуляции. Полигоны могут также быть разделены на жесткие и мягкие.

TIN поддерживают разнообразные виды анализа поверхности, такие как вычисления высоты, крутизны и экспозиции склона, выполнение вычислений объемов, создание профилей по трассе линии, анализ зон видимости, построение изолиний поверхности [5, 6].

Построение цифровой модели рельефа территории УГС «Западная Березина» способом TIN производилось с использованием четырех классов объектов. Слой с отметками высот указывался как mass points со значениями координаты Z по полю Н; слой горизонтали указывался как hard lines с полем значений высот Н; слой с реками указывался как hard lines без значений высот; слой с озерами указывался как hard replace.

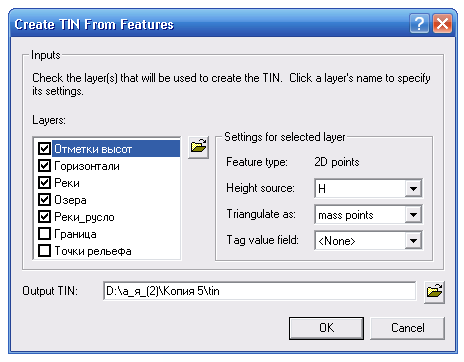
Рис. 3.9. Параметры построения TIN

В результате был построен довольно корректный TIN территории УГС «Западная Березина», были соблюдены расположения рек и озер. Однако стоит отметить, что, при большой точности, TIN сильно уступает всем методам растровой интерполяции в плане наглядности. Строится TIN гораздо быстрее всех остальных методов, однако для корректного отображения требуется более мощный компьютер, чем при работе с цифровыми моделями рельефа на основе гридов.

Таким образом, в конце можно сделать вывод, что метод создания цифровой модели рельефа необходимо выбирать в первую очередь в зависимости от поставленных задач, затем – от имеющихся данных, а уже потом все остальное.

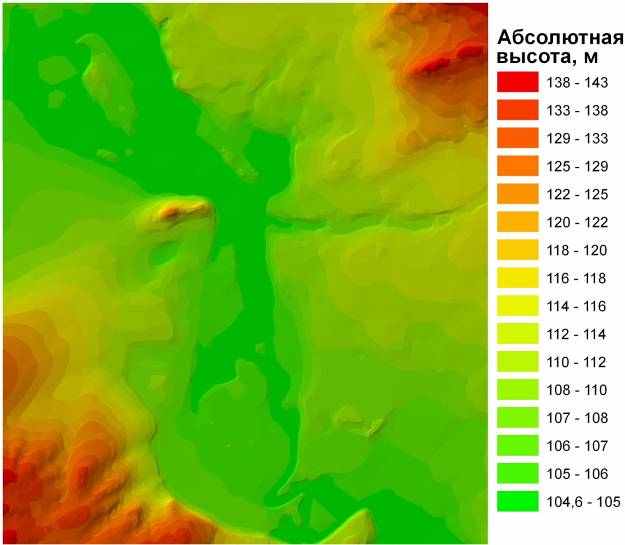
Рис. 3.10. Модель TIN

Модели TIN менее широко распространены, чем грид-модели, так как их создание оказывается более дорогим, что связано с необходимостью наличия высокоточных исходных данных для построения корректных моделей. В то время как грид-модели более просты и удобны для использования, требуют меньших затрат и меньшей производительности компьютеров для работ с ними.

TIN-модели более подходят для решения крупномасштабных задач на небольших территориях, где используются высокоточные данные. Так как в такой модели нет изменений исходных данных, то возможно широкое применение TIN в проектных инженерных приложениях для перспективного отображения строений на рельефе, вычисления объемов земельных выемок и иных задач. Модели на основе гридов более подходят для целей мелкомасштабного отображения, идентификации водосборных бассейнов, анализ зон затопления, моделирования рельефа поверхности, распространения загрязнений, геохимических, гидрологических, климатических и многих других данных.

Blog