Метод Лагранжа широко используется в различных областях экономической теории для решения задач на нахождение условного экстремума

Вид материала

Содержание

1. Анализ равновесия на дуопольном рынке: модель А.Курно
2. Анализ равновесия по Штекельбергу и по сговору

Подобный материал:

Чахоян В.А.

Об одном применении метода Лагранжа

Метод Лагранжа широко используется в различных областях экономической теории для решения задач на нахождение условного экстремума. С одной стороны, экономический образ мышления, нацеленный на поиск рациональных решений, приводит экономистов к описанию исследуемого явления в виде задачи на нахождение условного экстремума. С другой - математическое образование (в частности, знание метода Лагранжа в аналитической и геометрической формах) позволяет увидеть и глубже понять экономические взаимосвязи, по - новому их интерпретировать.

Приведем пример анализа известных моделей равновесия на дуопольном рынке, основанного на применении основных математических понятий теории экстремума (условного и безусловного) функций нескольких переменных и их содержательной интерпретации. Приведенный ниже пример применения метода Лагранжа для анализа равновесия на дуопольном рынке еще раз говорит о том, что математическое образование должно составлять неотъемлемую часть культурного багажа экономиста, а основной целью этого образования должно быть не формальное изучение отдельных математических методов, а развитие способа мышления, “который заставляет человека с математическим образованием думать о всех реалиях окружающего мира с помощью (сознательного или бессознательного) мягкого математического моделирования”.¹⁾

1. Анализ равновесия на дуопольном рынке: модель А.Курно

Рассмотрим ситуацию, когда на рынке некоторого однородного продукта взаимодействуют только две конкурирующие фирмы (дуопольный рынок).В этом случае фирмы принимая решения, ориентируются не только на условия спроса и свои издержки, но и на действия конкурирующей фирмы. Существует несколько моделей, описывающих как фирма-дуополист определяет свой равновесный объем выпуска. Рассмотрим самую простую из них, соответствующую подходу, предложенному французским экономистом А.Курно (модель Курно).

1)Арнольд В.И.,”Жесткие” и “мягкие” математические модели, доклад на научно-практическом семинаре”Аналитика в государственных учреждениях”, М, 1997.

Основное предположение модели Курно о поведении конкурента говорит о том, что каждая из фирм, принимая решение, действует так, как будто не ожидает от своего конкурента изменения объема выпуска, если даже сама сделает это. Традиционно в учебниках по экономической теории после формулирования данного предположения выписываются функции прибылей фирм, исследуются необходимые условия их максимизации, из которых выводятся линии реакции фирм и делается вывод о том, что равновесие на рынке определяется точкой пересечения линий реакции.

По нашему мнению, математическое описание модели будет более корректным, а экономическая интерпретация результатов анализа равновесия более содержательной, если рассматривать принятие решения каждой из фирм как решение задачи на нахождение условного максимума функции прибыли фирмы. Роль условия при этом играет формализованное описание сформулированного выше предположения о поведении конкурента. Приведем описание модели дуополии Курно с позиции предложенного подхода.

Обозначим через Х₁объем выпуска фирмы 1, через Х₂ – объем выпуска фирмы 2. Тогда объем предложенной на рынок продукции Х = Х₁ + Х₂. Допустим функция спроса на продукцию дуополии линейная: Р(Х) = b - aX .

Обозначим через Z₁(Х₁) функцию издержек фирмы 1, через Z₂(Х₂) - функцию издержек фирмы 2. Допустим, что функции издержек фирм также линейные: Z₁ = cX₁ + d₁, Z₂ = cX₂+ d₂.

Прибыль каждой из фирм может быть представлена как разность между общей выручкой фирмы и издержками: PR₁ = TR₁ – Z_1,PR₂ = TR₂ – Z_2,где TR₁и TR₂ - величина выручки для фирмы 1 и фирмы 2, соответственно.

В соответствии с предположением Курно, фирма 1 определяет объем выпуска, обеспечивающий ей максимальную прибыль при условии, что объем фирмы 2 равен некоторой величине С₂ = const. Аналогично фирма 2 определяет объем выпуска, обеспечивающий ей максимальную прибыль при условии, что объем фирмы 1 равен некоторой величине С₁ = const.

Тогда задача максимизации прибыли фирмой 1 при предположении, что объем выпуска фирмы 2 равен С2, формулируется следующим образом:

PR₁(Х₁,Х₂)= (b - aX₁ – aX₂)X₁ – cX₁ - d₁ max (1)

Х₂= С₂ (2)

Задача максимизации прибыли фирмой 2 при предположении, что объем выпуска фирмы 1 равен С₁ формулируется аналогично:

PR₂(Х₁,Х₂) = (b – aX₁ – aX₂)X₂ – cX₂ - d₂ max (3)

Х₁= С₁ (4)

Задачи (1), (2) и (3), (4) являются задачами на нахождение условного максимума. Для их решения можно применить метод Лагранжа. На примере фирмы 1 рассмотрим как можно найти решение задачи (1), (2) и приведем геометрическую интерпретацию этого решения.

Согласно необходимому условию локального условного экстремума функции (1) при наличии ограничения (2) в геометрической форме, если Х* = (Х₁*, Х₂*) – точка условного локального максимума, то линия уровня функции прибыли, соответствующая величине прибыли в точке Х*: PR₁(Х₁,Х₂)=PR₁(Х₁*,Х₂*)= PR₁* ( изопрофита фирмы 1, проходящая через точку Х* ) и линия уровня функции

G(X₁, X₂) = С₂ – X₂, содержащая точку (Х₁*, Х₂*), касаются в этой точке. Это означает, что градиент функции прибыли (gradPR₁) и градиент функции-условия

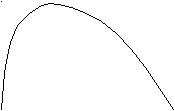
G(X₁, X₂) (gradG) коллинеарны в точке условного максимума Х*.Графически эта ситуация изображена на рис. 1 для некоторой точки локального максимума Х* = (Х₁*, С₂).

Х₂

С₂ Х*

gradG

gradPR₁ PR₁*

Х₁

Рис.1

Очевидно, что прямая Х₂ = С₂ = const. проходит через точку Х* и является нулевой линией уровня функции G (X₁, X₂) = C₂ – X₂. Что касается изопрофиты PR₁* фирмы 1 (линии уровня прибыли фирмы 1), проходящей через точку Х*, то ее графическое конфигурация нуждается в обосновании. Покажем, что изопрофита фирмы 1, при введенных предположениях о линейности функции спроса на продукцию дуополии и функции издержек фирмы 1, имеет именно такую форму.

PR₁(Х₁, Х₂)= (b - aX₁ – aX₂)X₁ – cX₁ - d₁ = (b – c)X₁- aX₁² – aX₁X₂ – d₁. (5)

Построим нулевую изопрофиту функции прибыли фирмы 1, т.е. PR₁(Х₁, Х₂) = 0 (будем обозначать ее PR₁⁰). В соответствии с (5) Х₂ можно выразить в явном виде как следующую функцию от Х₁:

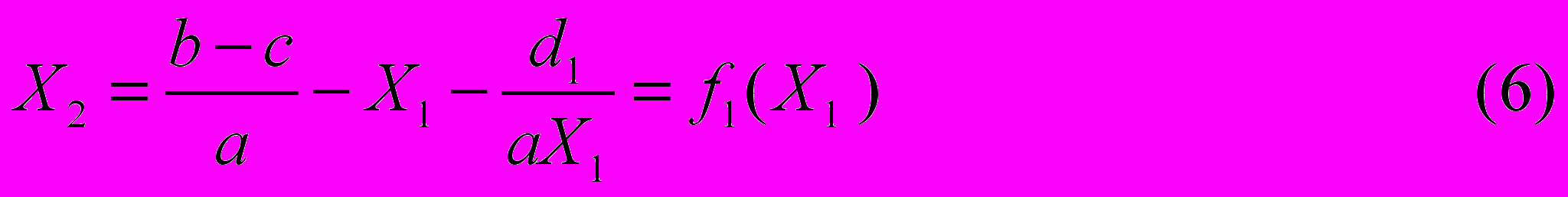
Для построения графика функции f₁(X₁) проведем необходимое исследование.

Функция f₁(X₁) определена для всех неотрицательных объемов выпуска фирмы 1: Х₁ > 0.
Она достигает максимума при Х₁⁰ = +√(d₁/a) (dX₂/dX₁ = 0 при Х₁⁰ = +√(d₁/a)).

При этом Х₂⁰ = (b-c)/a - 2√(d₁/a). Наличие максимума функции f₁(X₁) в точке Х₁⁰ подтверждает отрицательность второй производной Х₂ по Х₁(см.3).

Последнее неравенство, кроме того, говорит о выпуклости вверх графика нулевой изопрофиты фирмы 1.

Нули функции f₁(X₁) могут быть найдены как решение уравнения (см.(6)):

a Х₁² – (b - c)Х₁ + d₁ = 0.

5) Далее можно показать, что график изопрофиты фирмы 1 (функция (6)) имеет вертикальную и наклонную асимптоты. Вертикальной асимптотой является вертикальная прямая Х₁= 0. Наклонная асимптота описывается уравнением:

Х

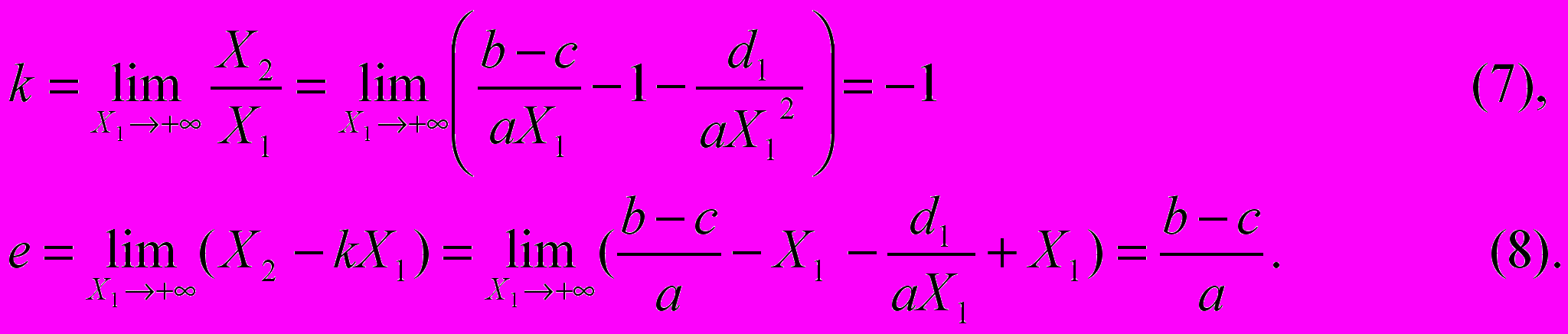
₂= - Х₁+ (b – c)/a. Действительно, если уравнение наклонной асимптоты записать в виде Х₂ = kX₁ + e, то коэффициенты k и e находятся как пределы следующих соотношений:

На основании проведенного анализа функции (6) можно изобразить графически изопрофиту фирмы 1 PR₁⁰,соответствующую нулевому значению прибыли (см.рис.2).

Рассмотрим градиенты функции прибыли фирмы 1 (gradPR₁(Х₁,Х₂)) и функции-условия G(X₁, X₂) (gradG(X₁, X₂)) в точке максимума функции f₁(X₁), то есть в точке Х⁰ = (Х₁⁰, Х₂⁰) .

Имеем: gradPR₁(Х₁,Х₂) = [(b-c) – 2aX₁ – aX₂; - aX₁]. В точке Х⁰

gradPR₁(Х₁⁰, Х₂⁰) = (0; - √(d₁/a)). (9)

X₂

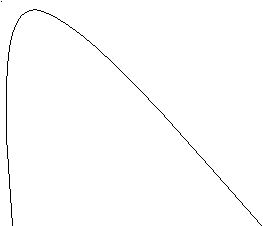PR₁^

(b-c)/a-2√(d₁/a) X⁰

PR₁⁰

PR₁⁺

X₁

√(d₁/a)

Рис.2

Градиент функции-условия имеет одинаковые координаты в любой точке пространства выпусков: gradG(X₁, X₂) = (0; -1). (10 )

Сравнение градиентов функций PR₁(Х₁,Х₂) и G(X₁, X₂) в точке Х⁰ показывает, что gradPR₁(Х₁⁰, Х₂⁰) =  gradG(Х₁⁰, Х₂⁰), где  = √(d₁/a).

На рис.2 изображены: изопрофита фирмы1, соответствующая нулевой прибыли - PR₁⁰ , а также изопрофиты PR₁^ и PR₁⁺. Согласно (9) градиент функции прибыли направлен вниз и, следовательно, прибыль фирмы растет (становится положительной) при перемещении изопрофиты PR₁⁰ вниз до положения, например PR₁⁺ и уменьшается (становится отрицательной) при перемещении изопрофиты PR₁⁰ вверх, например до положения PR₁^^-.

Приведем аналитическое решение задач (1), (2) и (3), (4) и геометрическую интерпретацию равновесия по Курно на дуопольном рынке. Обозначим через L(Х₁,Х₂,)функцию Лагранжа для для задачи (1), (2), и заменим решение этой задачи поиском точки максимума функции L(Х₁,Х₂,).

L(Х₁,Х₂,) = PR₁(Х₁,Х₂) + G(X₁, X₂)  max или

L

(Х₁,Х₂,) = (b - aX₁ – aX₂)X₁ – cX₁ - d₁ + (C₂ – X₂)  max

Если фирма 1 предполагает, что объем выпуска фирмы 2 равен С₂ , то решением системы (11) – (13) будут:Х₁= (b - c)/2a – (1/2)C₂, X₂ = C₂,  = (c – b +2aC₂)/2. Приведем экономическую интерпретацию уравнений (11) – (13).

Уравнение (11). Если предполагаемый объем производства фирмы 2 изменяется, то оптимальный объем выпуска (максимизирующий прибыль) фирмы 1 также меняется и может быть найден из уравнения (11), которое описывает зависимость оптимальных объемов выпуска фирмы 1 от предполагаемого объема выпуска фирмы 2. Уравнению (11) соответствует линия в пространстве Х₁, 0, X₂, которая называется линией реакции фирмы 1.

Уравнение (12). Легко показать, что, если построить косвенную функцию прибыли для фирмы 1 PR₁* = PR₁(a,b,c,d,C₂) т.е. выразить максимальную прибыль фирмы 1 как функцию от параметров исходных функций спроса и издержек и предполагаемого объема выпуска фирмы 2, то частная производная функции прибыли PR₁*/C₂ = . Следовательно,  может интерпретироваться в данной задаче как предельная прибыльность предполагаемого дополнительного выпуска фирмы 2. Согласно (12) скорость изменения прибыли фирмы 1 пропорциональна ее объему производства с коэффициентом (-a).

Уравнение (13) задает конкретную количественную оценку предполагаемого объема производства фирмой- конкурентом.

Теперь можно установить зависимость между изопрофитой фирмы 1 и ее линией реакции. Покажем, что вершины изопрофит фирмы 1 лежат на ее линии реакции, т.е. изопрофиты “как бы висят” на линии реакции Курно своей фирмы.

Выпишем уравнение изопрофиты фирмы 1, соответствующее значению прибыли, равному PR₁. Согласно (5) имеем:

PR₁(Х₁, Х₂)= (b – c)X₁ - aX₁² – aX₁X₂ – d₁  PR₁. (14)

Тогда

Максимум функции X₂ достигается при Х₁^PR = √(d/a) и равняется:

X₂^PR = (b - c)/a - 2√(d/a). Покажем, что, если фирма 1 предполагает, что объем производства фирмы 2 равен X₂^PR = (b - c)/a - 2√(d/a), то объем выпуска фирмы1

в соответствии с линией реакции фирмы 1 (11) равен Х₁^PR = √(d/a).

Действительно,

Проведенный анализ позволяет представить графически результаты принятия решений об объемах выпуска фирмой 1 и фирмой 2 (см. рис.3 и 4).

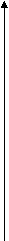
X₂ X₂

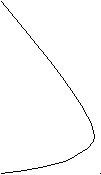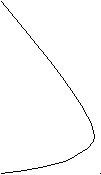(b-c)/a

Ф1 С₁ – Х₁ = 0

PR₂

С₂С₂ – Х₂ = 0 (b-c)/2a

PR₁ Ф2

X₁

(b-c)/2a С₁ (b-c)/a

Рис.3 Рис.4

Фирма 1 предполагает, что фирма 2 Фирма 2 предполагает, что фирма 1

произведет Х₂=С₂единиц продукции произведет Х₁=С₁единиц продукции

Равновесие на дуопольном рынке, согласно модели Курно имеет место, если фирмы“угадали”предполагаемые объемы производства друг друга.В этом случае точка равновесия (обозначим ее Cu) имеет координаты Х₁^Cu= С₁; Х₂^Cu= С₂. При этом вершина изопрофиты фирмы 1(обозначим ее PR₁^Cu), соответствующая значению функции прибыли в этой точке, касается прямой Х₂^Cu= С₂, а вершина изопрофиты фирмы 2 (обозначим ее PR₂^Cu) касается прямой Х₁^Cu= С_1.

Следовательно, обе изопрофиты проходят через точку Cu = (С₁; С₂) и их вершины пересекаются в этой точке. Учитывая, что вершины изопрофит лежат на линиях реакции фирм, можно утверждать, что точка равновесия Курно является точкой пересечения линий реакций фирм 1 и 2.

Тогда легко найти координаты этой точки как решение следующей системы уравнений с двумя неизвестными:

Х₁= (b-c)/2a – (1/2)Х₂,

X₂.= (b-c)/2a – (1/2)X₁

В результате несложных алгебраических преобразований имеем:

Х₁^Cu= (b – c)/3a , Х₁^Cu= (b – c)/3a (Х^Cu = 2(b – c)/3a , p^Cu = (b + 2c)/3).

X₂

Ф1

PR₂^Cu

C₂ Сu

PR₁^Cu Ф2

С₁Х₁

Рис.5

Количественные характеристики равновесия по Курно такие как цена продукции, прибыль каждой из фирм и суммарная прибыль приведены в таблице 1 (см. стр. ). Графическая интерпретация равновесия по Курно в терминах изопрофит приведена на рис.5.

2. Анализ равновесия по Штекельбергу и по сговору

Рассмотрим модель равновесия по Штекельбергу, когда лидером является одна из фирм, допустим фирма 1. Согласно основному предположению этой модели фирма-лидер, принимая решение об объеме выпуска, считает, что другая фирма ориентируется на объем выпуска фирмы-лидера. Последнее означает, что фирма 2 ведет себя согласно линии реакции Курно.

В этом случае задача максимизации прибыли фирмой-лидером может быть сформулирована как задача определения условного максимума функции прибыли. Условие описывается функцией G(X₁, X₂) = (b - c)/2a – (1/2)X₁ – X₂, где X₂= (b - c)/2a – (1/2)X₁ – линия реакции фирмы 2.

Приведем математическую формулировку этой задачи:

PR₁(Х₁,X₂)= (b - aX₁ – aX₂)X₁ – cX₁ - d₁ max (16)

G(X₁,X₂) = (b - c)/2a– (1/2)X₁ - X₂ = 0 (17)

Анализ решения задачи на условный экстремум, проведенный в параграфе 1, позволяет легко воспроизвести геометрическую интерпретацию решения (см. рис.6). Изопрофита PR₁^S¹фирмы 1(лидера) касается линии реакции фирмы 2 в точке равновесия по Штекельбергу S₁. Сравнение расположения изопрофит PR₁^S¹ и PR₂^S¹ позволяет сделать вывод о том, что прибыль фирмы 1 существенно больше чем прибыль фирмы 2. Аналитическое решение задачи методом Лагранжа позволяет увидеть, что изменяется зависимость между оптимальным объемом выпуска фирмы 1 и объемом выпуска фирмы 2, т.е. линия реакции

X₂

PR₂^S1

Ф1^S1

S₁ Ф2

PR₁^S1

X₁

Рис. 6

фирмы 1 изменяет свое положение (Ф1^S¹).Уравнение новой линии реакции имеет вид:

а координаты точки равновесия определяются как решение системы уравнений (17) и (18), что соответствует точке S₁- пересечения линий реакций Ф1^S¹ и Ф2 на рис.6.

Точка S₁ имеет координаты: Х₁^S1= (b – c)/2a , Х₂^S1= (b – c)/4a (Х^S1= 3(b – c)/4a, p^S1 = (b +3c)/4). Прибыли фирм в состоянии равновесия S₁равны:

Сравнение графических иллюстраций равновесия по Курно и по Штекельбергу позволяет увидеть, что фирма 1 увеличивает свою прибыль (изопрофита фирмы 1 опустилась вниз), а прибыль фирмы 2 уменьшается (изопрофита фирмы 2 сместилась вправо вдоль линии реакции фирмы 2). Аналогичную картинку можно получить и для ситуации, когда лидером является фирма 2.

Анализ графического изображения равновесия позволяет сделать вывод о наличии возможностей увеличения прибылей фирмами. Изопрофиты фирм пересекаются. Следовательно, можно двигать их вниз по линиям реакции, пока останется лишь одна общая точка.

Допустим фирма 1 стремится увеличить свою прибыль по сравнению с величиной PR₁^S¹ . Анализ ситуации, представленной на рис.6 показывает, что такие возможности существуют. Если фирма 1 предполагает, что фирма 2 согласится на получение такой же прибыли, как и в равновесии по Штекельбергу (PR₂^S¹), то она определит свой объем выпуска как решение следующей задачи на нахождение условного экстремума:

PR₁(Х₁ X₂)= (b – c)X₁ - aX₁² – aX₁X₂ – d₁  max (19)

PR₂(Х₁ X₂) = (PR₂^S¹) (20)

Графическое решение задачи (19), (20) легко просматривается на рис. 6. Для того, чтобы найти точку максимума прибыли фирмы 1 следует двигать изопрофиту PR₁^S¹ вниз до тех пор, пока она не коснется изопрофиты фирмы 2 - PR₂^S¹(см. рис.7). Точка k₁ – точка касания вышеназванных изопрофит. Координаты точки к1 могут быть найдены как решение задачи на определение

X₂

PR₂^S¹

Ф1 Х₁ = 3Х₂

PR₁^k¹

S₁ Ф2

^К1 PR₁^S1

X₁

Рис. 7

безусловного максимума следующей функции Лагранжа:

L(Х₁,Х₂,) = (b – c)X₁- aX₁² – aX₁X₂ – d₁+ (PR₂^S1– (b – c)X₂ + aX₂² + aX₁X₂ – d₂).

Х₁^к1 = 3(b - c)/8a, Х₂^к1 = (b - c)/8a (Х^к1 = (b - c)/2a, p^k¹ = (b + c)/2).

П

рибыль фирмы 1 при объеме выпуска Х₁^к1 равняется:

Можно показать, что такую же величину прибыли фирма 1 может получить при сговоре с фирмой 2, если суммарный, максимизирующий общую прибыль объем выпуска (Х), будет поделен в отношении 3 к 1 в пользу фирмы 1 (Х₁ = 3Х₂). В этом случае фирма 1 решает задачу максимизации прибыли при условии, что Х₁ = 3Х₂:

PR₁(Х₁ X₂)= (b – c)X₁ - aX₁² – aX₁X₂ – d₁  max (19)

Х₁ - 3Х₂ = 0 (21)

Графическим решением задачи (19), (21) является точка к1 (см. рис. 7), которая является точкой касания изопрофиты PR^k¹ и нулевой линии уровня функции условия G(X₁,X₂) = Х₁ - 3Х₂ = 0. Решение задачи (19), (21) методом Лагранжа позволяет убедиться, что Х₁^к1 = 3(b - c)/8a и Х₂^к1 = (b - c)/8a и , следовательно, изопрофиты максимальной прибыли задач (19),(20) и (19), (21) совпадают.

Если рассмотреть ситуацию, когда лидером будет фирма 2, то решая задачу аналогичную задаче (16), (17), можно вывести новую линию реакции этой фирмы:

Тогда фирма 1, предполагая, что фирма 2 ведет себя как лидер (в соответствии с линией реакции (22)), может определить возможный объем выпуска как решение следующей задачи на условный экстремум:

PR₁(Х₁ X₂)= (b – c)X₁ - aX₁² – aX₁X₂ – d₁  max (19)

Х₂ = 2 (b – c)/3a – (2/3)X₁ (23)

Решением задачи (19), (23) явлются следующие объем выпуска и прибыль фирмы 1: Х₁ = (b – c)/2a и PR₁ = (b – c)²/12a. Такую же величину прибыли фирма 1 получит и в случае сговора с фирмой 2 при условии, что Х₂= 2Х₁(см.таблицу 1 на стр.14,15). На рис. 9 изопрофита, соответствующая данному значению прибыли фирмы 1 проходит через точки L₁ и К₁, которые являются решениями задачи (19), (23) и сформулированной ниже задачи (19), (24).

PR₁(Х₁ X₂)= (b – c)X₁ - aX₁² – aX₁X₂ – d₁  max (19)

Х₂= 2Х₁ (24)

Остановимся подробнее на ситуации сговора двух фирм. В этом случае суммарный объем производства фирм определяется как решение задачи:

PR₁(Х₁ X₂) + PR₂(Х₁ X₂)  max (25)

Обозначим суммарный объем выпуска, максимизирующий суммарную прибыль фирм Х^к. Легко показать, что Х^к = (b - c)/2a. Учитывая, что Х^к = Х₁^к + Х₂^к, получаем уравнение контрактной (договорной) линии (см. (26)), на которой расположены различные комбинации объемов выпуска фирм, сумма которых равняется (b - c)/2a и при которых суммарная прибыль фирм максимальна при сложившемся спросе на продукцию фирм и имеющихся функциях издержек.

Следовательно, имеем: Х₁^к + Х₂^к = (b - c)/2a. (26)

Общий объем производства для сговорившихся фирм определен. Проблема в том, как поделят его между собой сговорившиеся и одновременно конкурирующие фирмы. Традиционно в экономической литературе рассматривается ситуация, когда фирмы делят объем выпуска пополам. Она называется равновесием по сговору. Эту ситуацию также можно описать в терминах задачи на условный максимум, а именно:

Фирма 1: PR₁(Х₁,X₂) = (b – c)X₁- aX₁² – aX₁X₂ – d₁ max (19)

X₁ = X₂(27)

Фирма 2: PR₂(Х₁,X₂) = (b – c)X₂ - aX₂² - aX₁X₂ – d₂  max (28)

X₂ = X₁(27)

Геометрическая интерпретация решения задач (19), (27) и (28), (27) позволяет понять почему достигаемая в этой ситуации прибыль максимально возможная для каждой из фирм как равноправных конкурентов (см. рис.8). Более того, можно убедиться, что прибыли фирм в состоянии равновесия по сговору при условии, что X₂ = X₁совпадают с прибылями фирм в состоянии равновесия по Штекельбергу.

Обозначим точку равновесия по сговору при X₂ = X₁ через К. Тогда К = (Х₁^К, Х₂^К) = ((b-c)/4a; (b-c)/4a) , р^К = (b + c)/2a. Прибыли фирм в точке К равны:

Легко убедиться, что прибыли фирмы 1 и фирмы 2 в состоянии равновесия по сговору (в точке К) совпадают с их прибылями в состоянии равновесия S₁(для фирмы 1) и в состоянии равновесия S₂ (для фирмы 2). Графическая иллюстрация равновесия по сговору приведена на рис.8.

Х₂

PR₂^K X₂ = X₁

S₂

S₁

K PR₁^K

Рис.8 X₁

В общем случае фирмы могут поделить суммарный объем выпуска Х^к = (b-c)/2a в любой пропорции. Допустим X₂ = kX₁, где k > 0. В этом случае каждая из фирм, принимая решение об объеме выпуска, решает следующую задачу на условный экстремум:

Фирма 1: PR₁(Х₁,X₂) = (b – c)X₁- aX₁² – aX₁X₂ – d₁ max (19)

X₁ =1/ kX₂(30)

Фирма 2: PR₂(Х₁,X₂) = (b – c)X₂ - aX₂² - aX₁X₂ – d₂  max (28)

X₂ = kX₁(31)

Согласно геометрической интерпретации решения задач (19), (30) и (28), (31) изопрофиты фирм будут касаться в точке пересечения контрактной линии (26) и луча, задаваемого уравнениями (30) или (31). Приведем графическую интерпретацию решения задачи (19), (30) для фирмы 1 при к = 1/2 , 1 и 2 (см. рис. 9).

Х2

Х₂ = 2Х₁ Х₂ = Х₁

Ф2^н

(b – c)/2a L₁ Х₂ = (1/2)Х₁

K₂ S₁

K Ф2

K₁

X₁

(b – c)/2a (b – c)/a

Рис. 9

В равновесии по сговору (обозначим точку рановесия К), изображенному на рис.9 фирма 1 производит больший объем продукции, чем в точке К₂, когда суммарный объем поделен между фирмами в пользу фирмы 2 (к =2,т.е. Х₂ = 2Х₁) и получает большую долю суммарной прибыли. Положим к = 1/2, т.е. Х₂= (1/2)Х₁. Тогда суммарный объем поделен в пользу фирмы 1. И, следовательно, в точке К₁ фирма 1 производит больший объем продукции, чем в К₂ и К, и получает наибольшую прибыль (с учетом того, что р^к= (b + c) /2a для любых к ).

Как было отмечено выше, прибыль фирмы 1 при сговоре с фирмой 2 в пользу фирмы 2 (К₂) совпадает величиной прибыли, получаемой при объеме производства, соответствующему точке L₁ , когда фирма 1, как бы продолжает борьбу за лидерство. Поэтому изопрофита, проходящая через точки К₂ и L₁ касается, с одной стороны, прямой Х₂ = 2Х₁, с другой – новой линии реакции фирмы 2 (Ф2^н). В то же время изопрофита, соответствующая равновесию по сговору, касается как прямой Х₂ = Х₁ (в точке К) и одновременно линии реакции фирмы 2 (Ф2) в точке S₁.

В таблице 1 приведены результаты расчета по различным моделям стратегического взаимодействия фирм в случае линейных функций спроса и издержек. Для упрощения сранения показателей прибыли, соответствующих различным состояниям равновесия, в выражении прибылей опущены величины постоянных общих издержек d₁и d₂.

Данные приведенные в таблице 1позволяют продолжить анализ различных случаев взаимодействия фирм. При этом обращение к геометрическим интерпретациям решений задач на условный экстремум в терминах изопрофит и нулевых линий уровня функций–условий, подобным приведенным выше, позволит, по нашему мнению, выявить такие свойства решений, которые не являются очевидными и последующее экономическое объяснение которых позволит глубже понять реальные процессы взаимодействия фирм на дуопольном рынке.

Таблица 1

№	Модель		Фирма 1		Фирма 2		Отрасль		Рыночная цена
			Объём выпуска	Прибыль	Объём выпуска	Прибыль	Объём выпуска	Прибыль	Рыночная цена
			x₁	PR₁	x₂	PR₂	X	PR	P
1	Курно		b – c 3a	(b – c)² 9a	b - c 3a	(b – c)² 9a	2(b-c) 3a	2(b – c)² 9a	b + 2c 3
2	Штекельберг	Фирма 1-лидер	b - c 2a	(b – c)² 8a	b – c 4a	(b – c)² 16a	3(b – c) 4a	3(b – c)² 16a	b + 3c 4
2	Штекельберг	Фирма 2-лидер	b – c 4a	(b – c)² 16a	b - c 2a	(b – c)² 8a	3(b - c) 4a	3(b – c)² 16a	b + 3c 4
3	Борьба За Лидерство	Независимые конкуренты	2(b - c) 5a	2(b – c)² 25a	2(b - c) 5a	2(b – c)² 25a	4(b - c) 5a	4(b – c)² 25a	b + 4c 5
		Фирма 1 – лидер	b - c 2a	(b – c)² 12a	b - c 3a	(b – c)² 18a	5(b-c) 6a	5(b – c)² 36a	b + 5c 6
		Фирма – 2 лидер	b - c 3a	(b – c)² 18a	b - c 2a	(b – c)² 12a	5(b - c) 6a	5(b – c)² 36a	b + 5c 6
		Сговор при борьбе за лидерство	3(b - c) 8a	3(b – c)² 32a	3(b - c) 8a	3(b – c)² 32a	3(b - c) 4a	3(b – c)² 16a	b + 3c 4
4	К А Р Т Е Л Ь	Равноправные партнеры	b - c 4a	(b – c)² 8a	b - c 4a	(b – c)² 8a	b - c 2a	(b – c)² 4a	b + c 2
		Пропорция в пользу фирмы 1(Х₁ = 2Х₂)	b - c 3a	(b – c)² 6a	b - c 6a	(b – c)² 12a	b - c 2a	(b – c)² 4a	b + c 2
		Пропорция в пользу фирмы 2(Х₂ = 2Х₁)	b - c 6a	(b – c)² 12a	b - c 3a	(b – c)² 6a	b - c 2a	(b – c)² 4a	b + c 2
		Пропорция в пользу фирмы 1(Х₁ = 3Х₂)	3(b – c) 8a	3(b – c)² 16a	b - c 8a	(b – c)² 16a	b - c 2a	(b – c)² 4a	b + c 2
		Пропорция в пользу фирмы 2(Х₂ = 3Х₁)	b - c 8a	(b – c)² 16a	3(b – c) 8a	3(b – c)² 16a	b - c 2a	(b – c)² 4a	b + c 2

Blog

Метод Лагранжа широко используется в различных областях экономической теории для решения задач на нахождение условного экстремума

Содержание

Курно