В электрических и магнитных полях

Вид материала

Лабораторная работа

Содержание Объект исследования Движение электрона в электрических полях Порядок выполнения работы 13ЛО6И (большой экран), сдвоенный источник питания (или два источника питания) и вольтметр В7-22. Движение электрона в магнитном поле Общее смещение электрона Порядок выполнения работы Движение электрона по винтовой линии Порядок выполнения работы 8ЛО29И (маленький экран), сдвоенный источник питания (или два источника питания) и вольтметр В7-22.

Подобный материал:

• Аннотация дисциплины, 34.98kb.
• Методика и техника реологических исследований магнитных жидкостей в электрическом, 230.2kb.
• Магнитное поле в вакууме, 56.29kb.
• Отчет по лабораторной работе должен содержать: наименование работы и номер, схемы, 365.83kb.
• Рабочая программа учебной дисциплины "электротехника и электроника" Цикл, 182.88kb.
• Самостоятельная работа Кредитная стоимость, 122.1kb.
• Аннотация дисциплины, 39.03kb.
• Оглавление цена дипломной работы с чертежом 500 рублей, 26.6kb.
• Лабораторная работа №3 исследование гистерезиса ферромагнетиков в переменном магнитном, 139.03kb.
• Взаимосвязи магнитных и электрических свойств пород островов аргентинского архипелага, 205.14kb.

Лабораторная работа № 3


ИЗУЧЕНИЕ ДВИЖЕНИЯ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ

В ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ПОЛЯХ


Цель работы: применение законов кинематики и динамики к описанию движения электрических зарядов в электрических и магнитных полях, экспериментальная их проверка.

Приборы и принадлежности: два макета с различными электронно-лучевыми трубками, два спаренных источника питания, цифровой вольтметр.


Подготовка к работе


Перед тем, как приступить к выполнению работы, необходимо повторить основные понятия кинематики, законы динамики и ответить на следующие вопросы:

1. Какое движение называется равномерным? Дать определение средней и мгновенной скорости движения. Написать формулы для вычисления пути при равномерном движении.

2. Какое движение называется равноускоренным? Дать определение среднего и мгновенного ускорения движения. Написать формулы для вычисления пути и скорости при равноускоренном движении.

3. Какое движение называют поступательным?

4. Какое движение называют вращательным?

5. Какое движение называют равномерным вращательным? Дать определение средней и мгновенной угловой скорости. Как находят угловой путь при равномерном вращательном движении?

6. Какое движение называют равноускоренным вращательным? Дать определение среднего и мгновенного углового ускорения. Написать формулы для вычисления углового пути и угловой скорости при равноускоренном вращательном движении.

7. Как связаны линейные и угловые скорости и ускорения при криволинейном движении?

8. Как формулируются законы Ньютона?


Поскольку работа предполагает изучение движения электрических зарядов в электрических и магнитных полях, необходимо вспомнить их основные характеристики и ответить на следующие вопросы:

1. Что называется напряженностью электрического поля? Как вычисляется сила, действующая на заряд в электрическом поле (сила Кулона)?

2. Как связаны в однородном электрическом поле напряженность и разность потенциалов?

3. В каких единицах измеряется индукция магнитного поля?

4. Как находится сила, действующая на электрический заряд, движущийся в магнитном поле (сила Лоренца)?

Объект исследования

В качестве объекта исследования используется макет, состоящий из ЭЛТ и источников питания, обеспечивающих ее работу. ЭЛТ представляет собой электронно-вакуумный прибор, состоящий из электронной пушки, отклоняющей системы X₁,X₂ и Y₁,Y₂ и экрана (рис. 1).




Электронная трубка состоит из подогревного оксидированного катода К, модулятора М и двух анодов А₁ и А₂. Оксидный катод выполнен в виде небольшого никелевого цилиндра, на дно которого нанесен активированный слой, эмитирующий при нагревании электроны. Вокруг катода располагается управляющий электрод (модулятор), выполненный в виде никелевого цилиндра с небольшим отверстием. На модулятор подается отрицательное относительно катода напряжение несколько десятков вольт, под действием которого создается электрическое поле, прижимающее электроны к оси трубки, благодаря чему осуществляется предварительная фокусировка электронного луча. Кроме того, электрическое поле модулятора, являясь тормозящим для электронов, отталкивает некоторые из них обратно на катод. Следовательно, регулируя значение отрицательного потенциала на модуляторе, можно изменять количество электронов, движущихся к экрану трубки, и, следовательно, яркость свечения экрана.

Ускорение электронов и дальнейшая их фокусировка в узкий пучок обеспечивается системой двух анодов, выполненных в виде полых металлических цилиндров. Чтобы получить достаточные скорости движения электронов, на аноды подаются большие положительные напряжения (на первый анод несколько сот вольт, на второй несколько киловольт). Качество фокусировки зависит от потенциала первого анода, необходимое значение которого устанавливается с помощью резистора. В соответствии с назначением и действием система электродов катод – модулятор – первый анод – второй анод образуют так называемую электронную пушку.

На пути к экрану электронный луч проходит между двумя парами взаимно перпендикулярных пластин, называемых электростатической отклоняющей системой.

Пластины Y₁, Y₂, расположенные горизонтально, отклоняют луч в вертикальном направлении и называются вертикально отклоняющими. Пластины X₁, X₂, расположенные вертикально, отклоняют луч в горизонтальном направлении и называются горизонтально отклоняющими.

В данной работе для создания электрического поля между отклоняющими пластинами от источника питания будет подаваться напряжение. Приближенно электрическое поле между пластинами можно считать однородным, т.е.

,

где E – напряженность электрического поля, U – напряжение на пластинах, d – среднее расстояние между пластинами.

Таблица 1.



Магнитное поле, направленное перпендикулярно к оси ЭЛТ, в макете с большим экраном создается при пропускании электрического тока через катушки, установленные внутри макета, причем

B = kI ,

где B – магнитная индукция, измеренная в теслах (Тл); I – ток в катушках, измеряется в амперах (А); K – постоянная катушек, зависящая от конструкции и числа витков катушек, приведена в таблице 1. Расстояние, на котором магнитное поле можно считать приблизительно однородным, следует принять равным ширине отклоняющих пластин ℓ.

В макете с малым экраном магнитное поле, направленное вдоль оси ЭЛТ, создается электрическим током, протекающим через соленоид, ось которого совпадает с осью трубки. Магнитное поле на оси соленоида находится по формуле:

B = ₀nI , (1)

где _ = 410^-7 (Гн / м), I – ток в соленоиде; n – число витков на единицу длины соленоида (n= N/L) . Количество витков N соленоидов для различных макетов указаны в таблице 2, L – длина соленоида и равна 0.18 м.


Таблица 2.




Движение электрических зарядов в электрических и

магнитных полях.


На движущуюся заряженную частицу в электрических и магнитных полях действует сила Лоренца



где e – заряд частицы (заряд электрона e = 1.6 10^–19 (Кл)); E – напряженность электрического поля (В / м); v – скорость частицы (м / с); B – индукция магнитного поля (Тл);

В соответствии со вторым законом Ньютона скорость изменения импульса пропорциональна действующей силе

(2)

где m – масса частицы (масса электрона m=9.1110^-31 (кг)); mv - импульс частицы.

Заметим, что скорость электрона, прошедшего разность потенциалов порядка 1000 В, значительно меньше скорости света; значит, в данной работе возможно использование нерелятивистских уравнений движения.

Для решения задач о движении электрона в электрических и магнитных полях, кроме уравнения (2), необходимы начальные условия. Сложные задачи надо расчленять на ряд простых. Рассмотрим несколько примеров.

Движение электрона в электрических полях

Движение электрона от катода до экрана является сложным (рис 2), поэтому разделим его на три простых.




1. Движение электрона между катодом К и анодом А₂


Электроны, эмитируемые подогревным катодом, ускоряются системой электродов (электронная пушка), проходя разность потенциалов Uz. Скорость электронов на выходе из пушки можно определить из закона сохранения энергии:



где V_k – скорость электрона при выходе из катода; V_z – скорость электрона за анодом; eU_z – потенциальная энергия, приобретенная электроном в ускоряющем поле.

Кинетическая энергия, определяемая тепловым движением электронов, обычно много меньше потенциальной энергии eU_z , значит, величину скорости электрона можно найти из формулы




2. Движение электрона в электрическом поле вертикально (горизонтально)

отклоняющих пластин


Если на пластины Y₁, Y₂ подать постоянное напряжение U_y, то между пластинами возникает электрическое поле, отклоняющее пучок электронов. Найдем величину отклонения y₁ и скорость V_y в момент вылета из отклоняющих пластин. Допустим, что электрическое поле между пластинами однородное, тогда

(3)

где d – расстояние между пластинами.

Электрон, двигаясь равномерно вдоль оси Z, под действием силы

F_y = eE_y (4)

будет двигаться равноускоренно в направлении оси Y с ускорением

. (5)

Время пролета электрона между пластинами t₁ можно определить, учитывая, что движение вдоль оси Z равномерное, т.е.

,

где ℓ – ширина пластин.

Пролетая между пластинами, электрон приобретает скорость в направлении оси Y, равную

, (6)

и сместится вдоль оси Y на расстояние, равное

(7)

Движение электрона от отклоняющих пластин до экрана будет равномерным и прямолинейным, потому что здесь на него не действуют силы.

Это движение электрона можно представить как два равномерных и прямолинейных в направлении оси Z со скоростью v_z и в направлении оси Y со скоростью v_y. Время пролета электрона от пластин до экрана найдем по формуле

(8)

где L – расстояние от пластин до экрана.

Отклонение от оси Z за это время определим по формуле

(9)

Общее смещение луча на экране

(10)

Подставляя в формулу (10) выражения (9), (8), (7), (6), (5), (4), (3) и упрощая, получим

(11)

Из формулы (11) видно, что наблюдаемое смещение луча пропорционально напряжению, поданному на отклоняющие пластины, и обратно пропорционально ускоряющему напряжению между катодом и анодом.

Зависимость (5) является следствием решения уравнения (2) (второго закона Ньютона) и подлежит экспериментальной проверке. В макетах не предусмотрено изменение ускоряющего напряжения U_z, поэтому возможна только проверка пропорциональности смещения луча отклоняющему напряжению:



Коэффициент  можно вычислить, зная геометрические размеры элементов ЭЛТ и величину ускоряющего напряжения:

(12)

Для экспериментальной проверки надо получить зависимость y = f (U_y), построить график и найти

.

Сравнить вычисленное значение  и полученное экспериментально _э, оценить погрешность.

Порядок выполнения работы

ВНИМАНИЕ ! Поскольку некоторые напряжения превышают 1000 В, пп. 1-3 выполняются только преподавателем или в присутствии преподавателя и под его наблюдением. Если такие измерения провести невозможно, то у преподавателя необходимо узнать напряжение между катодом и вторым анодом для используемого макета.

Приготовить макет с электронно-лучевой трубкой 13ЛО6И (большой экран), сдвоенный источник питания (или два источника питания) и вольтметр В7-22.

1. Измерить напряжение между катодом и модулятором. Определить возможные пределы регулировки напряжения, наблюдая за изменением яркости светящегося пятна на экране. Установить нормальную яркость. Результаты записать.

2. Измерить возможные пределы регулировки напряжения между катодом и первым анодом, наблюдая за фокусировкой луча. Сфокусировать луч. Результаты записать.

3. Измерить напряжение между катодом и вторым анодом. Рассчитать скорость электронов. Результаты записать.

4. Подключить источник напряжения к вертикально отклоняющим пластинам ЭЛТ и, увеличивая напряжение Uy, определить смещение y как функцию напряжения. Изменив полярность, измерения повторить. Результаты записать в таблицу (U_y,y) и построить график y = f (U_y).

5. Зная U_z, измерить параметры L, ℓ, d ЭЛТ 13ЛО6И и по формуле (12) вычислить .

6. Результаты пп. 4 и 5 сравнить, оценив погрешность измерения.

Движение электрона в магнитном поле

В качестве примера рассмотрим следующую задачу. Пучок электронов, ускоренный напряжением U_z, вылетая из электронной пушки, попадает в магнитное поле с индукцией B_x, действующее на расстоянии ℓ, пролетает его, попадая на экран (рис.3). Определить смещение луча y и сравнить его с экспериментальным.



Рис. 3

На электрон, движущийся со скоростью v_z , действует сила Лоренца

(13)

Так как скорость электрона v_z перпендикулярна вектору магнитной индукции B_x, то модуль силы находим по формуле

(14)

Эта сила F_л, перпендикулярная скорости v_z, являясь центростремительной силой, не изменяет величины скорости, а, изменяя направление скорости, двигает электрон по дуге с радиусом R. Скорость электрона v₀, направленную по касательной к дуге, разложим на две:

(15)

где  – угол, на который отклоняется вектор скорости v₀, равный центральному углу, опирающемуся на дугу O O`.

Поскольку v_z = v₀, ℓ << L, а угол будем считать достаточно малым. Учитывая, что для малых углов sin  , cos 1, будем иметь

v_y1v_z_, v_z1v_z.

Считая движение электрона по дуге равномерным движением по окружности, находим

, (16)

где t₁ – время пролета магнитного поля с индукцией B_x;

. (17)

Угловую скорость электрона находим из выражений (14), (15) и, учитывая, что v₀=R, получим:

, (18)

т.е. угловая скорость движения электрона пропорциональна индукции магнитного поля.

Из выражений (16), (17) находим

. (19)

Допуская, что второй закон Ньютона справедлив и движение в направлении оси y равноускоренное, а скорость изменялась от 0 до v_y1, находим среднюю скорость

(20)

Отклонение электрона магнитным полем вдоль оси y найдем по формуле

(21)

Электрон, двигаясь равномерно в направлении экрана со скоростью V_z, за время



достигнет экрана и одновременно отклонится в направлении оси y на

Общее смещение электрона

y = y₁ + y₂ . (22)

Подставив в выражение (22) формулы (21), (20), (19), (18), получим



Откуда видно, что смещение электрона прямо пропорционально B_x:



Коэффициент пропорциональности

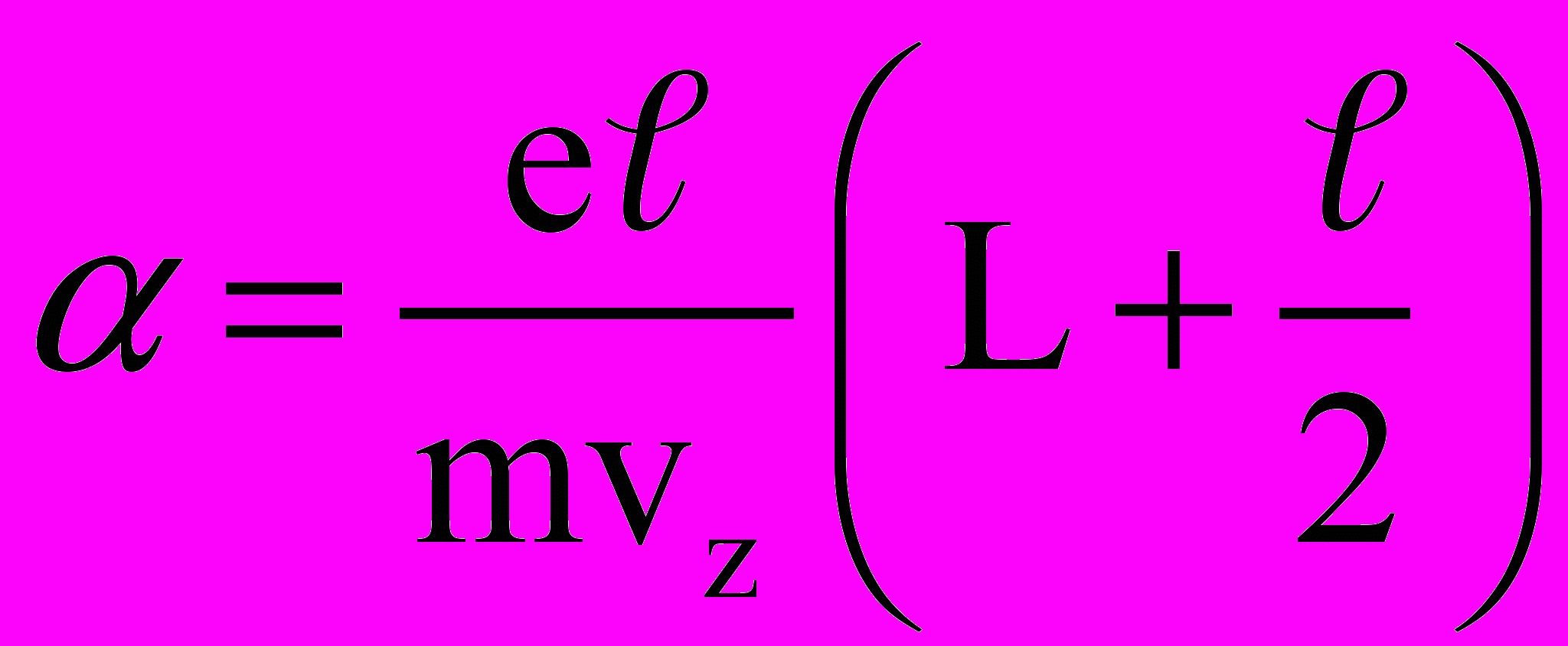(23)

можно определить из геометрических размеров ЭЛТ, зная e, m и ускоряющее напряжение U_z .

Известно, что B = kI. Экспериментально найдите зависимость смещения y = f (I), постройте график и вычислите



Сравните вычисленное  и экспериментально определенное _э, оцените погрешность.

Порядок выполнения работы

Приготовить макет с электронно-лучевой трубкой 13ЛО6И (большой экран), сдвоенный источник питания (или два источника питания) и вольтметр В7-22.

1. Подключить источник тока к вертикально отклоняющим катушкам. Увеличивая ток, определить смещение луча как функцию тока и, изменив полярность, повторить измерения. Результаты записать в таблицу (I, y) и построить график y=f(B_x). Вычислить _э.

2. Зная U_z и параметры ЭЛТ 13ЛО6И L и ℓ , массу электрона m и заряд электрона e, вычислить  по формуле (23).

3. Результаты пп. 1 и 2 сравнить и оценить погрешность.

Движение электрона по винтовой линии

1. Если электрон движется со скоростью v, не совпадающей по направлению с направлением индукции магнитного поля B_z, то возникает сила Лоренца



Величина силы F=evB_zsin, где  - угол между направлением скорости v и направлением магнитного поля B_z.

Для анализа движения электрона удобно разложить скорость электрона v на две составляющие: перпендикулярную и параллельную оси Z (рис.4).

2. Если электрон движется параллельно магнитному полю со скоростью V_z, то угол  равен нулю и сила отсутствует. Таким образом, электрон, первоначально двигавшийся параллельно магнитному полю, будет продолжать движение с постоянной скоростью.



Рис. 4

3. Если электрон движется со скоростью V_y, а V_z = 0, то возникает сила Лоренца, перпендикулярная скорости V_y. Под действием этой силы электрон будет двигаться в плоскости (x,y) по окружности равномерно. Угол поворота радиуса-вектора  будет равен

 =  t .

Так как сила Лоренца является центростремительной (F_л = F_цс),

F_лх = eV_у B_z .

Зная, что V_у = R, можно найти угловую скорость  .

, (24)

(25)

Из (24), (25) видно, что угловая скорость  не зависит от скорости V_у и пропорциональна величине магнитной индукции. Радиус окружности прямо пропорционален поперечной скорости и обратно пропорционален B_z.

4. Если v_y и v_z, то электрон, вращаясь в плоскости (x,y), будет равномерно двигаться вдоль оси Z :

Z = v_zt.

Расстояние, пройденное в направлении оси Z за время одного оборота электрона в плоскости (x,y), называют шагом винта, а траекторию электрона – винтовой линией.

Учитывая, что период обращения электрона T = , можно найти шаг винта по формуле

h = V_z T = V_z . (26)

5. Рассмотрим случай винтового движения электронного пучка в электронно-лучевой трубке. Электронный пучок, ускоренный вторым анодом, двигается со скоростью V_z в направлении магнитного поля B_z. Если на вертикально отклоняющие пластины приложить напряжение U_y, то электронный пучок отклонится на угол . Найдем tg. Для этого из формул (6), (5), (4), (3) выразим значения V_y и V_z , подставим в формулу tgV_y/V_z (рис.4) , получим



где ℓ – ширина отклоняющих пластин, d – расстояние между пластинами.

Из рис.4 видно, что электроны приобретут поперечную скорость, равную

V_y = V_z tg.

Электроны будут двигаться вдоль трубки по винтовой линии радиусом

(27)

с шагом винта

.

6. Рассмотрим, как меняется положение пятна на экране. Следует помнить, что электроны движутся по винтовой линии, ось которой смещена от центра экрана на радиус R. Чтобы найти уравнение траектории пятна на экране при увеличении магнитного поля, воспользуемся полярными координатами , . Из рис. 5 видно, что ,

 (28)

Время пролета электрона от отклоняющих пластин до экрана t₂:



За это время в плоскости (x,y) радиус-вектор R, вращаясь с угловой скоростью , повернется на угол , т.е.

t₂= . (29)



Рис. 5

Приравнивая (28) и (29), получаем

,

откуда

. (31)

Подставляя (27),(31) в (28), получаем



Это уравнение кривой, называемой кохлеоидой.


Определение удельного заряда электрона методом магнитной

фокусировки


Электрон в магнитом поле B_z движется по винтовой линии, если имеются продольные V_z и поперечные V_y составляющие скорости. Радиус винтовой линии находится по формуле (25), шаг винта – по формуле (26), угловая скорость – по формуле (24). Подставив в формулу (26) значение угловой скорости (24), получим

,

откуда видно, что шаг винта не зависит от поперечной скорости V_y, а определяется отношением e /m, которое называют удельным зарядом.

Если пучок состоит из электронов, влетевших в магнитное поле с разными поперечными скоростями V_y и одинаковыми скоростями V_z, то через период Т пучок соберется в одной точке, отстоящей от точки входа на расстоянии шага винта. На экране будет наблюдаться пятно малого размера (первая фокусировка). Увеличив магнитное поле, можно наблюдать вторую фокусировку, при этом на расстоянии L укладывается два шага винта.

Таким образом, зная величину шага винта h, продольной скорости V_z и индукции магнитного поля B_z, можно найти удельный заряд

(32)

Подставив в (50) значение V_z, получим

(33)

Возведя в квадрат и упростив выражение (33), получим



Величину индукции магнитного поля B_z найти по формуле (1).

Порядок выполнения работы

ВНИМАНИЕ! Поскольку некоторые напряжения превышают 1000 В,

п.1 выполняется только преподавателем или в присутствии преподавателя и

под его наблюдением. Если такие измерения провести невозможно, то у

преподавателя необходимо узнать напряжение между катодом и вторым анодом для используемого макета.

Приготовить макет с электронно-лучевой трубкой 8ЛО29И (маленький экран), сдвоенный источник питания (или два источника питания) и вольтметр В7-22.

1. Выполнить измерения, записать и сравнить результаты, следуя пп. 1–6 с.9

2. Подключить источник напряжения к вертикально отклоняющим пластинам. Увеличивая напряжение, сместить пятно на экране на 3-4 деления.

3. Подключить источник тока. Плавно увеличивая ток, проследить за изменением положения пятна на экране. Траекторию перемещения пятна по экрану зарисовать для отчета.

4. Рассчитать кохлеоиду, задавая изменение угла  по 10 - 15 градусов и начертить её в отчете. Сравнить с кривой, полученной в п.3 .

5. Измерить токи, при которых наблюдаются первая и вторая фокусировки, и рассчитать величину удельного заряда e/m.


Контрольные вопросы.


1. В каких видах движения участвует электрон, перемещаясь от катода к экрану? Напишите формулы пути и скорости для всех этих видов движения.

2. Какие силы действуют на электрон при движении от катода к экрану?

3. Какой вид имеет траектория движения электрона внутри отклонящих пластин?

4. Какой вид имеет траектория движения электрона в магнитном поле, направленном перпендикулярно его скорости?

5. Как изменяется форма траектории движения электрона при изменении величины продольного магнитного поля?

6. Как определяют удельный заряд электрона, используя магнитную фокусировку?