Конспект лекций по курсу "Алгоритмические языки и программирование". Тема "Множества"
| Вид материала | Конспект |
- Конспект лекций по курсу "Алгоритмические языки и программирование". Тема "Рекурсия", 178.49kb.
- Пояснительная записка Ккурсовой работе по дисциплине "Алгоритмические языки и программирование", 121.92kb.
- Рабочая программа курса "Алгоритмические языки программирования, 25.98kb.
- Организация и планирование производства Программирование на языке высокого уровня., 17.16kb.
- Программа дисциплины по кафедре Прикладная математика т информатика алгоритмические, 564.02kb.
- Програма курсу за вибором Технологія програмування на С++, 340.55kb.
- Конспект лекций по курсу макроэкономика для студентов заочников факультета бухгалтерского, 2421.87kb.
- Конспект лекций по курсу «Организация производства», 2034.84kb.
- Конспект лекций по курсу «Организация производства», 2032.47kb.
- Конспект лекций по курсу "Начертательная геометрия и инженерная графика" Кемерово 2002, 786.75kb.
Иванова Г.С., Ничушкина Т.Н.
Конспект лекций
по курсу "Алгоритмические языки и программирование".
Тема "Множества".
Понятие множество является одним из основных в современной математике и трактуется как бесповторная неупорядоченная совокупность объектов. В Турбо Паскале есть структуры, отражающие это математическое понятие.
Определение: Множество - это набор однотипных объектов, каким либо образом связанных друг с другом. Характер связей между объектами только подразумевается программистом и никак не контролируется Турбо Паскалем. В общем случае множество может не содержать ни одного элемента. Такое множество называется пустым.
При задании множественного типа определяется некоторый тип (базовый), из значений которого и создаются конкретные значения множественного типа. После того, как базовый тип задан, совокупность значений множественного типа определяется автоматически. Синтаксическая диаграмма описания множественного типа представлена на рисунке 1.
 Рис. 1
Рис. 1Некоторые особенности реализации множеств в Турбо Паскале:
- Допускаются только конечные множества.
- Количество элементов, входящих во множество, может меняться в пределах от 0 до 256.
- Базовым типом может быть любой порядковый тип за исключением типов integer и longint, количество возможных значений которых превышает 256 (в качестве базового типа могут использоваться диапазоны значений этих типов).
- Порядок расположения элементов во множестве и количество повторений некоторых из них никак не фиксируется. Это соответствует принятой в математике трактовке множества.
При использовании множественных типов данных новый тип обычно определяется в разделе описания типов, а затем используется при описании переменных и констант соответствующих типов.
Примеры задания множественного типа:
TYPE Digits = set of 1..100; {множество целых чисел от 1 до 100}
Setchar = set of char; {множество символов таблицы ASCII}
letter = set of ‘a’..’z’; {Множество прописных латинских букв}
logic = set of boolean; {множество логических значений}
CONST letgl: letter=[‘a’,’i’,’e’,’u’,’o’,’y’];{типизированная константа -множество гласных букв}
operation: setchar = [‘+’,’-‘,’*’,’/’]; {типизированная константа - множество знаков операций}
VAR mychar: setchar; {переменная типа множество символов таблицы ASCII}
bool: logic; {переменная типа множество логических значений}
mydig: Digits; {переменная типа множество символов таблицы ASCII}
simst: letter; {переменная типа множество прописных латинских букв}
Переменную множественного типа можно определить и непосредственно в разделе описаний переменных программы.
Примеры определения переменных множественного типа:
TYPE dayn=(sun,mon,tue,wed,thu,fri,sat); {перечислимый тип дни недели}
CONST weekend=[sun,sat]; {константа - множество выходных дней}
VAR number: set of 1..31;{переменная - множество целых чисел от 1 до 31}
cif: set of 0..9; {переменная - множество цифр}
kods: set of #0..#255;{переменная - множество кодов таблицы ASCII}
workweek, week: set of dayn;{переменная - множество дней недели}
Значением множественного типа в Паскале является множество. Конкретные значения множественного типа (постоянные и переменные) задаются с помощью так называемого конструктора множества, представляющего собой список элементов множества, заключенный в квадратные скобки. Элементы множества могут задаваться константами, переменными и выражениями базового типа.
Синтаксическое определение конструктора множеств в форме Бэкуса-Наура выглядит следующим образом:
<конструктор множества>::=[ ] | [<элемент>{,<элемент>}]
<элемент>::=<выражение>|< выражение >. .< выражение >
Примеры множеств на Паскале, заданных с помощью конструктора:
[ ] - пустое множество
[2,3,5,7,11] - множество, содержащее в качестве своих элементов целые числа;
[‘a’,’d’,’f’,’h’] - множество, содержащее в качестве своих элементов латинские литеры;
[1,k] - множество, состоящее из целого числа 1 и текущего значения переменной k;
[k..2*k] - множество целые чисел от значения переменной k до значения выражения 2*k;
[2..100] - множество последовательных целых чисел от 2 до 100;
[red,yellow,green]- множество, состоящее из трех элементов некоторого перечислимого типа.
Для работы со значениями множественного типа в Паскале предусмотрен довольно богатый набор операций. В основном этот набор отражает те операции над множествами, которые предусмотрены в теории множеств. Для получения новых множественных значений в Паскале введены в употребление операции объединения, пересечения и разности множеств.
Эти двуместные операции, операндами которых являются множественные константы, переменные - множества и выражения, принимающие значение множественного типа. Оба операнда должны принадлежать одному и тому же множественному типу. Обозначения этих операций в Паскале и их геометрическая интерпретация представлены в таблице 1 применительно к некоторым множествам А и Б.
Таблица 1.
| А+Б - объединение множеств А и Б - множество, состоящее из элементов, принадлежащих множествам А и Б. |  |
| А*Б - пересечение множеств А и Б - множество, состоящее из элементов, принадлежащих одновременно и множеству А и множеству Б. | 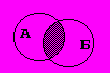 |
| А-Б - вычитание множеств А и Б - множество, состоящее из тех элементов множества А, которые не принадлежат множеству Б. | 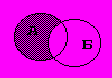 |
Примеры использования перечисленных операций:
[1,2]+[3,4]=[1,2,3,4];
[1..10]*[3,8,9,15,23,45]=[3,8,9];
[1..15]-[3,8,9,15,23,45]=[1,1,4..7,10..14];
[red,blue,green,black]*[blue,magenta,yellow]=[blue];
Наряду с рассмотренными выше операциями, над значениями множественного типа определены и некоторые операции отношения. Операндами отношений в этом случае являются множественные выражения.
Пусть А и Б - множества, принадлежащие одному и тому же множественному типу. В таблице 2 приведены операции отношения над множествами в Паскале, соответствующая математическая запись этих операций и дано их объяснение.
Таблица 2.
| Запись на Паскале | Математическая запись | Значение логической операции | |
| | | TRUE | FALSE |
| А=Б | А=Б | множества А и Б совпадают | множества А и Б не совпадают |
| А<>Б | А¹Б | множество А и Б не совпадают | множество А и Б совпадают |
| А<=Б | АÍБ | все элементы множества А принадлежат множеству Б. | Не все элементы множества А принадлежат множеству Б. |
| А>=Б | АÊБ | все элементы множества Б принадлежат множеству А | не все элементы множества Б принадлежат множеству А |
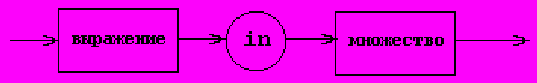
Среди операций отношения над значениями множественного типа особое место занимает специальная операция проверки вхождения элемента во множество, обозначаемая служебным словом in. В отличие от остальных операций отношения, в операции in первый операнд должен принадлежать базовому типу, а второй - множественному типу значений, построенному на основе этого базового типа. Результатом операции in, как во всех операциях отношения, является логическое значение. Синтаксическая диаграмма операции представлена на рисунке 2.
Рис. 2.
Примеры применения операций отношения и операции вхождения и результат их применения представлены в таблице 3.
Таблица 3.
| Операция отношения | Результат |
| [‘a’,’b’]=[‘b’,’a’]; | TRUE |
| [4,5,6]=[4..6]; | TRUE |
| [c’,’b’]=[‘c’,’b’,’d’] | FALSE |
| [2,3,5,7]<=[1..9]; | TRUE |
| [3,6..8]<=[2..7,9]; | FALSE |
| [5..8,9..12]>=[6,8,11]; | TRUE |
| 10 in [2,4,6,8,10,12,14]; | TRUE |
| k in [1,3,5,7,9]; | TRUE при k=1,3,5 и FALSE при k=2,4,6 |
При использовании множественных типов в программах возникают задачи формирования множества и его вывода на печать.
Первая задача может быть решена как с помощью уже упоминавшегося конструктора множеств, так и по определенному алгоритму, выбранному программистом в соответствии с целями решаемой задачи.
Печать множества выполняется поэлементно в цикле. Напечатать множество одним оператором, как строку, не возможно.
Ниже приведены некоторые примеры использования множественных переменных при решении конкретных задач.
Пример 1. Программа формирует множество символов, заполняя его случайными символами из таблицы ASCII.
program exmnoj1;
TYPE mnchar=set of char; {новый тип - множество символов таблицы ASCII}
VAR m:mnchar; {множество символов таблицы ASCII}
c:char; {вспомогательная переменная типа символ}
k:word; {количество элементов множества}
n:word;
begin
randomize;
m:=[ ]; {задание начального значения множества - пустое множество}
writeln(' введите количество элементов K <=256 ');
readln(k);
repeat
n:=0;
for c:=#0 to #255 do if c in m then n:=n+1; {подсчет количества элементов множества}
if n
until n=k;
{печать элементов множества m}
for c:=#0 to #255 do if c in m then write(c:2);
end.
Пример 2. Программа формирует и печатает в алфавитном порядке все элементы множества А, имеющего тип - множество строчных латинских букв.
program exmnoj2;
TYPE letter=set of 'a'..'z'; {новый тип - множество латинских букв}
VAR A:letter; {множество латинских букв}
c:char;
begin
A:=['a','c'..'k','o'..'w']; {задание значения множества с помощью операции присваивания}
{печать элементов множества}
for c:='a' to 'z' do if c in A then write(c:2);
end.
Пример 3. Программа находит и напечатает в порядке убывания все простые числа в диапазоне 2- 201. Для решения задачи использован метод, известный как РЕШЕТО ЭРИСТОФАНА.
program exmnoj3;
CONST n=201;m=2; {константы, позволяющие менять диапазон анализируемых чисел, может меняться}
TYPE number=set of m..n;
VAR numset, { множество анализируемых чисел}
rez:number; { множество простых чисел}
next, nn, i:integer;
begin
if m=1 then begin numset:=[m+1..n];rez:=[1];next:=m+1 end
else begin numset:=[m..n];rez:=[ ];next:=m; end;
while numset <> [ ] do
begin
nn:=next;
while nn <= n do
begin
numset:=numset -[nn]; { удаление числа nn и кратных ему из множества}
nn:=nn+next;
end;
rez:=rez+[next];
repeat
inc(next);
until (next in numset) or (next > n)
end;
writeln(' Простые числа в диапазоне ',m:3,'..',n:3,' в обратном порядке:');
for i:=n downto m do if i in rez then write(i:4);
readln;
end.
Пример 4. Программа подсчитывает количество различных цифр в десятичной записи натурального числа.
program exmnoj4;
TYPE long=0..maxlongint;
FUNCTION count(n:longint):word;
TYPE cifra=set of 0..9; {новый тип - множество десятичных цифр}
VAR sd:cifra; {множество десятичных цифр}
k:word;d:0..9;
begin
sd:=[ ]; {задание значения множества с помощью операции присваивания: в начале sd пустое множество}
k:=0;
repeat
d:=n mod 10;
sd:=sd+[d];{ определение очередной цифры числа n и запись ее во множество}
n:=n div 10;{ определение очередного значения числа n}
until n=0;
for d:=0 to 9 do if d in sd then k:=k+1;
count:=k
end;
VAR mn:long;
begin
writeln('Введите десятичное число');
readln(mn);
writeln(' В числе ',mn,' ',count(mn):5,' различных десятичных букв ');
end.
Пример 5. Для каждой строки символов, введенной с клавиатуры и состоящей из нескольких слов разделенных пробелами, программа создает множество гласных, которые:
1 - встречаются в каждом слове строки;
2 - встречаются только в одном слове строки;
3 - встречаются хотя бы в одном слове строки;
4 - встречаются более чем в одном слове строки;
слова разделены пробелами
program exmnoj5;
TYPE simv=set of char;
CONST b: simv = ['a','e','i','o','u','y'];
VAR rezul: simv;
st: string;
key: integer;
ch: char;
PROCEDURE prinmn(kl:integer;s:string;var rez:simv);
VAR mnsl, {множество гласных, встречающихся в текущем слове}
mn:simv; { множество гласных, встречающихся в строке}
sl:string; z,m,i,j,k:integer; ch:char;
begin
z:=0;
mn:=[ ];
k:=length(s);
i:=1; { номер символа в строке}
j:=1; { номер первого символа в очередном слове}
while i<=k do
begin
while (s[i]<>' ') and (i<=k) do i:=i+1;
sl:=copy(s,j,i-j); { выделение слова}
z:=z+1; { номер слова}
mnsl:=[ ];
if z=1 then begin
for m:=1 to i-j do
if sl[m] in b then mnsl:=mnsl+[sl[m]];
case kl of
1,3: rez:=mnsl; { rez - результат}
2,4: begin
rez:=mnsl;
mn:=mnsl;
end
end
end
else begin
mnsl:=[];
for m:=1 to i-j do
if (sl[m] in b) then mnsl:=mnsl+[sl[m]];
case kl of
1: rez:=rez*mnsl;
3: rez:=rez+mnsl;
2,4: begin
rez:=rez+mnsl-(mnsl*mn);
mn:=mn+mnsl;
end
end
end;
i:=i+1; j:=i;
end;
if kl=4 then rez:=mn-rez;
end;
begin
repeat
writeln(' Введи ключ = 1..4 ');
readln(key);
writeln(' введите исходную строку или ввод');
readln(st); { чтение исходной строки}
if length(st)<>0 then
begin
writeln('Исходная строка');
writeln(st);
prinmn(key,st,rezul);
case key of
1: writeln(' гласные, которые входят в каждое слово');
2: writeln(' гласные, входящие только в одно слово');
3: writeln(' гласные, входящие хотя бы в одно слово');
4: writeln(' гласные, входящие более чем в одно слово');
end;
for ch:=#0 to #255 do if ch in rezul then write(ch:2);
writeln;
end
until length(st)=0;
end.
