Многогранники
| Вид материала | Пояснительная записка |
- Многогранники, правильные многогранники, 77.69kb.
- Тема реферата, 246kb.
- Тема реферата, 244.57kb.
- Составьте конспект правильные многогранники Полуправильные многогранники Это интересно, 136.81kb.
- Региональный методический конкурс образовательных учреждений Костромской области Методическая, 197.94kb.
- «Многогранники», 183.59kb.
- Пискун Юлия Смирнова Ксения «Многогранники» реферат, 14.25kb.
- Многогранники в природе, 74.46kb.
- Тема урока: «Введение в стереометрию». «Правильные многогранники» (9класс, 2 часа),, 124.03kb.
- Программа V всероссийской научной школы «математические исследования в естественных, 30.28kb.
МОУ ЛИЦЕЙ №49
МНОГОГРАННИКИ
Автор: Бугрышева
Татьяна Николаевна
Калининград, 2007
Пояснительная записка.
Данный урок по теме: «Многогранники» в 10 филологическом классе был представлен в ходе проведения педсовета «Возможности и приемы взаимодействия в процессе работы с информацией. Обмен информацией». Учитывая тему педсовета и профиль класса, я выбрала 2 основных направления и попыталась реализовать их на уроке:
| Работа с текстом и приемы работы с ним:
| Взаимодействие учащихся в процессе работы с информацией:
Задачи:
|
Основной целью этого урока является формирование у школьников целостного представления о картине мира путем организации многостороннего анализа предмета изучения (темы)
P.S. Пункты хода урока (1, 2 и т.д.) соответствуют номерам страниц прилагаемой рабочей тетради, созданной для этого урока.
Эпиграфы
Однажды обыкновенный английский мальчик Джеймс, увлекшись изготовлением моделей многогранников, написал в письме отцу: «…я сделал тетраэдр, додекаэдр и еще два эдра, для которых не знаю правильного названия». Эти слова ознаменовали рождение в пока еще ничем не примечательном мальчике великого физика Джеймса Кларка Максвелла.
«Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук».
Льюис Кэролл
Введение.
Учитель: Тема нашего урока «Многогранники». Когда Вы спросили меня: «Это будет урок по алгебре или по геометрии?» Я ответила: «По геометрии». Интересно, а если в конце урока я задам вам встречный вопрос: «А сколько именно чисто геометрического материала было сегодня нами охвачено? Были ли найдены точки соприкосновения с другими предметами?»
Сейчас, учитывая тему, давайте попытаемся сформулировать задачи, которые мы поставим перед собой на этот урок (их формулируют дети, выдвигая свои вопросы и пожелания, что бы они хотели узнать на этом уроке). Например:
- Сколь значимы многогранники в нашей жизни?
- Являются ли они абстракцией, выдумкой человека, лишь искусственно привязанной к реальной жизни?
- К чему привело изучение многогранников учеными древности, средних веков и настоящих дней?
Обозначенная нами проблема получилась скорее не математического, а философского плана. В конце урока мы вернемся к поставленным вопросам и попытаемся ответить на них.
1
Знакомимся с определением пирамиды и из 5 предложенных геометрических тел выбираем те, которые являются пирамидами (индивидуальная работа).
Есть ли среди них «знакомые незнакомцы?» (Да, тетраэдр). Ученица читает стихотворение В. Брюсова, посвященное пирамидам.
Ощущение незыблемости и вечности пирамид всегда приводило воображение в трепет. Сколько столетий простояли они и сколько им еще предстоит нести над пустыней свой гордый и божественно простой очерк!
Все минет. Как льется вода,
Исчезнут в веках города,
Разрушатся стены и своды,
Но будет звучать наш завет
Сквозь сонмы мятущихся лет!
Что в нас, то навек неизменно, -
Все призрачно, бренно и тленно, -
Песнь лиры, созданье резца,
Но будем стоять до конца,
Как истина под покрывалом Изиды,
Лишь мы, Пирамиды!
Строители наши в веках
Осилили сумрачный прах,
И тайну природы постигли,
И вечные знаки воздвигли,
Мечтами в грядущем паря.
Пусть канул их мир как заря
В пыланиях нового века, -
Но смутно душа человека
Хранит в глубине до сих пор,
Что знали – Орфей, Пифагор,
Христос, Моисей, Заратустра, друиды,
И мы, Пирамиды!
Используя определенные призмы, выясняем, являются ли оставшиеся объекты призмами. Названия каких призм вы уже знаете (параллелепипед, куб).
Какой многогранник называется правильным?
2
И все-таки самым интригующим свойством правильных тел является то, что их всего 5. Не случайно доказательством этого факта завершалась последняя, 13 книга «Начал» Евклида. Перейдем к работе со второй страницей нашей рабочей тетради. Ребята сами заполняют пропущенные места определения, затем определяют геометрию грани каждого объекта (используются слайды и модели тел).
Следующий очень важный момент – предлагается найти в таблице некоторую закономерность в графах «грани» и «вершины»; вводится понятие дуальности.
Заполняя последнюю колонку, учащиеся проделывают путь Декарта и Эйлера и пытаются сформулировать свой вывод. (Формула Эйлера)
Учитель:
Совершенство форм, присущее правильным многогранникам, являлось причиной того, что им приписывались различные магические свойства.
3
Учитель:
Во времена пифагорейского союза, а возможно, и в нем самом, в древнегреческой философии родилась концепция 4 стихий – первооснов материального мира: огня, воздуха, воды и земли. Согласно некоторым античным источникам, четыре космические стихии были геометризированы самим Пифагором: атом каждой стихии мыслился в виде определенного правильного многогранника. Видимо, это близко к истине, т.к. впоследствии, когда эта идея была блестяще развита Платоном в диалоге «Тимей», это послужило поводом для обвинения Платона в плагиате пифагорейских книг.
Ученик:
Попытаемся восстановить пропущенные места цитат из диалога Платона «Тимей» и распределить правильные многогранники по стихиям. Но стихий всего 4, а многогранников – 5. Для 5ого Платон вводит пятый элемент – «пятую сущность», атомам которого придается форма наиболее близкого к шару, самому совершенному телу на земле, многогранника - … (додекаэдр). Атомам земли Платон придал форму самого неподвижного и устойчивого многогранника, ибо земля неподвижна и устойчива – это … (куб). Атом огня символизировал многогранник, острый, похожий на пламя свечи - … (тетраэдр). Вода отличается текучестью, и ее атомы символизировали самый «катящийся» многогранник – это … (икосаэдр). Воздух движется в разные стороны и оставшийся многогранник – октаэдр, как бы направленный в разные стороны, символизирует атом воздуха.
(У каждого ученика на парте рисунки 5 многогранников, обсуждая, ребята распределяют их по стихиям и расклеивают их в соответствующие окошки таблицы)
Учитель:
Конечно, пифагорейско-платоновская теория пяти стихий Мировоздания вызывает сегодня лишь вежливую улыбку. Но это была одна из первых попыток - чего? ( Обсуждение – возможно, кто-то из участников обсуждения предложит вариант «систематизация»).
4
Учитель:
Правильные многогранники на протяжении всей истории человечества не переставали восхищать пытливые умы симметрий, мудростью и совершенством форм. Леонардо Да Винчи любил мастерить каркасы правильных тел и преподносить в дар знатным особам, возможно, пытаясь таким образом приобщить сильных мира сего к философским размышлениям о красоте вечных истин.
Другим знаменитым художником эпохи Возрождения, увлекавшимся геометрией, был Альберт Дюрер. В его известной гравюре «Меланхолия» на переднем плане изображен додекаэдр. В 1525г. Дюрер написал трактат, где представил 5 правильных многогранников, поверхности которых служат хорошими моделями перспективы.
На картине Сальвадора Дали «Тайная вечеря» (1955г.) Христос и его ученики изображены сидящими внутри огромного прозрачного додекаэдра.
К 4 листу рабочей тетради задания по группам:
1группа: найти и выделить в тексте, что называется полуправильными телами Архимеда, сколько их, как они могут быть получены.
2группа: в тексте найдите объяснение того, что означают слова «снятие равных фасок».
3группа: найти и выделить в тексте материал, касающийся звездчатых многогранников.
4группа: в тексте этой страницы встречается довольно много фамилий знаменитостей. Из работы, подготовленной учениками заранее, выбрать самые интересные сведения о некоторых из них.
На работу этих 4-х групп отводится 3-4 минуты, затем группы прекращают обсуждения и выслушивают ответ представителя каждой группы, делая необходимые пометки на широких полях этой страницы. Таким образом, у каждого ученика должно быть представление и верный ответ на задания всех групп.
5
Но созвездию 5-ти Платоновых тел суждено было еще раз вспыхнуть на небосводе естествознания.
Сообщение ученика:
Модель Солнечной системы «космический кубок Кеплера» (во время прослушивания сообщения учащиеся записывают в рабочей тетради основные положения выступления).
Все та же пифагорейская вера в гармонию привела Иоганна Кеплера к озарению: существует 5 Платоновых тел и только 6 планет (известных на то время). Вряд ли это случайно, рассуждал Кеплер, значит, сферы планет связаны между собой вписанными в них Платоновыми телами. Вся модель будет иметь единый центр, которым и будет наше светило Солнце.
Остальное было делом техники. Проделав огромную вычислительную работу, испытав сотни вариантов, в 1596г. безызвестный 24-летний учитель Иоганн Кеплер в маленькой книжке «Тайна мироздания» опубликовал формулу своего открытия. В сферу обриты Сатурна он вписывает куб, в куб – сферу Юпитера, в сферу Юпитера – тетраэдр. И так далее последовательно вписываются друг в друга сфера Марса – додекаэдр, сфера Земли – икосаэдр, сфера Венеры – октаэдр. В едином центре всей системы коперниканец Кеплер помещает Солнце. Тайна мироздания кажется раскрытой! Вселенная устроена на основе единого геометрического принципа! Ликующий Кеплер мечтает изготовить свою модель Вселенной в виде серебряного кубка. Сегодня, когда открыты еще 3 планеты, таинственная связь между планетными расстояниями и свойствами правильных многогранников рассыпалась окончательно и модель Кеплера может служить не более чем изящным упражнением по стереометрии. Однако червь сомнения поселился в душе Кеплера из-за того, что не все вычисления были столь точны, как хотелось педантичному ученому. Можно сказать, что оставшиеся 30 лет жизни Кеплер посвятил спасению своей модели Вселенной от самого себя. Эта работа привела к открытию истинных астрономических законов – 3-х знаменитых законов Кеплера, на базе которых Ньютон построил свою теорию тяготения. Сам же Кеплер, «светлый мистик», так в полной мере и не осознал своих истинных открытий и до конца жизни больше всего ценил свою изящную юношескую работу.
Сообщение ученика:
Гипотеза об икосаэдро-додекаэдровой структуре Земли. (Во время прослушивания сообщения учащиеся фиксируют в рабочей тетради основные положения, тезисы).
Идеи Пифагора, Платона, Кеплера о связи правильных многогранников с гармоничным устройством мира нашли свое продолжение в интересной научной гипотезе, которую в начале 80-х годов прошлого столетия высказали московские инженеры В.Макаров и В.Морозов. Они считают, что ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете. Лучи этого кристалла, а точнее, его силовое поле, обуславливает икосаэдро-додекаэдровую структуру Земли. Она проявляется в том, что в земной коре проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра. Многие залежи полезных ископаемых тянутся вдоль этой сетки: 62 вершины и середины ребер многогранников, называемых авторами узлами, обладают рядом специфических свойств. В них располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити, Обская культура. В этих точках наблюдаются максимуму и минимумы атмосферного давления, гигантские завихрения Мирового океана. В этих узлах находятся озеро Лох-Несс, Бермудский треугольник.
6
Задания к таблице: Заполнить пропущенные колонки, слушая сообщения учителя и учеников, записывая вывод после коллективного обсуждения.
Учитель:
В связи с правильными многогранниками возник вопрос: можно ли ими заполнить пространство так, чтобы не было просветов? Оказалось, что есть только один способ заполнить пространство многогранниками только одного вида. Для этого нужно выбрать куб. В детстве каждый из нас, играя в кубики, много раз проделывал опыт такого «заполнения пространства». Но оказывается, что если использовать Платоновы тела 2-х видов: тетраэдры и октаэдры, то ими можно заполнить пространство таким образом (решетка Фуллера) – эта изящная решетка нашла широкое применение в строительных конструкциях, созданных архитектором Р.Б. Фуллером. Система Фуллера создается из алюминиевых трубок, образующих ребра своеобразных сот, ячейки которых имеют форму правильных тетраэдров и октаэдров. Знаменитые сетчатые перекрытия Фуллера – это решетчатые конструкции, в которых максимальная жесткость достигается при минимальных массе и стоимости.
Ученик:
Правильные многогранники встречаются и в живой природе. Например, скелет одноклеточного организма феодарии (Circogonia icosahedra) по форме напоминает икосаэдр. Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Интересно, чем может быть вызвана такая природная геометризация феодарий? Тем, по-видимому, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объем при наименьшей площади поверхности. (Что дает феодарии это свойство?)
Также икосаэдр оказался в центре внимания биологов в их спорах относительно формы некоторых вирусов.
Учитель (используя модели молекул химических элементов):
Природа широко пользуется тем, что правильные многогранники – самые выгоднее фигуры. Это подтверждает форма некоторых кристаллов. Например, поваренная соль, без которой мы не можем обойтись. Кристаллы поваренной соли имеют форму куба. Икосаэдр передает форму кристаллов бора. Получение серной кислоты, особых сортов цемента, железа не обходится без сернистого колчедана. Кристаллы этого химического вещества имеют форму додекаэдра. Кристалл алмаза – октаэдра. Давайте подробнее остановимся на прекрасных кристаллах алмаза.
7
Учитель:
Алмаз – самый дорогой и таинственный камень на Земле. Считается, что кристаллы алмазов обладают огромной энергетикой и являются носителями исторической информации, впитывая ее. В России лучшими друзьями девушек они стали не сразу, а всегда считались камнями царей. Природа алмаза капризна и для того, чтобы камень «заиграл», очень важно, чтобы он побывал в руках опытного гранильщика. Ведь только после огранки алмаз превращается в бриллиант. Поговорка «глаз-алмаз» тоже имеет смысл, т.к. природные алмазы используются в офтальмологии, для изготовления хрусталика глаза. Но, конечно, главное место алмазов – на ювелирном олимпе.
Задание ученика по группам:
Определить вид огранки коронки кольца (каждая группа получает свое кольцо для экспертизы).
Учитель:
Огранка розой состоит из полусферы с нанесенными на нее 24 правильно расположенными треугольными гранями. Изобретение этой формы огранки часто приписывают кардиналу Мазарини. (Жюль Мазарини стал кардиналом в 1640г, в 1842г заменил Рифелье на посту первого министра Франции и занимал эту должность до смерти. Он собрал великолепную коллекцию алмазов и завещал ее Французской короне). Существует несколько вариантов огранки розой.
Задание ученикам по группам:
Определить количество граней и их вид у голландской, полуголландской, антверпенской и крестовой розы.
Учитель:
Представленная в этом разделе информация – материал из книги Герберта Смита «Драгоценные камни» - эта книга уже много лет является одной из наиболее популярных книг, посвященной полезным ископаемым.
Заключение.
Обсуждаем поставленные в начале урока задачи (выступления учеников): идеи Пифагора и Платона оказались удивительного современными – это были первые попытки систематизации окружающего нас мира. Да, сегодняшнее Мироздание объемлет не 5 стихий, а чуть более 100 атомов элементов, из которых состоит вся материя.
Гениальное предвидение Пифагора о том, что математика откроет человечеству двери к тайне Мироздания, сбылись, хотя ждать пришлось более 2-х тысячелетий.
Спасибо за урок!
Рабочая тетрадь
- Многогранник, составленный из n-угольника A1А2…Аnи n треугольников называется пирамидой.
- Многогранник, составленный из двух равных многоугольников A1A/…An и B1B2…Bn, расположенных в параллельных плоскостях, и n параллелограммов, называется призмой.
- Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники в каждой его вершине сходится одно и то же число ребер.
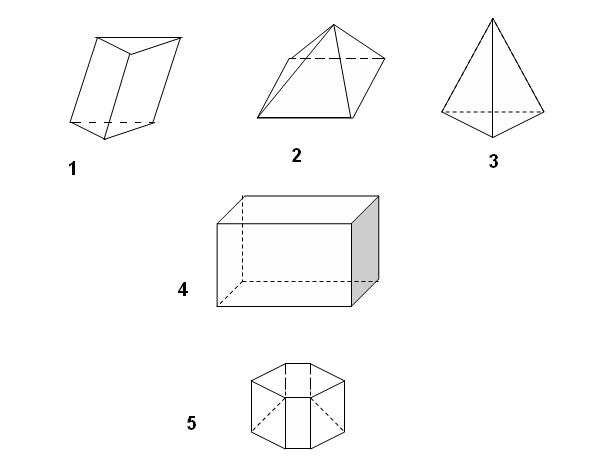

| Тетраэдр | Куб | Октаэдр | Додекаэдр | Икосаэдр |
Правильные многогранники.
Их форма – образец совершенства. Вы можете заметить ряд интересных особенностей, благодаря которым они получили свое название. Так, у каждого из них все грани – одинаковые , в каждой вершине многоугольника сходится одно и то же число ребер, а соседние грани сходятся под равными углами.
Подсчитаем число вершин (B), ребер (P) и граней (Г) у каждого многогранника и запишем результат в таблицу.
| название | Геометрия грани | Грани (Г) | Вершины (В) | Ребра (Р) | В+Г-Р |
| Тетраэдр | | 4 (тетра) | 4 | 6 | |
| Октаэдр | | 8 (окто) | 6 | 12 | |
| Гексаэдр | | 6 (гекса) | 8 | 12 | |
| Икосаэдр | | 20 (икоси) | 12 | 30 | |
| Додекаэдр | | 12 (додека) | 20 | 30 | |
«Эдра»(греч.) – грань.
| В+Г-Р = |
Эта формула была «подмечена» Декартом в 1640г., а позже доказал это удивительное соотношение Леонард Эйлер (1707-1783), один из величайших математиков, поэтому формула названа его именем. Она верна не только для правильных, но и для всех выпуклых многогранников.
Пять стихий мироздания Платона.
«… всему, что имело произойти, надлежало, конечно, быть телесным, видимым и осязаемым. Но быть видимым ничто не может без посредства , точно так же и осязаемым ничто не может быть без чего-нибудь твердого, твердым же ничто не может быть без ».
Платон, «Тимей».
«Невозможно чтобы две вещи совершенным образом соединялись без третьей».
Платон, «Тимей»
Поэтому между основными стихиями: и помещались две средние: и . В итоге все стихии оказывались связанными пропорцией:
Земля/вода = воздух/огонь
| Вселенная (Мировой эфир) | |
| Земля (устойчивость, неподвижность) | Воздух (движется во всех направлениях) |
| Вода (текучесть). Из всех правильных тел - самое «катящееся» | Огонь (острый, похожий на пламя свечи) |
Правильные многогранники называются также Платоновыми Телами.
Но на пяти правильных телах история многогранников не остановилась. Вслед за правильным телами Платона были открыты полуправильные тела Архимеда, грани которых составлены из правильных многоугольников нескольких видов, причем в каждой вершине сходится одно и то же число одинаковых граней в одинаковом порядке и многогранные углы при вершинах равны. Заметим, что тела Архимеда могут быть получены из соответствующих тел Платона снятием равных фасок. Тел Архимеда всего 13. Любопытно, что во второй половине ХХ в. Было обнаружено еще одно тело Архимеда - псевдоромбокубооктаэдр, которое не может быть получено путем однотипных усечений тела Платона и поэтому в течение 2000 лет оставалось незамеченным.
В XVII в. Кеплером и в XVIII в. Пуансо были найдены различные формы звездчатых невыпуклых многогранников, получаемых продолжением граней правильного или полуправильного тела до самопересечения. Простейшее тело такого типа – «Звезда Кеплера» - было обнаружено Кеплером в 1619г. и получается продолжением граней октаэдра. Впрочем, это же тело можно представить и как пересечение двух тетраэдров. Звездчатые многогранники поражают воображение красотой и причудливым разнообразием своих форм. Тем, кого вдохновит эта форма, мы рекомендуем книгу М. Венниджера «модели многогранников» (М.: Мир, 1974), познакомившись с которой можно на свой вкус выбрать и сделать самый экзотический звездчатый многогранник.
И все-таки знакомство с многогранниками мы советуем начать с «Начал» Евклида, ибо, как сказал Альберт Эйнштейн, «Тот не рожден для теоретических исследований, кто в молодости не восхищался этим творением».
Правильные звездчатые многогранники (Тела Кеплера – Пуансо)

Модель Солнечной системы «Космический кубок «Кеплера»»

Гипотеза об икосаэдро-додекаэдровой структуре Земли.
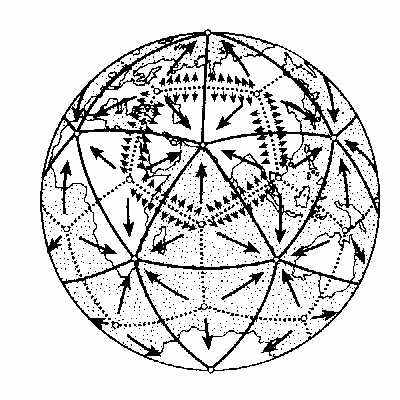
Благодаря правильным многогранникам открываются не только удивительные свойства геометрических фигур, но и пути познания природной гармонии…
| Объект | Виды многогранников. Свойства объекта. | Область знаний. |
| Решетка Фуллера  | | |
| Ф  еодария еодария | Circogonia icosahedra | |
| Поваренная соль (NaCl)  | | |
| Бор (B) 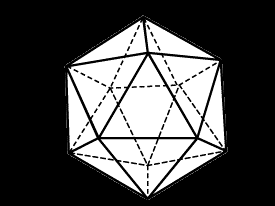 | | |
| Сернистый колчедан (FeS) 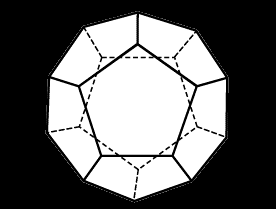 | | |
| Кристаллы алмаза  | | |
