Arch процессы. Определение, модели, приложения

Вид материала

Документы

Содержание 2.3 Обобщенный метод моментов ОMM оценки асимптотически более эффективны, чем оценки МКМП

Подобный материал:

• Служебные программы : очистка диска, восстанов­ле­ние системы (точки отката), дефрагментация, 21.88kb.
• Эконометрика2 Лекция 6 arch, garch модели, 12.91kb.
• Определение системы. Сложные системы. Системный подход, 23.24kb.
• Лекция: Спецификация функциональных требований к ис: Процессные потоковые модели. Процессный, 308.8kb.
• Программа дисциплины Многомерные модели для волатильности и их приложения в финансовых, 97.34kb.
• Шкаберин В. А. Определение математической модели. Преимущества математического моделирования., 66.58kb.
• Лекция №2 Тема: «Алгоритм информационная модель явления, процесса или объекта», 95.01kb.
• Программа заседаний Секции Математической экономики Международной школы семинара «Методы, 32.87kb.
• Краткое содержание: Прямая задача динамики машин. Понятие о динамической модели машины, 252.59kb.
• Математическое моделирование и методы оптимизации Общая трудоемкость изучения дисциплины, 22.02kb.

2.3 ОБОБЩЕННЫЙ МЕТОД МОМЕНТОВ

Обобщенный метод моментов (ОMM) обладает следующими достоинствами:

1. не требует явных предположений относительно плотности условного распределения и допускает присутствие ненулевых куртозиса и асимметрии;
   
2. использует лишь производные первого порядка функци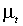й и 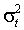и позволяет избежать тем самым применения методов численного дифференцирования;
   
3. асимптотически более эффективен, чем МКМП. Проверка метода на выборочных данных, демонстрирующих экстремально высокие коэффициенты асимметрии и куртозиса, свидетельствует о значительном выигрыше в эффективности.
   

Дополним модель (М.1)-(М.4) предположениями относительно третьего и четвертого моментов распределения :

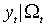(М.5)

(М.6) ,

где - постоянные коэффициенты асимметрии и куртозиса. Стандартизованные остатки в точке 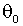тогда имеют первые четыре момента, равные соответственно 0, 1, . Гипотеза нормальности формулируется как .

Спецификация (М) обеспечивает две группы уравнений, идентифицирующих истинные значения параметров. Пусть



– строка из двух элементов, которую далее будем обозначать, опуская аргументы 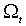и . Мат. ожидания существуют для всех    и обращаются в ноль единственным 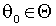. В этом смысле система уравнений

(3.19)

идентифицирует истинный вектор параметров. Определим условные матрицу ковариации и якобиан в точке 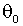как

(3.20)

(3.21) .

Класс оценок ОММ порождается различными наборами инструментальных переменных, выбор которых ограничен последовательностью 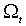. Асимптотическая ковариационная матрица ОММ оценок ограничена снизу, причем существует набор оптимальных инструментов, приводящий к эффективным оценкам.

Пусть l инструментов могут быть организованы в матрицу размерности l 2n, где - часть матрицы размерности l 2, относящаяся к наблюдению t (вклад данного наблюдения в матрицу инструментов). Требуется, чтобы число инструментов было не меньше числа оцениваемых параметров, т.е. l  m, и чтобы к моменту t значения были известны: ; можно указать бесконечное число инструментальных переменных. Эмпирические моменты, соответствующие данному набору инструментов могут быть выражены как

(3.21) .

Матрица условной ковариации эмпирических моментов в точке 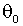равна

(3.22) .

Если l=m, то оценки 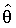находятся решением системы m уравнений

(3.23) ,

если l>m, то минимизацией критериальной функции – квадратичной формы, построенной из (3.21) и (3.22):

(3.24) .

При любом выборе инструментов оценки, определяемые (3.23) или (3.24), состоятельны и асимптотически нормальны с асимптотической матрицей ковариации

(3.25)

.

Инструменты W, такие что , приводят к оценкам, эффективным в классе ОММ. Существует ровно m оптимальных инструментов, поэтому эффективные оценки находятся решением системы

(3.26) .

Асимптотическая матрица ковариации таких оценок меньше, чем при любом ином выборе инструментов:

(3.27) .

Воспользуемся матрицами размерности l 2n, размерности m 2n, блочно-диагональной матрицей  размерности 2n 2n с диагональными блоками . Тогда участвующие в (3.25) и (3.27) суммы записываются как , , . Опустим знаки plim, множители и рассмотрим разность



между обращенными матрицами ковариации, относящимися к оптимальному и произвольному наборам инструментов, соответственно. Если симметричная 2n 2n матрица  такова, что , то разность данная равна

.

Эта матрица положительно полуопределена, поскольку матрица в больших скобках идемпотентна. Отсюда немедленно следует положительная полуопределенность

.

Оптимальные в классе ОMM оценки асимптотически более эффективны, чем оценки МКМП. Достаточно показать, что асимптотическая матрица ковариации последних приводима к виду (3.25) с помощью какого-либо набора неоптимальных инструментов. Вклад наблюдения t в этот набор инструментов представляет собой матрицу , вычисленную при :

(3.28) .

Если коэффициенты асимметрии и куртозиса действительно равны нулю, то такой набор инструментов является оптимальным. Следовательно, при верной гипотезе (N) методы моментов и максимального правдоподобия асимптотически эквивалентны.

Выбор инструментов (3.28) приводит к следующим совпадениям:

 

• эмпирических моментов и градиента критериальной функции