Учебно-методический комплекс учебной дисциплины «механика, основы механики сплошных сред» вузовского компонента цикла опд. Ф. 1 для специальностей 010400 физика и 013800 радиофизика и электроника составитель

Вид материала

Подобный материал:

1 2 3 4 5 6 7 8 9 10 11

ТЕСТИРОВАНИЕ

ТЕСТЫ

Число степеней свободы частицы в поле тяжести
1. 1
2. 2
3. 3
Число колебательных степеней свободы молекулы из N атомов
1. 3N
2. 3N-3
3. N
4. 3N-6
Функция Лагранжа 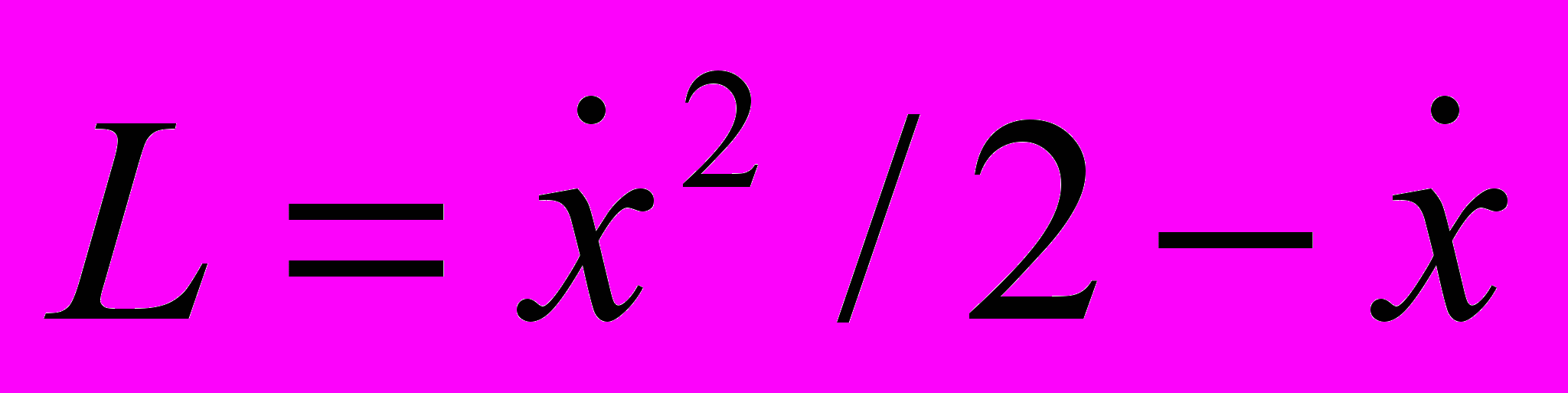есть функция Лагранжа
1. Свободной частицы
2. Частицы в ускоренной системе отсчета
3. Частицы в среде с линейной вязкостью
Полный интеграл уравнения Гамильтона-Якоби свободной частицы имеет вид
1. S = ax + bxt + c
2. S = ax + bt + c
3. S = (ax + bt)x + c
У частицы в поле тяжести (ось z направлена вертикально) сохраняются
1. Энергия и полный импульс
2. Энергия и x, y-компоненты импульса
3. Момент мпульса и x, y-компоненты импульса
Частица с функцией Лагранжа 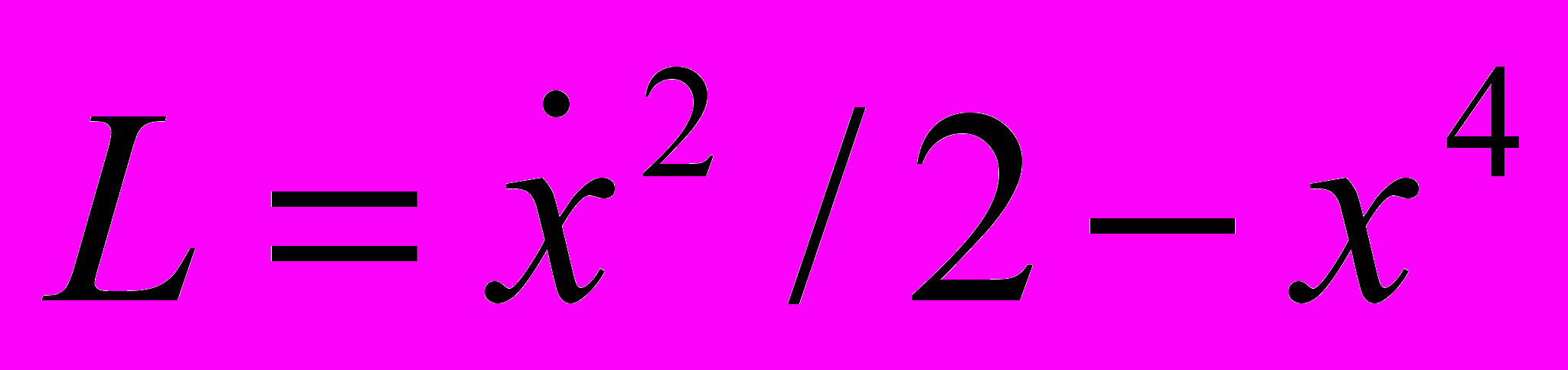совершает при всех начальных условиях
1. Инфинитное движение
2. Гармонические колебания
3. Нелинейные колебания
Функция Гамильтона гармонического осциллятора имеет вид
1. H = p²/2 + x
2. H = p²/2 – x²
3. H = p²/2 + x²
Сила инерции, действующая на частицу массы m в системе отсчета, движущейся с ускорением W, равна
1. mdW/dt
2. –mW
3. mW
4. -mW²/2
Число степеней свободы трех частиц, связанных стержнями, равно
1. 3
2. 2
3. 6
Внутренняя энергия системы взаимодействующих частиц зависит
1. От относительных скоростей частиц
2. От положения их центра масс
3. От внешнего поля
Круговой конус расположен вертикально в поле тяжести вершиной вниз. Частица, движущаяся по внутренней поверхности конуса (трением пренебречь),
1. При некоторых начальных условиях упадет на вершину конуса
2. Упадет при всех начальных условиях
3. Не упадет ни при каких начальных условиях
Скорость диссипации энергии у гармонического осциллятора в среде при наличии гармонической вынуждающей силы
1. Не зависит от частоты вынуждающей силы
2. Растет с ростом частоты вынуждающей силы
3. Падает с удалением частоты вынуждающей силы от собственной частоты осциллятора
С уменьшением прицельного расстояния при рассеянии в кулоновском поле угол рассеяния
1. Ведет себя не монотонно (убывает, затем возрастает)
2. Монотонно убывает
3. Монотонно возрастает
Уравнение движения плоского математического маятника (угол φ отсчитывается от направления вниз) имеет вид
1. φ’’ = -sinφ
2. φ’’ = -φ
3. φ’’ = sinφ
Функция Гамильтона гармонического осциллятора с частотой ω после канонического преобразования к переменным действие J угол w имеет вид
1. H = Jw
2. H = ωJ
3. H = J²/2
Частица в виде бусинки насажена на стержень и может двигаться без трения. Стержень равномерно вращается около перпендикулярной ему оси. Сила реакции со стороны стержня
1. Не действует на частицу
2. Компенсирует силу Кориолиса
3. Вызывает центробежное ускорение
Направление оси симметрии свободного симметрического волчка
1. Всегда остается неизменным в пространстве
2. Равномерно вращается вокруг направления момента импульса
3. Колеблется по отношению к направлению момента импульса
Энергия свободного симметрического волчка с заданными моментами инерции
1. Не зависит от момента импульса
2. Зависит от момента импульса
3. Зависит только от величины момента импульса
Амплитуда колебаний гармонического осциллятора пропорциональна
1. Энергии
2. Квадратному корню из энергии
3. Квадрату энергии
Действие свободной классической частицы с единичной массой на прямой x и на интервале [(t=0,x=0); (t=1,x=1)] равно
1. ¾
2. ½
3. 1
Действие свободной релятивистской частицы с единичной массой на прямой x и на интервале [(t=0,x=0); (t=1,x=1/2)] равно (скорость света равна 1)
1. -√¾
2. ½
3. -1

ОТВЕТЫ НА ТЕСТЫ

Вопрос	1	2	3	4	5	6	7	8	9	10	11
Ответ	с	d	a	b	b	c	c	b	b	a	a

Вопрос	12	13	14	15	16	17	18	19	20	21
Ответ	c	b	a	b	b	b	b	b	b	a

ГЛОССАРИЙ

Ансамбль Гиббса	Совокупность одинаковых механических систем, находящихся в разных состояниях.
Аддитивность интегралов движения	Интегралы движения, значения которых для системы, состоящей из отдельных частей, взаимодействием которых можно пренебречь, равно сумме значений для каждой из частей в отдельности.
Апериодическое затухание	Движение, наблюдаемое при сильном трении и состоящее в асимптотическом приближении к состоянию равновесия
Биения	Вынужденные колебания, наблюдаемые при приближении частоты вынуждающей силы к собственной частоте системы. При биениях амплитуда колеблется с частотой, равной разности частот вынуждающей силы и собственных колебаний
Вариация	Функция, определяющая малые отклонения некоторой наперед заданной функции.
Внутренняя энергия	Энергия покоящейся как целое механической системы
Волчок	Шаровой волчок – твердое тело с одинаковыми главными моментами инерции, симметрический волчок – два из трех главных момента совпадают, асимметрический волчок – общий случай твердого тела с разными главными моментами инерции
Герполодия	Кривая, описываемая эллипсоидом инерции на неподвижной плоскости
Главные колебания	Колебания многомерного гармонического осциллятора, совершающиеся с определенными частотами
Действие	1.Функционал траектории в пространстве событий, вычисляемый как интеграл от функции Лагранжа системы по времени в некоторых фиксированных пределах. 2.Функция положения и времени, вычисляемая вдоль истинной траектории движения системы в пространстве событий. 3.Одна из канонических переменных, равная интегралу от импульса по замкнутой траектории движения.
Декремент затухания	Логарифмическим декрементом затухания называют произведение коэффициента затухания на период колебаний
Диссипативная функция	Определяет интенсивность диссипации энергии в системе
Задача двух тел	Задача о движении замкнутой системы взаимодействующих частиц
Закон инерции	В инерциальной системе отсчета всякое свободное движение происходит с постоянной по величине и направлению скорости
Законы Кеплера	1.Планеты движутся по эллипсам, в одном из фокусов которых находится Солнце. 2.За равные промежутки времени радиус-вектор планеты описывает равные площади 3.Квадраты времен обращения планет по орбитам пропорциональны кубам их размеров
Замкнутая система	Система частиц, взаимодействующих только друг с другом, но ни с какими посторонними телами
Замкнутые траектории	Траектории, формирующие замкнутые кривые
Звуковое поле	Поле, отвечающее гармоническим колебаниям среды около состояния равновесия
Изотропия пространства	Независимость уравнений движения системы от направления в пространстве
Инерциальная система отсчета	Система отсчета, по отношению к которой свободная частица движется равномерно и прямолинейно
Интеграл движения	Функция состояния, не изменяющая своего значения в процессе движения системы
Канонические уравнения	Форма записи уравнений движения механической системы, описываемой функцией Гамильтона
Ковариантность	Независимость формы записи уравнений от выбора переменных, определяющих состояние или положение системы
Линия узлов	Линия пересечения подвижной и неподвижной плоскостей XY при описании ориентации твердого тела в пространстве
Мгновенная ось вращения	Если поступательная и угловая скорости твердого тела взаимно перпендикулярны в некоторый момент времени, то всегда можно выбрать такое начало подвижной системы координат, что движение твердого тела в данный момент будет представлено как чистое вращение вокруг оси, проходящей через это начало.
Момент силы	Вектор, равный векторному произведению радиус-вектора частицы твердого тела в подвижной системе координат на силу, действующую на эту частицу
Нормальные колебания	Колебания (так же именуемые главными), которые совершаются многомерным гармоническим осциллятором с определенными (собственными) частотами
Обобщенная координата	Любая из полного набора величин, вполне характеризующих положение системы
Обобщенный импульс	Производная функции Лагранжа системы по обобщенной скорости
Однородное поле	Поле, во всех точках которого на частицу действует одна и та же сила.
Однородность времени, пространства	Не зависимость от времени уравнений движения. Обычно, так же, независимость от времени функции Лагранжа системы. То же для пространства – независимость от координаты (или всех координат)
Осциллятор	Система, совершающая малые колебания
Переменная действия	Интеграл по циклу изменения координаты от импульса. Используется в качестве одной из канонических переменных в гамильтоновой механике задач с ограниченным движением
Перигелий	Точка максимального сближения частицы с центром поля в задаче Кеплера
Полный интеграл	Решение уравнения Гамильтона-Якоби, зависящее от постоянных, число которых равно числу аргументов неизвестной функции действия
Преобразования Галилея	Преобразования координат в классической механике при переходе от одной системы отсчета к другой, движущейся равномерно и прямолинейно относительно первой. В релятивистской механике аналогичные преобразования называются преобразованиями Лоренца
Прецессия	Вращение оси симметрии свободного симметрического волчка относительно направления момента импульса
Производящая функция	Функция канонических переменных из новой и прежней системы фазовых координат, которая определяет преобразование (каноническое) от одной системы координат к другой
Резонанс	Явление возрастания амплитуды гармонических колебаний с приближением частоты вынуждающей силы к собственной частоте колеблющейся системы
Ротатор	Твердое тело, все частицы которого расположены вдоль прямой
Связи	Ограничения на положения и/или скорости частиц системы, фиксированные внешними условиями (физическими телами)
Секториальная скорость	Скорость, с которой радиус-вектор частицы описывает площадь
Собственная частота	Одна из частот колебаний многомерного гармонического осциллятора
Степени свободы	Число независимых координат, однозначно описывающих положение механической системы
Точка остановки	Точка, в которой скорость одномерной системы обращается в ноль
Угловая переменная	Одна из канонических переменных в описании движения интегрируемой ограниченной системы.
Фаза	Аргумент гармонической функции в законе движения осциллятора
Фазовая траектория	Траектория, вдоль которой изменяется состояние механической системы
Фазовое пространство	Область, заполненная всеми возможными фазовыми траекториями механической системы
Финитное движение	Движение, происходящее в ограниченной области пространства. Если область движения не ограничена, то движение называют инфинитным
Циклическая координата	Координата, от которой не зависит функция Лагранжа. Импульс, отвечающий циклической координате, сохраняется
Циклическая частота	Частота гармонических колебаний
Эксцентриситет	Безразмерный параметр траектории движения в задаче Кеплера
Эффективное сечение	Отношение потока рассеянных частиц пучка к плотности потока налетающих частиц в теории рассеяния

Blog

ТЕСТИРОВАНИЕ

ТЕСТЫ

ОТВЕТЫ НА ТЕСТЫ

ГЛОССАРИЙ