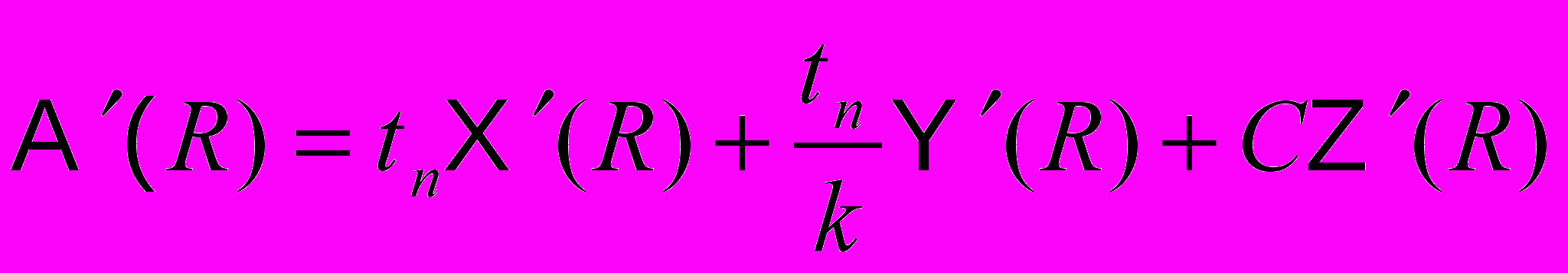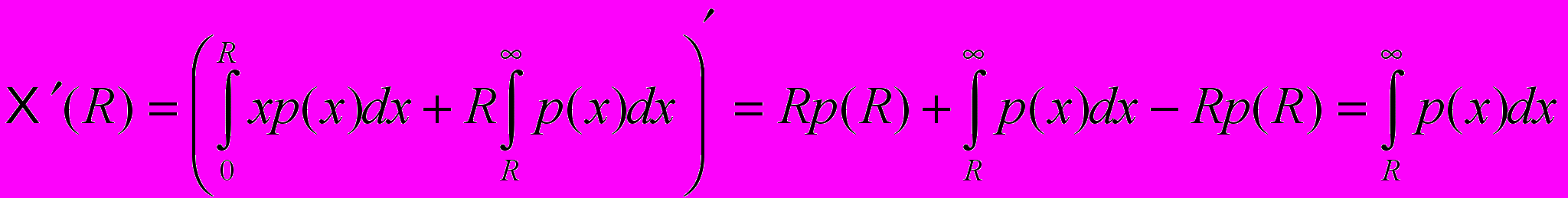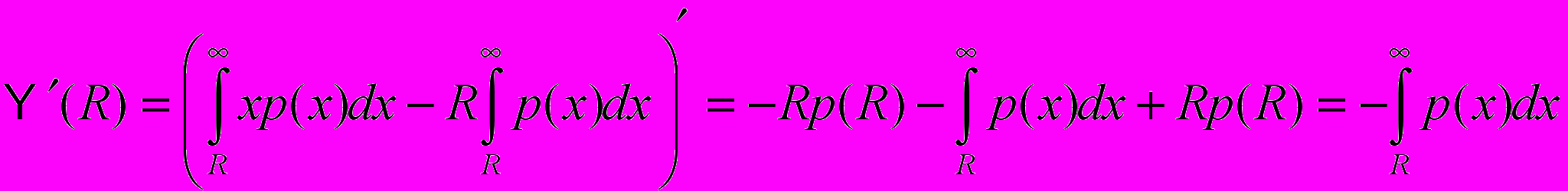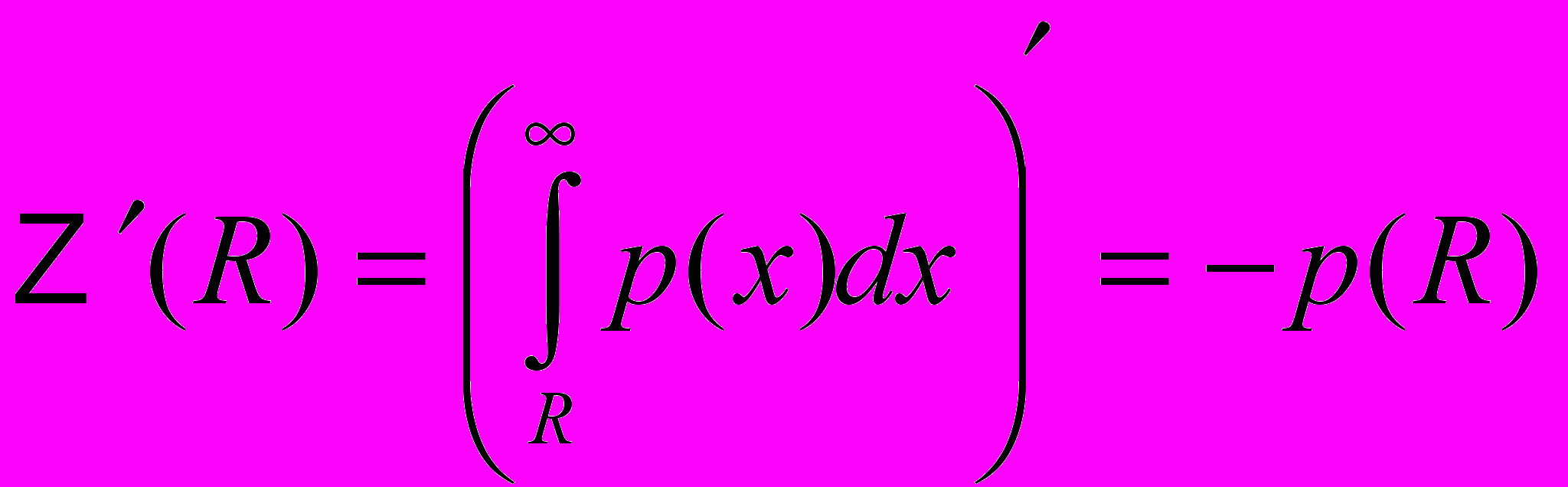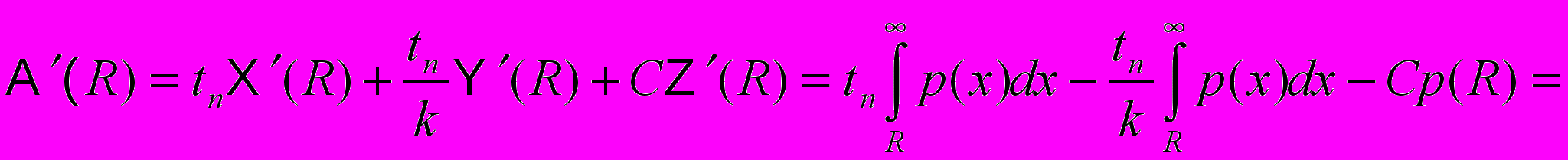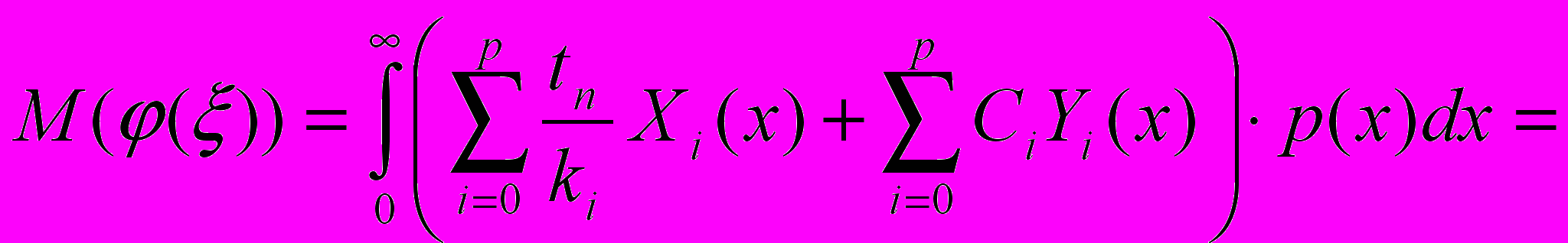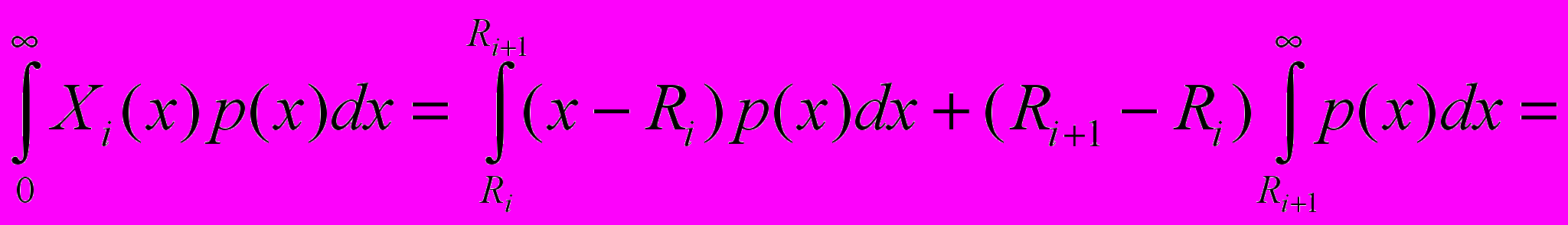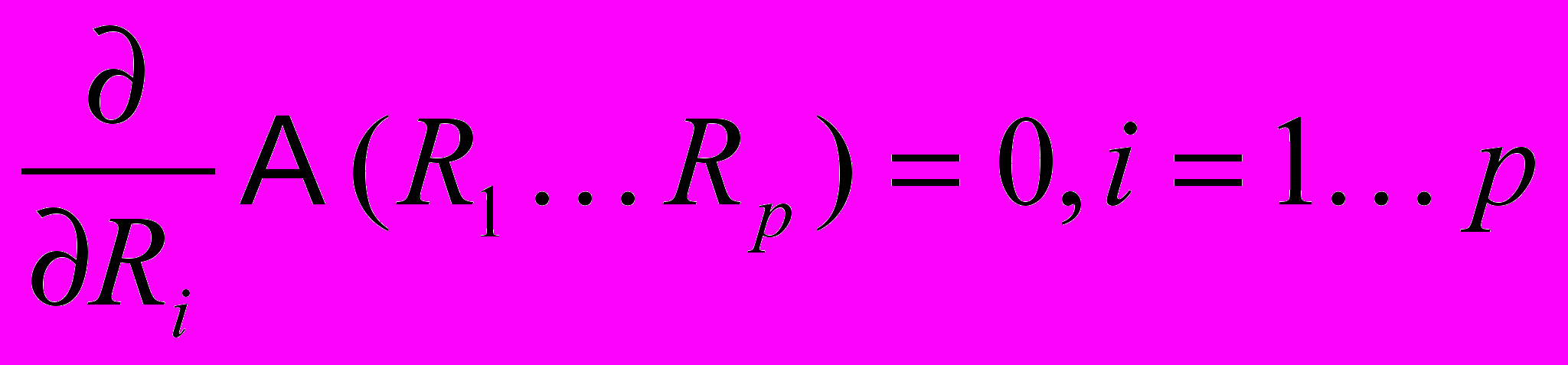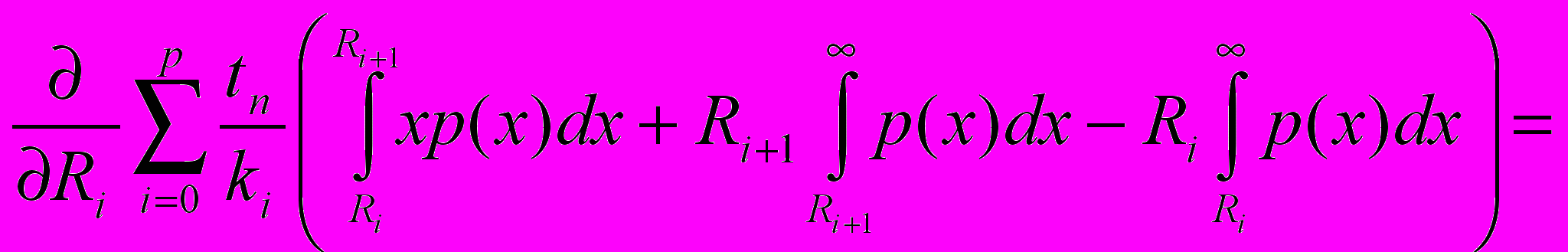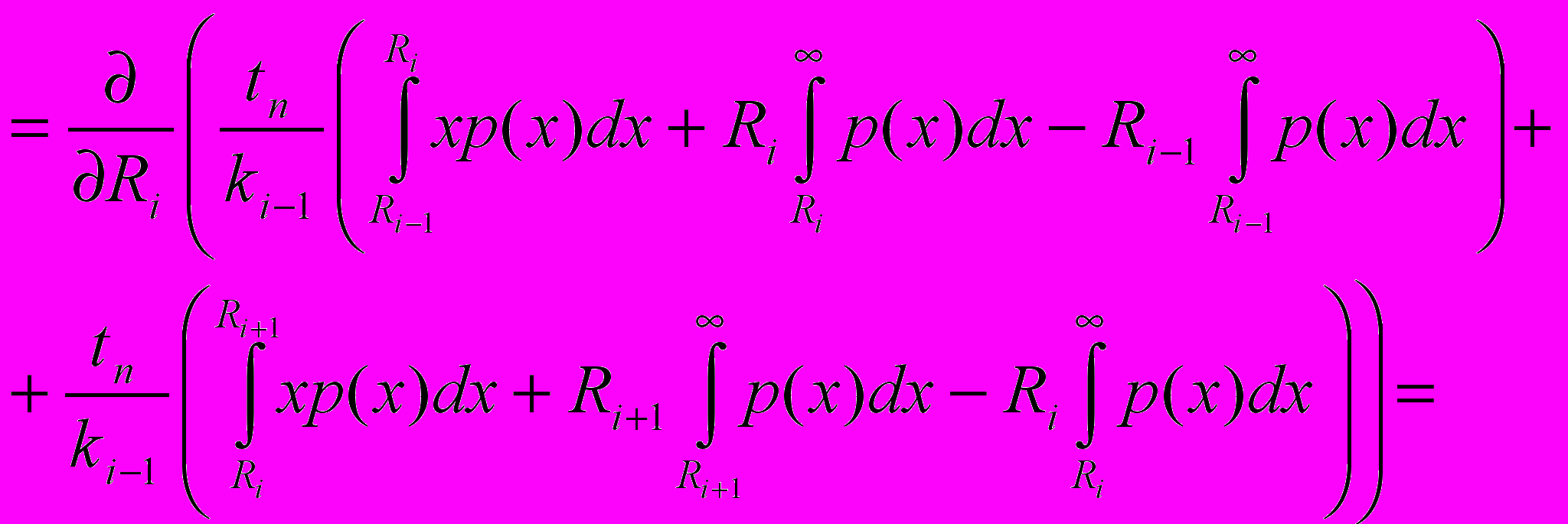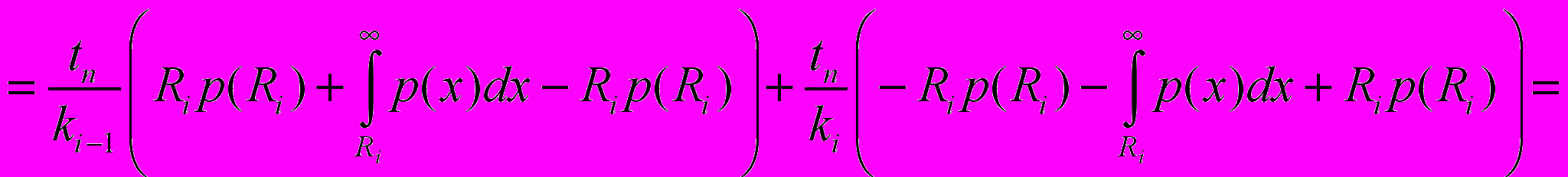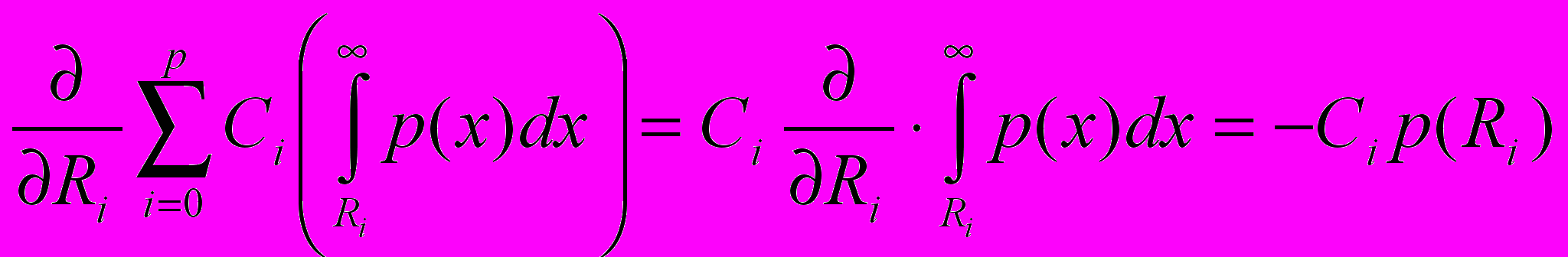Методы определения порогов активизации динамического оптимизирующего транслятора

Вид материала

Документы

Содержание 3. Нахождение статистически оптимального времени начала оптимизаций. 4. Нахождение статистически оптимального времени начала оптимизаций в многоуровневой системе.

Подобный материал:

• Соловьёва Марина Константиновна учитель истории. Г. Углич 2010 год Формы и методы активизации, 258.05kb.
• Программа курса лекций «Методы исследования макромолекул», 15.25kb.
• Разработка программы и определение методики изучения загрязнения почв при использовании, 202.22kb.
• «Методы обучения» содержание, 325.13kb.
• Пряжников Н. С. П77 Методы активизации профессионального и личностного самоопределения:, 5492.26kb.
• 1. Модели и критерии эффективности, 68.04kb.
• Экскурс в историю Простое и сложное поведение. Порядок в хаосе Прообразы динамического, 24.79kb.
• Семинар. Грабовой Г. П. «Система динамического управления» 17. 02. 2005, 2014.82kb.
• Лекция: История обнаружения и исследования динамического, 46.97kb.
• 1 Пути, формы и методы активизации познавательной деятельности младших школьников, 583.3kb.

3. Нахождение статистически оптимального времени начала оптимизаций.

Найдём минимум функции 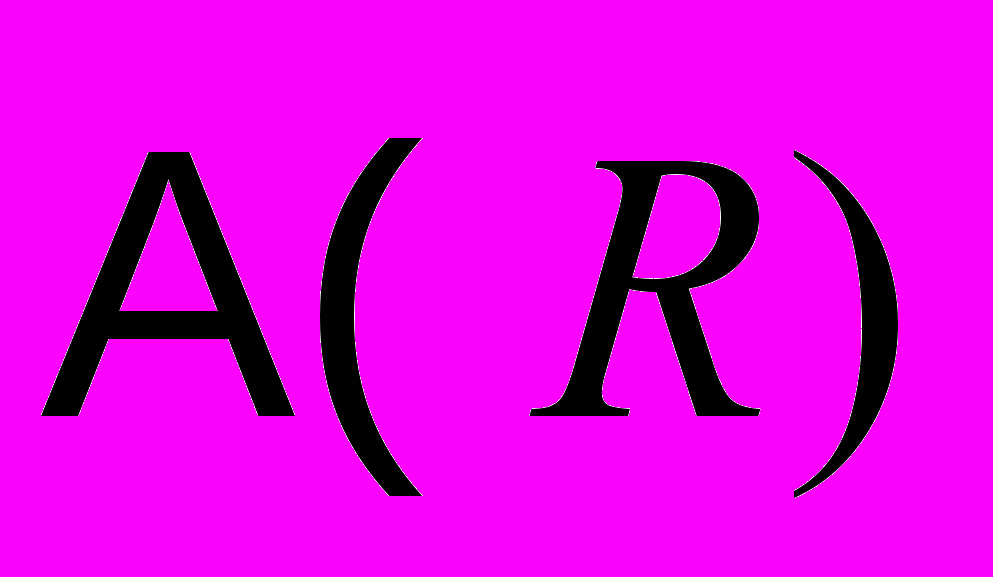из (1). Сначала преобразуем :

















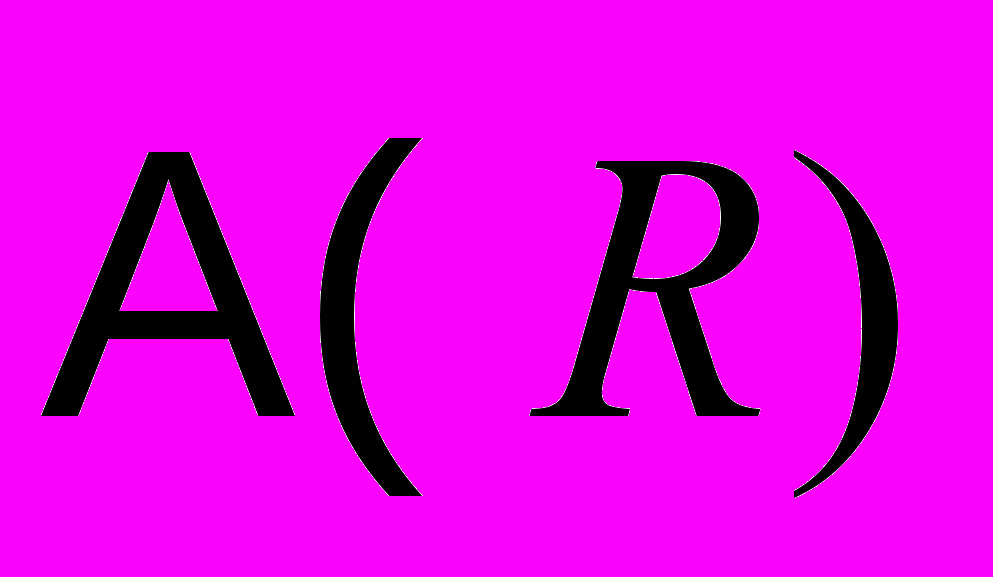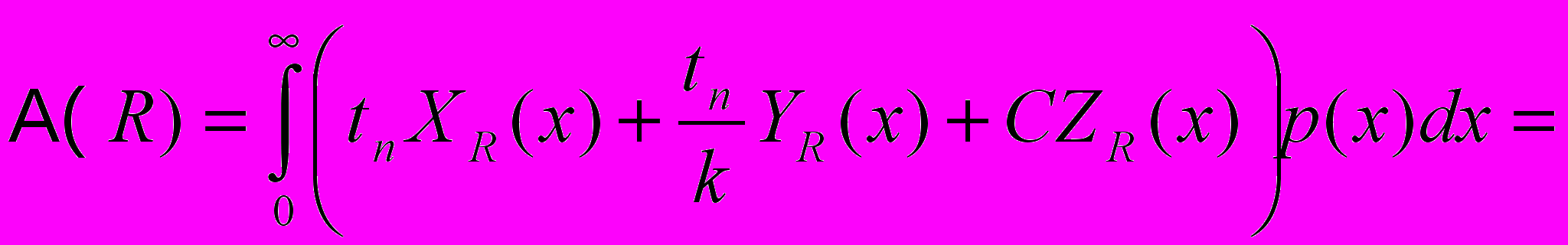
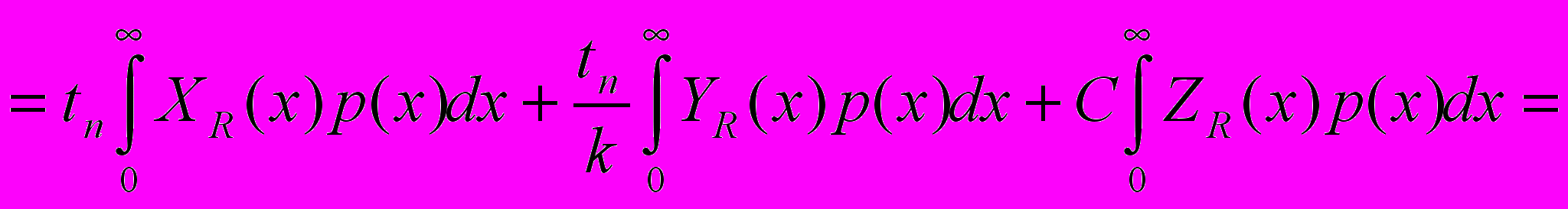
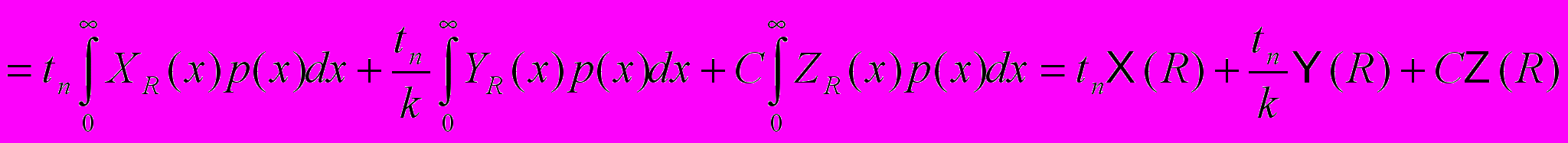
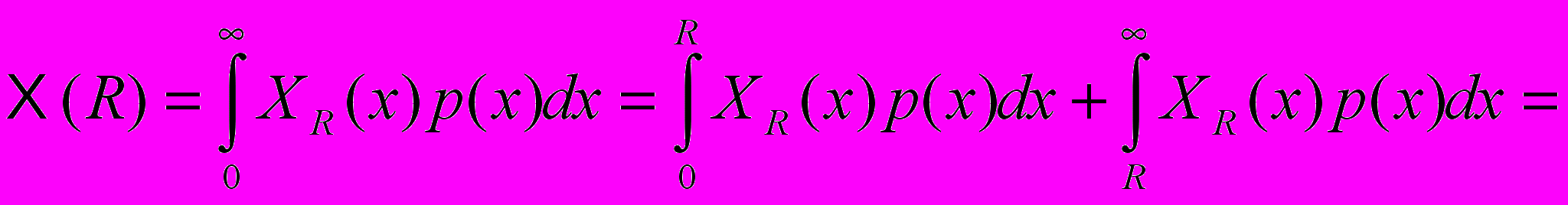
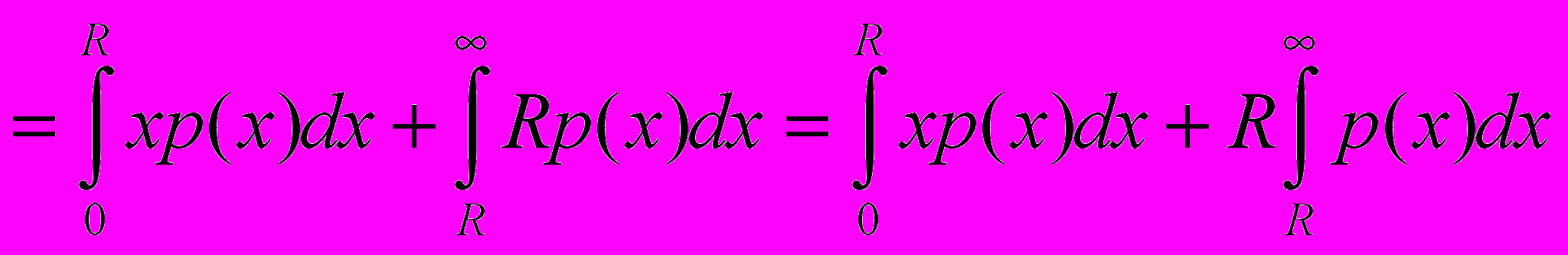
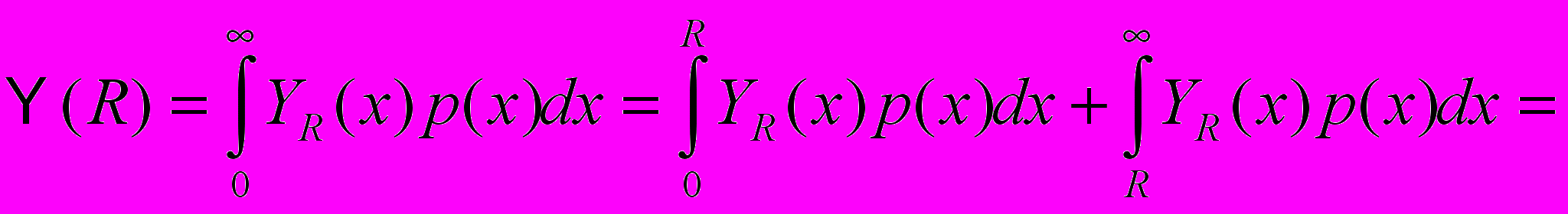
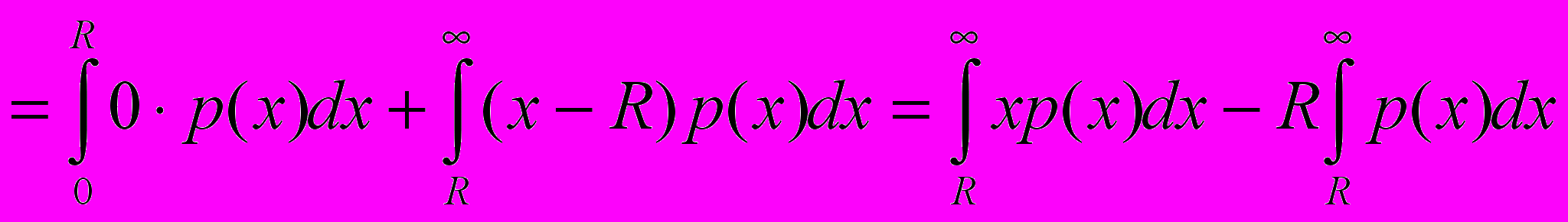
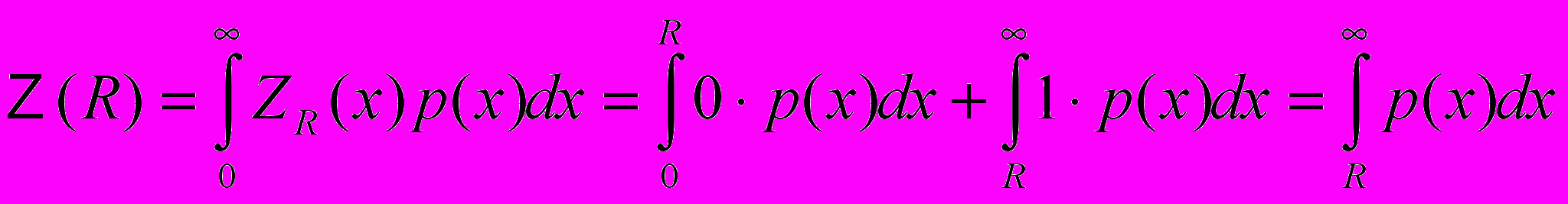
Найдём теперь производную :

2. 
   
3. 
   
4. 
   
5. 
   

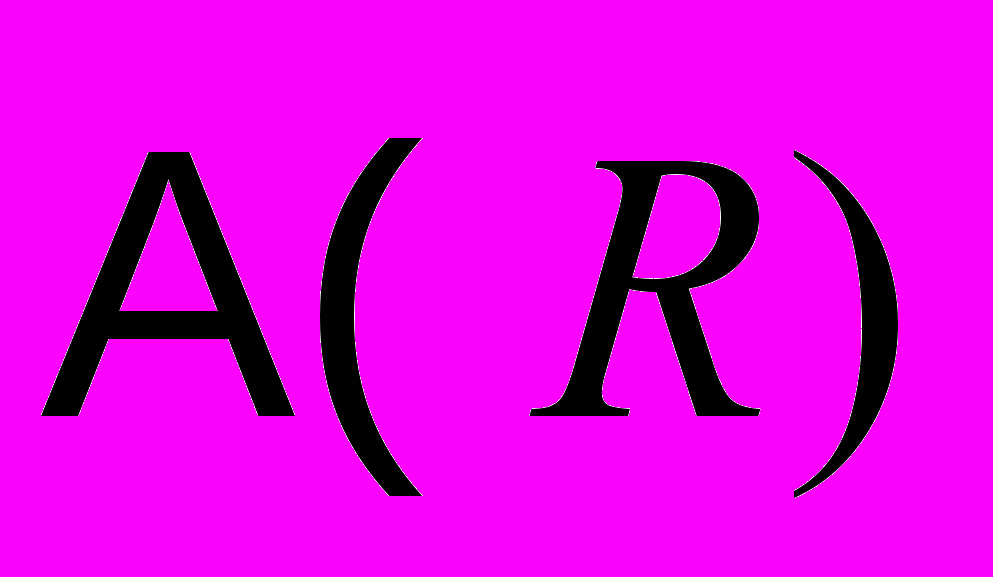Подставляя (3), (4), (5) в (2) получаем:

6. 
   

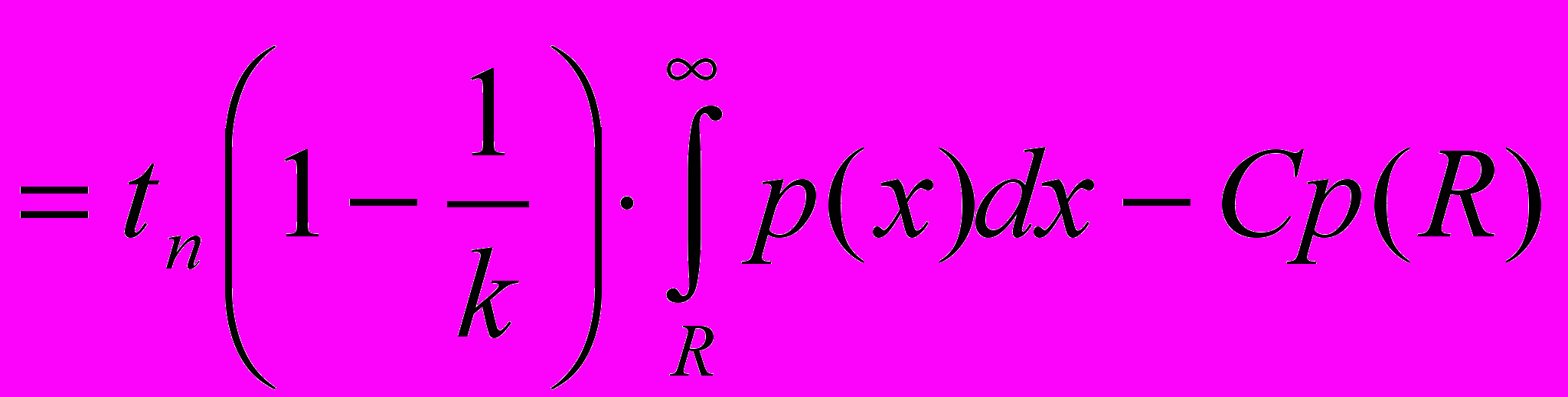
Приравнивая 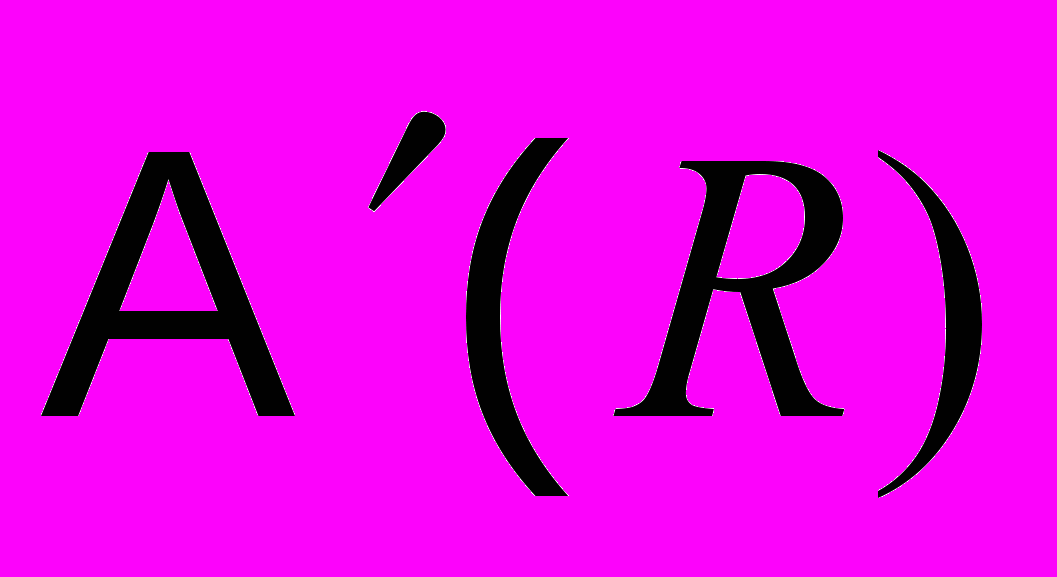нулю, получаем, что точки экстремума 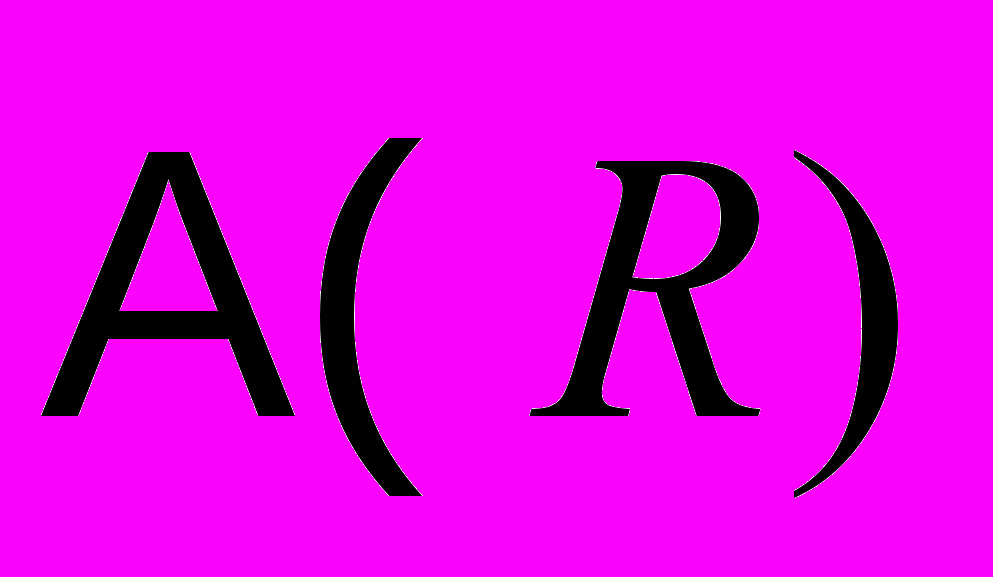достигаются в точках удовлетворяющих уравнению:

7. .
   

Таким образом, уравнения (7) является необходимым условием статистически оптимального время начала оптимизаций для двухуровневого двоично-оптимизирующего комплекса.

4. Нахождение статистически оптимального времени начала оптимизаций в многоуровневой системе.

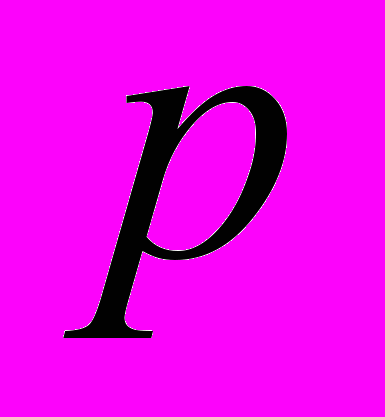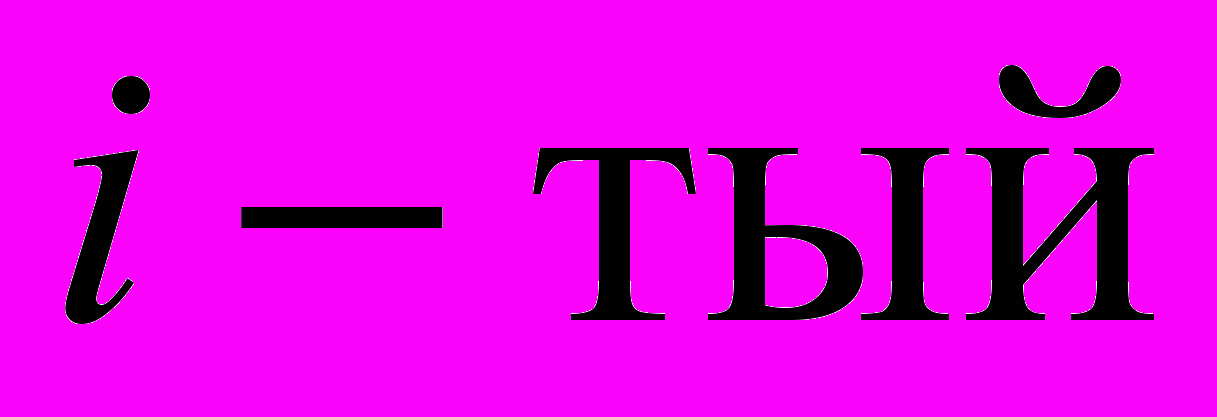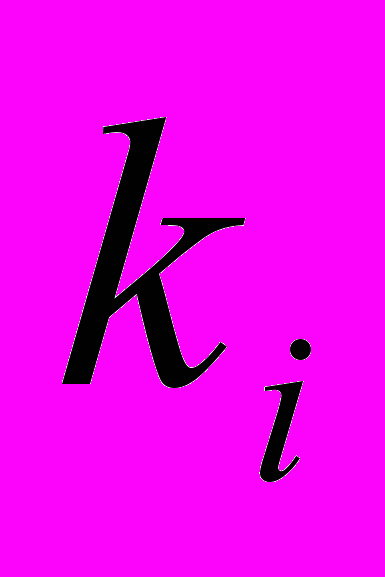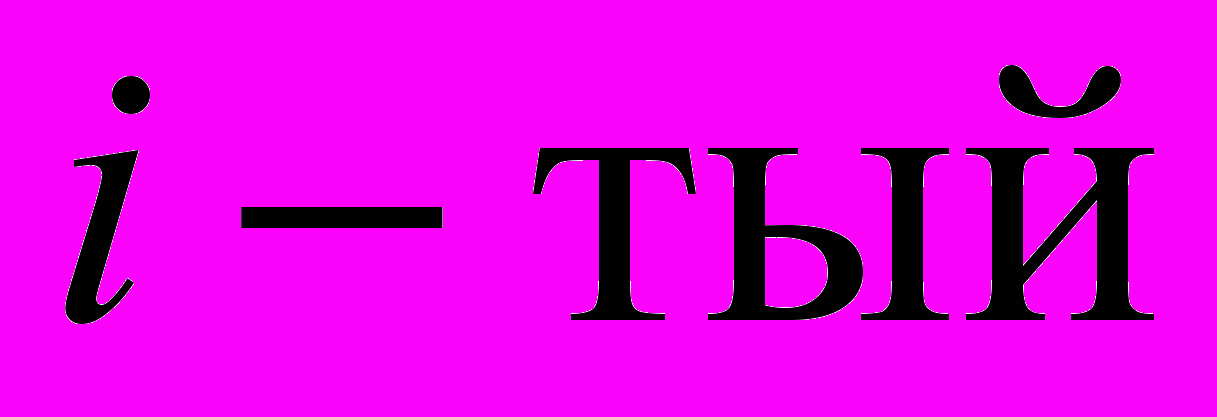Рассмотрим случай многоуровневой системы. Пусть имеется уровней оптимизаций в двоично-оптимизирующей системе. Пусть уровень улучшает код в раз и выполняет оптимизацию одной инструкции за тактов. Пусть также уровень начинает работать после 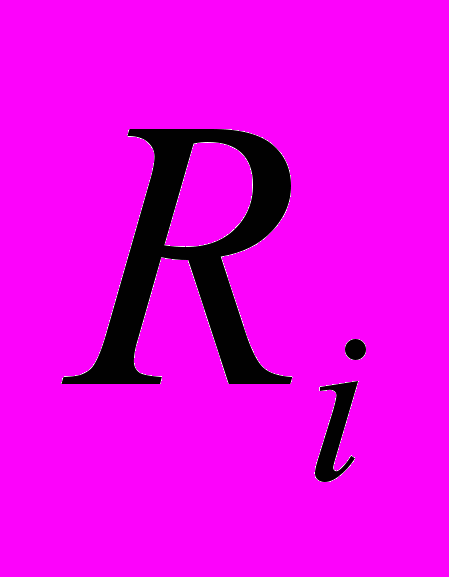повторения кода. Положим также 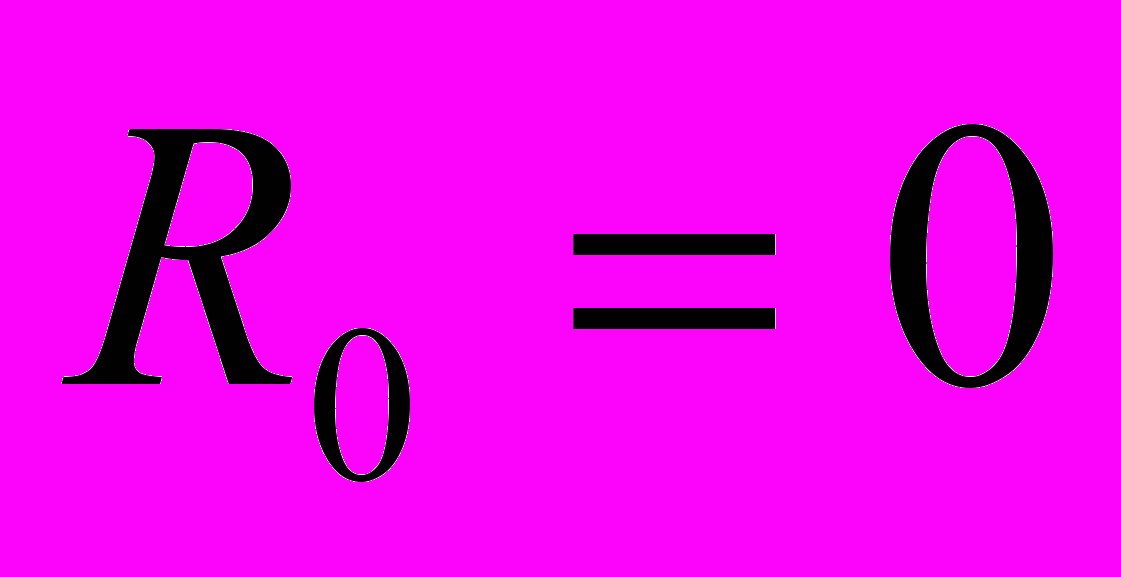и 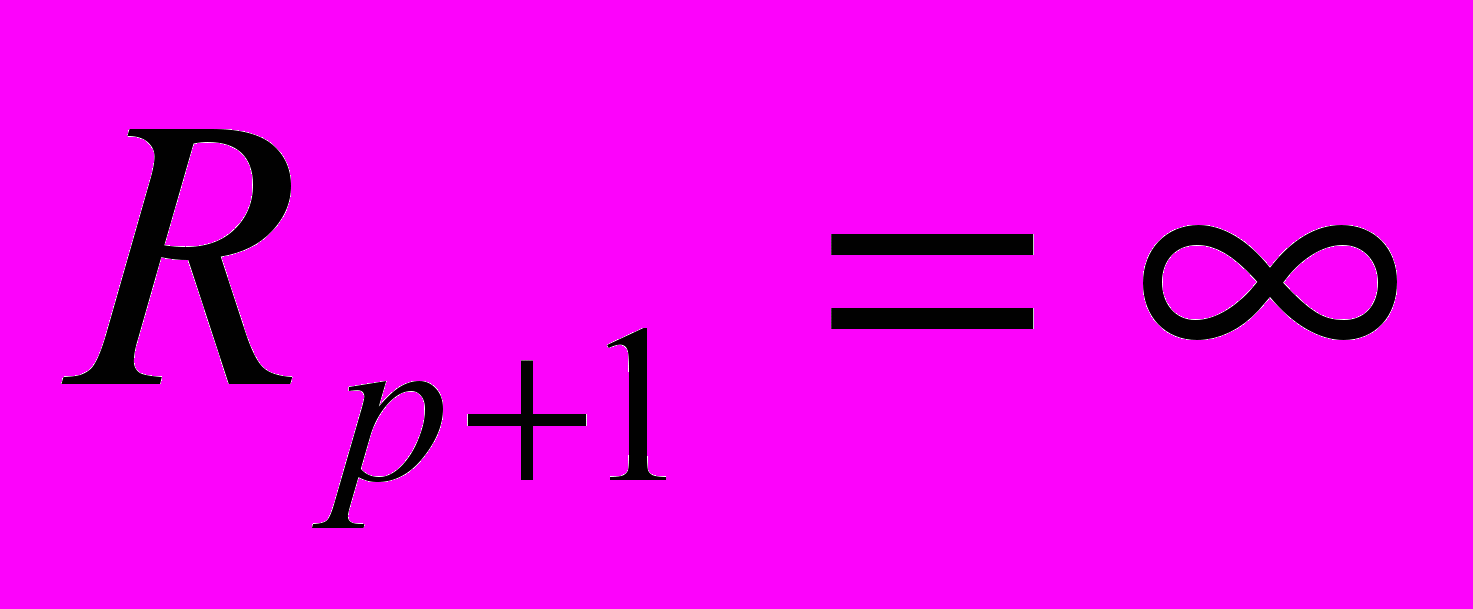. Тогда время, затраченное на выполнение одной инструкции исходной платформы, равняется:

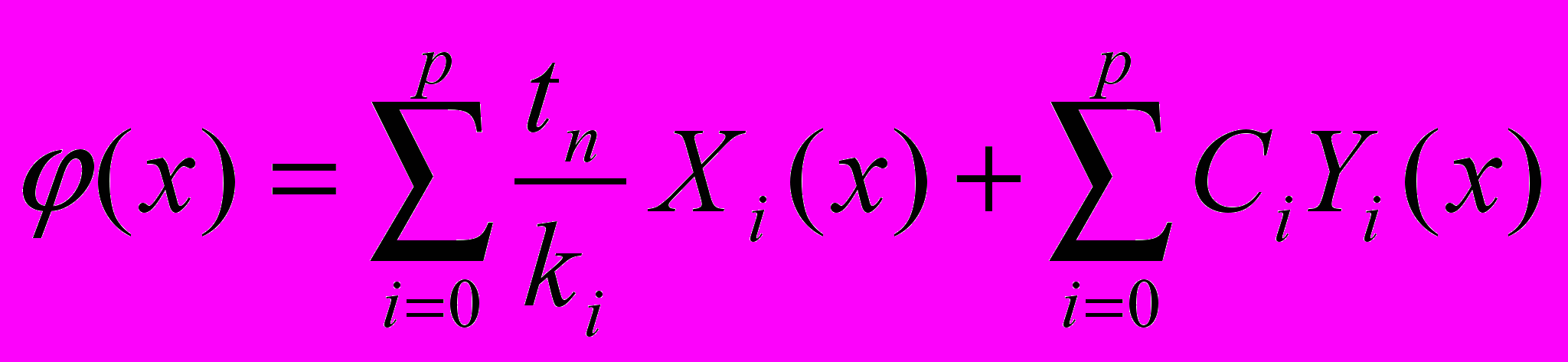, где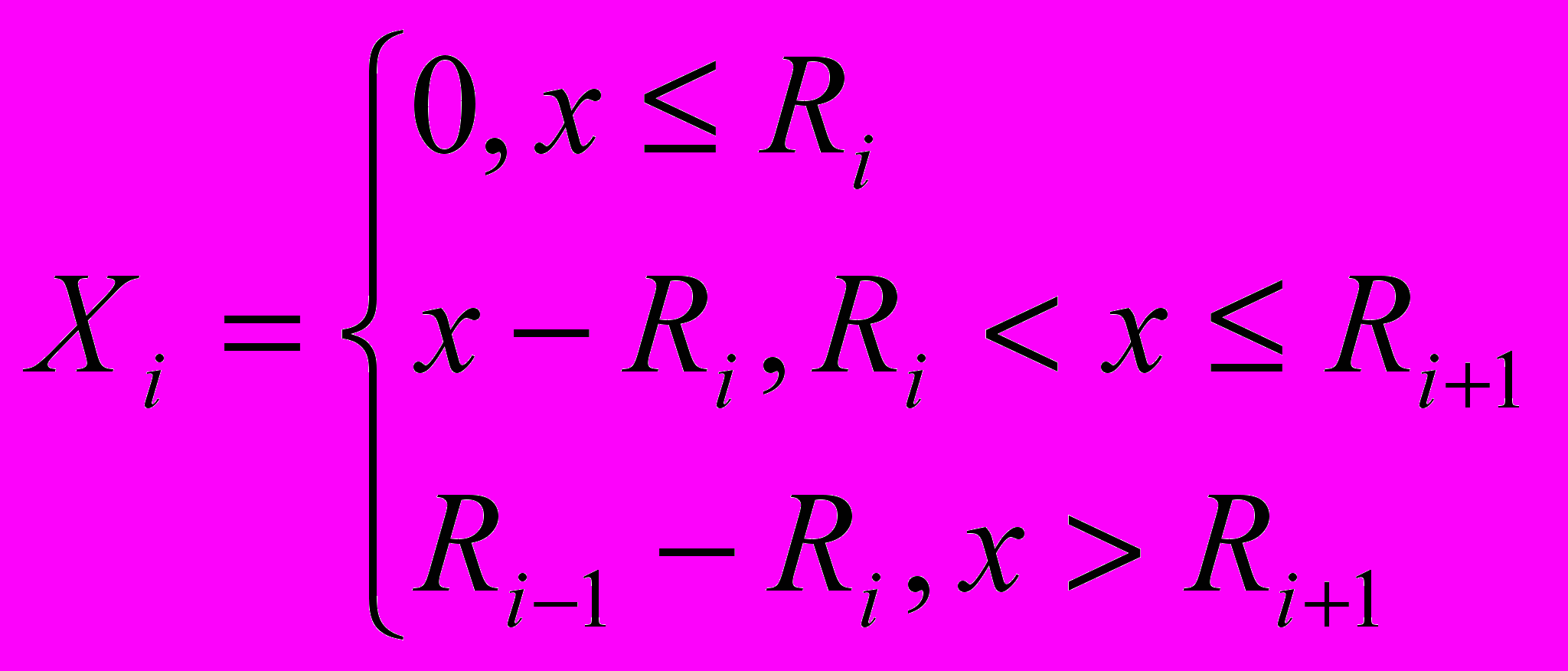

, .

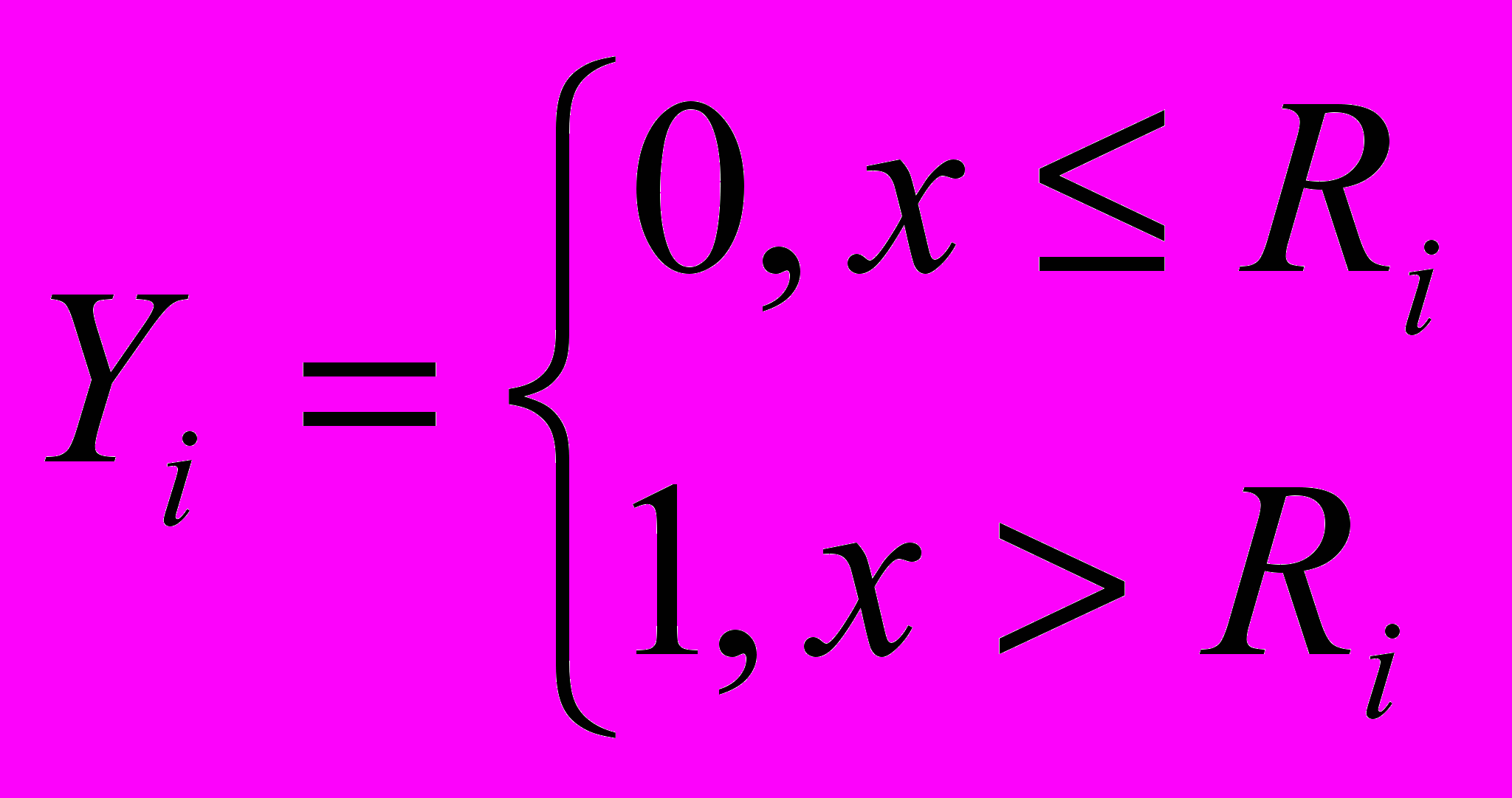Посчитаем теперь математическое ожидание времени выполнения одной инструкции (оно определено, так как имеет конечное математическое ожидание):

8. 
   

9. 
   

10. 
    

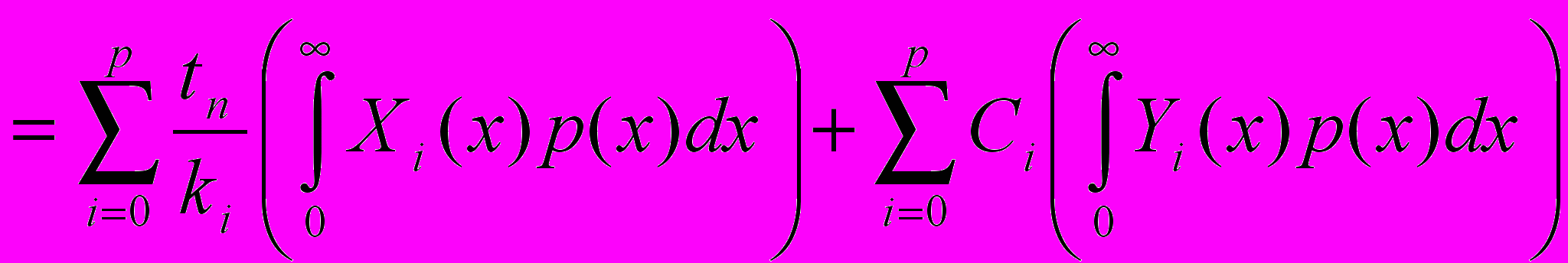
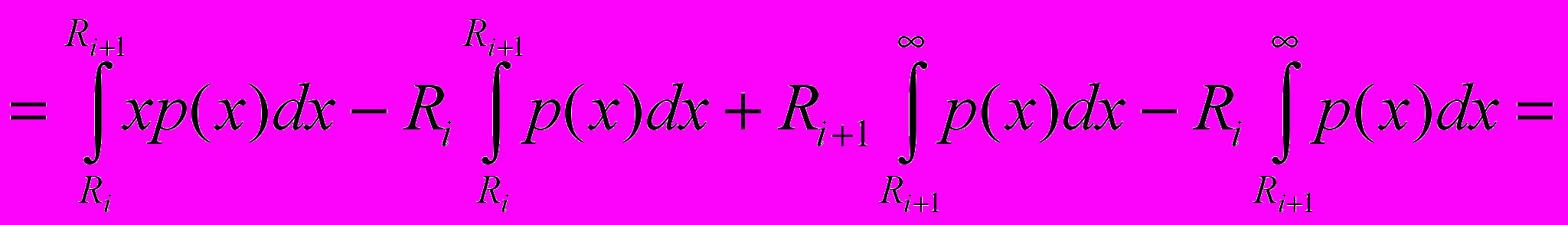
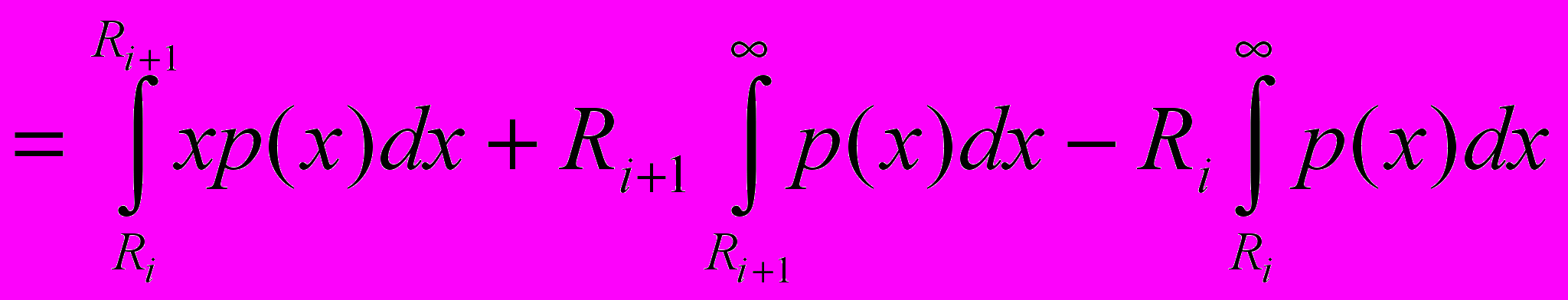
подставляя (9) и (10) в (8):



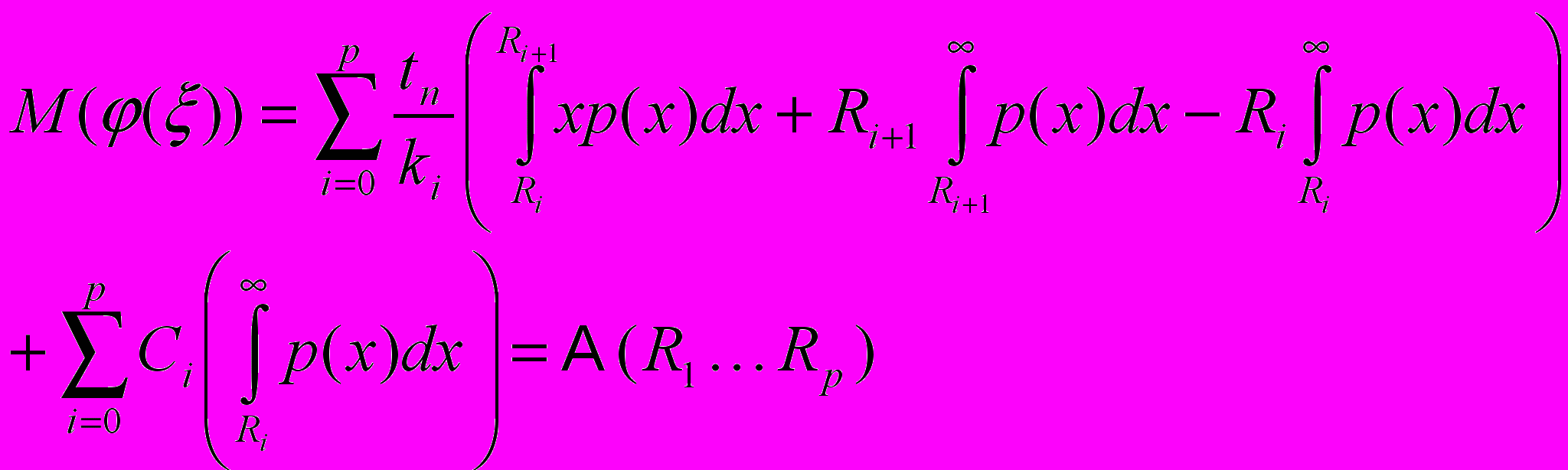
Теперь, также как и для двухуровневой схемы, для нахождения статистически оптимальных времён 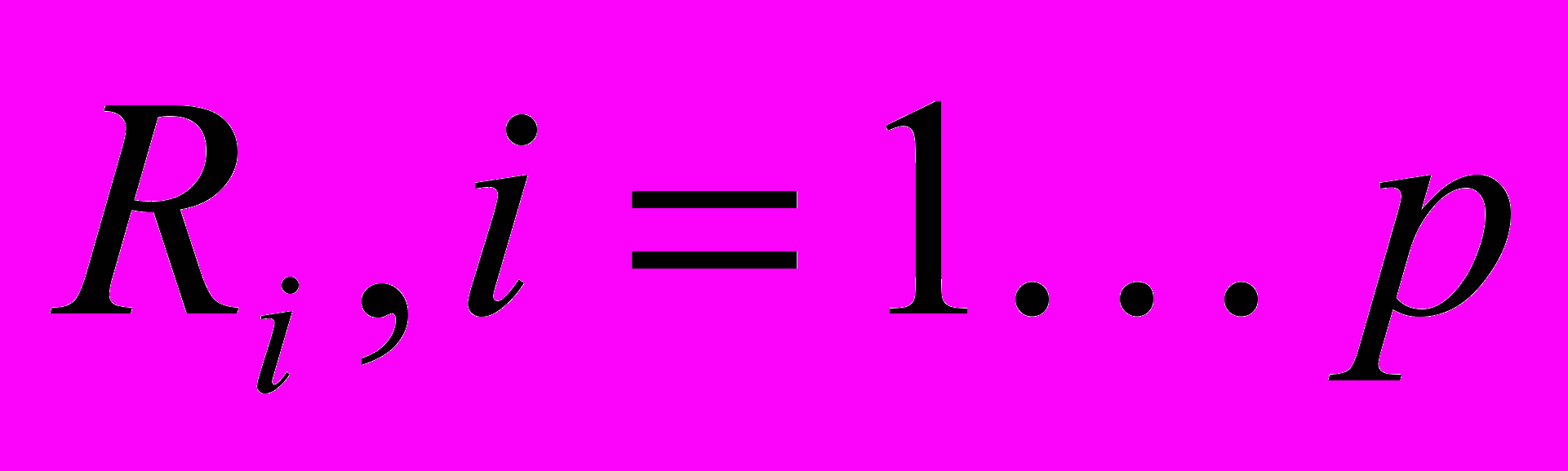, необходимо найти минимум функции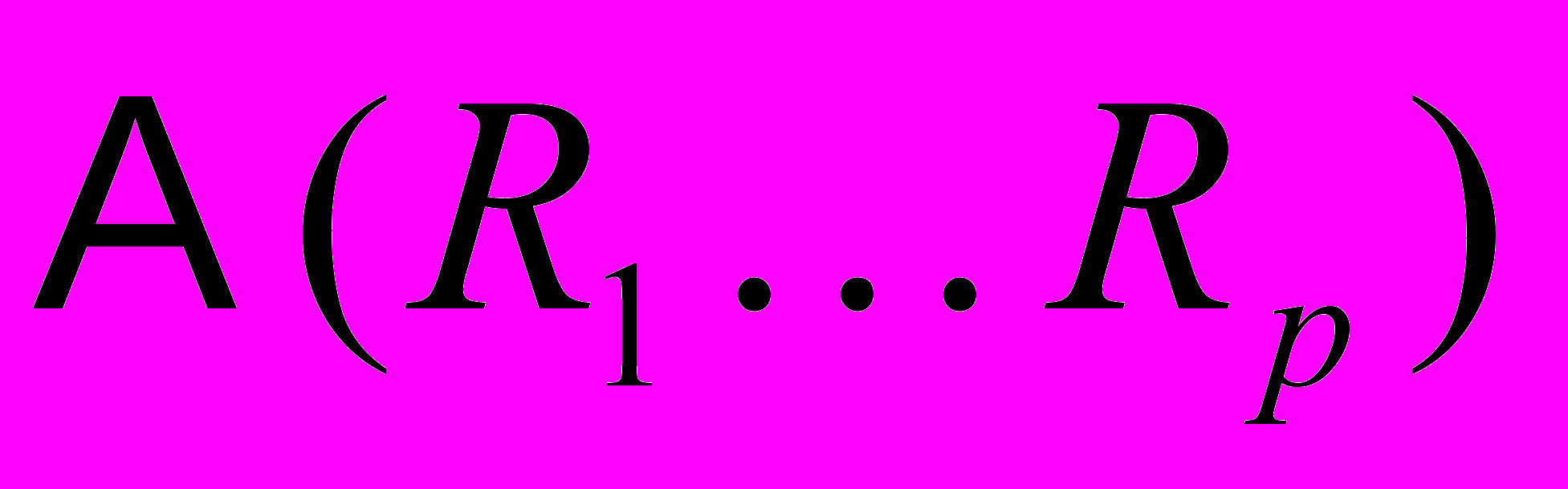. Необходимым условием минимума функции от многих переменных является равенство нулю всех частных производных:

11. 
    

Посчитаем 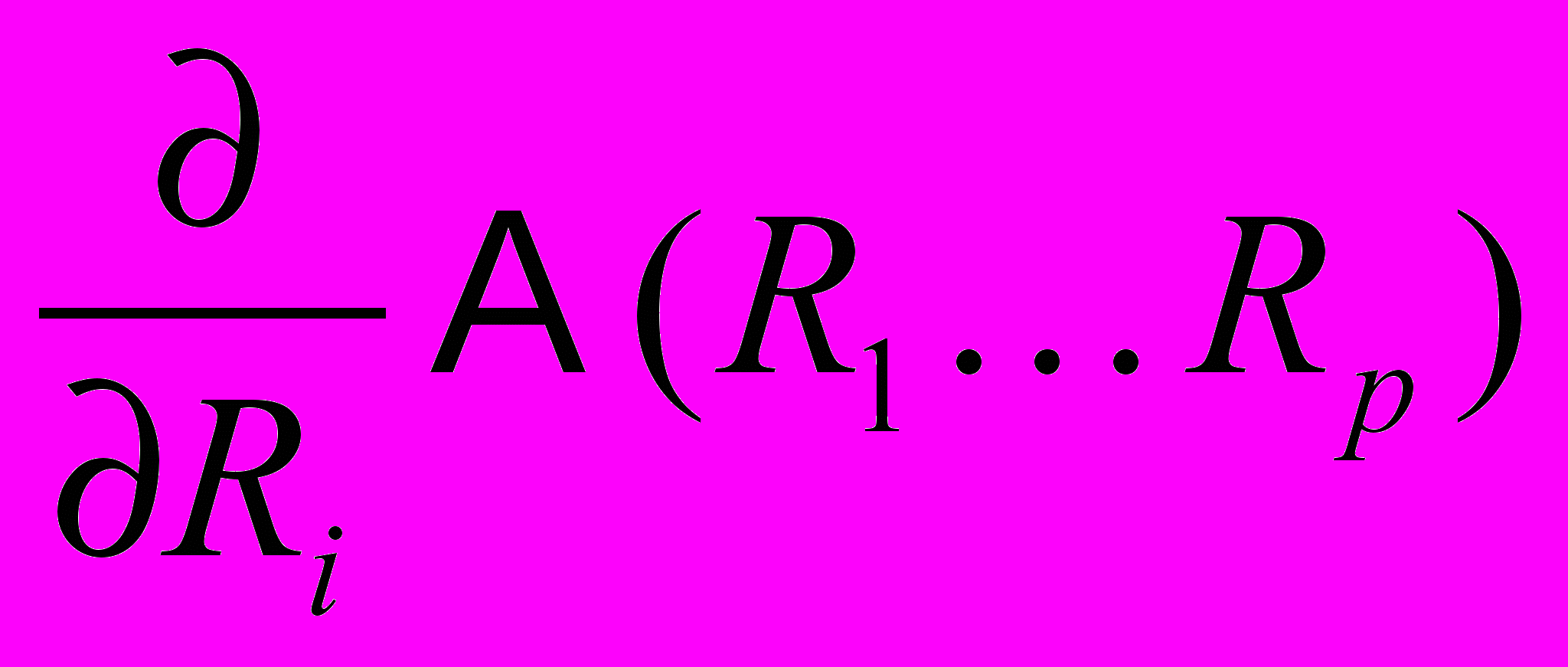для всех :

12. 
    
13. 
    

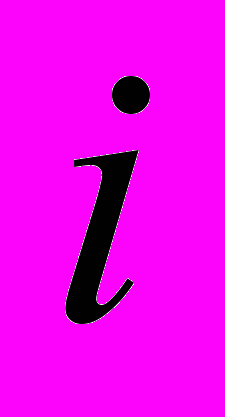Подставляя теперь (12) и (13) в (11) получаем необходимые условия минимума:

14. .
    

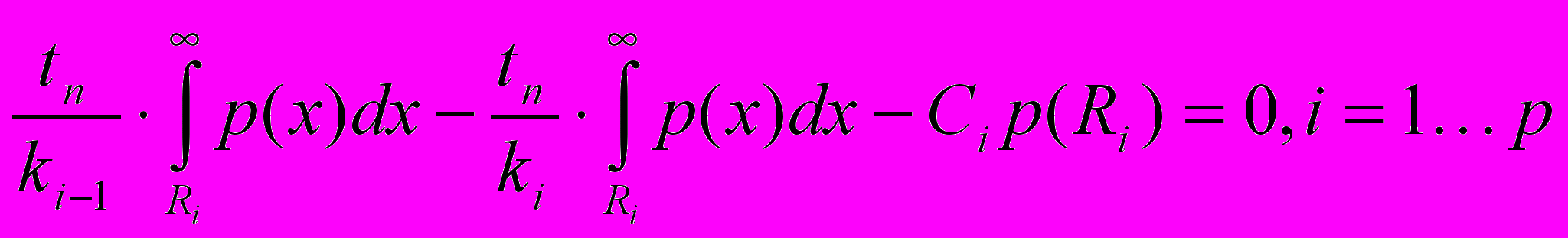Таким образом, уравнения (14) являются необходимыми условиями статистически оптимальных времён начала оптимизаций в многоуровневом двоично-оптимизирующем комплексе.