Ч. Т. Айтматова п г. т. Кукмор Программа курса

Вид материала

Программа курса

Содержание 6. Самостоятельная работа с самопроверкой по эталону 8. Рефлексия деятельности. 4) зафиксировать неразрешённые затруднения как направления будущей учебной деятельности Основная цель 1. Самостоятельная работа № 1. 2. Подробный образец решения самостоятельной работы № 1. 3. Эталон для самопроверки самостоятельной работы № 1. 4. Алгоритм исправления ошибок (урок – 6) 6. Подробный образец решения дополнительных заданий. 7. Самостоятельная работа № 2. 8. Эталон для самопроверки самостоятельной работы № 2. 9. Задания для выбора. Домашнее задание I. Проверка домашнего задания. Ход занятия Решение задач на сохранения массы и концентрации вещества Учащиеся решают самостоятельно, один из учеников коммен­тирует решение. 0,4ту - масса золота во 2-м слитке, (ту + 0,4ту) Домашнее задание. I. Решение задач. Ход урока ... Полное содержание

Подобный материал:

• Всероссийский конкурс профессионального мастерства педагогов «Образ няни в стихотворениях, 56.72kb.
• М. А. Булгакова и Ч. Айтматова     реферат, 668.87kb.
• Ч. Т. Айтматова «плаха». Цели урок, 62.67kb.
• Проблема свободы и несвободы в романах М. Булгакова и Ч. Айтматова, 671.89kb.
• «Пора возвращать человека к себе!», 159.27kb.
• А. М. Булатова п г. т. Кукмор Согласовано: Утверждаю: Заместитель директора по ур директор, 133.13kb.
• Логвина Ольга Васильевна, вторая квалификационная категория д. Шелоховская 2010-2011, 135.54kb.
• Гарифуллина Фарида Шараповна учитель биологии Iквалификационной категории Кукмор 2010, 1315.88kb.
• Творчество Чингиза Айтматова в контексте межнационального культурного диалога и гуманизации, 104.32kb.
• Г. Р. Державина программа курса история политических учений специальность «Политология», 530.36kb.

– Какую закономерность вы заметили? (Каждое следующее число в 2 раза больше предыдущего).

2. Можно ли утверждать, что 15% от 30 равно 30% от15? Всегда ли так происходит? Докажите своими примерами.

3. Длина отрезка МК составляет 63% от длины отрезка MN. Сколько процентов длина отрезка KN составляет от длины отрезка MN? (37%). На сколько процентов (от длины MN) длина отрезка MK больше длины отрезка KN? (40%).

63%

M

K N

3. Индивидуальное задание:

Во сколько раз увеличилась стоимость товара, если она выросла на 25%, на 50%, на 75%, на 100%.

4. Построение проекта выхода из затруднения.

Цель этапа: 1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного

затруднения;

2) зафиксировать новый способ действия в знаковой, вербальной форме и с помощью эталона.

Организация учебного процесса на этапе 4.

– Сформулируйте условие утверждения таким образом, чтобы смысл её остался тем же, но задача была бы на части. (Цена товара повысилась на

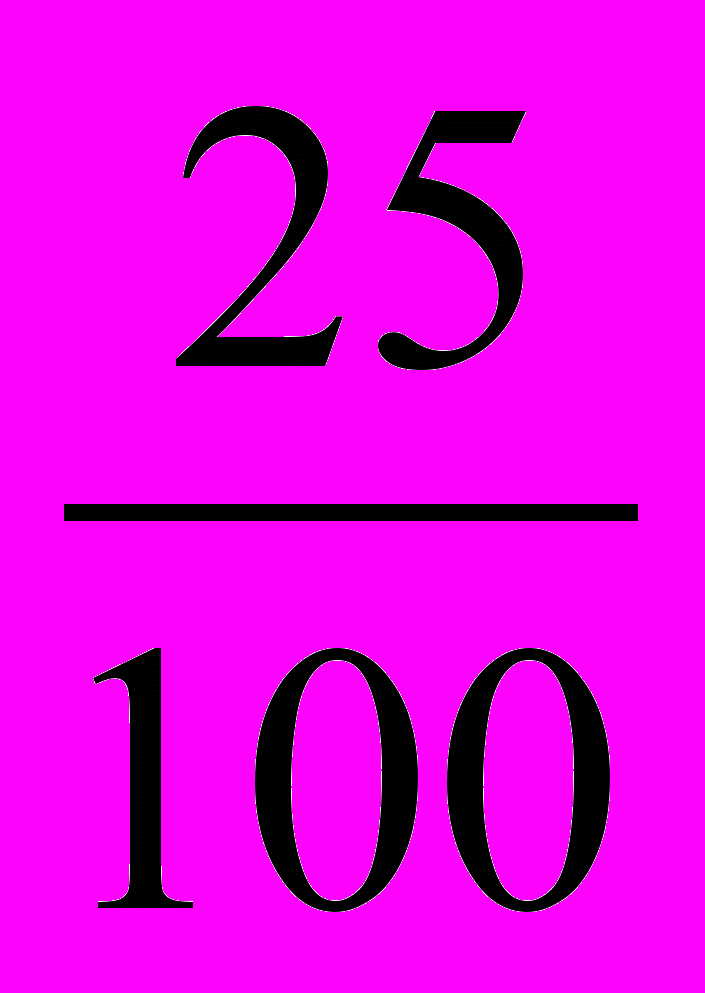
16


или 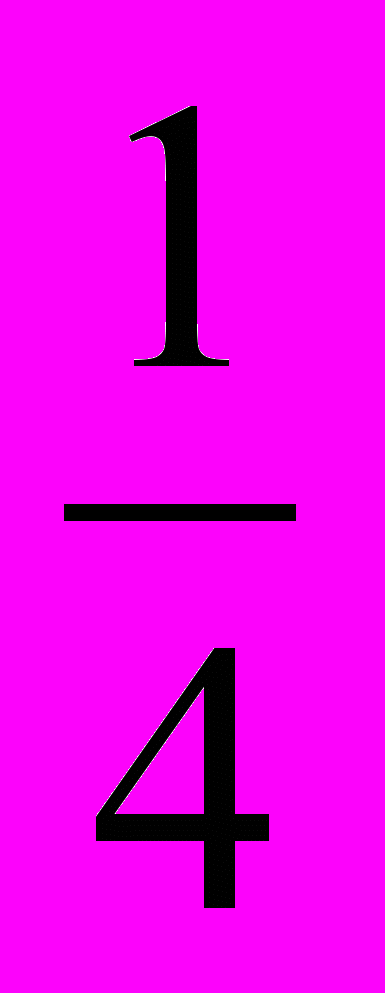от первоначальной цены).

– Постройте графическую модель получившейся задачи.


Цена – 1







Увеличилась –

– Измените схему так, чтобы было видно, что в утверждении говорится о процентах.


Цена – 100%







Увеличилась – 25%

– Что вы можете сказать об утверждениях, содержащих проценты? (Утверждения, содержащие проценты – это те же утверждения, которые содержат части).

– Какой стала стоимость товара? (125%)

– Ответьте на вопрос? (125 : 100 = 1,25 (раз))

– Во сколько раз увеличилась стоимость товара, если она выросла на 50%? Нарисуйте схему.

100% 50%







150%

– Какова новая стоимость? (150%, 150 : 100 = 1,5 (раза))

– Во сколько раз увеличилась стоимость товара, если она выросла на 75%? Сделайте схему.

100% 75%







175% 17


(Новая стоимость 175%, 175 : 100 = 1,75 (раз))

– Во сколько раз увеличилась стоимость товара, если она выросла на 100%? (Новая стоимость 200%, 200 : 100 = 2 (раза))

– Как же найти взаимосвязь между в несколько раз и на сколько то процентов? (Надо сначала выяснить сколько процентов стала новая величина, а затем разделить на 100 получим во сколько раз данная величина увеличилась или уменьшилась).

1) 25% от 20 клеток (100%) - 5 клеточек;

2) 25% от 20 клеток (125%) – 4 клеточки.

17

6. Самостоятельная работа с самопроверкой по эталону

7. Включение в систему знаний и повторение.

а) 100% - вся сумма

75% + 20% = 95% (всей суммы)

б) 100% - 75% = 25% - 100% для второго случая

25% от 25%

8. Рефлексия деятельности.


Цель этапа: 1) зафиксировать новое содержание, изученное на уроке;

2) оценить собственную деятельность на уроке;

3) поблагодарить одноклассников, которые помогли получить результат урока;

4) зафиксировать неразрешённые затруднения как направления будущей учебной деятельности;

5) обсудить и записать домашнее задание.


Занятие 4

Тема урока: «Процентные вычисления в жизненных ситуациях».


Основная цель: тренировать способность к выражению в процентах части величины, выраженной дробью и наоборот, способность к рефлексии собственной деятельности; повторить и закрепить множество и операции над ними, диаграммы Венна.


Оборудование.

Демонстрационный материал

Эталоны.


П
P % = p : 100 = 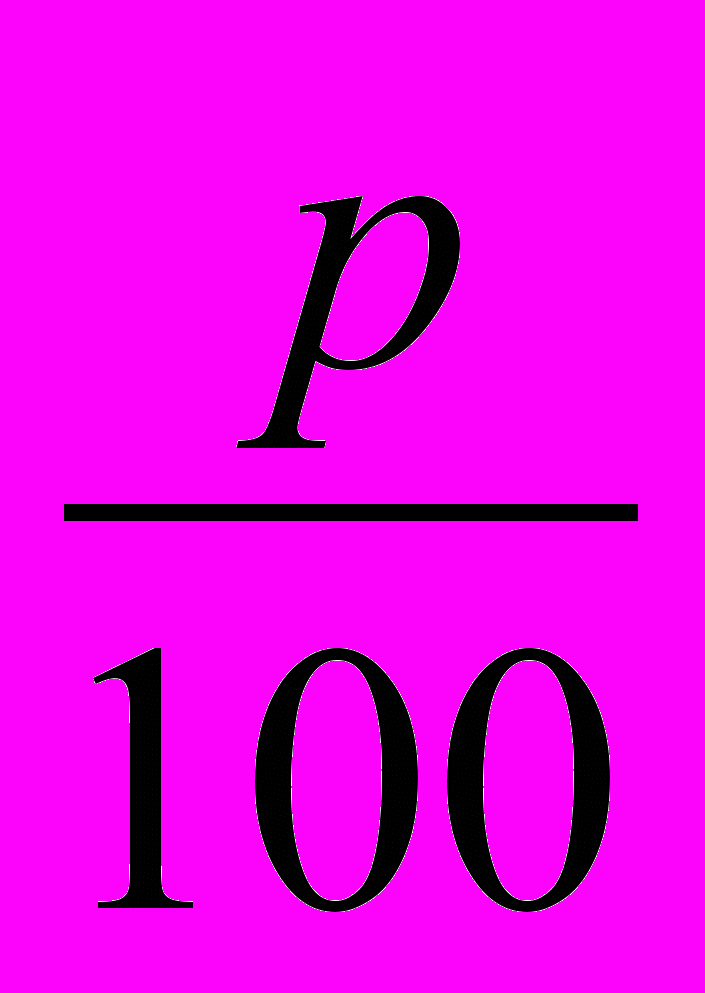= 0,01p
₁

(А  100) %

П₂


П

1. 100%•а;
   
2. 100%•а – 100%
   

₃


П

1. 100% : а;
   
2. 100% - 100% : а
   

₄


18

1. Самостоятельная работа № 1.

1. Выразите в процентах:

0,004; 2,5; 0,125.

2. Вырази десятичной дробью или натуральным числом:

46%; 0,4%; 300%.

3. На сколько процентов изменилась величина, если она:

а) увеличилась в 3 раза;

б) уменьшилась в 10 раз.

2. Подробный образец решения самостоятельной работы № 1.

1. 0,004 = 0,4%; 2,5 = 250%; 0,125 = 12,5%.

2. 46% = 0,46; 0,4% = 0,004; 300% = 3

3. а) увеличилась на 200%;

б) уменьшилась на 90%

3. Эталон для самопроверки самостоятельной работы № 1.

1. (А  100) %

0,004 • 100 = 0,4(%) (перенести запятую на два знака вправо);

2,5 • 100 = 250(%) (перенести запятую на два знака вправо);

0,125 • 100 = 12,5(%) (перенести запятую на два знака вправо).


2. P % = p : 100 = 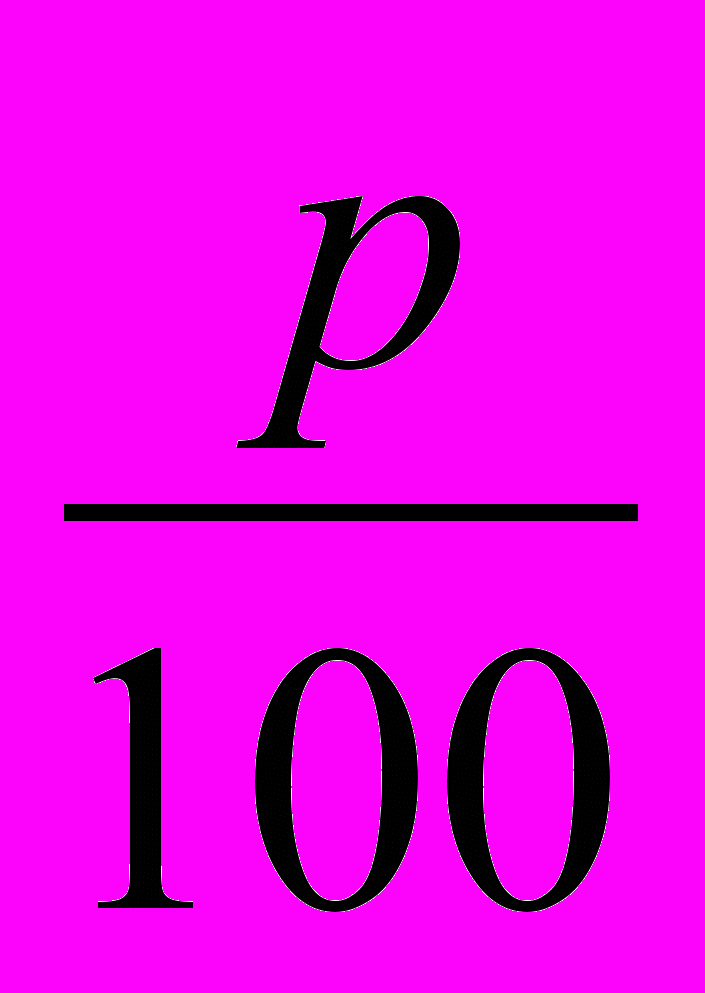= 0,01p

46% : 100% = 0,46 (перенести запятую на два знака влево);

0,4% : 100% = 0,004 (перенести запятую на два знака влево);

300% : 100% = 3 (перенести запятую на два знака влево).


3. а) 100%•3 = 300(%); 300% - 100% = 200% увеличилась на 200%; 100%•а;

100%•а – 100%


б) 100% : 10 = 10%; 100% - 10% = 90% уменьшилась на 90% 100% : а;

100% - 100% : а

4. Алгоритм исправления ошибок (урок – 6)

5. Дополнительные задания.

В автобусном парке 50% составляют городские автобусы, 80% остальных – автобусы междугородного класса. Каких автобусов больше – городских или междугородного класса?

1) В классе мальчиков на 25% больше, чем девочек. На сколько процентов девочек в этом классе меньше, чем мальчиков?

2) В первом квартале доля продажи товаров отечественных производителей увеличилась с 20% до 25%, а во втором – с 25% до 30%. В каком квартале

увеличение было более значительным?

19

6. Подробный образец решения дополнительных заданий.

Все автобусы – 100%

Городские – 50%

Остальные – 100%



Международные – 80%

Городских автобусов больше, т.к. международные автобусы составляют 80% оставшихся, а оставшиеся составляют половину всех. Половина больше, чем часть от половины.

1) Девочек – 100%, мальчиков – 125%

100 : 125•100 = 80(%) – составляют девочки от количества мальчиков100% - 80% = 20%

Девочек меньше мальчиков на 20%.

2) В первом квартале увеличение составило 5% от 20%, т.е. 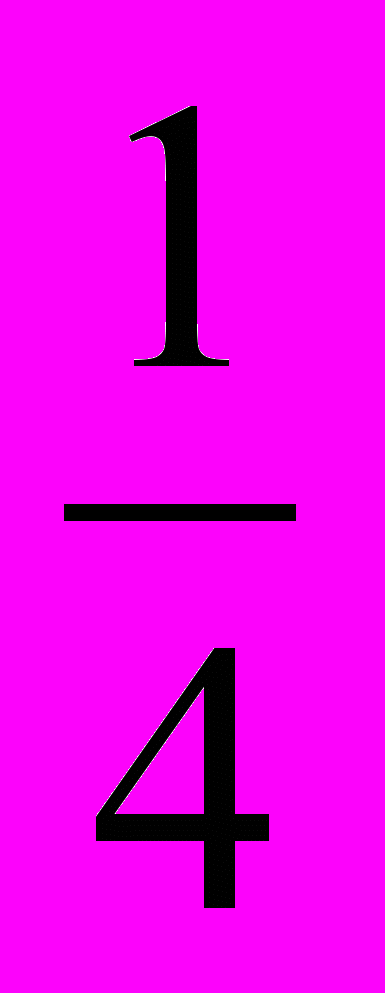, а во втором – 5% от 25%, т.е. 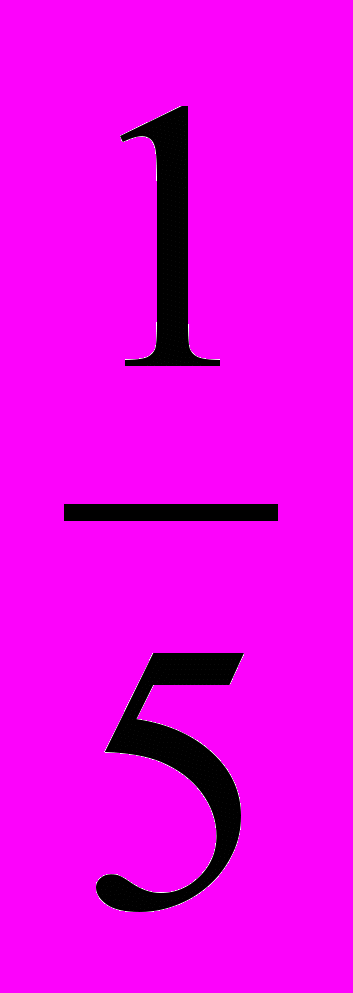. 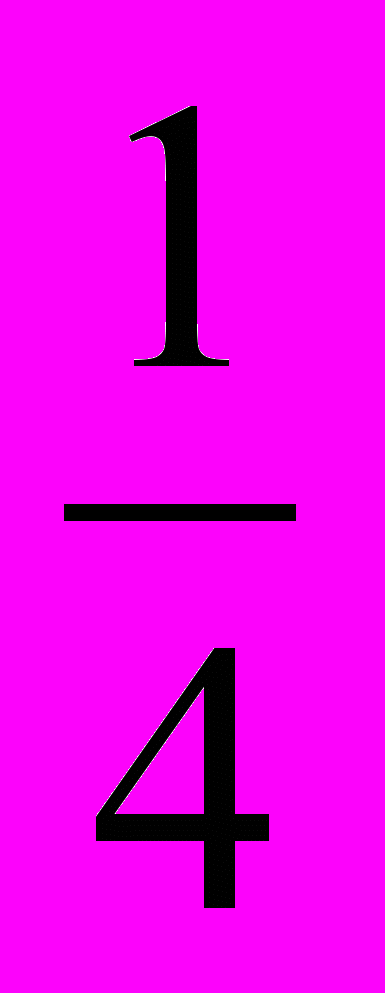> 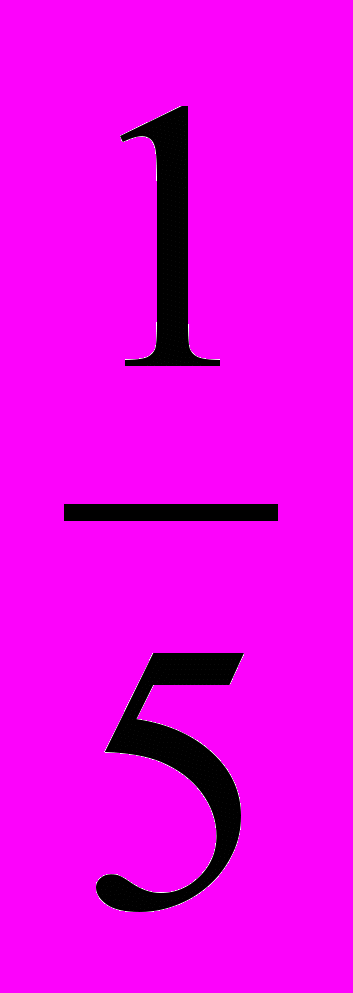, значит, в первом квартале увеличение было больше.

7. Самостоятельная работа № 2.

1. Выразите в процентах:

0,008; 3,4; 0,375.

2. Вырази десятичной дробью или натуральным числом:

24%; 0,7%; 400%.

3. На сколько процентов изменилась величина, если она:

а) увеличилась в 8 раз;

б) уменьшилась в 4 раза.

8. Эталон для самопроверки самостоятельной работы № 2.

1. (А  100) %

0,008 • 100 = 0,8(%) (перенести запятую на два знака вправо);

3,4 • 100 = 340(%) (перенести запятую на два знака вправо);

0,375 • 100 = 37,5(%) (перенести запятую на два знака вправо).


2. P % = p : 100 = 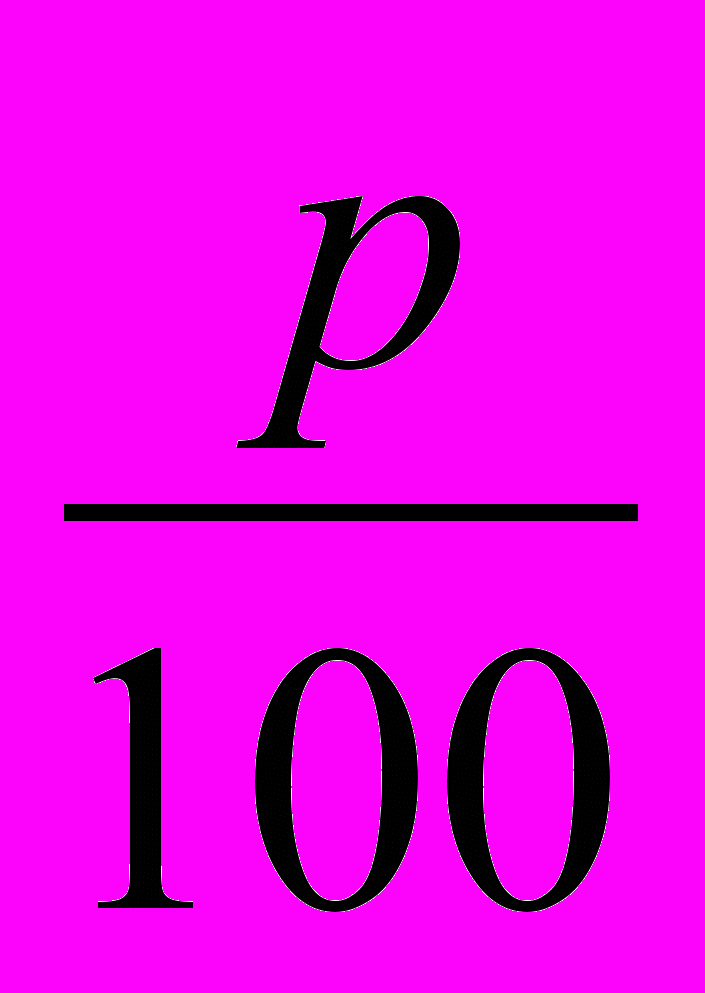= 0,01p

24% : 100% = 0,24 (перенести запятую на два знака влево);

0,7% : 100% = 0,007 (перенести запятую на два знака влево);

400% : 100% = 4 (перенести запятую на два знака влево).


3. а) 100%•8 = 800(%); 800% - 100% = 700% увеличилась на 700%; 100%•а;

20


100%•а – 100%

б) 100% : 4 = 25%; 100% - 25% = 75% уменьшилась на 75% 100% : а;

100% - 100% : а

9. Задания для выбора.

1. Замени проценты числами

а) 6%; 56% 90%;

б) 0,8% 0,03% 104,5%;

в) ;

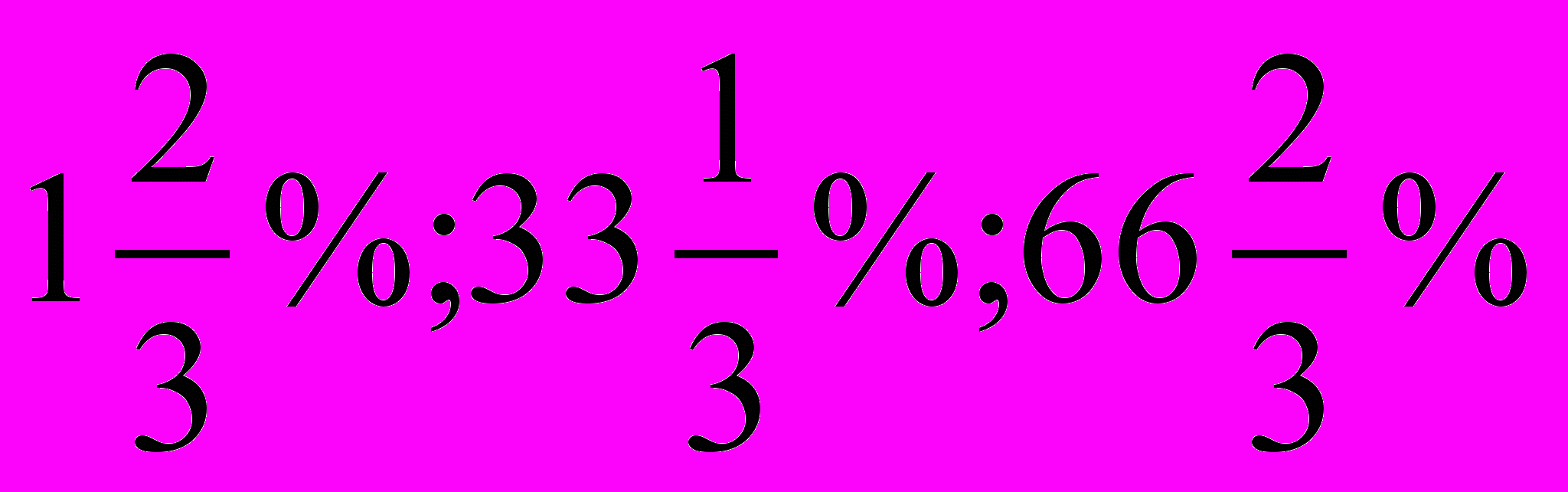г) 150%; 200%; 450%; 800%;.

На сколько процентов изменилась величина, если она:

а) увеличилась в 1,5 раза;

б) уменьшилась в 1,5 раза;

в) увеличилась в 5 раз;

г) уменьшилась в 5 раз;

д) увеличилась в 10 раз;

е) уменьшилась в 10 раз.

1. Верно ли утверждение, что корни предложенных уравнений равны?

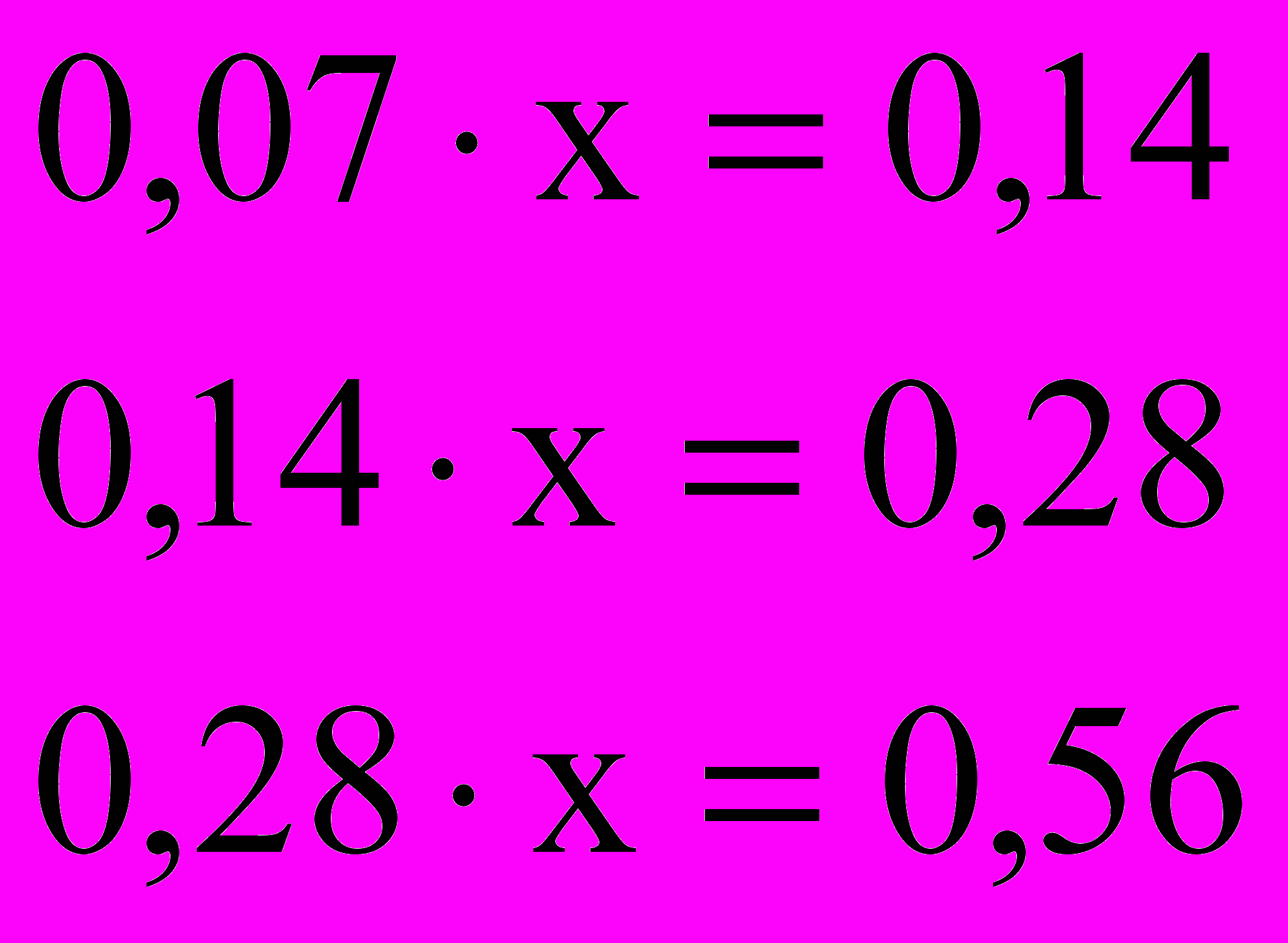(Да верно)

– Измените уравнение 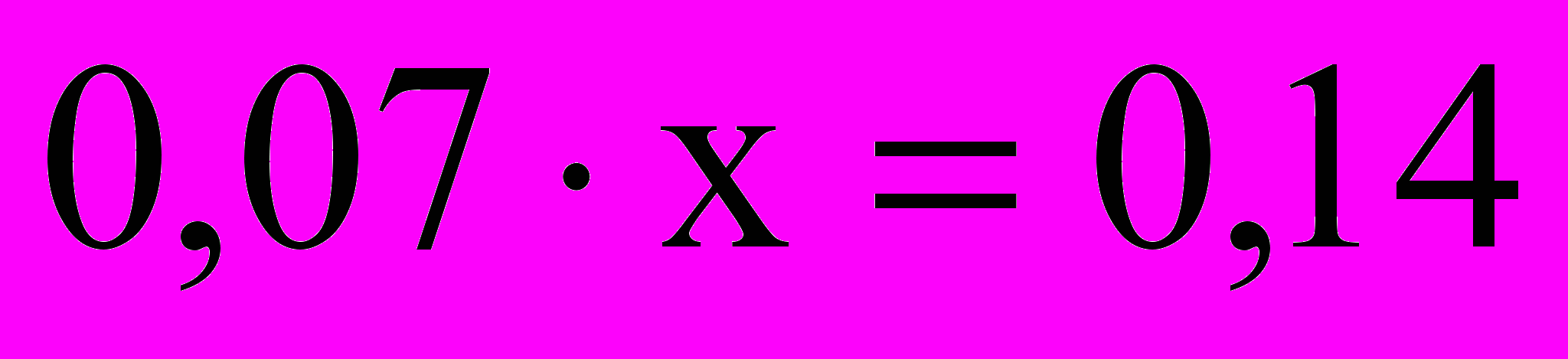так, чтобы корень нового уравнения составлял 10% от старого. (Новый корень должен быть равен 20, значит, 0,07x = 1,4)

– Как вы нашли новый корень? (2 : 10•100 или 2 : 0,1)


Задача 1.

В газете сообщается, что с 10 июня согласно новым тарифам стоимость отправления почтовой открытки составит 3 р. 15 к. вме­сто 2 р. 27 к. Соответствует ли рост цен на услуги почтовой связи росту цен на товары в этом году, который составляет 14,5 %.

Решение.

Разность тарифов составляет 0,4 р., а ее отношение к старому тарифу равно 0,14545... Выразив это отношение в процентах, по­лучим примерно 14,5 %.

О т в е т: да, соответствует.

Задача 2.

Дополнительный вопрос. Сколько будет стоить отправ­ка заказного письма, если эта услуга сейчас оценивается в 5 р. 50 к?

21

Решение.

Цена услуги увеличивается на 14,5 %, т. е. станет 5,5-1,145 = = 6,3 (р.).

Ответ: 6 р. 30 к.


3. В одном банке вложенная сумма увеличивается каждый месяц на 10%, а в другом банке вложенная сумма увеличивается на 30% каждые три месяца. В каком банке выгоднее хранить свои сбережения? (Одинаково).

– Для выполнения работы повторим основные алгоритмы.

– Какие операции мы можем выполнять, используя эти алгоритмы? (Переводить проценты в числа и числа в проценты).

– Как определить, на сколько процентов изменилась величина? (Надо 100% умножить или разделить на соответствующее число раз, а затем либо из

получившегося числа вычесть 100%, либо из 100% вычесть, получившееся число)

– Что мы использовали для выхода из затруднений? (Алгоритм работы над ошибками).

Домашнее задание: задания для выбора из дидактического материала.

Занятие 5

Цели: сформировать умение работать с законом сохранения массы; обеспечить усвоение учащимися понятий концентрации вещества, процентного раствора; обобщить полученные знания при решении задач на проценты.

Форма занятия: комбинированное занятие.

Методы обучения: рассказ, объяснение, практическая работа.

Формы контроля: проверка самостоятельно решенных задач.

Ход занятия

I. Проверка домашнего задания.

II. Рассказ учителя.

Данный тип задач охватывает большой круг ситуаций - смеше­ние товаров разной цены, жидкостей с различным содержанием соли, кислот различной концентрации, сплавление металлов с раз­личным содержанием некоторого металла и пр. Связь различных задач между собою станет яснее, если рассматривать типичные си­туации в общем виде. При решении задач данного типа использу­ются следующие допущения:

1. Всегда выполняется «Закон сохранения объема или массы»:
если два раствора (сплава) соединяют в «новый» раствор (сплав),
то выполняются равенства:

V = V₁ + V₂ - сохраняется объем;

т =m₁+ т₂~ закон сохранения массы.

2. Данный закон выполняется и для отдельных составляющих частей
   

(компонентов) сплава (раствора).

22

3. При соединении растворов и сплавов не учитываются хими­ческие взаимодействия их отдельных компонентов.

Задачи на смеси, растворы и сплавы называют еще задачами на процентное содержание или концентрацию. Введем основные по­нятия. Говоря о смесях, растворах и сплавах, будем употреблять термин «смесь» независимо от ее вида (твердая, жидкая, газообразная, сыпучая и т. д.). Смесь состоит из «чистого вещества» и «при­меси». Долей а чистого вещества в смеси называется отношение количества чистого вещества т в смеси к общему количеству М смеси при условии, что они измерены одной и той же единицей массы или объема: а = т/М. Отсюда получаем т = аМ, М = т/а. Понятие доли чистого вещества можно вводить следующей услов­ной записью:

Доля чистого вещества в смеси равна количеству чистого веще­ства в смеси, деленному на общее количество смеси. Заметим, что складывать и вычитать доли и процентные содержания нельзя.

Процентным содержанием чистого вещества в смеси с называ­ют его долю, выраженную процентным отношением: с = а 100 %, а = с/100%.

Считаем полезным предложить школьникам формулу, по кото­рой рассчитывают концентрацию смесей (сплавов):

п = т_в: т_р

где п - концентрация,

т_е - масса вещества в растворе (сплаве), т_р - масса всего раствора (сплава).

III. Решение задач.

Задача 1.

Сколько граммов воды надо добавить к 50 г раствора, содер­жащего 8 % соли, чтобы получить 5 % раствор?

Решение.

Пусть х - количество воды, которое надо добавить. Новое ко­личество раствора - (50 + х) г. Количество соли в исходном раство­ре 50-0,08 г. Количество соли в новом растворе составляет 5 % от (50+х)г,т. е. 0,05(50+ х)

Так как количество соли от добавления воды не изменилось, то оно одинаково в исходном и новом растворах. Получаем уравнение. Иногда в химии это уравнение называют кратко «баланс по соли».

50-0,08 = 0,05(50+х),

50-8 = 5(50+х),

80 = 50+х,

х = 30.

Ответ: 30 г.

Задача 2.

Сколько граммов 30 %-го раствора надо добавить к 80 г 12 %-го раствора этой же соли, чтобы получить 20 %-й раствор соли?

23

Решение.

Пусть надо добавить х г 30 % раствора соли. Получится (80 + х) г 20 % раствора. В 80 г 12 % раствора содержится 80-0,12 г соли 0,3* г соли - в х г 30 % раствора, 0,2(80 + х) г соли - в (80 + х) г 20 % рас­твора.

Получаем уравнение:

0,3х + 0,12-80 = 0,2(80 + х)- это и есть «баланс по соли».

0,3х:+ 9,6=16 + 0,2х,

0,3х - 0,2х-= 16-9,6,

0,1х-= 6,4,

х = 64.

Ответ: 64 г.

Занятие 6

Цель: углубить и систематизировать знания учащихся при решении задач на «смеси» и «сплавы».

Ход занятия Решение задач на сохранения массы и концентрации вещества

Задача 1.

Даны два куска с различным содержанием олова. Первый, мас­сой 300 г, содержит 20 % олова. Второй, массой 200 г, содержит 40 % олова. Сколько процентов олова будет содержать сплав, по­лученный из этих кусков.

Ответ: 28%.

Учащиеся решают самостоятельно, один из учеников коммен­тирует решение.

Задача 2.

Имеется два куска сплава олова и свинца, содержащие 60 % и 40 % олова. По сколько граммов от каждого куска надо взять, что­бы получить 600 г сплава, содержащего 45 % олова?

Решение.

Пусть масса куска, взятого от первого сплава т_х г, тогда масса куска от второго сплава будет 600 - т\, составим уравнение

т_х 0,6 + (600 - 1й,)-0,4 = 600-0,45,

6 т_х + 2400 - 4 т_х = 2700,

20 т_х = 3000, т_х = 150, 600 - т_х = 450, т₂ =450.

Ответ: 150 г; 450 г.

Задача 3. (Задача из разряда олимпиадных.)

Имеются два слитка золота с серебром. Процентное содержа­ние золота в первом слитке в 2,5 раза больше, чем процентное со­держание золота во втором слитке. Если сплавить оба слитка вме­сте, то получится слиток, в котором будет 40 % золота. Найдите, во сколько раз первый слиток тяжелее второго, если известно, что при сплаве равных по весу частей первого и

24

второго слитков получает­ся сплав, в котором 35 % золота.

Решение.

Задача ус­ложняется тем, что вводятся четыре переменные, от которых легко освобождаемся при решении системы двух уравнений. Напоминаем учащимся формулу, по кото­рой рассчитываем концентрацию смеси и сплава.

Пусть

х кг - масса 1 -го слитка, тогда кх - масса 2-го слитка.

у% -процентное содержание золота в 1 -м слитке,

0,4у % - процентное содержание золота во 2-м слитке,

ху - масса золота в 1 -м слитке,

0,4хук - масса золота во 2-м слитке.

(ху + 0,4хук) - масса золота в первом сплаве,

(х + кх) - масса первого сплава.

По условию концентрация золота в первом сплаве равна 40 %.

т кг - масса 1-го или 2-го слитков второго сплава, 2т - масса второго сплава, ту - масса золота в 1-м слитке, 0,4ту - масса золота во 2-м слитке, (ту + 0,4ту) - масса золота во втором сплаве. По условию концентрация золота во втором сплаве равна 35 %. Составим второе уравнение системы:

Итак, 1-й слиток в два раза тяжелее 2-го.

Домашнее задание. № 107, 109, 114.


Занятие 7

Цели: углубить и систематизировать знания учащихся.

Метод обучения: беседа.

Формы контроля: проверка самостоятельно решенных задач.

I. Решение задач.

Задача (на производительность).

В бассейн проведена труба. Вследствие засорения ее приток воды уменьшился на 60 %. На сколько процентов вследствие этого увеличится время, необходимое для заполнения бассейна Решение.

1. 100 % - 60 % = 40 % или 0,4 - такую часть составляет ос­тавшийся приток воды;
   
2. 1 : 0,4 = 2,5 (раза) - во столько раз увеличится время, необ­ходимое для наполнения бассейна, т. е. увеличится на 150 %.
   

Ответ: на 150 %.

Задача (содержание влаги).

Арбуз весил 20 кг и содержал 99 % воды, когда он немного усох, то стал содержать 98 % воды. Сколько теперь весит арбуз?

Решение.

Вес «сухого вещества» в арбузе составляет 100 - 99 = 1 (%) или 0,01, т. е. 200,01 =0,2 (кг).

25

После «усыхания» арбуза вес «сухого вещества» составляет 100 - 98 = 2 (%) или 0,2 : 0,02 = 10 (кг).

Ответ: 10 кг.

Задача

В референдуме приняли участие 60 % всех жителей одного из регионов города 14, имеющих право голоса. Сколько человек при­няли участие в референдуме, если в районе около 180 тыс. жите­лей, а право голоса имеют 81 %?

Решение.

Найдем, сколько человек имеют право голоса

180-0,81 = 145,8 (тыс. чел.) Из них 60 % приняли участие в референдуме, т. е.

145,8-0,6 = 87,48 (тыс. чел.).

Ответ: 87 480 человек.

Самостоятельно с комментариями с места решить задачу № 128.

П. Итоги занятия.

Домашнее задание. № 117, 120, 127.


Занятие 8.

Тема урока: "Задачи на проценты".

Тип урока: решение задач, теста


Основные цели: тренировать способность к решению простых и составных в 2-3 действия на проценты; повторить и закрепить решение уравнений, упрощение выражений, запись выражений в виде дроби и их сокращение.


Оборудование

Демонстрационный материал

Э
1. Первое число разделить на второе.

2. Результат умножить на 100%.
талон


Раздаточный материал

Эталон для самопроверки

а) 1) Находим какую часть 16 с составляет от 50 с: 16 : 50 = 0,32;

2) Выражаем, получившееся число в процентах: 0,32•100 = 32 (%)

3) Находим какую часть 2а составляет от 8а: 2а : 8а = 0,25

4) Выражаем, получившееся число в процентах: 0,25•100 = 25 (%).

26

Ход урока

Актуализация знаний и фиксация затруднения в деятельности.

1. Найдите x, если:

9% от x равно 8,1; (8,1 : 0,09 = 810 : 9 = 90)

7% от x равно 4,2; (4,2 : 0,07 = 420 : 7 = 60)

4% от xравно 1,2. (1,2 : 0,04 = 120 : 4 = 30)

– Вычислите сумму всех полученных результатов и уменьшите её в 100 раз. ((90 + 60 + 30) : 100 = 1,8)

2. По какому правилу составлен ряд чисел: 1,8; 3,6; 7,2.

– Установите закономерность и назовите ещё два числа данной последовательности. (Каждое последующее в 2 раза больше предыдущего: 1,8; 3,6; 7,2; 14,4; 28,8).

– Какое число в данной последовательности, по-вашему мнению, «лишнее»?

3. В коллекции 180 марок. 36 марок с изображением птиц. Какую часть от всех марок составляют марки с изображением птиц? Выразите, получившийся результат в процентах. (36 : 180 = 0,2; 20%).

4. Какую часть числа составляют:

Проценты	5%	10%	20%	40%	80%
Десятичная дробь	(0,05)	(0,1)	(0,2)	(0,4)	(0,8)
Обыкновенная дробь	(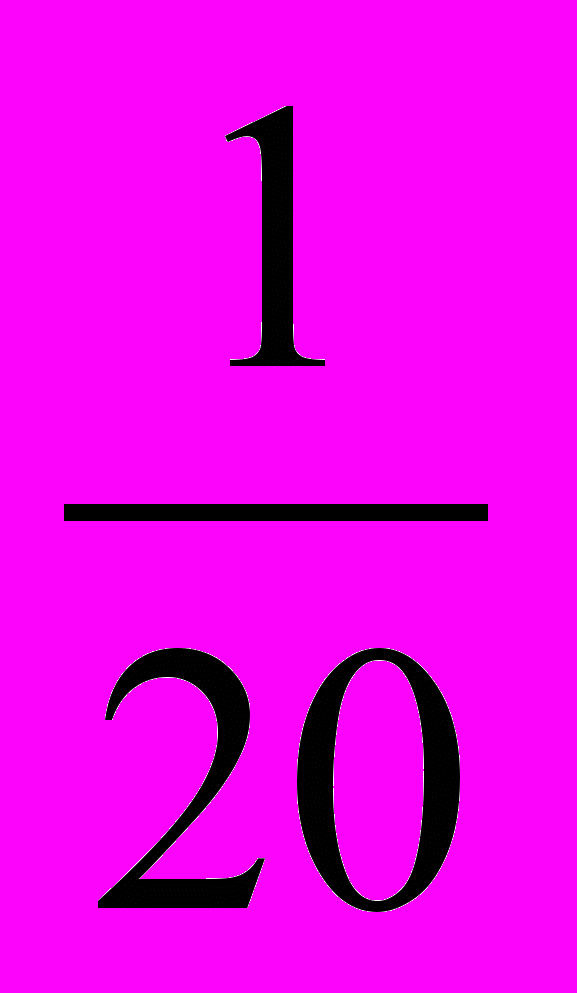)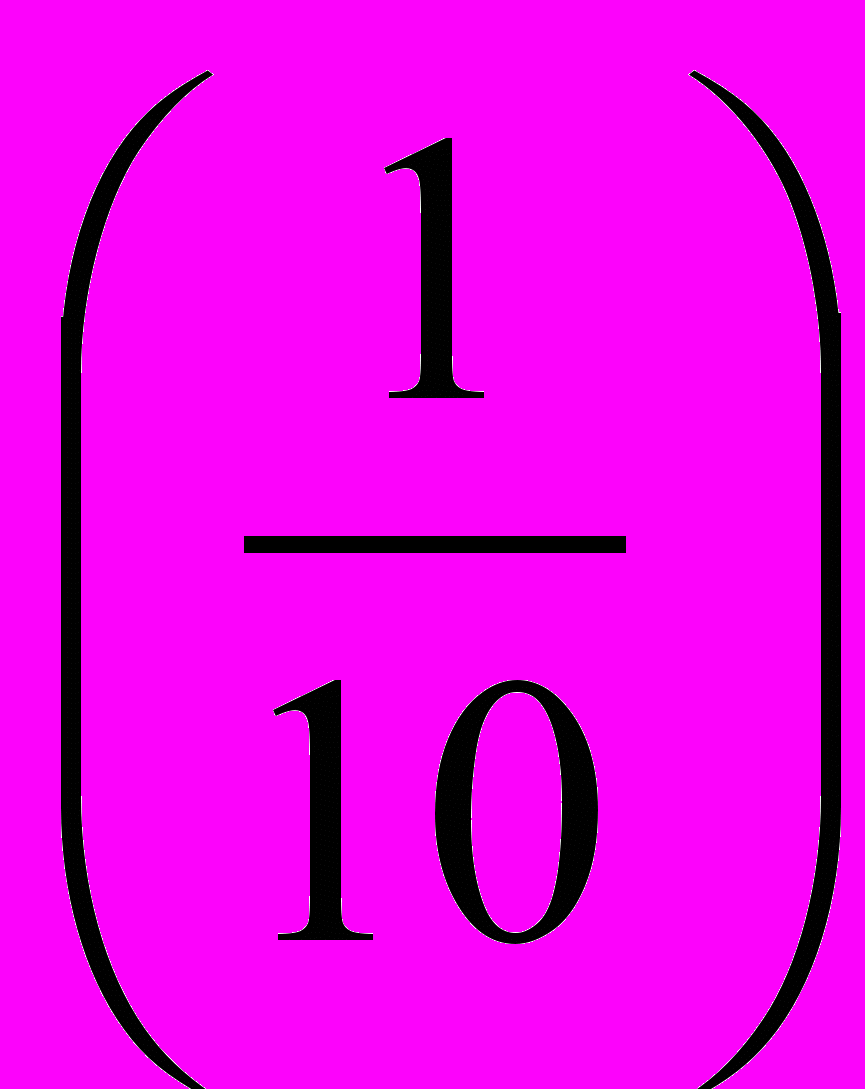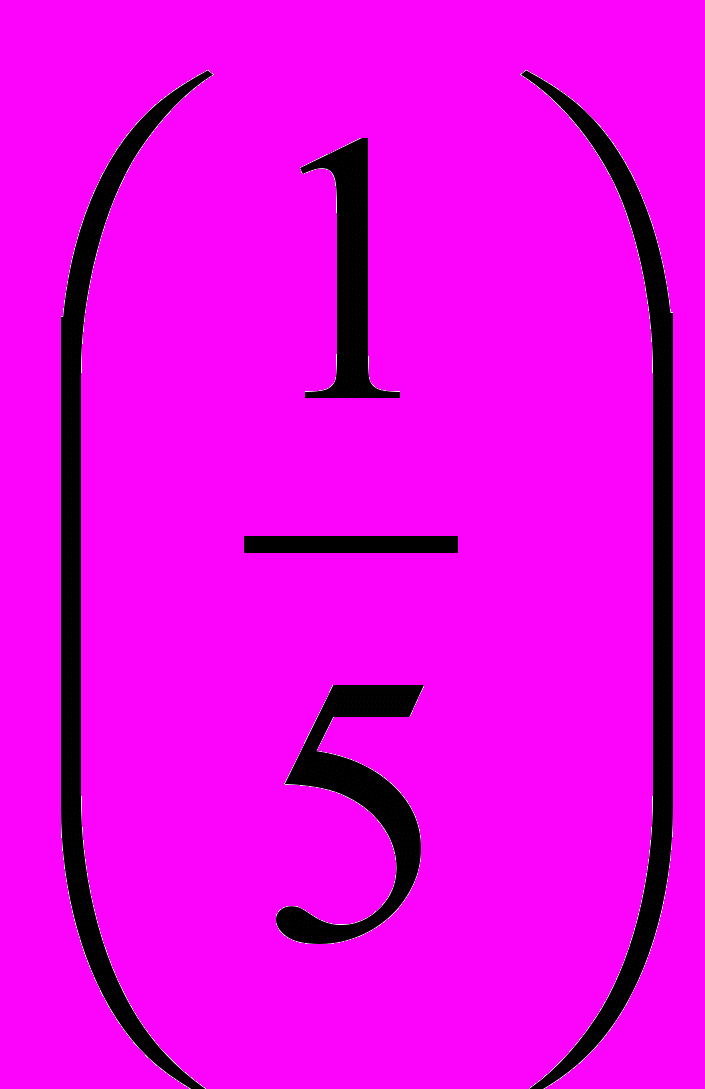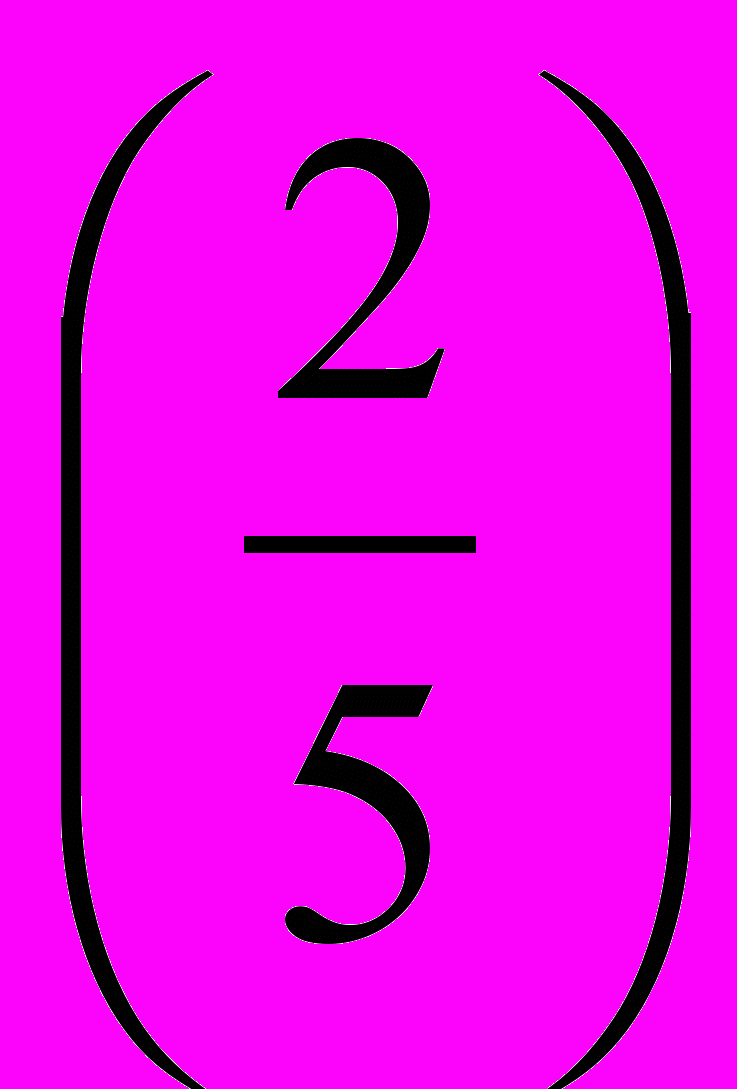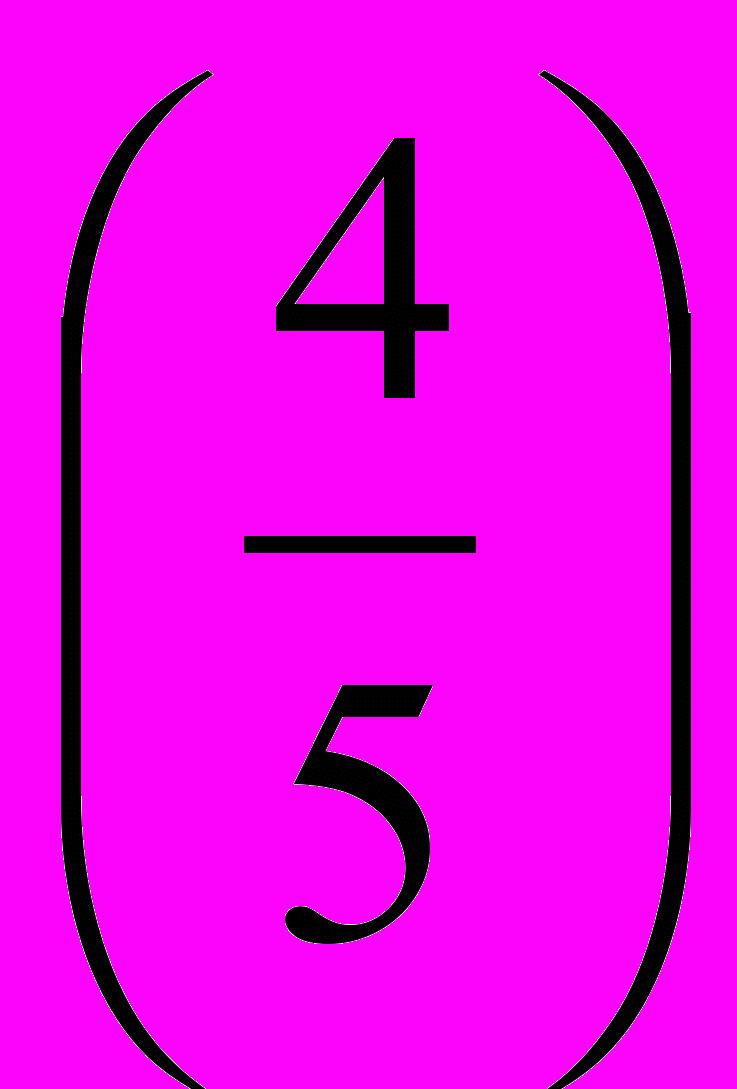