Контроль и диагностика общеучебных умений и навыков

Вид материала

Реферат

Содержание Общеучебные умения и навыки Уровень развития организационных ОУУН Коммуникативные ОУУН Уровень развития организационных ОУУН Информационные ОУУН Навык смыслового чтения Навык «сворачивания» и «разворачивания» информации Информационные ОУУН Мыслительные ОУУН Методика проведения контрольно – методического среза мыслительных ОУУН Библиографический список Тема: «Квадратные уравнения»(1 вариант) 3 уровень (Понимание) 5 уровень (Анализ) Контрольно-методический срез по геометрии в 8 классе по теме «Площади». 2 уровень (Осмысление) 3 уровень (Применение) 4 уровень (Анализ) 5 уровень (Синтез) 6 уровень (Оценка) ... Полное содержание

Подобный материал:

• «Формирование общеучебных умений и навыков», 225.06kb.
• Доклад на рмо на тему: «Диагностика общих учебных умений и способов учебной деятельности,, 136.47kb.
• «Укрупнение дидактических единиц (уде) с целью формирования общеучебных умений и навыков», 110.15kb.
• Стимулирование познавательной деятельности учащихся как средство повышения уровня сформированности, 57.94kb.
• Владение различными методами обучения, значение дидактических методов, приёмов и умений,, 1003.02kb.
• Программа : Лекция «Психологические особенности ребёнка». Роль семьи в формировании, 26.68kb.
• Урока:  «Природные  источники  углеводородов», 118.23kb.
• Опыта, 246.98kb.
• И. Я. Лернер признает: Задача состоит в том, чтобы список общеучебных умений был учтен, 192.18kb.
• Втечение всей работы у меня возникали такие вопросы, 128.94kb.

Министерство образования и науки Удмуртской Республики

Муниципальное общеобразовательное учреждение

Средняя общеобразовательная школа № 65


Реферат


Тема: Контроль и диагностика общеучебных умений и навыков.

Контрольно-методический срез по теме «Квадратные уравнения».


Выполнил: учитель математики МОУ СОШ №65 Васильева Галина Павловна, высшая квалифицированная категория




Научный руководитель: зам. директора по НМР Волкова Галина Серафимовна, высшая квалификационная категория


^{Ижевск, 2010}


Оглавление


Введение…………………………………………………………………………...…3


Глава 1. Общеучебные умения и навыки……………………………….......….4

1.1 Оганизационные ОУУН…………………………..……………..…..4

1.2 Коммуникативные ОУУН………………………..…...……………..5

1.3Информационные ОУУН…...………………………….………..……6

1.4 Мыслительные ОУУН…………………….……………………..….8

Глава 2.Критерии сформированности ОУУН…………..……………………10

2.1 Критерии сформированности ОУУН…………………………...…10

2.2 Методика проведения контрольно - методического среза

мыслительных ОУУН……………………………….…………...….11

Заключение……………………………………………………….………..….....14

Библиографический список……………………………………………….……15

Приложение 1 КМС на определение уровня сформированности

мыслительных ОУУН по теме «Квадратные уравнения»……………………16

Приложение 2 КМС на определение уровня сформированности

мыслительных ОУУН по теме «Решение линейных

и квадратных неравенств»…………………………………………………….………17

Приложение 3 КМС на определение уровня сформированности

мыслительных ОУУН по теме «Площади фигур»……………………………24

Введение


« Уже сегодня надо знать, какие требования к образованию предъявляют стандарты второго поколения…»( 10, с. 2).

Многие годы единственной формой итогового контроля знаний, умений и навыков учащихся оставалась контрольная работа, при этом личностный рост ребенка оставался вне поля зрения педагога. Сегодня в условиях гуманизации школьного математического образования изменение форм обучения влечет за собой изменение в системе контроля. Она становится более гибкой, позволяющей, с одной стороны, организовывать контроль знаний, умений и навыков, а с другой стороны – находить возможность развития интеллектуальных и творческих способностей учащегося.

В проекте Официальных документов сказано: «Функции универсальных учебных действий:

-обеспечение возможностей учащегося самостоятельно осуществлять деятельность учения, ставить учебные цели, искать и использовать необходимые средства и способы их достижения, контролировать и оценивать процесс и результаты деятельности, обеспечение успешного усвоения знаний, формирования умений и навыков и компетентностей в любой предметной области… .» ( 9 , с. 2).

Одной из задач реализации деятельностного подхода ставится определение основных результатов обучения и воспитания в зависимости от сформированности личностных качеств и универсальных учебных действий, а так же разработка системы типовых задач для диагностики сформированности универсальных учебных действий на каждом этапе образовательного процесса. ( 9 , с. 2).

Мы рассматриваем возможности контроля и оценки знаний с позиций личностно-ориентированного обучения. Под личностно-ориентированным будем понимать обучение, которое реализуется посредством совместной деятельности, саморазвитие субъективного процесса.

То есть при выборе форм и методов проверки знаний учитель понимает важность активной деятельности ученика, превращающего его из пассивного объекта воздействия в активного субъекта деятельности.

Деятельность на уроке рассматривается как последовательность действий: актуализация→ целеполагание → определение критериев успеха→ планирование собственной деятельности → реализация плана → рефлексия → оценивание →коррекция собственной деятельности.

Определить «профиль» коррекции позволяет сформированность общеучебных умений и навыков (ОУУН-ов), т.е. выявить несформированные общеучебные умения и навыки для целенаправленной работы по их формированию, а так же отметить те ОУУН, которые на данное время станут «опорными» для обеспечения успешной деятельности учащегося по предмету.( 8, с. 15) .


Общеучебные умения и навыки


Описанные в литературе (3, с.3) ОУУН разнообразны и по форме и по содержанию. В школе создана целостная программа развития всех четырех групп:

• информационных,
  
• коммуникативных,
  
• организационных,
  
• мыслительных.
  

Организационные ОУУН


Организационные ОУУН – это общеучебные умения и навыки, обеспечивающие ученику самостоятельность действий и оптимизацию деятельности на уроках и при выполнении домашних заданий.

Для учителя эти данные являются исходными для организации самостоятельной деятельности учащегося.

1. Навык планирования собственной деятельности (определяется и развивается при выполнении учащимися заданий типа проектных).
   
2. Навык организации и ведения записей в собственной тетради.
   
3. Навык самооценки (способность самостоятельно оценить и способ достижения результата, и сам результат) и другие навыки.
   

Для обеспечения педагогической поддержки уровня развития общеучебных навыков достаточно определять как достаточный, критический и недостаточный уровень.

Таблица 1

Уровень развития организационных ОУУН
Недостаточный (воспроизведение)	Критический (конструктивный)	Достаточный (творческий)
Самостоятельно планировать свою деятельность, прогнозировать ее результаты, контролировать выполнение и оценивать адекватно результаты своей работы практически не может, все делает только с помощью учителя.	Может сам организовать рабочее место, работает по плану, способен к самоконтролю по алгоритму, но самостоятельно ставить учебную задачу и выбирать оптимальный способ работы не может.	Приняв и осознав цель работы, может самостоятельно приготовить рабочее место, спланировать последовательность действий, выбрать оптимальный способ работы, оценить результат.

Коммуникативные ОУУН


Коммуникативные ОУУН определяют формы и виды участия в коллективной учебной деятельности учеников с разными характеристиками развития сферы общения.

Для учителя это очень важные параметры при планировании и организации многих социализирующих форм и видов работы – дискуссий, коллективной работы на единую цель и т.д.

1. Монологическая речь (устная или письменная);
   
2. Способность вести конструктивный диалог;
   
3. Способность работать в команде (подчиняться, руководить , делиться знаниями, полномочиями) и др.
   

Для обеспечения педагогической поддержки уровни развития общеучебных навыков достаточно определять как достаточный, критический и недостаточный уровень.

Таблица 2

Уровень развития организационных ОУУН
Недостаточный	Критический	Достаточный
Речь развита плохо, в диалоге участвует односложными ответами, работая в группе, только слушает. Навык активного слушания не сформирован – не отслеживает логику рассказа, не задает вопросов по ходу рассказа учителя.	Устный полный ответ может построить только по алгоритму. В группе может участвовать в дискуссии. Услышанное анализирует, иногда может задать вопрос. При работе в команде хорошо выполняет четко определенную деятельность, без собственной активности.	Свободно рассуждает на заданную тему в рамках полученных знаний. В диалоге активен, умеет внимательно слушать собеседника. В группе может организовать обсуждение. При работе в команде может как подчиняться, так и руководить одинаково успешно, сохраняет в команде способность к творчеству.

Информационные ОУУН


Информационные ОУУН определяют для ученика возможность самостоятельного поиска и осмысления информации.

Для учителя определяют выбор форм подачи материала на этапе объяснения и диагностики. А также выбор системы заданий для целенаправленного развития информационных ОУУН.

1. Навык смыслового чтения (умения осмыслять прочитанное на высоком уровне: «читать и понимать, что написано» Я.Б. Княжин). Этот навык диагностируется и развивается «слепыми» текстами и различными заданиями типа: «озаглавь текст», «поставь вопросы к тексту из текста» и т.д.
   
2. Навык «сворачивания» и «разворачивания» информации (составление и «чтение» таблиц, графиков, схем и т.д.).
   
3. Навык использования технических средств (ТСО, ПК, TV, мультимедиа) – для поиска, планирования, организации и оформления учебной работы и другие навыки.
   

Для обеспечения педагогической поддержки уровни развития общеучебных навыков достаточно определять как достаточный, критический и недостаточный уровень.

Таблица 3

Информационные ОУУН	Уровень развития информационных ОУУН
	Недостаточный	Критический	Достаточный
Смысловое чтение	При чтении с трудом выделяет главную мысль, ошибается при заполнении простого «слепого» текста	Может проанализировать прочитанное по вопросам, осмыслить текстовую задачу, задание.	Может «читать и понимать, что написано» Я.Б. Княжин), легко справляется с заданиями, требующими осмысления текста.
Преобразование информации	С трудом анализирует таблицы или составляет их; практически не способен самостоятельно построить схему по тексту, прочитать график функции.	При небольшой помощи учителя может справиться с преобразованием информации из вербальной в графическую или символическую (формулы).	Легко «читает» графики, схемы, формулы, преобразует их в текст. Способен без ошибок проделать обратную процедуру преобразовать текст в рисунок, график, таблицу и т.д.
ТСО	Использовать ТV,РС только как пользователь: без учебных познавательных целей.	При использовании ТV,РС способен работать с ними как с источниками знаний, но требует постановки учебной задачи учителем.	Способен использовать самостоятельно технические средства для поиска информации, для оформления работ.
Наблюдение	Не умеет осмыслять конкретную информацию, полученную путем наблюдения или непосредственных ощущений.	Умеет наблюдать, может перевести ощущения в сознательную смысловую информацию, однако, требует педагогической помощи - алгоритмов, вопросов.	Легко осмысляет информацию, полученную непосредственнее через эмоции и органы чувств: осязание, обоняние, зрение.

Мыслительные ОУУН


Мыслительные ОУУН - это реализованные в онтогенезе психофизиологические функции головного мозга, лежащие в основе сознательного мышления учащихся.

Уровень развития того или иного мыслительного навыка у учащихся устанавливается психологами, но учитель должен определять его на материалах своего предмета с помощью специального контрольно-методического среза.

Уровни мыслительных ОУУН-ов:

1. Распознавание
   
2. Понимание
   
3. Применение
   
4. Анализ
   
5. Синтез
   
6. Оценка
   

Таблица 4

Основные категории учебных целей	Примеры обобщенных типов учебных целей
Распознание Эта категория обозначает запоминание и воспроизведение неученого материала. Речь может идти о различных видах содержания – от конкретных фактов до целых сведений	Ученик знает употребляемые термины, знает конкретные факты, знает методы и процедуры, знает основные понятия, знает правила и принципы
2. Понимание Показателем способности понимать значение изученного может служить преобразование (трансляция) материала из одной формы выражения в другую, «перевод» его с одного «языка» на другой (например, из словесной формы в математическую). В качестве показателя понимания может также выступать интепретация материала учеником ( объяснение, краткое изложение) или же предположение о дальнейшем ходе явлений, событий (предсказание последствий, результатов). Такие учебные результаты превосходят простое запоминание материала.	Ученик понимает факты, правила, принципы, интерпретирует словесный материал, интерпретирует схемы, графики, диаграммы, преобразует словесный материал в математические выражения, предположительно описывает будущие последствия, вытекающие из имеющихся данных, непосредственно подставляет данные в формулу.
3. Применение Эта категория обозначает умение использовать неученый материал в конкретных условиях и новых ситуациях. Сюда входит применение правил, принципов, законов, теорий. Соответствующие результаты превосходят простое владение материалом, чем понимание.	Ученик использует понятия и принципы в новых ситуациях, применяет законы, теории в конкретных практических ситуациях, демонстрирует правильное применение метода или процедуры, решая задачу в один шаг.
Анализ Эта категория обозначает умение разбить материал на составляющие так, чтобы ясно выступала его структура. Сюда относятся: вычисление частей целого, выявление взаимосвязей между ними, осознание принципов организации целого. Учебные результаты при этом характеризуются более высоким интеллектуальным уровнем, чем понимание и применение, поскольку требуют осознания как содержания учебного материала, так и его внутреннего строения.	Ученик выделяет скрытые(неявные) предположения, видит ошибки и упущения в логике рассуждения проводит различия между фактами и следствиями, оценивает значимость данных, решает задачу в два шага.
Синтез Эта категория обозначает умение комбинировать элементы, чтобы получить целое, обладающее новизной. Таким новым продуктом может быть сообщение (выступление, доклад), план действий или совокупность обобщенных связей (схемы для упорядочения имеющихся сведений). Соответствующие учебные результаты предполагают деятельность творческого характера с акцентом на создание новых схем и структур.	Ученик пишет небольшое творческое сочинение, предлагает план проведения эксперимента, использует знания из разных областей, чтобы составить план решения той или иной проблемы, решает задачи повышенного уровня.
Оценка Эта категория обозначает умение оценивать значение того или иного материала (утверждение художественного произведения, исследовательских данных) для конкретной цели. Суждения ученика должны основываться на четких критериях. Категории могут быть как внутренними, так и внешними(соответствие намеченной цели). Критерии могут определяться самим учеником или же задаваться ему извне( например, учителем). Данная категория предполагает достижение учебных результатов по всем предшествующим на категориях оценочные суждения, основанные на явно очерченных критериях.	Ученик оценивает логику построения материала в виде письменного текста, оценивает соответствие выше имеющихся данных, оценивает значимость того или иного продукта деятельности исходя из внутренних критериев, решает задачи творческого уровня.

Критерии сформированности ОУУН.


В основу систематизации требований к оцениванию освоения учащимися общеучебных умений могут быть положены следующие стратегии:

• нормативно-индивидуальная стратегия, предполагающая оценивание результатов ученика на основании их сравнения с установленной нормой;
  
• нормативно-групповая стратегия, предполагающая оценивание результатов ученика на основании сравнения с выполнением нормы другими учениками;
  
• нормативно-ретроспективная стратегия, предполагающая оценивание результатов ученика на основании сравнения сегодняшних результатов ученика с выполнением нормы в прошлом.
  

В своей практике мы применяем все три оценочных суждения о качестве общеучебных умений, комментируя это в классе (в зависимости от того, за какой этап изучения темы ставится оценка).

Основой развития оценочной деятельности является групповое обсуждение в классе вопросов: эталонная работа, правильно ли оценена выполненная работа, в чем причины ошибок и что нужно сделать, чтобы их устранить? Такая работа позволяет не только формировать и развивать общеучебные умения, но и более эффективно организовывать деятельность учащихся по освоению содержания традиционных учебных дисциплин.

Уровень сформированности информационных, коммуникативных и организационных навыков учащихся оценивается на уроках и при самоподготовке и оценивания их по следующим уровням:

В – воспроизводящий по образцу;

К – конструктивный;

Т – творческий.

Мониторинг результатов проводится первый раз в учебном году в сентябре и второй раз – в марте-апреле. Данная работа отражает методическую тему школы «Формирование ключевых компетенций». Сформированность мыслительных ОУУН (Приложения1,2,3) оценивается в ходе выполнения специальных заданий с предметным содержанием (контрольно-методических срезов – КМС) и отмечается знаком «+» (справился) или «–» (не справился).


Методика проведения контрольно – методического среза мыслительных ОУУН


Обычно разрабатываю КМС на 3-4 варианта по одной теме. Каждый уровень помечен определенным цветом.

Накануне учащихся предупреждаю о предстоящем КМС. На проведение контрольно-методического среза выделяется два урока. В начале первого урока раздаю учащимся задания первого уровня, помеченные обычно коричневым цветом. На отдельном столе выложены задания на карточках последующих уровней по вариантам.

Учащиеся выполняют задание первого уровня, подходят к учителю, показывают и рассказывают свое решение. Если учащийся справился с заданием, то ему предлагается подойти к столу с выложенными на него карточками, положить карточку с заданием на свой вариант и на соответствующий уровень и взять карточку с заданием следующего уровня. Если учащийся не справился с заданием, то он получает консультацию учителя или принимающего у него консультанта, эту карточку возвращает на свой вариант на соответствующий уровень. Затем он берет карточку этого же уровня с другого варианта. Как правило, учащиеся, решающие повторно задание одного уровня, быстро справляются с заданием и переходят на следующий уровень. Учитель сразу результаты КМС на определение уровня сформированности мыслительных ОУУН оформляет в виде таблицы (например, таблица 5). Нормы оценок оговариваются в начале урока, поэтому учащийся знает, какую оценку он получит.


Тема: «Квадратные уравнения».

Класс: 8.

Таблица 5

	Уровни мыслительной деятельности
Фамилия и имя учащегося	распознавание	осмысление	понимание	применение	анализ	оценка
	+	+	+	+	+	+
	+	+	+	+	-
	+	+	+	+
	+	+	+	+
	+	+
	+	+	+	+
	+	+	+	+	+
	+	+	+	+	+
	+	+	+	+	+	+
	+	+	+	+
	+	+	+	+
	+	+	+	+
	+	+	+	+	+	+
	+	+	+	+
	+	+
	+	+	+	+

Оценка «3» ставится за выполнение заданий 1 – 3 уровней, «4» – 1 – 5 уровней, «5» – 1 – 6 уровней.

На таких уроках обычно присутствует рабочий шум, который ни в коей мере не уменьшает эффективности урока. Урок проходит плодотворнее, если на уроке принимают ответы учащихся два учителя математики. Иногда к такой работе привлекаю в качестве консультантов старшеклассников. В 2009-2010 учебном году КМС по теме « Рациональные неравенства» проводила только для слабых учащихся девятых классов.

Таким образом, в классе создается деятельностная ситуация:

исключено списывание с решебника, с соседа по парте, бессмысленное списывание с доски готового решения, угадывания ответа , как это зачастую происходит при тестовой форме контроля. На уроке нет учащихся, которые пришли в класс просто отсидеться и поиграть на телефоне. В противовес этому поставлены: самостоятельная учебная деятельность, осознанность цели работы и ответственность за собственный результат; реализация индивидуальных интересов учащихся.

После таких уроков слабые учащиеся начинают активнее работать и на последующих уроках математики . Указанная форма работы отличается от традиционной работы с учащимся своей нестандартностью и позволяет решать актуальные проблемы образования и воспитания в соответствии с требованиями времени.


Заключение


В составе основных видов универсальных учебных действий, соответствующих ключевым целям общего образования, четыре блока: личностный регулятивный, познавательный, коммуникативный. ( 9 ,с. 3).

Эффективная деятельность учителя математики по формированию и развитию ОУУН основывается на овладении учащимися ценностями познавательной культуры, на целостном видении общеучебных умений и освоении школьниками теоретических и технологических позиций их осуществления.

Ценности, знания, умения, освоенные на специальных занятиях, позволяют учителю более эффективно формировать, совершенствовать и использовать общеучебные умения.

Проектирование совершенствования и использования общеучебных умений целесообразно осуществлять в процессе планирования системы уроков по учебной теме.

Учителю важно, чтобы учащиеся не только получили, но и осмыслили информацию, поэтому учебный процесс обязательно включает такие ступени, как распознавание и осмысление. Однако мы окажем плохую услугу ученикам, если не будем требовать от них практического применения знаний, если не привьем навыки анализа и синтеза, не научим оценку фактам. Чтобы наладить полноценный процесс обучения, недостаточно лишь задавать нужные вопросы и ставить оценки. Учебный процесс должен предусматривать разнообразные виды работ, способствующих развитию мышления, необходимо при планировании урока учитывать психофизические особенности учащихся, внешней и внутренней мотивации, ведущей модальности восприятия. Наша задача – научить молодых людей глубоко мыслить, поэтому необходимо стараться включать соответствующие виды учебной деятельности в план каждого урока.(4, с.5)

Проведенные КМС показали, что в работе активно участвуют все учащиеся, заинтересованы в переходе на следующий уровень; время на уроке используется рационально каждым учеником; с урока учащиеся уходят а хорошем настроении и на следующих уроках по расписанию сохраняют хорошую работоспособность. В процессе такой работы поддерживается постоянная обратная связь учитель – ученик. Ученику сразу сообщается результат каждого действия.

Я считаю, что применяемые мною КМС могут способствовать формированию структуирования знаний, осознанного и произвольного построения речевого высказывания в устной и письменной речи , рефлексии способов и условий действия, контролю и оценке процесса и результатов деятельности; умения с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации, владения монологической и диалогической речи учащихся, о чем речь идет в проекте Официальных документов.(9, с.3)


Библиографический список

1. Бощенко О.В. «Математика. Итоговые работы». Волгоград: «Учитель», 2007 г.
   
2. Воровщиков С.Г. «Продуктивные деловые игры во внутришкольном управлении: теория, технология». М.: «ЦГЛ», 2005 г.
   
3. Галеева Н.Л. «Сто приемов для учебного успеха ученика на уроках биологии». М.: «5» за знания, 2006 г.
   
4. Козина М.Е., Фадеева О.М. «Математика 5–11 кл. Нетрадиционные формы контроля». Волгоград: «Учитель», 2007 г.
   
5. Мордкович А.Г., Мишустина Т.Н., Тульчинская Е.Е. «Алгебра - 8. Задачник. М.: Мнемозина, 2009 г.
   
6. Нечаев М.П. « Разноуровневый контроль качества знаний по математике». М.: «5» за знания, 2006 г.
   
7. Газета «Математика», № 7 (2007г.) , № 13 (2004 г).
   
8. Научно-практический журнал «Завуч», №2, 2003 г.
   
9. Газета «Математика», № 15 (2010г.) .
   
10. Примерные программы основного общего образования. Математика. – М.: Просвещение, 2009. (Стандарты второго поколения)
    

Приложение 1

КМС на определение уровня сформированности мыслительных ОУУН.

Тема: «Квадратные уравнения»(1 вариант)

Класс: 8

1 уровень

1.Какие из уравнений не являются квадратными?

2x – x² – 8 = 0

4x² + x = 4x – 2

3 + x² = 0

X² = (x – 2)(x + 1)

2.Определить коэффициенты в уравнениях, которые являются квадратными?

3.Выпишите неполные квадратные уравнения.

4.Выпишите приведенные квадратные уравнения.


2 уровень

1.Составить квадратное уравнение, у которого:

старший коэффициент равен 8, коэффициент при x равен 5, свободный член равен 1.

2.Преобразуйте уравнение к виду ax² + bx + c = 0

6x(2x + 1) = 5x + 1


3 уровень

1.Является ли число 3 корнем квадратного уравнения x² – 4x + 3 = 0 ?

2.Определите число корней квадратного уравнения:

X² – 8x – 84 = 0

X² + 3x – 24 = 0


4 уровень

Решите уравнения:

a) x² – 5x + 6 = 0

б) x² = 2x + 48

в) 6x(2x + 1) = 5x + 1

г)x² – 4 = 0

5 уровень

Решите уравнения:

а) (2х – 1) (2х + 1) + х (х – 1) = 2х (х + 1)

б) х² + 4 √3х + 12 = 0


6 уровень

Решите уравнения:

а) х⁴ – 17х² + 16 = 0

б) (3х – 4)² – 5 (3х – 4) + 6 = 0

в) (p – 4)x² + (2p – 4)x + p = 0

Оценка «3» - 1-3 уровень. Оценка «4» - 1-5 уровень. Оценка «5» - 1-6 уровень.


Приложение 2


КМС «Решение линейных и квадратных неравенств».

8-9класс

Основные темы:

1. Числовые промежутки.
   
2. Понятие линейного и квадратного неравенства.
   
3. Понятие решения неравенства.
   
4. Алгоритмы решения линейного и квадратного неравенства.
   
5. Нахождение ОДЗ для выражений, содержащих квадратные корни и алгебраические дроби.
   
6. Задачи с параметрами.
   

1 уровень (Распознавание)


1 вариант

Из предложенных неравенств выпишите:

а) линейные;

б) квадратные.

1. а + в > а ∙ в
   
2. x² > 4
   
3. (x – 3)∙5 ≤ 7
   
4. 25^-2 < 2⁶/₇ + 0,4
   

2 вариант

Из предложенных неравенств выпишите:

а) линейные;

б) квадратные.

1. c ∙ d < c – d
   
2. 3x + 7 ≥ 6x + 8
   
3. x² – 6x + 4 > 0
   
4. 37 – 2,5 > 2^-2 + 0
   

3 вариант

Из предложенных неравенств выпишите:

а) линейные;

б) квадратные.

1. m ∙ n < m : n
   
2. 3x + 2 ≤ 2 – 7x
   
3. 3 – x² ≥ 6x
   
4. 14 – 2⁵ < 7 + 6¹/₄
   

2 уровень (Осмысление)


1 вариант

Запишите неравенство на математическом языке:

а) Двучлен 5а – 3 принимает положительные значения.

б) Трехчлен 5m² + 8m + 3 принимает значения большие, чем 2.

в) Квадрат двучлена 13с – 22 принимает неотрицательные значения.


2 вариант

Запишите неравенство на математическом языке:

а) Двучлен 6х – 5 принимает отрицательные значения.

б) Трехчлен 6х² + 8х + 7 принимает значения меньшие, чем 3.

в) Разность квадратов х и 4 принимает неположительные значения.


3 вариант

Запишите неравенство на математическом языке:

а) Двучлен 7 – 3х принимает значения, не превосходящие 4.

б) Трехчлен 7 – 3х – х² принимает отрицательные значения.

в) Сумма квадратов х и 2 принимает неотрицательные значения.


3 уровень (Понимание)

1 вариант

1) Является ли решением неравенства 2а + 5 > 7а – 8 значение а, равное:

а) 2;

б) 6,5;

в) - √2;

г) √18.


2) Заполните пустые места в следующей таблице:

( таблицу чертить не нужно)

№ п/п	Условия	Название числового промежутка	Графическая модель	Аналитическая модель	Символическая запись
1	Все числа, большие или равные – 3
2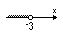
3				х ≥ 17
4					( - ∞; 8 ]
5
6	Все числа, большие -10 и одновременно меньшие -1
7				- 2 ≤ х ≤ 3
8					(15; 25)

Графической моделью числового промежутка может быть одна из геометрических фигур:

• Луч;
  
• Открытый луч (луч, начало которого ему не принадлежит);
  
• Отрезок;
  
• Интервал ( отрезок, концы которого ему не принадлежат).
  

2 вариант

1) Является ли решением неравенства 3а > а + 2 значение а, равное:

а) -1;

б) 7;

в) √5;

г) 3/7

2) Заполните пустые места в следующей таблице:

( таблицу чертить не нужно)

№ п/п	Условия	Название числового промежутка	Графическая модель	Аналитическая модель	Символическая запись
1	Все числа, меньшие или равные – 7
2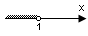
3					( - ∞; 45 ]
4				- 22 < х ≤ 0
5
6					( -23 ; 23 ]
7	Все числа, большие 0 и одновременно меньшие или равные 10
8				х ≥ 13

Графической моделью числового промежутка может быть одна из геометрических фигур:

• Луч;
  
• Открытый луч (луч, начало которого ему не принадлежит);
  
• Отрезок;
  
• Интервал ( отрезок, концы которого ему не принадлежат).
  

3 вариант

1) Является ли решением неравенства 9а + 1 > 7а значение а, равное:

а) 2;

б) – 0,5;

в) - √3;

г) √12.

2) Заполните пустые места в следующей таблице:

( таблицу чертить не нужно)

№ п/п	Условия	Название числового промежутка	Графическая модель	Аналитическая модель	Символическая запись
1	Все числа, большие или равные 7
2
3				х ≥ 17
4					( - ∞; 8 ]
5
6	Все числа, большие -10 и одновременно меньшие -1
7				- 2 ≤ х ≤ 3
8					(15; 25)

Графической моделью числового промежутка может быть одна из геометрических фигур:

• Луч;
  
• Открытый луч (луч, начало которого ему не принадлежит);
  
• Отрезок;
  
• Интервал ( отрезок, концы которого ему не принадлежат).
  

4 уровень (Применение)


1 вариант

Решите неравенство и изобразите его решение на координатной прямой.

а)x +1 > 0

б)- 8x > 24

в)3x + 2 ≥ 0

г)- 5x + 15 > 3x - 3

д)2 ∙ ( 3 – 2z ) + 3 ∙ ( 2 – z ) ≤ 40


2 вариант

Решите неравенство и изобразите его решение на координатной прямой.

а)x – 3 < 0

б)- 7x > 42

в)- 6x + 12 ≥ 0

г)-2m + 4 ≤ 3m – 6

д)3 – 11y ≤ - 3 ∙ ( y – 2 )


3 вариант

Решите неравенство и изобразите его решение на координатной прямой.

а)x – 7 < 0

б)- 5x < 25

в)- 5x – 1 ≤ 0

г)3 – 2x < 12 – 5x

д)2 ∙ (3 -4q ) – 3 ∙ ( 2 – 3q ) ≤ 0


5 уровень (Анализ)

1 вариант

Решите неравенство.

а) x² – 3x + 2 > 0

б) (2x + 1)(3x + 2) < 0

в) - 5x² < 6 – 2x

г) x² – 36 ≥ 0


2 вариант

Решите неравенство.

а) x² – 3x + 2 ≤ 0

б) (3 – 4x)(2x – 5) ≤ 0

в) - 2x² + x ≤ - 6

г) x² – 25 < 0


3 вариант

Решите неравенство.

а) x² – 3x + 2 ≥ 0

б) (7x + 3)(4x – 1) > 0

в) – x² < 4 – 4x

г) x² – 100 ≤ 0

6 уровень


1 вариант

1. Установите, при каких значениях х имеет смысл выражение:

a) √x² – 8x + 7

б) 1___

√6x² - 2x

в) __ 1______

√(x – 6)(2x + 3)

2. Найдите все значения параметра p, при которых не имеет действительных корней уравнение:

а) ( р – 1)х² – 4х + 5 = 0

б) ( 3р – 5 )х²– ( 6р – 2 )х + 3р – 2 = 0


2 вариант

1. Установите, при каких значениях х имеет смысл выражение:

a) √x² – 6x + 5

б) _ 1___

√3x² - 12x

в) ___ 1_____

√( x – 1 )( 2 - х )

2. Найдите все значения параметра p, при которых не имеет действительных корней уравнение:

а) ( р – 15)х² – 4рх - 3 = 0

б) ( р – 1 )х² – ( 2р – 3 )х + р + 5 = 0


3 вариант

1. Установите, при каких значениях х имеет смысл выражение:

a) √x + x - 2

б) 1___

√5x - x

в) __ 1______

√(x + 5) (4 - x)


2. Найдите все значения параметра p, при которых не имеет действительных корней уравнение:

а) (2р + 3)х² – 6х + 8 = 0

б) 3рх² – 6рх + 13 = 0


Оценка «3» - 1-3 уровень.


Оценка «4» - 1-5 уровень.


Оценка «5» - 1-6 уровень.


Приложение 3


Контрольно-методический срез по геометрии в 8 классе по теме «Площади».


1 уровень (Распознавание)

1 вариант

Выберите верное утверждение:

А) Площадь треугольника равна произведению основания на высоту.

Б) Площадь трапеции равна произведению полусуммы оснований на высоту.

В) Площадь параллелограмма равна произведению смежных сторон на синус угла между ними.


2 вариант

Выберите верное утверждение:

А) Площадь треугольника равна произведению полусуммы оснований на высоту.

Б) Площадь трапеции равна произведению суммы оснований на высоту.

В) Площадь параллелограмма равна произведению основания на высоту.

3 вариант


Выберите верное утверждение:

А) Площадь треугольника равна половине произведения двух смежных сторон на синус угла между ними.

Б) Площадь параллелограмма равна половине произведения основания на высоту.

В) Площадь трапеции равна половине произведения суммы оснований на высоту.


2 уровень (Осмысление)

1 вариант

Установите соответствие между формулами и фигурами:

S = ab

S =

S = *h







2 вариант

Установите соответствие между формулами и фигурами:

S = ab sinά

S = a

S = *h





3 вариант

Установите соответствие между формулами и фигурами:

S = ah

S = a


S = 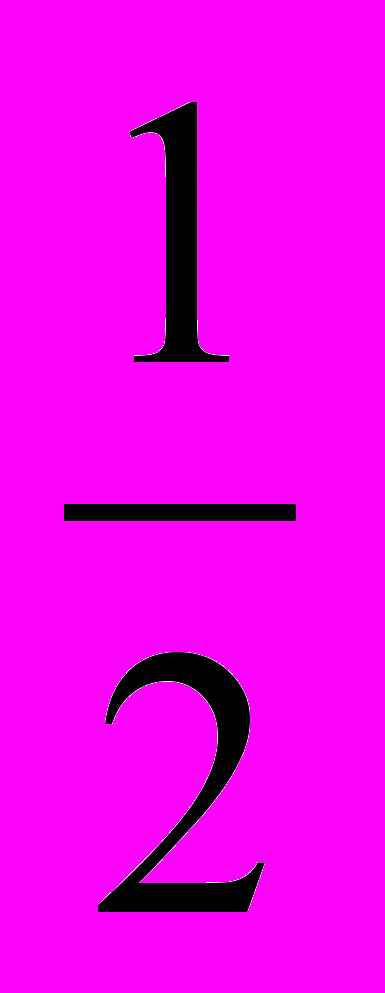dd




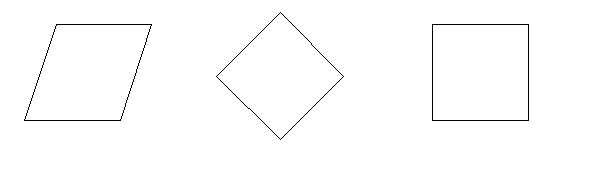
3 уровень (Применение)

1 вариант

Пусть a, b – стороны треугольника, h - высота, S - площадь, опущенная к стороне а . Найдите:

а) S, если a = 15см, h = 12см;

б) S, если a = 7см, b = 11см, C = 30;

в) S, a = 21см, b = 17см, C = 90.


2 вариант

Пусть a, b – стороны параллелограмма, h - высота, S - площадь, опущенная к стороне а . Найдите:

а) S, если a = 15см, h = 12см;

б) S, если a = 7см, b = 11см, C = 30;

в) S, a = 21см, b = 17см, C = 90.


3 вариант

Найдите площадь трапеции АВСД с основаниями АВ и СД, если

а) АВ = 21см, СД = 17 см, высота ВН = 7 см;

б) ВС перпендикулярна АВ, АВ = 5 см, ВС = 8 см, СД = 13 см.


4 уровень (Анализ)


1 вариант

Площадь трапеции равна 36 см, а основания 9 и 12 см. Найдите высоту трапеции.


2 вариант

Площадь треугольника АВС равна 21 см, а его высота СН равна 3 см. Найдите сторону АВ.

3 вариант


Площадь параллелограмма АВСД равна 48 см, сторона АВ равна 6 см. Найдите высоту, проведенную к данной стороне.


5 уровень (Синтез)


1 вариант

Две стороны треугольника 16 см и 22 см. Высота, проведенная к меньшей стороне, равна 11см. Найдите высоту, проведенную к большей стороне.


2 вариант

Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см, а больший угол равен 135˚.


3 вариант

Сторона параллелограмма равна 8 см. Диагональ, равная 14 см, образует с ней угол 30˚. Найдите площадь параллелограмма.


6 уровень (Оценка)


1 вариант

Две стороны треугольника равны 5,62 м и 7,19 м, а высота, проведенная к первой стороне, равна 4,35 м. Найдите высоту, проведенную ко второй стороне, с точностью до 1см.


2 вариант

Катеты прямоугольного треугольника равны 7,25 см и 3,67 см. Найдите гипотенузу с точностью до 0,01 см.


3 вариант

Стороны a и b прямоугольника измерены с точностью до 0,1 см. Можно ли, пользуясь этими измерениями, вычислить площадь прямоугольника S с точностью до 1 см, если в результате измерений получено: a = 2,5 см и b=1,7 см.