Лекция №2 Прикладная математика

Вид материала

Лекция

Содержание Операции над матрицами Транспонированная матрица

Подобный материал:

• «Математика. Прикладная математика», 366.03kb.
• Рабочая программа, 182.62kb.
• Рабочая программа, 160.99kb.
• Программа дисциплины Современная прикладная алгебра для направления 010500 Прикладная, 214.78kb.
• Цифровая обработка сигналов, 137.86kb.
• Проект постановление ученого совета сгту по вопросу: «О переименовании кафедры «Прикладная, 8.11kb.
• Программа вступительного экзамена по математике подготовки магистров по направлению, 86.94kb.
• «Прикладная математика и информатика», 3781.56kb.
• Рабочая программа дисциплины прикладная математика (Наименование дисциплины), 188.06kb.
• Программа вступительного экзамена вмагистратуру по направлению 010400 "прикладная, 204.27kb.

Элементы матричной алгебры

Опр. Матрицей называется упорядоченная совокупность чисел , расположенная в виде таблицы

.

Данная матрица имеет m строк и n столбцов, – элемент матрицы, расположенный на пересечении i-ой строки и j-го столбца.

Опр. Если матрица имеет m строк и n столбцов, то ее называют матрицей размерности

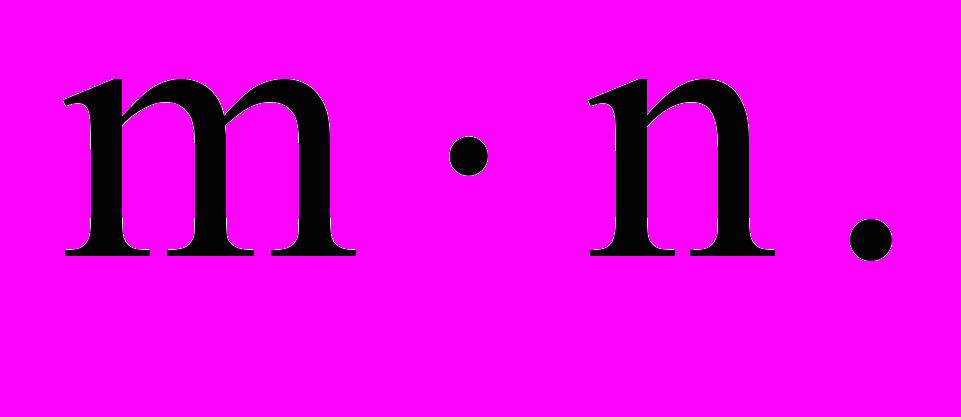
Опр. Если m=n, то матрица называется квадратной. Если 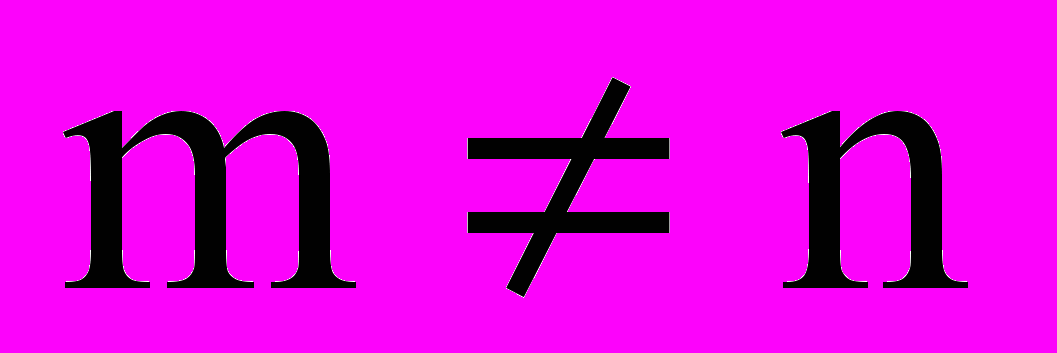, то – прямоу­гольной.

Опр. Матрица размерности 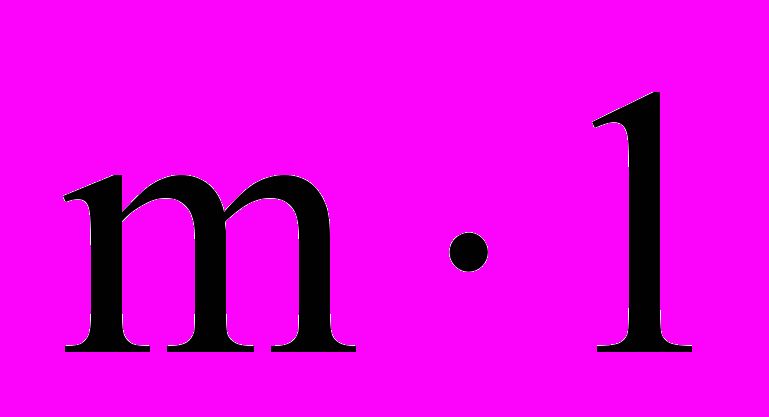называется вектором-столбцом или просто вектором. Матрица размерности 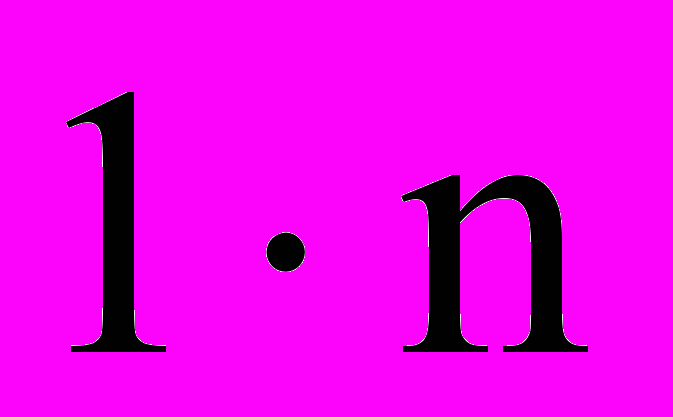называется вектором-строкой

, .

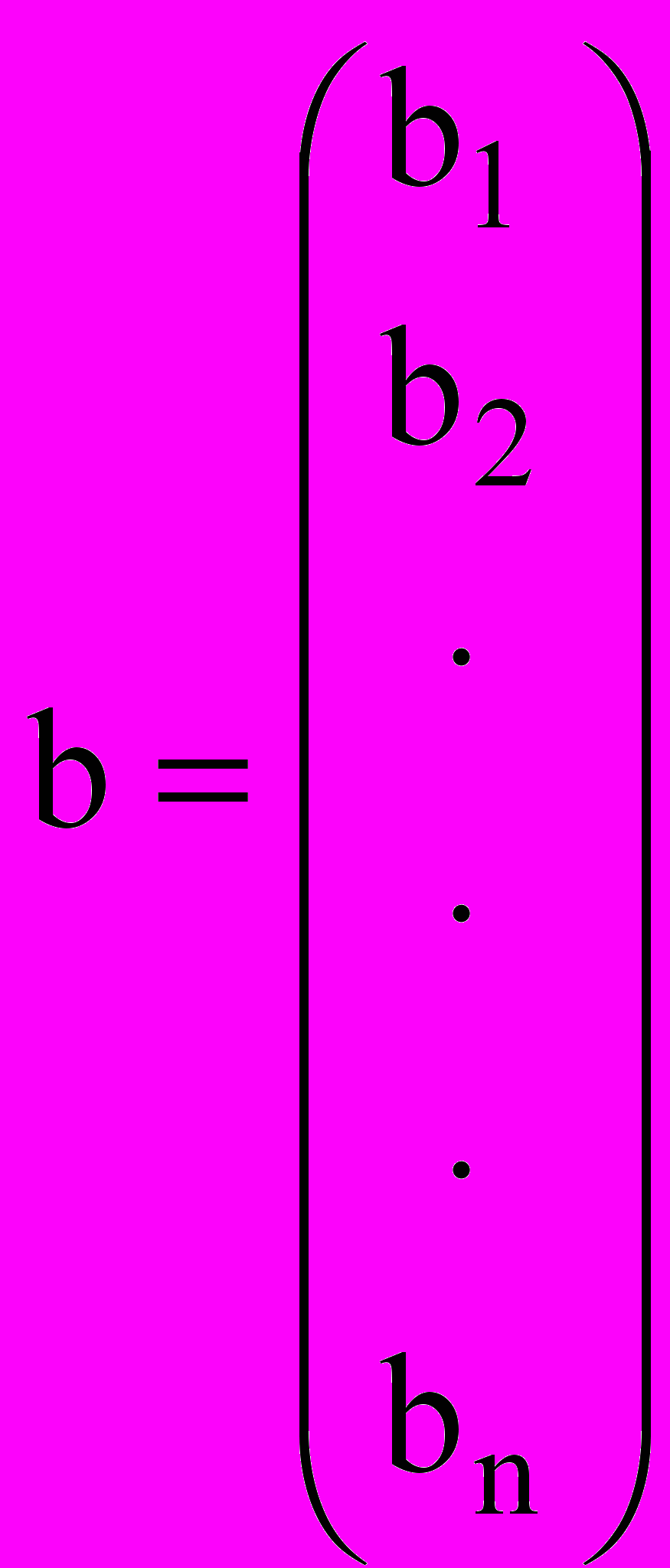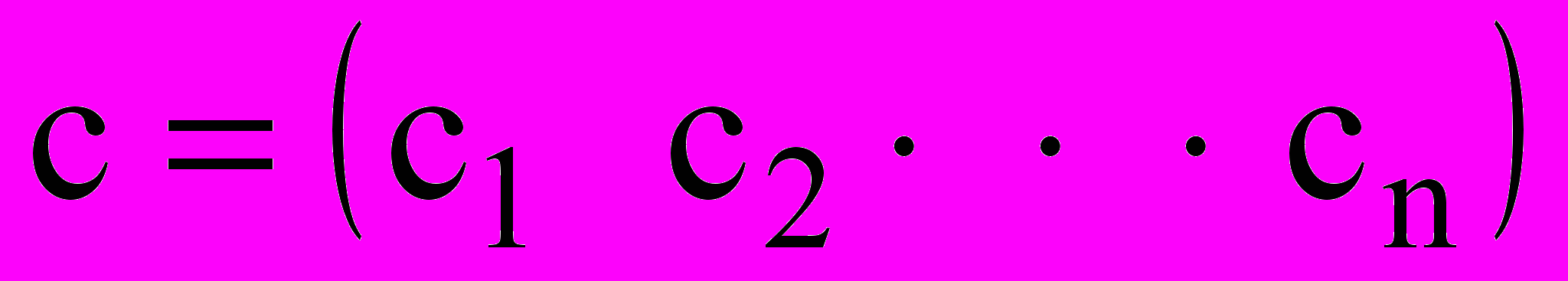В дальнейшем будем рассматривать в основном квадратные матрицы.

Опр. Элементы квадратной матрицы называется диагональными, элементы при 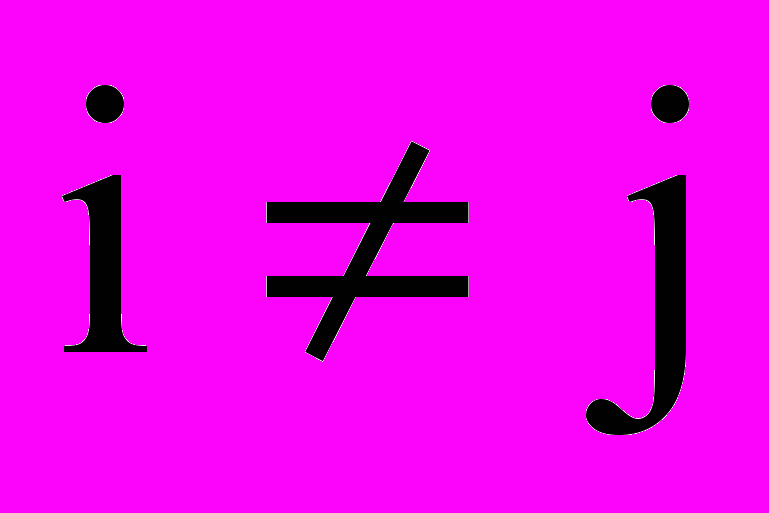называется внедиагональными.

Опр. Квадратная матрица, у которой все внедиагональные элементы равны нулю, называется диагональной

.

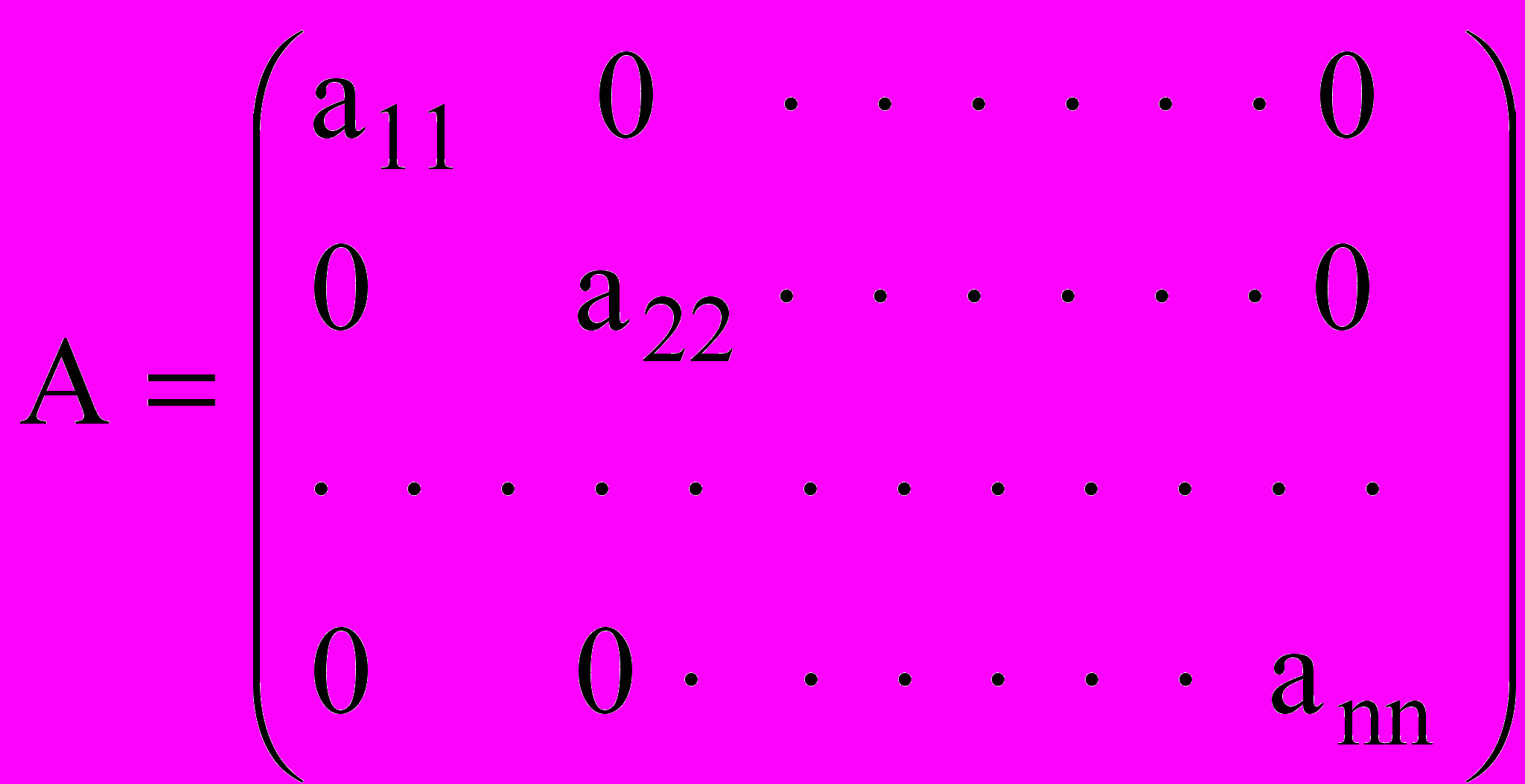Опр. Диагональная матрица, у которой все элементы равны единице, называется единичной

.

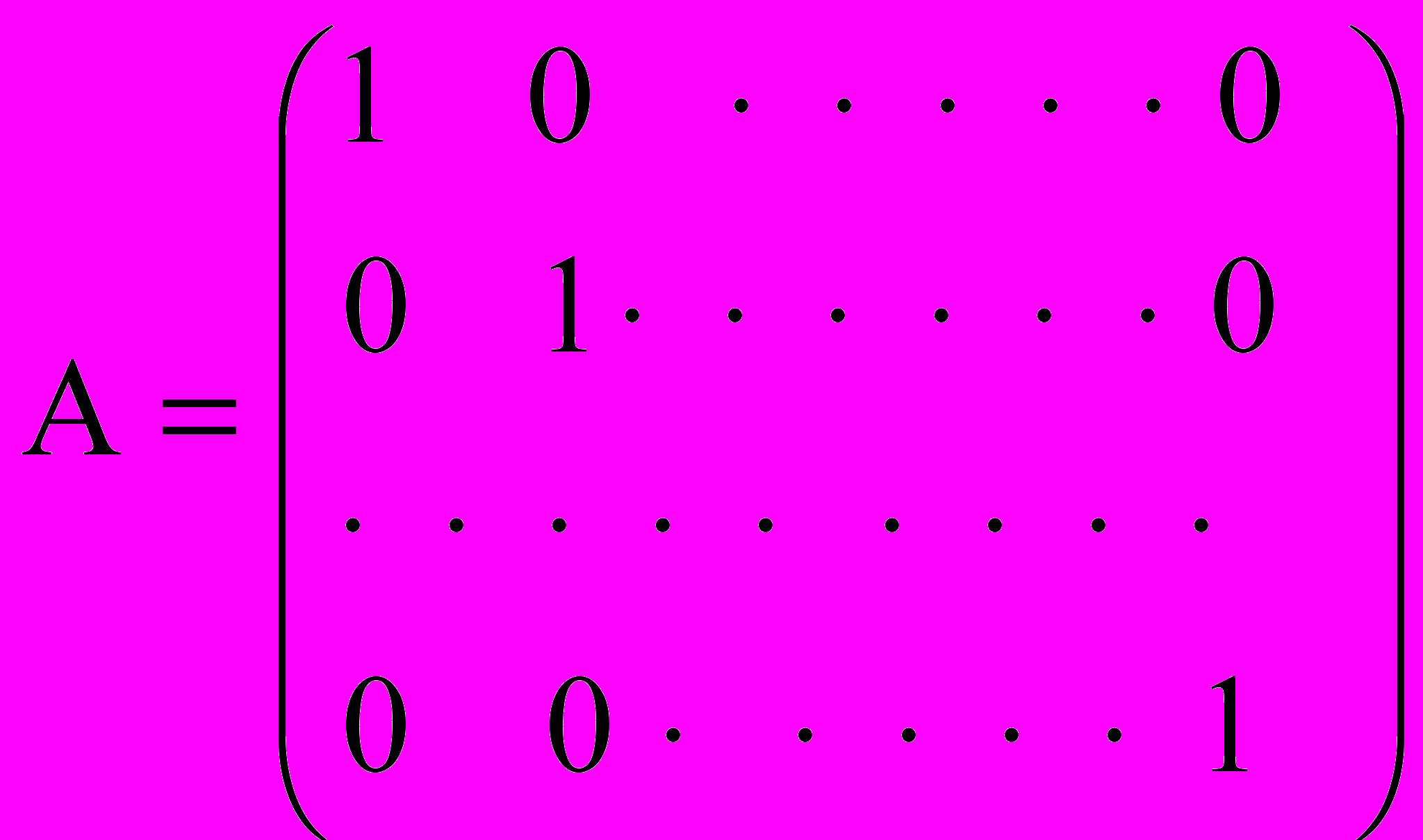Операции над матрицами

Опр. Матрицы A и B одной размерности называется равными, если 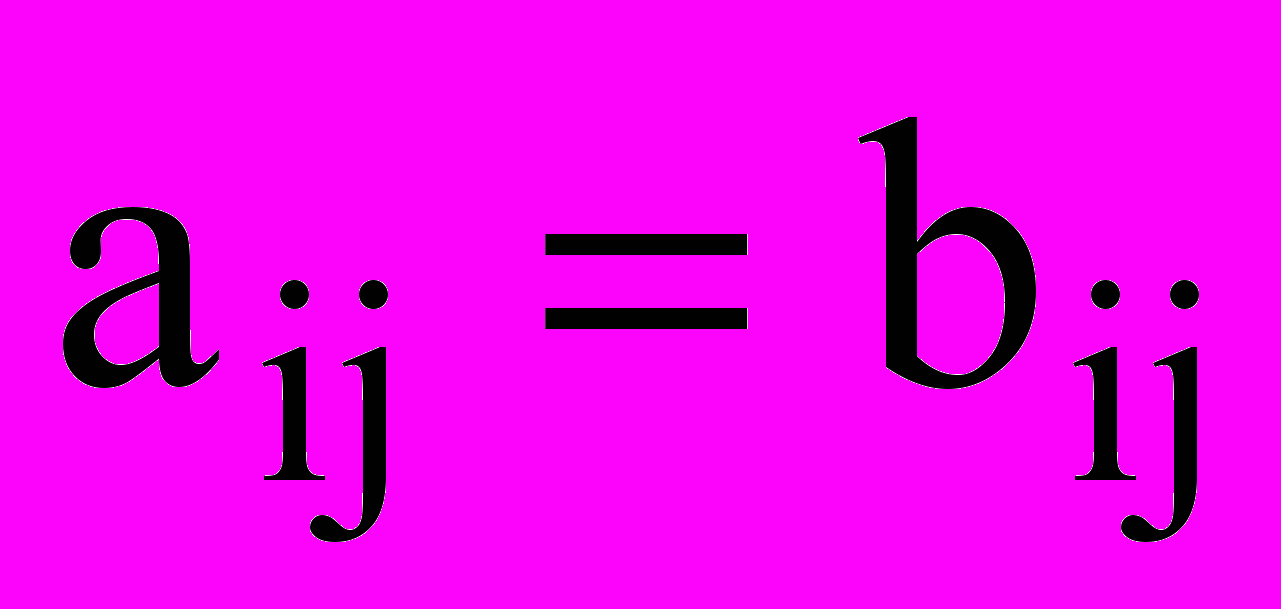для всех i и j. A=B

Опр. Суммой (разностью) матриц A и B одной размерности называется матрица C той же размерности, если 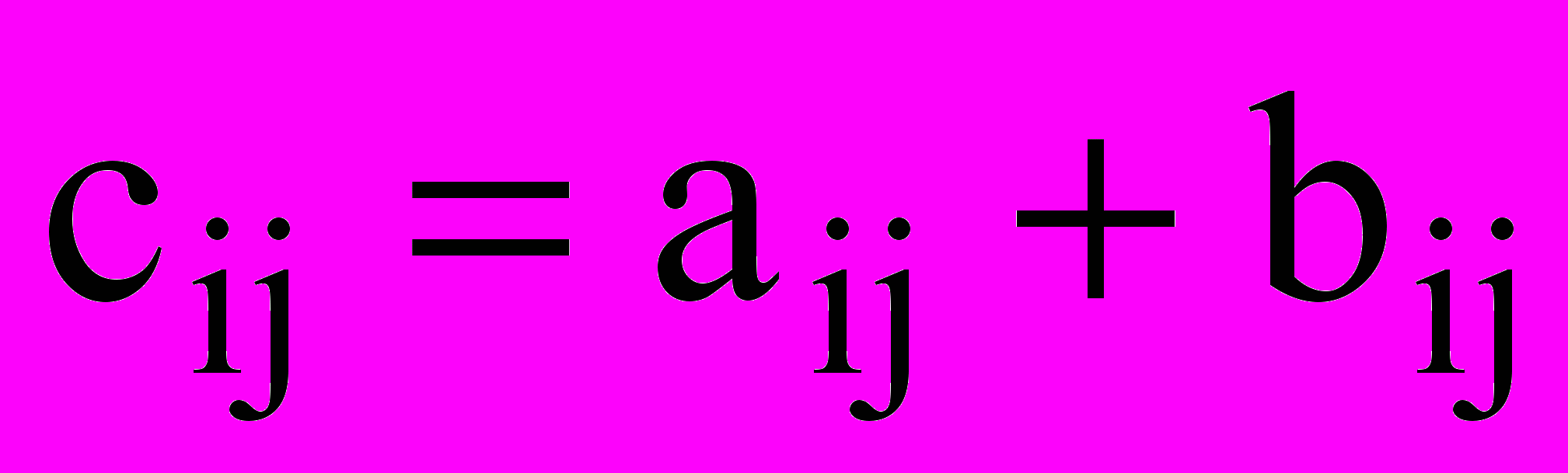(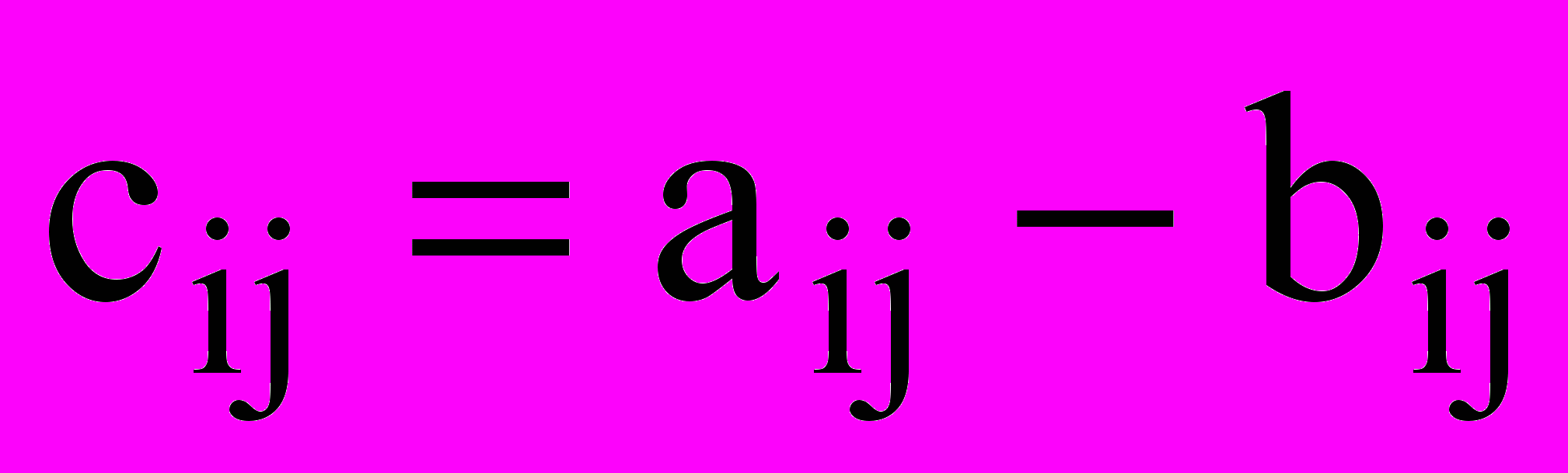) для всех i и j.

C=A+B (C=A–B).

Опр. Произведением матрицы A на число α называется матрица C той же размерности, если 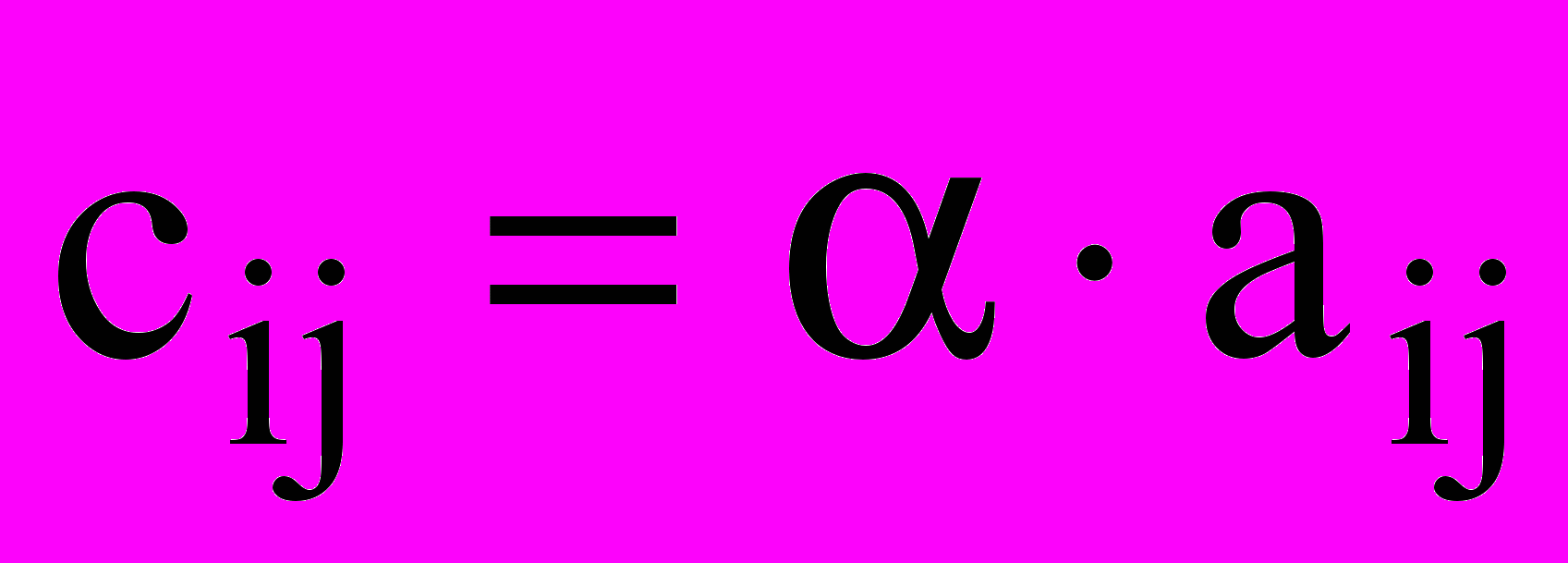для всех i и j .

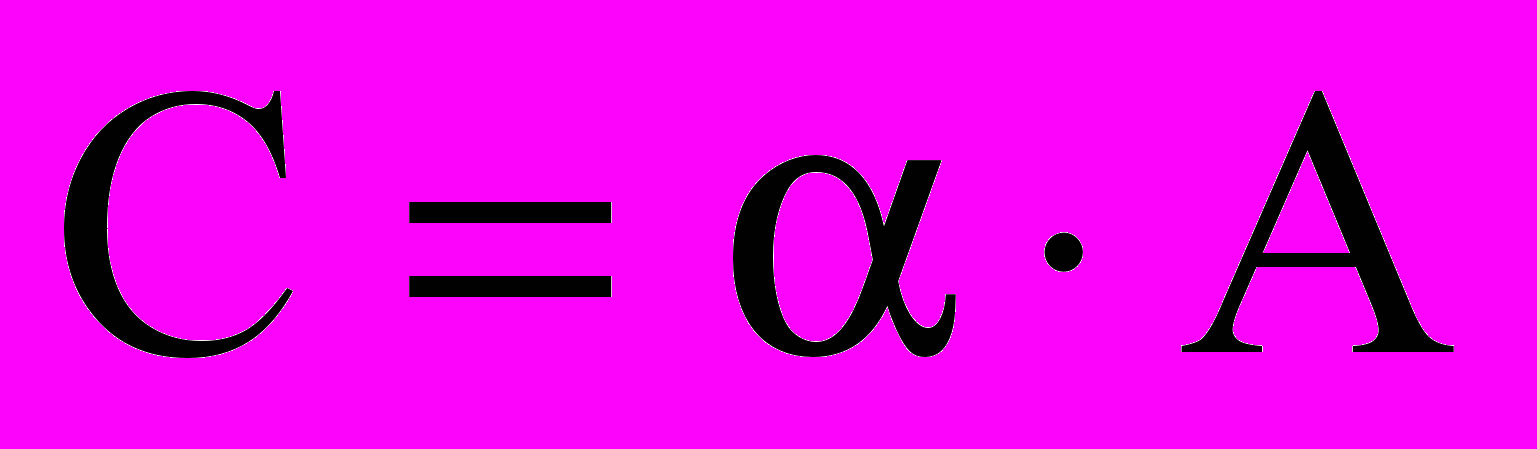Опр. Произведением матрицы A размерности 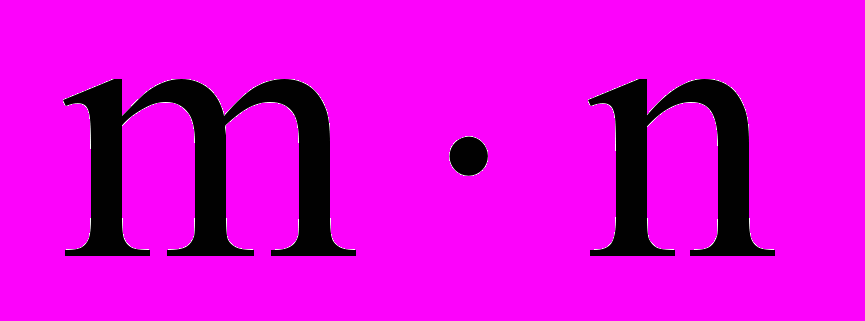и матрицы B размерности 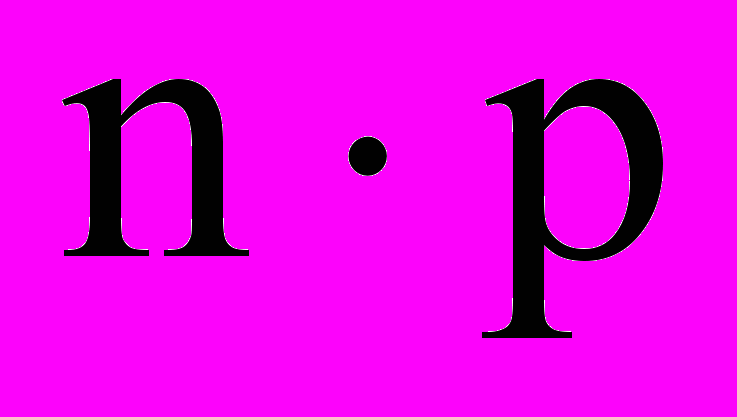называется матрица С размерности 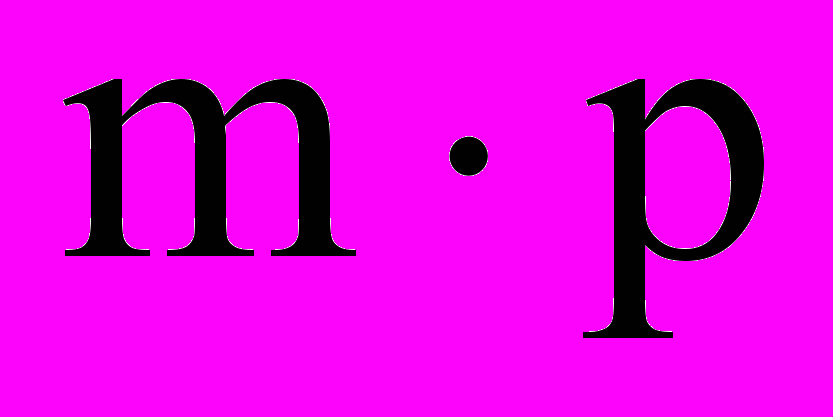, если

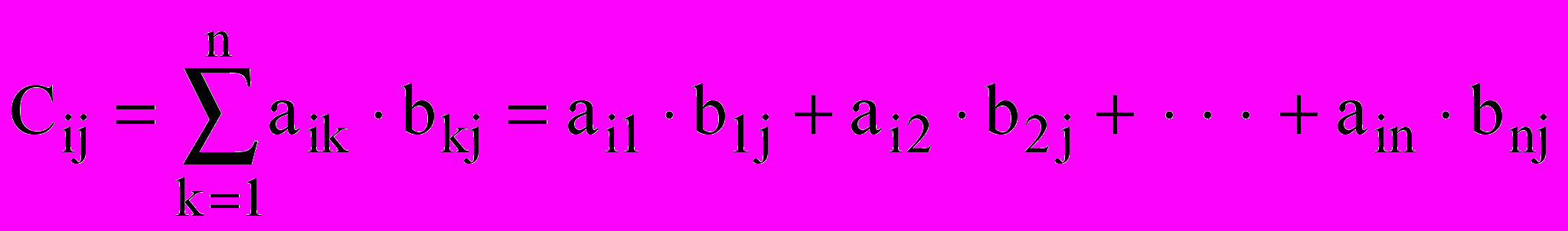для всех i и j .

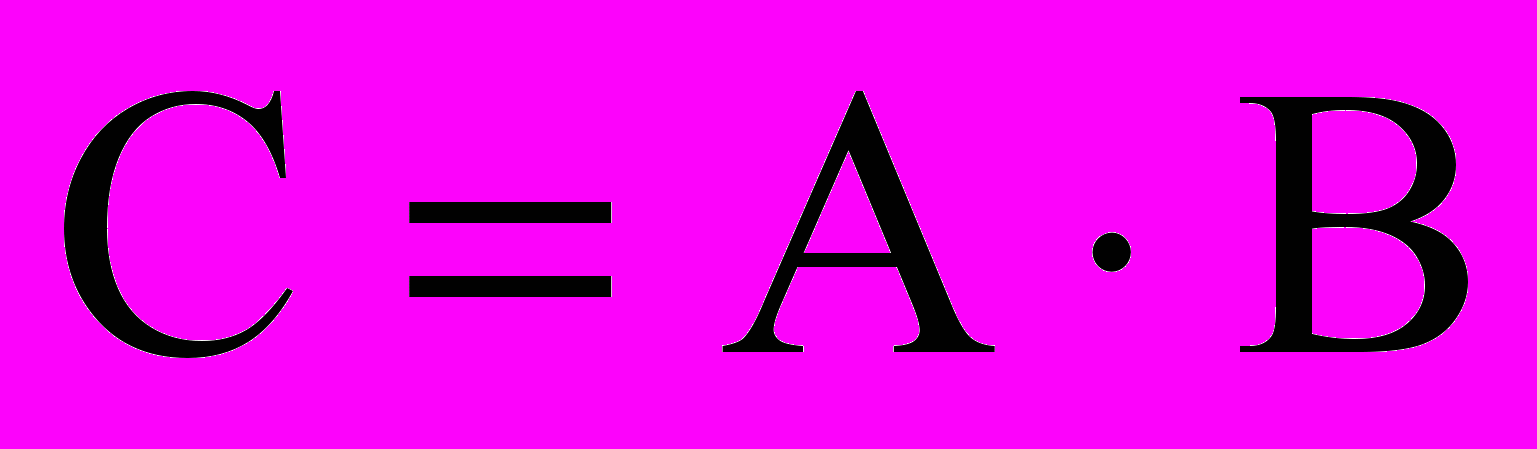Таким образом, чтобы найти элемент матрицы 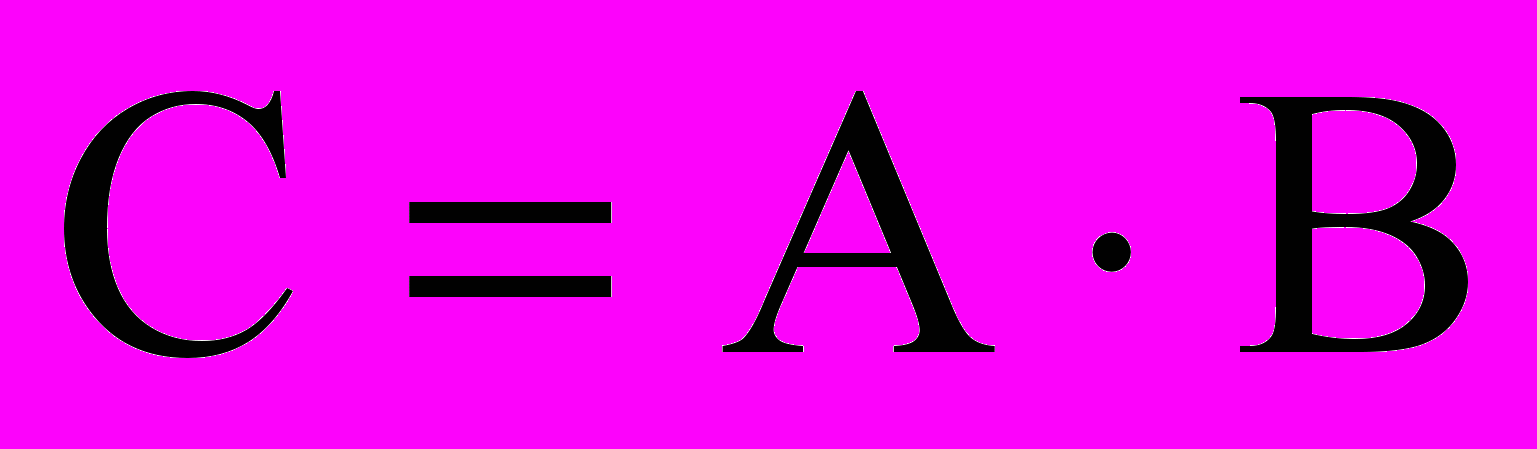, нужно все элементы
i-ой строки матрицы A умножить на соответствующие элементы j-го столбца матрицы B и полученные произведения сложить.

Замечание. Произведение прямоугольных матриц определено лишь в случае, когда число столбцов у матрицы A равно числу строк у матрицы B. Произведение квадратных матриц одной размерности определено всегда.

Примеры







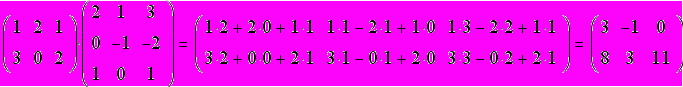
Произведение матрицы на вектор есть вектор.

Свойства произведения матриц (если оно определено)

1. 
   
2. 
   
3. В общем случае:
   

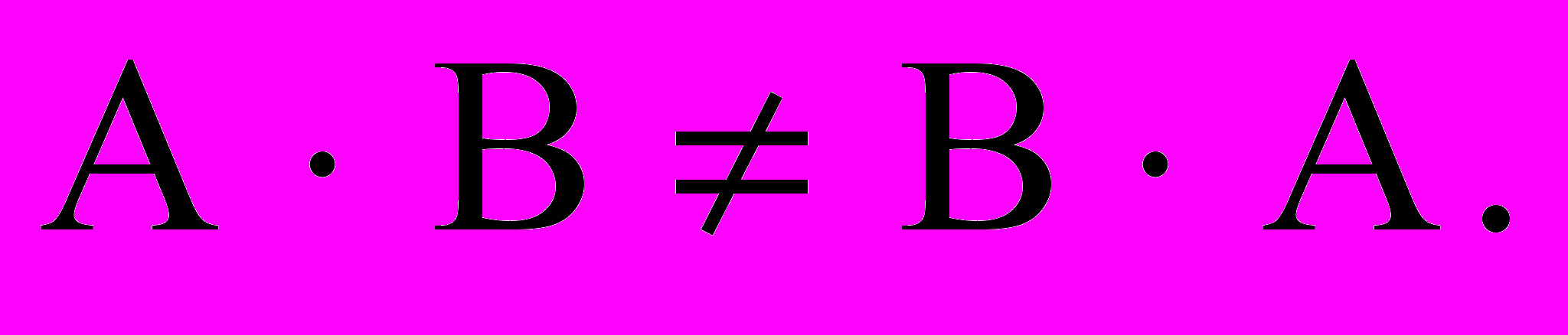
Опр. Если 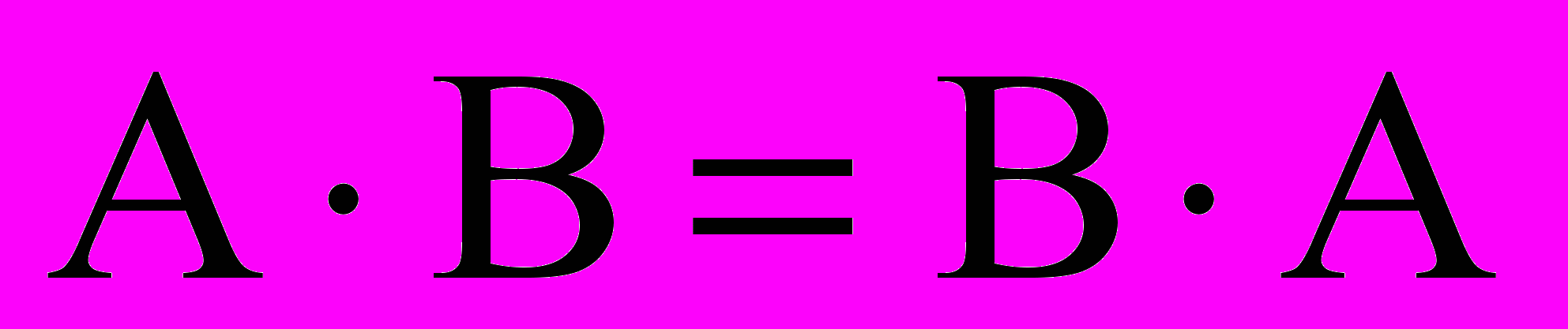, то матрицы называются перестановочными.

Единичная матрица перестановочна с любой квадратной матрицей той же размерности.



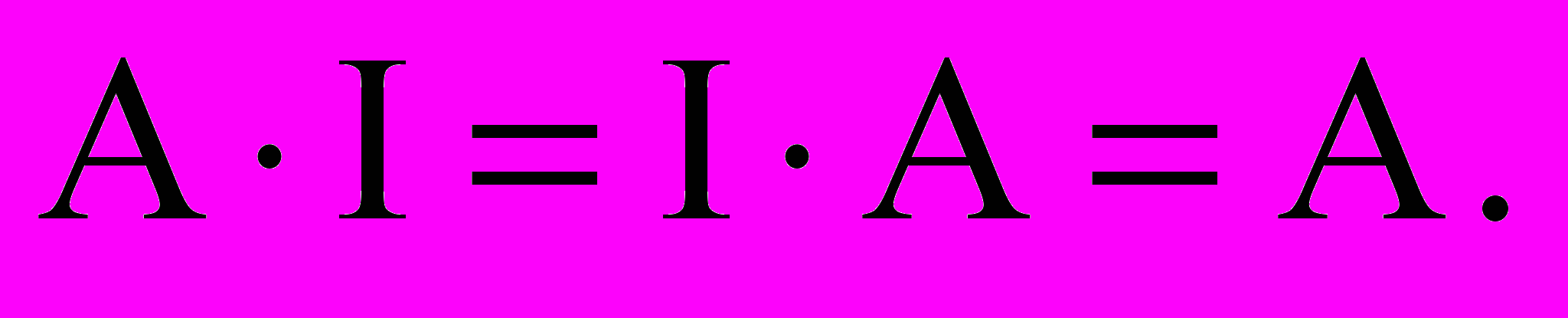
Транспонированная матрица

Опр. Матрица размерности 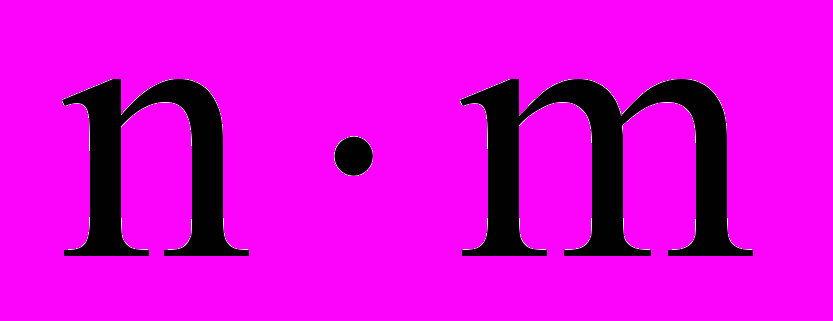называется транспонированной к матрице A размерности 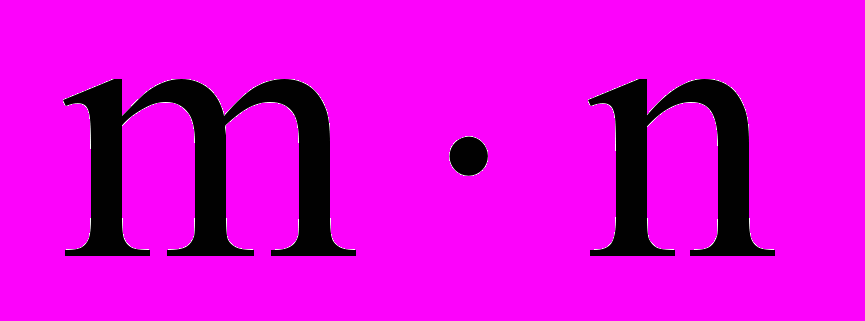, если 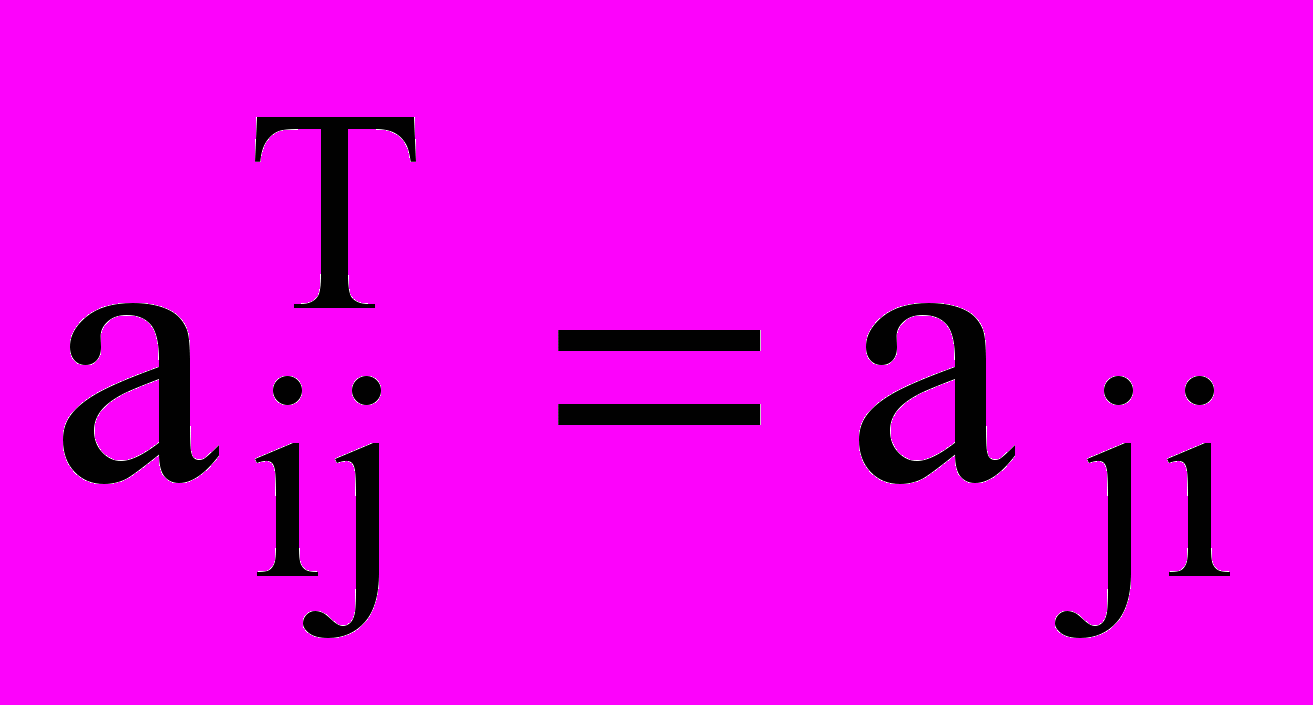для всех i и j (при операции транспонирования строки и столбцы меняются местами).

Примеры

,



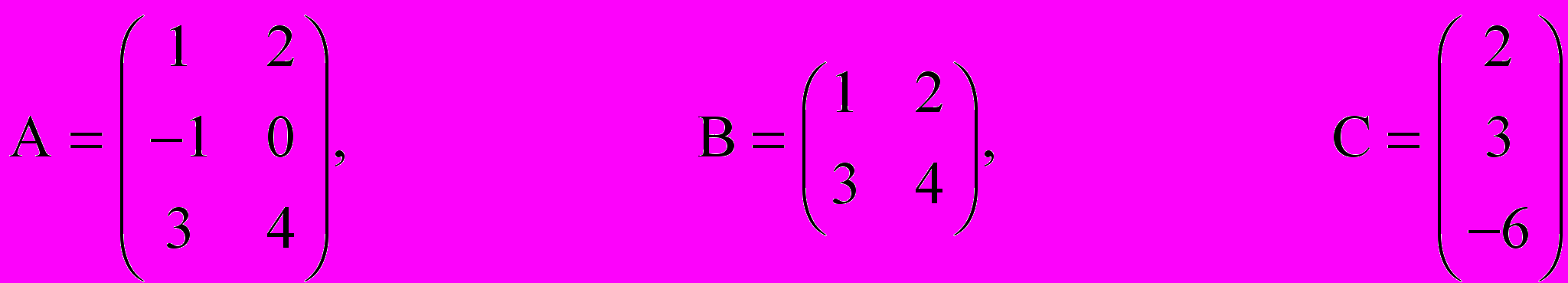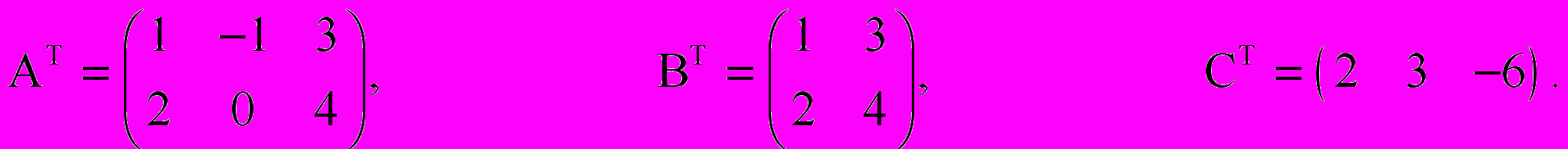
Свойства операции транспонирования

1. –  дважды транспонированная матрица совпадает с исходной матрицей.
   
2. 
   
3. 
   

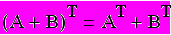
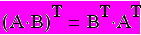
_{Опр. Квадратная матрица называется симметричной, если она совпадает со своей} транспонированной, то есть если _.

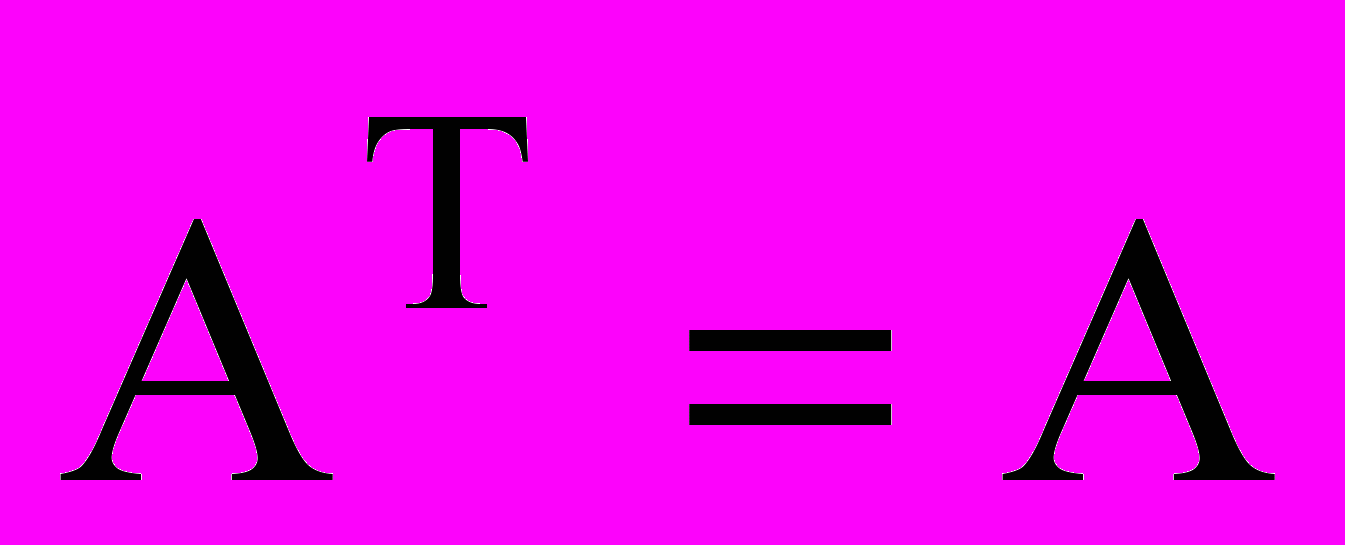У симметричной матрицы 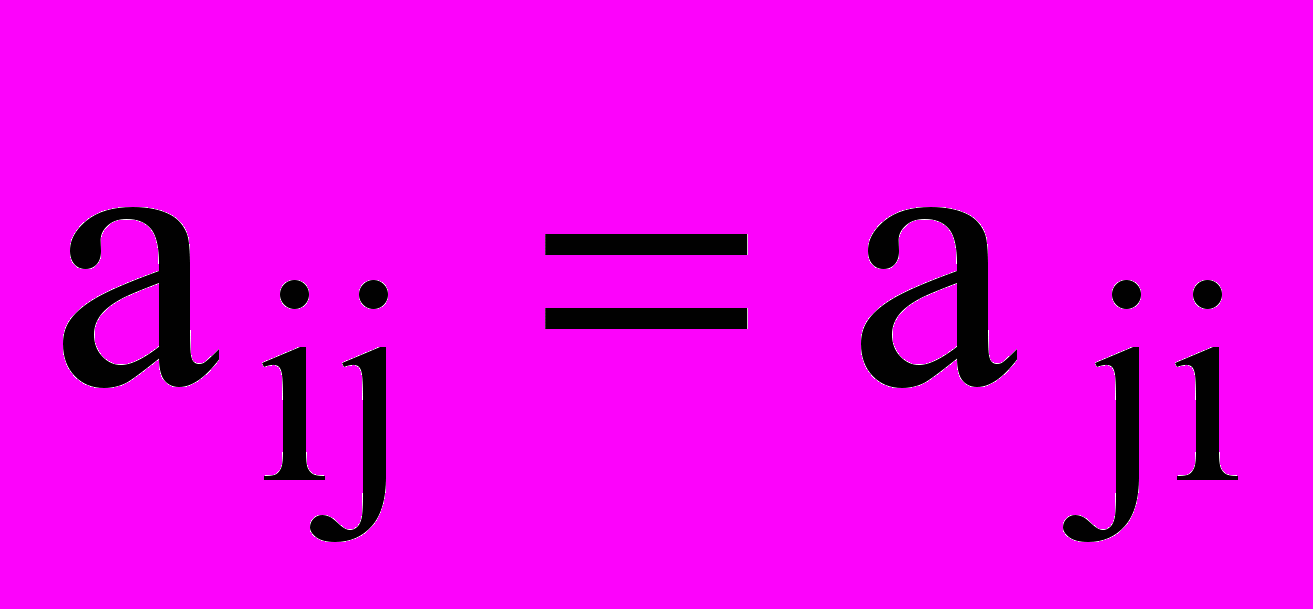для всех i и j.

Обратная матрица

Опр. Матрица 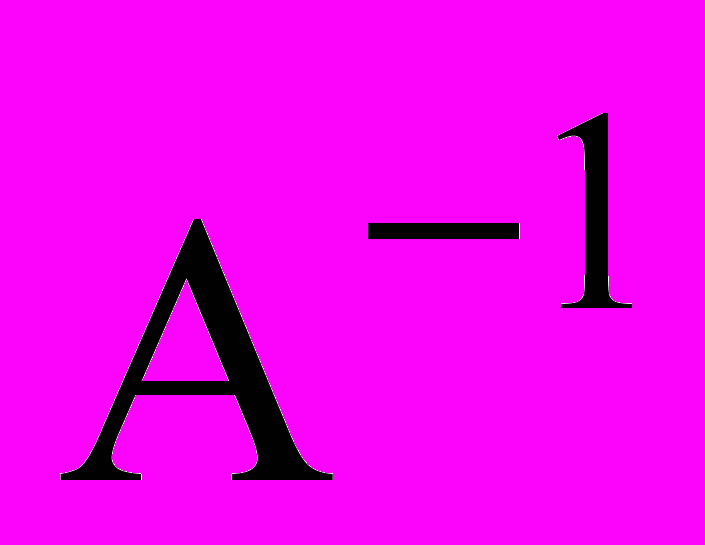называется обратной по отношению к квадратной матрице A, если выполняется равенство

.

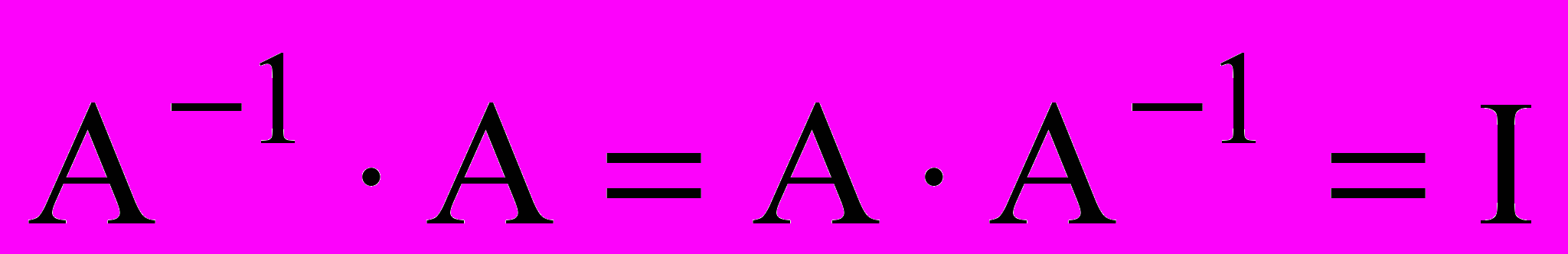Операция нахождения обратной матрицы называется обращением данной матрицы.

Обратная матрица существует только у невырожденных матриц, то есть у таких матриц, определитель которых отличен от нуля.

Свойства

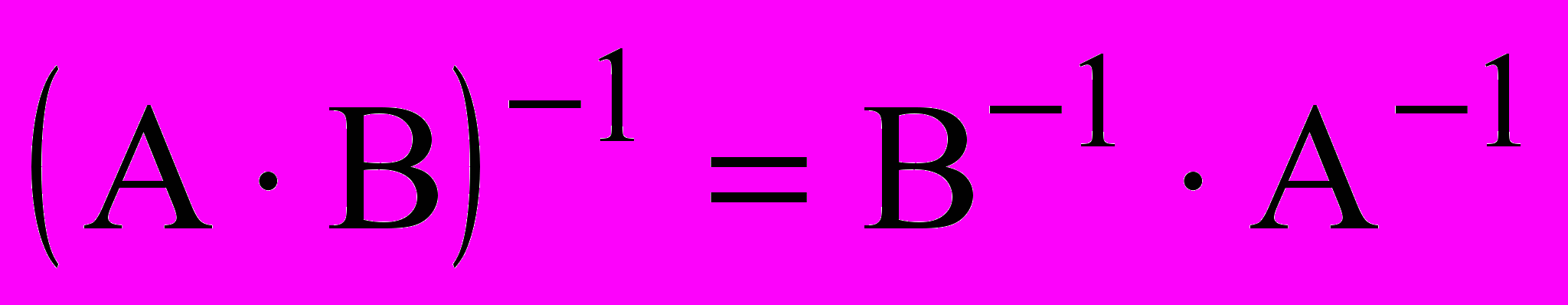1. ; 2.   .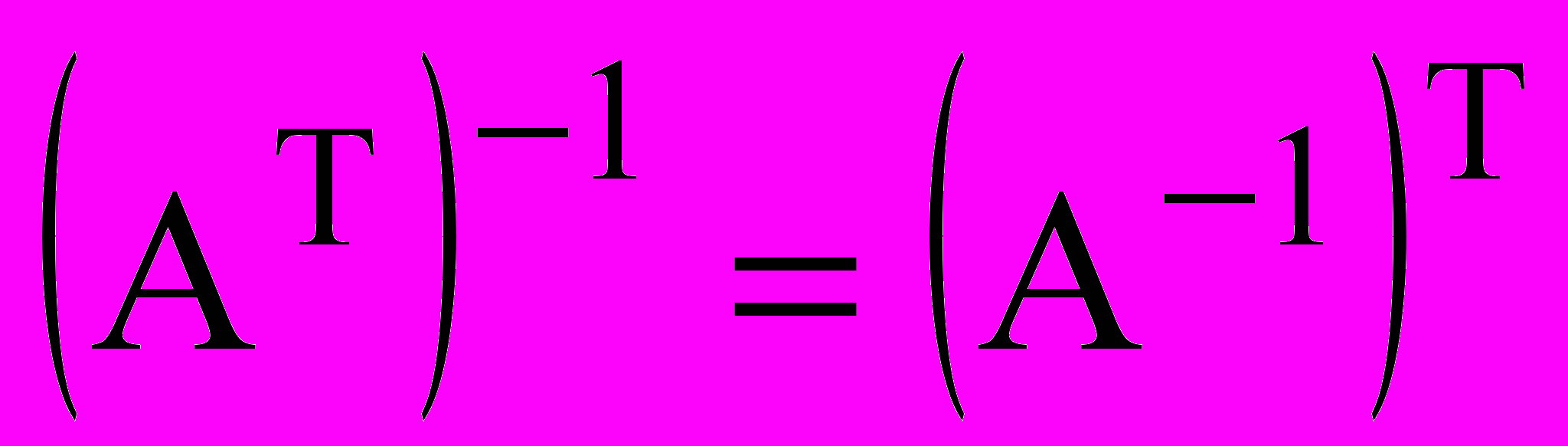
   

Определитель (детерминант) матрицы

Всякой квадратной матрице ставится в соответствие определитель, вычисляемый по определенным правилам. Обозначение .

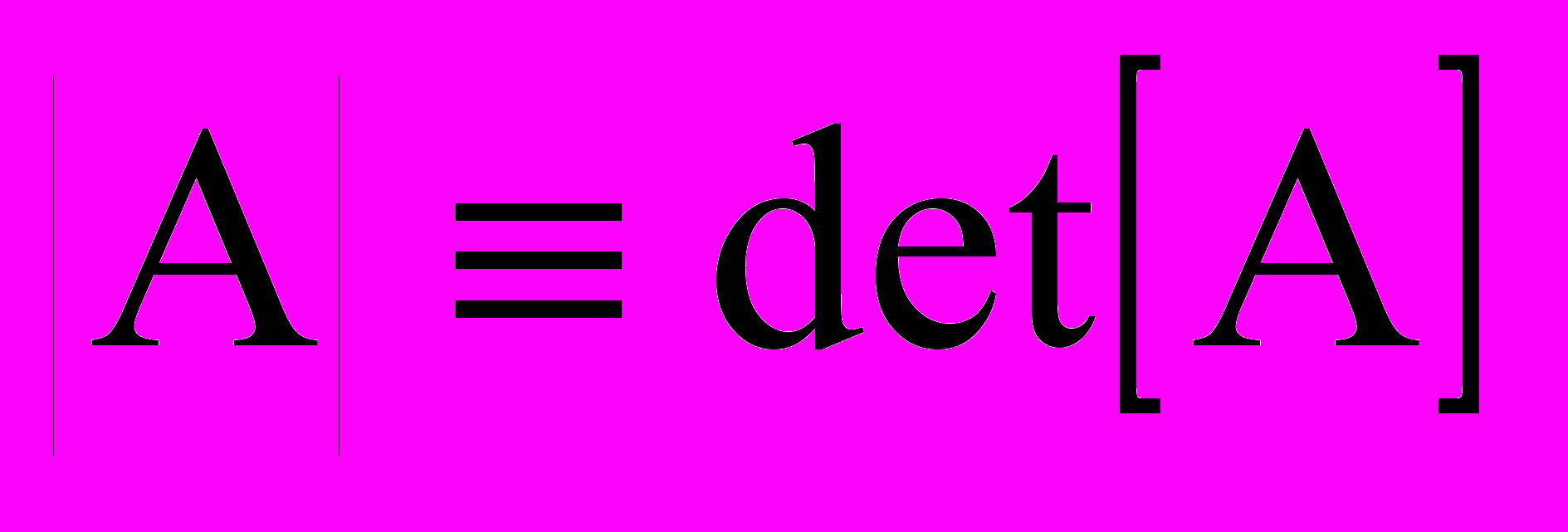Вычисление определителя

.

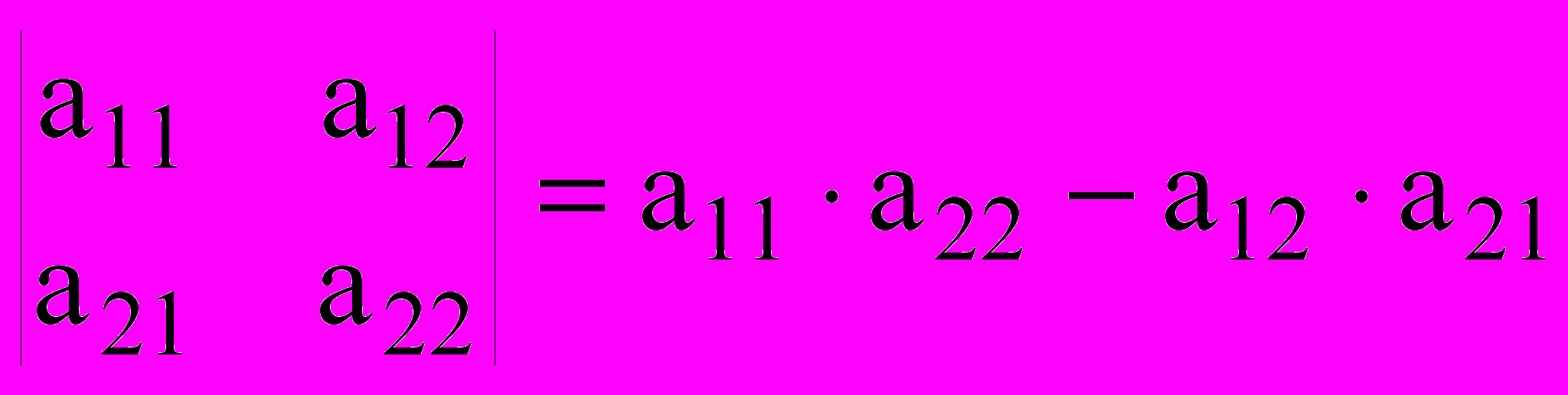Вычисление определителя матрицы размерности 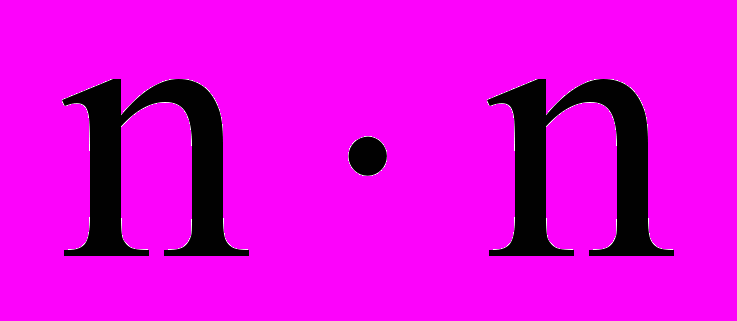можно свести к вычислению определителя матрицы размерности 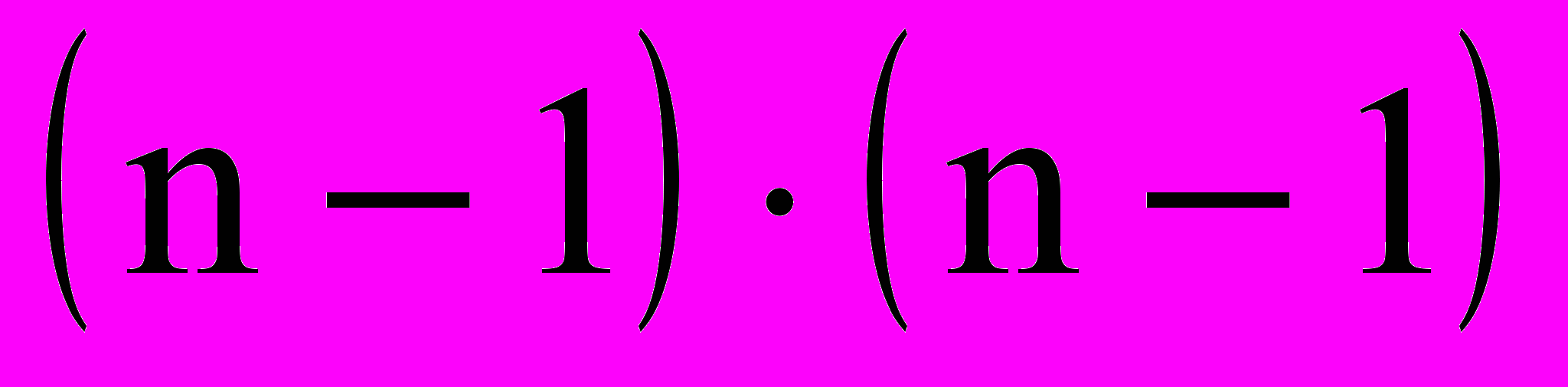и, таким образом, к вычислению определителя матрицы размерности .

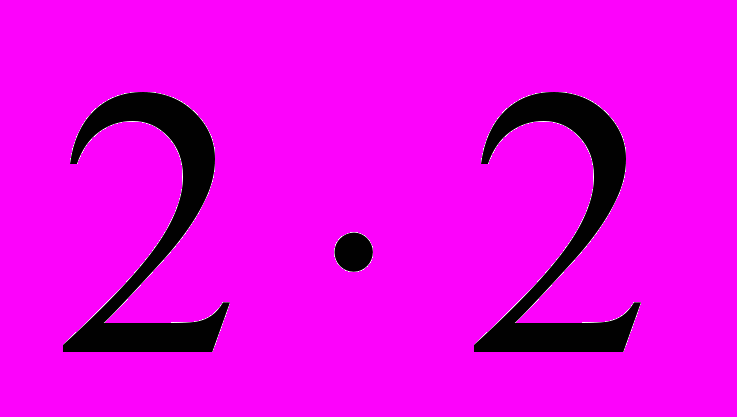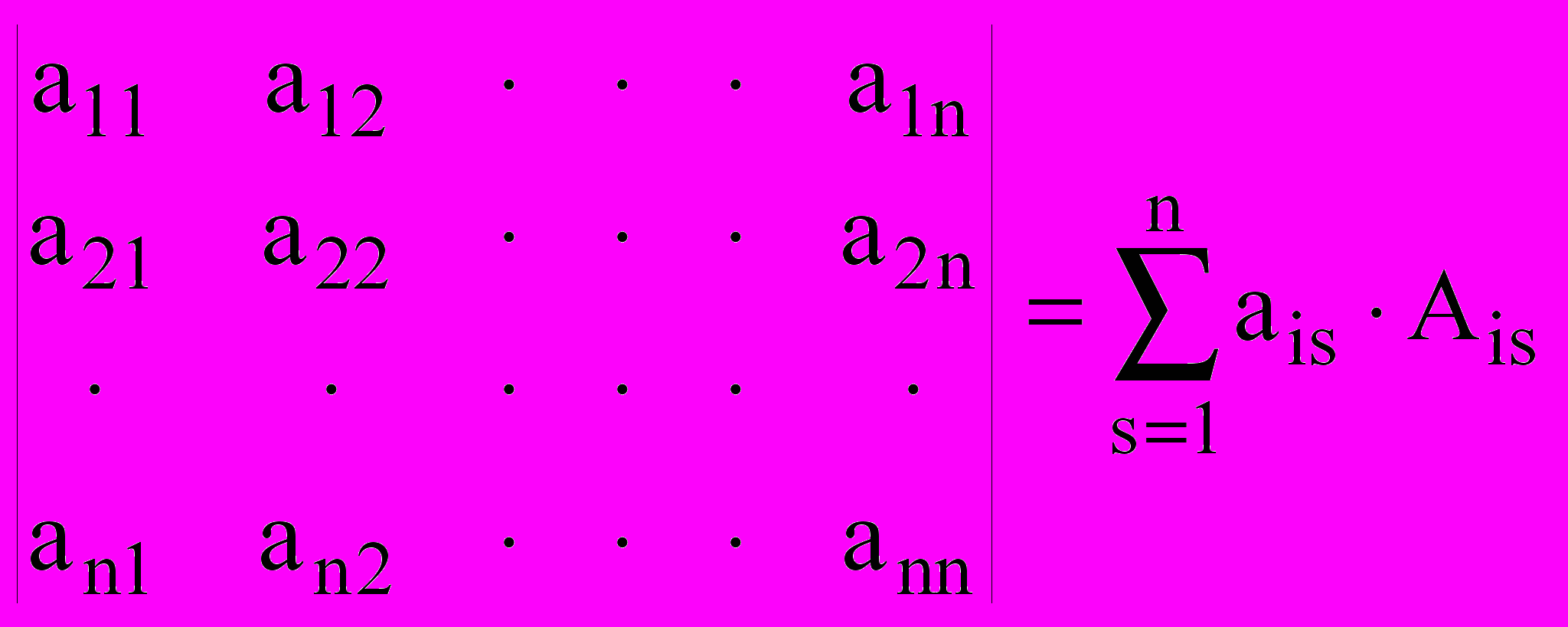– разложение определителя по элементам i-ой строки.

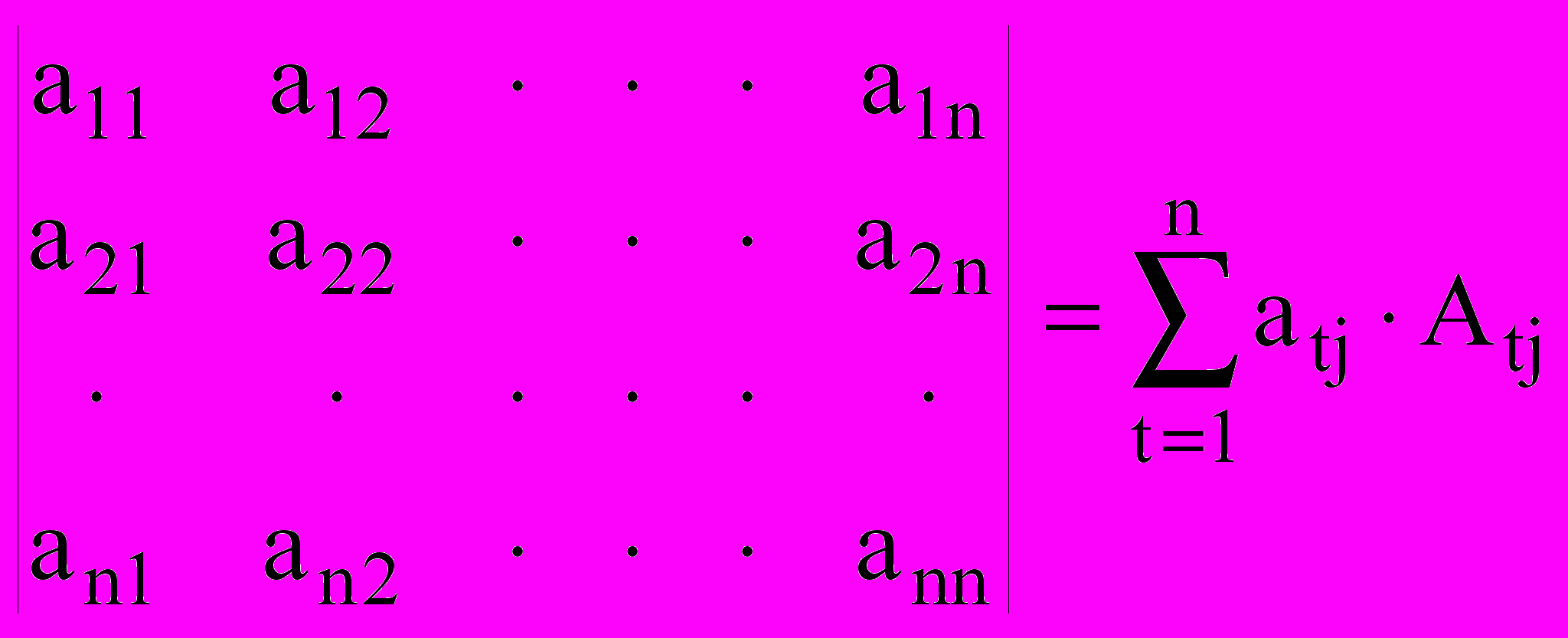– разложение определителя по элементам j-го столбца.

Здесь 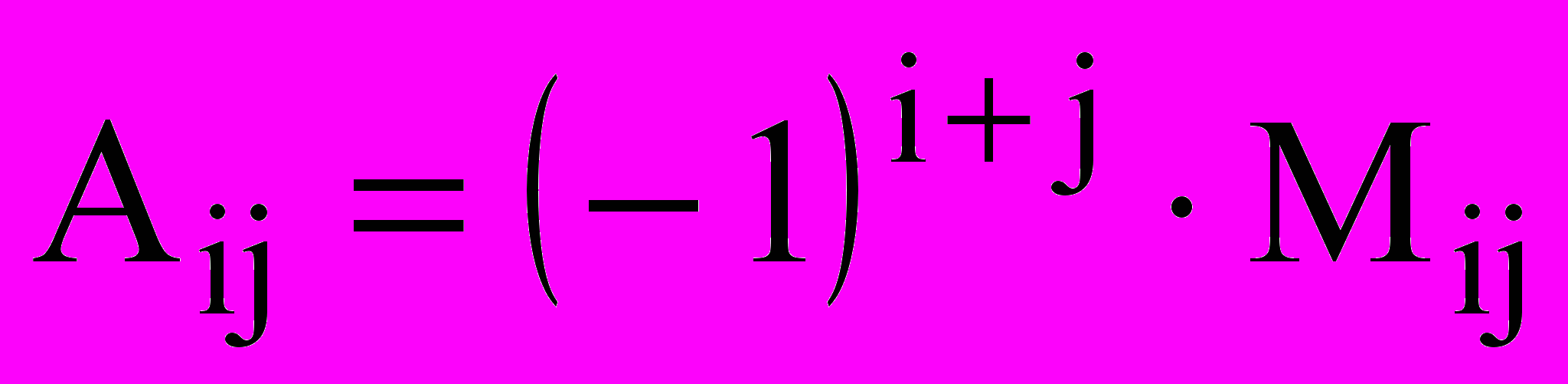– алгебраическое дополнение элемента ,  – минор элемента  –  определитель матрицы размерности (n-1), получаемой из исходной матри­цы вычеркиванием всех элементов i-ой строки и j-го столбца.

Пример



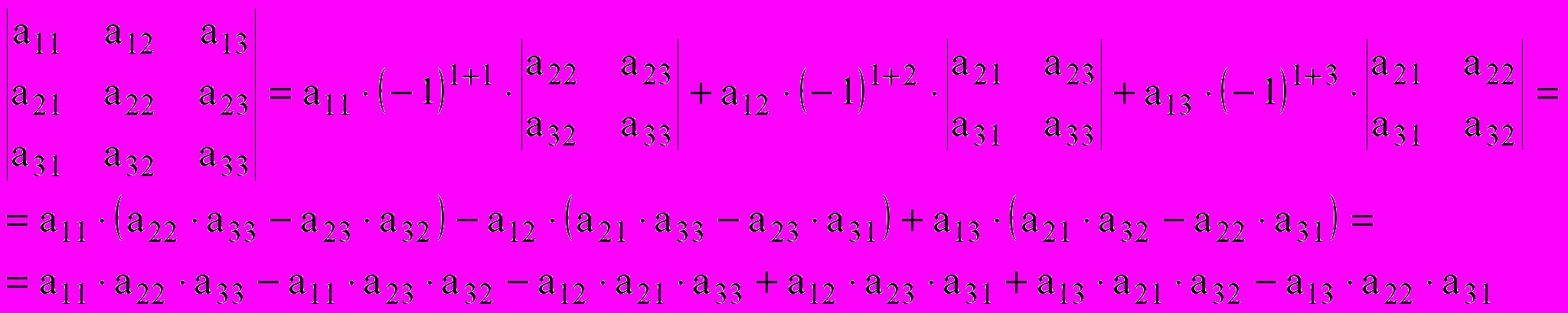
Свойства (A и B – квадратные матрицы размерности n)

1. 
   

5.

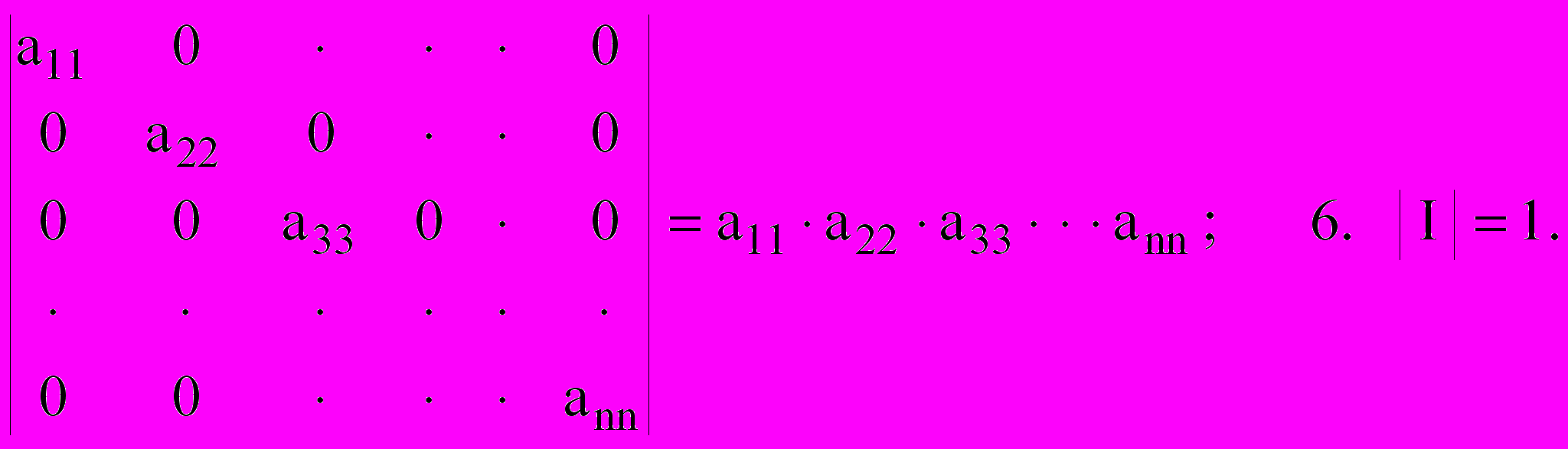
Верно равенство

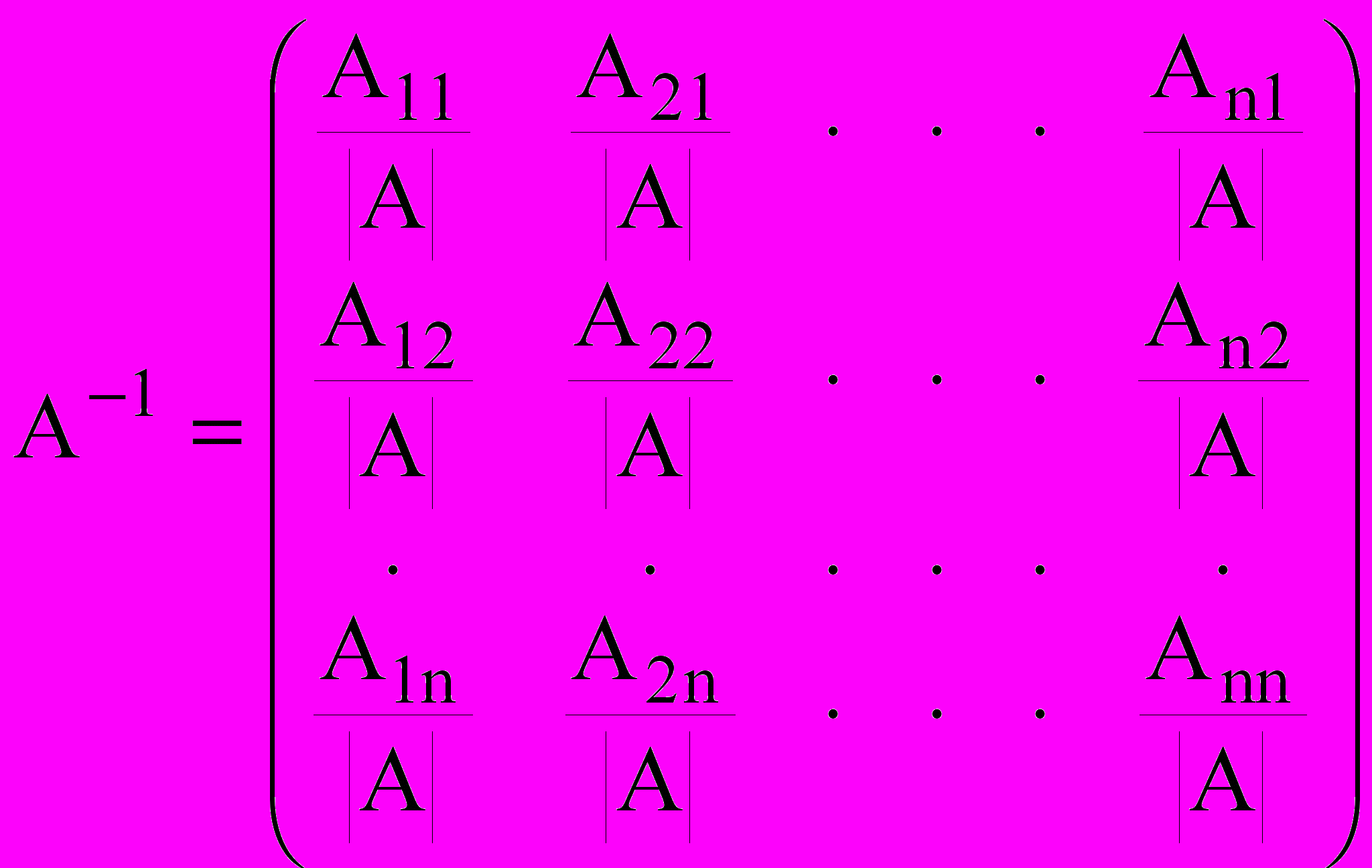, где – алгебраические дополнения; или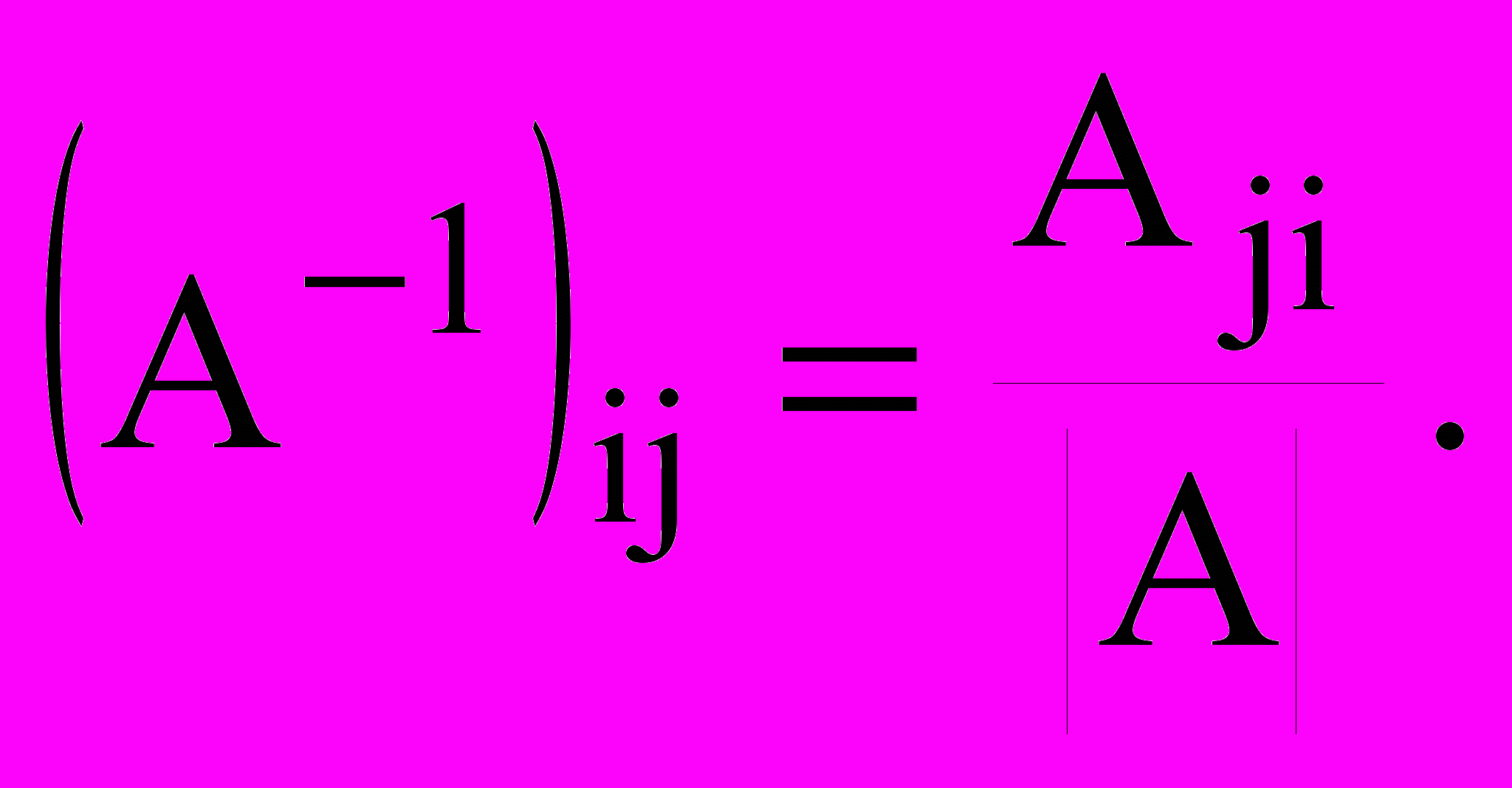

Пример

Дана матрица 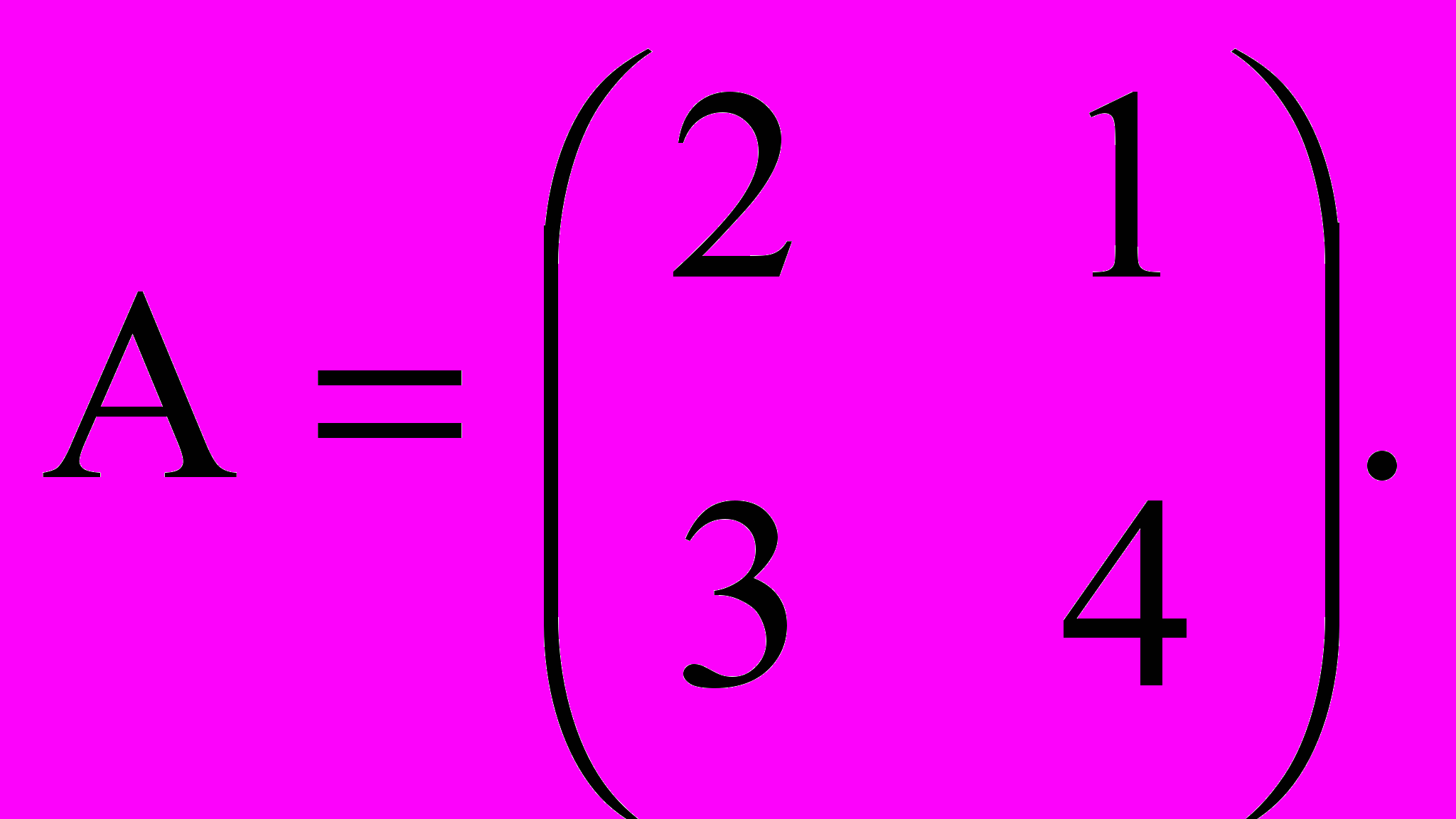Найти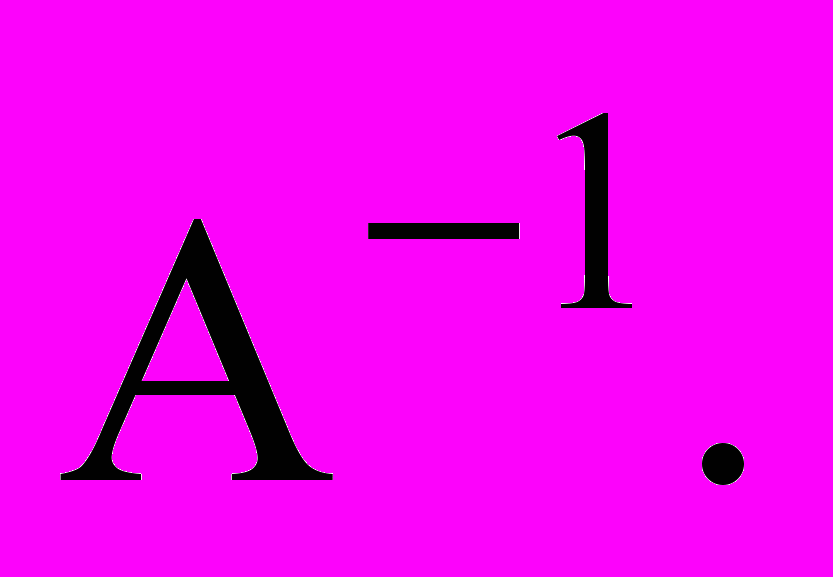

Решение:

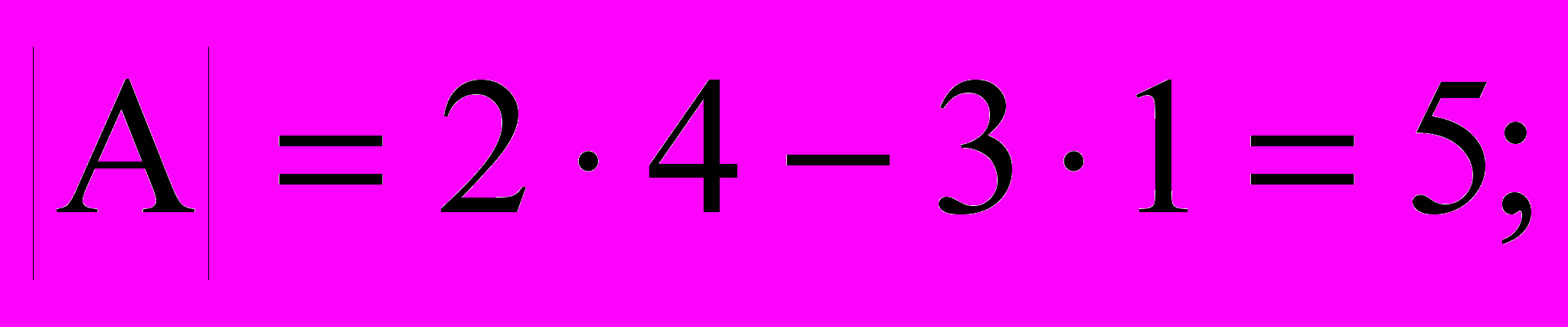
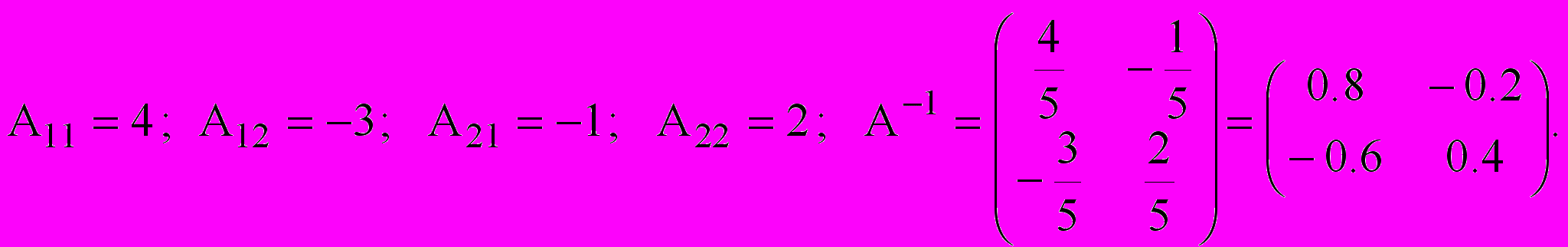
Проверка:

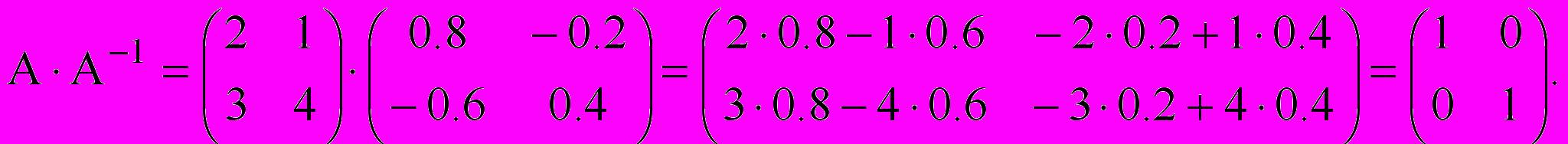
Ортогональная матрица

Опр. Матрица A с вещественными элементами называется ортогональной, если ее транспонированная матрица совпадает с обратной.

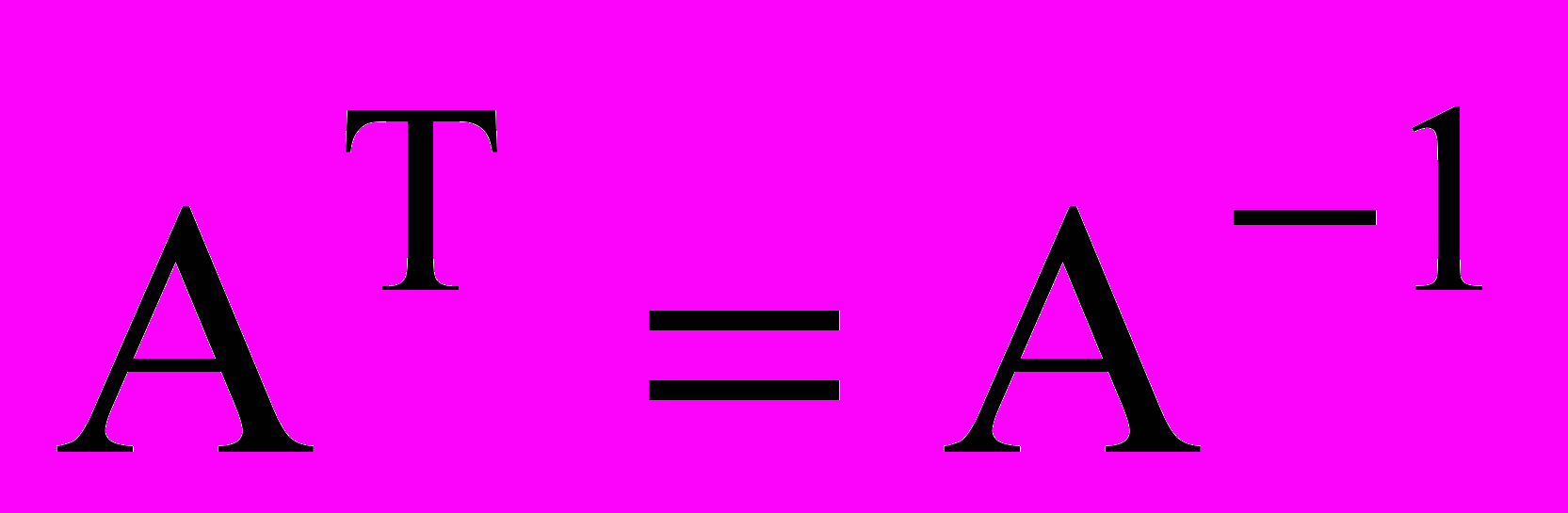или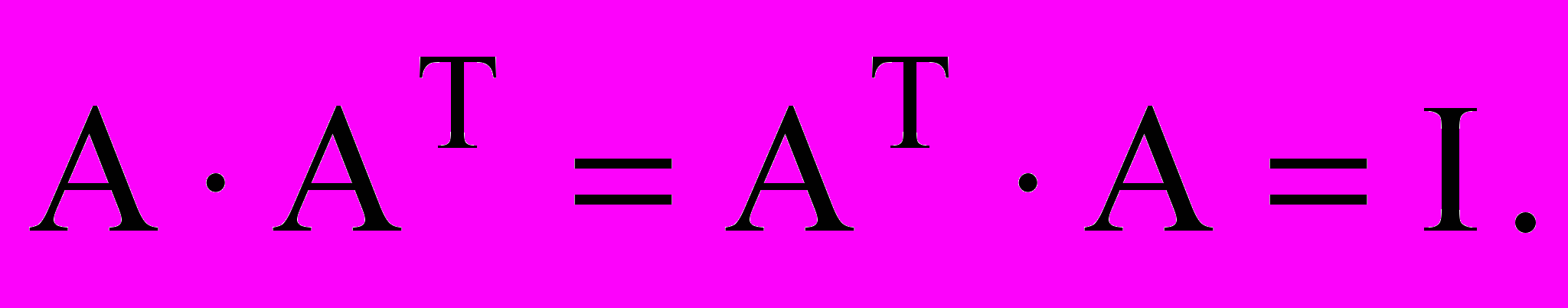

Отсюда следует, что у ортогональной матрицы определитель равен единице.

Пример

.
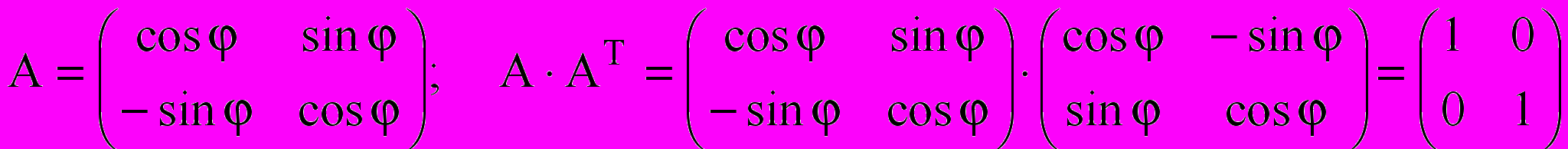