Geum.ru

Курсовой проект расчет определенного интеграла

Вид материалаКурсовой проект

Содержание


Математическая часть
Название процедуры
Label 1; label 2
Подобный материал:

МИРЭА


КУРСОВОЙ ПРОЕКТ


Расчет определенного интеграла


Кафедра РПУ

Выполнил ст.

гр. ВРУ-3-02


Проверил

Давлечин Д.И.


2003

Задание на курсовой проект

Сформировать матрицу С(5,5), элементы которой являются значениями определенного интеграла:





где f(x)




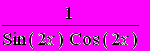
Заданный определенный интеграл необходимо рассчитывать по формуле Симпсона или методу трапеций с заданной точностью. Полученные данные записать в файл на диск. Предусмотреть в программе возможность для считывания данных из файла и их вывод на экран монитора (стандартное устройство вывода).


Математическая часть

Суть численного интегрирования сводится к тому, что приближенное вычисление интеграла



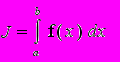
основано на его замене конечной суммой



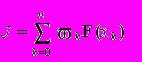
где - числовые коэффициенты, а xk – точки отрезка [a, b]. Приближенное равенство этих выражений называется квадратурной формулой.


Метод Ромберга (правило трапеций), описывается формулой:



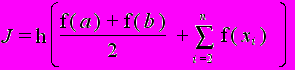
где xi – точка a+nh на каждом элементарном отрезке h:



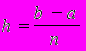
точки a = I/20, b = (I+J)/20.


Формула Симпсона описывается другой формулой:



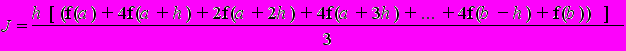
n должно быть четным.


Точность вычисления указывается пользователем и может быть указана как 1; 2; 3;… (количество цифр после запятой) или 0,1; 0,01; 0,06; 0,0002 и т.д. Программа автоматически распознает способ ввода точности и приводит его к виду 0,01; 0,002 и т.д. Если точность указана в пределах 0 … 1, программа оставляет ту точность, которая была введена и никак ее не корректирует.


Спецификация

В программе для очистки экрана используется процедура ClrScr из модуля Crt, собственные процедуры описаны в таблице 1.

Таблица 1.

Название процедуры
Функции, выполняемые процедурой

RadGrad
Вывод на дисплей задания; обеспечивает выбор метода интегрирования, выбор погрешности и ее преобразование.

MSimp
Расчет интеграла по формуле Симпсона.

MTrap
Расчет интеграла методом трапеций.

Matr
Создает матрицу, элементы которой являются значениями вычисленного интеграла. Может создавать сразу две матрицы, в зависимости от выбора параметра в процедуре RadGrad. В эту процедуру вложены процедуры MSimp и MTrap

Vyvod
Процедура выводит на монитор значения матрицы. В зависимости от выбора параметра в процедуре RadGrad может выводить значения двух матриц.

REC
Процедура записывает значения матриц в текстовый файл A:\Sluzh.txt

Pley
Процедура считывания информации из файла A:\Sluzh.txt



Описание переменных представлено в таблице 2.

Таблица 2

Переменная
Описание переменной

Файловые переменные

F1
Переменная связанная с текстовым файлом A:\Sluzh.txt

F2
Переменная связанная со стандартным устройством вывода – экраном.

Вещественные переменные типа “EXTEDED”

Cp1
Переменная используется для хранения текущего (нового) значения интеграла

Cp
Переменная используется для хранения предыдущего значения интеграла.

E
Переменная хранит введенную пользователем погрешность. Погрешность Е сравнивается с модулем разности Cp1-Cp. Если условие Cp1-Cp < Е не выполняется, значение Ср заменяется значением Ср1 и цикл повторяется. В случае выполнения условия, считается, что точность Е достигнута.

h
Элементарный отрезок функции (см. математическую часть).

a
Хранит значение нижнего предела интегрирования

b
Хранит значение верхнего предела интегрирования

Целочисленные переменные типа “LONGINT”

M
Используется в процедуре Vyvod в одном из циклов FOR… для создания второго столбца значений второй матрицы на экране.

V
Используется в процедуре RadGrad и непосредственно в теле программы в запросах. 1: Запрос на вычисление методом… 2: Запрос на повтор, выход, просмотр файла.

n
Используется в процедурах MSimp и MTrap в качестве входного параметра – число точек разбиения функции.

nn
Используется в процедурах MSimp и MTrap в качестве параметра цикла FOR…

I
Параметры циклов FOR…, которые отвечают за заполнение или считывание матриц, J параметр вложенного цикла. Параметрами обозначаются номера ячеек матриц.

J

D1; D2
Массивы 5×5

Символьные переменные

x1
Описывает тип данных в файле A:\Sluzh.txt


Запросы и сообщения программы




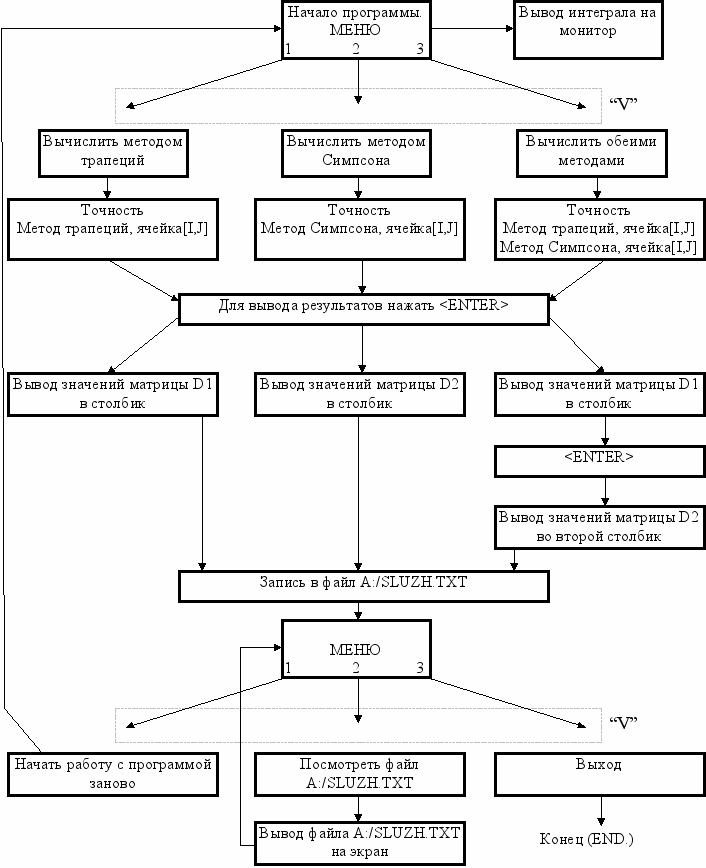
Алгоритм работы программы







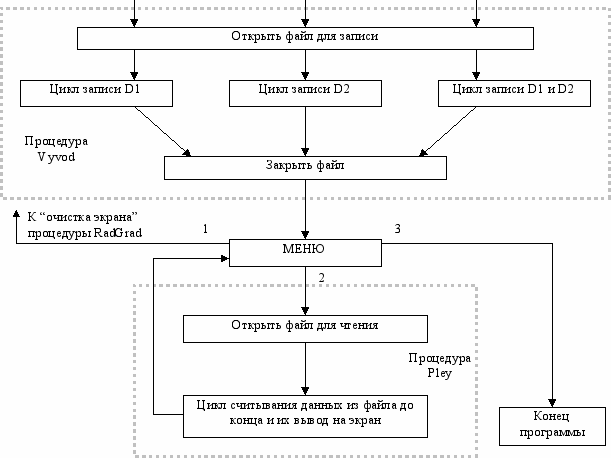
Описание и текст программы

Для удобства программа представлена в виде таблицы с нумерацией строк. Текст программы содержит 283 строки считая не компилируемые строки. Всего в программе 272 “чистых” строки.

Первая строка включает директиву компиляции, которая использует математический сопроцессор.

5…10 строки отведены под описание переменных (см. таблицу 2).

Тело программы начинается на 250 строке и запускает процедуру RadGrad (строка 13), далее запускается процедура очистки экрана и вывод в псевдографике заданного интеграла (строки 16…25). В строках 28…37 описан запрос программы на выбор действия. Функция GotoXY в строке 38 устанавливает курсор на заданную позицию на экране. Строка 40 – ввод значения, которое присваивается переменной V, в строках 41…46 значение V обрабатывается на предмет ошибочного ввода оператором, и в случае нахождения ошибки выдается соответствующее сообщение и метка GOTO1 возвращает программу на строку 16.

Если ошибка не найдена, в строке 49 предлагается ввести погрешность. В строке 52 введенная погрешность переводится в вещественный тип (0,0001), на чем процедура заканчивается. Цвет текста задается функцией “TextColor”.


Далее в теле программы запускается процедура Matr, которая в свою очередь использует процедуры MSimp и MTrap. Рассмотрим эти процедуры.

Процедура MSimp предназначена для расчета заданного интеграла методом Симпсона. В строках 60…62 задаются начальные значения переменных. В строке 63 вычисляется длина элементарного отрезка. В строке 64 задан цикл, в котором вычисляется ряд суммы по формуле. В строках 66…67 вычисляются крайние члены суммы, а в строках 68…69 – промежуточные. В строке 71 все полученные результаты вычисляются по заданной формуле, и в строке 72 сравнивается разница предыдущего и нового результатов с погрешностью. Если заданная погрешность Е меньше, n умножается на два и программа возвращается к строке 62. Если заданная погрешность Е больше, то значение запоминается в переменной Cp1.

Процедура MTrap отличается от процедуры MSimp только формулой. Принцип работы и переменные не изменились (строки 80…97).

Процедура Matr двумя циклами FOR, один из которых вложенный, формирует пределы интегрирования (строки 104, 105), номера ячеек массива (I,J) и запускает цикл с процедурой MTrap, MSimp, или с обеими сразу, в зависимости от параметра V.

Процедура Vyvod выводит на экран, в зависимости от значения параметра V, содержимое массивов D1 или D2 или обеих. Вывод значений массивов осуществляется двумя циклами FOR, один из которых вложенный (строки 156…158 для V = 1, 167…169 для V = 2 и 178…180, 190…195 для V = 3).

Далее процедура REC записывает данные из массивов D1 и D2 в файл SLUZH.TXT на дискете в корневой каталог (строки 204…209).

Далее в теле программы (строки 263…281) построено меню, аналогичное тому, которое построено в процедуре RadGrad. Это меню позволяет выбрать одно из действий: 1) возврат к началу программы (Goto 2); 2) чтение из файла процедурой Pley; 3) выход из программы.

Процедура Pley описана в строках 235…248. Строка 237 связывает переменную F1 с текстовым файлом на диске, строка 238 связывает переменную F2 со стандартным устройством вывода – дисплеем. Файл на диске открывается и информация с помощью цикла с предусловием считывается и выводится на дисплей (строки 241…244). По окончании чтения и вывода на экран содержимого файла метка Goto 1 переводит программу на строчку 262, т.е. к меню.


№ стр
Строка


{$N+}


Program Integral;


Uses CRT;


LABEL 1; LABEL 2;


Var


F1, F2 : text;


D1,D2: ARRAY[1..5, 1..5] OF Extended;


Cp, Cp1, Cp2, Cp3, E, h, a, b : Extended;


x1 : Char;


M, V, n, nn, I, J : Longint;


{***************************************}






PROCEDURE RadGrad;


Label 1;


BEGIN


1: ClrScr;


Textcolor(7);


Writeln('Vychislit'' integrall');


Textcolor(15);


Writeln;


Writeln(' (I+J)/20');


Writeln(' | 1');


Writeln('C(I,J)= S',#196,#196,#196,#196,#196,#196,#196,#196,#196,#196,#196,#196,#196,#196,#196,#196,' dx');


Writeln(' | sin(2x)*cos(2x)');


Writeln(' I/20');


Writeln;


TextColor(7);


Writeln('Vyberite deystvie');


Write('[1] Vychislit'' medodom ');


TextColor(15);


Writeln('Trapetsiy');


TextColor(7);


Write('[2] Vychislit'' medodom ');


TextColor(15);


Writeln('Simpsona');


TextColor(7);


Writeln('[3] Vychislit'' obeimi sposobami');


Writeln('[ ]');


GotoXY(2,13);


Readln(V);


IF NOT ((V=1) OR (V=2) OR (V=3)) then


begin


Textcolor(12);


Writeln('Nevernyy parametr');


Readln;


GOTO 1;


end;


Writeln;


Write('Vvedite pogreshnost'', E = ');


Textcolor(15);


Readln(E);


If E >= 0 then E:= 1/EXP((E+1)*Ln(10));


Textcolor(7);


END;


{***************************************}






Procedure MSimp;


Label 1;


begin


Cp:= 0;


n:= 4;


1: Cp1:= 0;


h:= (b-a)/n;


For nn:= 0 to n do


Begin


if nn = 0 then Cp1:= 1/(Sin(2*a) * Cos(2*a)) else


if nn = n then Cp1:= Cp1+(1/(Sin(2*b)*Cos(2*b))) else


If Odd(nn) then Cp1:= Cp1+4*(1/(Sin(2*(a+h*nn))*Cos(2*(a+h*nn)))) else


If Not (Odd(nn)) then Cp1:= Cp1+2*(1/(Sin(2*(a+h*nn))*Cos(2*(a+h*nn))))


end;


Cp1:= h/3*Cp1;


If ABS(Cp1 - Cp) > E then


Begin


Cp:= Cp1;


n:= n*2;


GOTO 1


end;


END;






Procedure Mtrap;


Label 1;


begin


Cp:= 0;


n:= 4;


1: Cp1:= 0;


h:= (b-a)/n;


For nn:= 2 to n do


Cp1:= Cp1+(1/(Sin(2*(a+h*nn))*Cos(2*(a+h*nn))));


Cp1:= Cp1+ (1/(Sin(2*a)*Cos(2*a)) + 1/(Sin(2*b)*Cos(2*b)))/2;


Cp1:= h*Cp1;


If ABS(Cp1 - Cp) > E then


Begin


Cp:= Cp1;


n:= n*2;


GOTO 1


end;


END;






Procedure Matr;


begin


For I:= 1 to 5 do


For J:= 1 to 5 do


begin


a:= I/20;


b:= (I+J)/20;


IF V = 1 Then


begin


MTrap;


D1[I,J]:= Cp1;


GotoXY(1,16);


Write('Metod trapetsiy, yacheyka N: ');


TextColor(15);


Writeln('[',I,',',J,']');


TextColor(7);


end else


IF V = 2 Then


begin


MSimp;


D2[I,J]:= Cp1;


GotoXY(1,16);


Write('Metod Simpsona, yacheyka N: ');


TextColor(15);


Writeln('[',I,',',J,']');


TextColor(7);


end else


IF V = 3 Then


begin


MTrap;


D1[I,J]:= Cp1;


MSimp;


D2[I,J]:= Cp1;


GotoXY(1,16);


Write('Metod trapetsiy, yacheyka N: ');


TextColor(15);


Write('[',I,',',J,']');


TextColor(7);


GotoXY(1,17);


Write('Metod Simpsona, yacheyka N: ');


TextColor(15);


Writeln('[',I,',',J,']');


TextColor(7);


end else Writeln('Sboy vybora');


end;


END;






Procedure Vyvod;


begin


ClrScr;


If V = 1 then


begin


Writeln('Metod trapetsiy');


TextColor(15);


Writeln(' I, J',#26,' znachenie;', ' pogreshnost'': ', E:2:16);


TextColor(7);


Writeln;


For I:= 1 to 5 do


For J:= 1 to 5 do


Writeln(' ',I,', ',J,' ', D1[I,J]:3:16);


end else


If V = 2 then


begin


Writeln('Metod Simpsona');


TextColor(15);


Writeln(' I, J',#26,' znachenie;', ' pogreshnost'': ', E:2:18);


TextColor(7);


Writeln;


For I:= 1 to 5 do


For J:= 1 to 5 do


Writeln(' ',I,', ',J,' ', D2[I,J]:3:16);


end else


If V = 3 then


begin


Writeln(' I, J',#26,' znachenie;', ' pogreshnost'': ', E:2:18);


TextColor(15);


Writeln(' Metod trapetsiy');


TextColor(7);


Writeln;


For I:= 1 to 5 do


For J:= 1 to 5 do


Writeln(' ',I,', ',J,' ', D1[I,J]:3:16);


Write('Dlya prodolzheniz nazhmite ');


TextColor(26);


Writeln('ENTER');


Readln;


GotoXY(29,2);


TextColor(15);


Writeln(' Metod Simpsona');


TextColor(7);


Write;


For I:= 1 to 5 do


For J:= 1 to 5 do


begin


M:= M+1;


GotoXY(29, 3+M);


Writeln(D2[I,J]:3:16);


end;


end;


END;






Procedure REC;


begin


Assign(F1, 'A:\Sluzh.txt');


Rewrite(F1);


If V = 1 then


begin


For I:= 1 to 5 do


begin


for J:= 1 to 5 do


Write(F1, D1[I,J]);


end;


end else


If V = 2 then


begin


For I:= 1 to 5 do


begin


for J:= 1 to 5 do


Writeln(F1, D2[I,J]);


end;


end else






If V = 3 then


begin


Writeln(F1,'Metod trapetsiy');


For I:= 1 to 5 do


for J:= 1 to 5 do


Writeln(F1, D1[I,J]);


Writeln(F1,'Metod Simpsona');


For I:= 1 to 5 do


for J:= 1 to 5 do


Writeln(F1, D2[I,J]);


end;


Close(F1);


END;






Procedure Pley;


begin


assign(F1, 'A:\Sluzh.txt');


assign(F2,'');


reset(f1);


rewrite(f2);


While not eof(f1) do


begin


read(f1,x1);


write(f2,x1);


end;


Close(F1);


readln;


end;






BEGIN


2: RadGrad;


Matr;


Writeln('Dlya vyvoda rezul''tatov nazhmite ENTER');


Readln;


Vyvod;


Writeln;


TextColor(15);


Writeln('Zapis'' v fayl A:/SLUZH.TXT');


TextColor(7);


REC;


Readln;


1: CLRSCR;


Writeln('[1] esche razok');


Writeln('[2] posmotret'' fayl');


Writeln('[3] nadoelo? konets');


Writeln('[ ]');


GotoXY(2,4);


Readln(V);


IF NOT ((V=1) OR (V=2) OR (V=3)) then


begin


Textcolor(12);


Writeln('Nevernyy parametr');


TextColor(7);


Readln;


GOTO 1;


end;


If V = 1 then GOTO 2 else


If V = 2 then


begin


Pley;


GOTO 1;


end;


end.


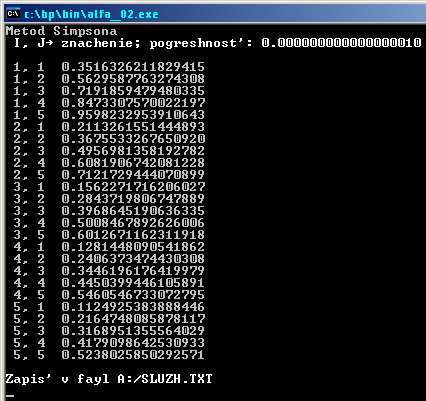
Результат работы программы

Приведенные ниже значения получены с помощью программы Mathematica 4.2,

номер ячейки, для которой просчитано значение, можно определить по верхнему пределу интегрирования.












































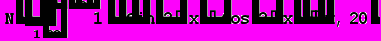
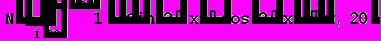
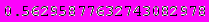
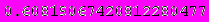
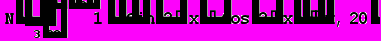
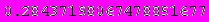
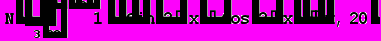
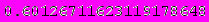
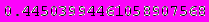
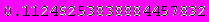
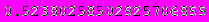
А теперь приведем скриншоты работы программы:





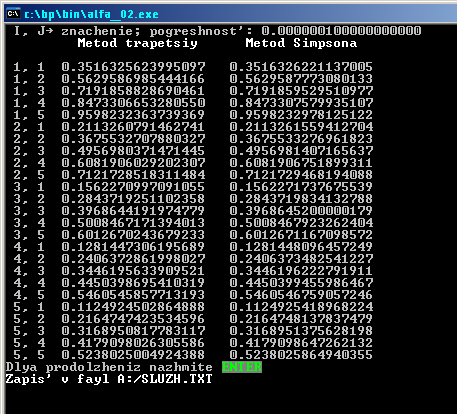
Точность вычисления указана на скриншоте.


Программа выполняет заданные функции и считает указанный в задании определенный интеграл с заданной точностью. Экспериментально определено, что в данном случае метод Симпсона работает в сотни, если не в тысячи раз быстрее метода трапеций.

Скриншот работы программы при вычислении интеграла методом Симпсона с точностью 16 знаков мантиссы показан ниже: