Конспект лекций для 16-и часового курса начертальная геометрия издание 2-ое
| Вид материала | Конспект |
Содержание3.4.Точка и линия на поверхности. |
- Конспект лекций по курсу "Начертательная геометрия и инженерная графика" Кемерово 2002, 786.75kb.
- Конспект лекций по курсу Начертательная геометрия (для студентов заочной формы обучения, 1032.28kb.
- Конспект лекций 2010 г. Батычко Вл. Т. Муниципальное право. Конспект лекций. 2010, 2365.6kb.
- Конспект лекций 2008 г. Батычко В. Т. Административное право. Конспект лекций. 2008, 1389.57kb.
- Конспект лекций 2011 г. Батычко В. Т. Семейное право. Конспект лекций. 2011, 1718.16kb.
- Конспект лекций 2011 г. Батычко Вл. Т. Конституционное право зарубежных стран. Конспект, 2667.54kb.
- Конспект лекций 2010 г. Батычко В. Т. Уголовное право. Общая часть. Конспект лекций., 3144.81kb.
- Программа курса Конспект лекций > Тесты Задачи > Вопросы к экзамену Методические рекомендации, 1693.2kb.
- Конспект лекций Батычко Вик. Т таганрог 2011, 2102.18kb.
- Конспект лекций организация производства и маркетинг для студентов 3 курса специальностей, 2989.73kb.
3.4.Точка и линия на поверхности.
Напомним уже известное, что точка принадлежит поверхности, если она на линии, принадлежащей поверхности. Хорошо, если эта линия имеет простые проекции. В противном случае приходится прибегать к способу случайной кривой на каркасе поверхности.
| Дано: Тор   _____________________ ?:  . . | Решение: 1).  , ,  , ,  . .2).  . . |
 |
| |
 , принадлежащей открытому тору
, принадлежащей открытому тору  .
.Для решения задачи можно использовать способ образующей с простыми проекциями. Поскольку через точку
 на торе можно провести окружность с проекциями в виде прямой и окружности для задания окружности используем горизонтальную проекцию точки
на торе можно провести окружность с проекциями в виде прямой и окружности для задания окружности используем горизонтальную проекцию точки  и точку 1 на меридиане
и точку 1 на меридиане 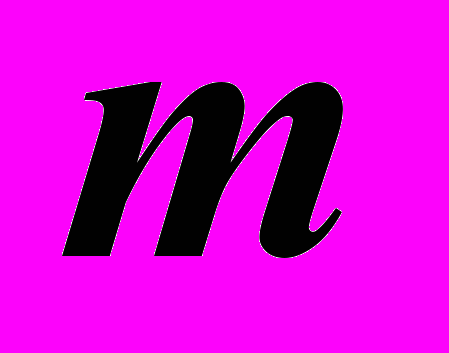 .
.Пример 2 (Рис.34). Построить горизонтальную проекцию точки
 , принадлежащей коноиду
, принадлежащей коноиду  .
.  |
| |
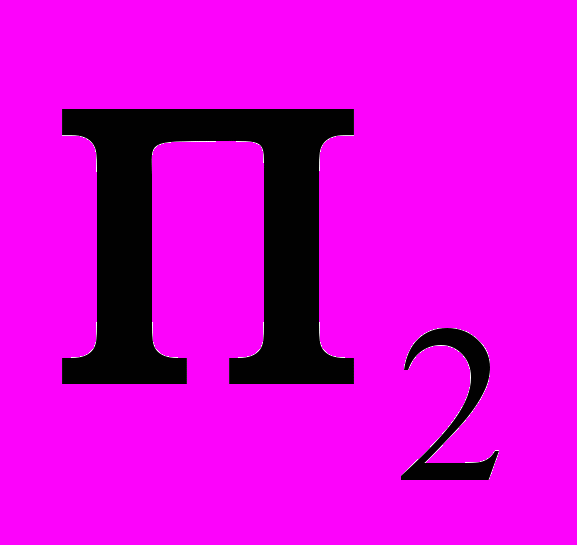 , то через любую точку на его поверхности из простых линий можно проводить только фронтали. Любую фронталь начинают строить с её горизонтальной проекции. Потому, что эта проекция всегда параллельна оси
, то через любую точку на его поверхности из простых линий можно проводить только фронтали. Любую фронталь начинают строить с её горизонтальной проекции. Потому, что эта проекция всегда параллельна оси 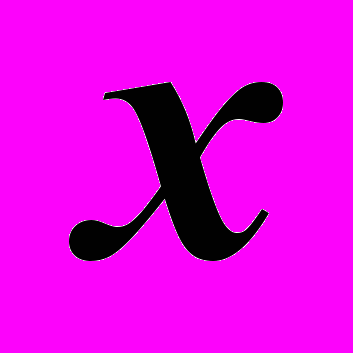 . Но точка
. Но точка 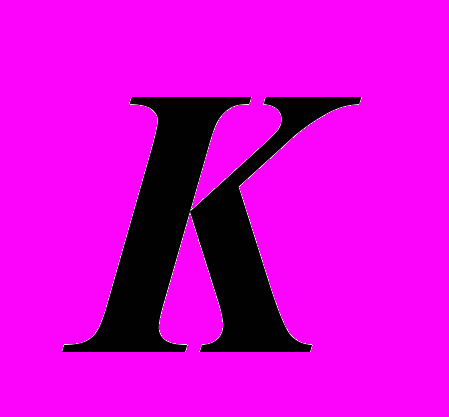 на поверхности коноида задана не горизонтальной проекцией, то остается решать задачу способом случайной кривой на каркасе поверхности.
на поверхности коноида задана не горизонтальной проекцией, то остается решать задачу способом случайной кривой на каркасе поверхности.| Решение: 1). Задать каркас поверхности семейством фронталей. 2). Через точку  провести фронтальную проекцию провести фронтальную проекциюпроизвольной линии  . .3). Построить точки пересечения линии 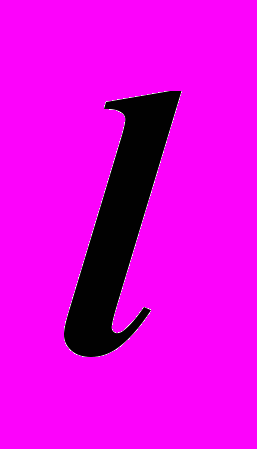 с элементами каркаса. с элементами каркаса.4). Используя горизонтальные проекции полученных точек, построить горизонтальную проекцию линии  . .5). Построить искомую проекцию точки  . . |
На примере данной задачи показан и способ задания линии на каркасе поверхности.
При построении линии на поверхности следует учитывать, что полностью или частично она может быть невидимой. Для наглядности и для удобства обводки чертежа невидимые проекции рекомендуется изображать в виде крестика. Должна соблюдаться и последовательность решения задачи:
1. Определить или построить опорные точки линии. Это начало и конец линии, очерковые точки (границы видимости ), экстремальные и другие чем-то особенные точки. Опорные точки следует обозначать прописными буквами, а промежуточные точки лучше обозначать цифрами
2. Построить необходимое число промежуточных точек.
3. Построить недостающую проекцию линии.
4. Окончательно обвести чертеж с учетом видимости, используя для этого стандартные типы линий.
Пример 3 (Рис.35). Построить фронтальную проекцию линию
 , инадлежащей закрытому тору. Для решения задачи есть возможность использовать способ образующих с простыми проекциями.
, инадлежащей закрытому тору. Для решения задачи есть возможность использовать способ образующих с простыми проекциями.  |
| |
| Решение: 1). Построить опорные точки. Точки  и и 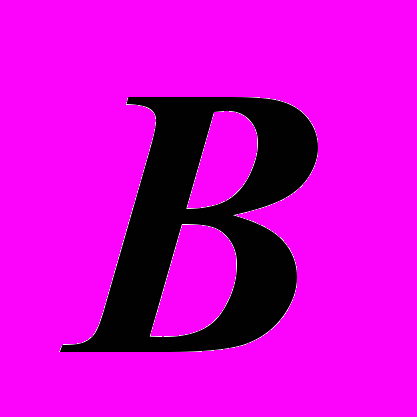 – на основании тора. Точка – на основании тора. Точка 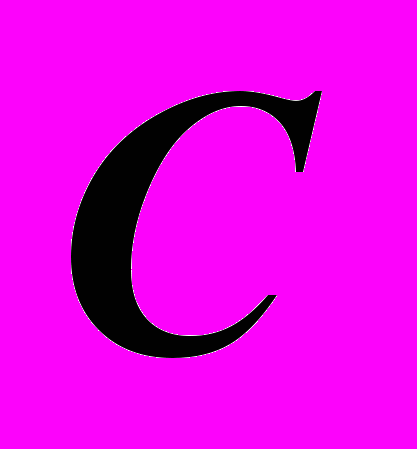 – на главном меридиане – на главном меридиане 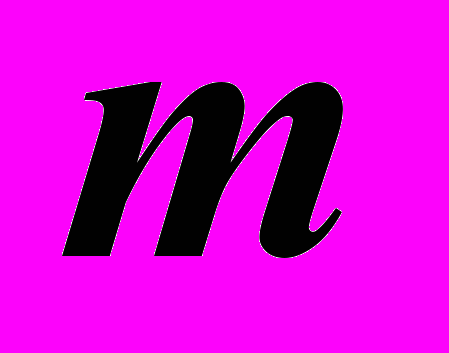 . Фронтальная ее проекция . Фронтальная ее проекция  – очерковая. Точка – очерковая. Точка  – самая высокая. Для ее построения использована окружность минимального радиуса. – самая высокая. Для ее построения использована окружность минимального радиуса.2). Построить несколько промежуточных точек, многократно решая задачу на принадлежность точки к поверхности. 3). По фронтальным проекциям опорных и промежуточных точек построить искомую проекцию линии  . .4). Обвести чертеж с учетом видимости. |
