Книга написана доступным языком и проиллюстрирована целым рядом художественных примеров из жизни людей, стран и цивилизаций
| Вид материала | Книга |
- Александр Лоуэн, 4552.11kb.
- Александр Лоуэн, 4361.84kb.
- Александр Лоуэн любовь и оргазм, 5727.34kb.
- Александр Лоуэн любовь и оргазм, 5727.33kb.
- Фритьоф Капра Дао физики, 4424.62kb.
- Фритьоф Капра Дао физики, 11823.64kb.
- Фритьоф Капра Дао физики, 3667.41kb.
- Фритьоф Капра Дао физики, 3577.57kb.
- Новая книга известного американского ученого посвящена строению и функционированию, 3776.88kb.
- Книга "Мистерии Мухомора" представляет собой научное исследование роли красною мухомора, 2743.14kb.
Тут должен прийти принц, склониться над спящей царевной, тогда она оживет и сможет отвечать на вопросы. Более того, сможет продолжить и себя, и пришедшего принца в потомстве, формируя и передавая словно эстафетную палочку генетическое знание, т.е. принцип генерации структуры, похожей на себя.
Сама Структура пришла к своему осознанию из человеческого языка, из речи, из рассказа у костра, где один Первобытный с большой буквы объяснял другому Первобытному с большой буквы, как пройти к дереву, дающему большие и сочные плоды. Возникнув, она уже была интересна тем, что пыталась аккумулировать знания, находя им место в себе, почти также, как это делает губка, всасывая воду, или конденсатор, поглощая электрическую энергию.
Было и есть такое направление в философии и языкознании как структурализм. Именно в этой пауке впервые речь пошла о мире (сознании) как о месте, в котором находятся взаимосвязанные развивающиеся ряды структур, где культура или искусство представляют собой «структуру структуры Ян Мукаржовский сформулировал для любого произведения искусства два важнейших понятия: преднамеренность и непреднамеренность. Первое у него являло ту силу, которая соеденяет воедино отдельные части и придает смысл любому произведению, представляя собой в искусстве семантическую энергию.
В нашей трактовке информационных самообучающихся систем преднамеренность трансформировалась не во что иное как в цель.
Все то, что для субъекта, воспринимающего произведение, сопротивляется в произведении этому объеденению, все то, что нарушает смысловое единство названо Муражковским непреднамеренностью .
Непреднамеренность - это то, что современниками воспринимается как ошибка.При этом ошибка имеет тенденцию к росту.Она постоянно растет. И через какое-то время все произведение становится одной большой ошибкой, а потом вобще теряет первоначальный смысл и преобретает совершенно другое прочтение, особенно если данное произведение являет собой исторический материал.
Непреднамеренность присуща не только произведениям искусства, но и любому продукту человеческого труда.
В нашей трактовке в приложении к информационным самообучающимся системам непреднамеренность это не что иное как ветер, сбивающий ракету с пути, призрак, прячущийся за деревьями и заманивающий путника в ловушку,ошибки, проникающие в любое достаточно емкое програмное обеспечение ЭВМ.Это сила внешнего по отношению к выделенной системе воздействия, находящая свое измерение в погрешности самообучающейся системы при реакции на входную информацию.
Вот так и жила-была Структура — одна одинешенька. Принцы для нее стали появляться в шестидесятых годах нашего столетия. Но появляться они стали достаточно агрессивно, выступая сразу под лозунгами типа «Мир — это процесс», а кто не согласен — будьте добры подвинуться. Структура подвинулась.
Но процессы могут существовать только в структуре, на структуре и за счет структуры.
В результате произошло проявление факта постоянной встречи главных персонажей, они получили прописку и относительную независимость в человеческом коллективном разуме.
Процесс стал искать свою материализацию в виде весомой микросхемы соответcтвyющero микропроцессора, про которую никак не скажешь, что ее нельзя увидеть и потрогать. Структура же, наоборот, от зримого порядка, с которым она всегда олицетворяется, сделала шаг в зыбкий мир связей различных полей баз данных, хранящихся на магнитных носителях.
В результате, с одной стороны возникли однопроцессорные и многопроцессорные вычислительные комплексы и компьютерные программы для них.
С другой — различные структуры для хранения данных: древовидная, сетевая и табличная.
Для таблиц была разработана серьезная математика, позволившая реляционным СУБД выйти победителем на рынке СУБД. И все потому, что в абстрактной алгебре было показано, как для определенного рода структур (пока только таблиц) выполняются удивительные вещи. Оказывается табличные структуры можно объединять, пересекать и каждый раз будет получаться новое знание, которого как бы и не было раньше. Мало того, доказанные теоремы гарантируют, что в результате подобных действий вновь рождающиеся структуры являются истинными для той модели мира, в которой мы и творим свои чудеса. Важность данного результата трудно переоценить. Еще бы: знания можно складывать, разбирать, а потом опять собирать в виде удобных для работы табличек. И они не портятся и не теряют свой товарный вид.
Следующим шагом, позволившим увидеть за тактовой частотой микропроцессора управляющую им структуру, стал шаг, определивший революцию в программировании, благодаря которому оно даже называться стало иначе и превратилось в структурное программирование, в котором только слепой не увидит положенную в основу структуру процесса.
В явном виде было продемонстрировано, что любой процесс тоже обладает структурой и никуда от нее он никогда не денется.
Однако, на столь безапелляционное заявление можно возразить: «А как же логическое программирование? В программе на языке Пролог нет никаких структур, но тем не менее того, что есть вполне достаточно, чтобы порождать процессы!»
Все дело в том, что языки логического программирования в большей степени ориентированы на описание имеющих место быть фактов, правил поведения и целей, которые есть у создателя программы. Но связи между элементами подобных программ спрятаны от зрителя. Они есть, они как бы заново рождаются каждый раз по определенным законам при активизация программы, а при достижении цели опять умирают. Получается, что Процесс как бы порождает Структуру, будит ее, заставляет ожить, заиграть всеми своими лабиринтами в поисках пути к поставленной цели; а наигравшись, засыпает сам и вместе с собой уносит очарование поиска цели в растворяющейся паутине дорог.
Программа — это способ представления знания о том. что и как надо делать. Иногда, в случае языков логического программирования остается только «что», потому что «как» скрыто на уровне транслятора или интерпретатора.
И если мы в своей жизни к чему-то стремимся, чего-то желаем, но не знаем как этого достичь, то это совсем не значит, что этого не знает тот интерпретатор, который переводит наши цели в мир наших действий. Было б, как говорится, желание.
О том как подобный интерпретатор может работать - это отдельный разговор. Сейчас важно отметить, что ничто не мешает подобному интерпретатору существовать либо в области коллективного бессознательного в "структуре структур" человечества, либо в области индивидуального бессознательного, в хаосе стремящихся к независимости структур собственного подсознания.
В свете сказанного любопытно наблюдать за развитием в мире программного обеспечения текстовых процессоров. Тексты создаваемые ими, становятся все более активными, приобретая спосбность влиять на окружающую их среду.
Глава 31 (3). Мир подобных структур
Несмотря на бесконечность многообразия и красочности внешних форм Проявления и свойств отдельных частностей, в их сущности продолжает оставаться нечто перманентное, только в различных условиях дающее себя различно чувствовать и различно проявляющееся во вне.
В.Шмаков
До сих пор в данной работе самозарождающиеся и саморазрушающиеся структуры рассматривались лишь исходя из возможности их применения в качестве самообучающихся систем. А для этого исследовались алгоритмы самомодификации, позволяющие осуществить аккумуляцию в результирующей структуре знания об окружающем мире на базе входной обучающей выборки.
При этом в стороне осталась задача поиска у подобных структур каких-либо интегральных характеристик. В частности, интересен вопрос о том, какими количественными или качественными параметрами можно охарактеризовать структуры:
—обладающие наибольшей устойчивостью к окружающему воздействию (речь идет именно о структуре, а не о ее элементах);
— в наибольшей степени тяготеющие к саморазрушению или самовозрождению;
— обладающие максимальным или минимальным знанием. Но и кроме того, хотелось бы получить ответ на вопрос: «А что могут означать понятия: «минимальное знание» и «максимальное знание»?
В качестве основного постулата было принято, об этом шла речь в предыдущих главах, что знание информационной системы выражается через ее структуру. Тогда для оценки количества воспринятой системой информации логично использовать такое понятие как степень модификации структуры входными данными. Изменились весовые коэффициенты нейронных связей одна информация, погибли или появились новые элементы— другая информация.
При этом было показано в первой части работы, что истинность знания определяется жизненной силой его носителей, т.е. жизненной силой элементов структуры (жизненная сила— показатель способности элемента противодействовать внешней силе, т.е. новому знанию).
Прежде чем сделать следующий шаг. вздохнем глубже и еще раз повторим — носителем знания является структура.
Чем можно охарактеризовать структуру?
В качестве характеристик структур предлагается определить:
1) количество элементов;
2) общее количество связей между элементами;
3) распределение связей между элементами:
4) «жизненная сила» элементов системы;
5) операции, выполняемые элементами (алгоритмы функционирования элементов).
Как можно записать информацию о структуре? Предлагается следующая форма описания структуры с именем А:
A:{a1(a i,aj, ak,..), a2(), a3(),...an(), ...(1)
a1:: =<операции, выполняемые первым элементом, — алгоритм, записанный на одном из известных языков программирования>
ai:: =<операции, выполняемые i-ым элементом, — алгоритм, записанный на одном из известных языков программирования>
an:: =<операции, выполняемые n элементом, — алгоритм, записанный ва одном из известных языков программирования> здесь:
ai — номер элемента;
n — общее количество элементов;
i≤n, j≤n, k≤n;
в круглых скобках перечислены номера элементов, с которыми Дивен тот элемент, чей номер записан перед открывающейся скобкой.
Приведем примеры описания структур.
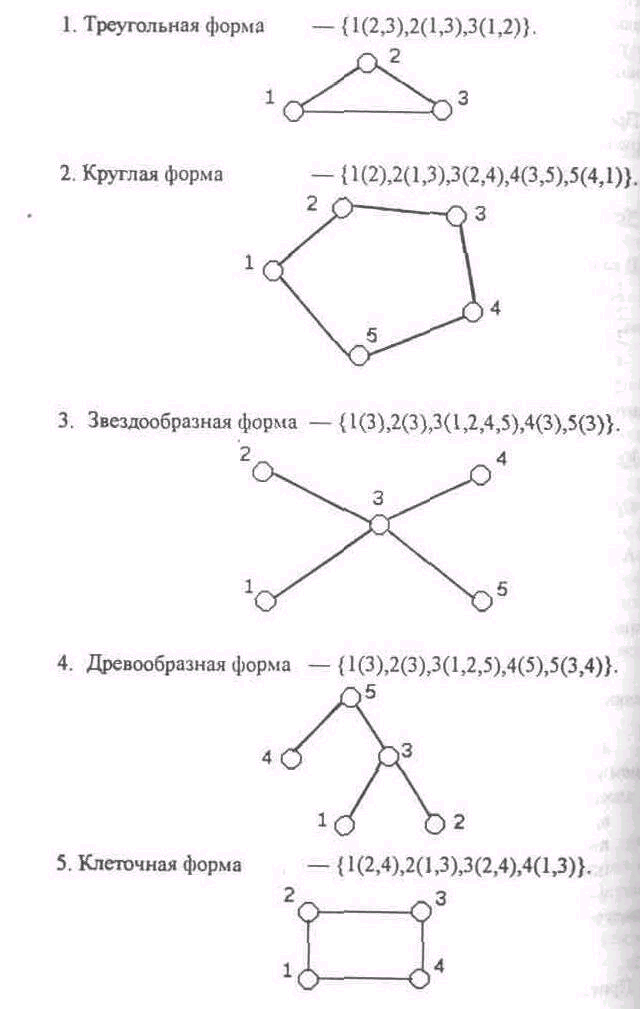
Иногда требуется в описании структуры указать «жизненную силу» ее элементов. В этом случае значения показателя «жизненная сила» проставляется в виде индекса над номером элемента, например:
треугольная форма — {11(2, 3), 22(1, 3), 3200(1, 2)}.
Легко показать, что при небольшой детализации предлагаемая форма описания структуры и запись алгоритмов па языках высокого уровня станут эквивалентным. Введена была данная форма записи исключительно для удобства преобразования структур и поиска наиболее уязвимых мест тех же алгоритмов и программ, составляющих базу информационного оружия.
Существуют различные способы сравнения структур.
Равенство структур. Две структуры будем называть равными, если описание одной из них можно наложить на описание другой и они совпадут, вплоть до совпадения значений «жизненной силы» элементов. При этом алгоритмы работы совпавших элементов являются равносильными.
Алгоритмы назовем равносильными, если по одинаковым входным данным они будут выдавать совпадающие результаты.
Две структуры назовем почти равными, если описание одной из них можно наложить на описание другой и они совпадут, при этом разница между значениями жизненной силы элементов, имеющих одинаковые номера, не будет превышать некоторой наперед заданной величины. При этом алгоритмы работы совпавших элементов являются функционально подобными.
Алгоритмы назовем функционально подобными, если одинаковое изменение входных данных приводит к одинаковому изменению результатов работы.
Подобие структур. Две структуры назовем подобными, если описание Одной из них можно наложить на аналогичное описание другой и они совпадут (без учета значений «жизненной силы» элементов).
В основе алгоритма определения подобия и равенства структур лежит переномерация элементов.
Покажем как это может быть сделано. Например, надо проверить подобны ли следующие две структуры А и В?
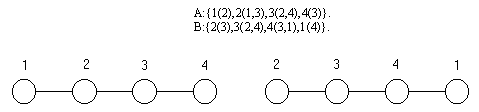
Если в описании структуры В произвести замену номеров в соответствии со следующим правилом:
2 -> 1,
3 ->2,
1 ->.
4 ->3,
то описания структур А и В совпадут. А это значит, что структуры А и В подобны.
Ранее, особенно в первой части работы, неоднократно упоминалось понятие «информационная емкость». Попробуем обосновать необходимость его введения и определить, что такое «информационная емкость». Значимость этого понятия вытекает из решения практических задач, в большинстве которых важно суметь ответить на вопросы: «Как велик багаж знаний у конкретной системы? Способна ли эта система освоить дополнительно еще что-то? Насколько быстро она способна это сделать?» Первый вопрос имеет отношение к текущему состоянию системы, вторые два— к ее будущему. Поэтому предлагается для оценки текущего состояния ввести понятие «информационная емкость». Что же касается оценки возможности системы, то здесь определяющую роль играет не столько исходная структура, сколько входная/выходная информация (обучающая выборка). Отвечать на вопросы о будущих состояниях следует только с учетом прогноза событий, способных затронуть данную систему.
Так как знание понимается через структурную сложность системы, то представляется разумным определить «информационную емкость» пропорциональной количеству элементов структуры и числу связей между ними
E = s+ n, где
s — общее число связей между элементами;
n — количество элементов в системе.
Глава 32 (4). Преобразование структур
Вот неделя, другая проходит, Еще пуще старуха одурилась;
Опять к рыбке старика посылает.
А.С.Пушкин
Считаем, что элементы структуры не способны поддерживать между собой связи, если сила внешнего давления превосходит их среднюю жизненную силу, умноженную на некоторый коэффициент ослабления, определяемый особенностями среды. Безусловно, можно ввести любые другие правила, определяющие гибель связей, и зависящие от того. какой процесс предполагается моделировать. В данном случае важно исследовать саму технологию преобразования структур без привязки к конкретным предметным областям. Например, в первой части работы, говоря о СР-сетях, предполагалось, что внешнее давление направлено в первую очередь на уничтожение элементов, а не их связей, а вот гибель элементов уже приводит к уничтожению связей. Понятно, что в каждом конкретном случае модель будет своя.
Исходя из сказанного, предлагается к выбору правил гибели элементов и их связей подойти несколько волюнтаристически, например:
1) элемент гибнет, если сила воздействия превышает его жизненную силу;
2) связь между элементами уничтожается, если сила внешнего воздействия на эту связь превышает силу сцепления, представляющую собой среднюю «жизненную силу» элементов, образовавших и поддерживающих эту связь, умноженную на некоторый коэффициент ослабления, который определяется условиями среды, типа: удаленность элементов друг от друга, частота взаимодействия, относительный объем передаваемой информации и т.п.
Силой сцепления двух элементов ai(gi) и aj(gj) назовем величину (первая форма) zi,j = Gi,j (gi+ gj)/2 или (вторая форма) zi,j = Gi,j (gi/si+ gj/sj)/2 где
Gi,j — коэффициент ослабления, Gi,j меньше 1, когда i ≠ j и равен 1, если i = j gi — «жизненная сила» i элемента;
si — число связей i элемента с остальными элементами данной системы,
Вполне допустимы и любые другие формы задания силы сцепления которые определяются исследуемой предметной областью и решаемыми задачами.
Внешнее давление (напряжение) может быть одинаково для все» элементов структуры, а может быть целенаправленным.
Предлагается первоначально рассмотреть процесс модификации структуры системы при постепенном увеличении внешнего равномерно распределенного давления на систему. А затем попытаться ответить на вопрос о том, что можно делать с системой в случае целенаправленного внешнего давления.
Итак, дана структура А.
а: {11(2, 3, 5), 22(1, 4), 32(1, 4, 5), 43(2, 3, 5), 51(1, 3, 4)},
форма которой для наглядности представлена на рис.6.1.

рис. 6.1.
Предположим, что коэффициент ослабления одинаков для всех связей данной структуры и равен 1.
Пусть на структуру А оказывается внешнее давление с силой в одну условную единицу. Под действием внешнего равномерного давления структура А, в соответствии с введенными правилами, приобретет следующий вид:
а: {11(2, 3), 22(1, 4), 32(1, 4, 5), 43(2, 3, 5), 51( 3, 4)},
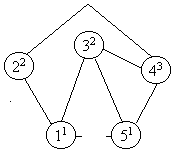
рис. 6.2.
Если давление будет усилено, то структура системы примет вид (внешнее давление соответствует двум условным единицам):
А: {22(4), 32(4), 43(2, 3)}.
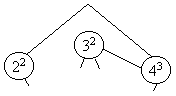
рис. 6.3.
Дальнейшее увеличение внешнего давления, в случае превышения двух услолвных единиц, приведет к тому, что система перестанет существовать, хотя отдельные элементы еще будут «живы».
Как видно из приведенного примера, поэтапное усиление внешнего давления приводит к поэтапному изменению структуры системы.
Первый этап: исходное состояние напоминает хаос — каждый соединен с каждым ; второй этап: структура приобретает древовидную форму, начинается выделение явного лидера, имеющего максимальную «жизненную силу»; третий структура приобретает явно выраженную звездообразную форму; четвертый этап: система растворяется в окружающем мире.
Чем можно охарактеризовать состояние структуры системы на каждом из этапов? Для ответа на этот вопрос хотелось бы опереться на такое понятие как энтропия, но на сегодняшний день оно уж очень тесно связано со статистической неопределенностью, с мерой хаоса. В нашем же случае аппарат
теории вероятностей и математической статистики не используется в силу того что исследуемые события являются в большинстве своем уникальными. Не бывает двух одинаковых информационных войн.
Действительно, как посчитать эту самую вероятность события, если любое событие в конечной человеческой жизни уникально по своей природе и совершенно непонятно, как вырезать его из всей ткани событийного мира?
Как рассчитать вероятность появления события в момент времени t если момент времени t уникален и в принципе неповторим, а поэтому говорить о статистических данных применительно к конкретному моменту времени все равно, что после драки махать кулаками.
Глава 33 (5). Хаос в принятии решения
...Все дороги занесло! Хоть убей следа не видно, Сбились мы, что делать нам! В поле бес нас водит, видно, Да кружит по сторонам.
А.С.Пушкин
Понятие энтропия в наше время как только не определяют. Наиболее традиционно— это мера неопределенности, существовавшая до наблюдения случайной величины, но она может быть и информационным расстоянием Кульбака-Лейблера, взятое с обратным знаком. Наиболее полно на сегодняшний день исследование данного понятия сделано С.Д.Хайтуном [102].
Не претендуя на данный термин во всем его многообразии, попробуем предложить собственную интерпретацию процессов, происходящих в структуре.
Известно, что скорость реагирования системы пропорциональна числу подсистем, с которыми согласуется решение и которые могут принять участие в его реализации. Функциональная зависимость скорости реагирования от числа подсистем может быть самая разнообразная в зависимости от решаемых системой задач, сложности структуры, процедуры принятия решения и т.п.
Предположим, что исследуемая нами структура состоит из n элементов и имеет вид соединений «каждый с каждым». При этом процедура принятия решения даже в этой полносвязной структуре может быть различна.
Вариант 1.
В структуре существует элемент, называемый руководитель, который с каждым членом «коллектива» согласовывает свое решение, либо выясняет способность любого из членов решить поставленную перед системой задачу, например: способный слышать как растет трава, будет предупреждать об опасности, способный делать семимильные шаги, поможет принести весть, а силач будет защищать.
Вариант 2.
Не только руководитель, но и каждый из элементов системы должен согласовывать свое мнение с каждым.
Второй вариант, несмотря на кажущуюся похожесть обоих вариантов предполагает получение ответов па такие вопросы, на которые в случае работы по первой схеме правильного ответа может и не быть. Подобное возможно благодаря тому, что любой из элементов дополняет собственное знание процессе согласования решения по схеме «каждый с каждым». «Умнеет» не только руководитель, но и все члены коллектива.
Однако, если допустить, что во втором варианте время взаимодействия между элементами много меньше времени обработки входных данных самими элементами, то образование, которое благодаря сделанному допущению возникнет, назвать системой можно будет с большой натяжкой— оно по существу является единым и неделимым элементом.
Предположим, что задержка на создание интерфейса между двумя элементами и передачу информации все же значительна и составляет t условных единиц. Попробуем оценить временную задержку в принятии системой решения для второго варианта.
Пусть на один из элементов подан входной сигнал. Представим, что элемент, принявший сигнал, сам не в состоянии его отработать, т.е. выдать результат. Тогда он формирует сообщение, включающее в себя полученный запрос и собственное мнение, и рассылает его по всем своим каналам. Каждый из получивших сообщение, если не может сформулировать ответ, поступает аналогично.
(n-1) — количество посылок на первом этапе (кроме себя самого) выполняются параллельно за одно и то же время t;
(n-l) x (n-l) — количество посылок на втором этапе, каждый обменивается с каждым собственной информацией и т.д.
При этом, если t — время пересылки сообщения от одного элемента к другому, то общее время, которое затратила система на принятие решения, равно 2хt.
В случае, если структура системы типа «звезда» и количество связей n-1, то общее время принятия решения также будет равно 2xt (передал, получил, обобщил).
В данном случае получается, что скорость реагирования системы прямо пропорциональна числу этапов.
Вполне возможно, что именно на подобный режим работы переходит система в случае опасности, т.к. в данном случае время реакции не зависит от числа элементов, участвующих в принятии решения. Когда употребляют при описании работы мозга биологической системы термин «сверхпроводимость», то может быть за ним кроется именно подобный механизм принятия системой решения.
Можно подойти с другой стороны к оценке времени реагирования системы. Например, пусть среди множества элементов системы (n штук) только комбинация выходов k элементов способна составить ответ на заданный
системе вопрос Наличие дополнительных элементов будет только мешать системе, искажая ответ.
Тогда, для того чтобы отобрать из всех n элементов именно k нужных, системе понадобится задать самой себе kxlog2(n) вопросов (в соответствии с формулой Хартли). Если вопросы задаются последовательно, то для этого ей понадобится
kxlog (n) xt единиц времени
