Теория графов и их применение

Вид материала

Курсовая

Содержание Смежность, инцидентность, степени Некоторые специальные графы Графы и матрицы

Подобный материал:

• 1. Элементы теории графов Введение в теорию графов: основные понятия и определения., 32.17kb.
• «Теория графов», 114.81kb.
• Задача является np-полной для кубических планарных графов, реберных графов, ориентированных, 39.45kb.
• «Применение информационный технологий в теории графов», 272.84kb.
• Билеты по Дискретной математике «Теория Графов», 12.79kb.
• Программа вступительного экзамена в аспирантуру по специальностям 05. 13. 05 - "Элементы, 88.59kb.
• Спецкурс «Теория графов» пм 4 курс История возникновения и развития теории графов., 13.97kb.
• Задание графов соответствием 9 > Матричное представление графов 10 Вопросы применения, 230.14kb.
• Знать содержание программы курса; иметь навыки структурного моделирования типовых объектов;, 56.2kb.
• Теория конечных графов и её приложения прак зан, 29.91kb.

Смежность, инцидентность, степени

Если в графе имеется ребро 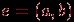, то говорят, что вершины и 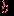смежны в этом графе, ребро инцидентно каждой из вершин , , 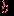а каждая из них инцидентна этому ребру.

Множество всех вершин графа, смежных с данной вершиной , называется окрестностью этой вершины и обозначается через .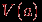

На практике удобным и эффективным при решении многих задач способом задания графа являются так называемые списки смежности. Эти списки могут быть реализованы различными способами в виде конкретных структур данных, но в любом случае речь идет о том, что для каждой вершины перечисляются все смежные с ней вершины, т.е. элементы множества 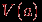. Такой способ задания дает возможность быстрого просмотра окрестности вершины.

Число вершин, смежных с вершиной , называется степенью вершины и обозначается через .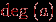

Если сложить степени всех вершин некоторого графа, то каждое ребро внесет в эту сумму вклад, равный 2, поэтому справедливо следующее утверждение:

Теорема 2. .

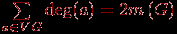Это равенство известно как "лемма о рукопожатиях". Из него следует, что число вершин нечетной степени в любом графе четно.

Вершину степени 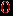называют изолированной.

Граф называют регулярным степени 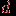, если степень каждой его вершины равна .

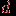Набор степеней графа - это последовательность степеней его вершин, выписанных в неубывающем порядке.

Некоторые специальные графы

Рассмотрим некоторые особенно часто встречающиеся графы.

Пустой граф - граф, не содержащий ни одного ребра. Пустой граф с множеством вершин обозначается через .

Полный граф - граф, в котором каждые две вершины смежны. Полный граф с множеством вершин обозначается через .

Граф 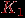, в частности, имеет одну вершину и ни одного ребра. Очевидно, . Будем считать также, что существует граф 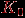, у которого .

Цепь(путь) - граф с множеством вершин и множеством ребер .

Цикл - граф, который получается из графа добавлением ребра .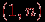

Все эти графы при показаны на рис. 1.6


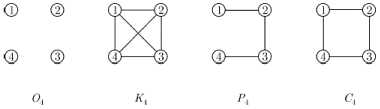
Рис. 1.6. 

Графы и матрицы

Пусть - граф с 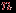вершинами, причем 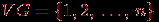. Построим квадратную матрицу 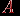порядка 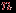, в которой элемент 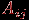, стоящий на пересечении строки с номером 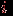и столбца с номером 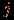, определяется следующим образом: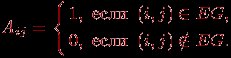



Она называется матрицей смежности графа. Матрицу смежности можно построить и для ориентированного графа, и для неориентированного, и для графа с петлями. Для обыкновенного графа она обладает двумя особенностями: из-за отсутствия петель на главной диагонали стоят нули, а так как граф неориентированный, то матрица симметрична относительно главной диагонали. Обратно, каждой квадратной матрице порядка 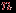, составленной из нулей и единиц и обладающей двумя указанными свойствами, соответствует обыкновенный граф с множеством вершин .

Другая матрица, ассоциированная с графом - это матрица инцидентности. Для ее построения занумеруем вершины графа числами от 1 до 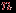, а ребра - числами от 1 до 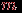. Матрица инцидентности 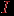имеет 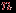строк и столбцов, а ее элемент 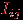равен 1, если вершина с номером 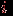инцидентна ребру с номером 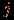, в противном случае он равен нулю. На рис. 1.7 показан граф с занумерованными вершинами и ребрами и его матрицы смежности и инцидентности.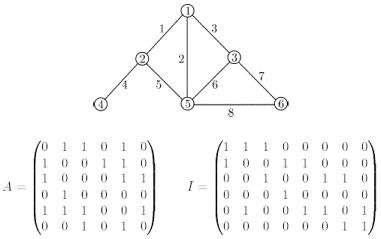


Рис. 1.7. 

Для ориентированного графа матрица инцидентности определяется несколько иначе: ее элемент 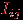равен 1, если вершина 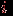является началом ребра 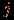, и равен , если она является концом этого ребра, и он равен 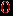, если эта вершина и это ребро не инцидентны друг другу.