Программа элективного курса "Компьютерное моделирование"

Вид материала

Программа

Содержание Компьютерные исследования Приложение к спецкурсу «Компьютерное моделирование» Алгоритм выполнения работы с помощью компьютерной модели «Графер» Карточки с заданием

Подобный материал:

• Программа дисциплины дпп. Дс. 01 Компьютерное моделирование в химии цели и задачи дисциплины, 281.91kb.
• Учебно-методический комплекс по дисциплине "компьютерное моделирование" (факультет, 384.08kb.
• Программа элективного курса "Компьютерное делопроизводство", 80.98kb.
• Программа дисциплины Компьютерное моделирование в экономике и менеджменте для направления, 192.72kb.
• Программа спецкурса "Компьютерное моделирование нелинейных волновых процессов" Специальность, 27.11kb.
• Программа элективного курса компьютерное делопроизводство, 155.02kb.
• Программа элективного курса Ставрополь, 186.92kb.
• Программа элективного курса по русскому языку и литературе 9 класс, 83.37kb.
• Программа элективного курса «Решение задач по физике» (1ч в неделю, всего 34часа), 115.81kb.
• Программа элективного курса «Решение ключевых задач по физике» (1ч в неделю, всего, 130.63kb.

Компьютерные исследования:

Приложение к спецкурсу «Компьютерное моделирование»
Тема: «Преобразования фигур»

Цель занятия:

• Развитие самостоятельности и творческой активности учащихся.
  
• Формирование умения анализировать, сравнивать и обобщать полученные результаты.
  

Описание работы:

• Откройте в разделе «Модели» окно модели «Движение».
  
• Нажмите кнопку «Старт», рассмотрите данные на экране.
  
• 
  Рассмотрите все виды преобразования, обратите внимание на свойства.
  
• Смоделируйте свою ситуацию для каждого вида преобразования.
  

Рис. 1 модель Движение.

• На интерактивной модели «Чертёж» для точек А(1;2), В(-3;3), С(-1;2), Е(5;-1) постройте симметричные им относительно оси ох, оу, начала координат.
  
• Для точки М(а;в) найдите симметричную ей относительно оси абсцисс точку М^{`</sup>. Какие координаты имеет точка М<sup>`}?
  
• Для точки Е(x;y) найдите симметричную ей относительно начала координат точку Е^{`</sup>. Какие координаты имеет точка Е<sup>`}?
  
• Какова зависимость между координатами точек М и М^`?
  
• Какова зависимость между координатами точек Е и Е^`?
  
• Какими формулами можно задать центральную симметрию относительно начала координат?
  
• Какими формулами задается поворот вокруг начала координат на угол φ против часовой стрелки?
  
• Какими формулами задается параллельный перенос? Найдите точки, в которые переводятся точки А(1;4), В(-5;1), С(-1,2;0,3), О(0;0)?
  
• С
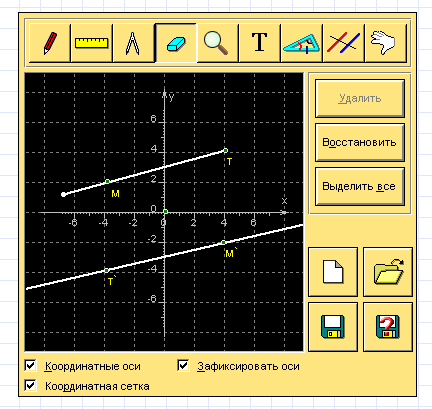
  делайте теоретические и практические выводы.
  

Рис. 2 модель Чертёж.

Приложение к спецкурсу «Компьютерное моделирование»
Тема: «Преобразование графиков функций»

Цель:

• Воспитание навыков самообучения.
  
• Развитие поисковой самостоятельности.
  

Оборудование:

• Программа для компьютера: «Функции и графики», ООО «ФИЗИКОН», М.2003г;
  
• Индивидуальные задания;
  
• Инструкция перед каждым компьютером или в документе Word.
  

Описание работы

Учащиеся делятся на группы по два человека. Каждая группа знакомится с заданием, содержанием и описанием работы. При необходимости используют электронный учебник, калькулятор, компьютерную модель 2.17. или «Графер».

Задания для повторения темы:

Подготовка к работе.

1. В чём сходство графиков y=1/3x², y=1/3(x+2)² , y=1/3x²+3 и
   
   1. y=-/3x²?
      
2. Сравните координаты точек с равными абсциссами.
   
3. Сравните координаты точек с равными ординатами.
   
4. Выполняя компьютерное моделирование, заполните пустые клетки таблицы:
   

   Данная функция	Новая функция	Описание преобразования
   y=x2		Перенос на 2 единицы вверх
   y=x2	y=x2-4
   y=x2	y=-2x2
   	y=(x+2)2	Перенос на 2 единицы влево
   y=x2		Перенос на 2 единицы вправо
   y=x2		Сжатие в 3 раза по оси ох

5. Постройте график функции y=(2x+3)². Опишите последовательность построения.
   
6. Выполните на одной плоскости графики данной последовательности.
   
7. *Сделайте вывод, записав формулы преобразований координат в общем виде.
   
8. *Проверьте свой вывод, выполнив 1-2 задания, выбранные самостоятельно.
   

Задания к исследовательской работе

Подготовка к работе.

Электронный курс. 1.4.1, вопрос3, задача1,2 с ответами, задачи 1,2 с решением.

1. Выполняя компьютерное моделирование для точек А(3,4), В(-1,-2), С(-3,2), Д(5,-3) постройте симметричные им
   
   1. Относительно оси ох по формуле
      
   2. Относительно оси оу, запишите формулу,
      
   3. Относительно начала координат, запишите формулу
      
2. Найдите точки, в которые переводятся указанные выше точки при параллельном переносе, заданном формулой , если а=4, в=1
   
3. В какую фигуру перейдёт окружность x²+y²=9, если а=2, в=4? Запишите формулу, постройте график уравнения.
   
4. Для точек п.1 постройте точки, в которые преобразует:
   

Растяжение, сжатие от оси ох k=2, k=0,5 по формуле

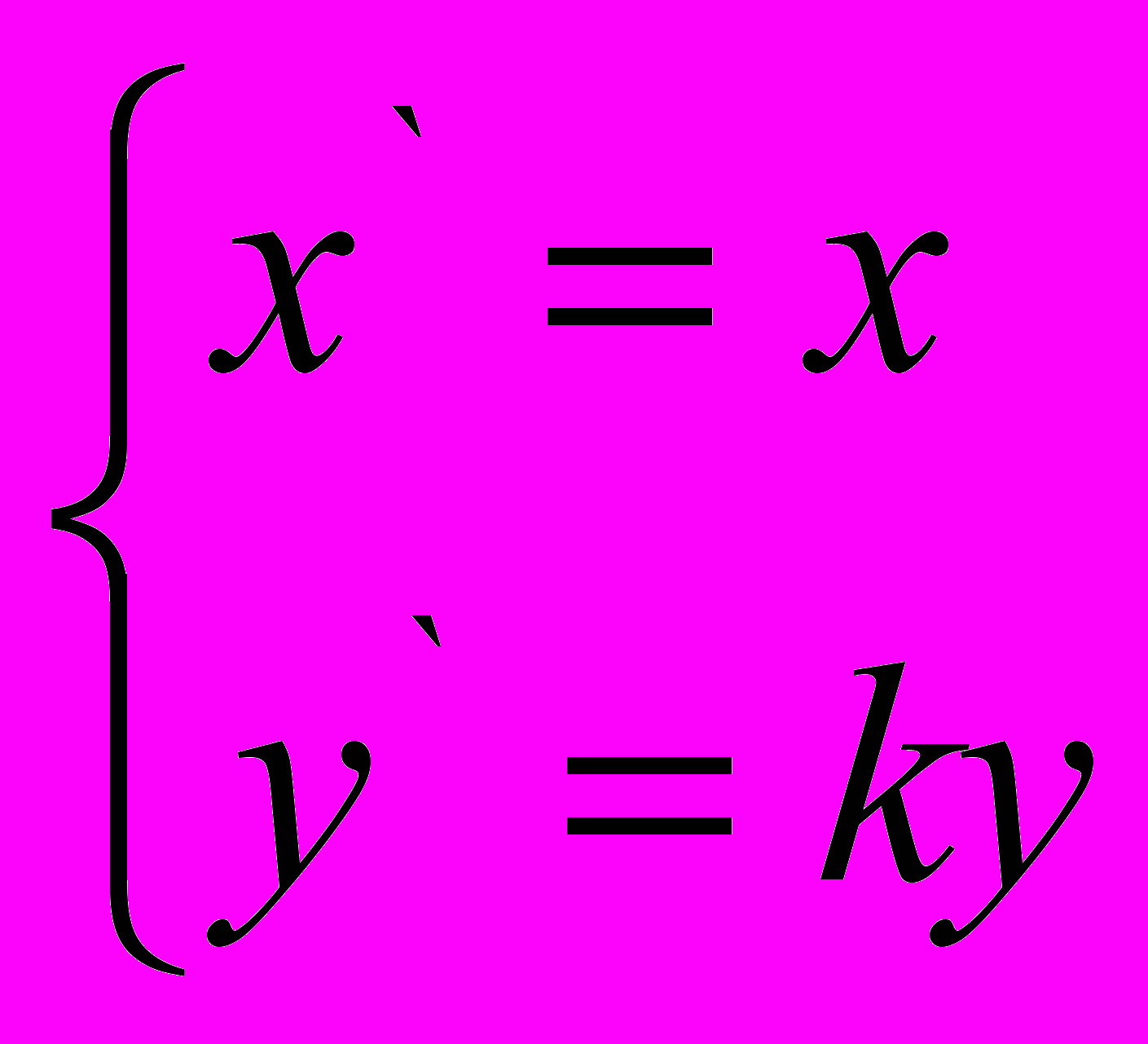
Запишите их координаты.

5. С помощью какого преобразования может быть получена парабола:
   

• y=0,5x²
  
• y=3x²
  
• y=-3x²
  
• y=(x-2)²
  
• y=x²-1
  
• y=(x-2)²-1
  
• y=2(x-2)²-1
  

Форма отчета

Фамилия _______________________

Вариант _______________________

Задания
1 задание:	Формула преобразования
относительно оси оу Формула преобразования относительно начала координат
2 задание координаты точек при параллельном переносе А В С Д
3 задание
4 задание
5 задание
6 задание опишите преобразования

Приложение к спецкурсу «Компьютерное моделирование»
Тема: «Координатная плоскость»

Цель занятия:

• Повторение темы «Построение точек по заданным координатам. Определение координат точек».
  
• Развитие наблюдательности, внимания по отношению к замеченным свойствам модели.
  
• Формирование умения обобщить и сделать выводы.
  

Оборудование:

• Компьютерный курс «Открытая математика 2.5. Функции и графики» ООО «ФИЗИКОН».
  
• Карточки с заданием:
  

«Многоугольник ABCDE, построенный на координатной плоскости, где А(1,2), В(-3,3), С(-1,2), Д(-3,-4), Е(4,-5)» (координаты вершин для учащихся не указаны).

Задания:

1. Какие координаты имеют вершины многоугольника ABCDE?
   
2. Найдите координаты середины отрезка ВЕ.
   
3. Определите координаты точки К пересечения отрезков АD и ВЕ.
   
4. Постройте четырёхугольник MNPQ: M(x₁, y₁), N(x₂, y₂), P(x₃, y₃), Q(x₄, y₄).
   
5. Постройте ещё два четырёхугольника, вершины которых были бы симметричны вершинам четырёхугольника MNPQ:
   
6. Относительно оси Ox;
   
7. Относительно оси Oy.
   
8. Сделайте вывод относительно координат симметричных точек.
   
9. Постройте на координатной плоскости точки: A(-4; -2); В(-3; -1), С(-2, 0), Д(-1; 1). Эти точки располагаются в определённой последовательности. Уловив её, отметьте ещё 2-3 точки. Постройте фигуру, симметричную данной относительно осей.
   

Алгоритм выполнения работы с помощью компьютерной модели «Графер»:

• Запишите координаты многоугольника ABCDE в отчёте л/р;
  
• При помощи команды «Точка» отметьте точку на координатной плоскости, обозначьте её при помощи команды «Фигуры. Ввод текста».
  
• Запишите координаты точки в отчёте л/р;
  
• Постройте новую координатную плоскость, команда «Главная. Построение координатной плоскости».
  
• Отметьте точки, команда «Точка».
  
• Обозначьте их, команда «Фигуры. Ввод текста».
  
• Определите их координаты, запишите координаты многоугольника в отчёт л/р;
  
• Выполните задание 5, команда «Преобразования». (Задание 6 носит исследовательский характер).
  
• Сохраните данные изображения, команда «Главная. Сохранение файла», введя свою фамилию, класс.
  

Карточки с заданием:

варианты	1	2	3	4
X1	4	5	6	7
Y1	2	3	4	5
Y2	2	3	4	5
X2	5	6	7	8
X3	1	3	4	5
Y3	4	3	4	5
X4	2	-1	0	1
Y4	2	4	5	6