Решение задачи одним из математических методов
| Вид материала | Решение |
- Задачи нелинейной и дискретной оптимизации. Методы решения. Постановка и экономико-математическая, 25.18kb.
- Задачи линейного программирования и задачи математической экономики Методика преподавания, 19.49kb.
- Бравый Евгений Ильич, 55.95kb.
- Тематический план учебной дисциплины, 52.63kb.
- Анализ методик использования моделирования в процессе обучения дошкольников математике, 472.24kb.
- Одним из эффективных математических методов для определения зависимости по множеству, 139.29kb.
- Д э. н. М. В. Грачева, зав кафедрой «Математических методов анализа экономики», 20.32kb.
- Задачи внеклассного занятия: Рассмотреть практическое применение математических знаний, 95.15kb.
- Практических: 0 Лабораторных, 16.63kb.
- Практических: 34 Лабораторных, 24.5kb.
19. Метод невязок.
Часто при решении задачи линейного программирования используется искусственный базис. Метод решения при помощи искусственного базиса называется методом невязок. Рассмотрим в качестве примера задачу линейного программирования с пятью неизвестными:
Z = c1x1 + c2x2 + c3x3 + c4x4 + c5x5 (max) (1)
a1x1 + a2x2 + a3x3 + a4x4 + a5x5 = a
b1x1 + b2x2 + b3x3 + b4x4 + b5x5 = b (2)
c1x1 + c2x2 + c3x3 + c4x4 + c5x5 = c
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0, x5 ≥ 0 (3)
a ≥ 0, b ≥ 0, c ≥ 0 (4)
Если одно или несколько условий (4) не выполняются, например a < 0, то, умножив обе части первого равенства на -1, получим уравнение, в котором свободный член больше. нуля.
Наряду с исходной задачей (1) – (4) рассмотрим другую задачу линейного программирования, которая является вспомогательной:
Т = c1x1 + c2x2 + c3x3 + c4x4 + c5x5 + М (V1 + V2 + V3) (max)
при условиях
a1x1 + a2x2 + a3x3 + a4x4 + a5x5 + V1 = a
b1x1 + b2x2 + b3x3 + b4x4 + b5x5 + V2 = b
c1x1 + c2x2 + c3x3 + c4x4 + c5x5 + V3 = c
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0, x5 ≥ 0, V1 ≥ 0, V2 ≥ 0, V3 ≥ 0
где М – некоторое число.
Эта задача называется М-задачей. Неизвестными в ней являются x1, x2, x3, x4, x5, V1, V2, V3. При этом неизвестные V1, V2, V3 называются искусственными.
При решении задачи линейного программирования используется следующая теорема:
- Если в оптимальном решении М-задачи все искусственные переменные равны нулю, то соответствующие значения остальных переменных дают оптимальное решение исходной задачи.
- Если имеется оптимальное решение М-задачи, в котором одна из искусственных переменных отлична от нуля, то система ограничений (исходная задача не имеет допустимого решения).
- Если М-задача не имеет оптимального решения, то исходная задача не разрешима.
20. Двойственные задачи.
С каждой задачей ЛП тесным образом связана, строящаяся определенным образом задача, называемая двойственной по отношению к исходной. Прямая и двойственная к ней задачи удовлетворяют следующим условиям:
- число переменных двойственной задачи равно числу условий ограничений прямой задачи (не считая условий неотрицательности переменных) и наоборот число условий ограничений двойственной задачи равно числу переменных исходной задачи;
- коэффициентами целевой функции двойственной задачи служат свободные члены системы ограничений прямой задачи, а свободными членами системы ограничений двойственной задачи – коэффициенты целевой функции исходной задачи;
- матрицей коэффициентов при переменных двойственной задачи будет транспонированная матрица из коэффициентов при переменных системы ограничений исходной задачи;
- если исходная задача решается на max и ее неравенства приведены к виду ≤ то двойственная к ней задача решается на min и ее неравенства в системе ограничений должны быть вида ≥ (целевая установка);
- каждому i-ому ограничению-неравенству прямой задачи соответствует в двойственной задачи условие неотрицательности i-ой переменной (yi ≥ 0), а ограничению-равенству соответствует переменная без ограничений. И наоборот, неотрицательной переменной прямой задачи соответствует в двойственной задачи k-ое ограничение-неравенство, а произвольной переменной – ограничение-равенство.
Соотношение двойственности взаимное, т. е. задача двойственная по отношению к двойственной совпадает с прямой, т. е. речь будет идти о паре двойственных задач.
Исходная и двойственная к ней задачи могут быть экономически интерпретированы следующим образом:
Исх. задача: составить план выпуска продукции, обеспечить ее max выпуск в стоимостном выражении.
Двойственная: какова должна быть цена единицы каждого из ресурсов для минимизации общей стоимости затрат.
В паре двойственных задач каждая является самостоятельной задачей ЛП и может быть решена независимо одна от другой, но тем не менее по решению одной из пары двойственных задач находится и решение двойственной к ней.
Существующие зависимости между решениями прямой и двойственной задач характеризуются сформулированными ниже леммами и теоремами двойственности.
Лемма 1. Если Х – некоторый план исходной задачи (43) – (45), a Y – произвольный план двойственной задачи (46), (47), то значение целевой функции исходной задачи при плане Х всегда не превосходит значения целевой функции двойственной задачи при плане Y, т. е. F(x)≤F*(Y) или j=1Σn CjXj ≤ i=1Σm biyi.
Лемма 2. Если
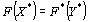для некоторых планов X* и Y* задач (43) – (45) и (46), (47), то X* – оптимальный план исходной задачи, а Y* – оптимальный план двойственной задачи.22-23. Симметричные и несимметричные двойственные задачи. Нахождение оптимального решения. Пример.
Пары двойственных задач делятся на симметричные и несимметричные. Если в системе ограничений нет ограничений вида равенства и в обеих задачах нет произвольных переменных, то такая пара задач называется симметричной. В противном случае задачи несимметричны.
Решение двойственных задач:
Z = c1x1 + c2x2 + … + cnxn (max)
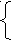x1x1 + … + anxn b1…
anx1 + … + amnxn bm
xj 0; j=1,n
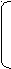
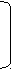
an … am b1 an … am1 c1
… …
A am1…amn bm AT am … amn cn
c1 … cn Zmax b1 … bm Zmax
T + biyi + … + amiyn (min)
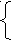anyi + … amj c1…
ainyi + … + amnyn cn
yi 0; i=1,m
Далее смотрят какую из пары задач выгоднее решать. Выгоднее решать ту задачу, в которой переменных больше чем уравнений системы ограничений.
Далее решают задачу симплекс-методом.
Далее находят решение двойственной задачи по решению исходной.
Если задачи симметричны, то решение двойственной находят по строке последней симплекс-таблице решенной задачи.
исходные балансовые
x1 x2 x3 x4 x5 x6
y4 y5 y6 y1 y2 y3
1 2 3 4 5 5
Если задачи несимметричны, то решение находят по формуле Yопт = Сб Вб-1 где Сб – матрица-строка (вектор) коэффициентов при базовых переменных целевой функции в оптимальном решении исходной задачи, Вб-1 – обратная матрица матрицы коэффициентов базовых переменных уравнений системы ограничений исходной задачи в оптимальном решении.
24. Теоремы двойственности. Основное неравенство двойственности.
Основное неравенство двойственности.
Пусть имеется пара двойственных задач. Скажем, что для любых допустимых решений X(x1,…,xn) и Y(y1,…,yn) исходной и двойственной задач справедливо неравенство: Z(x) T(y) или
n m
cjxj biyi
j=1 i=1
Доказательство:
Умножим обе части неравенств системы ограничений исходной задачи соответственно на переменные и сложив левые и правые части получим неравенство
m n m
yi aijxj biyi
i=1 j=1 i=1
Аналогично преобразовав систему ограничений двойственной задачи путем умножения обеих частей неравенства на (x1,…,xn) и последующего сложения, получим неравенство
n m n
xj aijyi cjxj
j=1 i=1 j=1
Так как левые части этих неравенств представляют собой одно и то же выражение D, то получаем:
n m
cijxi D bijyi
j=1 i=1
Отсюда из свойства транзитивности имеем неравенство
n m
cjxj biyi
j=1 i=1
что и требовалось доказать.
Теоремы двойственности.
1) Если одна из задач двойственной пары имеет оптимальный план, то и другая имеет оптимальный план и значения целевых функций задач при их оптимальных планах равны между собой, т. е.
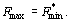Если же целевая функция одной задачи из двойственной пары неограничена сверху или снизу, то другая задача вообще не имеет планов.2) План
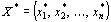исходной задачи и план 
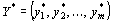двойственной задачи являются оптимальными планами этих задач тогда и только тогда, когда для любого 
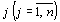выполняется равенство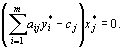 
Пары двойственных задач делятся на симметричные и несимметричные. Если в системе ограничений нет ограничений вида равенства и в обеих задачах нет произвольных переменных, то такая пара называется симметричной. В противном случае – несимметричной.
25. ТЗ. В общем случае имеется m пунктов производства и n пунктов потребления. Пункты производства пронумеруем числами от 1 до m. Номер пункта производства будем обозначать буквой i (таким образом, 1 i m). Пункты потребления пронумеруем числами от 1 до n. Номер пункта потребления будем обозначать буквой j (таким образом, 1 j n). Рассмотрим некоторый период времени. Пусть ai - объем производства за период времени в i-м пункте производства, bi - количество продукции, требуемое за период времени в j-м пункте потребления. Пусть cij - стоимость перевозки единицы груза из i-го пункта производства в j-й пункт потребления.
Требуется определить план перевозок, удовлетворяющий условиям по пунктам производства и потребления и соответствующий наименьшим затратам на перевозки.
Для построения математической модели следует ввести переменные. Для каждой пары поставщик-потребитель, то есть для каждой пары (i,j) введем переменную хij - объем перевозки от пункта производства i к пункту потребления j.
Математическая модель транспортной задачи записывается следующим образом:
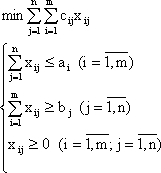
Целевая функция модели представляет собой общую стоимость всех перевозок. В модели указано, что целевую функцию следует минимизировать. Таким образом, модель предписывает искать план перевозок наименьшей общей стоимости.
В системе ограничений представлены три группы неравенств. В первой группе m неравенств, соответствующих пунктам производства. Каждое неравенство утверждает, что из соответствующего пункта не может быть вывезено больше, чем в нем имеется. Во второй группе n неравенств, соответствующих пунктам потребления. Каждое из них требует, чтобы в соответствующий пункт было привезено не меньше, чем требуется. В третьей группе m ´ n неравенств, обеспечивающих неотрицательность объема перевозок.
Представленная модель транспортной задачи с ограничениями-неравенствами называется открытой моделью. Задача разрешима в том и только в том случае, когда общий объем груза у поставщиков не меньше суммарной потребности потребителей, то есть когда выполнено неравенство:
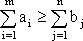. Если общий объем груза у поставщиков в точности равен общей потребности потребителей, то есть если имеет место равенство: 
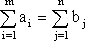, то указанная выше открытая модель эквивалентна более простой закрытой модели, в которой основные неравенства заменены равенствами. Закрытая модель имеет следующий вид: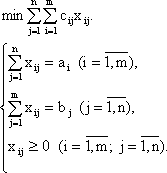 
26-27. Теорема о разрешимости транспортной задачи. Доказательство ограниченности функции на множестве планов транспортной задачи.
Теорема
Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы грузов в пунктах отправления были бы равны потребностям в грузах в пунктах потребления
m n ── ──
∑ ai = ∑ bi, i=1,m, j=1,n (1)
i=1 j=1
Для доказательства теоремы необходимо показать, что при заданных условиях существует хотя бы один план задачи и линейная функция на множестве планов ограничена.
Пусть выполняется условие
m n ── ──
∑ ai = ∑ bi = M>0, i=1,m, j=1,n
i=1 j=1,
тогда величины
aibi ── ──
xij= ── (i=1,m, j=1,n)
M
являются планом, так как они удовлетворяют системе ограничений
n
∑ xij=ai, (2)
j=1
m ── ──
∑ xij=bi, (3), i=1,m, j=1,n
i=1
Действительно, подставляя значения xij в 2 и 3, находим
n n aibi ai n ai
∑ xij=∑ ── = ─ ∑bj = ─ M = ai,
j=1 j=1 M M j=1 M
m m aibi bi m bi
∑ xij=∑ ── = ─ ∑ai = ─ M = bi
i=1 i=1 M M i=1 M
Выберем из значений Cij наибольшее C*=maxCij и заменим в линейной функции
m n
Z=∑ ∑ Cij xij все коэффициенты на на С*. Тогда, учитывая 2, получим
i=1 j=1
m n m n m
∑ ∑ = Cij xij <=C*, ∑ ∑ xij=C*, ∑ ai=C*M
i=1j=1 i=1j=1 i=1
Выберем из значений Сij наименьшее С**=minСij, и заменим в линейной функции все коэффициенты на С**, тогда, учитывая 2, имеем
m n m n m
∑ ∑ = Cij xij <=C**, ∑ ∑ xij=C**, ∑ ai=C**M
i=1j=1 i=1j=1 i=1
Объединяя два последних неравенства в одно двойное, окончательно получаем
С**<=Z<=С*М,
т.е. линейная функция ограничена на множестве планов транспортной задачи.
28. Теорема о ранге матрицы коэффициентов ТЗ
Теорема
Ранг r системы уравнений ТЗ при условии
m n ── ──
∑ ai = ∑ bi, i=1,m, j=1,n (1)
i=1 j=1
равен p+q-1.
Доказательство.
Действительно, сравним ∑ первых p уравнений. Согласно условию 1, правые части совпадают. Тогда совпадают и левые части, а сами уравнения линейно зависимы, а значит, r<= p+q-1.
Докажем, что r≥ p+q-1.
Из линейной алгебры известно, что если некоторые k переменных произвольной системы линейных уравнений можно выразить через остальные переменные системы, то ранг этой системы не меньше, чем k. Выразим переменные xik, входящие в первый столбец и первую строку таблицы.
p
xij=b1- ∑xij (8)
i=2
q
xik=a1-∑xij (9)
i=2
Подставим вместо xik его выражение из уравнения 8. Т.о., p+q-1 переменных можно выразить через остальные переменные pq-p-q+1.
r= p+q-1.
Следствие:
Число r основных (базисных) переменных закрытой модели ТЗ равно p+q-1, где p – число поставщиков, q – потребителей.
29. Нахождение исходного опорного решения транспортной задачи
Опорным решением транспортной задачи называется любое допустимое решение, для которого вектор-условия, соответствующие положительным координатам, линейно независимы.
Ввиду того, что r= p+q-1, опорное решение не может иметь отличных от нуля координат более p+q-1. Число отличных от нуля координат невырожденного опорного решения равно p+q-1, а для вырожденного опорного решения меньше.
- Метод северо-западного угла
- Метод минимальной стоимости
- Метод двойного предпочтения
- Начинают с того, что приписывают переменной x11, стоящей в северо-западном углу таблицы, минимальное из значений a1 и b1.
x11=min a1b1
Двигаются в соседнюю клетку по строке вправо, если a1>b1, или по столбцу вниз если a1
Недостаток этого метода – он не учитывает значений коэффициентов затрат, но он допускает модификацию и очень удобен для работы на машине (первой берут не клетку северо-западного угла, а клетку с минимальным значением. При этом распределение поставок будет ближе к оптимальному).
- Из всей таблицы стоимостей выбирают наименьшую и в клетку, которая ей соответствует, помещают меньшее из чисел ai и bi. Затем из рассмотрения исключают или строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.
- В каждом столбце отмечают знаком √ клетку с наименьшей стоимостью. Затем то же проделывают в каждой строке. В результате некоторые клетки имеют отметку √√. В оставшейся части таблицы перевозки распределяют по наименьшей стоимости.
Цикл – набор клеток вида (i1k2,i2k1), в котором только две соседние клетки расположены в одном столбце или одной строке распределительной таблицы, причем последняя клетка находится в том же столбце или в той же строке, что и первая.
Графически циклу соответствует замкнутая ломаная линия. Допустимое решение транспортной задачи является опорным в том случае, если из занятых этим решение клеток нельзя образовать ни одного цикла. Если в распределительной таблице содержится опорное решение, то для каждой свободной клетки можно образовать только 1 цикл.
30. Переход к новому опорному решению ТЗ
В ТЗ переход от одного опорного решения к другому осуществляется с помощью цикла. Для некоторой свободной клетки таблицы строится цикл, содержащий часть клеток, занятых опорным решением. По этому циклу перераспределяются объемы перевозок. Для определения количества единиц груза, подлежащих распределению, отмечаем знаком + клетку, которую надо загрузить. Это означает, что клетка присоединяется к занятым клеткам. В таблице занятых клеток стало p+q, поэтому появляется цикл, все вершины которого, за исключением клетки, отмеченной знаком +, находятся в занятых клетках, причем этот цикл единственный. Отыскиваем цикл и, начиная движения от клетки, отмеченной знаком +, поочередно проставляем знаки + и -. Затем находим ג=minxij, где xij – перевозки, стоящие в вершинах цикла, отмеченных знаком -. Величина ג определяет, сколько единиц груза можно перераспределить по найденному циклу. Значение ג записываем в незанятую клетку, отмеченную знаком +, двигаясь по циклу, вычитаем ג из объемов перевозок, находящихся в клетках, отмеченных знаком +. Если ג соответствуют несколько минимальных перевозок, то при вычитании оставляем в соответствующих клетках нулевые перевозки в таком количестве, чтобы во вновь полученном опорном плане занятых клеток было p+q-1.
Проверяем полученный план на оптимальность. Ищем потенциалы последней матрицы. Так как отрицательных оценок нет, построенный план является оптимальным. Если полученный план окажется неоптимальным, то следует выполнить перечисленные вычисления еще раз. Процесс выполняют до тех пор, пока все незанятые клетки не будут удовлетворять условию оптимальности.
Циклы
Циклом называется набор клеток, вида: (L1;K1);( L1;K2);( L2;K2)…( Ls;K1) или (L1;K1);( L2;K1);( L2;K2)…( L1;Kl), в которых две и только две соседние клетки расположены в распределительной таблице, причем последняя клетка находится в том же столбце или той же строке, что и первая. Графически циклу соответствует замкнутая ломанная линия с прямыми углами. Допустимые решения ТЗ являются опорными, лишь в том случае, если из занятых этим решением клеток нельзя образовать ни одного цикла. Если в распределительной таблице содержится опорное решение, то для каждой свободной клетки можно образовать один цикл, содержащий данную свободную и некоторую часть занятых клеток.
Все вершины цикла кроме одной находятся в занятых клетках; углы прямые, число вершин четное. никакие 3 соседние клетки не могут быть в одной строке или в одном столбце. Около свободной клетки цикла ставится знак (+), затем поочередно проставляются знаки(-)и (+). У вершин со знаком (-) выбирают минимальный груз, его прибавляют к грузам, стоящих у вершин со знаком (+), и отнимают от грузов у вершин со знаком (-).В результате перераспределения груза получается новое опорное решение
32. Метод потенциалов.
1. Строят исходное опорное решение (план).
2. Выписывают матрицу затрат С и находят потенциалы Ui и Vk по формуле Cik+Ui+Vk=0 для все занятых клеток. Один из потенциалов полагают равным произвольнному числу (обычно полагают Ui=0 потенциал в троке или в столбце с наибольшим количеством занятых клеток).
3. Переходят к оценочной матрице С’, элементы которой находят по формуле C’={Cik}, Cik’=Cik+Ui+Vk.
4. Если все оценки Δst≥0 для свободных клеток, то полученное решение оптимально и найдено.
5. Если хотя бы одна оценка Δst<=0, то для клетки с максимальной по абсолютной величине отрицательной оценкой строят цикл и переходят к новому опорному решению. Процесс продолжается до тех пор, пока не будет получено решение, для которого все оценки свободных клеток будут ≥0.
33. Теорема об эквивалентных преобразованиях матрицы затрат.
Добавление ко всем элементам любой строки или столбца матрицы затрат одного и того же числа, не меняет оценок свободных клеток.
Эти числа Ui, где i=1,p Vk, где k=1,q добавляют ко всем элементам соответствующей строки или столбца. Выбирают их или находят из условия (1) Ci k + Ui+ Vk=0 для всех занятых клеток. Т.к в этой системе p+q неизвестных, а занятых клеток p+q-1, то для определения чисел Ui; Vk одной из переменных можно придать произвольное значение, тогда остальные неизвестные определяться однозначно, тогда от матрицы затрат легко перейти к матрице, элементы которой находятся по формуле: ∆ st=Cst'= Cst+ Us+Vt Для того, чтобы некоторое опорное решение X={Xik} i=1,p k=1,q было оптимальным, необходимым и достаточно, чтобы существовала система p +q чисел Ui и Vk , которые удовлетворяли бы условиям (1) Ci k + Ui+ Vk=0 где i=1,p k=1,q для всех занятых клеток и (2) Ci k + Ui+ Vk ≥0 где i=1,p k=1,q для всех свободных клеток. Эти два условия и есть критерии оптимальности опорного решения ТЗ. Эти условия (1) и(2) называются условиями потенциальности, сами числа Ui и Vk называются потенциалами, а сам метод называется методом потенциалов.
Приращение целевой функции ТЗ
Рассмотрим какое изменение целевой функции Z вызывает перемещение по циклу, начинающее со свободной клетки(S;T) числа λ.
∆Z=∑λCik-∑λCik=λ( ∑Cik-∑Cik )
Неч четн неч четн
Величина в скобках не зависит от λ, а только от структуры цикла и величины Сik т к с любой свободной клеткой связан только один цикл. Эта величина однозначно определяется для выбранной свободной клетки. Т.е. называют оценкой свободной клетки и обозначается: ∆st=∑Cik-∑Cik => ∆Z=λ∆st т.к λ>0, то для уменьшения Z необходимо чтобы ∆st была меньше 0 (∆st<0)
35. Оценка свободной клетки.
Потенциал Ui u Vj находят из равенства Ui+Vj=Cij, справедливого для занятых клеток. Одному из потенциалов дается произвольное значение, например U1=0, тогда остальные потенциалы определяются однозначно. Так, если известен потенциал Ui, то Vj = Cij -Ui ; если известен потенциал Vj, то Ui = Cij –Vj. Обозначим ∆ij= Ui+Vj-Cij. Эту оценку называют оценкой свободных клеток. Если ∆≤0, то опорное решение является оптимальным. Если хотя бы одна из оценок ∆>0, то опорное решение не является оптимальным и его можно улучшить, перейдя от одного опорного решения к другому.
Обоснование перехода к новому опорному решению.
Переход к новому опорному решению. Пусть выбрана свободная клетка(S;T) это значит, что Хst вводится в базис и для клетки (S;T) строится цикл. Клетки цикла мысленно нумеруют начиная с клетки (S;T). Заносится в свободную клетку неизвестное число λ. (λ>0). При этом значение переменных в нечетных клетках увеличиваются на величину λ, в четных-уменьшаются, такие преобразования называются перемещение по циклу числа λ. Выберем λ =min{Xik} стоящих в четных клетках цикла. Если при перемещении λ освободится сразу несколько клеток, оставляем свободную только одну, которой соответствует наибольшее значение Сik , а остальные клетки заполняем нулями. Рассмотрим какое изменение целевой функции Z вызывается перемещением по циклу начинающимся в свободной клетки (S;T) числа λ
∆Z=∑λCik-∑λCik=λ( ∑Cik-∑Cik )
Неч четн неч четн
Величина в скобках не зависит от λ, а только от структуры цикла и величины Сik т к с любой свободной клеткой связан только один цикл. Эта величина однозначно определяется для выбранной свободной клетки. Т.е. называют оценкой свободной клетки и обозначается: ∆st=∑Cik-∑Cik => ∆Z=λ∆st т.к λ>0, то для уменьшения Z необходимо чтобы ∆st была меньше 0 (∆st<0).
36. Критерий оптимальности. Переход к оценочной матрице.
От матрицы затрат переходят к оценочной матрице C’, элементы которой- дельта st= C’st находят по формуле - st= C’st= Cst+Us+Vt.
Для того, чтобы некоторые опорные решения X= {Xik}, i=1,p, k=1,q транспортной задачи было оптимальным, необходимо и достаточно чтобы существовала система p+q чисел Ui и Vk, которые удовлетворяли бы критериям оптимальности:
Cik+Ui+Vk=0 - для всех занятых клеток.
Cik+Ui+Vk>0 - для всех свободных клеток.
37.Открытая модель транспортной задачи.
Транспортная задача, в которой суммарные запасы и потребности совпадают, т.е. выполняется
условие i=1m ai=j=1n bj
Называется закрытой моделью;
в противном случае- открытой.
Для открытой модели может быть два случая:
а) суммарные запасы превышают суммарные потребности i=1m ai > j=1n bi ;
b) суммарные потребности превышают суммарные запасы;
Линейная функция одинакова в обоих случаях, изменяется только вид системы ограничений.
Найти минимальное значение линейной функции z = i=1m j=1n Cij Xij при ограничениях j=1n xij < ai, i=1,2,…,m,
i=1m xij=bj, j= 1,2,…,n; (случай а)
j=1n xij= ai, i= 1,2,…, m,
i=1m xij< bj, j= 1,2,…, n, (случай б)
Открытая модель решается привидением к закрытой модели .В случае (а), когда суммарные запасы превышают суммарные потребности, вводится фиктивный потребитель Вn+1, потребности которого bn+1 = i=1m ai – j=1n bi. В случае (b), когда суммарные потребности превышают суммарные запасы, вводится фиктивный поставщик Аm+1, запасы которого
am+1 = j=1n bj – i=1mai. Стоимость перевозки единицы груза как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика полагают равными нулю, т.к. груз в обоих случаях не перевозится.
После преобразований задача принимает вид закрытой модели и решается обычным способом. При равных стоимостях перевозки единицы груза от поставщиков к фиктивному потребителю, затраты на перевозку груза реальным потребителям минимальны, а фиктивному потребителю будет направлен груз от наименее выгодны поставщиков. То же самое получаем и в отношении фиктивного поставщика.
38. Распределительный метод
1. Строим исходное опорное решение, при этом должны оказаться занятыми p+q-1 клеток.
2. Производим оценку свободных клеток, начиная с клетки с наименьшими затратами путем построения цикла и вычитания по этому циклу величины Δst. Если Δst<0, то переходят к следующему пункту алгоритма.
3. Перемещают по циклу число А=min{xik}, возвращаются к п.2.
4. Если Δst≥0, то оценивают следующую свободную клетку и т.д.
Если оценки всех свободных клеток окажутся неотрицательными, то оптимальное решение найдено.
При решении ТЗ распределительным методом метод подсчета оценок свободных клеток оказывается довольно трудоемким. Этого недостатка лишен метод потенциалов.
39. Постановка задачи ЦП.
Значительная часть экономических задач, относящихся к задачам ЛП требует целочисленного решения. Это задачи, где переменные величины обозначают количество единиц неделимой продукции. Задача целочисленного программирования формулируется так же, как и задача ЛП, но включает дополнительное требование- значения переменных в оптимальном решении должны быть целыми неотрицательными числами.
Найти min или max значение линейной функции z= j=1n Cjxj при ограничениях j=1n aijxj= bi, i=1,2,…,m,
xj-целые. xj>0, j=1,2,…,n.
40.Метод Гомори.
Метод решения задачи, предложенный Гомори, основан на симплексном методе и состоит в следующем. Симплексным методом находится оптимальный план задачи без учета условия целочисленности. Если оптимальный план целочисленный, то вычисления заканчивают; если же оптимальный план содержит хотя бы одну дробную компоненту Xi, накладывают дополнительное ограничение, учитывающее целочисленность компонент плана, и вычисления симплексным методом продолжают до получения нового оптимального плана . Если и он является нецелочисленным, то составляют следующее ограничение, учитывающее целочисленность. Процесс присоединения дополнительных ограничений повторяют до тех пор, пока либо будет найден целочисленный оптимальный план, либо доказано, что задача не имеет целочисленных планов. Это наблюдается в случае, если для дробного Xi все Xij в этой строке окажутся целыми.
Недостатком метода Гомори является требование целочисленности для всех переменных: как основных, выражающих единицы продукции, так и для дополнительных, выражающих величину неиспользованных ресурсов, которые могут быть и дробными.
41. Понятие об игровых моделях
Если имеется несколько конфликтующих сторон, каждая из которых принимает некоторое решение, определяемое заданным набором правил, и каждой из этих сторон известно возможно конечное состояние конфликтной ситуации с заранее определенными для каждой из сторон платежами, то говорят, что имеет место игра. Ситуация называется конфликтной, если в ней участвуют стороны, интересы которых частично или полностью противоположны. Игра – это конфликт, в котором имеется по крайней мере два участника или игрока, каждый из которых стремится к достижению своих целей.
Задача теории игр состоит в выборе такой линии поведения игрока, отклонения от которой могут лишь уменьшить его выигрыш. При этом предполагается, что все игроки ведут себя рационально.
Допустимые действия каждого из игроков, направленные на достижение некоторых целей, называются правилами игры. Количественная оценка результатов игры называется платежом. Ход – это выбор игроком одного из действий, предусмотренных правилами игры. Ходы бывают личными и случайными. Однозначные описания выбора игрока в каждой из возможных ситуаций, при которой он должен сделать личный ход, называется стратегий игрока. Стратегия игрока называется оптимальной, если при многократном повторении игры она обеспечивает игроку максимальный возможный средний выигрыш.
Классификация игр.
1. Возможность образований коалиций.
Если правила игры разрешают объединение группы участников для получения ими лучших результатов по сравнению с теми, которых они бы добились, действуя самостоятельно, то такая игра называется кооперативной. В противной случае игра называется бескоалиционной или некооперативной.
2. По количеству стратегий.
Если у каждого игрока имеется в распоряжении конечное чило стратегий, то игра называется конченой, в противном случае - бесконечной.
3. По числу игроков.
В зависимости от числа участников они делятся на игры с двумя, тремя и более игроками. Игра с двумя игроками называется парной.
4. По свойствам выигрыша.
Игра называется игрой с нулевой суммой, если в любой партии сумма выигрышей всех игроков равна нулю, т.е. каждый игрок может выиграть лишь за счет проигрыша других игроков. Если это условие не выполнено, то такая игра называется игрой с ненулевой суммой. В парной игре с нулевой суммой выигрыш одного игрока всегда равен проигрышу другого. Такая игра называется антагонистической.
5. По количеству имеющейся априорной информации.
Различают игры с полной информацией о состоянии игры, о стратегиях действий сторон и о платежной матрице; игры с неполной (вероятностной) информацией о функциях выигрыша, о стратегиях сторон, об осведомленности сторон (каналах наблюдения); игры в условиях полной неопределенности.
42. Приведение экономических задач к теоретико-игровой форме.
Пусть имеется два игрока, один из которых может выбрать i-стратегию из m возможных (i=1,m), а второй, не зная выбор первого – j стратегию из n возможных (j=1,n). В результате игрок 1 выигрывает величину aij, а второй игрок проигрывает эту же величину. Ясно, что игрок 1 стремится максимизировать эту величину, а игрок 2 – минимизировать.
Составим матрицу А.
-
(
a11 a12 … a1n
)
A=(aij)=
a21 a22 … a2n
…
am1 am2 … amn
Строки этой матрицы соответствуют стратегиям 1 игрока. Столбцы соответствуют стратегиям второго игрока. Эти стратегии называются чистыми, а матрица А платежной матрицей или матрицей игры. Игру, определяемую матрицей А, имеющей m строк и n столбцов, называют конечной игрой размерности m x n. Если такая матрица составлена, то говорят, что игра приведена к матричной форме. К этой форме можно привести любую конечную парную игру. Поэтому такие игры называют матричными.
43. Парная конечная игра. Платежная матрица. Maxmin/minmax стратегии.
Пусть имеется два игрока, один из которых может выбрать i-стратегию из m возможных (i=1,m), а второй, не зная выбор первого – j стратегию из n возможных (j=1,n). В результате 1 игрок выигрывает величину aij, а второй игрок проигрывает эту же величину.
Составим матрицу А.
-
(
a11 a12 … a1n
)
A=(aij)=
a21 a22 … a2n
…
am1 am2 … amn
Строки этой матрицы соответствуют стратегиям 1 игрока. Столбцы соответствуют стратегиям второго игрока. Эти стратегии называются чистыми, а матрица А платежной матрицей или матрицей игры. Игру, определяемую матрицей А, имеющей m строк и n столбцов, называют конечной игрой размерности m x n.
| α=max(min aij) |
| i j |
| β=min(max aij) | |
| j i | |
Теорема 1. Нижняя цена игры всегда не превосходит верхней цены игры, т.е α≤β
Доказательство: Для любых индексов i и j справедливы соотношения:
| αi=min aij ≤ aij ≤ max aij = βj |
| j=1,n i=1.m |
| α=max aij≤βj |
| i=1.m |
Значит, для всех j выполнено неравенство.
| α≤max βj≤β |
| j=1,n |
т.е. α≤β, что и требовалось доказать.
44. Цена игры. Седловые точки.
Если α=β=V, то V называется ценой игры. Игра, в которой α= β, называется игрой с седловой точкой. Для игры с седловой точкой нахождение решения состоит в выборе максиминной и минимаксной стратегий, которые являются оптимальными. Каждому из игроков невыгодно отклоняться от своей оптимальной стратегии, так как это может привести лишь к ухудшению его положения. Пара оптимальных стратегий игроков образуют решение игры, которое называется равновесием.
Если игра, заданная матрицей, не имеет седловой точки, то для нахождения ее решения используются смешанные стратегии. Вектор, каждая из компонент которого показывает относительную частоту использования игроком соответствующей чистой стратегии, называется смешанной стратегией данного игрока => сумма компонент данного вектор =1, а сами эти коэффициенты не отрицательны. Обычно смешанную стратегию I игрока обозначают через U=(U1, …, Un). Ui≥0, i=1,m.
i=1Σm Ui=1
Стратегии 2 игрока:
Z=(Z1, …, Zn).
Zj≥0, j=1,n.
j=1Σn Zj=1
Всякая матричная игра с нулевой суммой имеет решение в смешанных стратегиях. Если U* - оптимальная стратегия I игрока, а Z* - оптимальная стратегия 2 игрока, то число V= j=1Σn i=1Σm aij Ui* Zj* является ценой игры, а совокупность {U*, Z*, V*} –решением игры. Для того, чтобы число V было ценой игры, а U* и Z* - оптимальными стратегиями, необходимо и достаточно, чтобы выполнялись следующие неравенства:
| i=1Σm aij Ui* ≥ V j=1,n | j=1Σn aij Zj*≤V i=1,m |
Если один из игроков применяет оптимальную смешанную стратегию, то его выигрыш равен цене игры V вне зависимости от того, с какими частотами будет применять 2 игрок стратегии, вошедшие в оптимальные ( в т.ч и чистые стратегии).
45. Графическо представление игры при n=2
Предположим, что игрок 1 имеет m чистых стратегий, а игрок 2 - две чистых стратегии.
Тогда платежная матрица игры выглядит так:
| | ( | a11 | a12 | ) |
| A= | a21 | a22 | ||
| | … | … | ||
| | am1 | am2 |
Множество смешанных стратегий игроков имеет следующий вид:
- для игрока 1 – U={u=(u1,….,um), u1 + … + um=1; xi>=0, i=1,m};
- для игрока 2 – Z={z=(1-t, t), 0=
Обозначим R1(t), i=1,m – проигрыш игрока 2 в ситуации, когда он выбрал смешанную стратегию y=(1-t, t), а игрок 1 – свою чистую стратегию. Тогда ясно, что R1(t)=ai1(1-t)+ai2t.
Обозначим R(t)=max Ri(t), 1=
Тогда согласно Теореме 1 все стратегии игрока 1, для которых R1(t*)=v*, могут быть отброшены. Как правило, активными будут лишь две стратегии этого игрока, что также позволяет свести решение игры m x 2 к случаю 2 х 2.
Теорема 1. Если выигрыш игрока 1 в ситуации, образованной его чистой стратегией и оптимальной стратегией другого игрока, меньше цены игры, то такая чистая стратегия не может быть активной, и в любой оптимальной чистой стратегии вероятность ее использования равна нулю.
Проиллюстрируем использование графического метода в этом случае на примере.
Нужно найти решение игры, задаваемое матрицей.
| | ( | -2 | 3 | ) |
| A= | 2 | -1 | ||
| | -1 | 1 |
Проверим, есть ли у этой игры решение в чистых стратегиях. Для этого найдем max(i)min(j) aij = max {-2, -1, 1}=-1 и min(j)max(i) aij = min {2, 3}=2. Так как они не равны друг другу, то решения в чистых стратегиях нет.
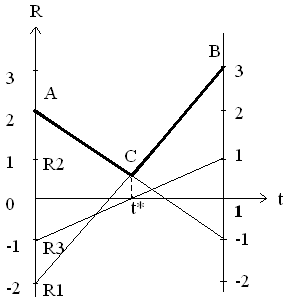
На оси Ot плоскости tOR отложим единичный отрезок [0, 1]. Каждой его точке t соответствует смешанная стратегия y=(1-t, t) игрока 2. Затем через точки 0 и 1 проведем линии, перпендикулярные оси Ot. На первом перпендикуляре, совпадающим с осью OR, отложим значения элементов первого столбца матрицы А – проигрыши игрока 2 при выборе им чистой стратегии В1. На втором перпендикуляре отложим значения элементов второго столбца – проигрыши игрока 2 при выборе им чистой стратегии В2. Затем соединим отрезками прямых точки на перпендикулярах, соответствующие чистым стратегиям игрока 1 – строкам матрицы А. Эти отрезки прямых являются графиками функций R1(t), задаваемых следующими уравнениями:
R1|(t) = -2(1-t) + 3t = -2+5t
R2|(t) = 2(1-t) - t = 2-3t
R3|(t) = -(1-t) + t = -1+2t
Затем построим из верхнюю огибающую – график функции R(t). На рисунке (1) она представлена ломаной АВС. Ее точка В, имеющая минимальную ординату, является графическим решением игры.
Из рисунка (1) видно, что точка В лежит на пересечении отрезков прямых R1 и R2. Значит, активными стратегиями игрока 1 являются стратегии А1 и А2. Стратегия А3 в его оптимальной стратегии не используется, т.е. х3*=0. Поэтому третью строку матрицы А можно вычеркнуть и рассмотреть игру с платежной матрицей
-
(
-2
3
)
x1
А’=
2
-1
x2
y1
y2
Д
ля определения цены этой игры и оптимальной смешанной стратегии игрока 1 следует решить систему уравнений:-2х1+2х2=v
3x1-x2=v
x1+x2=1.
x1*=3/8, x2*=5/8, v*=1/2.
Д
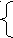ля нахождения коэффициентов активных стратегий игрока 2 нужно решить систему уравнений:-2y1+3y2=1/2
y1+y2=1
Ее решение y1*=1/2, y2*=1/2. Итак, исходная игра имеет решение: х*=(3/8; 5/8; 0), y*=(1/2; ½), v*=1/2.
Графический метод для игры 2 x n.
ГМ применяется к играм, в которых хотя бы один игрок имеет 2 стратегии. Рассмотрим игру 2 x n. Пусть игра не имеет седловой точки. Обозначим: х1 –вероятность применения первым игроком 1 стратегии, х2 – 2 стратегии. х2=1-х1; у1 – вероятность применения 2 игроком первой стратегии, yn – n-ой стратегии. Ожидаемый выигрыш первого игрока при применении вторым игроком 1 стратегии составляет: a11x1 + a21x2 = a11x1 + a21(1-x2) = a11x1 + a21 – a21x1 = (a11-a21)x1+a21. Ожидаемый выигрыш перового при применении вторым n стратегии (a1n-a2n)x1+a2n. Ожидаемый выигрыш первого зависит от х1. На оси Х1 строим выражения ожидаемых выигрышей первого. Оптимальная стратегия первого – точка пересечения прямых, максимизирующих его min ожидаемый выигрыш Оптимальная стратегия второго – точка пересечения прямых, минимизирующих его max ожидаемый проигрыш.