Лекция 4 Изображение кривых 3
| Вид материала | Лекция |
- С. В. Шадрина Лекция 5 сентября, 15: 00-16: 30, Введение в геометрию пространства модулей, 5.97kb.
- 12. ломаные и кривые линии (плоские и пространственные). Винтовая линия, 91.72kb.
- Лекция Растровое и векторное изображение. Понятие конвейеров ввода и вывода графической, 251.93kb.
- Тема 14. Модель is-lm и варианты экономической политики государства, 312.73kb.
- Нейросетевая аппроксимация векторных объектов кривыми безье, 82.29kb.
- Лекция №9 26. пересечение плоскости и поверхности, определение натуры сечения, 151.71kb.
- Рыночное равновесие, 130.99kb.
- Научная программа молодежной школы-конференции «Современные проблемы алгебры и математической, 48.63kb.
- | Основные правила построения кривых Adobe Illustrator Алгебра, 106.46kb.
- | Основные правила построения кривых Adobe Illustrator Алгебра, 127.02kb.
Лекция 4
Изображение кривых 3
| Данная лекция может содержать ошибки (как логические, так и грамматические). Авторы будут признательны за любые сообщения об ошибках, неточностях, а также за любые комментарии и дополнения, присланные по адресу Denis@fit.com.ru (Денису Иванову). |
I. Аппроксимация и интерполяция.
В этой лекции будут рассматриваться вопросы построения кривых по контрольным точкам. Нас будут интересовать две задачи:
Интерполяция - построение кривой, проходящей через контрольные точки.
Аппроксимация - приближение кривой (не обязательно проходит точно через данные точки, но удовлетворяет некоторому заданному свойству относительно этих точек).
II. Интерполяция.
Постановка задачи:
 Рис. 1. Постановка задачи. | Дано: 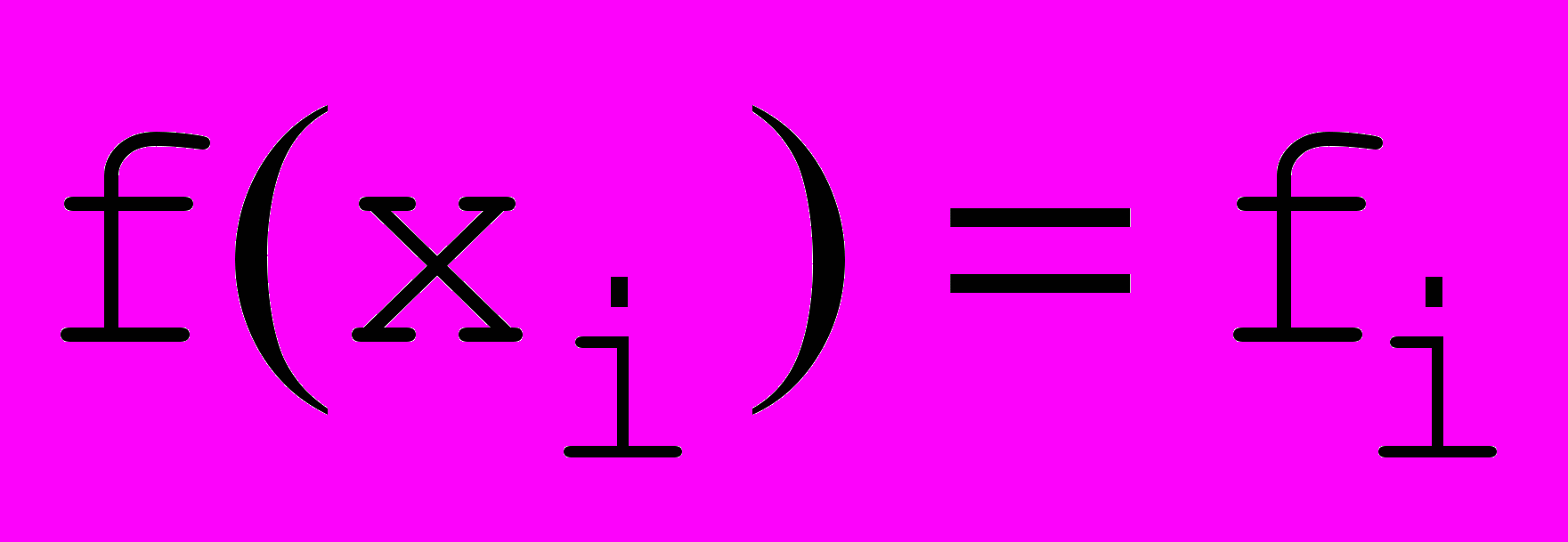 . . 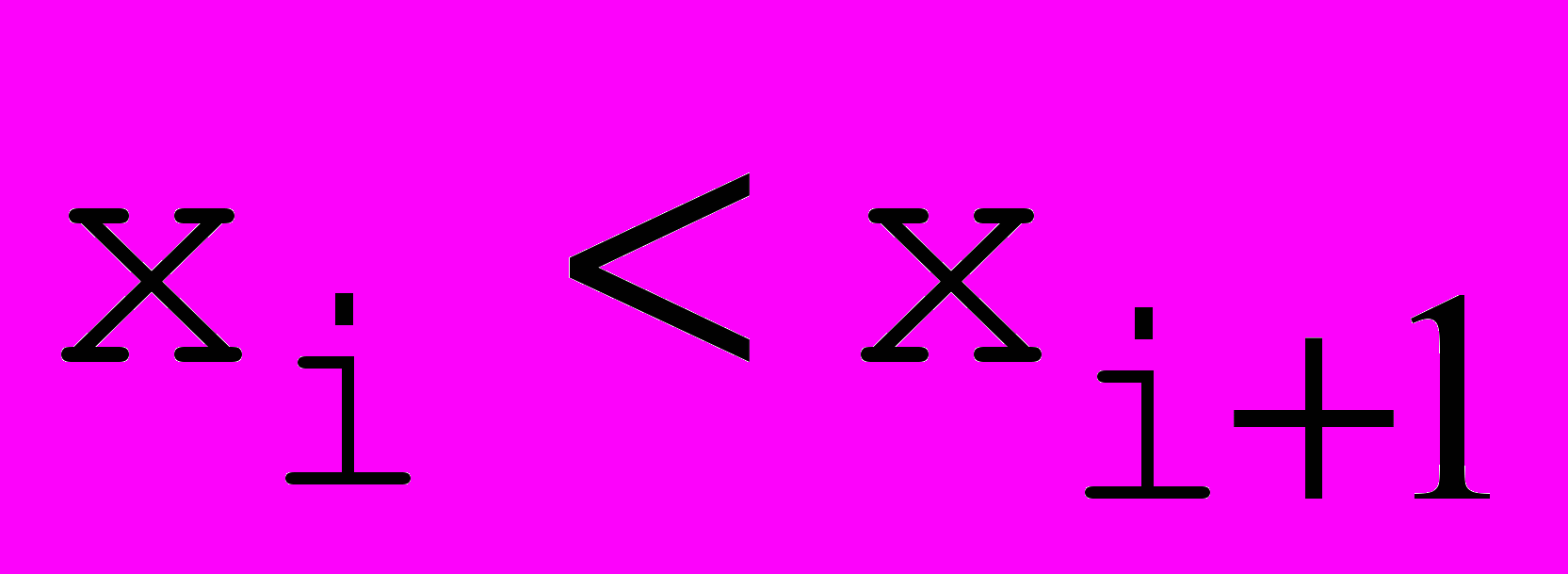 i i 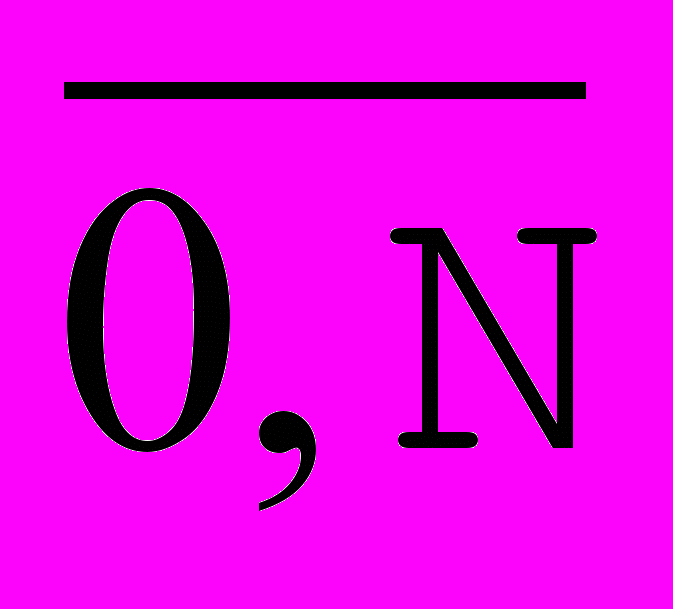 . Построить функцию f(x), удовлетворяющую этому условию. . Построить функцию f(x), удовлетворяющую этому условию. |
- Интерполяционный многочлен Лагранжа
 ;
;  ;
; 
Получаем непрерывную функцию, проходящую через все точки.
Минусы:
- Требует значительного объема вычислений для нахождения значения функции в произвольной точке.
- Неопределенное поведение построенной функции между узлами, в частности можно привести следующие результаты:
1916 Бернштейн :
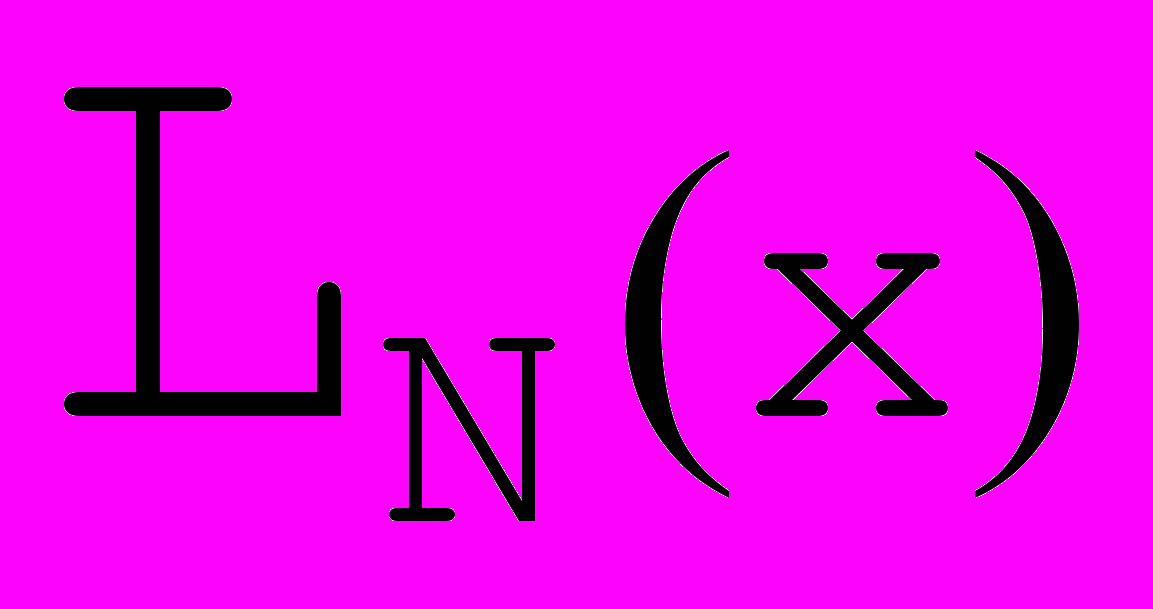

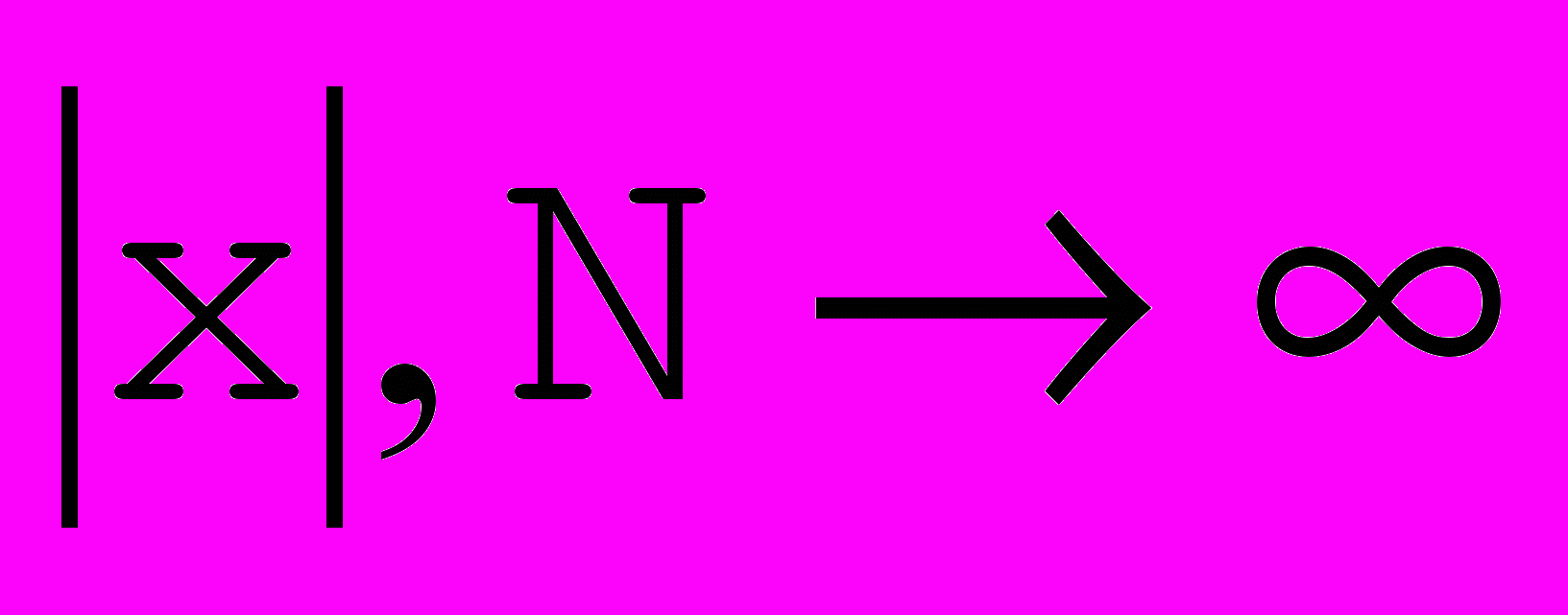
1925 Рунге :
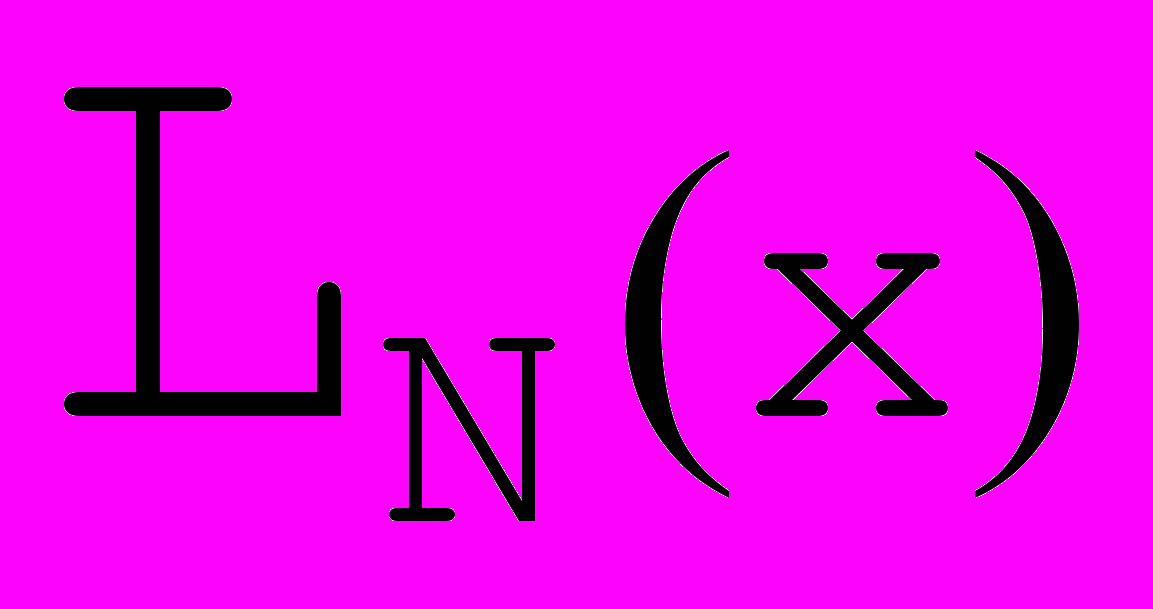


Далее будем рассматривать интерполирующие функции, которые задаются отдельно на каждом отрезке
 , что позволяет лучше учитывать локальное поведение требуемой функции и избежать громоздких вычислений (так как на каждом из отрезков интерполирующая функция имеет по возможности простой вид).
, что позволяет лучше учитывать локальное поведение требуемой функции и избежать громоздких вычислений (так как на каждом из отрезков интерполирующая функция имеет по возможности простой вид).2) Кусочно-линейная интерполяция
 Рис. 2. Кусочно-линейная интерполяция. |  Интерполяция следующей кусочно-линейной функцией: Интерполяция следующей кусочно-линейной функцией: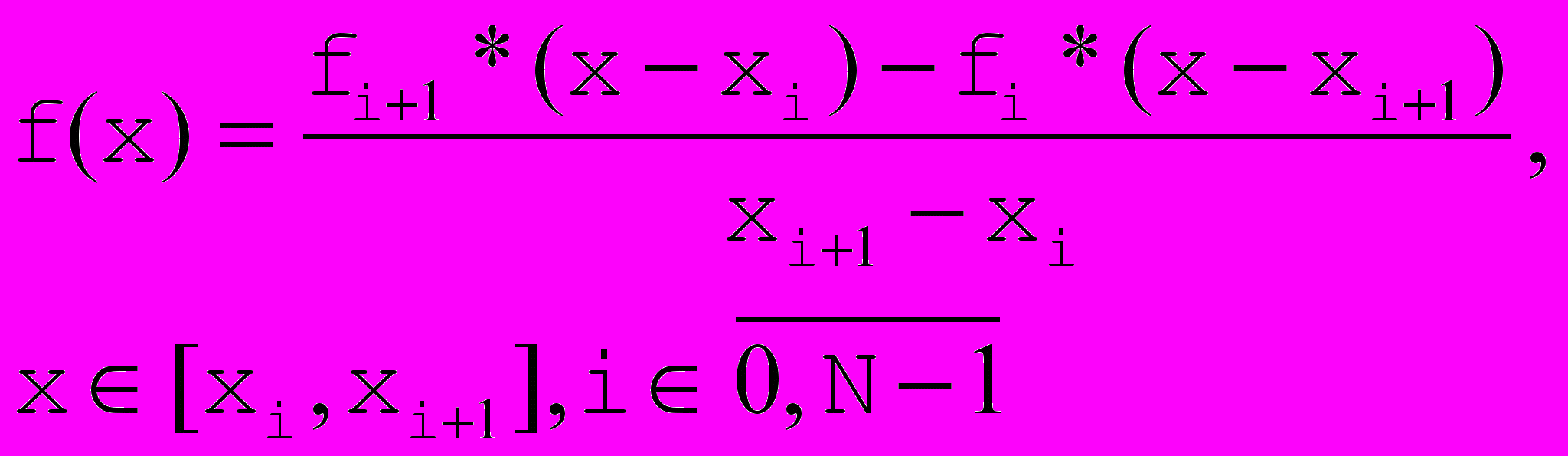 Класс  |
3) Кубическая интерполяция Эрмита
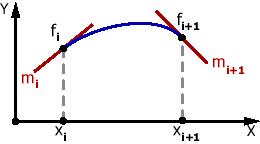 Рис. 3. Кубическая интерполяция Эрмита. |  Пусть заданы следующие условия: Пусть заданы следующие условия: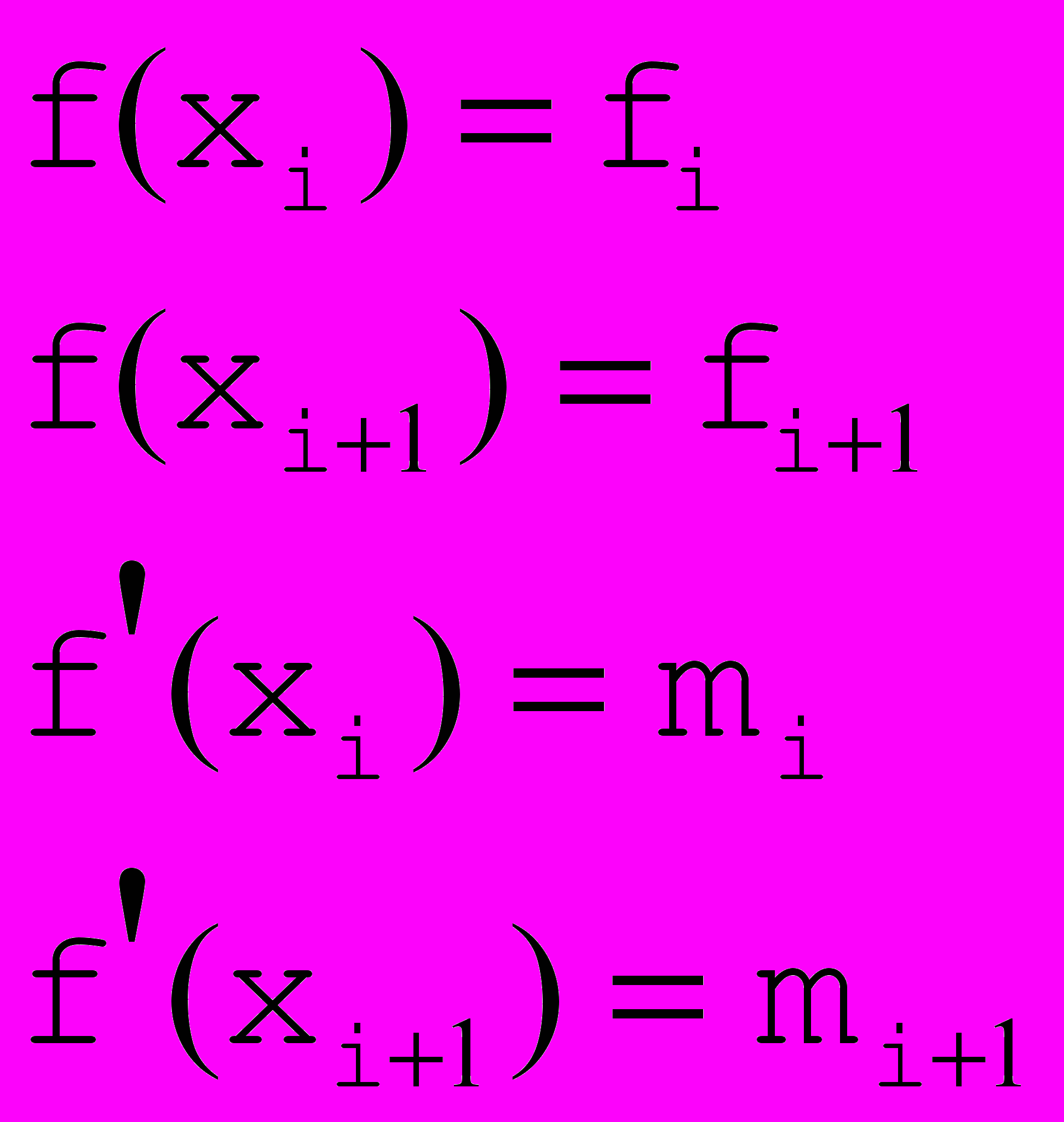 , ,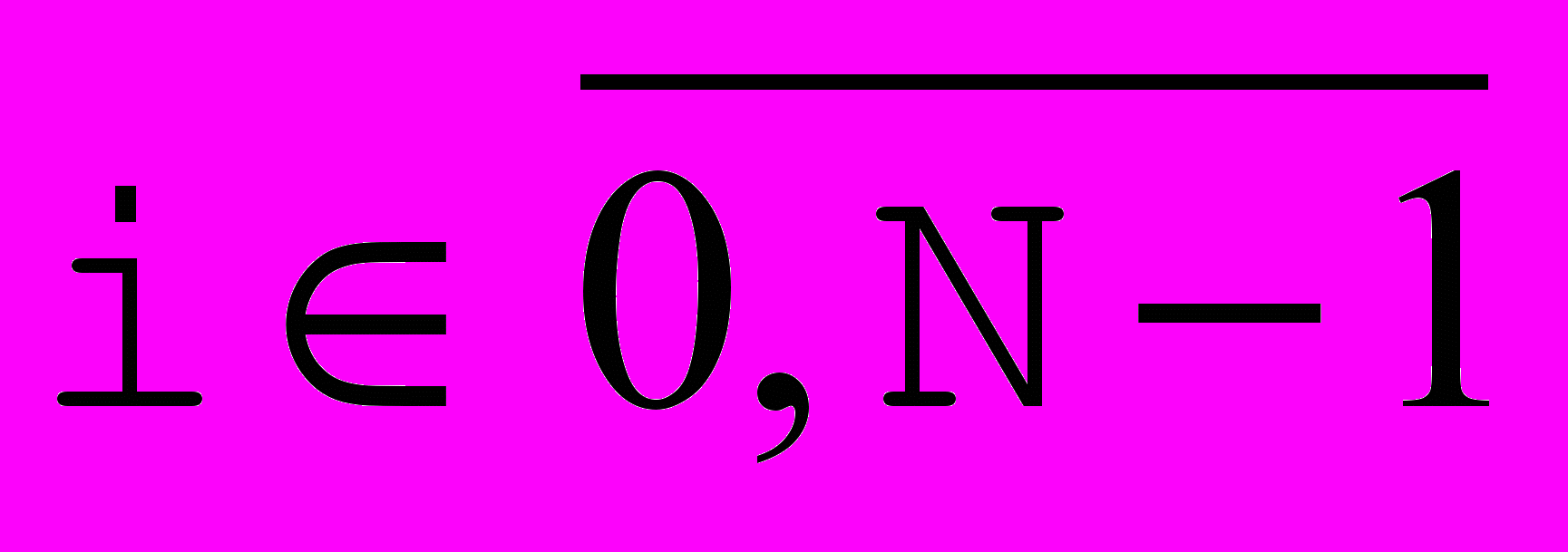 тогда для каждого i будем искать искомую функцию в виде 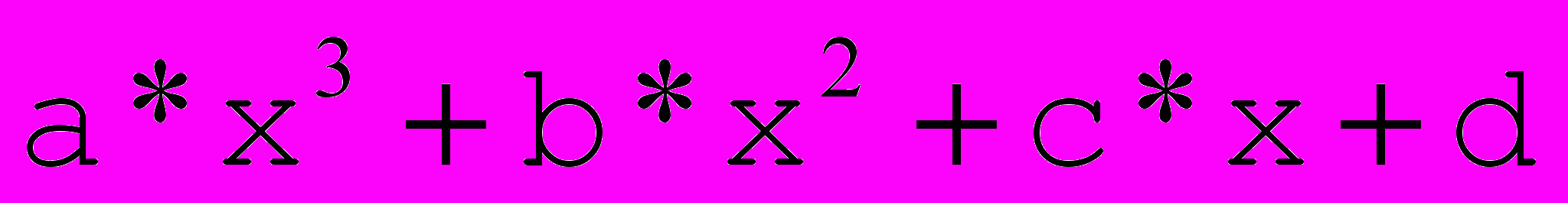 . Подставив эту функцию в уравнения условий получим линейную невырожденную систему из 4 уравнений с 4 неизвестными (a,b,c и d), т.е. решение существует и единственно. . Подставив эту функцию в уравнения условий получим линейную невырожденную систему из 4 уравнений с 4 неизвестными (a,b,c и d), т.е. решение существует и единственно.Класс  |
Проблемы:
- Непонятно откуда брать значения производных.
- Хотелось бы
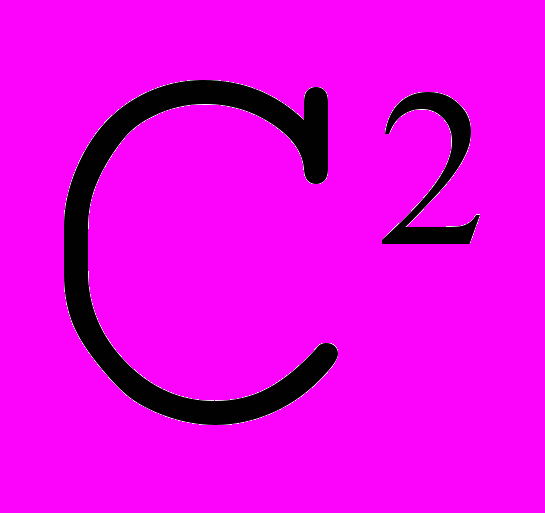 , а не только
, а не только 
4) Сплайны
Сплайн - кусочный полином степени K с непрерывной производной степени K-1 в точках соединения сегментов.
Далее нас будут интересовать кубические сплайны.
Понятие сплайна пришло из машиностроения, где сплайном называли гибкую линейку, закрепив которую в нужных местах, добивались плавной кривой, которую затем чертили по этой линейке (см. Рис. 4) Форма такой линейки, если ее рассматривать как функцию y(x), будет удовлетворять уравнению Эйлера-Бернулли:
 ,где M(x) - момент изгиба вдоль рейки, E - модуль Юнга. зависящий от свойств материала рейки, I - момент инерции, определяемый формой кривой. Если мы фиксируем некоторые точки подпорками, то момент изгиба на каждом отрезке
,где M(x) - момент изгиба вдоль рейки, E - модуль Юнга. зависящий от свойств материала рейки, I - момент инерции, определяемый формой кривой. Если мы фиксируем некоторые точки подпорками, то момент изгиба на каждом отрезке  меняется по линейному закону: M(x) = A*x + B , подставляя в исходное уравнение получаем:
меняется по линейному закону: M(x) = A*x + B , подставляя в исходное уравнение получаем:  , дважды интегрируя получаем уравнение кривой на данном
, дважды интегрируя получаем уравнение кривой на данном 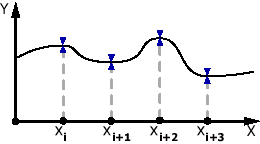 Рис. 4. Сплайн. | отрезке:  ; таким образом форма физического сплайна описывается кусочным кубическим полиномом. ; таким образом форма физического сплайна описывается кусочным кубическим полиномом.Теперь рассмотрим задачу построения системы таких кубических полиномов для всего отрезка  |
- Для N отрезков имеем 4N коэффициентов:
 для
для 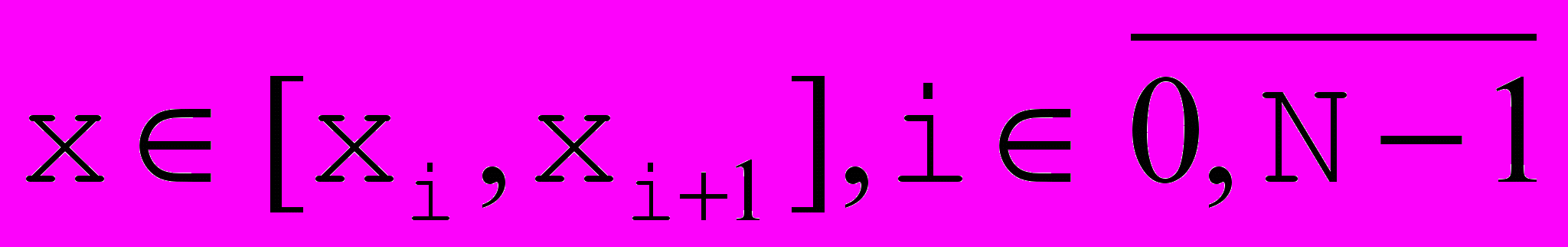 ;
;
- Условия
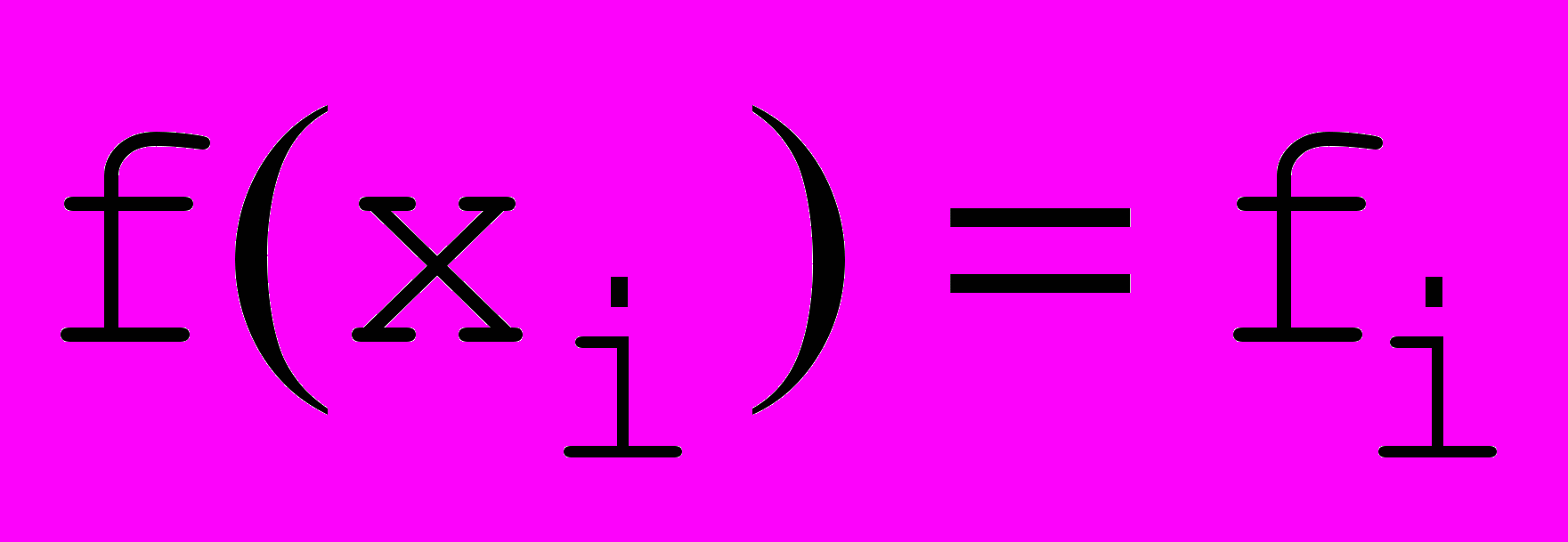 ( i
( i 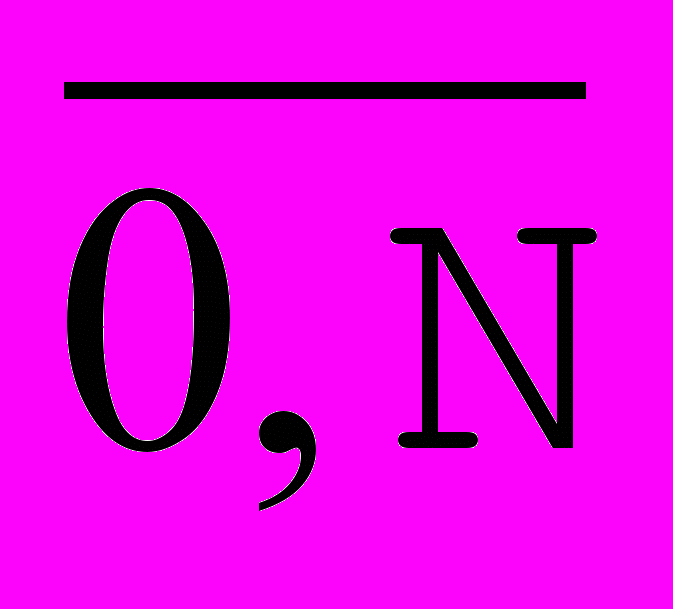 ) дают 2N уравнений;
) дают 2N уравнений;
- Требование
 в точках
в точках  ( i
( i 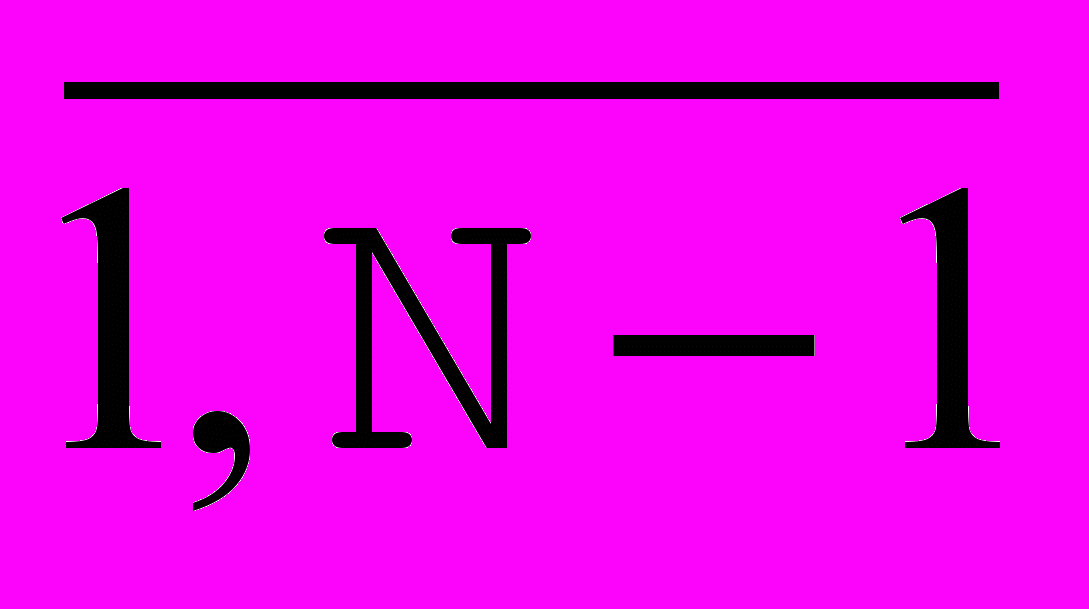 ) дает N-1 уравнений;
) дает N-1 уравнений;
- Требование
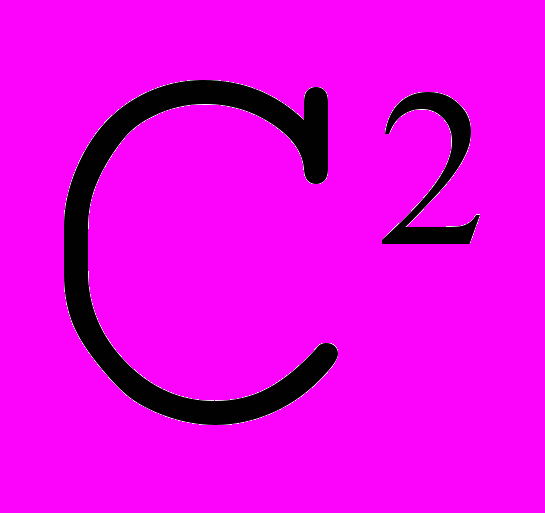 в точках
в точках  ( i
( i 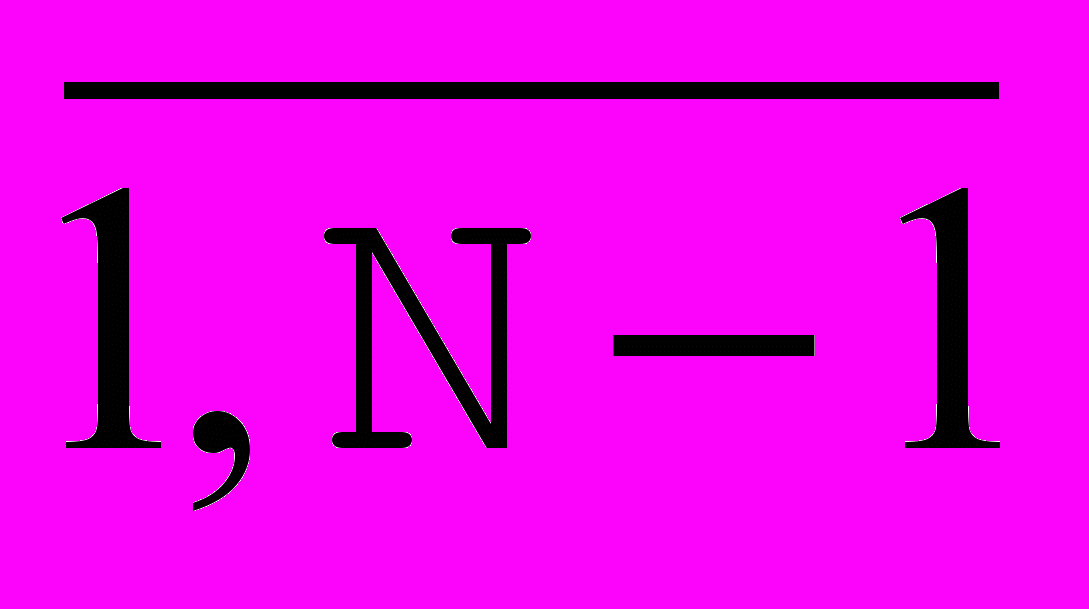 ) дает N-1 уравнений.
) дает N-1 уравнений.
Итого имеем 4N-2 уравнения; для того чтобы система была определенной, необходимы еще 2 уравнения; их можно вывести, например, из заданных значений производных на границах или или из условия периодичности. При корректно заданных условиях линейная относительно
 система имеет единственное решение. Подробнее смотри в [Роджерс, Адамс, 2001].
система имеет единственное решение. Подробнее смотри в [Роджерс, Адамс, 2001].III. Аппроксимация.
1) Кривые Безье
В настоящее время для задач аппроксимации наиболее широко применяются кривые Безье. Это связано с их удобством как для аналитического описания, так и для наглядного геометрического построения (применительно к компьютерной графике это означает, что пользователь может задавать форму кривой интерактивно, т.е. двигая опорные точки курсором на экране ).
Наглядный метод построения этих кривых был предложен de Casteljau в 1959 году. Построим кривую по 3 опорным точкам (Рис. 5). Метод de Casteljau основан на разбиении отрезков, соединяющих исходные точки в отношении t (значение параметра), а затем в рекурсивном повторении этого процесса для полученных отрезков.
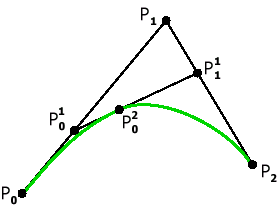 Рис. 5. Кривая Безье с 3 опорными точками. |  Обозначим опорные точки как 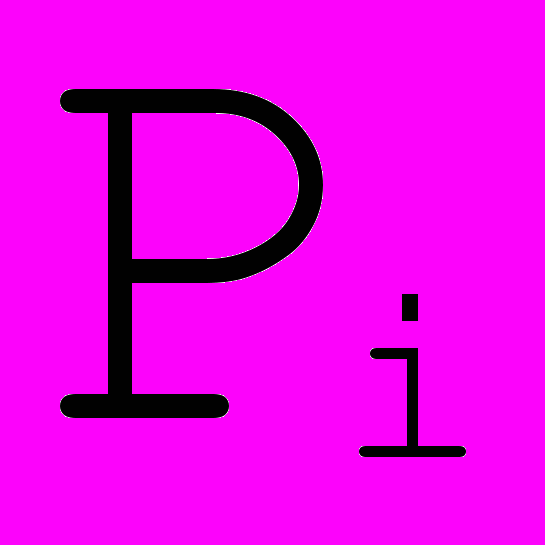 , , , начало кривой положим в точке , начало кривой положим в точке 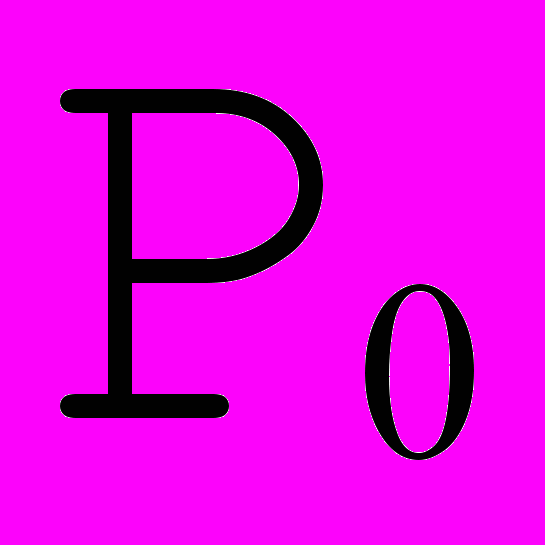 (t=0), а конец в точке (t=0), а конец в точке  (t=1), для каждого (t=1), для каждого 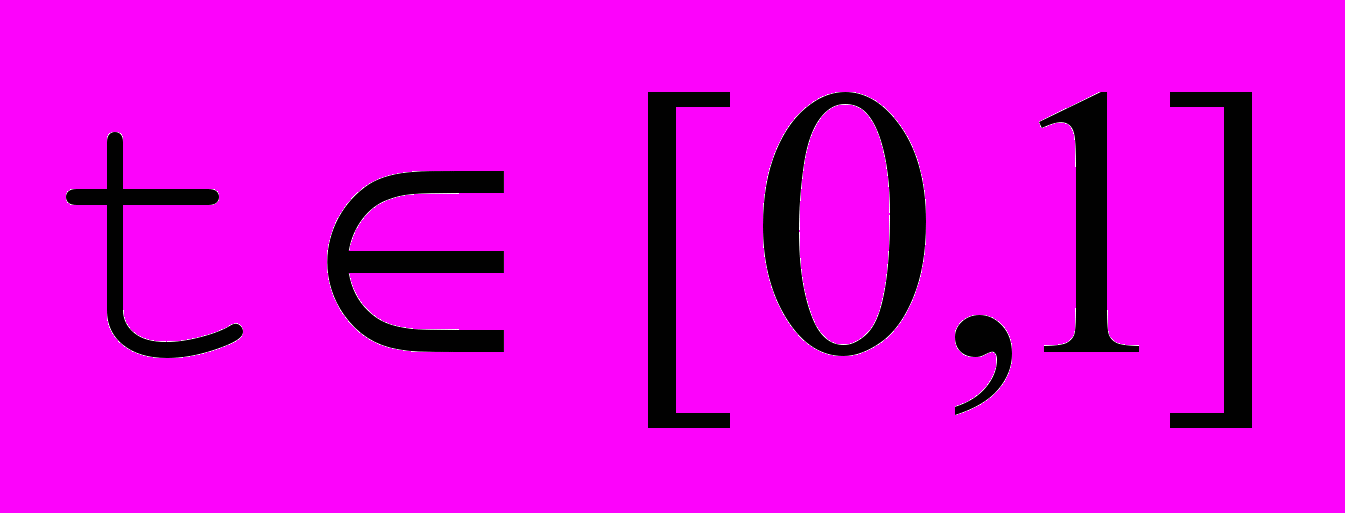 найдем точку найдем точку  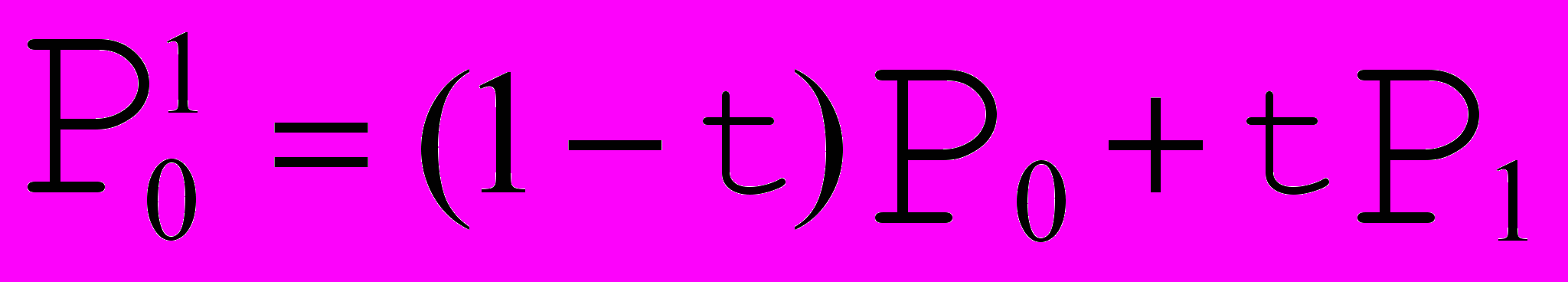   , ,таким образом, получим кривую второго порядка. |
Теперь постоим аналогичным методом кривую Безье с 4 опорными точками.
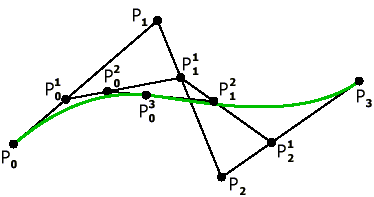 Рис. 6. Кривая Безье с 4 опорными точками. | 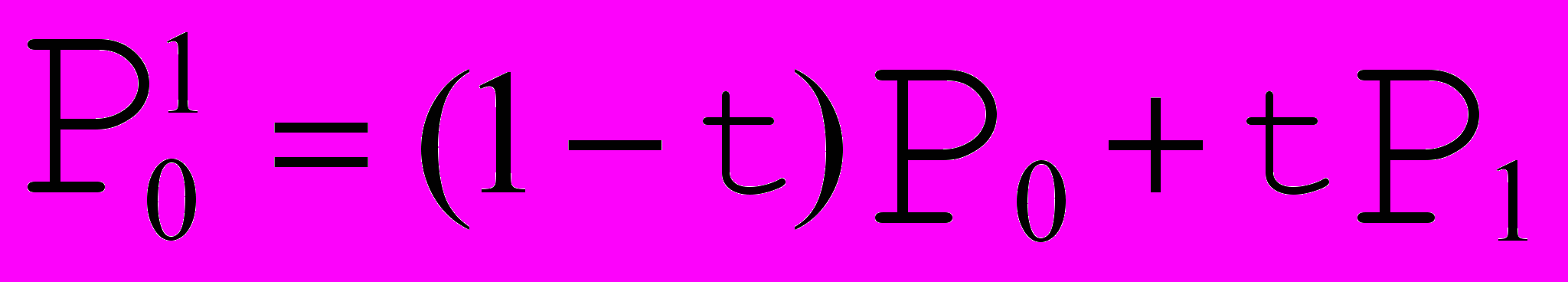     |
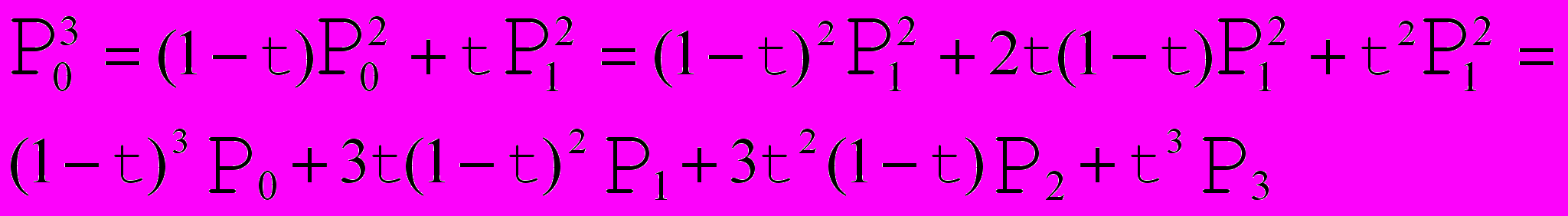
Можно продолжать подобные построения и для большего числа узлов, получая аналогичные выкладки. Запишем общее аналитическое представление для кривой Безье с N+1 опорной точкой:
 , где
, где 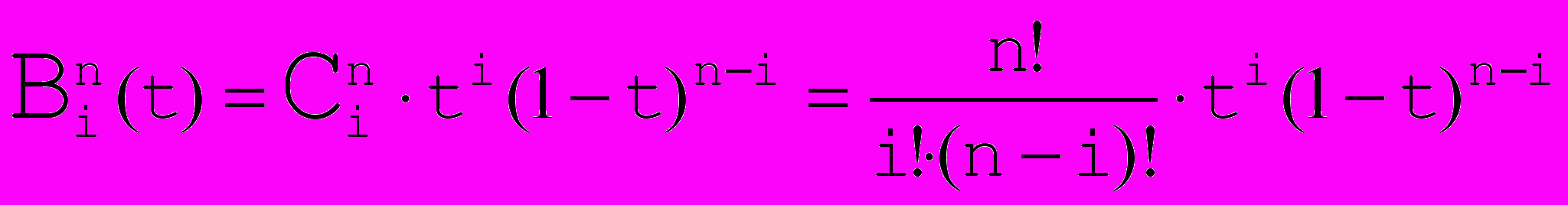 , где
, где  - биномиальные коэффициенты,
- биномиальные коэффициенты, 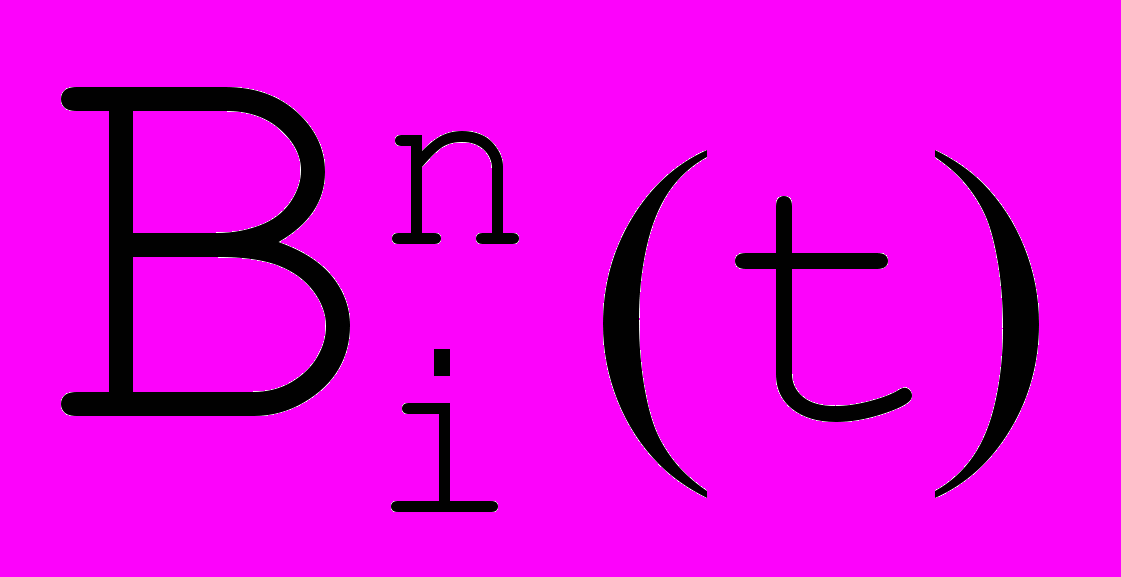 называются базисными многочленами Бернштейна n степени (а также весовыми функциями Безье/Бернштейна). На рисунках ниже изображены многочлены Бернштейна 3 и 4 степеней
называются базисными многочленами Бернштейна n степени (а также весовыми функциями Безье/Бернштейна). На рисунках ниже изображены многочлены Бернштейна 3 и 4 степеней

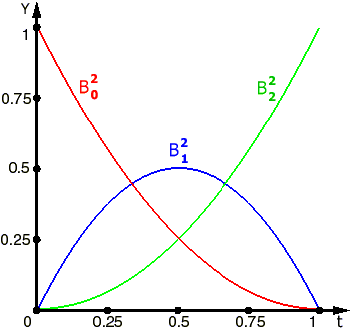 Рис. 7. Базисные функции Бернштейна для кривой Безье с 3 опорными точками. |  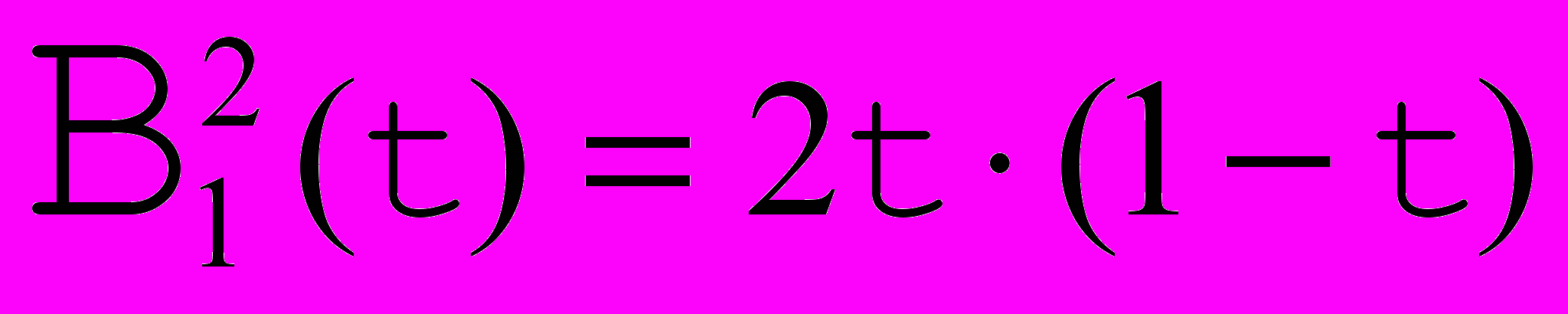 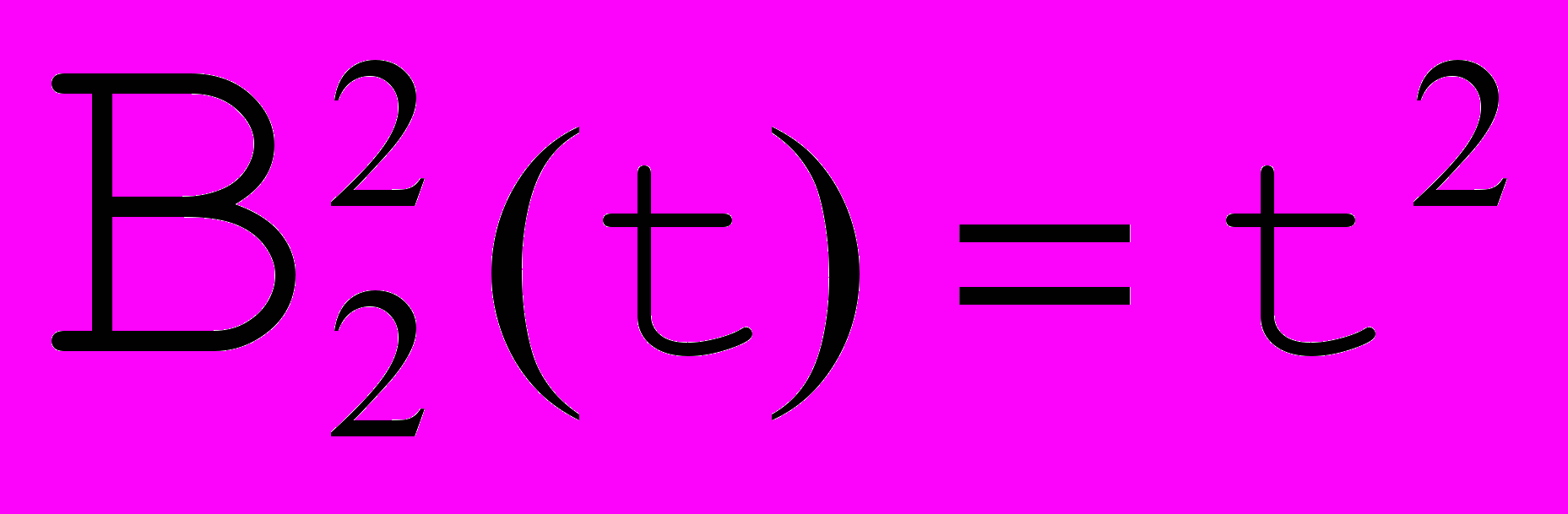 |
 Рис. 8. . Базисные функции Бернштейна для кривой Безье с 4 опорными точками. | 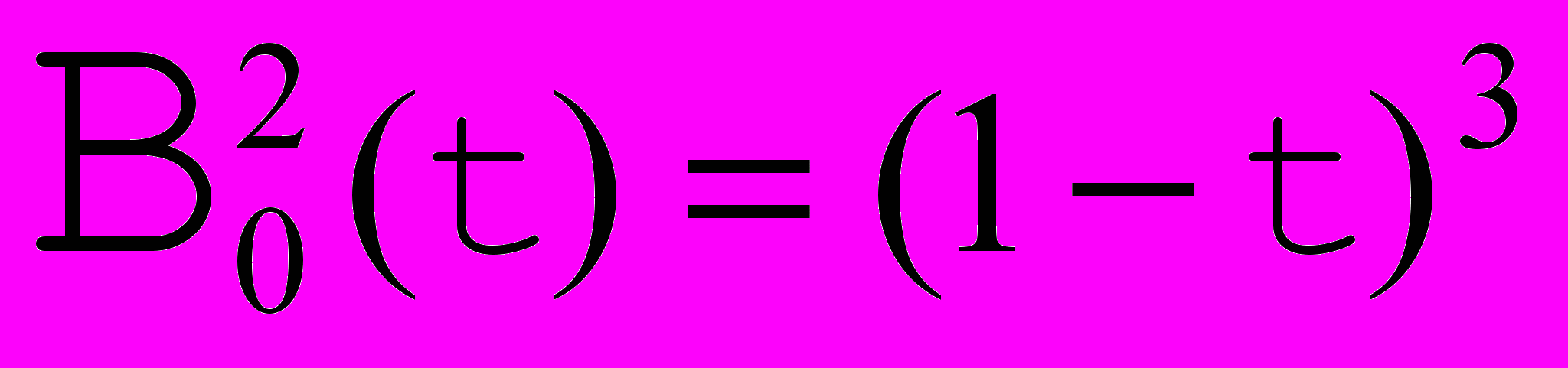  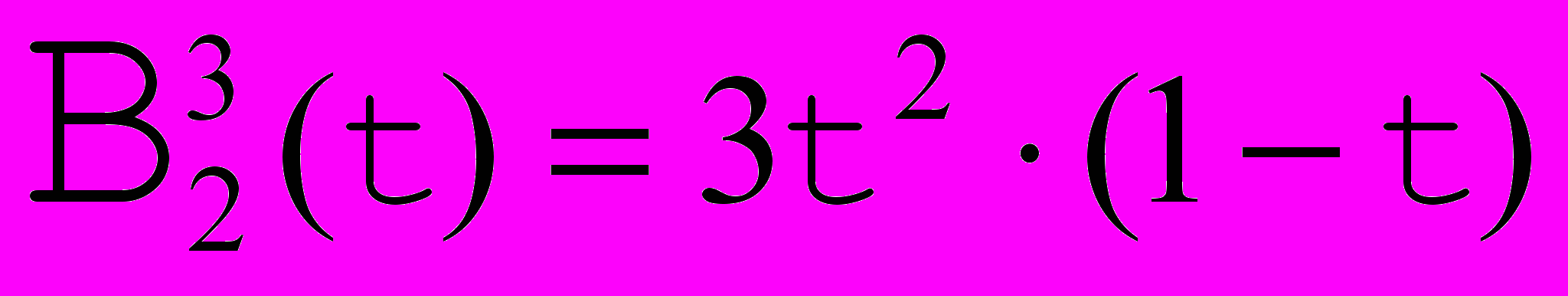  |
Свойства кривых Безье
1) Инвариантность относительно аффинных преобразований;
2) Инвариантность относительно линейных замен параметризации;
- Кривая Безье принадлежит выпуклой оболочке опорных точек (следует из геометрического способа построения);
Следствие: Если все опорные точки лежат на одной прямой, то кривая Безье вырождается в отрезок, соединяющий эти точки.
4) Кривая Безье проходит через
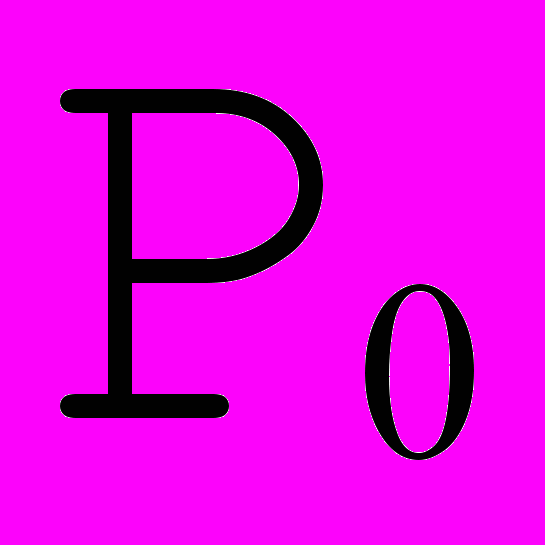 и
и 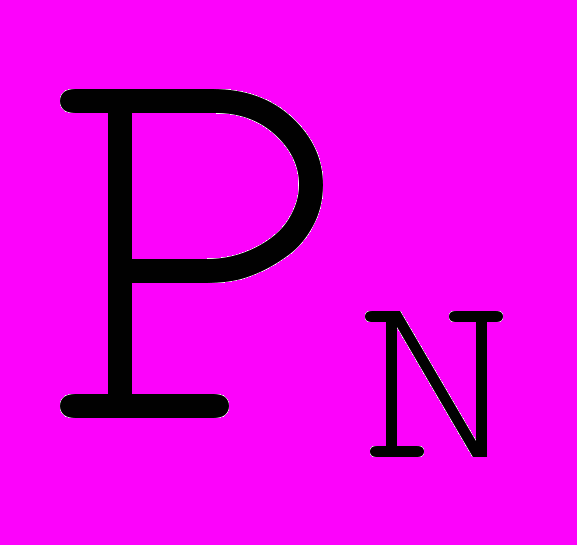 ;
;5) Симметричность: если рассматривать контрольные точки в противоположном порядке, то кривая не измениться;
6) Степень многочлена, представляющего кривую в аналитическом виде на 1 меньше числа опорных точек;
7) Векторы касательных в точках
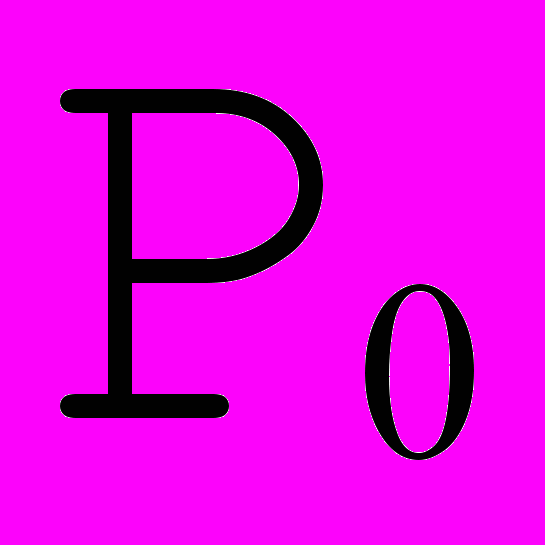 и
и 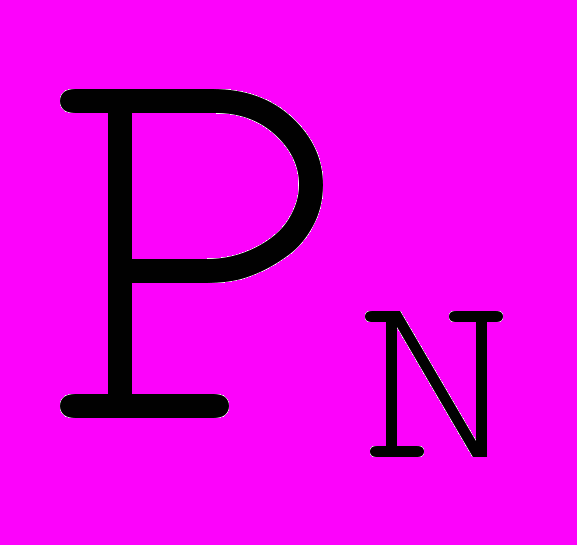 коллинеарны
коллинеарны  и
и 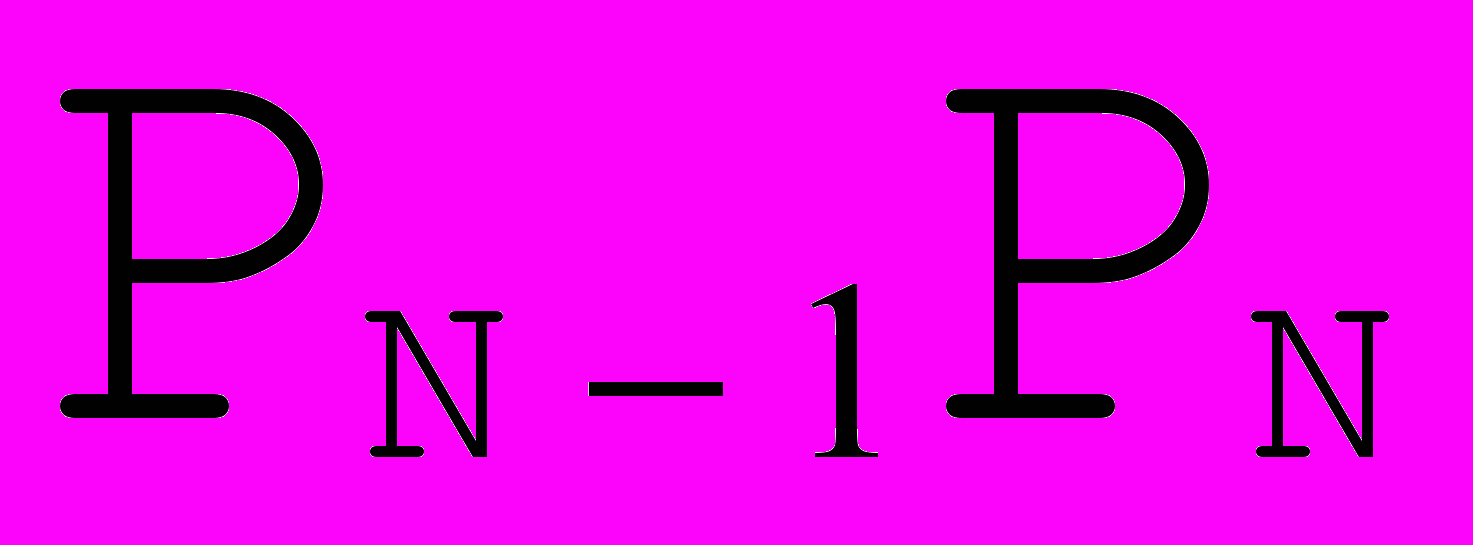 ,соответственно.
,соответственно.Замечание:
Хотя все выкладки проводились в
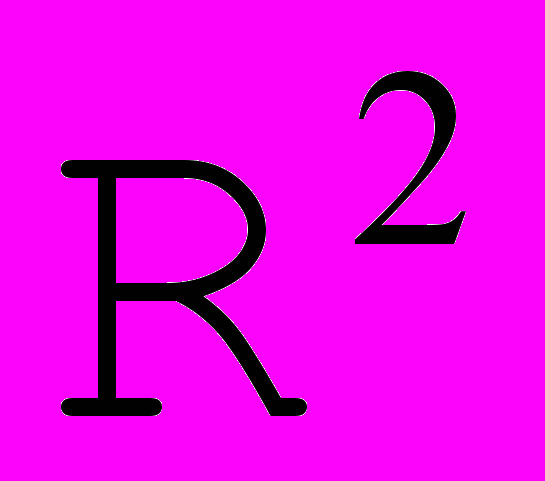 , аналогичные построения и свойства справедливы и в
, аналогичные построения и свойства справедливы и в 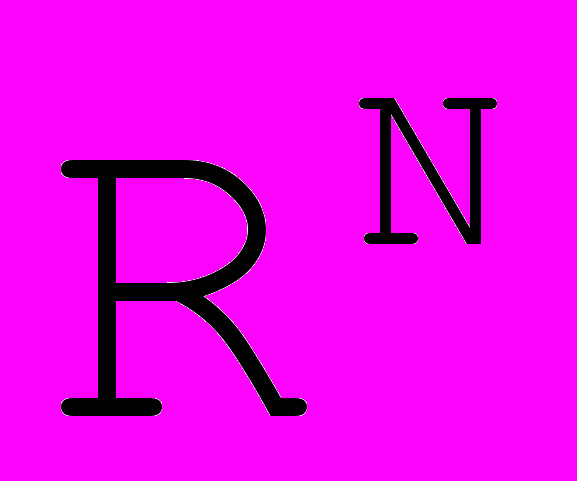 .
.Визуализация кривых Безье
1) Прямой метод
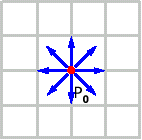 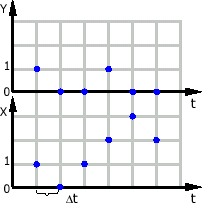 Рис. 9. Построение кривых Безье прямым методом. |  , , 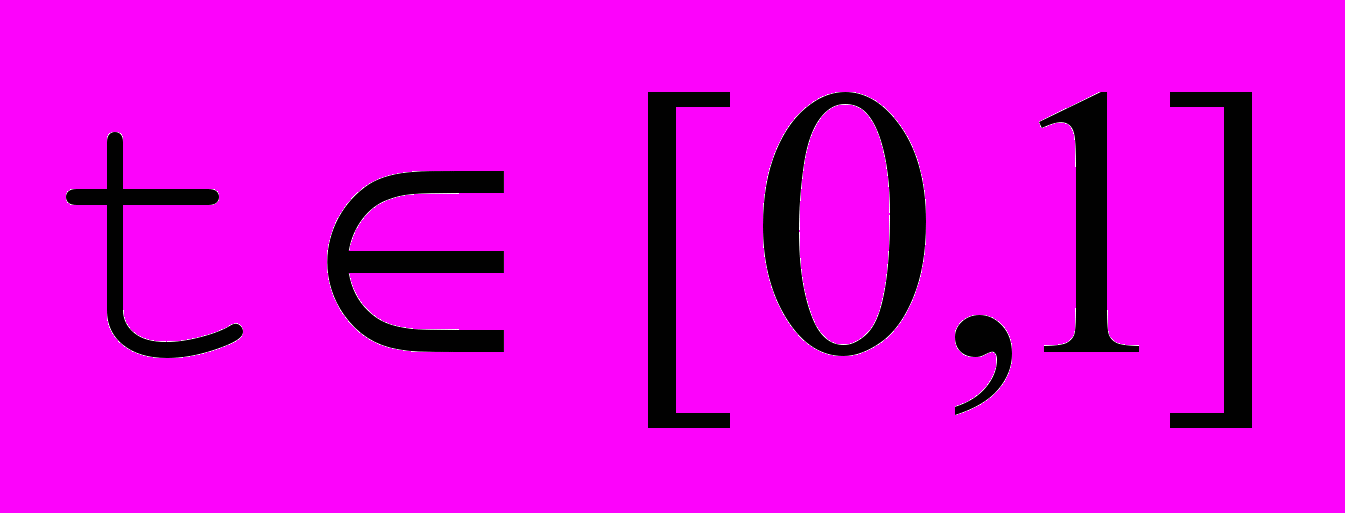 (Точную формулу см. выше) (Точную формулу см. выше)Подберем шаг dt так, чтобы dx и dy были <1 (т.е. мы не пропустим ни одного пиксела).  и и - многочлены, соответственно легко найти их максимумы - многочлены, соответственно легко найти их максимумы  и и 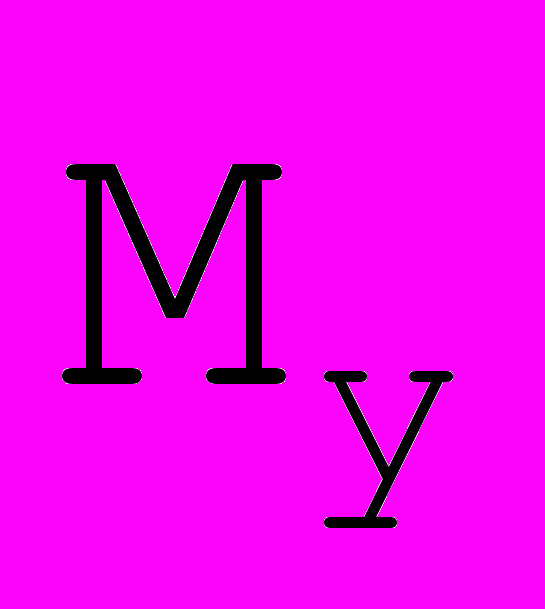 . Положим . Положим  =max ( =max ( , ,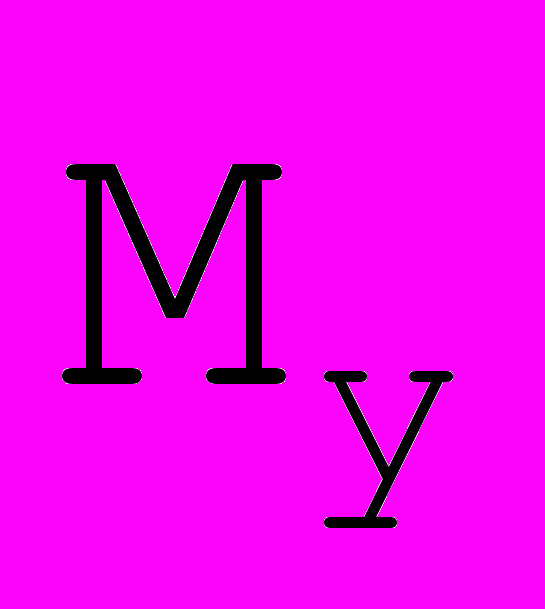 ), тогда взяв ), тогда взяв 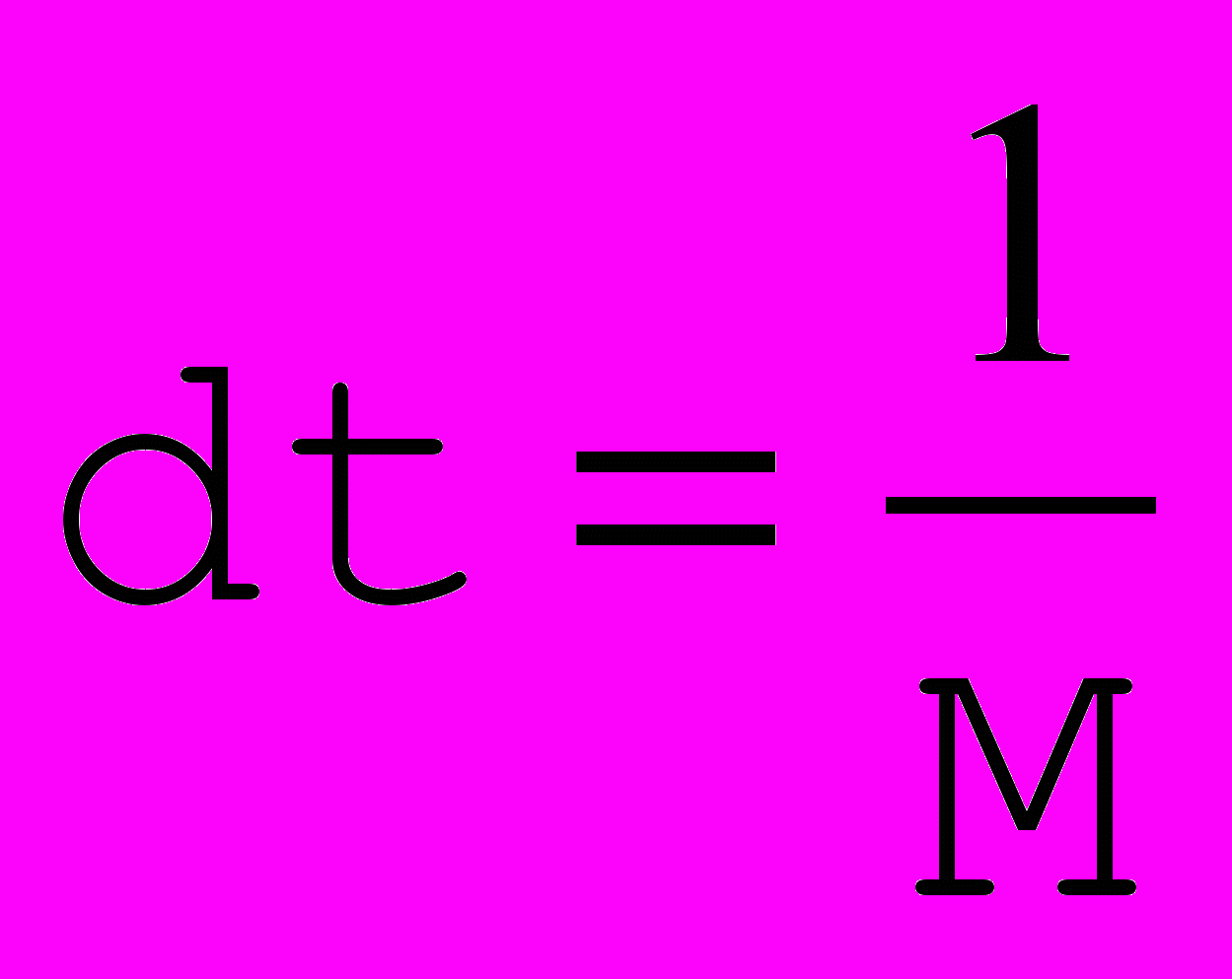 , получим что смещения по x и по y при каждом шаге не превосходят 1. , получим что смещения по x и по y при каждом шаге не превосходят 1.Алгоритм: t=0; while(t≤1) { x=x(t); y=y(t); plot(x,y); t+=dt; } Недостаток: при малых смещениях по x и y много итераций проходит зря. |
- Метод разбиения (subdivision)
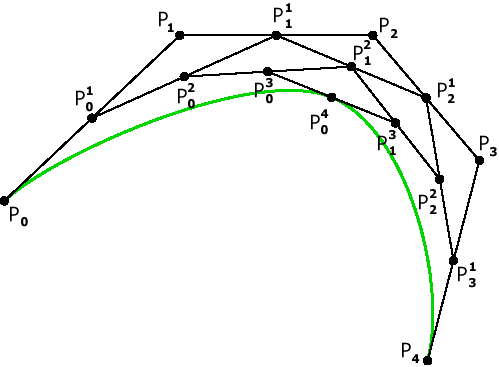 Рис. 10. Построение кривой Безье методом разбиения. | Предложен de Casteljau. 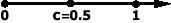 Если рассмотреть участок между  и и 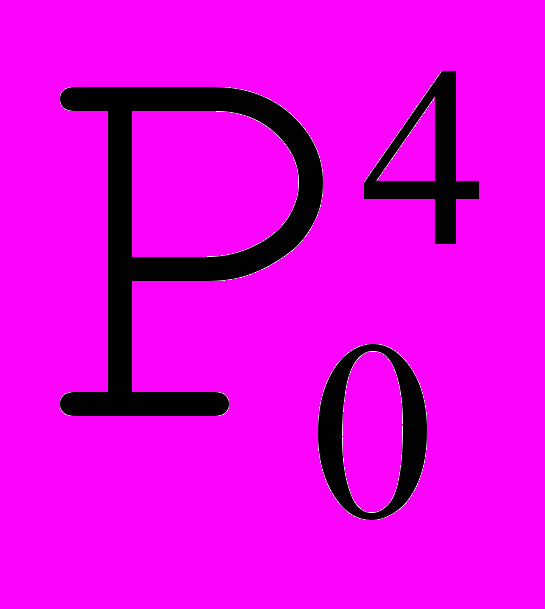 , взятых для t=0,5, то он может быть задан как кривая Безье с опорными точками , взятых для t=0,5, то он может быть задан как кривая Безье с опорными точками 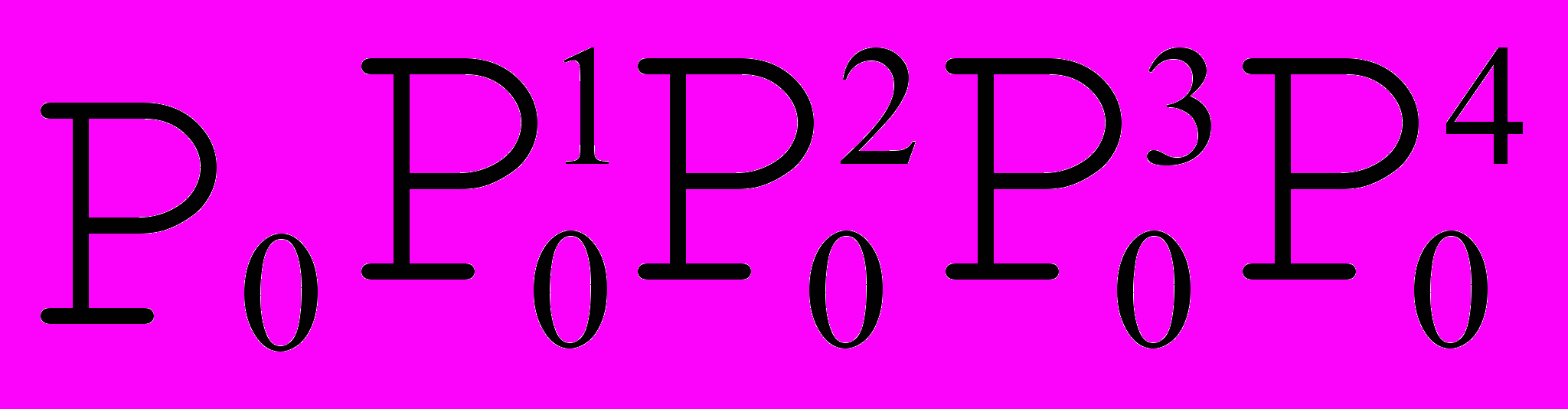 , аналогичные рассуждения справедливы и для участка между , аналогичные рассуждения справедливы и для участка между 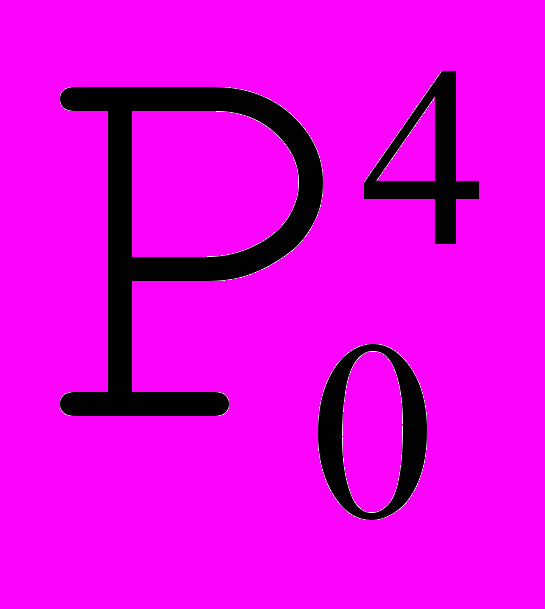 и и  . Таким образом будем применять этот алгоритм рекурсивно для левой и правой частей, пока размер кривой не станет меньше размера пиксела. . Таким образом будем применять этот алгоритм рекурсивно для левой и правой частей, пока размер кривой не станет меньше размера пиксела. |
Алгоритм:
PutPixel(
 );
);PutPixel(
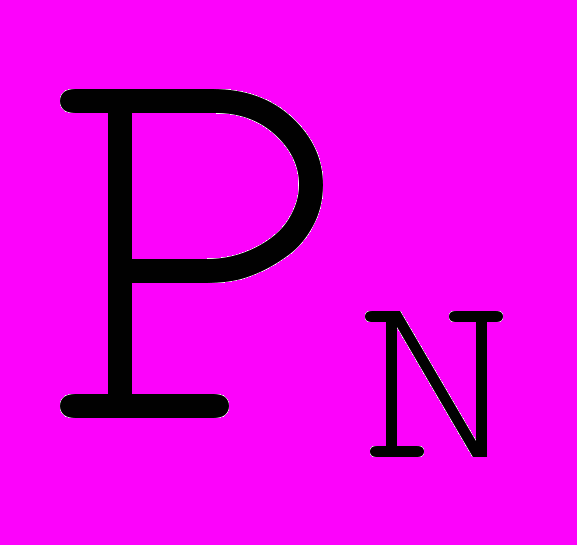 );
);DrawCurve (
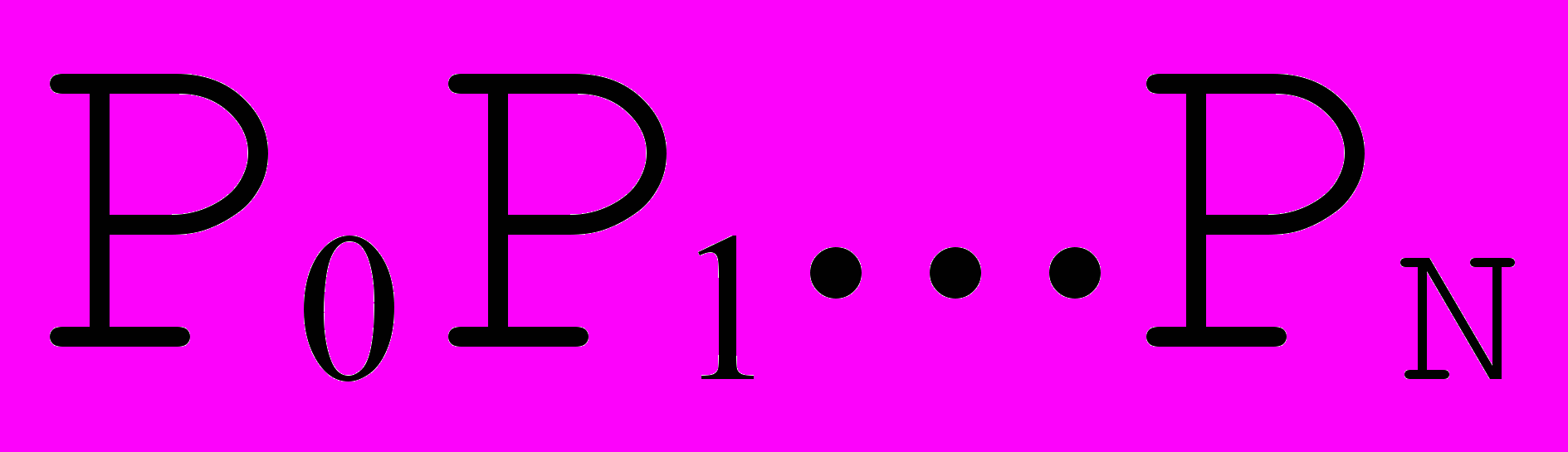 )
){
// Проверка на завершение
if ( BBox(
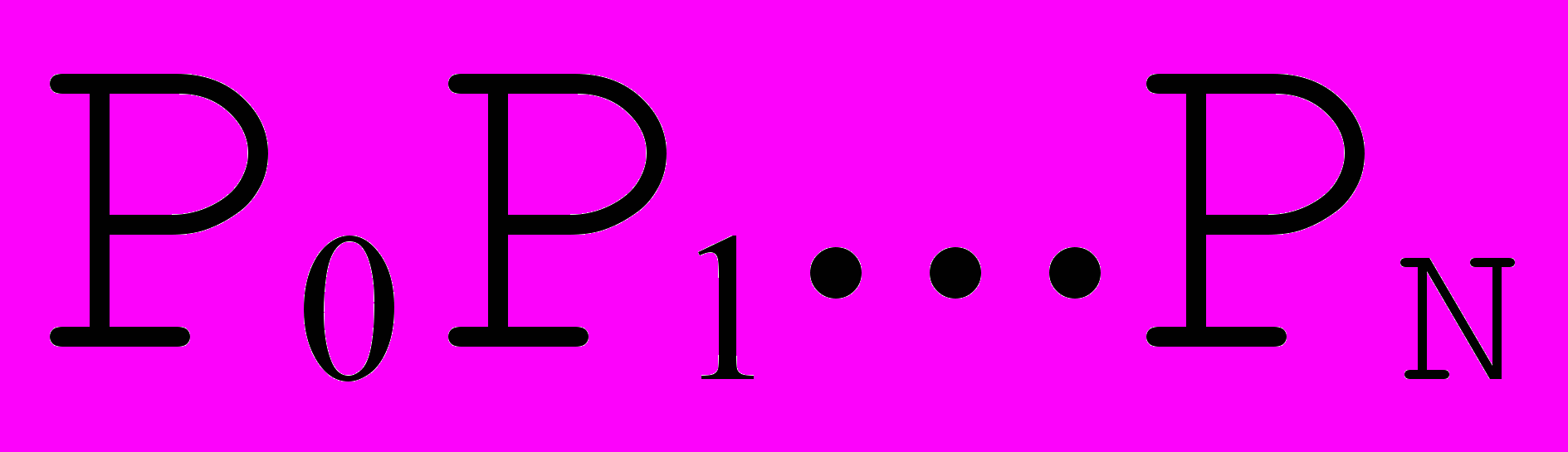 ) < pixelsize ) return;
) < pixelsize ) return;if (
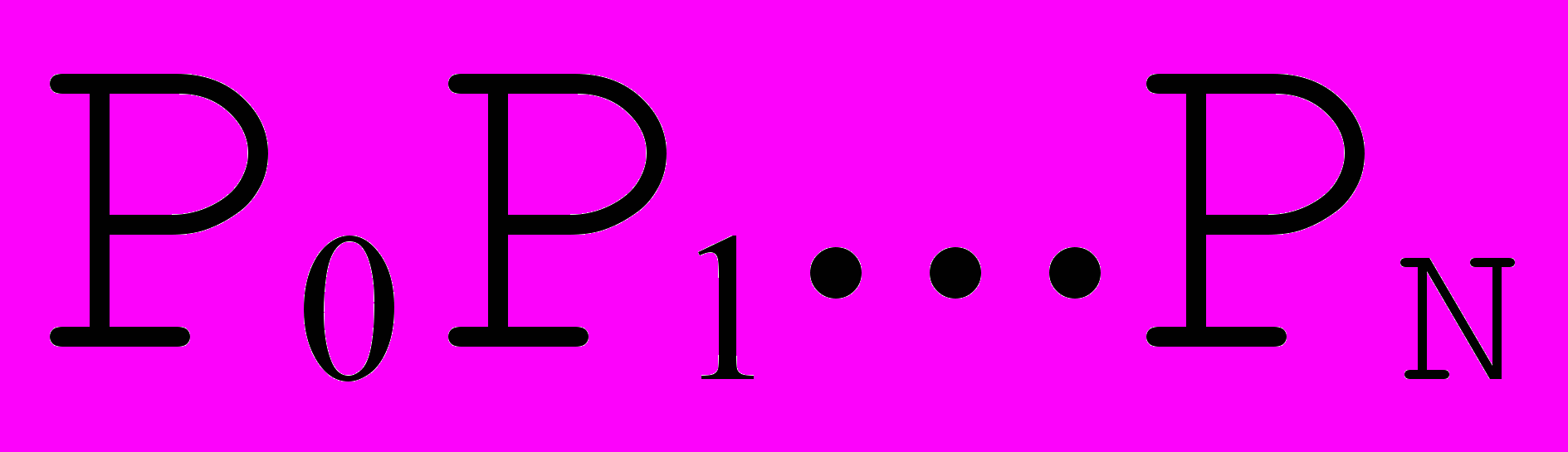 - прямая линия с точностью до пиксела )
- прямая линия с точностью до пиксела ){
Нарисовать эту линию;
return;
}
Найти
 ;
;PutPixel(
 );
);// Нарисовать половинки
DrawCurve(
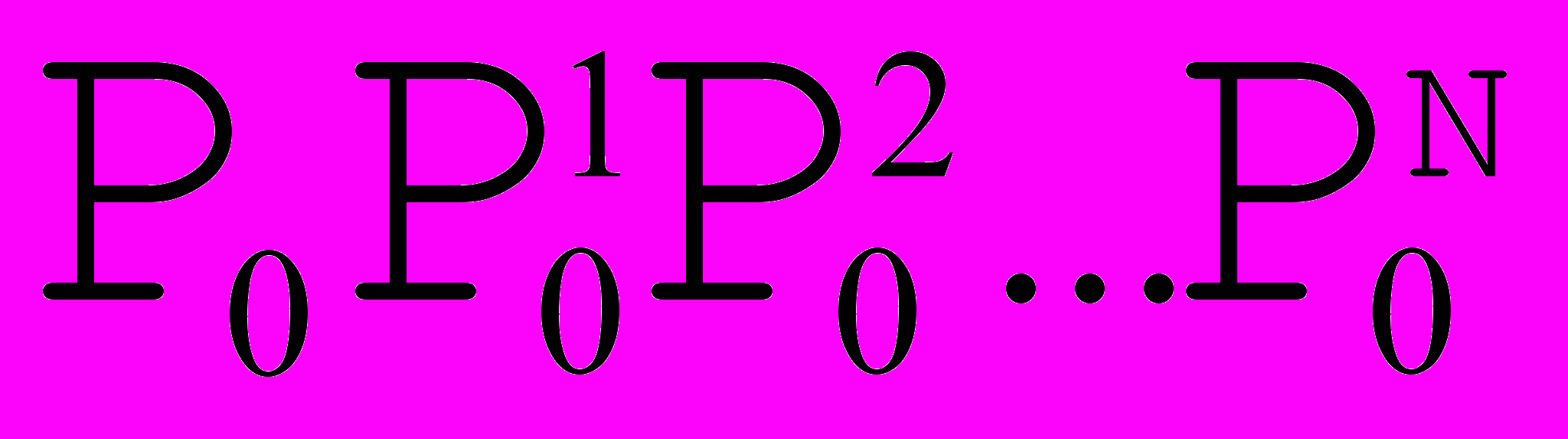 );
);DrawCurve(
 );
);}
2) Сплайны, составленные из кривых Безье
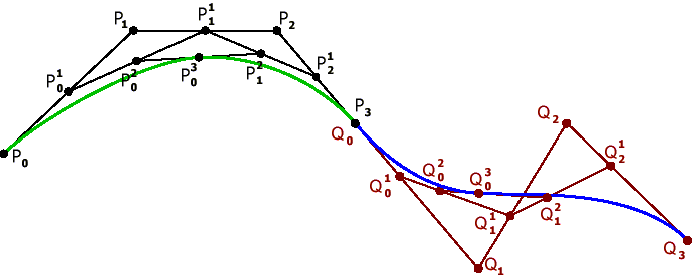
Рис. 11. Состыкованные кубические кривые Безье.
Д
 ля упрощения будем считать, что параметризация равномерная, т.е. длины отрезков, которые пробегает параметр на каждом из участков, равны.
ля упрощения будем считать, что параметризация равномерная, т.е. длины отрезков, которые пробегает параметр на каждом из участков, равны.Для того чтобы рассмотреть условия на
 и
и 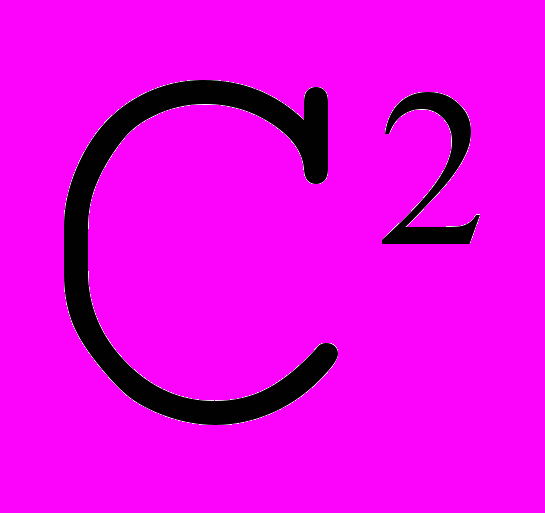 , необходимо найти производные кривых Безье:
, необходимо найти производные кривых Безье: , где
, где 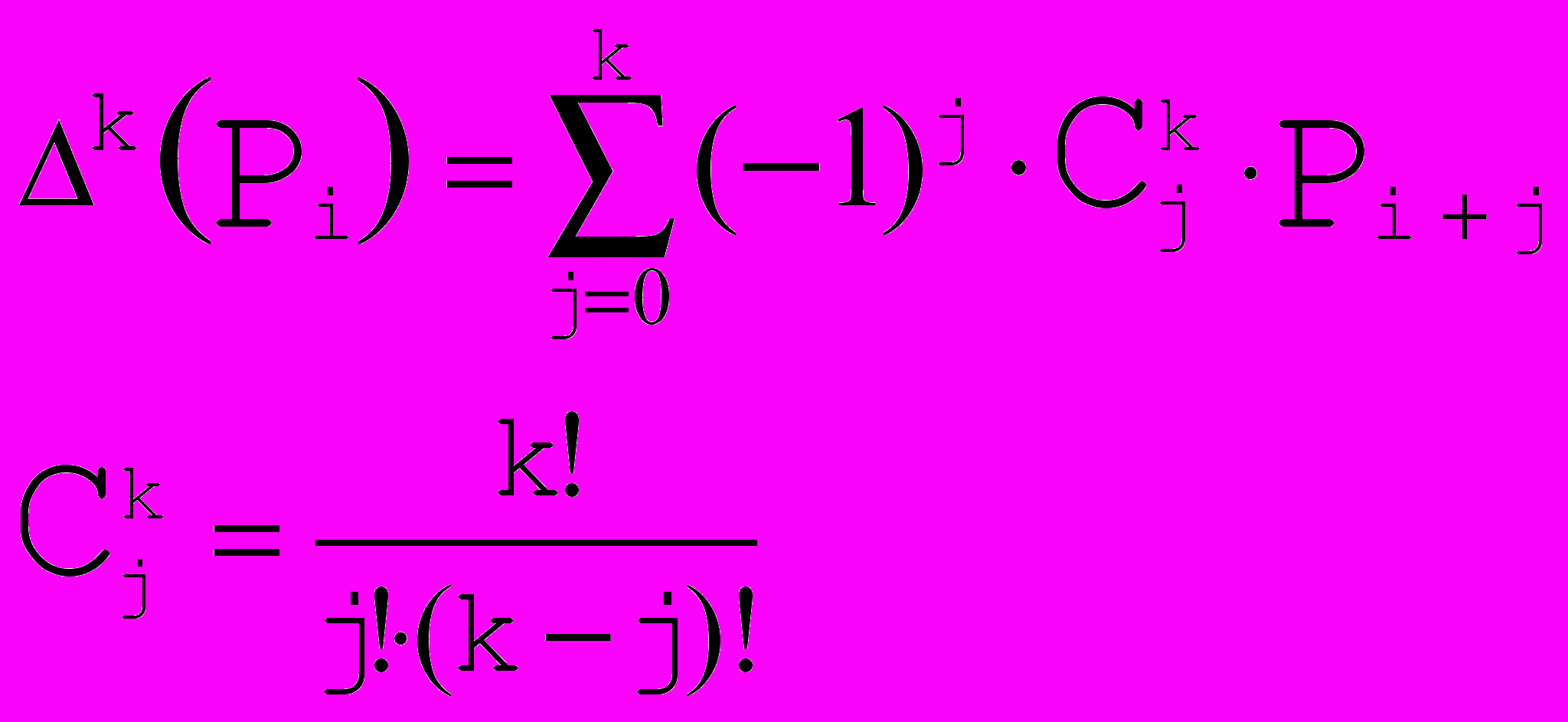
Ограничимся в рассмотрении кубическими кривыми Безье, которые более всего распространены.
1) Требование

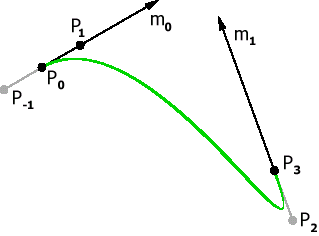 Рис. 12. Стыковка с требованием  | Пусть заданы значение производных на концах: m0 и m1 :  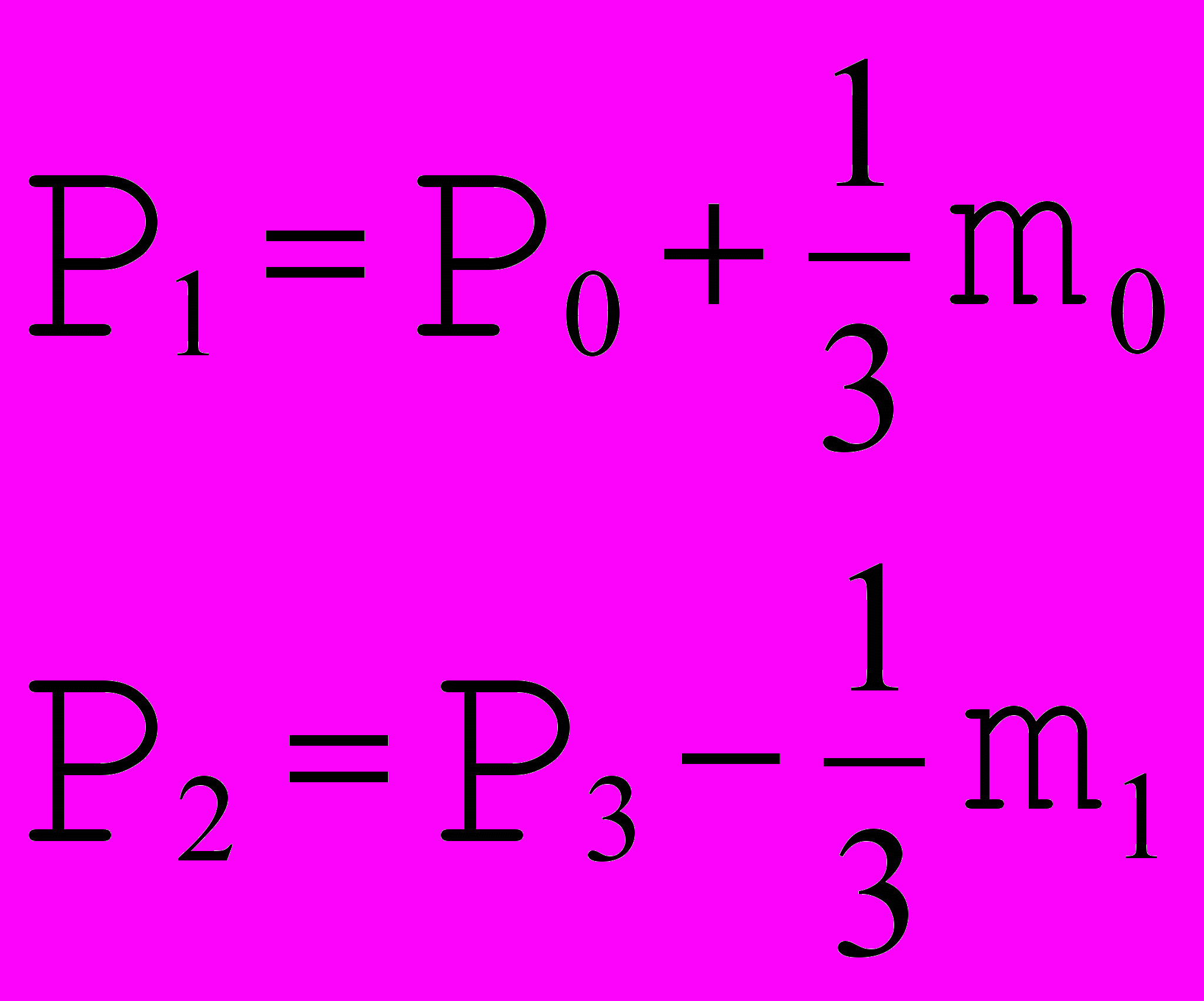 Таким образом, для того, чтобы в точках стыковки производные были равны необходимо, чтобы  , т.е. : , т.е. :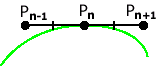 |
2) Требование
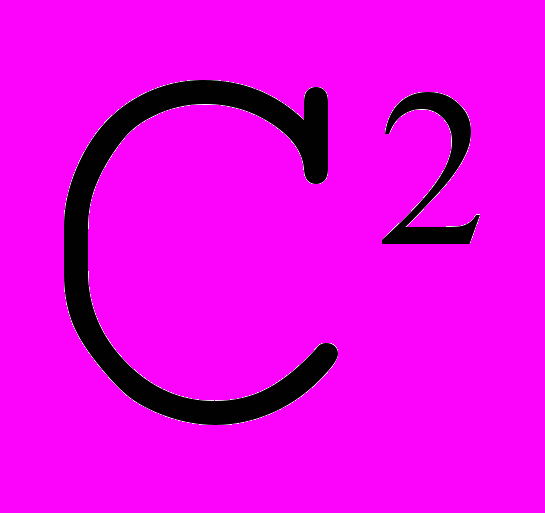
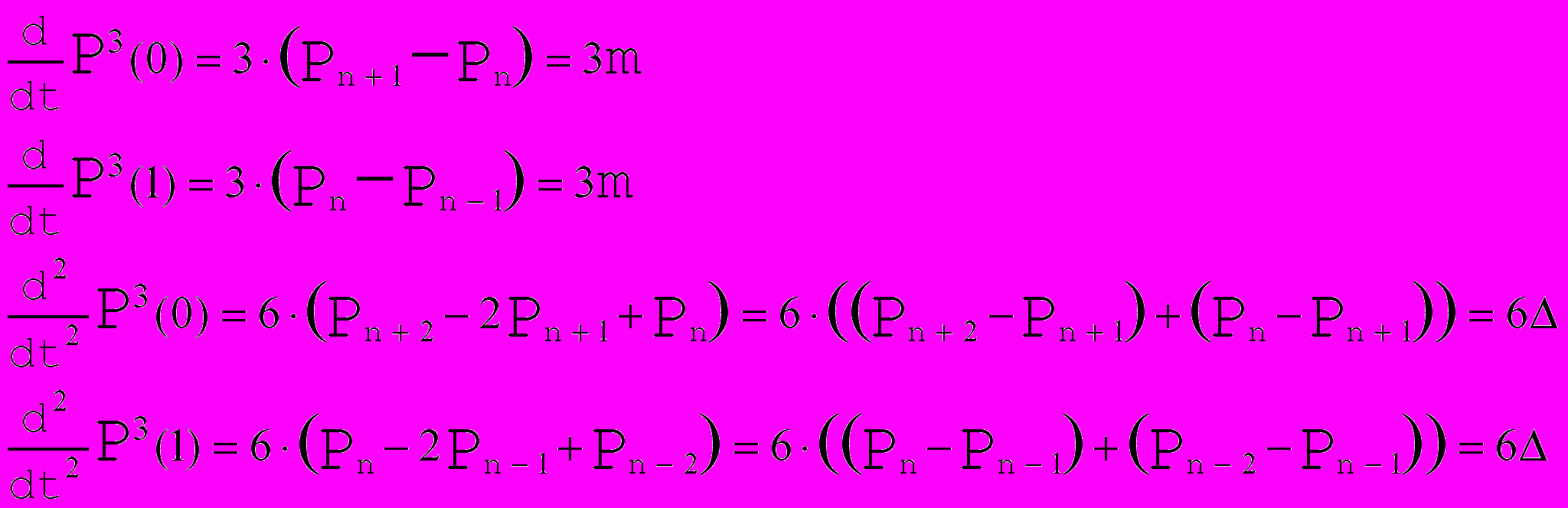
 Рис. 13. Стыковка с требованием 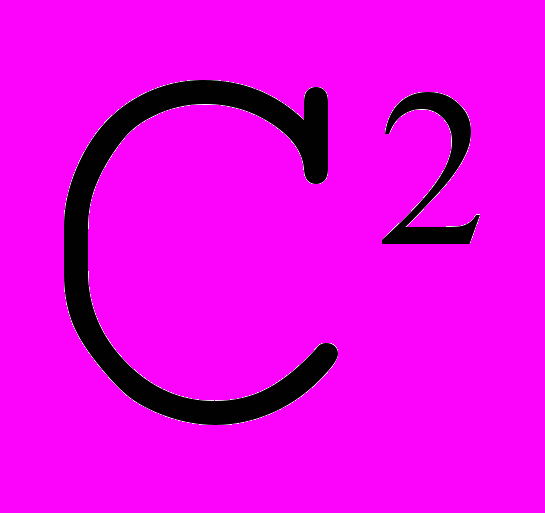 . . | Из требования  в точках стыковки получаем в точках стыковки получаем 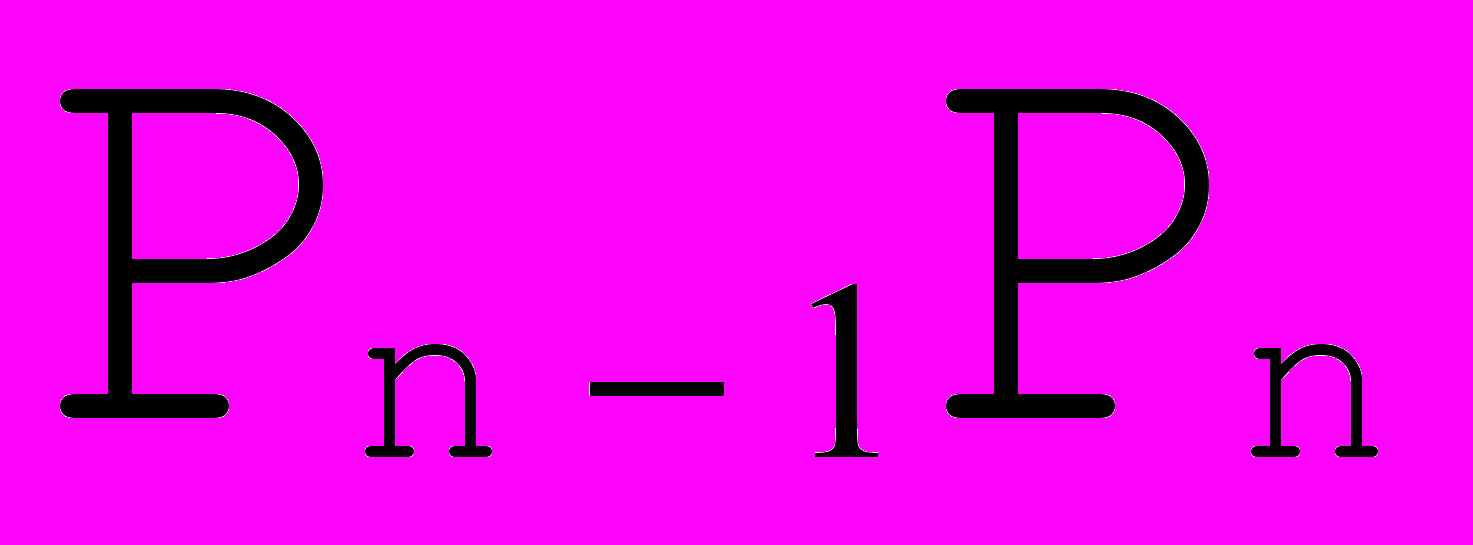 = =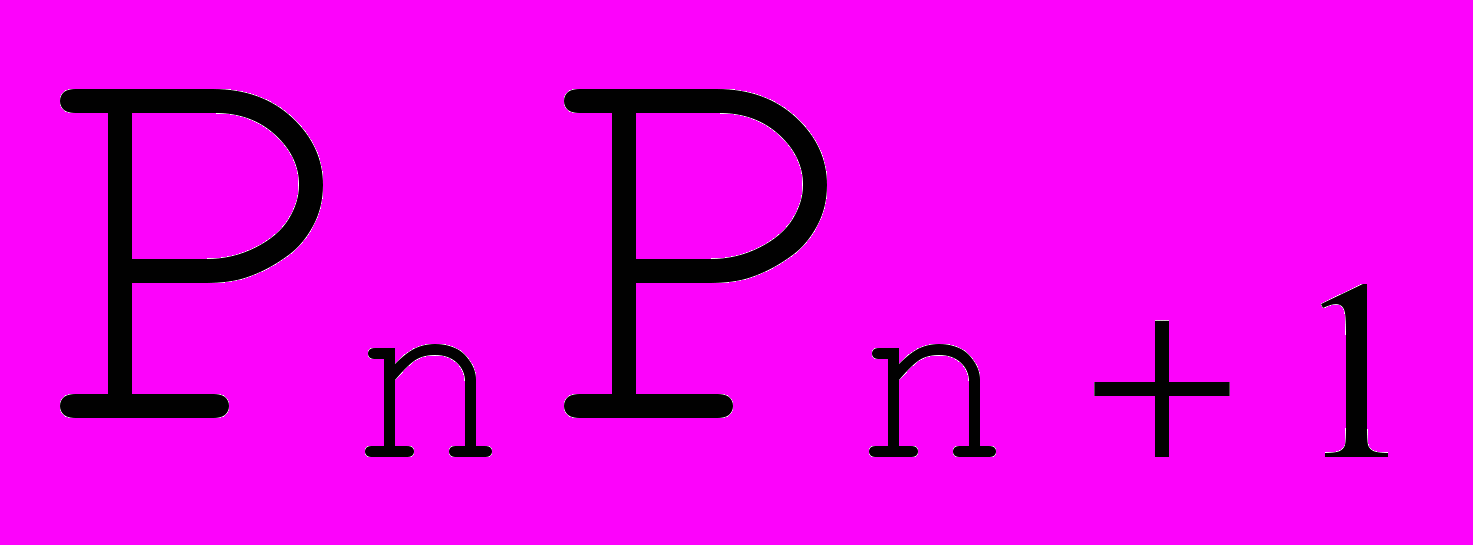 . Далее , из требования . Далее , из требования 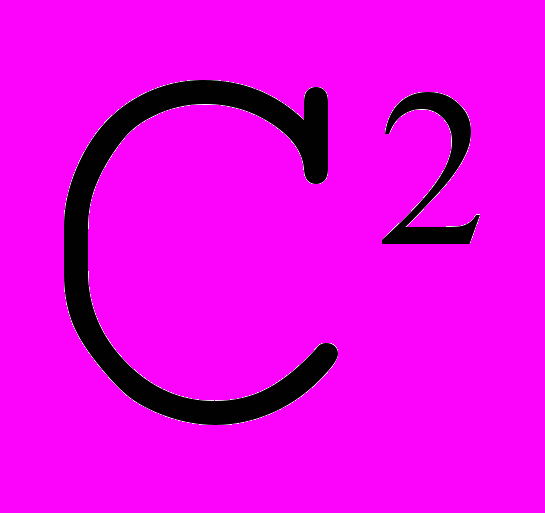 следует равенство , и так как получаются сложением соответствующих векторов по правилу параллелограмма, то следует равенство , и так как получаются сложением соответствующих векторов по правилу параллелограмма, то 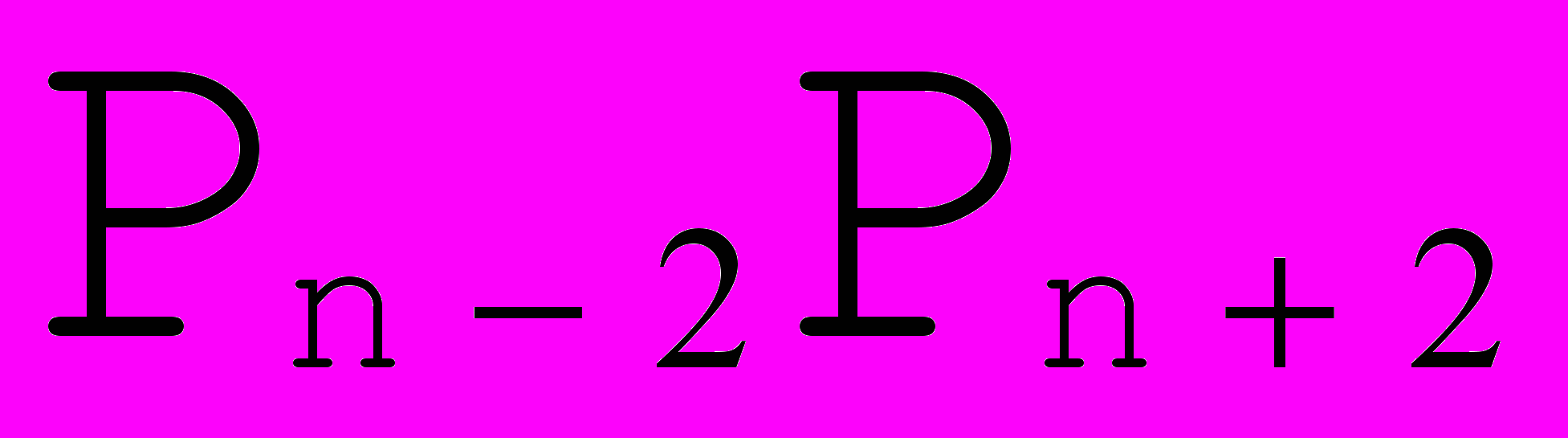 ││ ││ и, если обозначить точку пересечения и, если обозначить точку пересечения  и и 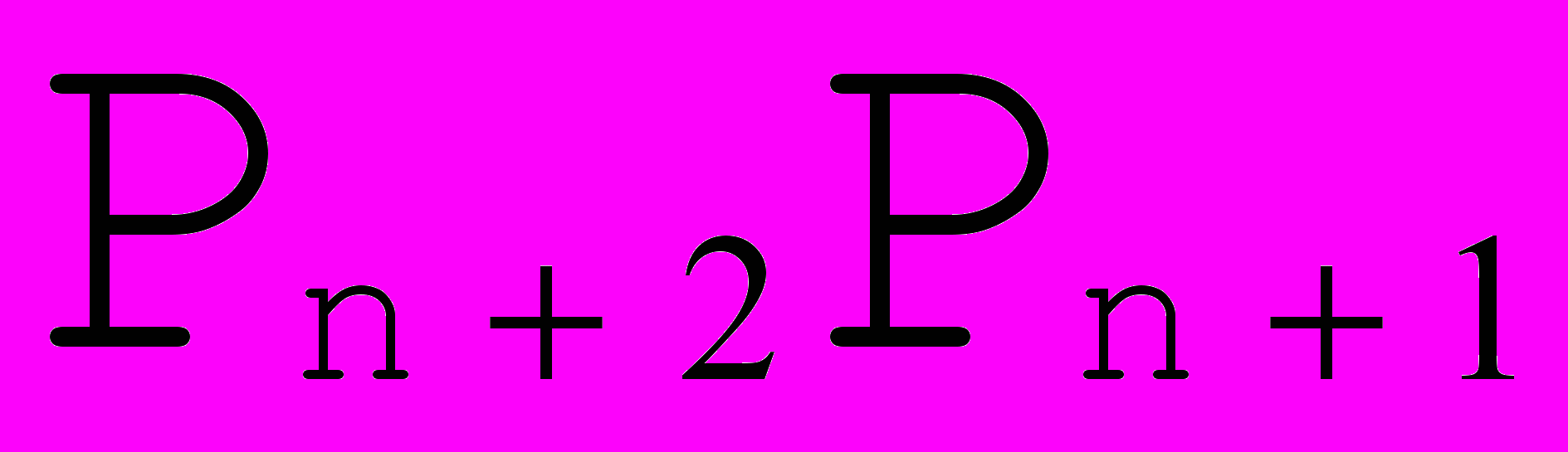 как как 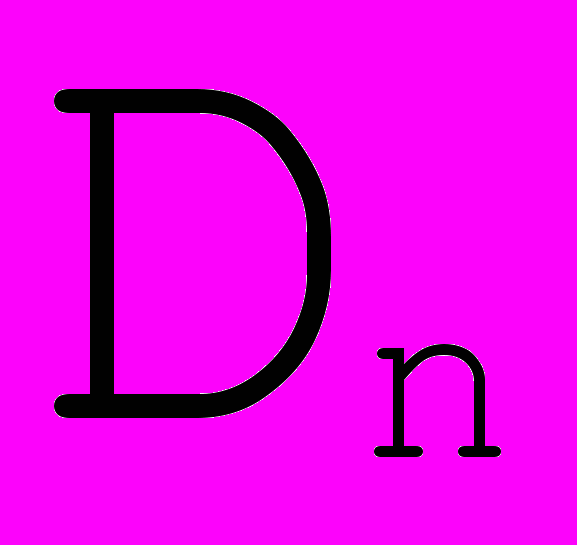 , то получим, что , то получим, что  - средняя линия треугольника - средняя линия треугольника 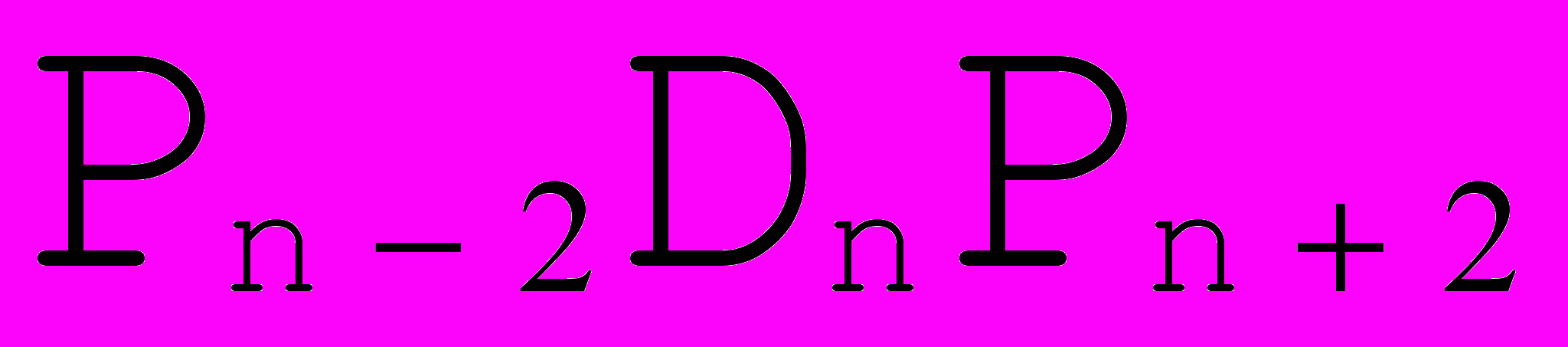 Распространяя эти рассуждения на все точки стыковки, получаем, что для задания формы такого сплайна достаточно задать точки 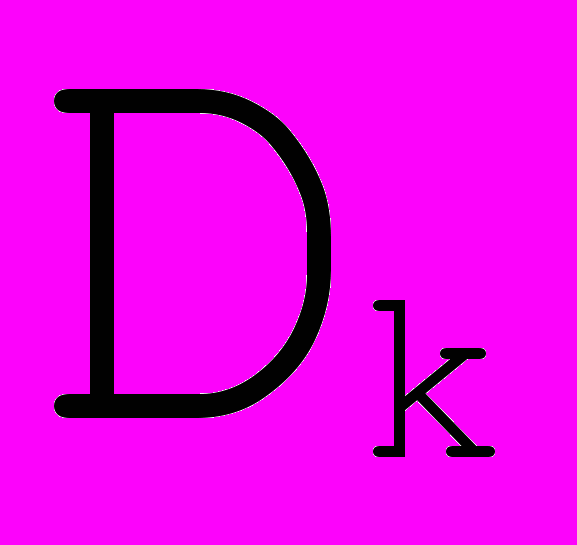 , где k = 3i , i , где k = 3i , i 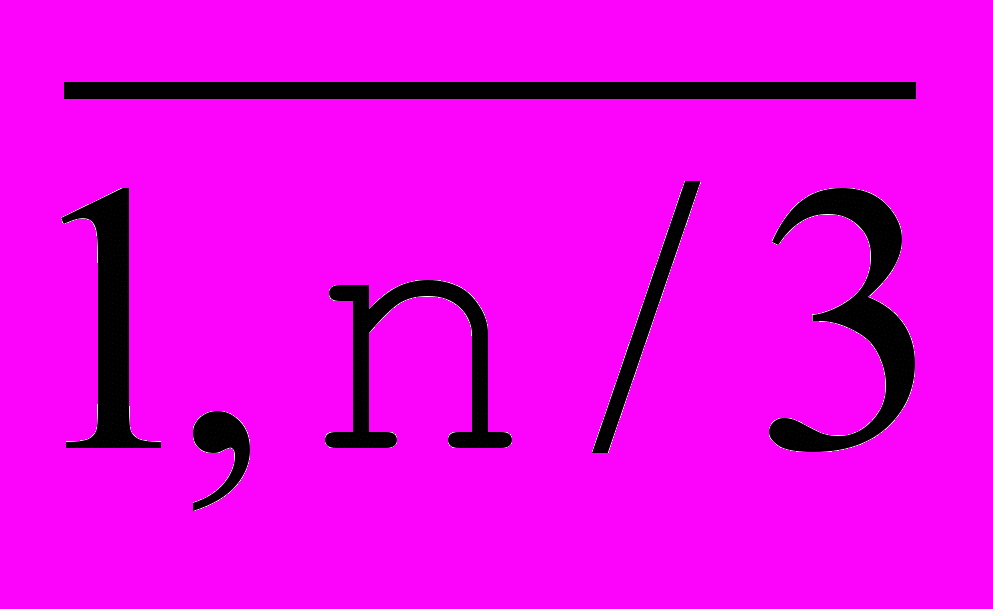 , где n+1 - число опорных точек и краевые точки , где n+1 - число опорных точек и краевые точки  и и  (см. Рис. 14) (см. Рис. 14) |
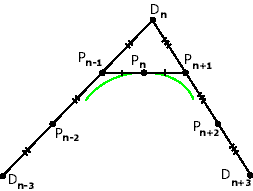 Рис. 14. Связь между точками 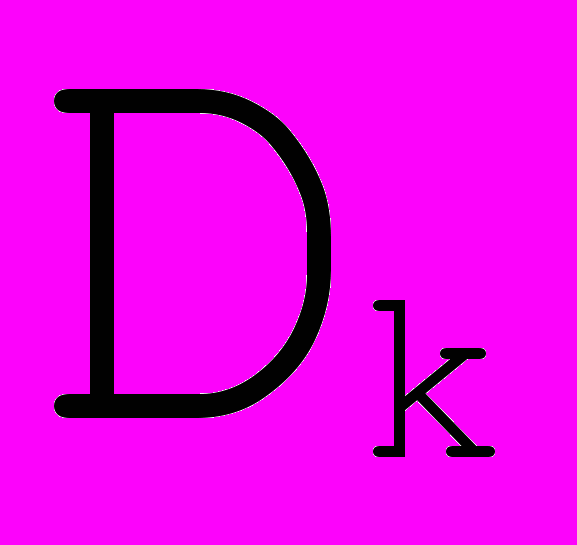 для соседних сегментов. для соседних сегментов. | Замечание: Для замкнутой кривой задание краевых точек не нужно. |
3) Сплайны, составленные из рациональных кривых Безье
Даже такие достаточно развитые средства аппроксимации кривыми Безье не позволяют построить окружность:
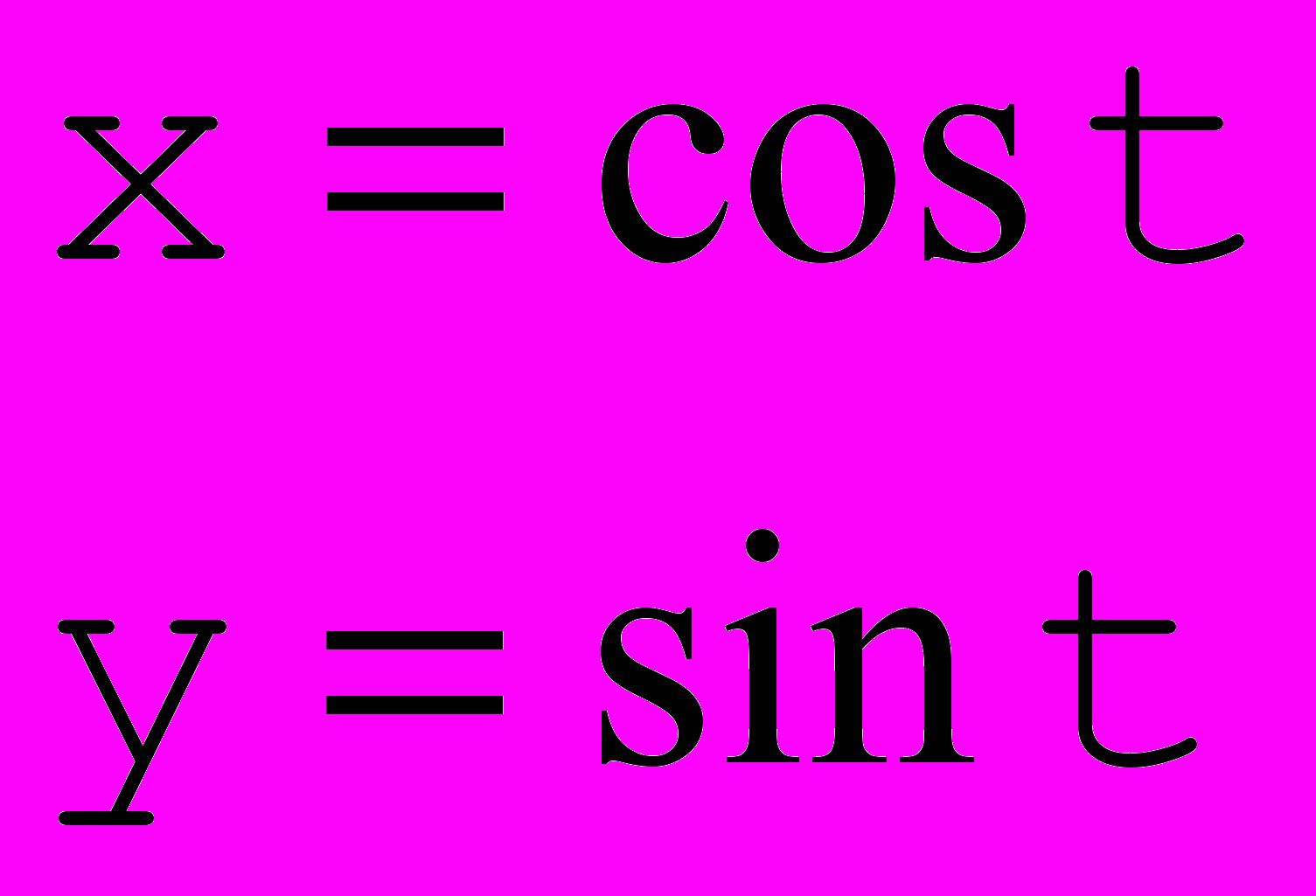 , так как sin и cos для достаточно хорошего приближения требуют многочленов высокой степени, поэту вводится более широкий класс кривых, способ построения которых связан с представлением о проективном пространстве.
, так как sin и cos для достаточно хорошего приближения требуют многочленов высокой степени, поэту вводится более широкий класс кривых, способ построения которых связан с представлением о проективном пространстве.  Рис. 15. Рациональная кривая Безье. | Пусть у нас есть пространственная кривая Безье 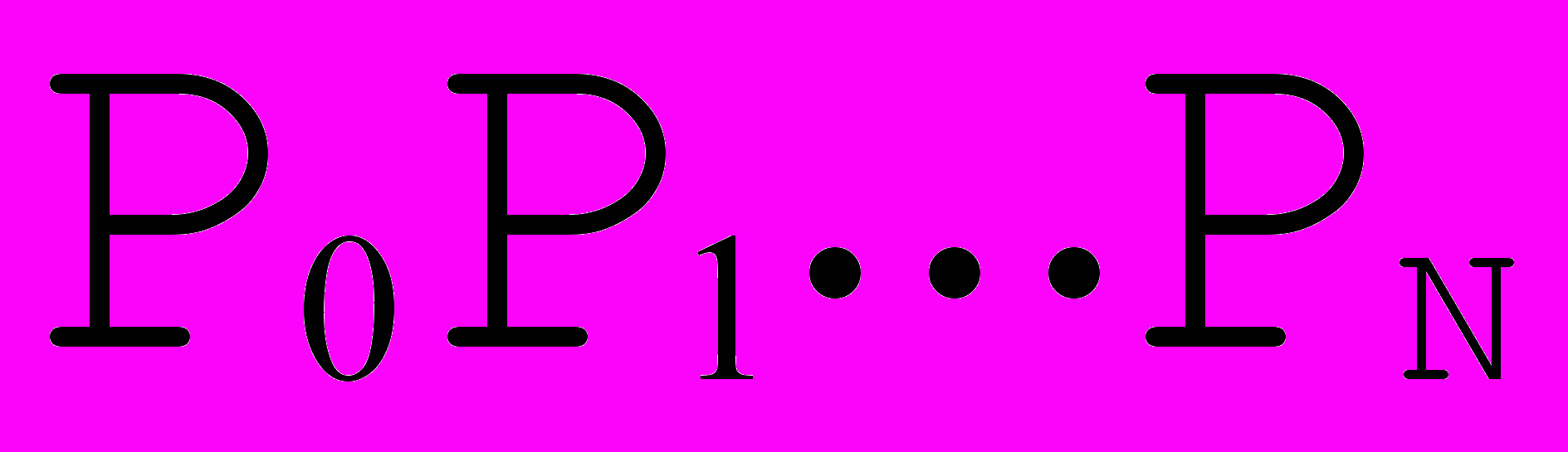 ,в системе координат OXYw, спроецируем все точки исходной кривой на плоскость w=1. Т.е. : ,в системе координат OXYw, спроецируем все точки исходной кривой на плоскость w=1. Т.е. : , где , где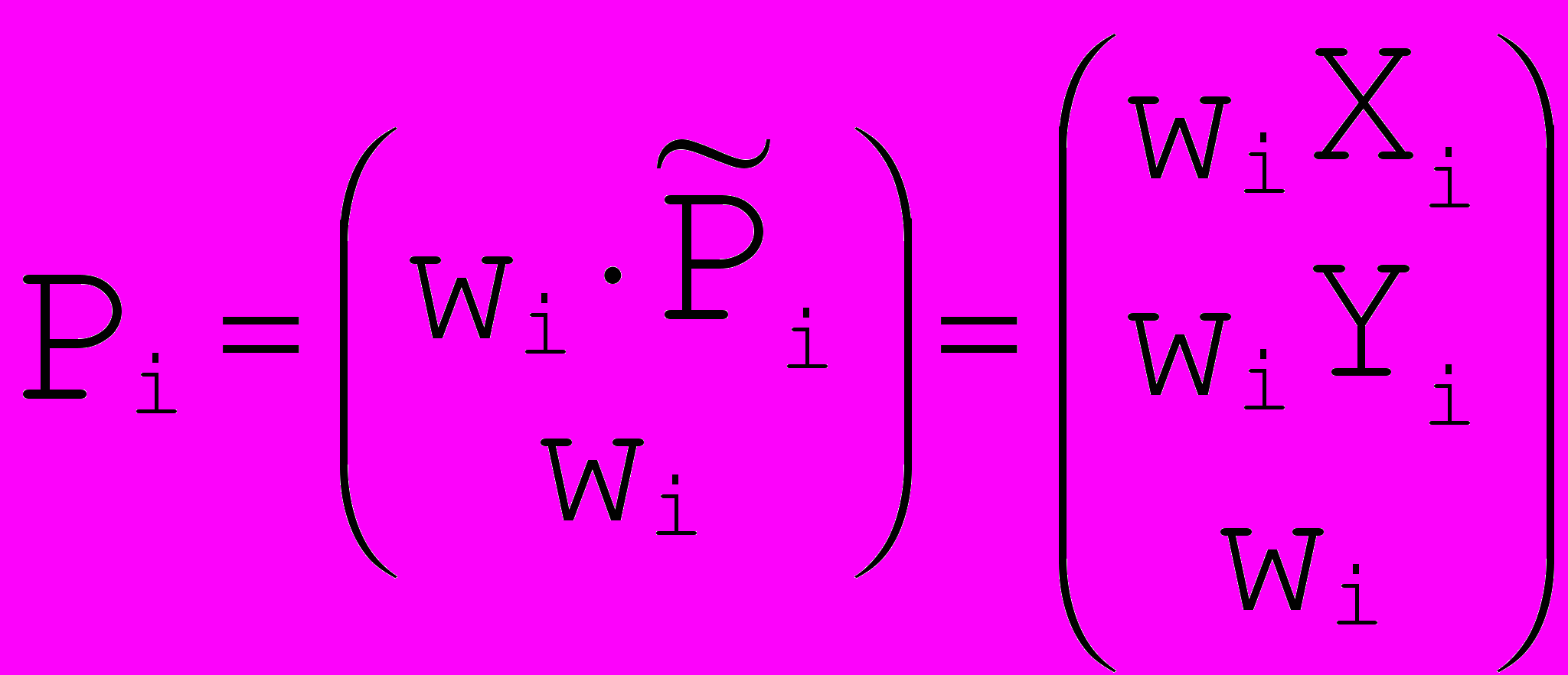 (см. Рис. 15). (см. Рис. 15).Полученная кривая, лежащая в плоскости w=1, и называется рациональной двумерной кривой Безье. |
Аналогичным образом можно получать рациональные кривые Безье и в пространстве большего числа измерений.
 будем называть опорными точками рациональной кривой Безье, а
будем называть опорными точками рациональной кривой Безье, а 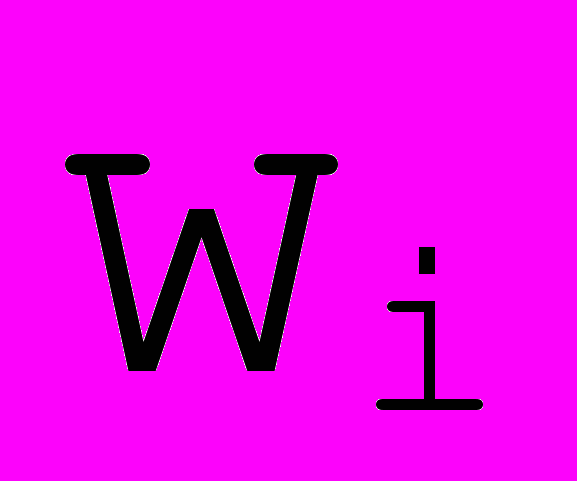 - весовыми функциями.
- весовыми функциями.Рассмотрим пример представления окружности составленной из 3-х рациональных кубических кривых Безье. Возьмем для примера один из сегментов. Положим
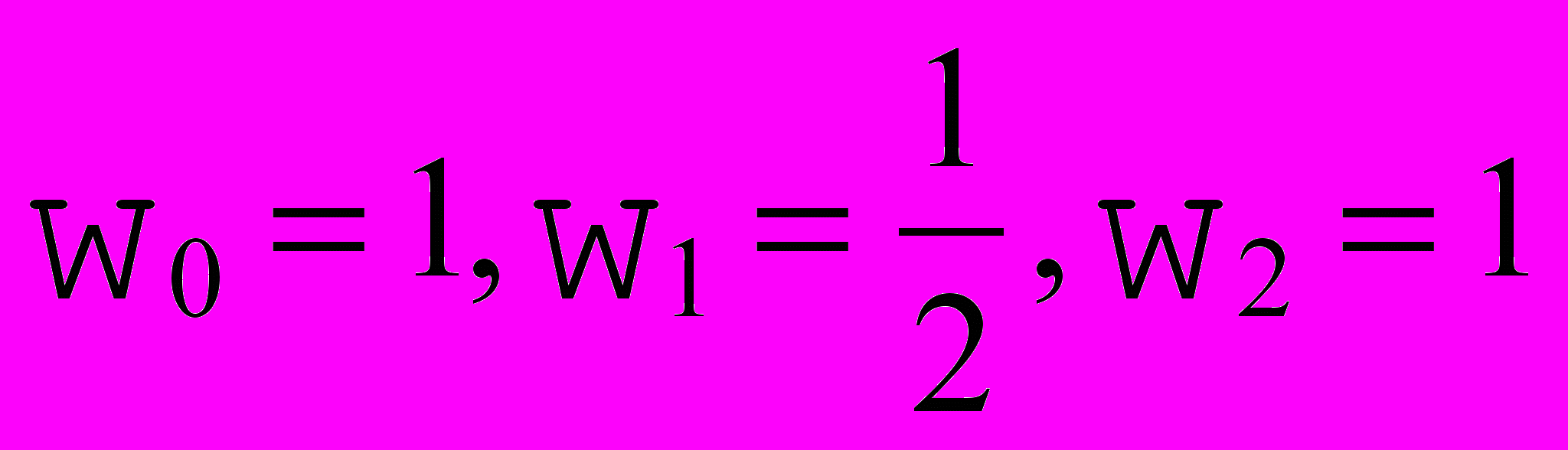 , а
, а  Рис. 16. Сегмент окружности, представленный рациональной кривой Безье. | 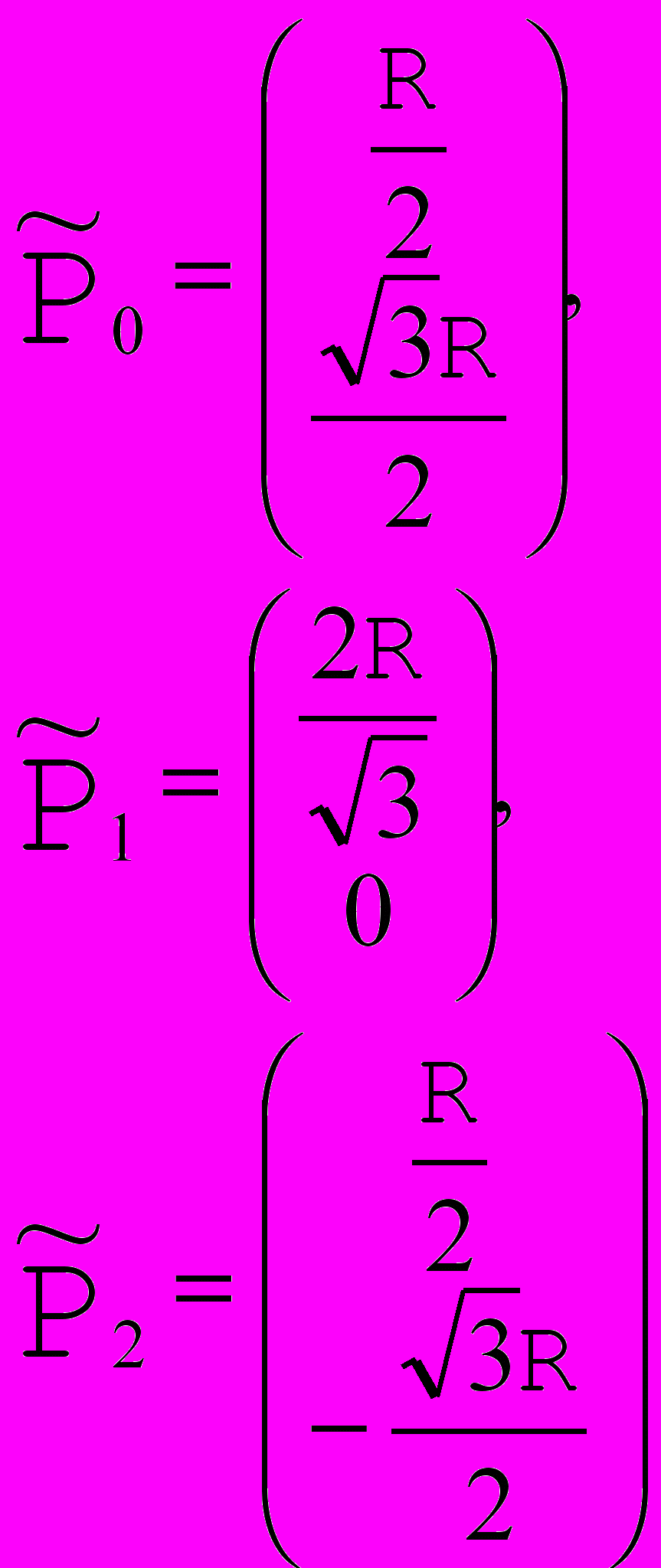 , где R - радиус окружности. , где R - радиус окружности. |
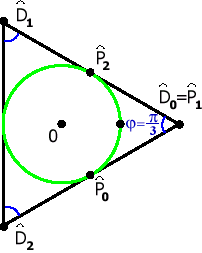 Рис. 17. Изображение окружности. | Итоговое изображение представлено на Рис. 17. Отметим, что за рамками данной лекции остались не разобранными многие важные вопросы, требующие более тщательного рассмотрения. Среди них следует отметить :
(Non-Uniform Rational B-Splines), которые в настоящее время являются фактически общепризнанным стандартом представления кривых, так как позволяют наиболее точно передавать форму кривой. 3) Аналогичную теорию можно строить и для поверхностей, что находит не меньшее, а, возможно, и большее применение в приложениях. Всех интересующихся описанием этих вопросов, а также тех, кто хотел бы узнать более подробно о вышеизложенном материале, отсылаем к замечательной книге [Роджерс, Адамс, 2001]. |
СПИСОК ЛИТЕРАТУРЫ
[Роджерс, Адамс, 2001] Роджерс.Д., Адамс.Дж. Математические основы машинной графики: Пер. с англ. - М.: Мир, 2001. - 604 с., ил.


