Geum.ru

Лекция Функция распределения

Вид материалаЛекция

Содержание


7.1. Свойства функции распределения
Прочие полезные свойства функций распределения
Функция распределения дискретного распределения
Подобный материал:

Лекция 7. Функция распределения


Далее в этом разделе
  • Свойства функции распределения
    • Прочие полезные свойства функций распределения
    • Функция распределения дискретного распределения



Заметим, что на том же отрезке [0,1] вероятности попадания в множества положительной меры совсем не нулевые. И термин «наудачу» мы когда-то описывали как раз в терминах вероятностей попадания в множества.

Может быть, разумно описать распределение случайной величины, задав для любого множества вероятность принять значения из этого множества? Это действительно полная характеризация распределения, но уж очень трудно с ней работать — слишком много множеств на прямой.

Нельзя ли обойтись заданием вероятностей попадания в какой-нибудь меньший набор множеств на прямой? Оказывается, что можно ограничиться только вероятностями попадания в интервалы 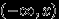для всех 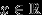, с помощью которых можно будет определить и вероятность попасть в любое другое множество.

Замечание 11. Можно с таким же успехом ограничиться набором вероятностей попадания в интервалы 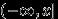, или в 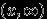, или в 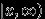, или в 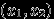. Впрочем, последних уже слишком много. :-)

Определение 28.

Функцией распределения случайной величины 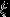называется функция 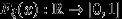, при каждом 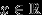равная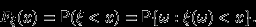



Пример 24.

Случайная величина 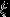имеет вырожденное распределение 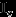. Тогда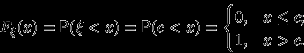



Пример 25.

Случайная величина 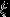имеет распределение Бернулли 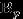. Тогда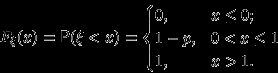



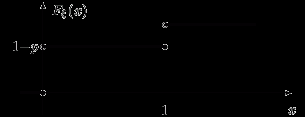
Пример 26.

Будем говорить, что случайная величина 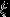имеет равномерное распределение на отрезке 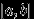и писать 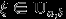(«uniform»), если 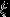— координата точки, брошенной наудачу на отрезок 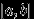числовой прямой. Это распределение можно задать и с помощью функции распределения: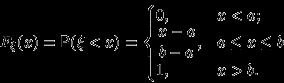



Упражнение 8.

Построить графики функций распределения для распределения Пуассона, биномиального и геометрического распределения.


7.1. Свойства функции распределения


Теорема 18.

Функция распределения 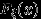обладает следующими свойствами:

F1) Функция распределения 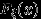не убывает: ;

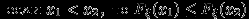F2) Существуют пределы 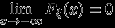и .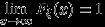

F3) Функция распределения 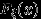непрерывна слева: .

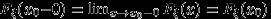Доказательство свойства (F1).

Если 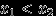, то 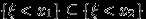. Поэтому .

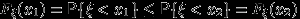Q.D.E.

Доказательство свойства (F2).

Замечание 12.

Если ряд, составленный из неотрицательных слагаемых 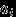, сходится, то есть существует 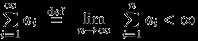, то «хвост» ряда стремится к нулю: .

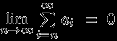Замечание 13.

Существование пределов в свойствах (F2), (F3) вытекает из монотонности и ограниченности функции 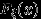. Так что остается доказать равенства

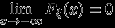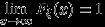, и .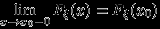

Замечание 14.

Если существует 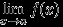, то для произвольной последовательности 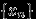такой, что 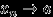, имеет место равенство .

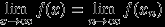По замечанию 14, для доказательства 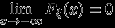достаточно доказать, что 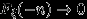при .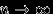

Представим событие 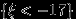(например) как счетное объединение событий: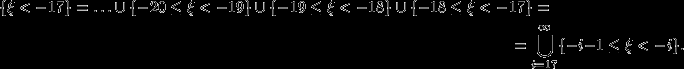




Используя 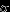-аддитивность вероятности, и помня, что 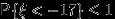, получим: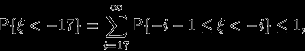



и, по замечанию 12,



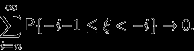
Но



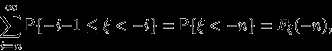
и сходимость 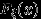к нулю при 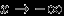доказана.

Итого: есть ряд, составленный из вероятностей, сумма которого тоже есть вероятность и, следовательно, конечна. А из того, что ряд сходится, по замечанию 12 вытекает сходимость «хвоста» ряда к нулю. Осталось посмотреть на этот хвост и убедиться, что он равен как раз той вероятности, сходимость к нулю которой нам нужно доказать. Точно так же докажем и остальные свойства.
По замечанию 14, для доказательства 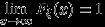достаточно доказать, что 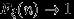при 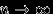, или что .

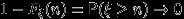Представим событие 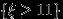(например :-)) как счетное объединение событий: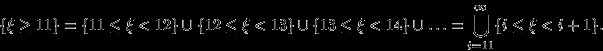



В силу -аддитивности вероятности,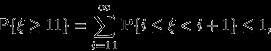



и, по замечанию 12,



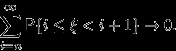
Но



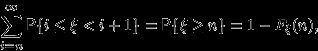
и сходимость 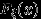к единице при 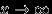доказана.

Q.D.E.

Доказательство свойства (F3).

Согласно замечанию 14, достаточно доказать, что 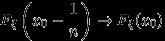при 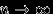. Или, что то же самое, доказать, что



(12)

Представим событие 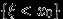как счетное объединение событий: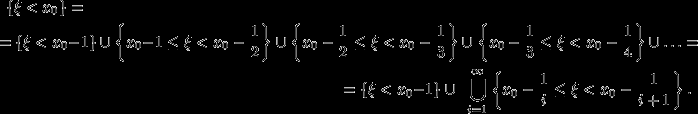




В силу 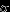-аддитивности вероятности,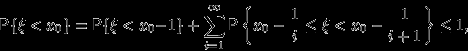



поэтому снова



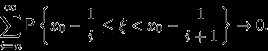
Но 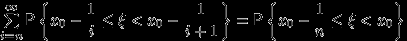, и эта вероятность, как мы только что видели, стремится к нулю с ростом 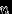. Тогда, по (12), 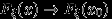при 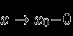(непрерывность слева).

Q.D.E.

Как утверждает следующая теорема, три доказанных свойства полностью описывают класс функций распределения. То, что любая функция распределения ими обладает, мы с вами доказали. Оказывается, верно и обратное: любая функция с такими тремя свойствами есть функция распределения.

Теорема 19.

Если функция 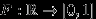удовлетворяет свойствам (F1)-(F3), то 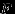есть функция распределения некоторой случайной величины 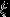, то есть найдется вероятностное пространство 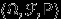и случайная величина 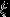на этом пространстве, что .

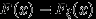Эту теорему мы доказывать не станем. Хотя ее можно попробовать доказать конструктивно — предъявив то вероятностное пространство (проще всего отрезок 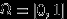с 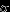-алгеброй борелевских множеств и мерой Лебега :-) и ту случайную величину, о существовании которых идет речь. Непременно попробуйте сделать это! Например, можно попробовать, не подойдет ли

.

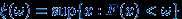Прочие полезные свойства функций распределения


F4) В любой точке 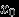разниц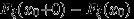а равна :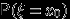






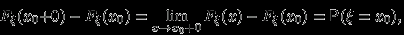
или, иначе,



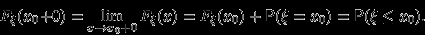
Упражнение 9.

Докажите сами (точно так же, как мы доказывали (F2) и (F3)).

Заметим, что разница 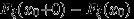между пределом при стремлении к 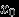справа и значением в точке 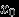есть величина скачка функции распределения, и равна нулю, если функция распределения непрерывна (справа) в точке 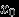. Слева, напомню, функция распределения непрерывна всегда.

Следствие 4.

Если функция распределения 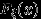непрерывна в точке 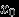, то .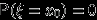

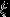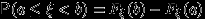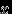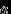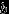F5) Для любой случайной величины имеет место равенство . Если же функция распределения непрерывна (для любого , или только в точках и ), то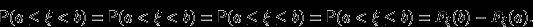



Доказательство.

Доказывать нужно только равенство 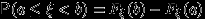, поскольку все остальные равенства следуют из него с учетом следствия 4. Напомню, что этим равенством мы уже много раз пользовались, доказывая свойства (F2), (F3).

Заметим, что 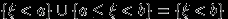, и первые два события несовместны. Поэтому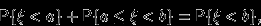



или

,

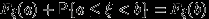что и требовалось доказать.

Q.D.E.

Функция распределения дискретного распределения


Мы уже видели, как выглядят функции распределения некоторых дискретных распределений.

Из свойств (F4), (F5) следует

Свойство 6.

Случайная величина имеет дискретное распределение тогда и только тогда, когда функция распределения 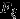— ступенчатая функция. При этом возможные значения 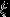— точки 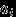скачков 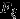, и 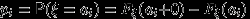— величины скачков.

Упражнение. Доказать, что любая функция распределения имеет не более чем счетное число точек разрыва (или «скачков»).

Указание. Сколько скачков величиной более 1/2 может иметь функция распределения? А величиной более 1/3? Более 1/4?

В следующей главе мы рассмотрим случайные величины, функции распределения которых не удовлетворяют свойству 6 хотя бы потому, что они вовсе не имеют разрывов. Более того, мы выделим класс функций распределения, которые «восстанавливаются по своей производной» с помощью интегрирования (так называемые абсолютно непрерывные функции).