Копенгагене Ганс Христиан Эрстед читал лекции
| Вид материала | Лекции |
Содержание3.4. Характеристики магнитного поля в магнетиках S, ограниченную контуром l |
- Родился Ганс Христиан Андерсен, датский писатель-сказочник. Андерсен Ганс Христиан, 113.53kb.
- Урок литературного чтения в 3-м классе "Ганс Христиан Андерсен. Сказка, 28.29kb.
- Ганс Христиан Андерсен. Снежная королева рассказ, 469.28kb.
- Ганс Христиан Андерсен. Снежная королева рассказ, 490.21kb.
- Ганс Христиан Андерсен, 1327.11kb.
- Ганс Христиан Андерсен! Априехал я сюда поработать. Акто знает, кем я работаю? Правильно,, 228.36kb.
- Ганс Христиан Андерсен. Очерк жизни и творчества. М. Детгиз. 1957 (любой другой год, 16.85kb.
- Г в селе Понино, Глазовского уезда, Вятской губернии / теперь уасср /. Впериод с 1909, 257.82kb.
- Ганс Христиан Андерсен. Осказочнике. Бал литературных героев. «Соловей» сказка, 31.71kb.
- Европейский Институт Общественной Администрации, Маастрих Дает лекции, 28.46kb.
3.4. Характеристики магнитного поля в магнетиках
Магнитное поле в магнетиках
 является результатом суперпозиции внешнего поля
является результатом суперпозиции внешнего поля 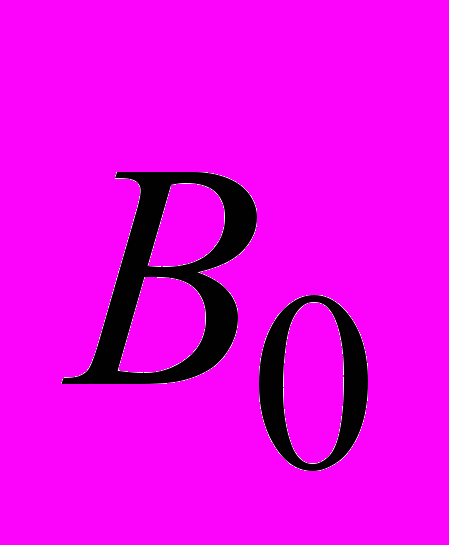 и собственного магнитного поля магнетика
и собственного магнитного поля магнетика 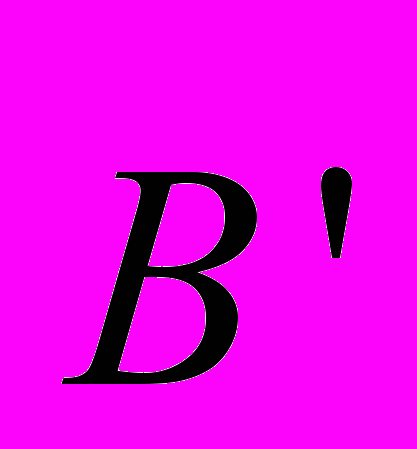 :
:
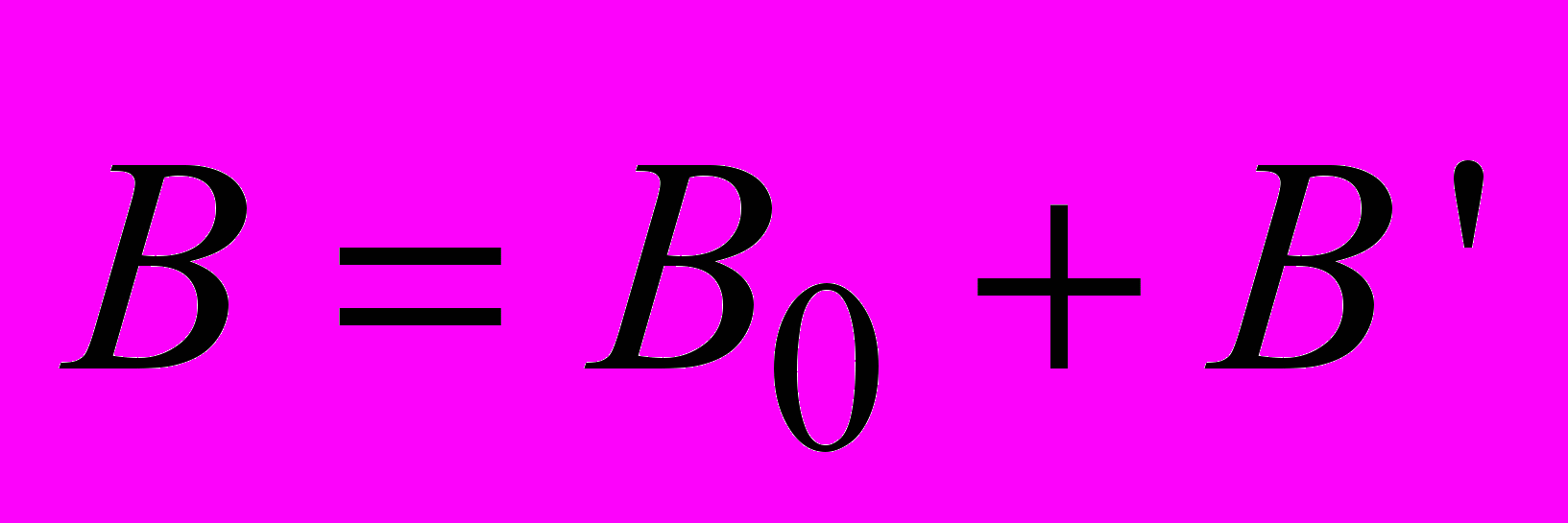 .
.В общем случае для произвольного замкнутого контура l в магнетике по теореме о циркуляции вектора магнитной индукции (подразд. 1.6) имеем
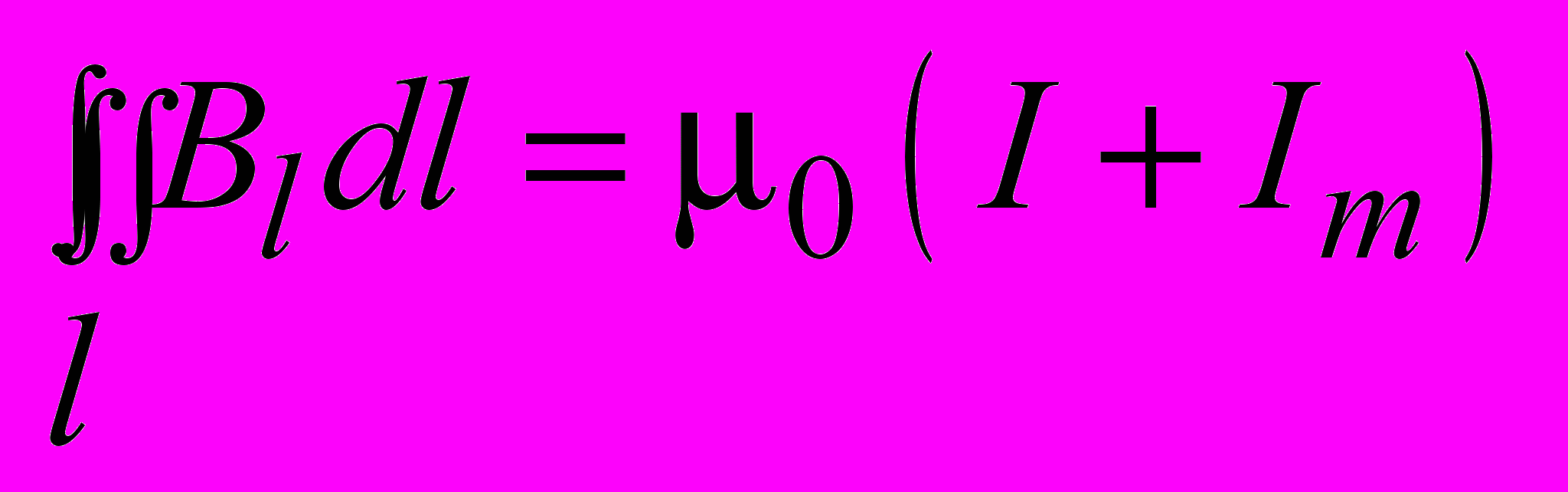 . (3.19)
. (3.19)Т
 ок, охватываемый контуром l, представлен как алгебраическая сумма токов проводимости
ок, охватываемый контуром l, представлен как алгебраическая сумма токов проводимости 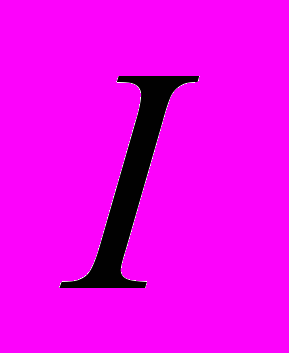 и алгебраическая сумма молекулярных токов Ампера
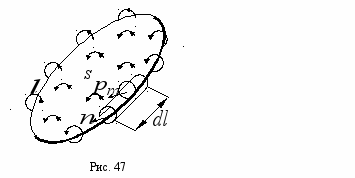
и алгебраическая сумма молекулярных токов Ампера 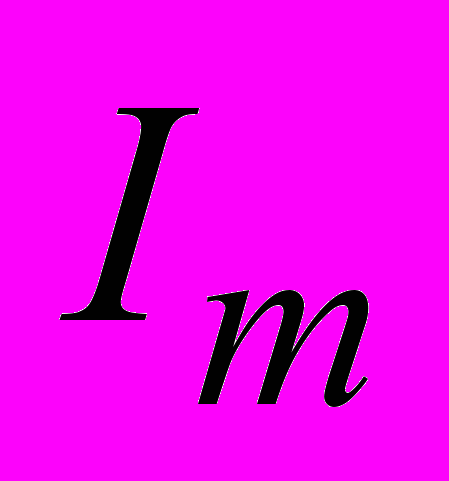 , проходящих через поверхность S, ограниченную контуром l (рис. 47).
, проходящих через поверхность S, ограниченную контуром l (рис. 47).Молекулярные токи, не охватывающие контур, дважды пересекают эту поверхность: один раз в одном направлении, другой раз – в противоположном. Вклад таких токов в суммарный ток
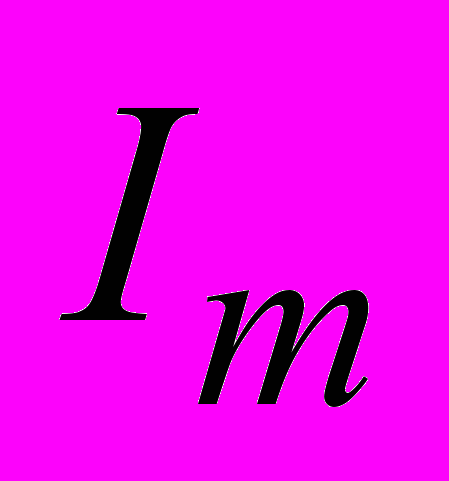 равен нулю. Молекулярные токи, охватывающие контур l, пересекают поверхность S один раз и должны быть учтены в сумме токов Ампера
равен нулю. Молекулярные токи, охватывающие контур l, пересекают поверхность S один раз и должны быть учтены в сумме токов Ампера 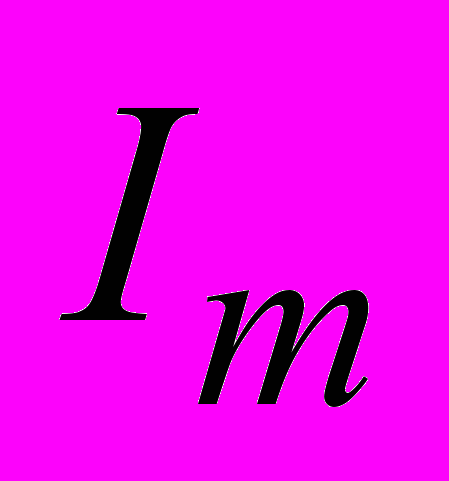 .
.Н
 айдем вклад
айдем вклад 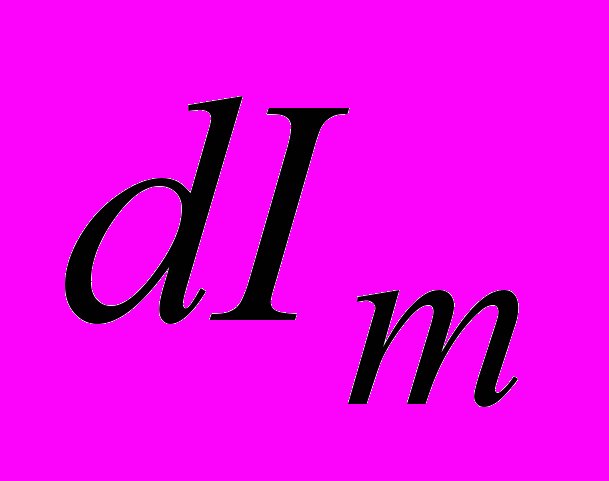 токов, которые охватывают малый элемент
токов, которые охватывают малый элемент  контура. Построим косой цилиндр, ось которого совпадает с
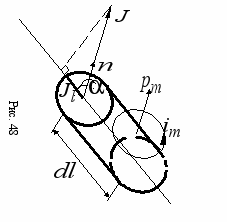
контура. Построим косой цилиндр, ось которого совпадает с  , основания параллельны плоскостям круговых молекулярных токов (рис. 48). Площадь основания косого цилиндра равна площади
, основания параллельны плоскостям круговых молекулярных токов (рис. 48). Площадь основания косого цилиндра равна площади 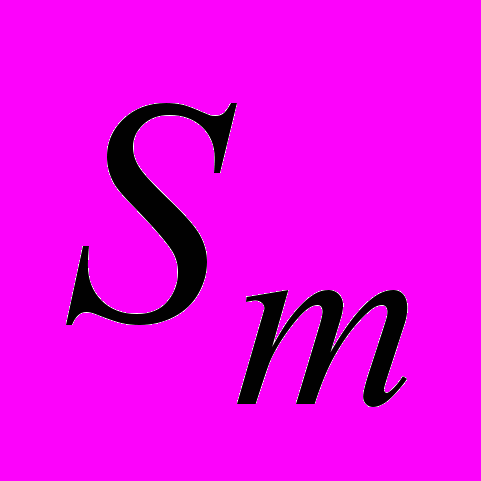 , ограниченной молекулярным током. Как видно из рис. 48, элемент контура
, ограниченной молекулярным током. Как видно из рис. 48, элемент контура  , образующий с направлением вектора намагничивания
, образующий с направлением вектора намагничивания 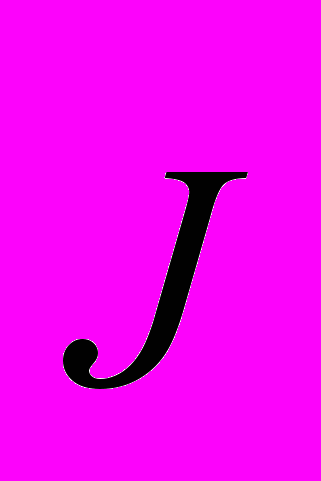 угол
угол 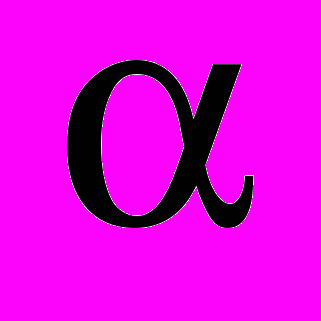 , охватывается теми молекулярными токами, центры которых попадают внутрь косого цилиндра объемом dV, который определяется формулой
, охватывается теми молекулярными токами, центры которых попадают внутрь косого цилиндра объемом dV, который определяется формулой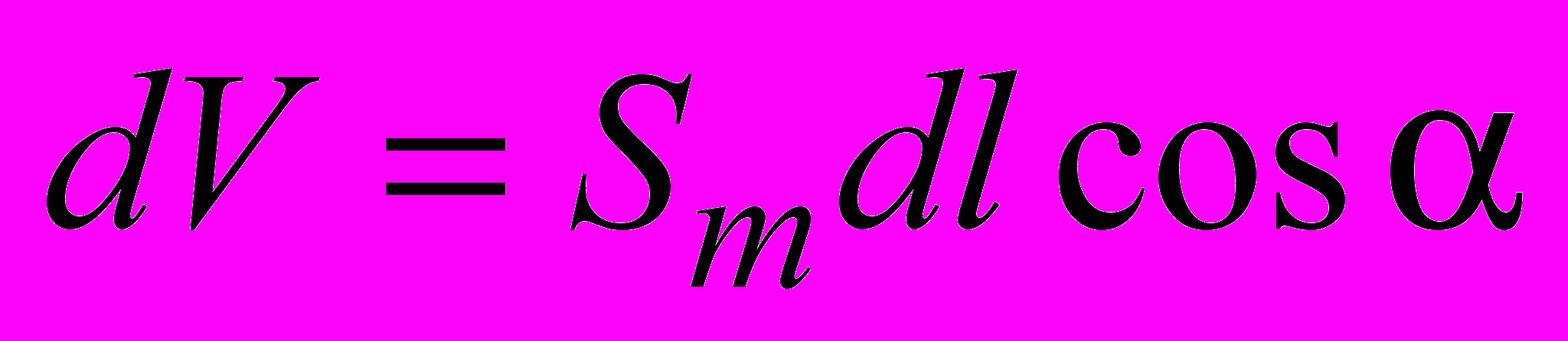 .
.Если n – число атомов (молекул) в единице объема магнетика, то для суммарного тока, охватывающего элемент
 , получаем
, получаем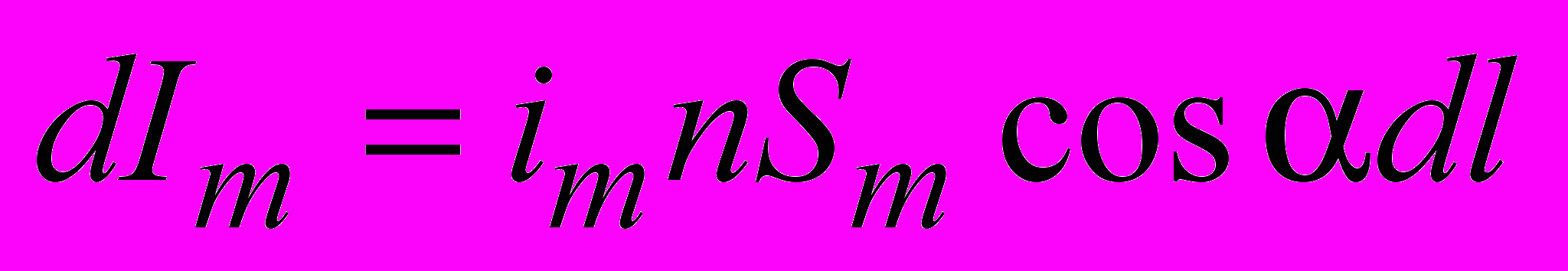 ,
,где
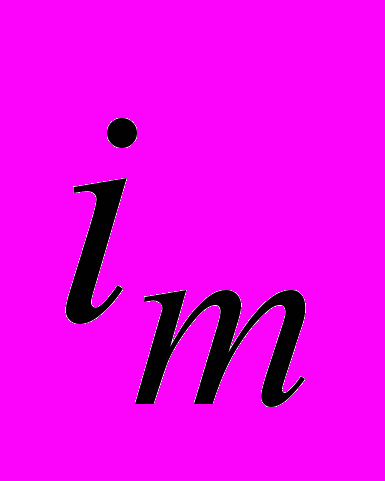 – сила молекулярного тока, магнитный момент которого
– сила молекулярного тока, магнитный момент которого 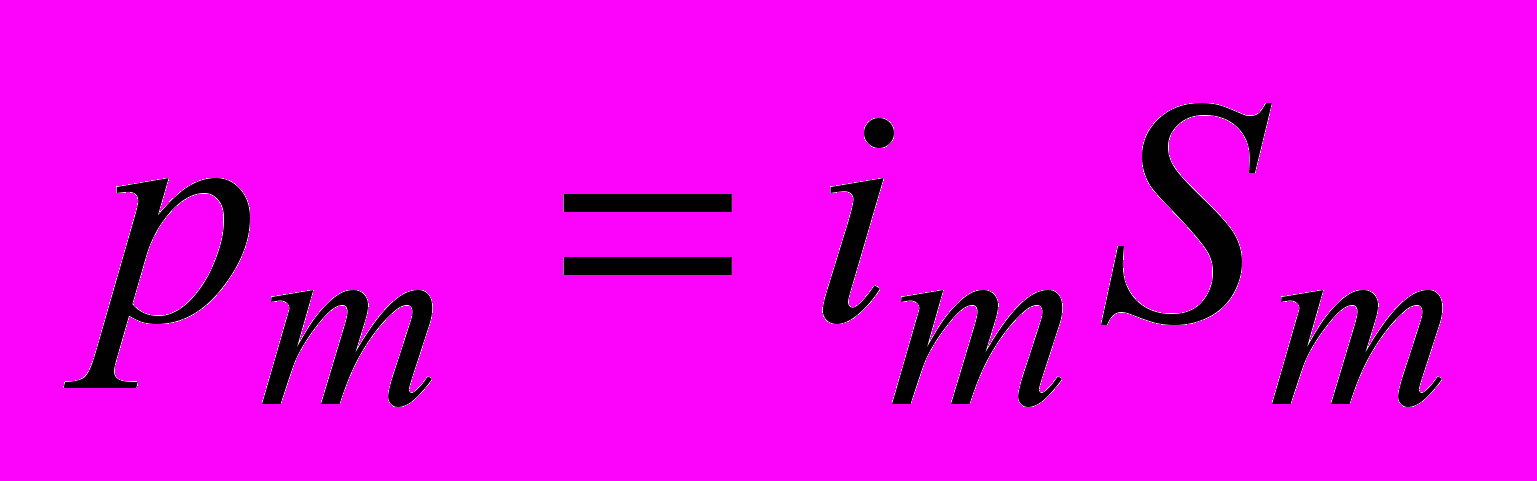 .
.Следовательно, выражение
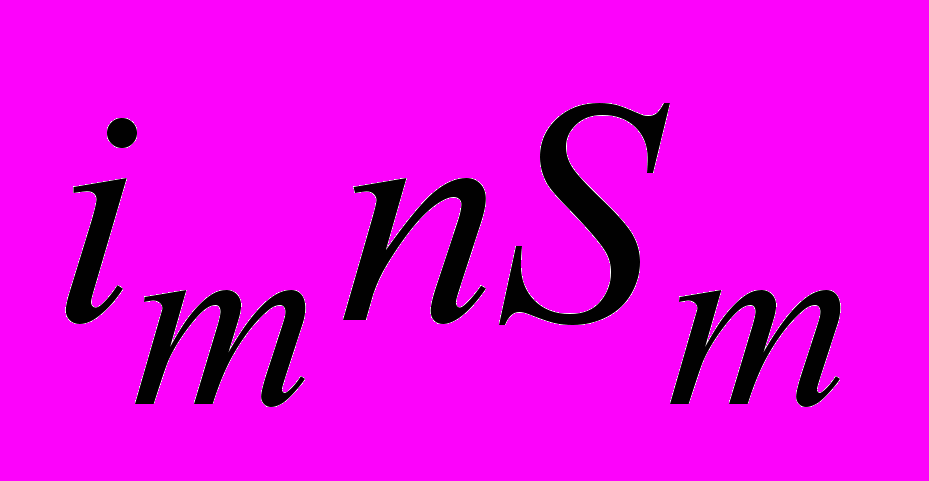 представляет собой магнитный момент единицы объема, т. е. модуль вектора
представляет собой магнитный момент единицы объема, т. е. модуль вектора 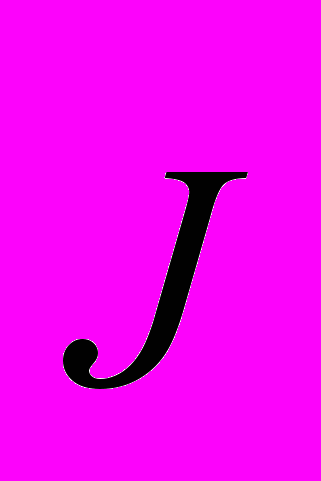 , а
, а 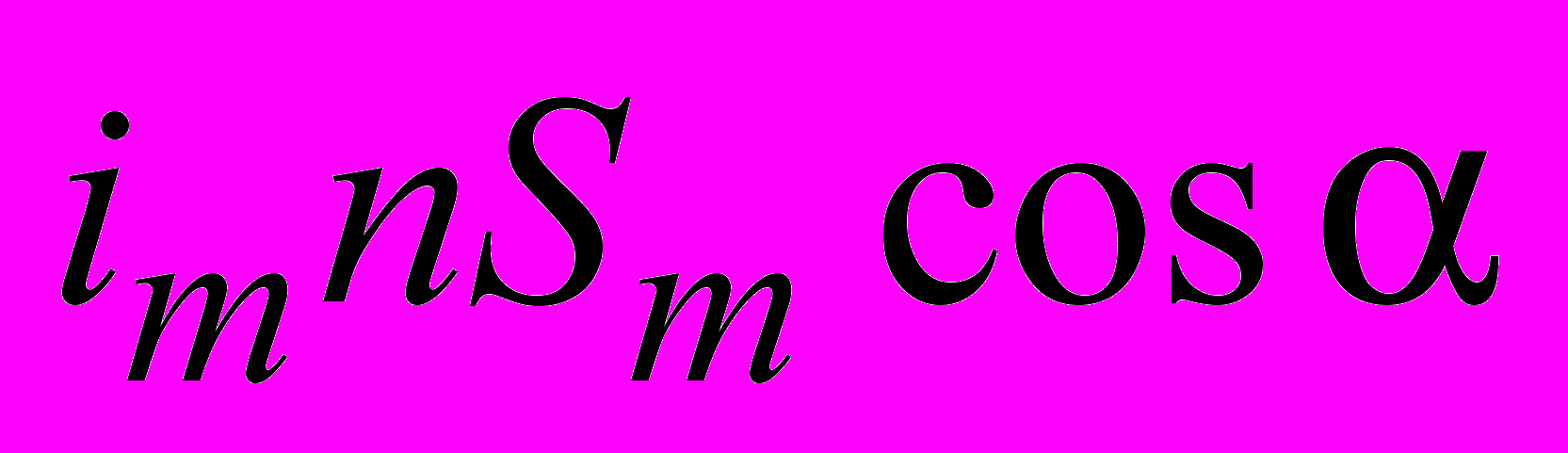 =
=  , где
, где  – проекция вектора
– проекция вектора 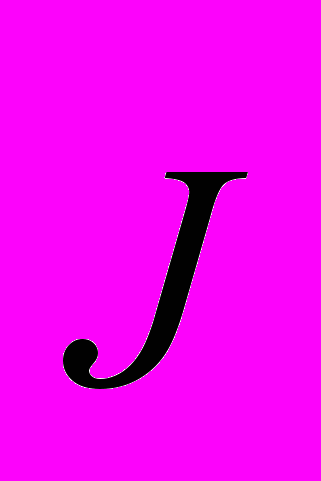 на направление элемента
на направление элемента 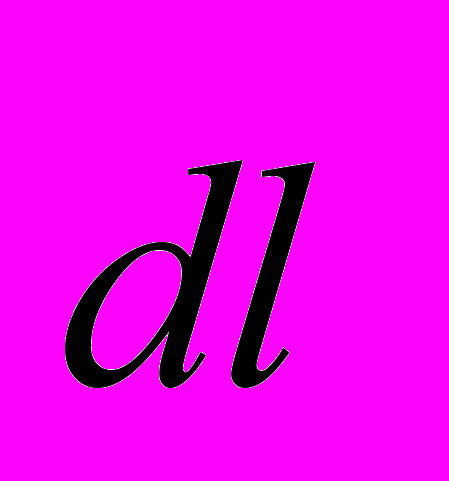 . Таким образом, для суммарного молекулярного тока, охватывающего элемент
. Таким образом, для суммарного молекулярного тока, охватывающего элемент 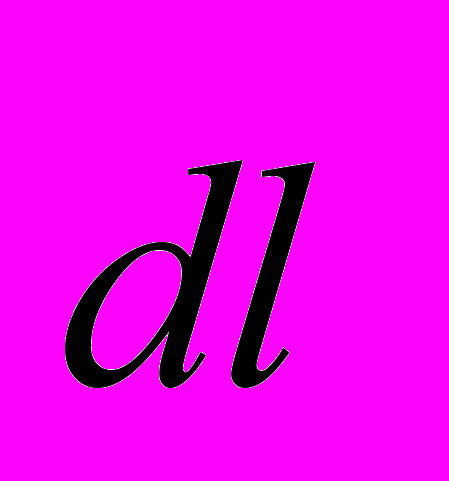 , получаем
, получаем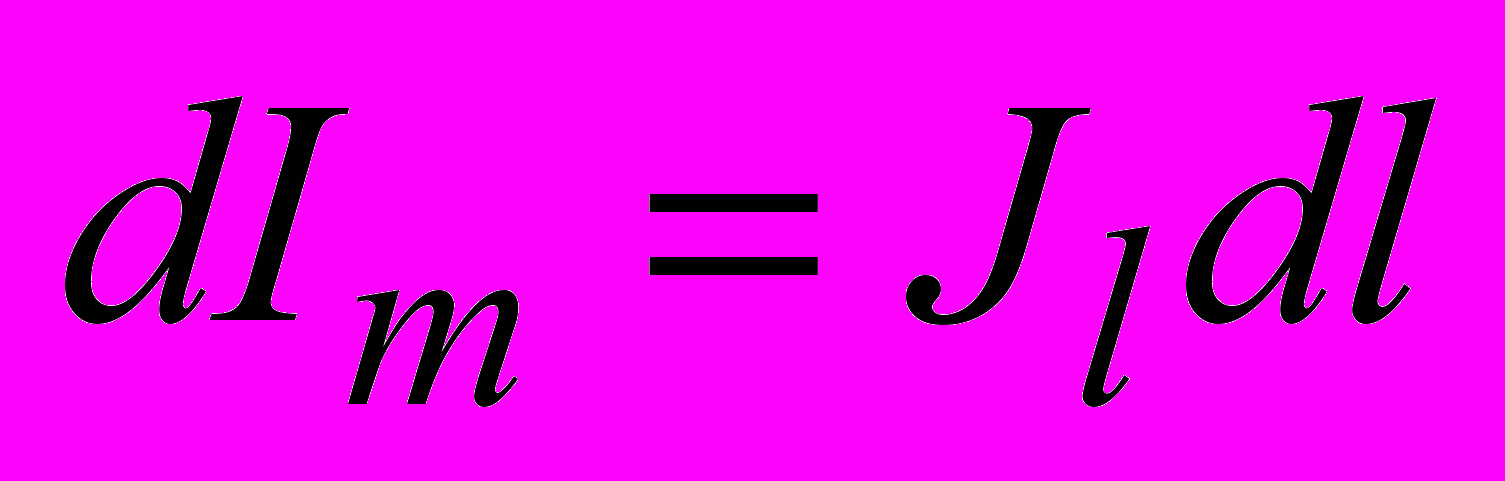 . (3.20)
. (3.20) Полную сумму молекулярных токов получим, проинтегрировав (3.20) по замкнутому контуру l:
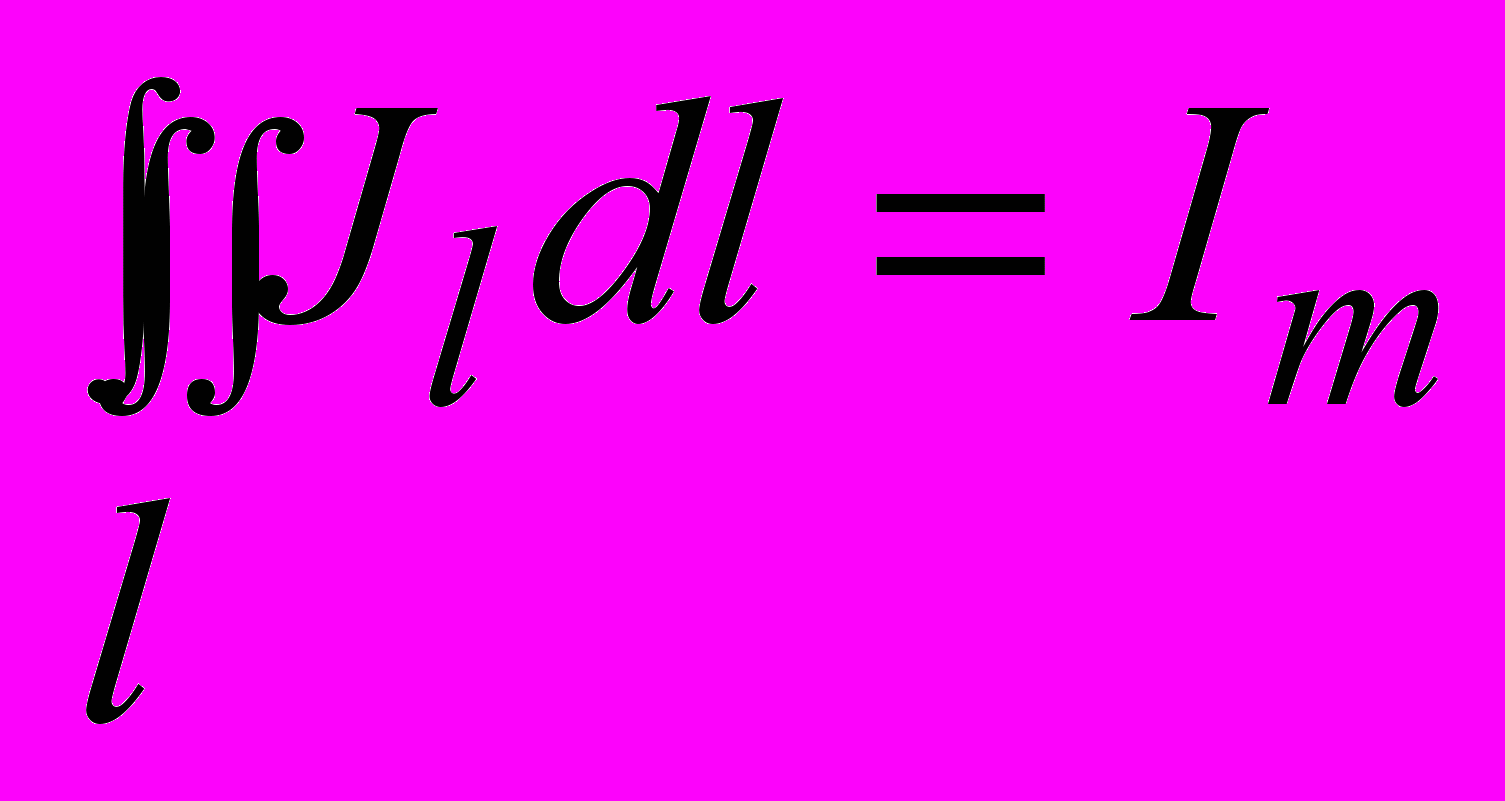 . (3.21)
. (3.21)Иными словами, циркуляция вектора намагничивания по произвольному замкнутому контуру равна алгебраической сумме молекулярных токов, проходящих через поверхность S, ограниченную этим контуром.
Подстановка (3.21) в (3.19) приводит к выражению
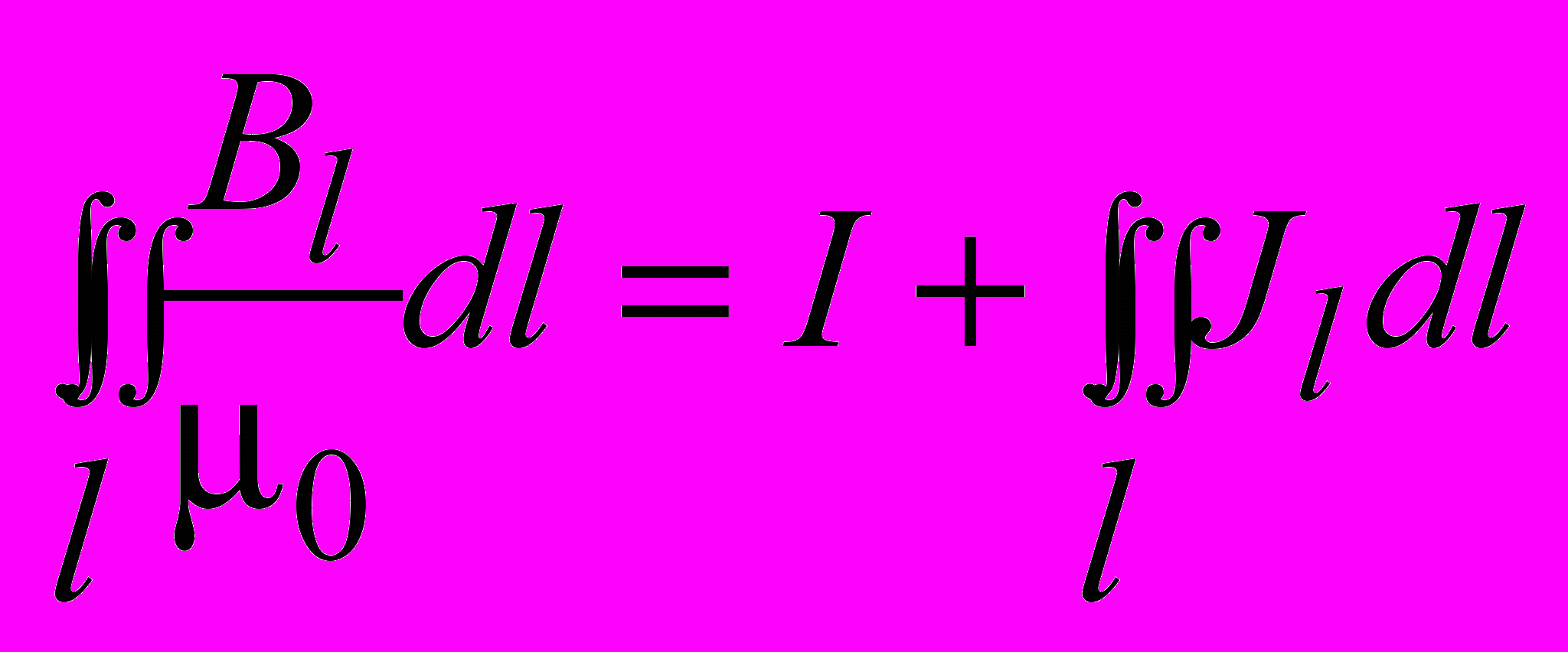 ,
,откуда
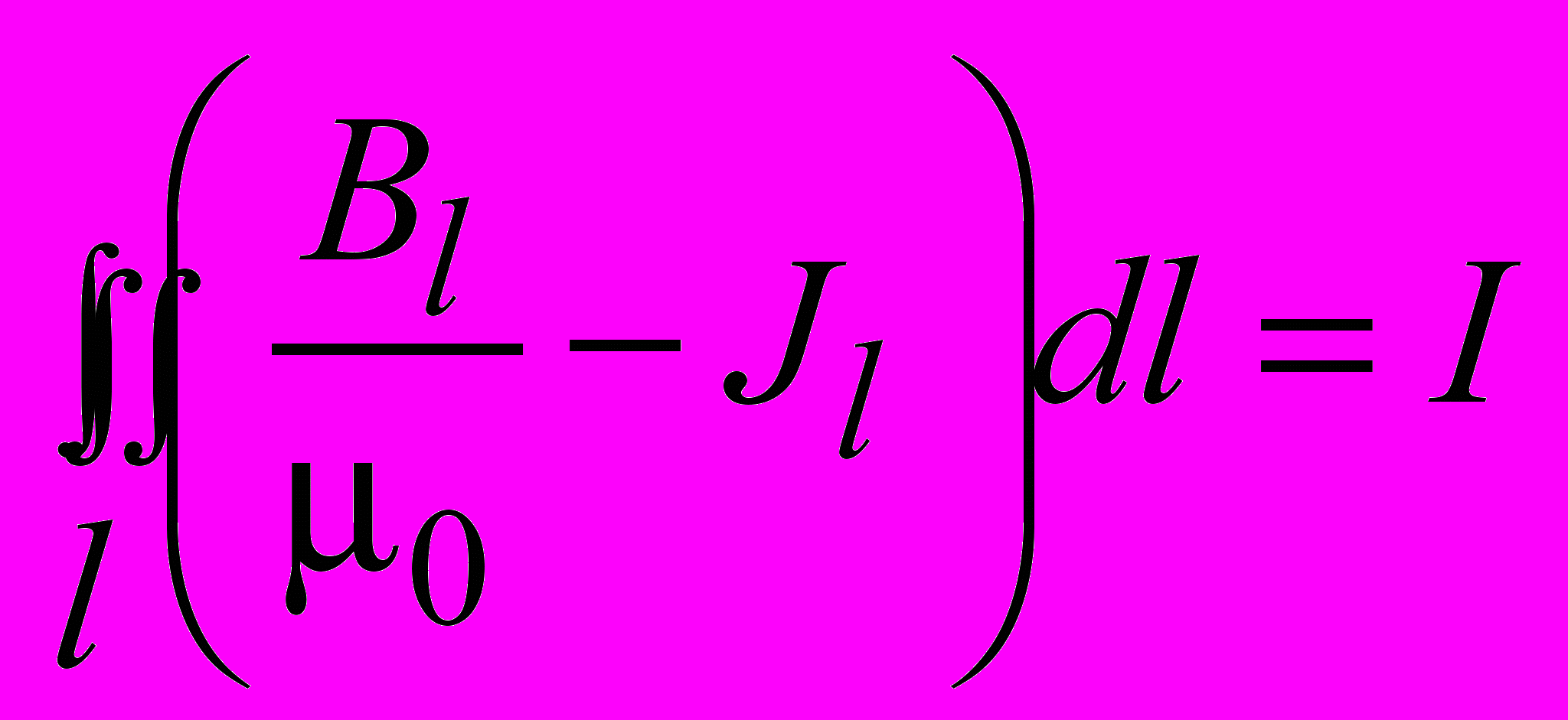 . (3.22)
. (3.22)Введем вектор напряженности магнитного поля
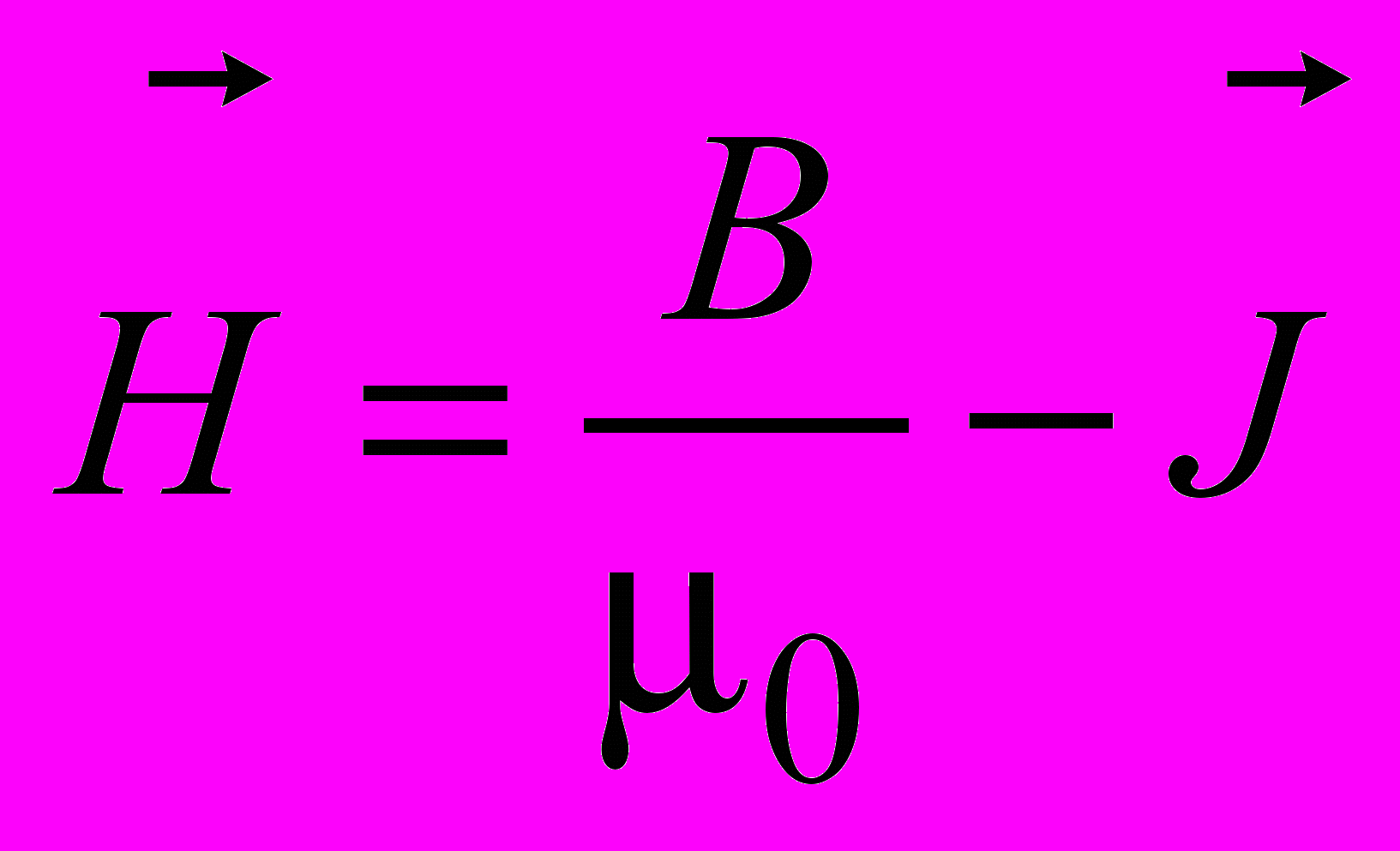 . (3.23)
. (3.23)Равенство (3.23) является определением напряженности магнитного поля. Тогда для проекции напряженности магнитного поля на направление элементарного перемещения получаем
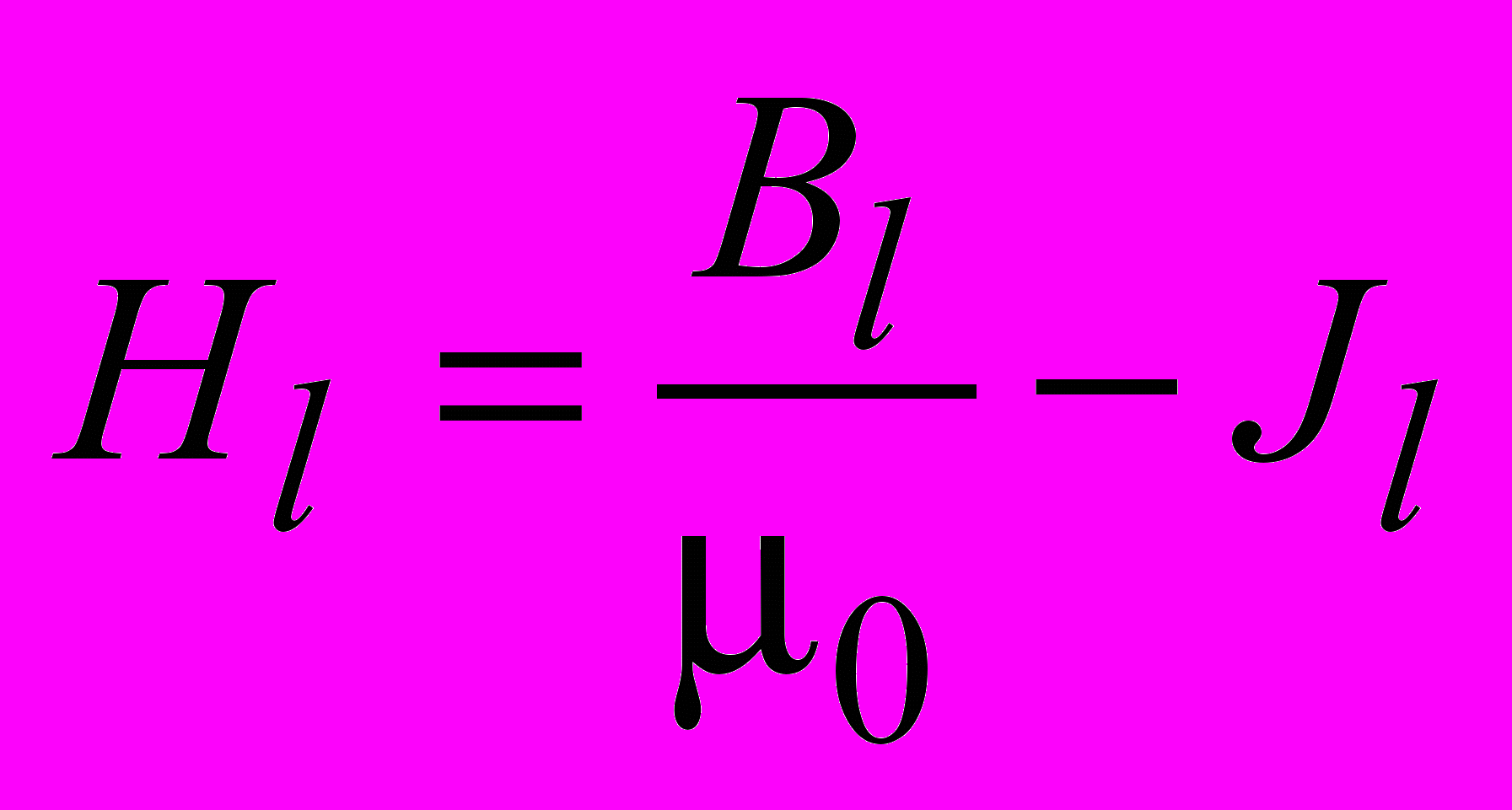 . (3.24)
. (3.24)Подстановка (3.24) в (3.22) приводит к теореме о циркуляции напряженности магнитного поля:
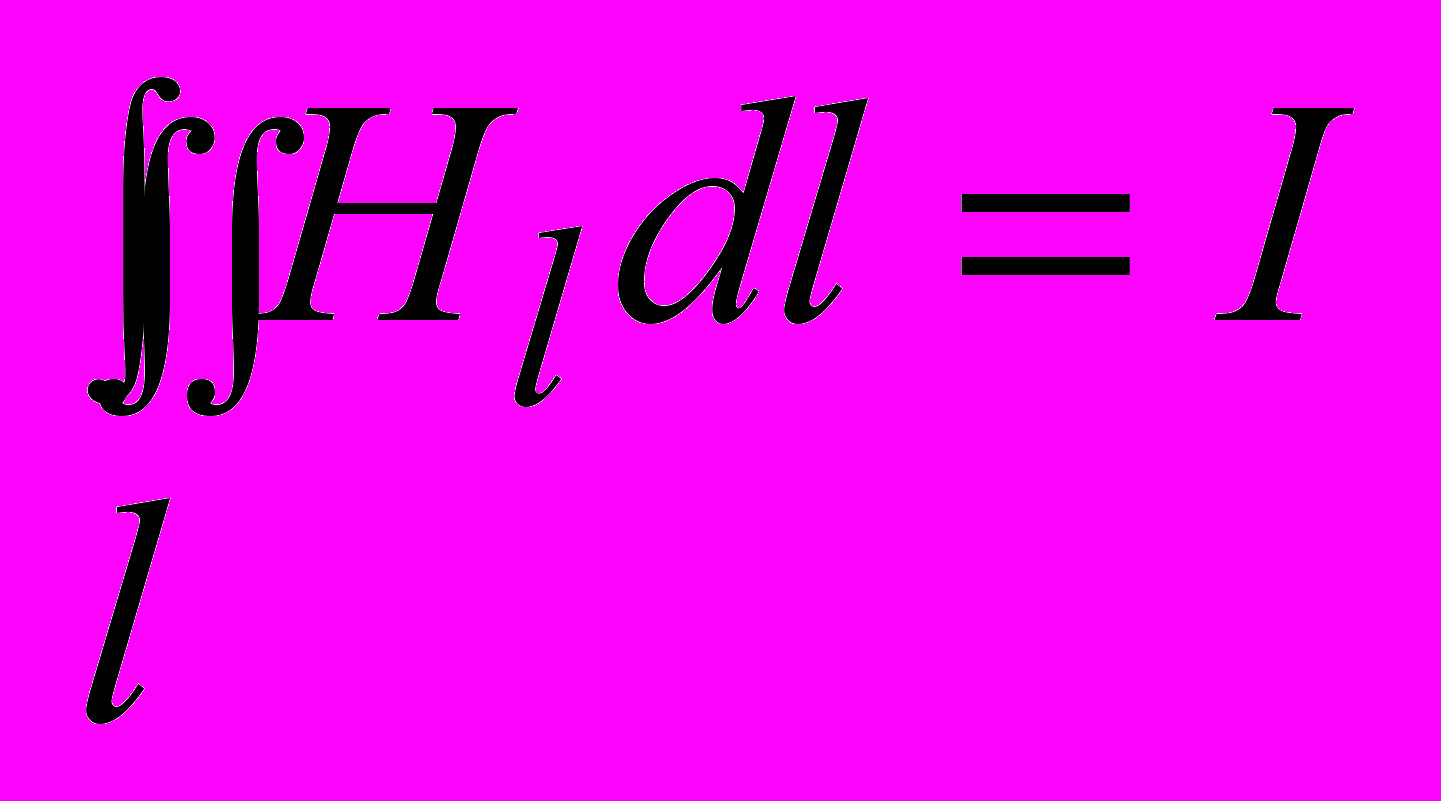 . (3.25)
. (3.25)Таким образом, циркуляция напряженности магнитного поля по произвольному замкнутому контуру равна алгебраической сумме токов проводимости, охватываемых этим контуром. Если контур проведен внутри проводящей среды, в которой текут токи проводимости, то (3.25) удобно представить в виде
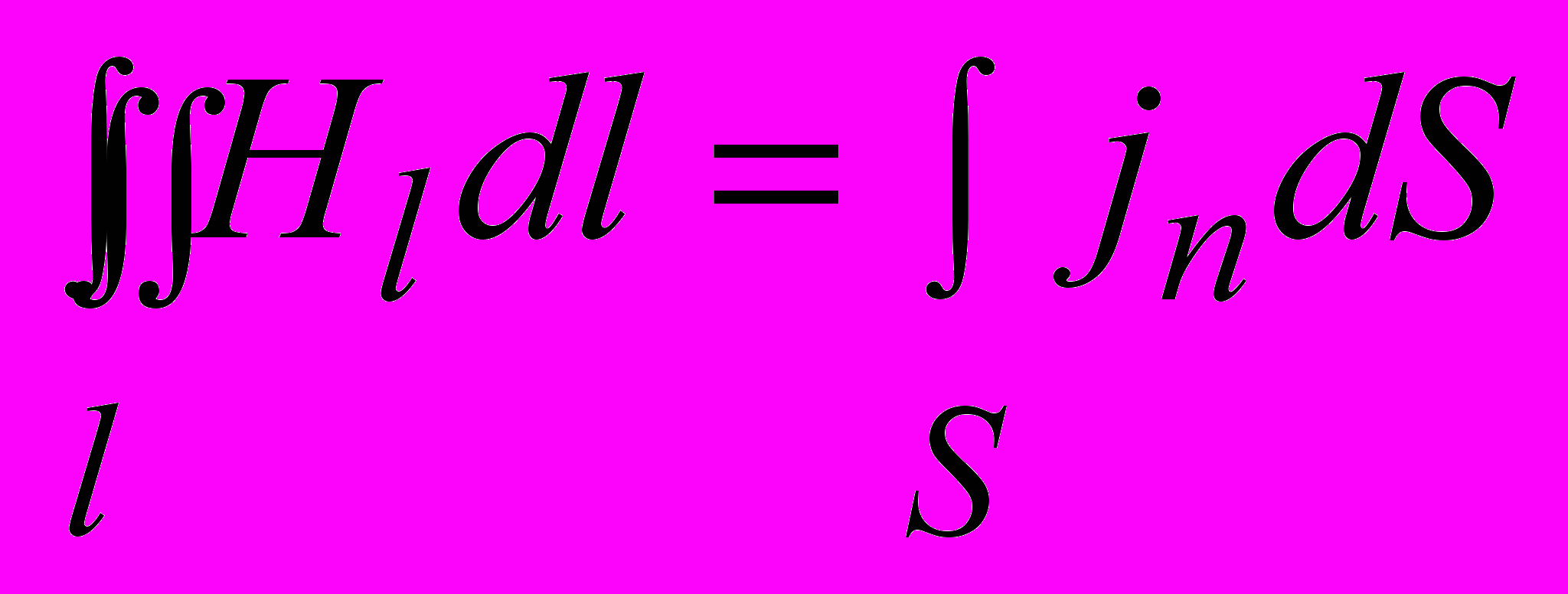 , (3.26)
, (3.26)где
 – проекция вектора плотности тока проводимости на направление нормали к элементу поверхности
– проекция вектора плотности тока проводимости на направление нормали к элементу поверхности  .
.Из (3.23) следует
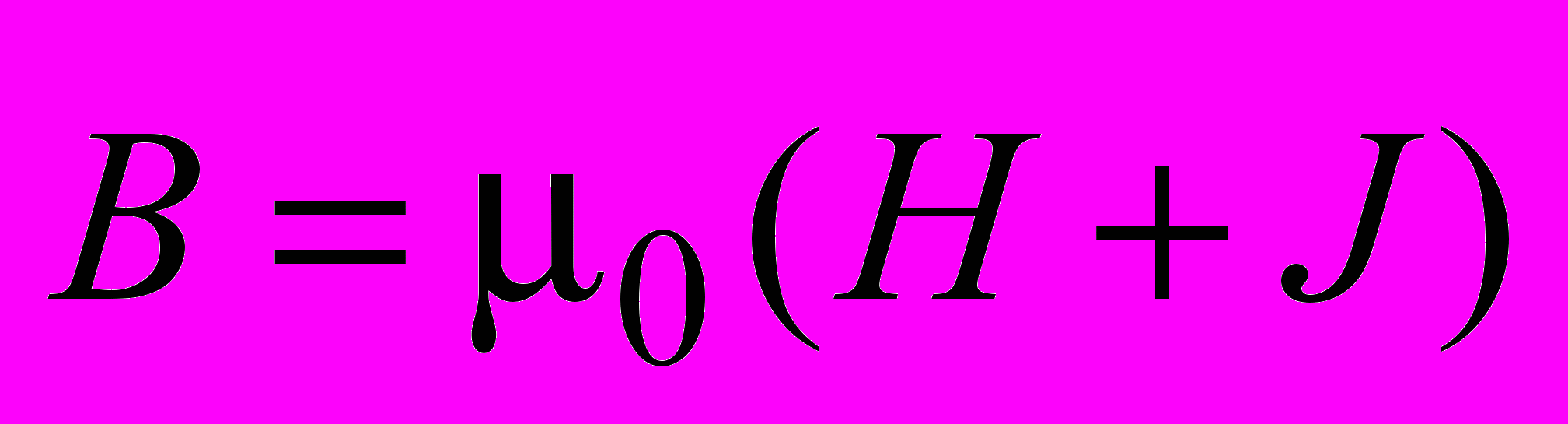 . (3.27)
. (3.27)Как показывает опыт, намагниченность
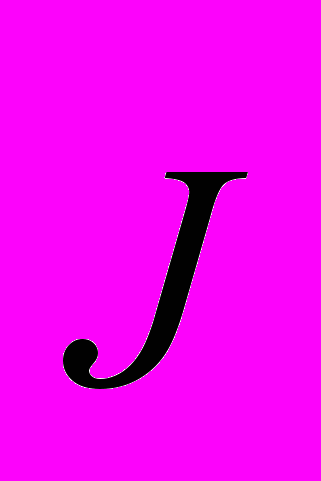 для пара- и диамагнетиков пропорциональна напряженности магнитного поля:
для пара- и диамагнетиков пропорциональна напряженности магнитного поля: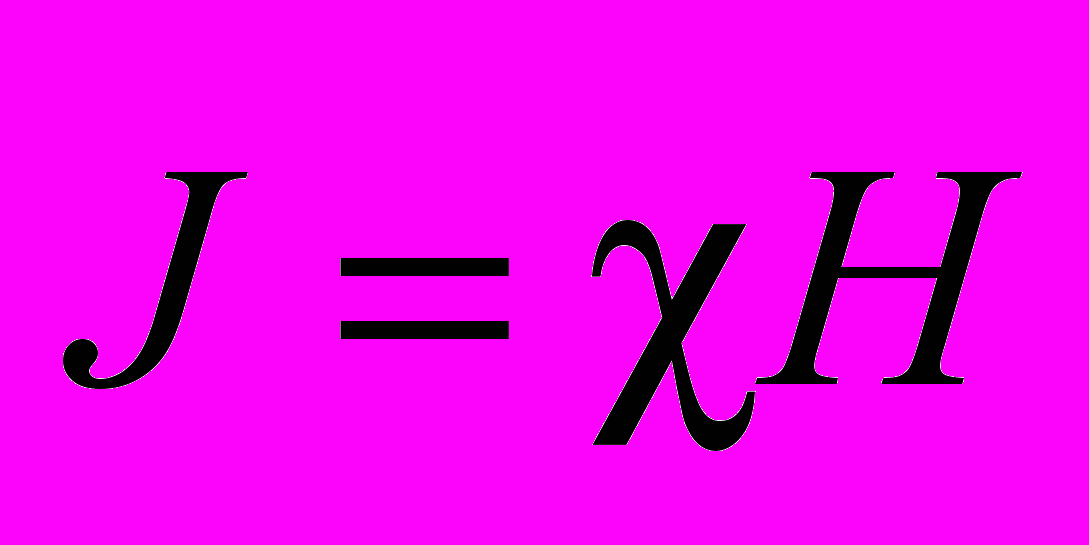 . (3.28)
. (3.28)Коэффициент пропорциональности
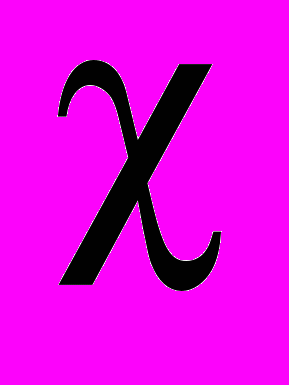 называется магнитной восприимчивостью.
называется магнитной восприимчивостью.Подстановка (3.28) в (3.27) дает связь между напряженностью и магнитной индукцией:
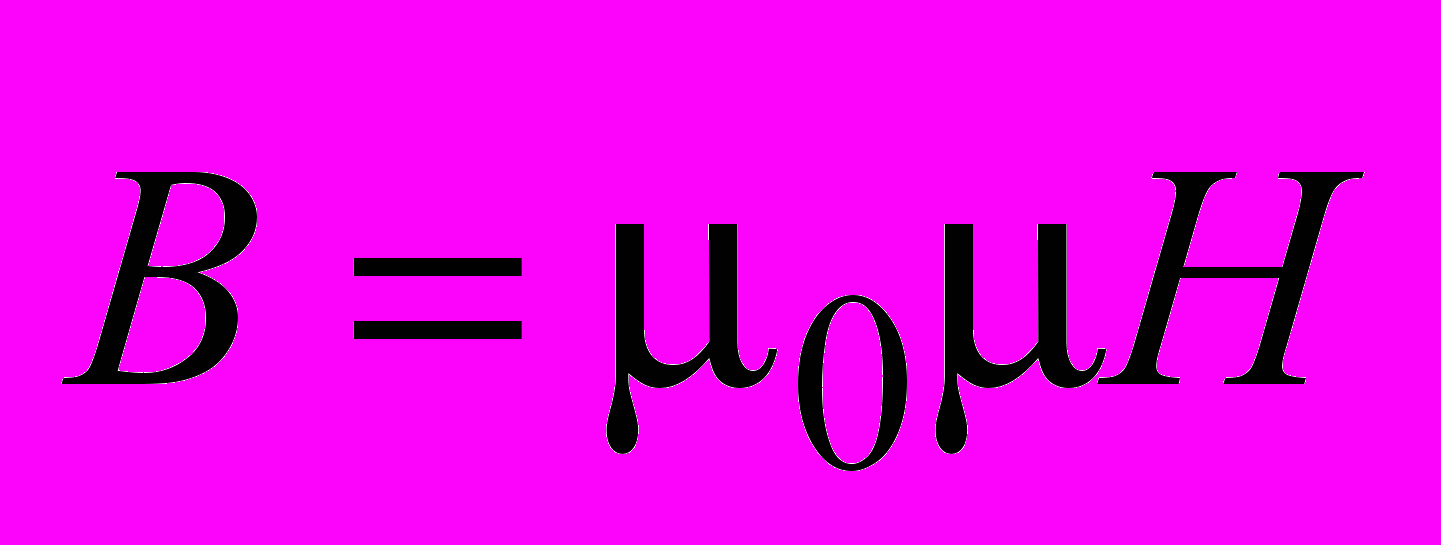 ,
,где
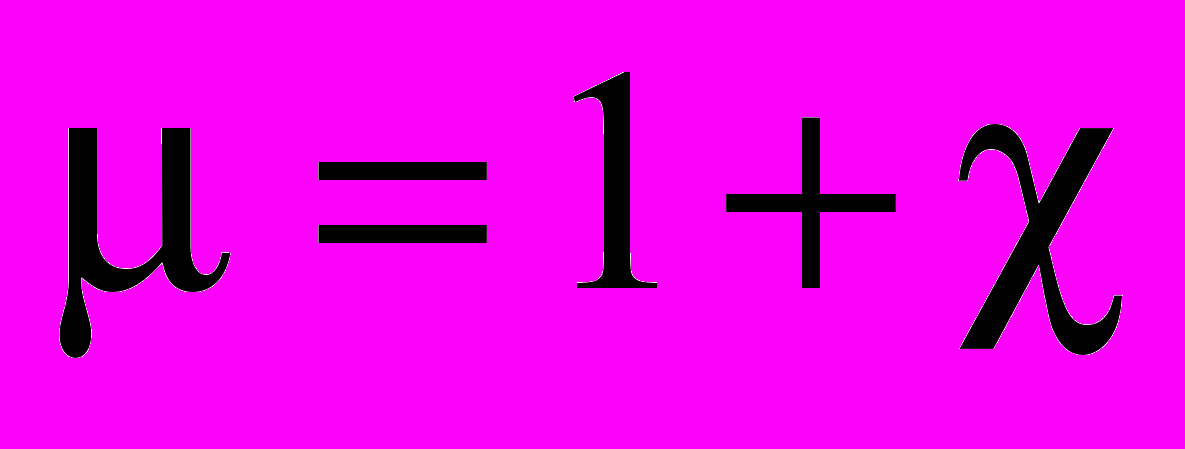 называется магнитной проницаемостью вещества. Магнитная восприимчивость
называется магнитной проницаемостью вещества. Магнитная восприимчивость 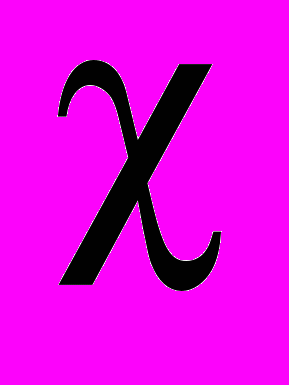 и магнитная проницаемость
и магнитная проницаемость 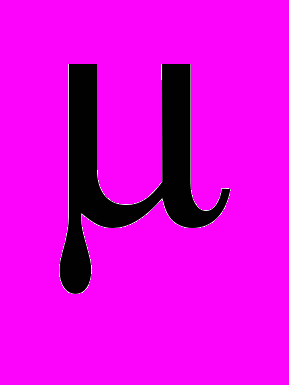 – величины, характеризующие магнитные свойства диамагнетиков и парамагнетиков.
– величины, характеризующие магнитные свойства диамагнетиков и парамагнетиков.У диамагнетиков магнитные моменты атомов (молекул) и вектор намагниченности
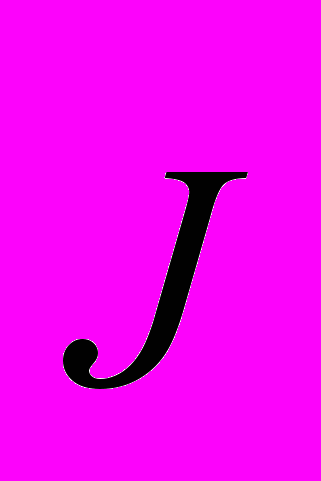 направлены противоположно вектору магнитной индукции и напряженности магнитного поля. Для диамагнетиков
направлены противоположно вектору магнитной индукции и напряженности магнитного поля. Для диамагнетиков 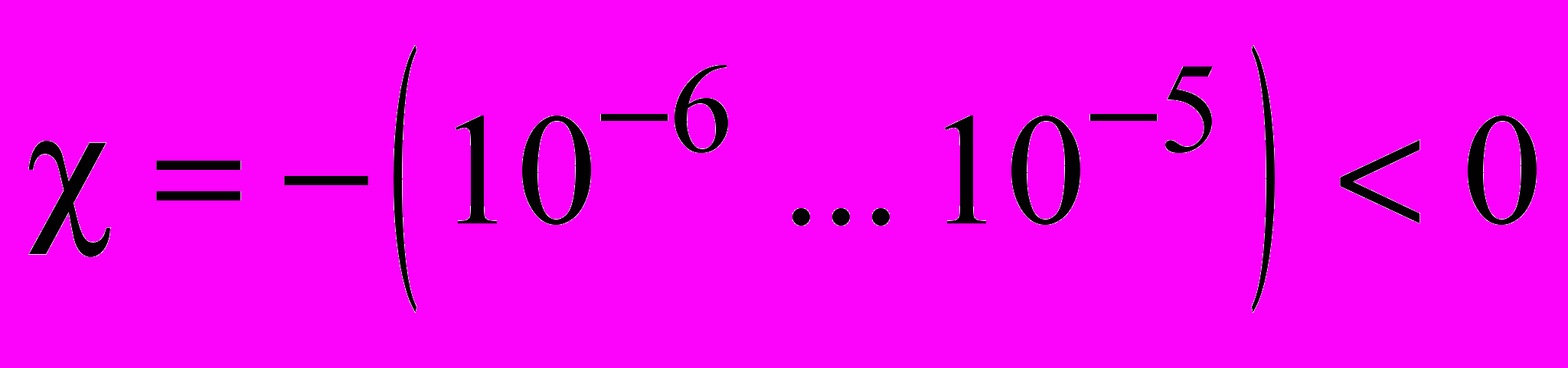 ,
, 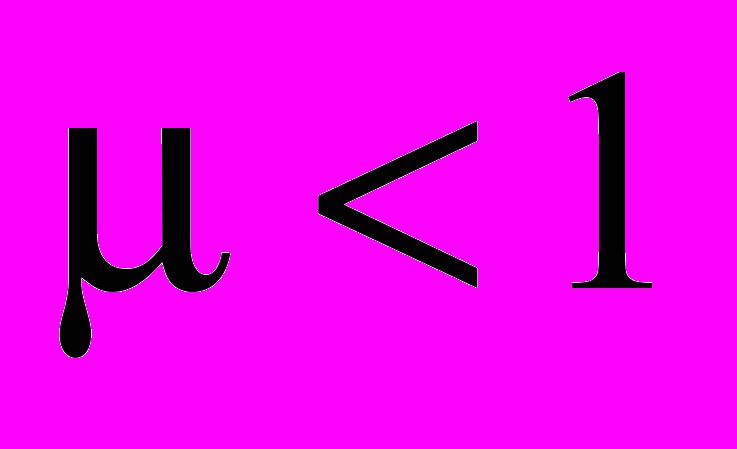 .
. У парамагнетиков магнитные моменты атомов (молекул), вектор намагниченности
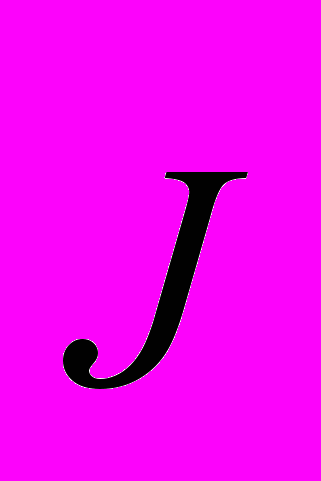 , вектор магнитной индукции и напряженность магнитного поля направлены в одну сторону. Для парамагнетиков при комнатных температурах
, вектор магнитной индукции и напряженность магнитного поля направлены в одну сторону. Для парамагнетиков при комнатных температурах 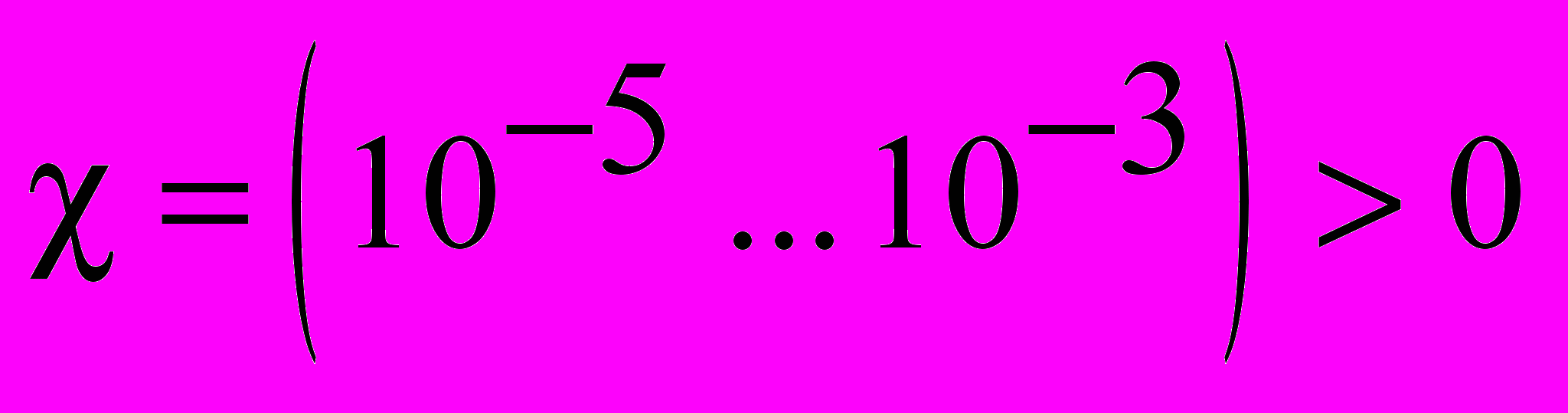 ,
, 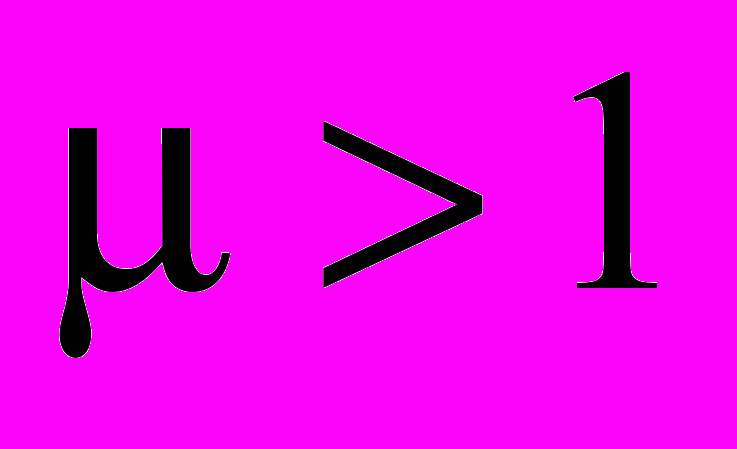 . С ростом температуры магнитная восприимчивость уменьшается (
. С ростом температуры магнитная восприимчивость уменьшается (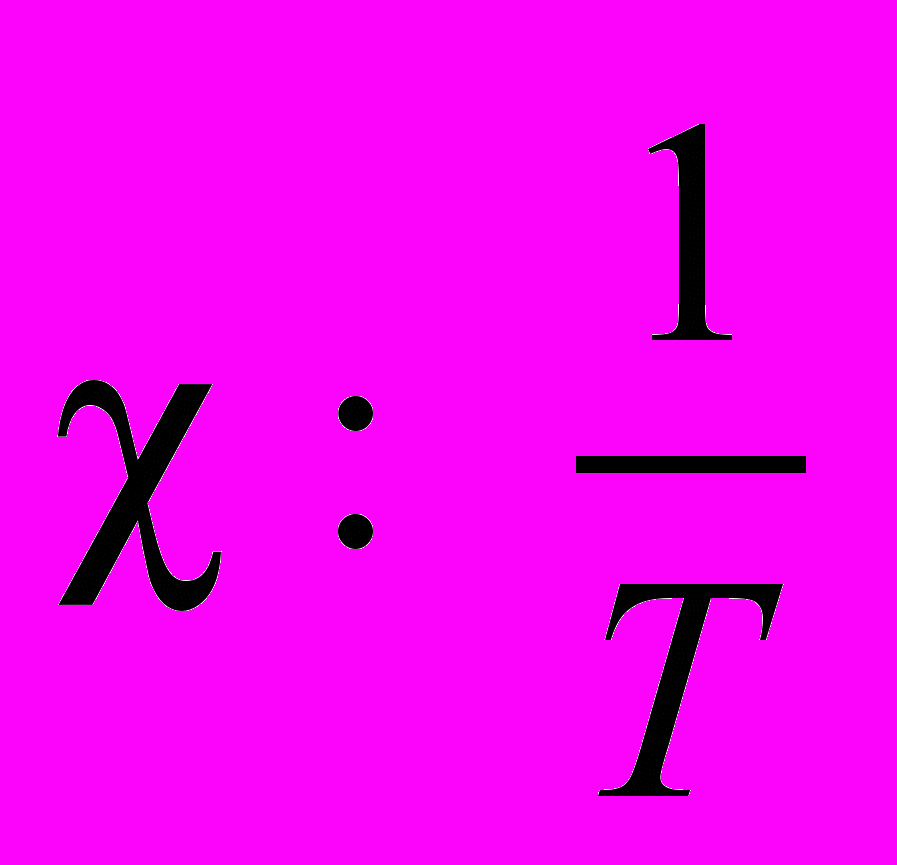 – закон Кюри).
– закон Кюри).