
Теорема о линейной сходимости градиентного метода с постоянным шагом
Доклад по математическим методам в экономике
Теорема о линейной сходимости градиентного метода с постоянным шагом
ДВГУ
Теорема о линейной сходимости градиентного метода с постоянным шагом.
Пусть выполнены словия: функция сильно выпукла с константой сходится со скоростью геометрической прогрессии
со знаменателем q = max<{|1 <-
|
||xn <- x*|| £ qn<||x0 <- x*||.
|
Д о к з т е л ь с т в о. Решение x* = argmin f(x) существует и единственно в силу теорем 1) и 2)[1]<. Для функции F(x) = f ¢(x) воспользуемся аналогом формулы Ньютона Ч Лейбница
|
F(y) = F(x) +
|
ò
|
1
0
|
F ¢[x + s(y <- x)](y<- x) ds,
|
|
или, для x = x* и y = xn, учитывая, что f ¢(x*) = Q,
|
f ¢(xn) =
|
ò
|
1
0
|
f ¢¢[x* + s(xn <- x*)](xn <- x*)
ds
|
|
(здесь воспользовались 3)[2]<).
Далее, в силу тверждения 4)[3]< m. Кроме того (в силу 5)[4]), по условию f ¢¢(x) ³
|
l<||h||2 £ (f ¢¢[x* + s(xn <-2,
|
выполнено неравенство
|
2 £
|
æ
è
|
æ
è
|
ò
|
1
0
|
f ¢¢[x* + s(xn <- ds
|
ö
ø
|
h, h
|
ö
ø
|
£ L ||h||2.
|
|
(10)
|
Интеграл, стоящий в этом неравенстве, определяет линейный (симметричный в силу симметричности f) оператор на Rm, обозначим его Ln. Неравенство (10) означает, что n £ L. В силу (9) градиентный метод (4) записывается в виде
|
xn+1 = xn <- n(xn <- x*).
|
Но тогда
|
||xn+1 <- xn|| = ||xn <- x* <-aLn(xn <- x*)||
=
= ||(I <- n)(xn <- x*)||
£ ||I <- n|| ||xn <- x*||.
|
Спектр n) оператора I
<- n состоит из чисел вида i = 1 <-ali, где i Î n). В силу (10) и неравенств i £ L ,
и следовательно
|
||I <- n|| £ max<{|1 <-al<|,
|1 <-
|
Таким образом,
|
||xn+1 <- xn|| £ q||xn <- x*||.
|
Из этого неравенства вытекает тверждение даннойа
теоремы.
Оптимальный выбор шага.
Константа q,
характеризующая скорость сходимости метода, зависит от шага
минимальна, если шаг рис. 1), т. е. если

Рис. 1.
В качестве рис. 2). Простейшим примером такой функции может служить функция на R2, задаваемая формулой
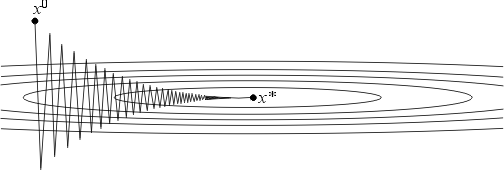
Рис. 2.
Поведение итераций градиентного метода для этой функции изображено на рис. 2 - они, быстро спустившись на "дно оврага", затем медленно "зигзагообразно" приближаются к точке минимума. Число
Но даже для хорошо обусловленных функций проблема выбора шага нетривиальна в силу отсутствия априорной информации о минимизируемой функции. Если шаг выбирается малым (чтобы гарантировать сходимость), то метод сходится медленно. величение же шага (с целью скорения сходимости) может привести к расходимости метода.
[1]< а1) Теорема единственности для строго выпуклой функции.
Задача f(x) о min , со строго выпуклой функцией
не может иметь более одного решения.
2) Теорема о разрешимости для сильно выпуклой функции.
Задач дифференцируемой сильно выпуклой
функцией разрешима.
[2]<а 3) [f ¢(x)]¢ = f ¢¢(x).
Поясним: здесь [f ¢(x)]¢ - производная функции x о f ¢(x),
действующей из Rm в Rm, f ¢¢(x) Ч вторая производная функции f: Rm о Rm.
[3]< а4) Пусть F: Rm оRk дифференцируема. Тогда F довлетворяет условию Липшица с константой L,
в том и только том случае, если ||F ¢(x)|| £ L при всех xа ( существует и обратное тверждение).
[4]<а 5)
f Î C2 сильно выпукла с константой c в том и только том случае, если f ¢¢(x) ³ c при всех x Î Rm.



