Метод построения графиков функций (с использованием теории относительности)
I. Введение
При рассмотрении различных явлений и процессов, происходящих в природе, приходится учитывать изменения одних величин в зависимости от изменения других. Например, при движении мы рассматриваем зависимость пройденного пути от времени, при нахождении площади круга рассматривается зависимость между площадью круга и его радиусом и т.д. Такие зависимости называют функциональными. В основе функциональной зависимости лежит не просто зависимость, полная определенность соответствия между переменными величинами.
Впервые определение функции было дано русским математиком Н.И. Лобачевским.
Переменную величину S называют функцией другой переменной величины t, если каждому значению величины t (из некоторой области) поставлено в соответствие вполне определенное значение величины S.
II. Преимущества и недостатки аналитического и графического способов задания 
Термин Уфункция введен Лейбницем, символическая запись функциональной зависимости 

 Такой способ часто применяется в естествознании, технике и т.д., например, при использовании самопишущих приборов, автоматически записывающих изменения одной величины от изменения другой. К недостаткам графического способа задания функции можно отнести:
нахождение приближенного значения функции при определенном значении аргумента,
функции заданные аналитически, могут быть изображены и графически, к графику нельзя непосредственно применить аппарат математического анализа, но график имеет преимущество - наглядность. По графику функции
Такой способ часто применяется в естествознании, технике и т.д., например, при использовании самопишущих приборов, автоматически записывающих изменения одной величины от изменения другой. К недостаткам графического способа задания функции можно отнести:
нахождение приближенного значения функции при определенном значении аргумента,
функции заданные аналитически, могут быть изображены и графически, к графику нельзя непосредственно применить аппарат математического анализа, но график имеет преимущество - наглядность. По графику функции 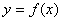 можно многое знать о поведении этой функции.
можно многое знать о поведении этой функции.
Для функции 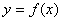 , график которой изображен на рисунке, можно казать несколько ее свойств.
, график которой изображен на рисунке, можно казать несколько ее свойств.
1) При 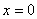
2)
 аи
аи 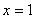 ) график функции пересекает ось абцисс, т.е. в этих точках
) график функции пересекает ось абцисс, т.е. в этих точках

3)
 аи при
аи при 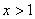 , график расположен выше оси абсцисс, т.е. функция принимает положительные значения. При
, график расположен выше оси абсцисс, т.е. функция принимает положительные значения. При  , функция принимает трицательные значения.
, функция принимает трицательные значения.
Рис.1
4)
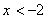 функция возрастает, при
функция возрастает, при 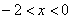 убывает. При х>0 функция только возрастает и т.д. Часто для получения графика функции наносят на координатную плоскость несколько точек графика, затем проводят через эти точки плавную кривую. Построение графика функции по точкам не является точным изображением графика функции, поэтому так важно проводить дополнительные исследования, чтобы построеный график был приближен к точному графику. Исследование функций, заданных аналитически,
проводится гораздо легче и становится наглядным, если параллельно рассматривать и графики этих функций. Т.о. мение строить графики функций, заданных аналитически, является важным элементом в общей математической подготовке учащихся.
убывает. При х>0 функция только возрастает и т.д. Часто для получения графика функции наносят на координатную плоскость несколько точек графика, затем проводят через эти точки плавную кривую. Построение графика функции по точкам не является точным изображением графика функции, поэтому так важно проводить дополнительные исследования, чтобы построеный график был приближен к точному графику. Исследование функций, заданных аналитически,
проводится гораздо легче и становится наглядным, если параллельно рассматривать и графики этих функций. Т.о. мение строить графики функций, заданных аналитически, является важным элементом в общей математической подготовке учащихся.
В школьном курсе математики рассматриваются элементарные функции.
. Элементарные функции.
К основным элементарным функциям относятся следующие функции:
1)а степенная функция 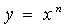 , где n - вещественное число.
, где n - вещественное число.
2)а показательная функция  , где
, где  .
.
3)а логарифмическая функция  где
где  .
.
4)а тригонометрические функции  а.
а.
5)а обратные тригонометрические функции  .
.
Функции 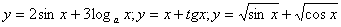 , так же являются элементарными.
, так же являются элементарными.
IV. Методы построения графиков функции
В школьном курсе математики построение графиков элементарных функций: 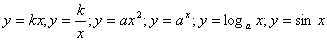 адаже для очень слабо подготовленных учащихся не составляет особого труда. Но если требуется построить график функции, тесно связанный с же известными функциями, для некоторых учащихся эта задача представляет трудность.
адаже для очень слабо подготовленных учащихся не составляет особого труда. Но если требуется построить график функции, тесно связанный с же известными функциями, для некоторых учащихся эта задача представляет трудность.
Например, при работе с такими функциями, как 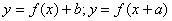
Кроме того, ошибки могут возникнуть на стадии выбора значений аргумента: их недостаточность или большой разрыв между соседними значениями аргумента. При работе с функцией необходимо учитывать область определения функции, т.е. отделить те значения аргумента, при которых выражение, задающее функцию, теряет смысл. Чтобы избежать этого, можно применить уже известные приемы.
В школьном курсе построение графика такой функции строится в два приема:
- Строится по точкам график функции
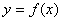 .
. - Выполняется параллельный перенос построенного графика на определенные расстояния в определенном направлении в зависимости от знаков
№ 1. Алгоритм построения.
1) Построим прямоугольную систему координат и выполним разметку по осям карандашом (впоследствии эта разметка нам не пригодится).
2)
К построенной системе координат построим график функции 
3) Выполним параллельный перенос оси Оу в положительном направлении на 3 единицы (вправо).
4) Выполним разметку (уже ручкой).
5)
В данной системе координат построенный график является графиком функции 
№3. Алгоритм построения.
1) Построим систему координат х/о/у/
2)
По точкам построим функции 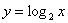
3) Выполним параллельный перенос оси о/х/ на 4 единицы в отрицательном направлении (вниз).
4) Выполним разметку в системе координат хоу.
Для более точного построения графика функции, 
 аи
аи 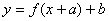
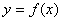 . При отсутствии шаблона построение графика функции
. При отсутствии шаблона построение графика функции 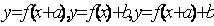 , становится более трудоемким. Особенно это относится к построению графика гармонического колебания.
, становится более трудоемким. Особенно это относится к построению графика гармонического колебания.
Упростить эту работу можно, с помощью следующих приемов.
Прием №1. Для того, чтобы построить график функции 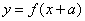
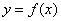 аи сдвинуть ось ОУ на |a<| единиц (точка О Уползет по оси Ох).
аи сдвинуть ось ОУ на |a<| единиц (точка О Уползет по оси Ох).
Если, а>0, то ось Оу надо сдвинуть в положительном направлении на |a<| единиц (т.е. вправо). Если же a<0, то ось Оу надо сдвинуть на |a<| единиц в отрицательном направлении (т.е. влево). а

1) х/о/у/
2)
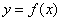
3) а.
4) Выполнить новую разметку.
Рассмотрим несколько примеров.
№1 Построить график функции 

лгоритм построения.
6) Построим прямоугольную систему координат и выполним разметку по осям карандашом (впоследствии эта разметка нам не пригодится).
7)
К построенной системе координат построим график функции 
8) Выполним параллельный перенос оси Оу в положительном направлении на 3 единицы (вправо).
9) Выполним разметку (уже ручкой).
10)
В данной системе координат построенный график является графиком функции 
№2 Построить график функции  а
а

лгоритм построения.
1)
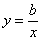 апо точкам ва х/о/у/
апо точкам ва х/о/у/
2)
3) Выполним новую разметку.
Рассмотрим построение графика функции  .
.
Прием №2. Для того, чтобы построить график функции  ,надо построить график функции
,надо построить график функции 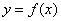 <|b<| единиц (точка О ползет по Оу).
<|b<| единиц (точка О ползет по Оу).
Если b>0, то ось Ох смещается на |b<| единиц в отрицательном направлении (вниз). Если же b<0, то ось Ох смещается на |b<| единиц в положительном направлении (вверх).
Составим алгоритм построения графика функции  .
.
1) х/о/у/
2)
Построить график функции 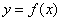
3) /х/а в зависимости от знака b.
4) хоу.
Рассмотрим несколько примеров
№3 Построить график функции 

лгоритм построения.
5) Построим систему координат х/о/у/
6)
По точкам построим функции 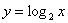
7) Выполним параллельный перенос оси о/х/ на 4 единицы в отрицательном направлении (вниз).
8) Выполним разметку в системе координат хоу.
№4 Построить график функции 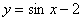 .
.
 Алгоритм построения.
Алгоритм построения.
1)
х/о/у/ построим график функции 
2)
3) Выполним разметку в хоу.
Правило 3.
Для построения графика функции  анадо использовать прием №1 и №2 последовательно.
анадо использовать прием №1 и №2 последовательно.
№5 Построить график функции 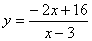

лгоритм построения.
1)

2)

№6 Построить график функции 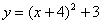
лгоритм построения.
1)
х/о/у/ построим график функции 
2)

Рассмотрим прием № 4
Для того, чтобы построить график функции  /(-а:b). Во вспомогательной системе координат построить график функции
/(-а:b). Во вспомогательной системе координат построить график функции 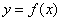 . Тогда в данной системе координат построенный график будет графиком функции
. Тогда в данной системе координат построенный график будет графиком функции 
лгоритм построения.
1) хоу.
2)
 о/
о/
3) х/о/у/, где о/х/ || ох и о/у/ || oy.
4)
х/о/у/ построим график 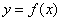 .
.
5)
6)

№7 а х/о/у/
построим график
х/о/у/
построим график 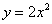 о/ (-3:-4)
о/ (-3:-4)
Прием № 4 более добен для работы по сравнению с приемами №1- №3, кроме того, этот прием более приближен к приемам построения кривых второго порядка, заданных общим каноническим равнением второго порядка в аналитической геометрии, изучаемой в вузах.
№8 Построить график функции: 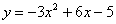 а
а
Во вспомогательной системе х/о/у/, где о/-вершина параболы 
О/ (Хо;Уо)

О/(1;-2).
№9 Построить график функции:
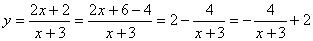
Во вспомогательной системе координатной х/о/у/,
где о/ (-3;2)
построим график функции 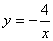

№10
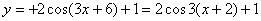
Во вспомогательной системе координат х/о/у/
построим график функции 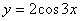
о/ (-2;1)
.

