Математика. Интегралы
1.
*1. Говорят, что функция
*2. Говорят, что функция Т1. Дифференцируемая на ( Док-во:
1) Достаточность. Пусть Т2. Для возрастания (убывания) Замечание1. Обратное к теореме 2 не имеет места,
т.е. если *3. Прямая х=а называется вертикальной асимптотой графика функций Замечание 2. Непрерывные функции вертикальных асимптот не имеют. *4. Прямая Т3. Прямая Замечание3. При 2. *1. Точку х0 назовем стандартной для функции *2. Необходимое словие экстремума. Если функция Замечание 1. Необходимое словие экстремума не является достаточным. Т1. (Первое достаточное словие экстремума). Пусть Замечание 2. Если Т2. (Второе достаточное словие экстремума). Пусть 3. *1. График функции *2. График функции Т1. Пусть *3. Точка ( Т2. (Необходимое словие перегиба). Если кривая Замечание1. Необходимое словие перегиба не является достаточным. Замечание2. В точке перегиба вторая производная может не существовать. Т3. (Первое достаточное словие перегиба). Пусть Т4. (Второе словие перегиба).
Если 4. *1. Первообразная от функции T1. Всякая непрерывная функция имеет бесчисленное множество первообразных, причем любые две из них отличаются друг от друга только постоянным слагаемым. Док-во: F( *2. Неопределенным интегралом от данной функции 5. Свойства неопределенного интеграла: Т2. (об инвариантности формул интегрирования): Пусть
ò 6. Метод замены переменных. 1)
Подведение под знак дифференциала. Т1. Пусть функция Замечание1. При интегрировании иногда целесообразно подбирать подстановку не в виде 2)
Подведение под знак дифференциала. F(x)dx=g( Интегрирование по частям: ò 7. Интегрирование по частям: ò Интегрирование функций,
содержащих квадратный трехчлен: Первый интеграл табличного вида: òduk: Второй интеграл сводится к нахождению интеграла: где Интегрирование рациональных функций: R( t
соответствует сумма Правила интегрирования рациональных дробей: Правую рац. дробь разлагают на сумму простейших дробей. Этим самым интегрирование правильной рац. дроби сводят к интегрированию простейших дробей. 8. Интегрирование тригонометрических функций: I.
1 Интеграл вида: 2
R( 3
R( 4
R( II.
1 2
Оба показателя степени .
ò IV.
ò V.
ò 9. Интегрирование иррациональных функций: I.
1 òR( 2
òR(x,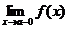 аравно +¥ или Ц¥.
аравно +¥ или Ц¥.
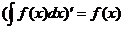


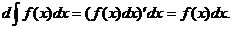
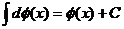


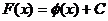

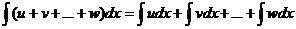
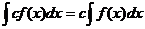

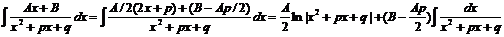
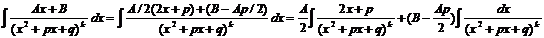
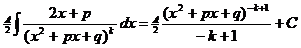

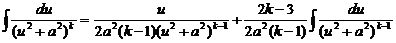
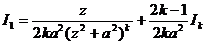 Ц рекуррентная формула.
Ц рекуррентная формула.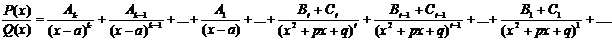
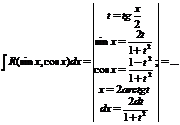
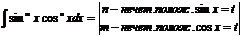
 ,Е)dx,
,Е)dx, 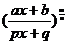
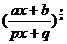

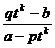
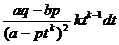


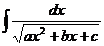 Вынести 1/Ö
Вынести 1/Ö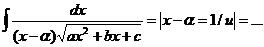
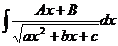 Разбить на два интеграла.
Разбить на два интеграла.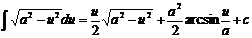
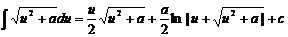
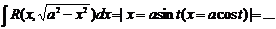
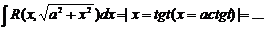
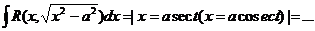
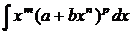 а 1)
а 1)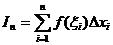 ,
где
,
где 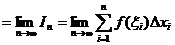 Ц этот предел (если он существует) называется определенным интегралом, или интегралом от функции
Ц этот предел (если он существует) называется определенным интегралом, или интегралом от функции