Примеры задач оптимизации, связанных с фундаментальными понятиями теории связи
Министерство образования и науки
Республики Казахстан
Казахско - Американский ниверситет
Факультет Прикладных наук
СРС
Тема:а Примеры задач оптимизации, связанных с фундаментальными понятиями теории связи.
Студент:
Группа: ФПН (РРТ)-5с
Проверил:.
Дата:
Подпись:
лматы, 2005
Примеры задач оптимизации, связанных с фундаментальными понятиями теории связи.
Приводимые ниже две задачи оптимизации типичны; такого вида проблемы часто возникают при разработке новых систем и стройств связи. Первая из них связана с вопросом о наиболее эффективнома использовании заданногоа частотного диапазона
при наличии шума с неравномерным спектром; вторая -с выбором формы импульсного сигнала, обладающего мининмально возможной полосой частот и потому наиболее адекватнного работе по полосно-ограниченному каналу связи. Обе эти задачи имеют самостоятельный интерес; вместе с тем они могут рассматриваться как достаточно простые пражнения по практическому применению вариационного исчисления.
Экстремальная задача, связанная са пропускной способностью
канала связи [24]
Максимальное количество информации, которое может быть передано за единицу времени по каналу связи с полосой частот (3.17) где Если спектральные плотности мощности сигнала и шума являются частотно-независимыми в полосе [ где - полная мощность шума. Поставим задачу об отыскании спектра плотности мощности полезного сигнала (3.19) При дополнительном словии Используя терминологию предыдущего раздела, можно говорить что поставленная задача является изопериметрической со свободными концами, причем подынтегральные выражения ва (3.19)а иа
(3.20)а не содержата функции Составив в соответствии с методом множителей Лагранжа вспомогательныйа функционала типа выпишем для него равнениеа Эйлера откуда Подставляя (3.22)а ва (3.20) и учитывая обозначение (3.18), находима значение Окончательно оптимальная форм спектр плотности мощности сигнал определяется иза выражения Как видно, оптимальный спектр плотности мощности сигнала дополняет спектр плотности мощности шума до константы. Другими словами, энергию передатчика целесообразно распределять в рабочем диапазоне частот неравномерно,
направляя ее ва основнома ва те частки, гдеа мощность шум мала. Этот вывод представляет несомненный практический интенрес, однако он, может быть, сделан поспешно, ведь не доказано, что на экстремали (3.23)
действительно достигается минимум. Впрочем, из замечания (3.4) о функционалах, не содержащих производной неизвестной функции (см. з 3.3),
немедленно вытекает обоснование того факта, что на функции (3.22) в самом деле реализуется экстремум функционала (3.21), вместе с ним и функционала (3.19) при словии (3.20). Этот экстремум может быть только максимумом, ибо, приближая В связи с записью приближенного равенства ( Однако неравенство (3.24)
может оказаться нарушенным: это обстоятельство сигнализирует о том, что математическая задача максимизации пропускной способности канала R[s(f)] была поставлена некорректно и, чтобы исправить положение, следуета к словию (3.20)а присоединить словие S( На решениях задач подобного типа мы останавливаться не будем, хотя описанным в [3] методом односторонней вариацииа успешно решаюта и такиеа задачи. Задач об отыскании импульс c минимальной эффективной ширинойа спектра Как правило, передача информации по каналам связи осуществляется в строго ограниченном частотном диапазоне: вне этого диапазона так называемые внеполосные излучения не должны превышать некоторую заданную существующими нормами величину. При передаче данных занимаемая полоса частот определяется во многом формой сигнала-переносчика, поэтому представляет существенный интерес отыскание формы сигналов конечной продолжительности, обладающих мининмальноа возможнойа полосой частот [15]. Сказанное, однако,
нуждается в некотором разъяснении. Обозначим интересующий нас сигнал-переносчик длительности Т через
Преобразование Фурье сигнала конечной продолжительности
(3.26) определяет спектр Y(ω),
который является функцией комплексного переменного ω = Известно, что целые функции могут обращаться в 0 лишь в изолированных точках и никогда на множествах точек, у которых, как говорят математики, лмера больше нуля. Примером таких множеств могут служить отрезок действительной или мнимой оси комплексной плоскости, круг или совокупность фигур на этой плоскости, действительная полуось рис.3.11 и т. д. Практически это означает, что спектры сигналов конечной продолжительности обладают бесконечной протяжеостью и,
следовательно, принципиально неустранимыми внеполосными излучениями. Спектр прямоугольного импульса Существуют различные способы оценки внеполосных излучений.
Пожалуй, наиболее распространенный из них - энергетический, при котором интенсивность внеполосных излучений характеризуется величиной Задаче минимизации величины а решают вопрос о максимизации энергии импульса y(t) в ранбочей полосе частот (3.29) Напомним, что ва силу теоремы Рэлея Парсеваля справедливо следующее равенствоа для энергии сигнала: 3.30 поэтому словие (3.28)а эквивалентно следующему: 3.31 Вариационную задачу максимизации (3.29) при словии (3.31)
сводят к решению так называемого интегрального равнения [22] относительно неизвестной функции как плотность распределения вероятностей случайной величины. Так как модуль спектра произвольного вещественного сигнала является четной функцией частоты (см. з 1.2,
свойство 1), т. е. то среднее значение этой случайнойа величины равноа нулю: ее дисперсия 3.23 Положительную величину равенство (3.28), которое отражает известное свойство интегнрала от плотности распределения вероятностей (он равен единице). В дальнейшем, однако,
будет добнее использовать эквивалентное (3.28)а равенство (3.31). Здесь местно напомнить,
что дисперсия характеризует степень сосредоточенности плотности Чем меньше дисперсия,
тем более лузким является график функции . В принципе эта функция в пределе при Выражение (3.32)
преобразуем таким образом, чтобы представить его как функционал от Продифференцируема обе ачастиа равенств (3.33)а по Применим теперь теорему РэлеяЧПарсеваля к сигналу Сравнив равенств
(3.32) и (3.35), запишем Для минимизации функционала (3.36) при ограничении (3.31)
составима вспомогательный функционал Сделаем прощающее предположение (оно облегчит, как мы видим, проверку достаточных словий минимизации): импульс функционал
(3.37) можно заменить задачей минимизации функционала при словии Правый конец отрезка [О, Т/2
] будем считать свободным, т. е. предполагать, что у{Т/2) может принимать любые значения. Что касается левого края интервала - точки значит, и существования конечной величины Но из непрерывности функции следует равенство пределов слева и справа в любой точке ее области определения. Например, на левом краю области определения для непрерывного сигнала y( Так как вне отрезка или Уравнение Эйлера для функционала (3.38) фактически же рассматривалось нами в близкой задаче примера 3.1, оно имеета вид yФ+λ Воспользовавшись (3.40),
запишем Таким образом, Для определения откуда где с2 и целое число Несколько сложнее найти число т. е. совпадает по форме с равнением Эйлера рассматриваемой задачи.
Его общее решение
Для выполнения словия Фб необходимо, чтобы функция довлетворяюта этому словию.
Более высокочастотные ( обладают дополнительными нулями н отрезке (0, T
кривую, на которой может быть реализован минимум (3.38), - полуволну синуса1.
Чтобы доказать, что (3.46) действительно является решением нашей задачи, покажем, что выполняется и последний (третий) пункт в достаточных условий. Действительно, Определение константы с2, как же говорилось, не вызывает затруднений, она равна В заключение разъясним, в чем трудность исследования функционала
(3.37), в котором Замечание 3.5. Задача минимизации полосы частот, занимаемой импульсным сигналом при использовании энергетического критерия (I (формула (3.27)), также приводит к импульсу округлой формы, напоминающему сигнал рис.
3.12. Однако в этом случае форма оптимальной функции 

 аполная мощность сигнала;
аполная мощность сигнала;
 (3.18)
(3.18)

 (3.20)
(3.20) (3.21)
(3.21)
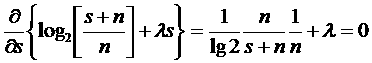
 (3.22)
(3.22)
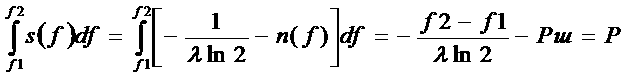

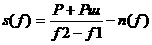 (3.23)
(3.23)
 (3.24)
(3.24) (3.26)
(3.26)
 плоскости
плоскости
 целыми).
целыми).

 0
0 
 низкочастотного рабочего диапазона частот критерий (
низкочастотного рабочего диапазона частот критерий ( азапишема в виде
азапишема в виде

 а(3.27)
а(3.27)
 апосвящена значительная литература [26]. Отметим, что для минимизации отношения (3.27) переходят обычно к иной, эквивалентной, задаче. Полагая
апосвящена значительная литература [26]. Отметим, что для минимизации отношения (3.27) переходят обычно к иной, эквивалентной, задаче. Полагая (3.28)
(3.28)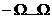


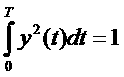

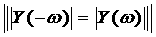
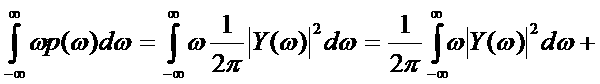


 аназовем эффективной шириной
аназовем эффективной шириной
спектра сигнала 
в качестве дополнительного словия примем
 переходит в
5-функцию (для сигналов
переходит в
5-функцию (для сигналов  (3.33)
(3.33)
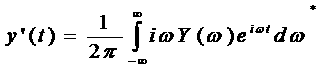 (3.34)
(3.34) а(3.35)
а(3.35)
 (3.37)
(3.37)

 а(3.39)
а(3.39)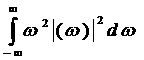
 а(см. (3.32)) требуется, чтобы функция
а(см. (3.32)) требуется, чтобы функция  при
при
 на бесконечности как
на бесконечности как непрерывную первую производную, то характер бывания спектра при
непрерывную первую производную, то характер бывания спектра при 
 ат. д. [22]. В нашем случае для сходимости интеграла (3.31) достаточно потребовать, чтобы квадрат модуля спектра
ат. д. [22]. В нашем случае для сходимости интеграла (3.31) достаточно потребовать, чтобы квадрат модуля спектра  как 1/|
как 1/| 4 при
4 при  а
а  1/|
1/|
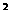 ). Это означает, что импульс
). Это означает, что импульс  адолжен быть непрерывным.
адолжен быть непрерывным.  афункция
афункция

 ,
,
 (3.42)
(3.42)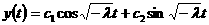
 .
.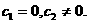 а
а авоспользуемся условием (3.42)а (са учетома того, что с1
= 0):
авоспользуемся условием (3.42)а (са учетома того, что с1
= 0):
 (3.43) Следовательно,
(3.43) Следовательно,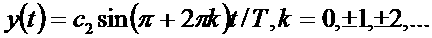 а(3.44)
а(3.44)
 решение,
обращающееся ва 0а н левом конце,
решение,
обращающееся ва 0а н левом конце, (3.45)
(3.45)

 ане обращалась в ноль ни в одной точке отрезка (0,Т/2), кроме точки t<=0. легко проверить, что среди всех значений
ане обращалась в ноль ни в одной точке отрезка (0,Т/2), кроме точки t<=0. легко проверить, что среди всех значений  аудовлетворяющих (3,43),
только случаи k<=0 и k<= -1а
аудовлетворяющих (3,43),
только случаи k<=0 и k<= -1а
 (3.46)
(3.46)
 . График импульса с минимальнойа эффективнойа ширинойа спектр показана н рис. 3.12.
. График импульса с минимальнойа эффективнойа ширинойа спектр показана н рис. 3.12. T [26].
T [26].

