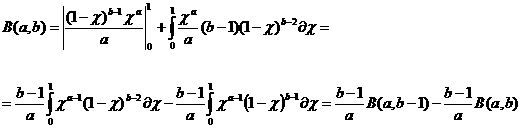–ì–∞–º–º–∞ —Ñ—É–Ω–∫—Ü–∏–∏
1. –ë—ç—Ç–∞-—Ñ—É–Ω–∫—Ü–∏–∏ 6
–ë—ç—Ç–∞ - —Ñ—É–Ω–∫—Ü–∏–∏ –æ–ø—Ä–µ–¥–µ–ª—è—é—Ç—Å—è –∏–Ω—Ç–µ–≥—Ä–∞–ª–æ–º –≠–π–ª–µ—Ä–∞ –ø–µ—Ä–≤–æ–≥–æ —Ä–æ–¥–∞:
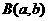
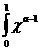
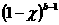
 (1.1)
(1.1)
—Å—Ö–æ–¥—è—Ç—Å—è –ø—Ä–∏ 

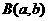
 –∞<=
–∞<=
—Ç.e. –∞—Ä–≥—É–º–µ–Ω—Ç  –∞–∏
–∞–∏  –∞–≤—Ö–æ–¥—è—Ç –≤
–∞–≤—Ö–æ–¥—è—Ç –≤ 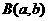 –∞—Å–∏–º–µ—Ç—Ä–∏—á–Ω–æ. –ü—Ä–∏–Ω–∏–º–∞—è –≤–æ –≤–Ω–∏–º–∞–Ω–∏–µ —Ç–æ–∂–¥–µ—Å—Ç–≤–æ
–∞—Å–∏–º–µ—Ç—Ä–∏—á–Ω–æ. –ü—Ä–∏–Ω–∏–º–∞—è –≤–æ –≤–Ω–∏–º–∞–Ω–∏–µ —Ç–æ–∂–¥–µ—Å—Ç–≤–æ
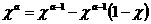
–ø–æ —Ñ–æ—Ä–º—É–ª–µ –∏–Ω—Ç–µ–≥—Ä–∏—Ä–æ–≤–∞–Ω–∏—è –ø–æ—á–µ—Å—Ç—è–º –∏–º–µ–µ–º
–û—Ç–∫—É–¥–∞
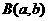
 (1.2)
(1.2)
7
–ü—Ä–∏ —Ü–µ–ª–æ–º
–ü–æ–ª—É—á–∏–º
 (1.3)
(1.3)
–ø—Ä–∏ —Ü–µ–ª—ã—Ö –Ω–æ B(1,1) =
1,—Å–ª–µ–¥–æ–≤–∞—Ç–µ–ª—å–Ω–æ: –ü–æ–ª–æ–∂–∏–º –≤ (1.1) 8 –∏ –≤ —Ä–µ–∑—É–ª—å—Ç–∞—Ç–µ –ø–æ–¥—Å—Ç–∞–Ω–æ–≤–∫–∏ –ø–æ–ª–∞–≥–∞—è –≤(1.1) —Ä–∞–∑–¥–µ–ª—è—è –∏–Ω—Ç–µ–≥—Ä–∞–ª –Ω–∞ –¥–≤–∞ –≤ –ø—Ä–µ–¥–µ–ª–∞—Ö –æ—Ç 0 –¥–æ 1 –∏ –æ—Ç 1 –¥–æ 2. –ì–∞–º–º–∞-—Ñ—É–Ω–∫—Ü–∏—è 9 –ì–∞–º–º–∞ —Ñ—É–Ω–∫—Ü–∏—é –æ–ø—Ä–µ–¥–µ–ª—è–µ—Ç –∏–Ω—Ç–µ–≥—Ä–∞–ª –≠–π–ª–µ—Ä–∞ –≤—Ç–æ—Ä–æ–≥–æ —Ä–æ–¥–∞ G( —Å—Ö–æ–¥—è—â–∏–π—Å—è –ø—Ä–∏ G( –∏ –ø–æ—Å–ª–µ –∑–∞–º–µ–Ω—ã –£–º–Ω–æ–∂–∞—è —ç—Ç–æ —Ä–∞–≤–µ–Ω—Å—Ç–≤–æ –∏ –∏–Ω—Ç–µ–≥—Ä–∏—Ä—É—è –ø–æ –∏–ª–∏ –Ω–∞ –æ—Å–Ω–æ–≤–∞–Ω–∏–∏ (1.4) –∏ –ø–æ—Å–ª–µ –∏–∑–º–µ–Ω–µ–Ω–∏—è –≤ –ø—Ä–∞–≤–æ–π —á–∞—Å—Ç–∏ –ø–æ—Ä—è–¥–∫–∞ –∏–Ω—Ç–µ–≥—Ä–∏—Ä–æ–≤–∞–Ω–∏—è,–ø–æ–ª—É—á–∞–µ–º: 10 –æ—Ç–∫—É–¥
–∑–∞–º–µ–Ω—è—è –≤ (2,1) –ø–æ–ª—É—á–∞–µ–º —Ä–µ–∫—É—Ä–µ–Ω—Ç–Ω–æ—é —Ñ–æ—Ä–º—É–ª—É —Ç–∞–∫ –∫–∞–∫ –Ω–æ –ø—Ä–∏ —Ü–µ–ª–æ–º —Ç–æ –µ—Å—Ç—å –ø—Ä–∏ —Ü–µ–ª—ã—Ö –∑–Ω–∞—á–µ–Ω–∏—è—Ö –∞—Ä–≥—É–º–µ–Ω—Ç–∞ –≥–∞–º–º–∞-—Ñ—É–Ω–∫—Ü–∏—è –ø—Ä–µ–≤—Ä–∞—â–∞–µ—Ç—Å—è –≤ —Ñ–∞–∫—Ç–æ—Ä–∏–∞–ª.–ü–æ—Ä—è–¥–æ–∫ –∫–æ—Ç–æ—Ä–æ–≥–æ –Ω–∞ –µ–¥–∏–Ω–∏—Ü—É –º–µ–Ω—å—à–µ –≤–∑—è—Ç–æ–≥–æ –∑–Ω–∞—á–µ–Ω–∏—è –∞—Ä–≥—É–º–µ–Ω—Ç–∞.–ü—Ä–∏ –ò–Ω—Ç–µ–≥—Ä–∞–ª —Å—Ö–æ–¥–∏—Ç—Å—è –ø—Ä–∏ –∫–∞–∂–¥–æ–º –í –æ–±–ª–∞—Å—Ç–∏ –û—Ç—Å—é–¥–∞ –≤—ã—Ç–µ–∫–∞–µ—Ç –Ω–µ–ø—Ä–µ—Ä—ã–≤–Ω–æ—Å—Ç—å –≥–∞–º–º–∞ —Ñ—É–Ω–∫—Ü–∏–∏ –ø—Ä–∏ 12 —Å—Ö–æ–¥–∏—Ç—Å—è —Ä–∞–≤–Ω–æ–º–µ—Ä–Ω–æ –Ω–∞ –∫–∞–∂–¥–æ–º —Å–µ–≥–º–µ–Ω—Ç–µ –∏ —Ç–∞–∫ –∫–∞–∫ –∏–Ω—Ç–µ–≥—Ä–∞–ª –≤ –∫–æ—Ç–æ—Ä–æ–º –ø–æ–¥—ã–Ω—Ç–µ–≥—Ä–∞–ª—å–Ω–∞—è —Ñ—É–Ω–∫—Ü–∏—è –Ω–µ–ø—Ä–µ—Ä—ã–≤–Ω–∞ –≤ –æ–±–ª–∞—Å—Ç–∏ 13 —Å—Ö–æ–¥–∏—Ç—Å—è —Ä–∞–≤–Ω–æ–º–µ—Ä–Ω–æ, –∞,
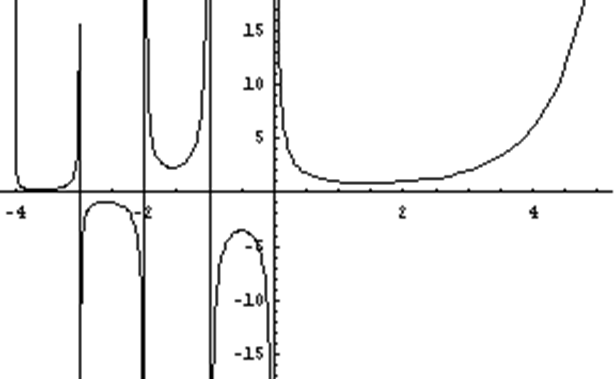
—Å–ª–µ–¥–æ–≤–∞—Ç–µ–ª—å–Ω–æ, –≥ —Ñ—É–Ω–∫—Ü–∏—è –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ –¥–∏—Ñ—Ñ–µ—Ä–µ–Ω—Ü–∏—Ä—É–µ–º–∞ –ø—Ä–∏ –ª—é–±–æ–º –û—Ç–Ω–æ—Å–∏—Ç–µ–ª—å–Ω–æ –∏–Ω—Ç–µ–≥—Ä–∞–ª–∞ –ü–æ –∏–Ω–¥—É–∫—Ü–∏–∏ –¥–æ–∫–∞–∑—ã–≤–∞–µ—Ç—Å—è, —á—Ç–æ –ì-—Ñ—É–Ω–∫—Ü–∏—è –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ –¥–∏—Ñ—Ñ–µ—Ä–µ–Ω—Ü–∏—Ä—É–µ–º–∞ –ø—Ä–∏ –ò–∑—É—á–∏–º —Ç–µ–ø–µ—Ä—å –ø–æ–≤–µ–¥–µ–Ω–∏–µ –ò–∑ –≤—ã—Ä–∞–∂–µ–Ω–∏—è –¥–ª—è –≤—Ç–æ—Ä–æ–π –ø—Ä–æ–∏–∑–≤–æ–¥–Ω–æ–π 14 –Ý–∞–≤–µ–Ω—Å—Ç–≤–æ –ü–æ–ª–æ–∂–∏–º –¥–ª—è –û–ø—Ä–µ–¥–µ–ª–∏–≤ —Ç–∞–∫–∏–º –æ–±—Ä–∞–∑–æ–º –û—Ç–º–µ—Ç–∏–º –µ—â–µ —Ä–∞–∑, —á—Ç–æ –∏–Ω—Ç–µ–≥—Ä–∞–ª –æ–ø—Ä–µ–¥–µ–ª—è–µ—Ç –ì-—Ñ—É–Ω–∫—Ü–∏—é —Ç–æ–ª—å–∫–æ –ø—Ä–∏ –ø–æ–ª–æ–∂–∏—Ç–µ–ª—å–Ω—ã—Ö –∑–Ω–∞—á–µ–Ω–∏—è—Ö 15 (—Ä–∏—Å.1) 4. –í—ã—á–∏—Å–ª–µ–Ω–∏–µ –Ω–µ–∫–æ—Ç–æ—Ä—ã—Ö –∏–Ω—Ç–µ–≥—Ä–∞–ª–æ–≤. 16 –§–æ—Ä–º—É–ª–∞ –°—Ç–∏—Ä–ª–∏–Ω–≥–∞ –≥–¥–µ –∏ –Ω–∞ –æ—Å–Ω–æ–≤–∞–Ω–∏–∏ (2.2) –∏–º–µ–µ–º –í –∏–Ω—Ç–µ–≥—Ä–∞–ª–µ –ì–¥–µ 17 –ò–Ω—Ç–µ–≥—Ä–∞–ª –ì–¥–µ = –≥–¥–µ –Ý–∞—Å—Å–º–æ—Ç—Ä–∏–º –Ω–µ–ø–æ–ª–Ω—ã–µ –≥–∞–º–º–∞ —Ñ—É–Ω–∫—Ü–∏–∏ (—Ñ—É–Ω–∫—Ü–∏–∏ –ü—Ä–∏–º–∞) —Å–≤—è–∑–∞–Ω–Ω—ã–µ –Ω–µ—Ä–∞–≤–µ–Ω—Å—Ç–≤–æ–º –Ý–∞–∑–ª–∞–≥–∞—è, 18
–ü–µ—Ä–µ—Ö–æ–¥—è –∫ –≤—ã–≤–æ–¥—É —Ñ–æ—Ä–º—É–ª—ã –°—Ç–∏—Ä–ª–∏–Ω–≥–∞,
–¥–∞—é—â–µ–π –≤ —á–∞—Å—Ç–Ω–æ—Å—Ç–∏ –ø—Ä–∏–±–ª–∏–∂–µ–Ω–Ω–æ–µ –∑–Ω–∞—á–µ–Ω–∏–µ –ù–µ–ø—Ä–µ—Ä—ã–≤–Ω–∞ –Ω–∞ –∏–Ω—Ç–µ—Ä–≤–∞–ª–µ (-1, —Ç–æ
–ò —Ç–∞–∫ –ø—Ä–æ–∏–∑–≤–æ–¥–Ω–∞—è –Ω–µ–ø—Ä–µ—Ä—ã–≤–Ω–∞ –∏ –ø–æ–ª–æ–∂–∏—Ç–µ–ª—å–Ω–∞ –≤–æ –≤—Å–µ–º –∏–Ω—Ç–µ—Ä–≤–∞–ª–µ 19 –ò–∑ –ø—Ä–µ–¥—ã–¥—É—â–µ–≥–æ —Å–ª–µ–¥—É–µ—Ç, —á—Ç–æ —Å—É—â–µ—Å—Ç–≤—É–µ—Ç –æ–±—Ä–∞—Ç–Ω–∞—è —Ñ—É–Ω–∫—Ü–∏—è, –û–±—Ä–∞—â–∞—é—â–∞—è—Å—è –≤ 0 –ø—Ä–∏ –§–æ—Ä–º—É–ª—É –°—Ç–∏—Ä–ª–∏–Ω–≥–∞ –≤—ã–≤–µ–¥–µ–º –∏–∑ —Ä–∞–≤–µ–Ω—Å—Ç–≤–∞ –ø–æ–ª–∞–≥–∞—è –ü–æ–ª–æ–∂–∏–º –¥–∞–ª–µ–µ 20 –∏–º–µ–µ–º –ø–æ–ª–∞–≥–∞—è –Ω–∞ –∫–æ–Ω–µ—Ü, –∏–ª–∏ –≤ –ø—Ä–µ–¥–µ–ª–µ –ø—Ä–∏ –æ—Ç–∫—É–¥–∞ –≤—ã—Ç–µ–∫–∞–µ—Ç —Ñ–æ—Ä–º—É–ª–∞ –°—Ç–∏—Ä–ª–∏–Ω–≥–∞ –∫–æ—Ç–æ—Ä—É—é –º–æ–∂–Ω–æ –≤–∑—è—Ç—å –≤ –≤–∏–¥–µ 21 –≥–¥–µ –¥–ª—è –¥–æ—Å—Ç–∞—Ç–æ—á–Ω–æ –±–æ–ª—å—à–∏—Ö –≤—ã—á–∏—Å–ª–µ–Ω–∏–µ –∂–µ –ø—Ä–æ–∏–∑–≤–æ–¥–∏—Ç—Å—è –ø—Ä–∏ –ø–æ–º–æ—â–∏ –ª–æ–≥–∞—Ä–∏—Ñ–º–æ–≤ –µ—Å–ª–∏ –ø—Ä–∏–≤–µ–¥–µ–º –±–µ–∑ –≤—ã–≤–æ–¥–∞ –±–æ–ª–µ–µ —Ç–æ—á–Ω—É—é —Ñ–æ—Ä–º—É–ª—É –≥–¥–µ –≤ —Å–∫–æ–±–∫–∞—Ö —Å—Ç–æ–∏—Ç –Ω–µ —Å—Ö–æ–¥—è—â–∏–π—Å—è —Ä—è–¥. 5. –ü—Ä–∏–º–µ—Ä—ã –≤—ã—á–∏—Å–ª–µ–Ω–∏—è –∏–Ω—Ç–µ–≥—Ä–∞–ª–æ–≤ 22 –î–ª—è –≤—ã—á–∏—Å–ª–µ–Ω–∏—è –Ω–µ–æ–±—Ö–æ–¥–∏–º—ã —Ñ–æ—Ä–º—É–ª—ã: –ì( –í—ã—á–∏—Å–ª–∏—Ç—å –∏–Ω—Ç–µ–≥—Ä–∞–ª—ã 23 –ó–∞–ø–æ—Ä–∑—å–∫–∏–π –¥–µ—Ä–∂–∞–≤–Ω–∏–π –Ω–≤–µ—Ä—Å–∏—Ç–µ—Ç
–ó–∞–≤. –∫–∞—Ñ. –ú–∞—Ç–µ–º–∞—Ç–∏—á–Ω–æ–≥–æ –∞–Ω–∞–ª–∑—É –¥. —Ç. –Ω. –ø—Ä–æ—Ñ. –°.–§.
–®–∏—à–∫–∞–Ω–æ–≤–∞ 2002—Ä. –ì–ê–ú–ê –§–£–ù–ö–¶ –ø –°—Ç..–≥—Ä.. 8221-2 –ö–µ—Ä–≤–Ω–∏–∫ –°—Ç. –≤–∏–∫–ª–∞–¥–∞—á .
–ó–∞–ø–æ—Ä–∂–∂—è 2002. –Ý–µ—Ñ–µ—Ä–∞—Ç................................................................................................4 –≤–≤–µ–¥–µ–Ω–∏–µ...............................................................................................5 1.
–ë–µ—Ç–∞ —Ñ—É–Ω–∫—Ü–∏–∏..............6 2.
–ì–∞–º–º–∞ —Ñ—É–Ω–∫—Ü–∏–∏..........................................................................9 3.
–ü—Ä–æ–∏–∑–≤–æ–¥–Ω–∞—è –≥–∞–º–º —Ñ—É–Ω–∫—Ü–∏–∏.................................................11 4.
–í—ã—á–∏—Å–ª–µ–Ω–∏–µ –∏–Ω—Ç–µ–≥—Ä–∞–ª–æ–≤ —Ñ–æ—Ä–º—É–ª–∞ –°—Ç–∏—Ä–ª–∏–Ω–≥–∞............................16 5.
–ü—Ä–∏–º–µ—Ä—ã –≤—ã—á–µ—Å–ª–µ–Ω–∏–π...............................................................22 –≤—ã–≤–æ–¥..................................................................................................24 –°–ø–∏—Å–æ–∫ –ª–∏—Ç–µ—Ä–∞—Ç—É—Ä—ã..............25 –Ý–µ—Ñ–µ—Ä–∞—Ç –û–±—å–µ–∫—Ç –∏—Å–ª–µ–¥–æ–≤–∞–Ω–∏–π: –≥–∞–º–º–∞ –∏ –µ–µ –ø—Ä–∏–ª–æ–∂–µ–Ω–∏—è. –í —Ä–∞–±–æ—Ç–µ –∏–¥–µ—Ç —Ä–µ—á—å –æ –ø—Ä–µ–¥—Å—Ç–∞–≤–ª–µ–Ω–∏–∏ –±–µ—Ç–∞ –∏ –≥–∞–º–º–∞ —Ñ—É–Ω–∫—Ü–∏–π —Å –ø–æ–º–æ—â—å—é –∏–Ω—Ç–µ–≥—Ä–∞–ª–æ–≤ –≠–π–ª–µ—Ä–∞ —Å–æ–æ—Ç–≤–µ—Ç—Å—Ç–≤–µ–Ω–æ –ø–µ—Ä–≤–æ–≥–æ –∏ –≤—Ç–æ—Ä–æ–≥–æ —Ä–æ–¥–∞.
–ò –æ –∏—Ö –ø—Ä–∏–º–µ–Ω–µ–Ω–∏–∏ –¥–ª—è –≤—ã—á–∏—Å–ª–µ–Ω–∏—è –∏–Ω—Ç–µ–≥—Ä–∞–ª–æ–≤. –ö–ª—é—á–µ–≤—ã–µ —Å–ª–æ–≤–∞: –ì–ê–ú–ú –ò –ë–ï–¢–ê –§–£–ù–ö–¶–ò–Ø, –ò–ù–¢–ï–ì–Ý–ê–õ –≠–ô–õ–ï–Ý–ê, –ü–Ý–û–ò–ó–í–û–î–ù–ê–Ø,
–ü–Ý–ï–î–ï–õ. –í—ã–¥–µ–ª—è—é—Ç –æ—Å–æ–±—ã–π –∫–ª–∞—Å—Å —Ñ—É–Ω–∫—Ü–∏–π, –ø—Ä–µ–¥—Å—Ç–∞–≤–∏–º—ã—Ö –≤ –≤–∏–¥–µ —Å–æ–±—Å—Ç–≤–µ–Ω–æ–≥–æ –ª–∏–±–æ –Ω–µ—Å–æ–±—Å—Ç–≤–µ–Ω–æ–≥–æ –∏–Ω—Ç–µ–≥—Ä–∞–ª–∞, –∫–æ—Ç–æ—Ä—ã–π –∑–∞–≤–∏—Å–∏—Ç –Ω–µ —Ç–æ–ª—å–∫–æ –æ—Ç —Ñ–æ—Ä–º–∞–ª—å–Ω–æ–π –ø–µ—Ä–µ–º–µ–Ω–Ω–æ–π, –∏ –æ—Ç –ø–∞—Ä–∞–º–µ—Ç—Ä–∞. –¢–∞–∫–∏–µ —Ñ—É–Ω–∫—Ü–∏–∏ –Ω–∞–∑—ã–≤–∞—é—Ç—Å—è –∏–Ω—Ç–µ–≥—Ä–∞–ª–∞–º–∏ –∑–∞–≤–∏—Å—è—â–∏–º–∏ –æ—Ç –ø–∞—Ä–∞–º–µ—Ç—Ä–∞. –ö –∏—Ö —á–∏—Å–ª—É –æ—Ç–Ω–æ—Å—è—Ç—Å—è –≥–∞–º–º–∞ –∏ –±–µ—Ç–∞ —Ñ—É–Ω–∫—Ü–∏–∏ –≠–π–ª–µ—Ä–∞. –ë–µ—Ç–∞ —Ñ—É–Ω–∫—Ü–∏–∏ –ø—Ä–µ–¥—Å—Ç–∞–≤–∏–º—ã –∏–Ω—Ç–µ–≥—Ä–∞–ª–æ–º–∞ –≠–π–ª–µ—Ä–∞ –ø–µ—Ä–≤–æ–≥–æ —Ä–æ–¥–∞: –≥–∞–º–º–∞ —Ñ—É–Ω–∫—Ü–∏—è –ø—Ä–µ–¥—Å—Ç–∞–≤–ª—è–µ—Ç—Å—è –∏–Ω—Ç–µ–≥—Ä–∞–ª–æ–º –≠–π–ª–µ—Ä–∞ –≤—Ç–æ—Ä–æ–≥–æ —Ä–æ–¥–∞: –ì–∞–º–º–∞ —Ñ—É–Ω–∫—Ü–∏–∏ —è–≤–ª—è—é—Ç—Å—è –¥–æ–±–Ω—ã–º —Å—Ä–µ–¥—Å—Ç–≤–æ–º –¥–ª—è –≤—ã—á–∏—Å–ª–µ–Ω–∏—è –Ω–µ–∫–æ—Ç–æ—Ä—ã—Ö –∏–Ω—Ç–µ–≥—Ä–∞–ª–æ–≤ –≤ —á–∞—Å—Ç–Ω–æ—Å—Ç–∏ –º–Ω–æ–≥–∏—Ö –∏–∑ —Ç–µ—Ö –∏–Ω—Ç–µ–≥—Ä–∞–ª–æ–≤, –∫–æ—Ç–æ—Ä—ã–µ –Ω–µ –ø—Ä–µ–¥—Å—Ç–∞–≤–∏–º—ã –≤ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã—Ö —Ñ—É–Ω–∫—Ü–∏—è—Ö. –ë–ª–∞–≥–æ–¥–∞—Ä—è —ç—Ç–æ–º—É –æ–Ω–∏ —à–∏—Ä–æ–∫–æ –ø—Ä–∏–º–µ–Ω—è—é—Ç—Å—è –≤ –º–∞—Ç–µ–º–∞—Ç–∏–∫–µ –∏ –µ–µ –ø—Ä–∏–ª–æ–∂–µ–Ω–∏—è—Ö, –≤ –º–µ—Ö–∞–Ω–∏–∫–µ, —Ç–µ—Ä–º–æ–¥–∏–Ω–∞–º–∏–∫–µ –∏ –≤ –¥—Ä—É–≥–∏—Ö –æ—Ç—Ä–∞—Å–ª—è—Ö —Å–æ–≤—Ä–µ–º–µ–Ω–Ω–æ–π –Ω–∞—É–∫–∏. 2. –ú–∞—Ç–µ–º–∞—Ç–∏—á–µ—Å–∫–∏–π –∞–Ω–∞–ª–∏–∑ —á–∞—Å—Ç—å 2: –ò–ª—å–∏–Ω –û.–ê., –°–∞–¥–æ–≤–Ω–∏—á–∏–π –í.–ê., –°–µ–Ω–¥–æ–≤ –ë–ª.–•.,–ú.,–ú–æ—Å–∫–æ–≤—Å–∫–∏–π –Ω–∏–≤–µ—Ä—Å–∏—Ç–µ—Ç,1987 3.
–°–±–æ—Ä–Ω–∏–∫ –∑–∞–¥–∞—á –ø–æ –º–∞—Ç–µ–º–∞—Ç–∏—á–µ—Å–∫–æ–º—É –∞–Ω–∞–ª–∏–∑—É: –î–µ–º–∏–¥–æ–≤–∏—á –ë.–ü.,–ú.,–ù–∞—É–∫–∞,1966 4. –ò–Ω—Ç–µ–≥—Ä–∞–ª—ã –∏ —Ä—è–¥—ã —Å–ø–µ—Ü–∏–∞–ª—å–Ω—ã–µ —Ñ—É–Ω–∫—Ü–∏–∏: –ü—Ä—É–¥–Ω–∏–∫–æ–≤ –ê.–ü., –ë—Ä—ã—á–∫–æ–≤ –Æ.–ê.,–ú.,–ù–∞—É–∫–∞,1983 5. –°–ø–µ—Ü–∏–∞–ª—å–Ω—ã–µ —Ñ—É–Ω–∫—Ü–∏–∏: –ö—É–∑–Ω–µ—Ü–æ–≤, –ú.,–í—ã—Å—à–∞—è —à–∫–æ–ª–∞,1965
 <=
<=




 –∞.–¢–∞–∫ –∫–∞–∫ –≥—Ä–∞—Ñ–∏–∫ —Ñ—É–Ω–∫—Ü–∏–∏
–∞.–¢–∞–∫ –∫–∞–∫ –≥—Ä–∞—Ñ–∏–∫ —Ñ—É–Ω–∫—Ü–∏–∏ 


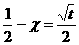
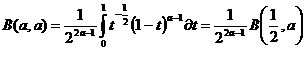
 ,–æ—Ç–∫—É–¥–∞
,–æ—Ç–∫—É–¥–∞ 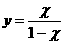
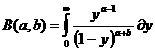 (1.4)
(1.4)
 –∞–∏ –ø—Ä–∏–º–µ–Ω–µ–Ω–∏–µ –∫–æ –≤—Ç–æ—Ä–æ–º—É –∏–Ω—Ç–µ–≥—Ä–∞–ª—É –ø–æ–¥—Å—Ç–∞–Ω–æ–≤–∫–∏
–∞–∏ –ø—Ä–∏–º–µ–Ω–µ–Ω–∏–µ –∫–æ –≤—Ç–æ—Ä–æ–º—É –∏–Ω—Ç–µ–≥—Ä–∞–ª—É –ø–æ–¥—Å—Ç–∞–Ω–æ–≤–∫–∏ 
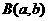


 (2.1)
(2.1)
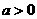 –∞0.–ü–æ–ª–æ–∂–∏–º
–∞0.–ü–æ–ª–æ–∂–∏–º 

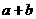 –∞–∏
–∞–∏
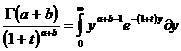

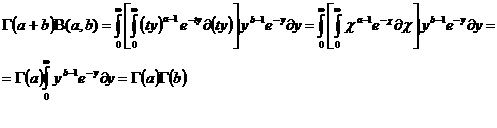
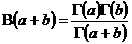 (2.2)
(2.2)
 ,–Ω–∞
,–Ω–∞  –∞–∏ –∏–Ω—Ç–µ–≥—Ä–∏—Ä—É–µ–º –ø–æ —á–∞—Å—Ç—è–º
–∞–∏ –∏–Ω—Ç–µ–≥—Ä–∏—Ä—É–µ–º –ø–æ —á–∞—Å—Ç—è–º
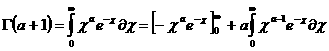

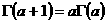 (2.3)
(2.3)

 –∞–∏–º–µ–µ–º
–∞–∏–º–µ–µ–º
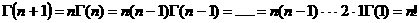 (2.4)
(2.4)

3.
–ü—Ä–æ–∏–∑–≤–æ–¥–Ω–∞—è –≥–∞–º–º–∞ —Ñ—É–Ω–∫—Ü–∏–∏ 11
 –∞
–∞ 
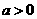


 –∞–ø—Ä–∏
–∞–ø—Ä–∏ 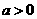

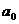
 –∞–∏ –º–æ–∂–Ω–∞ –ø—Ä–∏–º–µ–Ω–∏—Ç—å –ø—Ä–∏–∑–Ω–∞–∫ –í–µ–µ—Ä—à—Ç—Ä–∞—Å–∞. –°—Ö–æ–¥—è—â–∏–º—Å—è –ø—Ä–∏ –≤—Å–µ—Ö –∑–Ω–∞—á–µ–Ω–∏—è—Ö
–∞–∏ –º–æ–∂–Ω–∞ –ø—Ä–∏–º–µ–Ω–∏—Ç—å –ø—Ä–∏–∑–Ω–∞–∫ –í–µ–µ—Ä—à—Ç—Ä–∞—Å–∞. –°—Ö–æ–¥—è—â–∏–º—Å—è –ø—Ä–∏ –≤—Å–µ—Ö –∑–Ω–∞—á–µ–Ω–∏—è—Ö 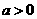 –∞—è–≤–ª—è–µ—Ç—Å—è –∏ –≤–µ—Å—å –∏–Ω—Ç–µ–≥—Ä–∞–ª
–∞—è–≤–ª—è–µ—Ç—Å—è –∏ –≤–µ—Å—å –∏–Ω—Ç–µ–≥—Ä–∞–ª  –∞—Ç–∞–∫ –∫–∞–∫ –∏ –≤—Ç–æ—Ä–æ–µ —Å–ª–æ–≥–∞–µ–º–æ–µ –ø—Ä–∞–≤–æ–π —á–∞—Å—Ç–∏ —è–≤–ª—è–µ—Ç—Å—è –∏–Ω—Ç–µ–≥—Ä–∞–ª–æ–º, –∑–∞–≤–µ–¥–æ–º–æ —Å—Ö–æ–¥—è—â–∏–º—Å—è –ø—Ä–∏ –ª—é–±–æ–º
–∞—Ç–∞–∫ –∫–∞–∫ –∏ –≤—Ç–æ—Ä–æ–µ —Å–ª–æ–≥–∞–µ–º–æ–µ –ø—Ä–∞–≤–æ–π —á–∞—Å—Ç–∏ —è–≤–ª—è–µ—Ç—Å—è –∏–Ω—Ç–µ–≥—Ä–∞–ª–æ–º, –∑–∞–≤–µ–¥–æ–º–æ —Å—Ö–æ–¥—è—â–∏–º—Å—è –ø—Ä–∏ –ª—é–±–æ–º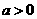

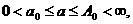 –∞–≥–¥–µ
–∞–≥–¥–µ  –∞–ø—Ä–æ–∏–∑–≤–æ–ª—å–Ω–æ.–î–µ–π—Å—Ç–≤–∏—Ç–µ–ª—å–Ω–æ –¥–ª—è –≤—Å–µ—Ö –∫–∞–∑–∞–Ω—ã—Ö –∑–Ω–∞—á–µ–Ω–∏–π
–∞–ø—Ä–æ–∏–∑–≤–æ–ª—å–Ω–æ.–î–µ–π—Å—Ç–≤–∏—Ç–µ–ª—å–Ω–æ –¥–ª—è –≤—Å–µ—Ö –∫–∞–∑–∞–Ω—ã—Ö –∑–Ω–∞—á–µ–Ω–∏–π 
 –∞
–∞

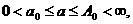
 —Ö–æ–¥–∏—Ç—Å—è —Ä–∞–≤–Ω–æ–º–µ—Ä–Ω–æ.
—Ö–æ–¥–∏—Ç—Å—è —Ä–∞–≤–Ω–æ–º–µ—Ä–Ω–æ.
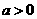
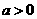 —Ñ—É–Ω–∫—Ü–∏—è
—Ñ—É–Ω–∫—Ü–∏—è –∞–Ω–µ–ø—Ä–µ—Ä—ã–≤–Ω–∞ –ø—Ä–∏
–∞–Ω–µ–ø—Ä–µ—Ä—ã–≤–Ω–∞ –ø—Ä–∏ 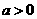 –∞–∏
–∞–∏

 –∞,
–∞,  –∞. –í—ã–±–µ—Ä–µ–º —á–∏—Å–ª–æ
–∞. –í—ã–±–µ—Ä–µ–º —á–∏—Å–ª–æ –∞—Ç–∞–∫, —á—Ç–æ–±—ã
–∞—Ç–∞–∫, —á—Ç–æ–±—ã 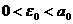
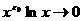 –∞–ø—Ä–∏
–∞–ø—Ä–∏ 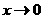
 –∞—Ç–∞–∫–æ–µ, —á—Ç–æ
–∞—Ç–∞–∫–æ–µ, —á—Ç–æ  –∞–∏
–∞–∏  –∞–Ω–∞
–∞–Ω–∞
 –∞—Å–ø—Ä–∞–≤–µ–¥–ª–∏–≤–æ –Ω–µ—Ä–∞–≤–µ–Ω—Å—Ç–≤–æ
–∞—Å–ø—Ä–∞–≤–µ–¥–ª–∏–≤–æ –Ω–µ—Ä–∞–≤–µ–Ω—Å—Ç–≤–æ
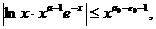
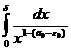 –∞—Å—Ö–æ–¥–∏—Ç—Å—è, —Ç–æ –∏–Ω—Ç–µ–≥—Ä–∞–ª
–∞—Å—Ö–æ–¥–∏—Ç—Å—è, —Ç–æ –∏–Ω—Ç–µ–≥—Ä–∞–ª  –∞—Å—Ö–æ–¥–∏—Ç—Å—è —Ä–∞–≤–Ω–æ–º–µ—Ä–Ω–æ –æ—Ç–Ω–æ—Å–∏—Ç–µ–ª—å–Ω–æ
–∞—Å—Ö–æ–¥–∏—Ç—Å—è —Ä–∞–≤–Ω–æ–º–µ—Ä–Ω–æ –æ—Ç–Ω–æ—Å–∏—Ç–µ–ª—å–Ω–æ  –∞–Ω–∞
–∞–Ω–∞ 
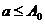 –∞—Å—É—â–µ—Å—Ç–≤—É–µ—Ç —Ç–∞–∫–æ–µ —á–∏—Å–ª–æ
–∞—Å—É—â–µ—Å—Ç–≤—É–µ—Ç —Ç–∞–∫–æ–µ —á–∏—Å–ª–æ

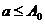 –∞–≤—ã–ø–æ–ª–Ω—è–µ—Ç—Å—è –Ω–µ—Ä–∞–≤–µ–Ω—Å—Ç–≤–æ
–∞–≤—ã–ø–æ–ª–Ω—è–µ—Ç—Å—è –Ω–µ—Ä–∞–≤–µ–Ω—Å—Ç–≤–æ 
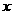 –∞–∏ –≤—Å–µ—Ö
–∞–∏ –≤—Å–µ—Ö 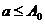 –∞–ø–æ–ª—É—á–∏–º
–∞–ø–æ–ª—É—á–∏–º 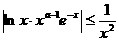 –∞ –≤ —Å–∏–ª—É –ø—Ä–∏–∑–Ω–∞–∫–∞ —Å—Ä–∞–≤–Ω–µ–Ω–∏—è —Å–ª–µ–¥—É–µ—Ç, —á—Ç–æ –∏–Ω—Ç–µ–≥—Ä–∞–ª
–∞ –≤ —Å–∏–ª—É –ø—Ä–∏–∑–Ω–∞–∫–∞ —Å—Ä–∞–≤–Ω–µ–Ω–∏—è —Å–ª–µ–¥—É–µ—Ç, —á—Ç–æ –∏–Ω—Ç–µ–≥—Ä–∞–ª 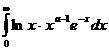 –∞—Å—Ö–æ–¥–∏—Ç—Å—è —Ä–∞–≤–Ω–æ–º–µ—Ä–Ω–æ –æ—Ç–Ω–æ—Å–∏—Ç–µ–ª—å–Ω–æ
–∞—Å—Ö–æ–¥–∏—Ç—Å—è —Ä–∞–≤–Ω–æ–º–µ—Ä–Ω–æ –æ—Ç–Ω–æ—Å–∏—Ç–µ–ª—å–Ω–æ  –∞–Ω–∞
–∞–Ω–∞ 

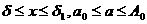

 –∞
–∞  –∞–∏–Ω—Ç–µ–≥—Ä–∞–ª
–∞–∏–Ω—Ç–µ–≥—Ä–∞–ª
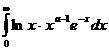
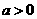 –∞–∏ —Å–ø—Ä–∞–≤–µ–¥–ª–∏–≤–æ —Ä–∞–≤–µ–Ω—Å—Ç–≤–æ
–∞–∏ —Å–ø—Ä–∞–≤–µ–¥–ª–∏–≤–æ —Ä–∞–≤–µ–Ω—Å—Ç–≤–æ
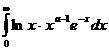
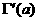
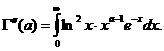
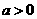

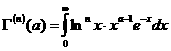


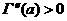 –∞–¥–ª—è –≤—Å–µ—Ö
–∞–¥–ª—è –≤—Å–µ—Ö 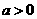
 –∞–≤–æ–∑—Ä–∞—Å—Ç–∞–µ—Ç. –ü–æ—Å–∫–æ–ª—å–∫—É
–∞–≤–æ–∑—Ä–∞—Å—Ç–∞–µ—Ç. –ü–æ—Å–∫–æ–ª—å–∫—É  [1,2]–ø—Ä–æ–∏–∑–≤–æ–¥–Ω–∞—è
[1,2]–ø—Ä–æ–∏–∑–≤–æ–¥–Ω–∞—è  –∞–ø—Ä–∏
–∞–ø—Ä–∏  –∞–∏
–∞–∏ –∞–ø—Ä–∏
–∞–ø—Ä–∏  –∞ –ú–æ–Ω–æ—Ç–æ–Ω–Ω–æ —É–±—ã–≤–∞–µ—Ç –Ω–∞
–∞ –ú–æ–Ω–æ—Ç–æ–Ω–Ω–æ —É–±—ã–≤–∞–µ—Ç –Ω–∞ 
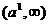
 –∞
–∞ 

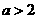 –∞–∏–∑ —Ñ–æ—Ä–º—É–ª—ã
–∞–∏–∑ —Ñ–æ—Ä–º—É–ª—ã  –∞
–∞  –∞–ø—Ä–∏
–∞–ø—Ä–∏ 

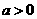


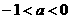
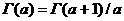
 –∞–∏–∑ (-1,0). –ü–æ–ª—É—á–∞–µ–º, —á—Ç–æ —Ç–∞–∫ –ø—Ä–æ–¥–æ–ª–∂–µ–Ω–Ω–∞—è —Ñ—É–Ω–∫—Ü–∏—è
–∞–∏–∑ (-1,0). –ü–æ–ª—É—á–∞–µ–º, —á—Ç–æ —Ç–∞–∫ –ø—Ä–æ–¥–æ–ª–∂–µ–Ω–Ω–∞—è —Ñ—É–Ω–∫—Ü–∏—è  –∞–ø—Ä–∏–Ω–∏–º–∞–µ—Ç –Ω–∞ (-1,0)
–æ—Ç—Ä–∏—Ü–∞—Ç–µ–ª—å–Ω—ã–µ –∑–Ω–∞—á–µ–Ω–∏—è –∏ –ø—Ä–∏
–∞–ø—Ä–∏–Ω–∏–º–∞–µ—Ç –Ω–∞ (-1,0)
–æ—Ç—Ä–∏—Ü–∞—Ç–µ–ª—å–Ω—ã–µ –∑–Ω–∞—á–µ–Ω–∏—è –∏ –ø—Ä–∏ 
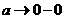 —Ñ—É–Ω–∫—Ü–∏—è
—Ñ—É–Ω–∫—Ü–∏—è 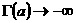
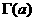
 –∞ —Ç–æ–π –∂–µ —Ñ–æ—Ä–º—É–ª–µ –ø—Ä–æ–¥–æ–ª–∂–∏—Ç—å –µ–µ –Ω–∞ –∏–Ω—Ç–µ—Ä–≤–∞–ª (-2,-1). –ù–∞ —ç—Ç–æ–º –∏–Ω—Ç–µ—Ä–≤–∞–ª–µ –ø—Ä–æ–¥–æ–ª–∂–µ–Ω–∏–µ–º
–∞ —Ç–æ–π –∂–µ —Ñ–æ—Ä–º—É–ª–µ –ø—Ä–æ–¥–æ–ª–∂–∏—Ç—å –µ–µ –Ω–∞ –∏–Ω—Ç–µ—Ä–≤–∞–ª (-2,-1). –ù–∞ —ç—Ç–æ–º –∏–Ω—Ç–µ—Ä–≤–∞–ª–µ –ø—Ä–æ–¥–æ–ª–∂–µ–Ω–∏–µ–º 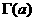 –∞–æ–∫–∞–∂–µ—Ç—Å—è —Ñ—É–Ω–∫—Ü–∏—è,
–ø—Ä–∏–Ω–∏–º–∞—é—â–∞—è –ø–æ–ª–æ–∂–∏—Ç–µ–ª—å–Ω—ã–µ –∑–Ω–∞—á–µ–Ω–∏—è –∏ —Ç–∞–∫–∞—è, —á—Ç–æ
–∞–æ–∫–∞–∂–µ—Ç—Å—è —Ñ—É–Ω–∫—Ü–∏—è,
–ø—Ä–∏–Ω–∏–º–∞—é—â–∞—è –ø–æ–ª–æ–∂–∏—Ç–µ–ª—å–Ω—ã–µ –∑–Ω–∞—á–µ–Ω–∏—è –∏ —Ç–∞–∫–∞—è, —á—Ç–æ 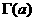
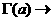

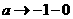 –∞–∏
–∞–∏ 
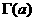





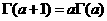
–∞ –ü—Ä–∏–º–µ–Ω–∏–º –≥–∞–º–º–∞ —Ñ—É–Ω–∫—Ü–∏—é –∫ –≤—ã—á–∏—Å–ª–µ–Ω–∏—é –∏–Ω—Ç–µ–≥—Ä–∞–ª–∞:



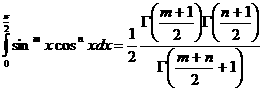 (3.1)
(3.1)
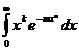
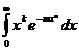

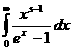
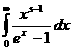




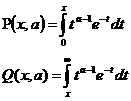


 –∞–≤ —Ä—è–¥ –∏–º–µ–µ–º
–∞–≤ —Ä—è–¥ –∏–º–µ–µ–º

 (3.2)
(3.2)

 –∞–¥–æ
–∞–¥–æ –∞–ø—Ä–∏ –∏–∑–º–µ–Ω–µ–Ω–∏–∏
–∞–ø—Ä–∏ –∏–∑–º–µ–Ω–µ–Ω–∏–∏ 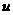 –æ—Ç
–æ—Ç 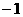 –¥–æ
–¥–æ –∞–∏ –æ–±—Ä–∞—â–∞—é—Ç—Å—è –≤ 0–∞ –ø—Ä–∏
–∞–∏ –æ–±—Ä–∞—â–∞—é—Ç—Å—è –≤ 0–∞ –ø—Ä–∏
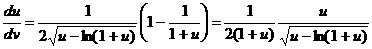
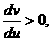
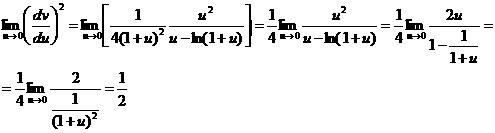
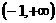
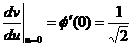
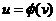 –∞–æ–ø—Ä–µ–¥–µ–ª–µ–Ω–Ω–∞—è –Ω–∞ –∏–Ω—Ç–µ—Ä–≤–∞–ª–µ
–∞–æ–ø—Ä–µ–¥–µ–ª–µ–Ω–Ω–∞—è –Ω–∞ –∏–Ω—Ç–µ—Ä–≤–∞–ª–µ  –∞–Ω–µ–ø—Ä–µ—Ä—ã–≤–Ω–∞—è –∏ –º–æ–Ω–æ—Ç–æ–Ω–Ω–æ –≤–æ–∑—Ä–∞—Å—Ç–∞—é—â–∞—è –≤ —ç—Ç–æ–º –∏–Ω—Ç–µ—Ä–≤–∞–ª–µ,
–∞–Ω–µ–ø—Ä–µ—Ä—ã–≤–Ω–∞—è –∏ –º–æ–Ω–æ—Ç–æ–Ω–Ω–æ –≤–æ–∑—Ä–∞—Å—Ç–∞—é—â–∞—è –≤ —ç—Ç–æ–º –∏–Ω—Ç–µ—Ä–≤–∞–ª–µ,

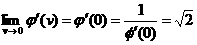 (3.3)
(3.3)
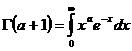


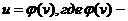
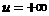 –∞–ø—Ä–∏
–∞–ø—Ä–∏ 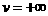 –∞.–ó–∞–º–µ—á–∞—è —á—Ç–æ(—Å–º.3.2)
–∞.–ó–∞–º–µ—á–∞—è —á—Ç–æ(—Å–º.3.2)

 ,
,
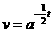
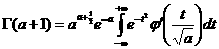

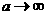



 (3.4)
(3.4)
 –∞,–ø—Ä–∏
–∞,–ø—Ä–∏ 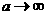

 –∞–ø–æ–ª–∞–≥–∞—é—Ç
–∞–ø–æ–ª–∞–≥–∞—é—Ç
 (3.5)
(3.5)
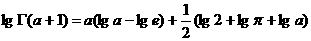
 –∞—Ü–µ–ª–æ–µ –ø–æ–ª–æ–∂–∏—Ç–µ–ª—å–Ω–æ–µ —á–∏—Å–ª–æ, —Ç–æ
–∞—Ü–µ–ª–æ–µ –ø–æ–ª–æ–∂–∏—Ç–µ–ª—å–Ω–æ–µ —á–∏—Å–ª–æ, —Ç–æ  –∞–∏ (3.5) –ø—Ä–µ–≤—Ä–∞—â–∞–µ—Ç—Å—è –≤ –ø—Ä–∏–±–ª–∏–∂–µ–Ω–Ω—É—é —Ñ–æ—Ä–º—É–ª—É –≤—ã—á–∏—Å–ª–µ–Ω–∏—è —Ñ–∞–∫—Ç–æ—Ä–∏–∞–ª–æ–≤ –ø—Ä–∏ –±–æ–ª—å—à–∏—Ö –∑–Ω–∞—á–µ–Ω–∏—è—Ö
–∞–∏ (3.5) –ø—Ä–µ–≤—Ä–∞—â–∞–µ—Ç—Å—è –≤ –ø—Ä–∏–±–ª–∏–∂–µ–Ω–Ω—É—é —Ñ–æ—Ä–º—É–ª—É –≤—ã—á–∏—Å–ª–µ–Ω–∏—è —Ñ–∞–∫—Ç–æ—Ä–∏–∞–ª–æ–≤ –ø—Ä–∏ –±–æ–ª—å—à–∏—Ö –∑–Ω–∞—á–µ–Ω–∏—è—Ö
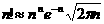

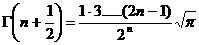




 –∞
–∞
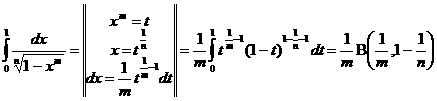



–ú–Ω—Å—Ç–µ—Ä—Å—Ç–≤–æ –æ—Å–≤—Ç–∏ –Ω–∞—É–∫–∏ –∫—Ä–∞ø–Ω–∏
–î–û –ó–ê–•–ò–°–¢–£ –î–û–ü–£–©–ï–ù–ò–ô
–ü–û–Ø–°–ù–Æ–í–ê–õ–¨–ù–ê –ó–ê–ü–ò–°–ö–ê –î–û –ö–£–Ý–°–û–í–û–ì–û –ü–Ý–û–ï–ö–¢–£
–Ý–æ–∑—Ä–æ–±–∏–≤
–°–∞–¥–∏–≥–æ–≤ –Ý.–ê.
–ö—É–¥—Ä—è –í.
–°–æ–¥–µ—Ä–∂–∞–Ω–∏–µ
–ó–∞–¥–∞–Ω–∏–µ –Ω–∞ –∫—É—Ä—Å–æ–≤—É—é —Ä–∞–±–æ—Ç—É..............................................................2
–ö—É—Ä—Å–æ–≤–∞—è —Ä–∞–±–æ—Ç–∞: 24 —Å—Ç., 5 –∏—Å—Ç–æ—á–Ω–∏–∫–æ–≤, 1 —Ä–∏—Å.
–í–≤–µ–¥–µ–Ω–∏–µ

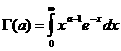
–í—ã–≤–æ–¥
–°–ø–∏—Å–æ–∫ –ª–∏—Ç–µ—Ä–∞—Ç—É—Ä—ã