Статические модели задачи размещения
РЕФЕРАТ
Статические модели задачи размещения.
Самара, 2006
Производственно-транспортные задачи оптимального размещения предприятий и применимость метода последовательных расчетов
1. Задача размещения предприятий с ограниченными объемами производства.
Имеется п пунктов потребления с заданными объемами потребления Необходимо определить такие объемы перевозок где при словиях Если все
Предполагается также, что либо так как в противном случае никакие значения Обозначим через при словиях Фиксирование некоторого варианта размещения налогичное словию (5). Значение
Задача,
собственно, состоит в отыскании среди всех возможных подмножеств (вариантов размещения) Функция После такого введения словного пункта производства словие (4.10) будет выполняться для любого Таким образом, на множестве всех подмножеств Покажем,
что к решению этой задачи применим метод последовательных расчетов. Для этого достаточно становить, что функция где Для доказательств рассмотрим вспомогательную функциюа
Таким образом, для каждого при словиях (7)<-(10). Эта задача отличается от задачи 1 тем, что некоторые предприятия при словиях где Предполагается, что так как в противном случае задача не имеет решения. Задача чрезвычайно прощается, когда в обоих случаях ее решение сводится к решению одной транспортной задачи. Поэтому будем в общем случае считать Обозначим через при словиях Так как с четом пустого множества для любого то методами линейного программирования определяется значение 1) 2) В случае 2) рассмотрим задачу отыскания наименьшего значения функционала при условиях где Значения
Для всех тельное число, но в то же время Для всех Условие этой задачи полностью совпадает с словием задачи 1, и поэтому решение ее сводится к отысканию такого подмножества 3. Задача размещения со ступенчатой функцией стоимости производства. Постановка этой задачи отличается от постановки задачи 1 другим заданием функций стоимости производства предприятий. В данном случае эта функция задается некоторой ступенчатой разрывной функцией
где Таким образом, задача состоит в следующем: определить совокупность значений где
При
4. Задачи размещения с ограничениями на суммарную продукцию. В этой задаче предполагается, что суммарный объем продукции, выпускаемой всеми предприятиями, задан и равен Тогда рассматриваемая задача принимает следующий вид: определить совокупность значений при словиях Будем считать, что Рассмотрим вначале задачу (32) -(36). Наиболее интересен случай, когда Все остальные предположения о расположении величины d относительно интервала Действительно, если при при Для любого Производственно-распределительные задачи оптимального размещения предприятий и применимость метода последовательных расчетов. 5. Производственно-распределительная задача размещения предприятий с ограниченными объемами производства и пропускными спонсобностями коммуникаций. Рассматривается задача нахождения наименьшего значения функционала при словиях В отличие от задач оптимального размещения предприятий и применимость метода последовательных расчетов, здесь имеются коэффициенты при словиях
(38)-(40), в которых I заменено на В случае отсутствия верхних ограничений на переменные Для решения сформулированной задачи также применим метод последовательных расчетов. 6. Производствснно-распределительная задача размещения предприятий с ограничениями на суммарную продукцию. Рассматривается задача нахождения наименьшего значения функционала при словиях Комбинаторная постановка задачи заключается в определении подмножества здесь при словиях (41) -(45),
в которых I заменено на Для решения этой задачи также применим метод последовательных расчетов.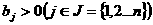 аи
аи  азаданы величины
азаданы величины 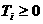 Ч постоянные затраты
(капиталовложения), не пропорнциональные объему производства
Ч постоянные затраты
(капиталовложения), не пропорнциональные объему производства 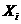 анеобходимые, например,
для строительства предприятий
анеобходимые, например,
для строительства предприятий 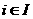
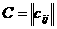 , где
, где 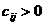 Ч стоимость перевозки единицы продукции из пункта производства
Ч стоимость перевозки единицы продукции из пункта производства
 затраты были минимальными, т.е. требуется найти наименьшее значение функционала
затраты были минимальными, т.е. требуется найти наименьшее значение функционала
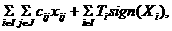
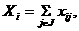
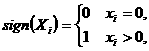 (1)
(1)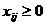
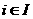 а
а 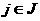 , (2)
, (2)
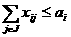 а
а (3)
(3)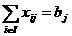 а
а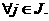 (4)
(4)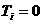 , то задача становится обычной транспортной задачей линейного программирования. В рассматриваемой задаче предполагается, что не все
, то задача становится обычной транспортной задачей линейного программирования. В рассматриваемой задаче предполагается, что не все 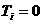 . В этом случае функционал (1) представляет собой разрывную функцию, обладающую,
вообще говоря, большим числом точек минимума над областью (2) - (4).
. В этом случае функционал (1) представляет собой разрывную функцию, обладающую,
вообще говоря, большим числом точек минимума над областью (2) - (4).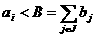 адля всех
адля всех 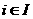 , либо
, либо 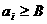 ане для всех
ане для всех 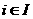 , так как в случае
, так как в случае 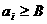 адля всех
адля всех 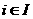 получаем задачу размещения с неограниченными объемами производства. Однако необходимо, чтобы суммарный объем потребления
получаем задачу размещения с неограниченными объемами производства. Однако необходимо, чтобы суммарный объем потребления 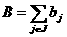 <- не превышал сумму верхних
<- не превышал сумму верхних
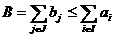 (5)
(5) ане довлетворяют словиям (2) -(4).
ане довлетворяют словиям (2) -(4).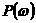 аминимальные суммарные затраты при фиксировании некоторого варианта размещения
аминимальные суммарные затраты при фиксировании некоторого варианта размещения 
 (6)
(6)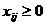
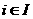 а
а 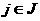 , (7)
, (7)
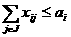 а
а (8)
(8)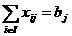 а
а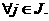 (9)
(9)
 апроизводится тем, что для всех
апроизводится тем, что для всех 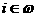 асчитается
асчитается 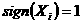 Для фиксированного со предполагается выполнение словия
Для фиксированного со предполагается выполнение словия (10)
(10)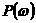 адля каждого
адля каждого  определяется решением обычной транспортной задачи линейного программирования. Таким образом, можно говорить об однозначной функции
определяется решением обычной транспортной задачи линейного программирования. Таким образом, можно говорить об однозначной функции 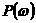 заданной на множестве всех
заданной на множестве всех  , для которых выполняются словия (10).
, для которых выполняются словия (10). апунктов производства
апунктов производства 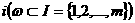 атакого подмножества (варианта)
атакого подмножества (варианта) 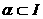 , при котором обеспечинваются с четом словий (7) - (10) наименьшие суммарные затраты
, при котором обеспечинваются с четом словий (7) - (10) наименьшие суммарные затраты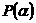 . Другими словами, требуется определить такое подмножество
. Другими словами, требуется определить такое подмножество 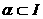 , для которого
, для которого 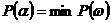 апо всем
апо всем  , довлетворяющим условию (10).
, довлетворяющим условию (10).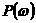 ане определена на множестве всех подмножеств
ане определена на множестве всех подмножеств  , не довлетворяющих словию (10). Для определения функции
, не довлетворяющих словию (10). Для определения функции 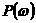 ана множестве всех
ана множестве всех  поступим следующим образом. Соотнесем пустому подмножеству
поступим следующим образом. Соотнесем пустому подмножеству 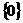 аусловный пункт производства
аусловный пункт производства 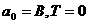
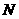
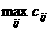 ). Так как пустое множество
). Так как пустое множество 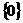 содержится в любом
содержится в любом  , то это означает, что словный пункт производства бундет содержаться в любом подмножестве (варианте размещения)
, то это означает, что словный пункт производства бундет содержаться в любом подмножестве (варианте размещения)  апунктов производства.
Поэтому в дальнейшем (чтобы не сложнять записи) под выражением
апунктов производства.
Поэтому в дальнейшем (чтобы не сложнять записи) под выражением 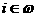
 все отличные от нуля значения элементов подмножества
все отличные от нуля значения элементов подмножества  , но и само значение 0, соответствующее словному пункту производства. В частности,
, но и само значение 0, соответствующее словному пункту производства. В частности, 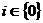
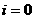 .
. , так как величина
, так как величина  аи поэтому значение
аи поэтому значение 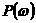 атеперь может быть определено для всех
атеперь может быть определено для всех  . Здесь необходимо отметить, что в силу выбора величин
. Здесь необходимо отметить, что в силу выбора величин 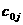
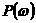 адля тех
адля тех  , для которых условие (10) выполняется лишь с четом
, для которых условие (10) выполняется лишь с четом 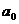 , будут сколь годно большими, для тех
, будут сколь годно большими, для тех  , для которых это словие выполняется и без чета
, для которых это словие выполняется и без чета 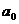 , наличие словного пункта производства не влияет на величину
, наличие словного пункта производства не влияет на величину 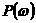 , т.е.
, т.е. 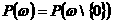 . Отсюда, в частности, следует, что искомое подмножество
. Отсюда, в частности, следует, что искомое подмножество 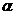
 , для которых
, для которых (11)
(11) амножества/опреденляется однозначная функция
амножества/опреденляется однозначная функция 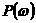 аи исходная задача сводится к отысканию такого подмножества
аи исходная задача сводится к отысканию такого подмножества 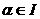
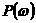 адостигает своего наинменьшего значения
адостигает своего наинменьшего значения 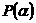 , т.е
, т.е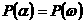 по всем
по всем  .
.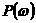 аудовлетворяет словию
аудовлетворяет словию
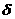 аи
аи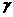 а<- произвольные подмножества
а<- произвольные подмножества 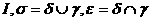
 адля всех
адля всех  Можно записать
Можно записать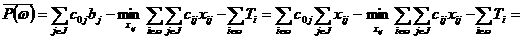


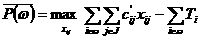
2. Задача размещения с фиксированными минимальными объемами производства.
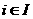 являются же действующими с мощностями
являются же действующими с мощностями  , закрытие их запрещено и возможно лишь величение их мощностей до некоторой величины
, закрытие их запрещено и возможно лишь величение их мощностей до некоторой величины 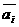 (
(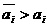 , что влечет дополнительные затраты
, что влечет дополнительные затраты  . Таким образом, ставится следующая задача: определить совокупность значений
. Таким образом, ставится следующая задача: определить совокупность значений  , при которых достигается минимум функционала
, при которых достигается минимум функционала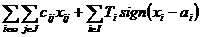 (12)
(12)
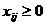
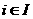 а
а 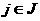 , (13)
, (13)
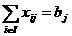 а
а (14)
(14)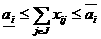 а
а (15)
(15)
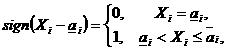
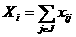 а<- возможный объем производства предприятия
а<- возможный объем производства предприятия 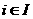 .
.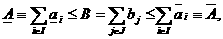
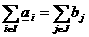 аили
аили 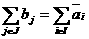
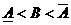 (16)
(16) амножество тех
амножество тех 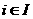 , для которых
, для которых 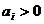 . Определим функцию
. Определим функцию 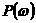 ана множестве всех подмножеств
ана множестве всех подмножеств  а(считаем для
а(считаем для 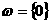 , как и прежде,
, как и прежде, 
 аполагать,
что
аполагать,
что 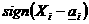 для всех
для всех 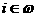 а(это означает, что для всех предприятий
а(это означает, что для всех предприятий 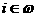 возможно расширение мощности до
возможно расширение мощности до  ), то минимальное значение функционала (12) для этого
), то минимальное значение функционала (12) для этого 
 (17)
(17)
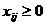
 а
а 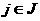 , (18)
, (18)
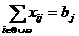 а
а (19)
(19)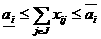 адля
адля 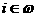 (20)
(20)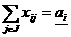 для а
для а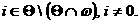
 авыполняется неравенство
авыполняется неравенство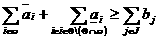 (22)
(22)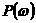 адля любого
адля любого  ва I определяется однозначная функция
ва I определяется однозначная функция 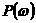 . Следовательно, задача 2 сводится к определению такого подмножества
. Следовательно, задача 2 сводится к определению такого подмножества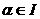 функция
функция 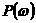 апринимает свое наименьшее значение
апринимает свое наименьшее значение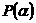 , т.е.
, т.е.  по всем
по всем  при словиях (18) - (21). Возможны два случая:
при словиях (18) - (21). Возможны два случая: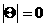 , т.е.
, т.е. 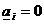 а
а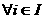 аи в этом случае получаем задачу 1;
аи в этом случае получаем задачу 1;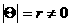 аможно записать
аможно записать 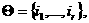 агде
агде  Ч элементы
Ч элементы 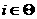 , расположенные в порядке возрастания
, расположенные в порядке возрастания
индексов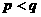 <
<
 (23)
(23)
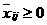
 а
а 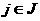 , (24)
, (24)
 а
а (25)
(25)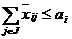 а
а 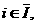 (26)
(26)
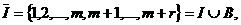
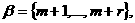 а
а 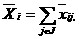
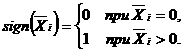

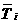
 аопределяются следующим образом.
аопределяются следующим образом.

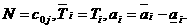
 апри любых
апри любых 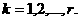
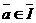
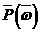
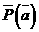
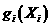 аименно:
аименно: (27)
(27) 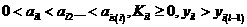 адля всех
адля всех 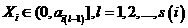 а(при
а(при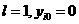
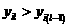 адля всех
адля всех 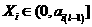 аследует,
что
аследует,
что  апри
апри
 адля всех
адля всех 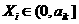
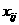 апри которых достигается минимум функционала
апри которых достигается минимум функционала (28)
(28) <- ступенчатая разрывная функция (27) при словиях
<- ступенчатая разрывная функция (27) при словиях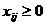
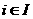 а
а 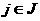 , (29)
, (29)
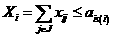 а
а (30)
(30)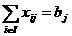 а
а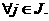 (31)
(31)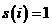 аполучаем задачу 1.
аполучаем задачу 1.
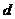 , объемы перевозок от предприятий до потребителей ограничены сверху величинами
, объемы перевозок от предприятий до потребителей ограничены сверху величинами 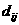 каждый потребитель должен получить продукцию в объеме,
не меньшем
каждый потребитель должен получить продукцию в объеме,
не меньшем 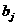 Остальные словия задачи 1 сохраняются.
Остальные словия задачи 1 сохраняются.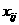 , при которых достигается минимум функционала
, при которых достигается минимум функционала
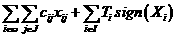 (32)
(32)
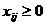
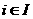 а
а 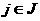 , (33)
, (33)
 а
а (34)
(34)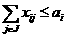 а
а (35)
(35)
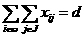 (36)
(36)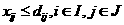
 ,
,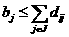
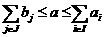
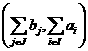 алибо делают задачу несовместной, либо позволяют освободиться от словия (4.53).
алибо делают задачу несовместной, либо позволяют освободиться от словия (4.53). , то
, то 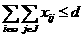 ;
;
 аусловия (33),
(34), (36) несовместны; при
аусловия (33),
(34), (36) несовместны; при 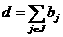 условие (36)а можно исключить, заменив словия (34) на
условие (36)а можно исключить, заменив словия (34) на 
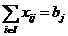 а
а
 аусловия (33), (34), (36)
несовместны;
аусловия (33), (34), (36)
несовместны;
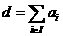 апри словие (36) можно исключить,
заменив словия (35) на
апри словие (36) можно исключить,
заменив словия (35) на 
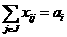 а
а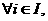
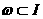 аопределение
аопределение 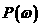 асводится к решению задачи (32)-(36),
где везде вместо I пишется
асводится к решению задачи (32)-(36),
где везде вместо I пишется  d для какого-либо
d для какого-либо 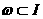 авыйдет из интервала
авыйдет из интервала 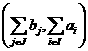 , то, как показано выше, либо условия (33)-(36)а становятся несовместными (в этом случае полагаем
, то, как показано выше, либо условия (33)-(36)а становятся несовместными (в этом случае полагаем 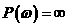 ), либо освобождаемся от словия (4.53) и определение
), либо освобождаемся от словия (4.53) и определение 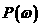 асводится к решению транспортной задачи типа 1.
асводится к решению транспортной задачи типа 1.
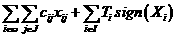 (37)
(37)

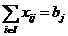 а
а (38)
(38)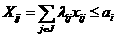 а
а (39)
(39)
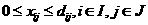 (40)
(40)
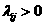 , называемые коэффициентами переработки. Комбинаторная постановка задачи (37)
- (40) состоит в определении подмножества
, называемые коэффициентами переработки. Комбинаторная постановка задачи (37)
- (40) состоит в определении подмножества 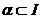 атакого, что
атакого, что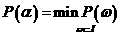 агде
агде 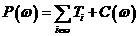

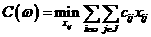
 .
.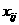 ав работе показывалось,
что функция
ав работе показывалось,
что функция 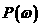 аудовлетворяет словию
аудовлетворяет словию 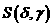 .
.
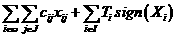 (41)
(41)

 а
а (42)
(42)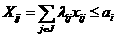 а
а (43)
(43)
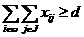 (44)
(44)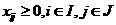 (45)
(45)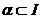 атакого, что
атакого, что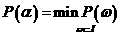 агде
агде 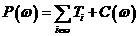

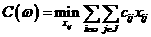 .
.

