Электромагнитные колебания
Министерство науки и образования Украины
Статья для учащихся школ, гимназий и лицеев
по теме:
Электромагнитные колебания<
Выполнил: преподаватель школы №1
Шкоропадо Александр Сергеевич
Одесса 2005г
Содержание
|
Введение |
3 |
|
Свободные и вынужденные электромагнитные колебания |
5 |
|
Собственные электрические колебания |
7 |
|
Уравнения собственных электрических колебаний (в отсутствие затухания и при наличии затухания) |
13 |
|
Вынужденные электрические колебания. Переменные токи |
16 |
|
Сопротивление в цепи переменного тока |
18 |
|
Емкость в цепи переменного тока |
21 |
|
Индуктивность в цепи переменного тока |
24 |
|
Резонанс в электрической цепи |
27 |
|
Заключение |
31 |
|
Литература |
32 |
Введение
В природе и технике, кроме поступательного и вращательного движений, часто встречается еще один вид механического движения это колебания.
Говоря колебания, мы сразу представляем себе колебание грузика, подвешенного к нити, или прикрепленного к пружине. Однако колебания означают не только механическое движение физического тела туда - обратно. Под колебаниями следует понимать изменение какой-либо величины, то есть изменение, при котором значение этой величины повторяется через определенный промежуток времени.
Среди различных механических движений особо важное значение имеют периодические движения, или колебания. Такие движения мы встречаем в небесной механике (движение планет) и в различных механических машинах. Они лежат в основе изменения времени (часы). Механическими колебаниями объясняются также звуковые явления.
Открытие электромагнитной индукции глубило наши представления об электромагнитном поле. Но дело не только в этом. Благодаря самоиндукции возможны колебания заряда, силы тока и других величин, характеризующих и имеют много общего с механическими колебаниями.
Подобно этому, среди различных электрических явлений особое место занимают электромагнитные колебания, при которых электрические величины (заряды, токи, электрические и магнитные поля) изменяются периодически. Электромагнитные колебания используют в различных важных технических стройствах и принимают для целей связи (телефония, телеграфия, радиосвязь). Технические переменные токи также являются электрическими колебаниями. кажем, наконец, что световые явления представляют собой не что иное, как электромагнитные колебания.
Таким образом, приступая к изучению электромагнитных колебаний, полезно вспомнить колебания механические, несколько точнить и расширить знания по данной теме.
Свободные и вынужденные электромагнитные колебания
Электромагнитные колебания были открыты в известной мере случайно. После того как изобрели лейденскую банку (первый конденсатор) и научились сообщать ей большой заряд с помощью электростатической машины, начали изучать электрический заряд банки. Замыкая обкладки лейденской банки с помощью проволочной катушки, обнаружили, что стальные спицы внутри катушки намагничиваются. В этом ничего странного не было: электрический ток и должена намагничивать стальной сердечник катушки. дивительным было то, что нельзя было предсказать, какой конец сердечника катушки окажется северным полюсом, какой - южным. Повторяя опыт примерно в одних и тех же словиях, получали в одних случаях один результат, в других - другой.
Далеко не сразу поняли, что при разрядке конденсатора через катушку возникает колебания. За время разрядки конденсатор спевает много раз перезарядиться, и ток меняет направление много раз. Из-за этого сердечник может намагничиваться различным образом.
Электромагнитные колебания - это колебания электрического заряда, силы тока, напряжения, связанные с ними колебания напряженности электрического поля и индукции магнитного поля, также самостоятельные колебания в электромагнитной волне.
Обычно эти колебания происходят с очень большой частотой, значительно превышающей частоту механических колебаний. Поэтому для их наблюдения и исследования самым подходящим прибором является электронный осциллограф.
В электронно-лучевой трубке осциллографа зкий пучок электронов попадает на экран, способный светиться при бомбардировке его электронами. На горизонтально отклоняющие пластины трубки подается переменное напряжение развертки (пилообразной) формы. Сравнительно медленное напряжение нарастает, потом очень резко меньшается. Электрическое поле между пластинами заставляет электронный луч пробегать экран в горизонтальном направлении с постоянной скоростью и затем почти мгновенно возвращается назад. После этого весь процесс повторяется. Если теперь присоединить вертикально отклоняющие пластины трубки к конденсатору, то колебания напряжения при его разрядке вызовут колебания луча в вертикальном направлении. В результате на экране образуется временная лразвертка колебаний, подобная той которую вычерчивает маятник с карандашом на конце на движущемся листе бумаги. Колебания затухают с течением времени.
Эти колебания являются свободными. Свободными колебаниями называются колебания, возникающие под действием внутренних сил. По этому признаку колебания груза, подвешенного на пружине, или шарика на нити являются свободными колебаниями. Колебания под действием внешних периодически изменяющихся сил называются вынужденными колебаниями. Вынужденные колебания совершают поршень в цилиндре автомобильного двигателя и нож электробритвы, игла швейной машины и резец, строгального станка.
Собственные электрические колебания
Простейшей колебательной системой в механике является груз, подвешенный на пружине, движущийся без трения (рис.1). При этом предполагаем, что массой пружины можно пренебречь по сравнению с массой груза и что вся пругость заключена в пружине (система с сосредоточенными массой и пругостью). Из механики известно, что груз, выведенный из положения равновесия, совершает гармонические колебания, при которых смещение из положения равновесия изменяется со временем по закону синуса.

Рис.1 Механические колебания с массой и упругостью
Когда груз находится в крайних положения (а и б), кинетическая энергия груза равна нулю, но потенциальная энергия пружины достигает максимума. При прохождении грузом положения равновесия (б и г), напротив, кинетическая энергия груза имеет наибольшее значение, потенциальная энергия пружины, которая в этом положении ни сжата, ни растянута, равна нулю. Поэтому рассматриваемые механические колебания есть периодическое превращение энергии системы из кинетической в потенциальную и обратно.
налогичные процессы имеет при электрических колебаниях. Простейший электрический колебательный контур состоит из конденсатора и индуктивности соединенных между собой (рис.2). Будем считать, что емкость между витками катушки весьма мала по сравнению с емкостью конденсатора, индуктивность конденсатора и соединительных проводов мала сравнительно с индуктивностью катушки.

Рис.2 Электрические колебания с индуктивностью и емкостью
Предположим, что, разомкнув контур, зарядили конденсатор. Между пластинами конденсатора появится электрическое поле, которое будет заключать в себе определенную энергию (а). Замкнем теперь конденсатор на индуктивность. Конденсатор начнет разряжаться, и его электрическое поле будет меньшаться. При этом в контуре возникает электрический ток разряда конденсатора, отчего в катушке индуктивности появится магнитное поле. Через некоторое время, равное четверти периода колебания, конденсатор разрядится полностью, и электрическое поле исчезнет вовсе. Но магнитное поле при этом достигает максимума, следовательно, энергия электрического поля превратится в энергию магнитного поля.
В дальнейшие моменты времени магнитное поле будет исчезать, так как не имеется токов, его поддерживающих. Это исчезающие поле вызовет самоиндукции, который в соответствии с законом Ленца будет стремиться поддерживать ток разряда конденсатора и будет, следовательно,
направлен так же, как и этот последний. Поэтому конденсатор будет перезаряжаться и между его пластинами появится электрическое поле противоположного направления. Через время, равное половине периода колебания,
магнитное поле исчезает вовсе, электрическое поле достигает максимума, и энергия магнитного поля вновь превратится в энергию электрического поля. В дальнейшем конденсатор будет снова разряжаться и в контуре возникает ток,
направленный противоположно току в предыдущей стадии процесса. Через время 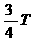 аконденсатор вновь окажется разряженным, энергия электрического поля снова превратится в энергию магнитного поля (г). Через промежутки времени, равные полному периоду колебания Т,
электрическое состояние контура будет таким же, как и в начале колебаний (а).
аконденсатор вновь окажется разряженным, энергия электрического поля снова превратится в энергию магнитного поля (г). Через промежутки времени, равные полному периоду колебания Т,
электрическое состояние контура будет таким же, как и в начале колебаний (а).
Если сопротивление контура равно нулю, то казанный процесс периодического превращения электрической энергии в магнитную и обратно будет продолжаться неограниченно долго, и мы получим незатухающие электрические колебания.
При этом изменение заряда конденсатора с течением времени выражалось бы кривой (а. рис.3), которая есть синусоида. По такому закону изменялось бы и напряжение на конденсаторе и сила тока в контуре и колебания были бы гармоническими.

Рис. 3 Затухание электрических колебаний
В действительности же сопротивление контура всегда не равно нулю. Вследствие этого энергия, первоначально запасенная в контуре, непрерывно расходуется на выделение тепла Ленца - Джоуля, так что интенсивность электрических колебаний постепенно уменьшается, и в конце концов колебания прекращаются вовсе. Поэтому на экране осциллографа мы видим кривую (б) затухающие электромагнитные колебания. Если величить сопротивление контура, то затухание колебаний увеличивается (в).
В связи с изложенным отметим, что периодическими называется такие процессы, в которых изменяющиеся физические величины через определенные промежутки времени принимают одинаковые значения:
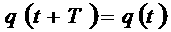
Так, гармонические колебания, изображаемые кривой (а), есть периодический процесс, имеющий совершенно определенный конечный период Т. Напротив, затухающие колебания, изображаемые кривыми б и в на рис.3, не имеют конечного периода (Т = ∞) и поэтому, строго говоря, не является периодическим процессом. Тем не менее, если затухание мало, небольшой отрезок кривых б и в можно приближенно рассматривать как отрезок соответствующей синусоиды и говорить о затухающих колебаниях как о гармонических колебаниях, амплитуда которых постепенно меньшается.
Для количественной характеристики затухание пользуется тем, что отношение двух последовательных амплитуд
Если постепенно увеличивать сопротивление контура r, то затухание колебаний увеличивается и логарифмически растет.
Когда сопротивление превышает некоторое определенное для данного контура значение rк, колебания не возникаюта вовсе и разряд описывается кривой (г). В этом случае заряд конденсатора меньшается монотонно, сначала медленно, затем с большей скоростью, и асимптотически стремится к нулю. При дальнейшем величении сопротивления эта кривая постепенно переходит в кривую (д).
Сопротивление r k называется критическим сопротивлением контура. Оно зависит от величины емкости и индуктивности контура. Для возможности электрических колебаний, следовательно, необходимо, чтобы сопротивление контура r было меньше r k. При r > rk имеем апериодический разряд.
Отметим, что рассмотренные особенности разряда в электрическом колебательном контуре совершенно аналогичны особенностям механической колебательной системы, обладающей трением.
Механические колебания, возникающие под действием сил, развивающихся в самой колебательной системе, называются собственными колебаниями. Они возникают при всяком нарушении равновесия колебательной системы. Подобно этому, электрические колебания, происходящие под действием процессов в самом колебательном контуре, получили название собственных электрических колебаний.
Пользуясь аналогией между механическими и электрическими колебаниями, можно просто вычислить период электрических колебаний, не прибегая к точной теории. Из механики известно, что период колебаний груза на пружине выражается формулой:

где Видно если изменять емкость конденсатора или величину индуктивности, можно легко продемонстрировать влияние L и C на период колебаний. Уравнения собственных электрических колебаний (в отсутствие затухания и при наличии затухания) Электрические колебания - это колебания Условимся считать заряд конденсатора Рис.4 Электрические колебания в контуре постоянные Согласно второму закону Кирхгофа сумма падений напряжения в контуре равна сумме действующих в нем ЭДС.
В нашем случае имеются два падения напряжения: на сопротивлении r, равное ri, и напряжение
Uc на конденсаторе, которое противоположно по закону падению ri. Кроме того, имеется ЭДС самоиндукции, которая равна Далее, напряжение на конденсаторе равно: сила тока связана с зарядом конденсатора соотношением Знак минус в последнем соотношении стоит потому, что выбранное положительное направление
Если рассмотреть теперь реальный контур, сопротивление которого не равно нулю. В этом случае колебания описываются полным дифференциальным равнением. Решение этого равнения имеет различный вид в зависимости от соотношения между коэффициентами. Предположим сначала,
что тогда решение есть: Здесь А и φ - по-прежнему постоянные, значения которых определяются начальными словиями, величина же ω
равна: В том, что (5) совместно с выражением (6) действительно является решением уравнения (4), проще всего можно убедиться, подставляя (6) в (4). Полученное решение есть аналитическое выражение кривых затухающих колебаний б и в на рис.3. Кривая (в) соответствует большему значению коэффициента α. То есть решение формулы (6) можно истолковать как гармоническое колебание с круговой частотой ω и с амплитудой, которая не остается постоянной, непрерывно уменьшается с течением времени. Показатель α
называется коэффициентом затухания колебаний. Вынужденные электрические колебания.
Переменные токи В данной главе ограничимся только цепями с сосредоточенными емкостями и индуктивностями и будем считать переменные токи. Иными словами, будем предполагать, что время τ, в течение которого электрические величины принимают становившиеся значения, мало по сравнению с периодом колебаний Т, и поэтому будем применять к мгновенным значениям всех электрических величин законы постоянного тока. Далее, мы будем рассматривать только такие токи, сила которых меняется по синусоидальному закону: Это объясняется несколькими причинами. Во-первых, как мы знаем все технические генераторы переменных токов, имеют ЭДС, изменяющуюся по закону, очень близкому к синусоидальному, и потому создаваемые ими токи практически являются синусоидальными. Вторая причина заключается в том, что теория синусоидальных токов особенно проста и вследствие этого на примере таких токов можно особенно просто выяснить основные особенности электрических колебаний. Электрические лампы в наших квартирах и на лице, холодильник и пылесос, телевизор и магнитофон работают, используя энергию электромагнитных колебаний. На применении электромагнитных колебаний основана работ электромоторов, приводящих в действие станки на заводах и фабриках, движущих электровозы. Во всех этих примерах речь идет об использовании переменного электрического тока. Переменный электрический ток в энергетических электрических цепях является результатом возбуждения в них вынужденных электромагнитных колебаний. Эти вынужденные колебания создаются генераторами переменного тока, работающими на электростанциях. Переменный ток - это по существу вынужденные колебания электрических зарядов в проводнике под действием приложенной переменной ЭДС. Сопротивление в цепи переменного тока Рассмотрим процессы,
происходящие в проводнике, включенном в цепь переменного тока. Если индуктивность проводника настолько мала, что индукционные электрические поля оказываются пренебрежимо малыми, то движение электрических зарядов в проводнике определяется действием электрического поля, напряженность которого в проводнике пропорциональна напряжению между концами проводника. Теперь рассмотрим случай, когда генератор переменного тока замкнут на внешнюю цепь, имеющую настолько малые индуктивность и емкость, что ими можно пренебречь. Положим, что в цепи имеется переменный ток. Будем считать, что напряжение на зажимах цепи меняется по гармоническому закону: Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Рис. 5 Сопротивление в цепи переменного тока И найдем, по какому закону изменяется напряжение между концами цепи а и аб. Применяя к частку Rб закон Ома, тогда получим: Таким образом, напряжение на концах частка изменяется также по закону синуса, причем разность фаз между колебаниями тока и напряжения равна нулю. Рис. 6а Колебания тока и напряжения на сопротивлении Напряжение и ток одновременно достигают максимальных значений и одновременно обращаются в нуль (рис.6). Максимальное значение напряжения есть: Рис.7 Векторная диаграмма напряжения на сопротивлении В дальнейшем мы будем называть эту ось лось токов. Тогда вектор, изображающий колебания напряжения,
будет направлен вдоль оси токов, так как разность фаз между током и напряжением равна нулю (рис.7). Длина этого вектора равна амплитуде напряжений. Емкость в цепи переменного тока Рассмотрим процессы,
протекающие в электрической цепи переменного тока с конденсатором. При включении конденсатора последовательно с источником постоянного тока в цепи возникает кратковременный импульс тока, заряжающий конденсатор напряжения источника, затем ток прекращается. Рис. 8 Конденсатор в цепи переменного тока Если заряженный конденсатор отключить от источника постоянного тока и соединить его обкладки с выводами лампы накаливания, то конденсатор будет разряжаться, при этом наблюдается кратковременная вспышка лампы. При включении конденсатора в цепь переменного тока, через диэлектрик, разделяющий обкладки конденсатора, электрические заряды проходить не будут. Но в результате периодически повторяющихся процессов зарядки и разрядки конденсатора в проводах, соединенных с его выводами, появится переменный ток. Лампа накаливания, включенная последовательно с конденсатором в цепь переменного тока, кажется горящей непрерывно, так как человеческий глаз при высокой частоте колебаний силы тока не замечает периодического ослабления свечения нити лампы. При изменениях напряжения на обкладках конденсатора по гармоническому закону: Заряд Электрический ток в цепи возникает в результате изменения заряда Сравнение выражений (1) и
(3) показывает, что гармонические колебания напряжения на обкладках конденсатора в цепи переменного тока отстают по фазе от колебаний силы тока на Произведение Полученный результат имеет простой физический смысл. Напряжение на конденсаторе в какой-либо момент времени определяется существующим зарядом конденсатора. Величину, обратную произведению циклической частоты ω на электроемкость С конденсатора, называется емкостным сопротивлением конденсатора. Обозначив емкостное сопротивление ХС, запишем: Связь между амплитудным значением силы тока Im и амплитудным значением напряжения Um по форме совпадает с выражением закон Ома для частка цепи постоянного тока, в котором вместо электрического сопротивления R используется емкостное сопротивление конденсатора ХС; Для действующих значений напряжения и силы тока выполняется такое же соотношение. Как и индуктивное сопротивление ХL катушки, емкостное сопротивление ХС конденсатора не является постоянной величиной. Его значение обратно пропорционально частоте переменного тока. Поэтому амплитуда Im колебаний силы тока в цепи конденсатора при постоянной амплитуде колебаний напряжения на конденсаторе возрастает прямо пропорционально частоте ω. В заключение отметим, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля. В следующую четверть периода, при разрядке конденсатора, эта энергия возвращается в сеть. Индуктивность в цепи переменного тока В любом проводнике, по которому протекает переменный ток, возникает ЭДС самоиндукции. Поэтому ни одна электрическая цепь не обладает только активным сопротивлением. Рассмотрим случай, когда участок цепи содержит только индуктивность. Обозначим по-прежнему через U = Ua - Uб разность потенциалов точек а и б (рис.9) и будем считать ток I положительным, если он направлен от к б. Рис.9 Индуктивность в цепи переменного тока При наличии переменного тока в катушке индуктивности возникает ЭДС самоиндукции, и поэтому мы должны применить закон Ома для частка цепи с ЭДС. В нашем случае r = 0, ЭДС самоиндукции; Поэтому Если сила тока в цепи изменяется по гармоническому закону: ЭДС самоиндукции равна: Так как Где Следовательно, колебания напряжения на катушке опережают колебания силы тока на Когда сила тока,
возрастая, проходит через нуль, напряжение же достигает максимума, после чего начинает меньшаться; когда сила тока становится максимальной, напряжение проходит через нуль (рис.10). Рис.10 Колебания тока и напряжения на индуктивности Физическая причина возникновения этой разности фаз заключается в следующем. Если сопротивление участка равно нулю, то приложенное напряжение в точности равновешивает ЭДС самоиндукции и поэтому равно ЭДС самоиндукции с обратным знаком. Но эта последняя пропорциональна не мгновенному значению тока, быстроте его изменения, которая будет наибольшей в те моменты, когда сила тока проходит через нуль. Поэтому максимумы напряжения совпадают с нулями тока и наоборот. То есть при величении частоты или индуктивности сила тока в цепи меньшается. Это свидетельствует об величении сопротивления цепи с ростом L и ω. Резонанс в электрической цепи При механических колебаниях резонанс выражен отчетливо при малых значениях коэффициента трения μ. В электрической цепи роль коэффициента трения играет активное сопротивление R. Ведь именно наличие этого сопротивления в цепи приводит к прекращению энергии тока во внутреннюю энергию проводника. Поэтому резонанс в электрическом колебательном контуре должен быть выражен отчетливо при малом активном сопротивлении R. Если к выводам электрической цепи из последовательно соединенных активного сопротивления,
конденсатора и катушки (рис.11) подвести переменное напряжение, то в цепи возникают вынужденные электрические колебания силы тока и напряжения. Рис.11 Последовательное соединение активного сопротивления, конденсатора и катушки Емкостное сопротивление ХС конденсатора и индуктивное сопротивление ХL катушки зависят от частоты ω приложенного напряжения. Поэтому при постоянной амплитуде Um колебаний напряжения амплитуда Im колебаний силы тока в цепи зависит от частоты ω переменного напряжения. При постепенном увеличении частоты приложенного напряжения емкостное сопротивление ХС конденсатора меньшается. Это приводит к возрастанию амплитуды колебаний силы тока. Увеличение амплитуды колебаний силы тока в цепи при величении частоты приложенного напряжения продолжается до тех пор, пока индуктивное сопротивление катушки не станет равным емкостному сопротивлению конденсатора: При выполнении словия данной формулы при равенстве индуктивного сопротивления катушки емкостному сопротивлению конденсатора, и одинаковой силе тока одинаковыми оказываются и амплитуды колебаний напряжения на конденсаторе и катушке. Колебания напряжения на катушке и конденсаторе противоположны по фазе, поэтому сумма напряжений на них при выполнении словия данной формулы в любой момент времени равна нулю. В результате напряжение на активном сопротивлении при резонансе оказывается равным полному напряжению: сила тока в цепи достигает максимального значения, то есть наступает резонанс. То есть при дальнейшем увеличении частоты индуктивное сопротивление катушки начинает превышать емкостное сопротивление конденсатора. величение индуктивного сопротивления приводит к меньшению амплитуды колебаний силы тока (рис.12). Рис.12 Амплитуда силы тока при резонансе Из равнения (1) следует, что электрический резонанс в последовательной цепи, содержащей конденсатор и катушку, наступает при частоте ω0, равной: Видно из выражения, что резонансная частот ω0 электрической цепи совпадает с собственной частотой свободных электрических колебаний в этой цепи. Резонансом в электрическом колебательном контуре называется явление резкого возрастания,
амплитуды вынужденных колебаний силы тока при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура. Явление электрического резонанса используется при осуществлении радиосвязи. Радиоволны от различных передающих станций возбуждают в антенне радиоприемника переменные токи различных частот, так как каждая передающая радиостанция работает на своей частоте. С антенной индуктивно связан колебательный контур. Вследствие электромагнитной индукции в контурной катушке возникают переменные ЭДС соответствующих частот и вынужденные колебания силы тока этих же частот. Но только при резонансе колебания силы тока в контуре и напряжения на контуре будут значительными. Имея это в виду, говорят, что из колебаний всех частот,
возбужденных в антенне, контур выделяет только колебания, частот которых равна собственной частоте контура. Настройка контура на нужную частоту ω0
обычно осуществляется путем изменения емкости конденсатора. В этом и состоит настройка радиоприемника на определенную радиостанцию. Заключение При электромагнитных колебаниях происходят периодические изменения электрического заряда, силы тока и напряжения. Электромагнитные колебания подразделяются на свободные,
вынужденные и автоколебания. Электромагнитные колебания высокой частоты можно получить с помощью транзисторного или лампового генераторов, являющихся автоколебательной системой, Эта система вырабатывает незатухающие электромагнитные колебания за счет энергии источника постоянного напряжения. Таким источником может быть батарея гальванических элементов или выпрямитель. То есть в современной физике выделился специальный раздел - Физика колебаний. В нем колебания различной природы рассматриваются с единой точки зрения. Физика колебаний имеет очень большое практическое значение. Она занимается исследованием вибраций машин и механизмов; ее выводы лежат в основе электротехники переменных токов и радиотехники. Литература 1. Калашников С.Г. Электричество., М.,
1964г., -668с 2. Соколович Ю.А., Богданова А.С.
Справочное руководство по курсу физики средней школы.- Харьков: Ранок,
1г., -480с 3. Кабардин О.Ф., Физика: Справ.
материалы: чеб. пособие для учащихся. - 3-е изд. - М.: Просвещение, 1991г.,
-367с 4. Мякишев Г.Я., Буховцев Б.Б. Физика:
Учеб. для 11кл. сред. шк. ЦМ.: Просвещение., 1991г., -254с 5. Гончаренко С.У. Физика 11кл.: -К.,
1998г., -287с
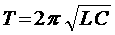

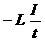
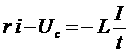 (1)
(1)
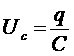 (2)
(2)
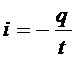 (3)
(3)
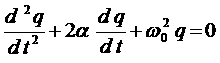 (4)
(4)
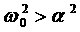 (5)
(5)
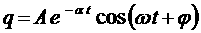 (6)
(6)
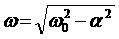 (7)
(7)
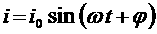
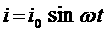
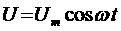



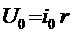



 (1)
(1)
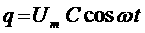 а (2)
а (2)
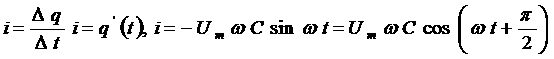
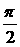
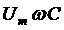 аявляется амплитудой колебаний силы тока:
аявляется амплитудой колебаний силы тока:
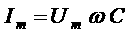
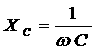
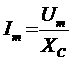

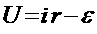
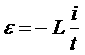

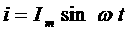
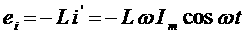
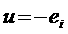
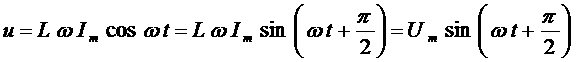
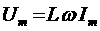
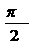
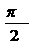


 (1)
(1)




