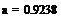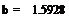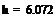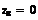Теория вероятностей и математическая статистика
Задача 1.
Генерация случайных чисел с заданным законом распределения с помощью случайных чисел, равномерно распределенных на интервале (0,1):
a)
b)
Решение:
С помощью сумм 6 независимых равномерно распределенных на интервале (0,1) случайных чисел получим 24 случайных числа со стандартным нормальным законом распределения по формуле
 , где zi - равномерно распределенные на интервале (0,1) случайные числа.
, где zi - равномерно распределенные на интервале (0,1) случайные числа.
Получены следующие числа:
|
-1.235 |
-0.904 |
-1.674 |
1.918 |
-0.335 |
|
1.082 |
-0.584 |
-0.565 |
0.149 |
0.528 |
|
1.076 |
1.011 |
0.671 |
-1.011 |
-1.502 |
|
0.627 |
-0.489 |
-0.486 |
1.022 |
-0.472 |
|
-0.844 |
0.92 |
-0.583 |
0.645 |
-0.495 |
Найдем выборочное среднее по формуле

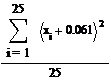
Найдем выборочную дисперсию по формуле
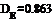
Получим 11 случайных чисел с законом распределения Стьюдента с 10 степенями свободы:

Случайные числа, распределенные по закону хи квадрат с 10 степенями свободы:
, где xi - нормальные независимые случайные величины.
Случайные числа, распределенные по закону Стьюдента с 10 степенями свободы:
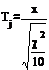
, где x - нормальная случайная величина, c2 - независимая от x величина, которая распределена по закону хи квадрат с 10
степенями свободы.
Получены следующие числа:
|
-0.58 |
-2.496 |
-0.06 |
-0.932 |
1.547 |
0.418 |
1.658 |
1.51 |
-0.171 |
-0.821 |
-1.728 |
Найдем выборочное среднее по формуле


Найдем выборочную дисперсию по формуле
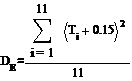

Задача 2.
Проверка статистической гипотезы:
a) 1,Е,x100}, распределенных по показательному закону с параметром l = 1/6, найти такое наименьшее целое число N, что N ³ xk для всех k = 1,Е,100;
b) разделить отрезок [0, N] на 10 равных отрезков;
получить группированную выборку {n1,Е,n10}, где ni
Ц число чисел, попавших в i-ый интервал; построить гистограмму относительных частот; по группированной выборке найти оценку c)
проверить с помощью критерия хи квадрат гипотезу о соответствии группированной выборки показательному распределению с параметром Решение: Получим 100 случайных чисел {x1,Е,x100},
распределенных по показательному закону с параметром l = 1/6: 4,9713 3,2905 2,7849 4,1093 2,1764 9,9659 10,343 4,6924 13,966 14,161 0,4258 0,6683 8,4 5,3392 2,7906 4,7696 3,0867 0,9414 2,8 3,4177 10,148 3,5312 8,4915 3,0179 3,2209 4,2259 1,8006 2,8645 1,3051 3,3094 0,7 1,9075 2,4227 6,9307 7,1085 13,322 0,9665 11,19 15,203 2,6685 3,6408 5,3646 4,5871 11,277 1,823 1,142 0,8126 7,3 12,371 1,4527 2,9692 15,762 2,5493 13,533 8,8944 0,5005 2,4678 4,2491 4,1972 4,0488 2,2424 3,0025 30,785 13,778 0,8824 1,7475 5,8036 3,5565 0,2718 10,404 12,166 0,297 21,487 17,302 12,166 0,875 1,9573 25,326 2,0727 9,1516 10,669 6,4 6,005 1,3209 3,8486 1,3525 11,593 5,4617 11,946 16,293 3,3376 3,6084 7,0011 1,279 7,5471 0,6641 1,776 6,1109 8,857 8,8327 Находим такое наименьшее целое число N, что N ³ xk для всех k = 1,Е,100: N = 31 Разделяем отрезок [0, 31] на 10 равных отрезков и получим группированную выборку {n1,Е,n10}, где ni - число чисел,
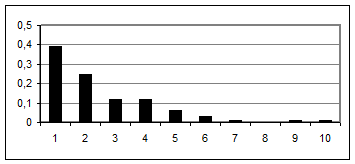
попавших в i-ый интервал: xi Xi+1 ni ni/n 0 3,1 39 0,39 3,1 6,2 25 0,25 6,2 9,3 12 0,12 9,3 12,4 12 0,12 12,4 15,5 6 0,06 15,5 18,6 3 0,03 18,6 21,7 1 0,01 21,7 24,8 0 0 24,8 27,9 1 0,01 27,9 31 1 0,01 Гистограмма относительных частот: Находим выборочное среднее по формуле По группированной выборке находим оценку Проверяем с помощью критерия хи квадрат гипотезу о соответствии группированной выборки показательному распределению с параметром Находим вероятности попадания X в частичные интервалы (xi, xi+1)
по формуле Вычисляем теоретические частоты по формуле xi Xi+1 ni Pi fi (ni - fi)2
/ fi 0 3,1 39 0,3955 39,55 0,0076 3,1 6,2 25 0,2391 23,91 0,0499 6,2 9,3 12 0,1445 14,45 0,4162 9,3 12,4 12 0,0874 8,74 1,2188 12,4 15,5 6 0,0528 5,28 0,0977 15,5 18,6 3 0,0319 3,19 0,0116 18,6 21,7 1 0,0193 1,93 0,4482 21,7 24,8 0 0,0117 1,17 1,1668 24,8 27,9 1 0,0071 0,71 0,1231 27,9 31 1 0,0043 0,43 0,7717 Находим наблюдаемое значение критерия по формуле По таблице критических точек распределения хи квадрат, по заданному ровню значимости 0.05 и числу степеней свободы 8 находим критическую точку Гипотезу о соответствии группированной выборки показательному распределению с параметром Задача 3. Проверка гипотезы о равенстве дисперсий: a)
b)
Решение: Получим 2 случайных числа,
распределенных по стандартному нормальному закону с помощью сумм 5 независимых равномерно распределенных на интервале (0, 1) случайных чисел по формуле Получены следующие числа: -0,848 -1,662 Получим 9 случайных числа,
распределенных по стандартному нормальному закону с помощью сумм 9 независимых равномерно распределенных на интервале (0, 1) случайных чисел по формуле Получены следующие числа: 0.885 1.25 -0.365 -1.139 0.891 -1.176 0.237 1.807 -0.96 Проверим гипотезу о равенстве генеральных дисперсий полученных совокупностей при ровне значимости 0.1:
Найдем выборочное среднее первой совокупности по формуле Найдем выборочное среднее второй совокупности по формуле Найдем исправленную дисперсию первой совокупности по формуле Найдем исправленную дисперсию второй совокупности по формуле Вычислим наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей) по формуле По таблице критических точек распределения Фишера-Снедекора, по заданному ровню значимости 0.1 и числам степеней свободы 1 и 9 найдем критическую точку Гипотезу о равенстве генеральных дисперсий полученных совокупностей при ровне значимости 0.1 не отвергается. Задача 4. Уравнение линии регрессии: a)
1,Е,x50}
случайной величины X, равномерно распределенной на интервале (0, 9); получить
50 случайных независимых значений {y1,Е,y50} случайной величины Y следующим образом: yi - случайное число, распределенное по показательному закону с параметром b)
c)
Dmax, Dmax]
на 5 равных частей, где Dmax
Ц наибольшее по абсолютной величине отклонение yi от линии регрессии. Решение: Получим 50 случайных независимых значений {x1,Е,x50} случайной величины X, равномерно распределенной на интервале (0, 9): 8.83174196071923 6.99053263384849 8.93890746776015 0.385410904884338 5.75393992289901 4.51090870331973 0.00656201597303152 7.97929550148547 6.6076143393293 4.54793028719723 1.40597840119153 2.18026433419436 5.0019520492 5.61958408355713 0.148365877147 4.25108801946044 4.77254802547395 1.53819094598293 6.14594876859337 0.812219920568168 6.2368449093774 1.69562757108361 0.272606268525 2.94200687524 7.07131071947515 2.973582518287 8.08092284202576 2.89726528152823 8.8169469544664 3.27939590346068 0.570096284151077 8.46246168483049 2.0076337551 2.70446146745235 8.67470343410969 1.92118153441697 1.92350933980197 1.31150823365897 1.80795181263238 3.65427995938808 8.97048242390156 2.54362053237855 0.0568648930639029 6.36279229167849 1.68422971665859 4.25911642424762 2.50030734948814 4.91532963048667 7.3589529544 4.39228433836252 Получим 50 случайных независимых значений {y1,Е,y50} случайной величины Y следующим образом: yi - случайное число, распределенное по показательному закону с параметром 24.9323592452182 15.7441606069719 15.5028112434691 2.87790855039727 4.16156795216443 0.190460347139702 0.252207251176988 5.55884492608762 11.5417165759534 11.8189116910915 9.57191092954621 6.48268208064067 10.6729845988228 11.9201379351172 0.0563900402236241 6.07239051882238 10.8341890845962 2.77373256689 1.4735808529829 0.683544240471081 1.536352690789 0.10049538246 6.48630115206778 1.01945703768 6.79791391486788 2.34472037157293 2.06912254815368 3.42524848981833 9.45107567296 3.18848770214796 1.69800713475763 2.42887690987151 6.18175839336735 4.85432860734921 3.12088295311468 0.14473630724364 0.312712437424258 1.16492882917332 2.95306149294792 6.38190212865322 0.293019110223049 0.664514453422601 3.47608211592645 20.3599120342622 1.45318365215952 9.23209976014301 0.965294785502523 6.29747102157127 6.46689933291391 3.14474865192493 Найдем равнение прямой линии регрессии Y на X по этим данным по формулам Уравнение прямой линии регрессии
Y на X: Получены следующие значения отклонений имеющихся данных от прямой регрессии: 15.1803992483 7.69319511536507 5.65184678474214 0.929060623659 -2.74697588437076 -5.56971364166513 -1.34664251825399 -3.40558552590376 3.84450875080244 6.024535447371 6.68021544884769 2.87566537149934 4.45916201865442 5.13571824955786 -1.67346851299683 0.55225091890577 4.83230056456327 -0.240106987952807 -5.79711892247662 -1.65960963866345 -5.81832115202078 -3.05879142493402 4.17543322148284 -3.29134973659658 -1.32767811582337 -1.99520044159931 -6.98919595084991 -0.844166923187427 -0.287216028830924 -1.43395767411 -0.421461708068378 -6.98192485416478 2.7342258747 0.763034293093572 -6.48599757504491 -3.92770452086 -3.0571021088348 -1.63949073262982 -0.305654309725 1.41312147312541 -9.58711575629829 -3.27818755099385 1.8307602174006 12.21627727 -1.69557328905632 3.70454314781532 -2.93739249325208 0.163674237751803 -1.9244299300759 -2.50583465164 Проверим с помощью критерия хи квадрат гипотезу о нормальном распределении с нулевым математическим ожиданием отклонений имеющихся данных от прямой регрессии при ровне значимости 0.05: Найдем наибольшее по абсолютной величине отклонение yi от линии регрессии: Рассмотрим группированную выборку, разделив отрезок [-Dmax,
Dmax] на 5 равных частей: zi zi+1 ni -15.1803992483 -9.10823954902661 1 -9.10823954902661 -3.03607984967554 12 -3.03607984967554 3.03607984967554 25 3.03607984967554 9.10823954902662 10 9.10823954902662 15.1803992483 2 Вычислим шаг: Вычислим выборочное среднее по формуле Вычислим выборочное среднее квадратическое отклонение по формуле Вычислим теоретические вероятности попадания в интервалы (zi, zi+1)
по формуле Вычислим теоретические частоты по формуле zi zi+1 ni Pi fi (ni - fi)2
/ fi -15.1803992 -9.10823954 1 0.02546995 0.02546995 0.02546995 -9.10823954 -3.03607984 12 0.23264461 0.23264461 0.23264461 -3.03607984 3.036079849 25 0.48256076 0.48256076 0.48256076 3.036079849 9.108239549 10 0.23264461 0.23264461 0.23264461 9.108239549 15.18039924 2 0.02546995 0.02546995 0.02546995 По таблице критических точек распределения хи квадрат, по заданному ровню значимости 0.05 и числу степеней свободы 3 находим критическую точку: Гипотезу о нормальном распределении с нулевым математическим ожиданием отклонений имеющихся данных от прямой регрессии при ровне значимости 0.05 не отвергаем.




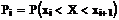

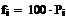
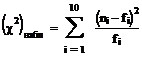
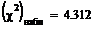


 , где zi -а равномерно распределенные на интервале (0, 1)
случайные числа.
, где zi -а равномерно распределенные на интервале (0, 1)
случайные числа.
 , где zi -а равномерно распределенные на интервале (0, 1)
случайные числа.
, где zi -а равномерно распределенные на интервале (0, 1)
случайные числа.


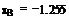
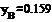
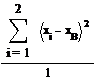
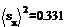




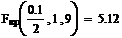
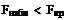
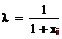
 :
: