Статистическое исследование количества потребляемой электроэнергии
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ ЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ НИВЕРСИТЕТ
(ГОУ ВПО ИГУ)
Физический факультет
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
ПО МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ
Выполнил студент гр. 1322
Конусов Н.Ю.
Иркутск 2007
Проводилось статистическое исследование количества потребляемой электроэнергии в течение каждого часа в дневное время на протяжении пяти дней в двухкомнатной квартире. Объем выборки n=90.
|
| 3 | ||
|
Время |
Показания счетчика кВт * час |
Потребление кВт * час |
|
5:00 |
30137,17 |
|
|
6:00 |
30137,25 |
0,08 |
|
7:00 |
30137,31 |
0,06 |
|
8:00 |
30137,58 |
0,27 |
|
9:00 |
30137,74 |
0,16 |
|
10:00 |
30137,86 |
0,12 |
|
11:00 |
30138,12 |
0,26 |
|
12:00 |
30138,82 |
0,70 |
|
13:00 |
30139,49 |
0,67 |
|
14:00 |
30139,82 |
0,33 |
|
15:00 |
30140,20 |
0,38 |
|
16:00 |
30141,77 |
1,57 |
|
17:00 |
30143,12 |
1,35 |
|
18:00 |
30143,57 |
0,45 |
|
19:00 |
30144,32 |
0,75 |
|
20:00 |
30145,00 |
0,68 |
|
21:00 |
30145,53 |
0,53 |
|
22:00 |
30145,84 |
0,31 |
|
23:00 |
30147,17 |
1,33 |
| 4 | ||
|
Время |
Показания счетчика кВт * час |
Потребление кВт * час |
|
5:00 |
30148,61 |
|
|
6:00 |
30148,68 |
0,07 |
|
7:00 |
30148,80 |
0,12 |
|
8:00 |
30148,88 |
0,08 |
|
9:00 |
30149,40 |
0,52 |
|
10:00 |
30150,32 |
0,92 |
|
11:00 |
30150,95 |
0,63 |
|
12:00 |
30151,10 |
0,15 |
|
13:00 |
30151,30 |
0,20 |
|
14:00 |
30151,67 |
0,37 |
|
15:00 |
30151,77 |
0,10 |
|
16:00 |
30152,16 |
0,39 |
|
17:00 |
30152,38 |
0,22 |
|
18:00 |
30153,00 |
0,62 |
|
19:00 |
30153,56 |
0,56 |
|
20:00 |
30154,29 |
0,73 |
|
21:00 |
30155,14 |
0,85 |
|
22:00 |
30155,66 |
0,52 |
|
23:00 |
30155,96 |
0,30 |
| 5 | ||
|
Время |
Показания счетчика кВт * час |
Потребление кВт * час |
|
5:00 |
30157,52 |
|
|
6:00 |
30157,55 |
0,03 |
|
7:00 |
30158,01 |
0,46 |
|
8:00 |
30158,15 |
0,14 |
|
9:00 |
30158,67 |
0,52 |
|
10:00 |
30159,59 |
0,92 |
|
11:00 |
30160,79 |
1,20 |
|
12:00 |
30161,20 |
0,41 |
|
13:00 |
30161,40 |
0,20 |
|
14:00 |
30161,77 |
0,37 |
|
15:00 |
30162,23 |
0,46 |
|
16:00 |
30162,57 |
0,34 |
|
17:00 |
30162,79 |
0,22 |
|
18:00 |
30163,41 |
0,62 |
|
19:00 |
30163,97 |
0,56 |
|
20:00 |
30164,70 |
0,73 |
|
21:00 |
30165,55 |
0,85 |
|
22:00 |
30165,98 |
0,43 |
|
23:00 |
30166,28 |
0,30 |
ПЕРВИЧНАЯ СТАТИСТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ
1. Точечный вариационный ряд. Распределение xi по частотам ni.
|
xi |
0 |
0,02 |
0,03 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
0,1 |
0,12 |
0,14 |
0,15 |
0,16 |
0,17 |
|
ni |
0 |
1 |
1 |
1 |
2 |
1 |
3 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
|
0,18 |
0,19 |
0,2 |
0,21 |
0,22 |
0,23 |
0,25 |
0,26 |
0,27 |
0,3 |
0,31 |
0,32 |
0,33 |
0,34 |
0,37 |
|
1 |
1 |
3 |
1 |
2 |
1 |
1 |
1 |
1 |
3 |
1 |
2 |
1 |
3 |
4 |
|
0,38 |
0,39 |
0,4 |
0,41 |
0,42 |
0,43 |
0,45 |
0,46 |
0,47 |
0,49 |
0,51 |
0,52 |
0,53 |
0,54 |
0,55 |
|
2 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
1 |
1 |
1 |
4 |
1 |
1 |
2 |
|
0,56 |
0,62 |
0,63 |
0,67 |
0,68 |
0,7 |
0,73 |
0,75 |
0,85 |
0,92 |
1,05 |
1,2 |
1,33 |
1,35 |
1,57 |
|
2 |
4 |
2 |
1 |
1 |
1 |
2 |
1 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
Переход к группированным выборочным данным.
xmin = 0,02 xmax = 1,57. Диапазон [xmin ; xmax] разбиваем на k равных интервалов. Воспользуемся формулой аk = log 2 n + 1. k = 7.
Вариационный размах R = xmax - xmin = 1,55. Длина интервала h = R / k = 0,221.
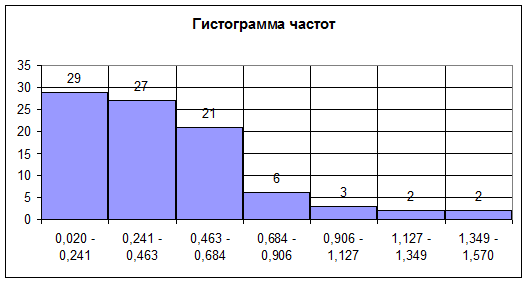
Интервальный ряда 
|
Ci - C i+1 |
0,02 - 0,241 |
0,241 - 0,463 |
0,463 - 0,684 |
0,684 - 0,906 |
0,906 - 1,127 |
1,127 - 1,349 |
1,34Ц 1,570 |
|
n*i |
29 |
27 |
21 |
6 |
3 |
2 |
2 |
Равноточечный ряд по частотам 
|
x*i |
0,131 |
0,352 |
0,574 |
0,795 |
1,016 |
1,238 |
1,459 |
|
n*i |
29 |
27 |
21 |
6 |
3 |
2 |
2 |
Равноточечный ряд по относительным частотам 
; 
|
x*i |
0,131 |
0,352 |
0,574 |
0,795 |
1,016 |
1,238 |
1,459 |
|
w i |
29/90 |
27 / 90 |
21 / 90 |
6 / 90 |
3 / 90 |
2 / 90 |
2 / 90 |
|
w i |
0,3 |
0,3 |
0,2 |
0,0667 |
0,0 |
0,0 |
0,0 |
Равноточечный ряд по накопительным частотам
|
x*i |
0,131 |
0,352 |
0,574 |
0,795 |
1,016 |
1,238 |
1,459 |
|
m*i |
29 |
56 |
77 |
83 |
86 |
88 |
90 |
ГРАФИКИ
|
|
|
|
|
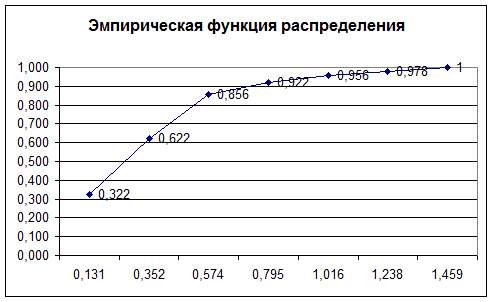
3. Построение эмпирической функции распределения
F* = nx / n , где nx Ц число элементов выборки (объема n), меньших, чем x.
|
x*i |
0,130714 |
0,352143 |
0,573571 |
0,795 |
1,016429 |
1,237857 |
1,459286 |
|
F* |
0,3 |
0,6 |
0,86 |
0,9 |
0,96 |
0,98 |
1 |
4. Числовые характеристики выборки по ряду
|
x*i |
0,131 |
0,352 |
0,574 |
0,795 |
1,016 |
1,238 |
1,459 |
|
n*i |
29 |
27 |
21 |
6 |
3 |
2 |
2 |
)а Выборочные среднее и дисперсия
< xв > = (1 / n) ´ å( xi ´ ni ) = 0,43
Dв = (1 / n) ´ å( xi - < xв >)2 ´ niа = 0,0955 sn = 0,309 = Dв2
б)а Мода - значение, которое чаще всего встречается в данном вариационном ряду.
xmod = 0,370
в)а Медиана - средневероятное значение.
xmed = 0,385
г)а Асимметрия
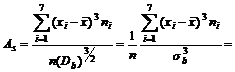1,297
д)а Эксцесс
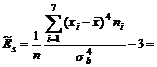
5. Оценка близости выборочных наблюдений к нормальному закону
Положительная асимметрия говорит о том, что длинная часть кривой распределения расположена справа от математического ожидания, положительный эксцесс - о том, что кривая распределения имеет более высокую и острую вершину, чем кривая нормального распределения.
СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
1. Несмещенная оценка математического ожидания - выборочное среднее.
_
M X = x = 0,4284
Несмещенная дисперсия - исправленная выборочная дисперсия.
0,096541
2. Построение доверительных интервалов для матожидания и дисперсии при неизвестных параметрах нормального закона с доверительной вероятностью, равнойа γ = 0,95 и 0,99.
а) γ=0,95 n = 90
МХ
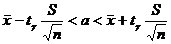
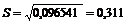
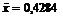
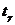
0,3633 а< MX < 0,4953
Дисперсия
α=1-γ=0,05;
а64,793
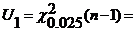116,989
0,073<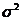 
< 0,133
б) γ=0,99 n = 90
МХ
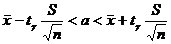
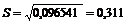
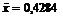
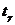
0,3420 < MX < 0,515
Дисперсия
α=1-γ=0,01;
а
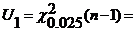116,989
0,068
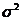< < 0,147
3. Используя таблицу случайных чисел получить 50 равномерно распределенных чисел из интервала (0; 10) X~R(a,b)
|
|
|
|
Вариационный ряд | ||||||||
|
1 |
2 |
Xi |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
2 |
2 |
ni |
6 |
11 |
7 |
5 |
4 |
3 |
2 |
8 |
4 |
|
2 |
5 |
|
|||||||||
|
4 |
6 |
|
|||||||||
|
1 |
5 |
|
|||||||||
|
2 |
1 |
|
|||||||||
|
5 |
2 |
|
|||||||||
|
2 |
8 |
|
|||||||||
|
3 |
3 |
|
|||||||||
|
8 |
1 |
|
|||||||||
|
8 |
3 |
|
|||||||||
|
8 |
9 |
|
|||||||||
|
1 |
4 |
|
|||||||||
|
2 |
9 |
|
|||||||||
|
4 |
6 |
|
|||||||||
|
9 |
3 |
|
|||||||||
|
5 |
9 |
|
|||||||||
|
2 |
3 |
|
|||||||||
|
4 |
7 |
|
|||||||||
|
3 |
2 |
|
|||||||||
|
6 |
8 |
|
|||||||||
|
1 |
2 |
|
|||||||||
|
8 |
3 |
|
|||||||||
|
7 |
8 |
|
|||||||||
|
8 |
4 |
|
Интервальный ряд
|
Ci-Ci+1 |
0-2 |
2-4 |
4-6 |
6-8 |
8-10 |
|
ni* |
17 |
12 |
7 |
10 |
4 |
Точечный ряд
|
xi* |
1 |
3 |
5 |
7 |
9 |
|
ni* |
17 |
12 |
7 |
10 |
4 |
|
xi*ni* |
17 |
36 |
35 |
70 |
36 |
|
(xi*)2ni* |
17 |
108 |
175 |
490 |
324 |
Методом моментов найдем оценки неизвестных параметров равномерного распределения:
Метод моментов заключается в приравнивании определенного числа выборочных моментов к соответствующим теоретическим моментам.
X~R(a,b)
f(x) = 1 / (b - a), если x Î [a; b]
f(x) = 0, в противном случае
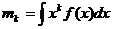
Þ
, 
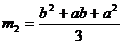
Получим систему равнений
b=7,76-a
a2+a(7.76-a)+60.2176-15.52a+a2=66.84
a2+7.76a-a2-15.52a+a2-6.6224=0
a2-7.76a-6.6224=0
D=60.2176-26.489633.728
Возможна пара решений
a = 6,7838 b = 0,9762
a = -0,9762 b = 8,7362
4. Методом максимального правдоподобия найдем точечную оценку параметра λ распределения Пуассона
X ~ П (λ)а
P(X=k) =
Функция правдоподобия:
L=
Ln L(λ)= 
Уравнение правдоподобия:
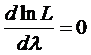а=> 
а=> 
Докажем несмещенность:
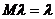
Докажем сосотоятельность:а
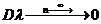
СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
1. Пусть случайная величина X~N(a,
), причем параметры распределения неизвестны.
а)а Проверим нулевую гипотезу H0: для 
, если альтернативная гипотеза H1: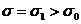 
.
Найдем наблюдаемое значение критерия:
.
По словию конкурирующая гипотеза имеет вид первого случая, поэтому критическая область правостороння, по ровню значимости равному
0,05 и числу степеней свободы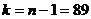
, находим критическую точку 
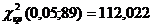, при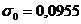 
. Так как 
Ц есть основание отвергнуть гипотезу.
б) Далее проверим следующую нулевую гипотезу 
если альтернативная гипотеза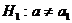 
. ровень значимости принимается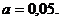 
Для этого вычислим наблюдаемое значение критерия:
По таблице критических точек распределения Стъюдента имеем :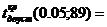 
Т.е. получилось, что 
, следовательно, нулевая гипотеза