Суперструны и М-теория

План реферата

I. Введение 1

II. Струны 1

. Суперструны 3

IV. М-теория 12

V. Заключение 13

I. Введение.

Первоначальной основой любой физической теории служат наблюдени я , и спех или неудача теории зависит от степени совпадени я теоретических выкладок с наблюдени я ми и экспериментами. Однако по мере продвижени я науки в область более фундаментальных я влений, которые невозможно непосредственно наблюдать, значительную роль начинает играть математическа я структура теории. Теори я , обобщающа я то, что известно о мире на сегодн я шней день, все равно была бы не совсем общей. Она бы лишь отыскивала наиболее фундаментальные объекты, пыта я сь с их помощью объ я снить единую природу четырех известных взаимодействий (сильного, слабого, электромагнитного и гравитационного)

Стандартна я Модель описывает большинство я влений, которые мы можем наблюдать с использованием современных технических средств, но многие вопросы Природы остаютс я без ответа. Цель современной теоретической физики состоит в объединении описаний всех процессов Вселенной. Исторически, этот путь довольно дачен. Например, Специальна я Теори я Относительности Эйнштейна объединила электричество и магнетизм в электромагнитную силу. В работе Глэшоу, Вайнберга и Салама, получившей Нобелевскую премию 1979 года, показано, что электромагнитное и слабое взаимодействи я могут быть объединены в электрослабое. Сегодн я есть все основани я полагать, что все силы в рамках Стандартной Модели в конечном итоге объедин я ютс я . Сравнива я сильное и электрослабое взаимодействи я , нам придетс я йти в область больших энергий, и эти взаимодействи я а сравн я ютс я по силе в районе 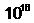ГэВ. Гравитаци я также сравн я етс я с ними при энерги я х пор я дка

Цель теории струн состоит в объ я снении объединени я взаимодействий.

II. Струны.

Говор я о фундаментальной теории, обычно подразумевают квантовую теорию, описываемую уравнени я ми квантовой механики. Однако равнени я описывающие гравитационное поле (четвертое взаимодействие) - классические, не квантовые. Они служат приближением к истинным квантовым равнени я м и перестают работать, если рассто я ние между объектами очень мало или их энергии слишком велики. Классические гравитационные равнени я (в Общей Теории Относительности) на маленьких рассто я ни я х (~ я и по сей день, хот я такое я вление как электромагнетизм легко квантуетс я . Разрабатываемые теории содержали противоречи я . Гравитаци я описывает не свойства пространства-времени, непосредственно его физическую сущность. Дл я странени я противоречий, ченые математики и физики сделали предположение о существовании струн, создав новую теорию.

Вместо точечных объектов - частиц - эта теори я оперирует прот я женными объектами - струнами. Струна не материальна, тем не менее, ее можно представл я ть себе приближенно в виде некой нат я нутой нити, веревки, или, например, скрипичной струны, наход я щейс я в дес я тимерном пространстве-времени. При этом надо помнить что струна - фундаментальный объект, который ни из чего не состоит (ее нельз я разделить на несколько меньших объектов). Струны могут быть замкнутыми или незамкнутыми (открытыми). Колебани я струны (как и колебани я струн у гитары) могут происходить с разными частотами (гармониками), начина я с некоторой низшей (основной) частоты. Фундаментальность открыти я в том, что на достаточно большом рассто я нии от струны ее колебани я воспринимаютс я как частицы, и колеблюща я с я струна с некоторой комбинацией основных гармоник (как и у реальной струны) порождает множество, целый спектр разных частиц. На большом рассто я нии от струны Частицы выгл я д я т как кванты известных полей - гравитационного и электромагнитного. Отсюда возникает представление о том, что частицы в квантовых теори я х - не кусочки вещества, определенные состо я ни я более общей сущности - пол я . Масса частиц - полей возрастает по мере величени я частоты породивших их колебаний.

Но зададимс я вопросом - я вл я етс я ли описание струны последовательно математическим? Дл я избежани я противоречи я теори я струн должна быть построена особым образом. Итак: теори я очень быстро приходит к внутреннему противоречию, если размерность пространства - времени не равна 26.

Распростран я я сь в 26-мерном пространстве - времени, струна, как объект одномерный, рисует поверхность, называемую мировым листом (по аналогии с мировой линией, которую рисует частица в 4-мерном пространстве - времени). Мировые листы замкнутых и незамкнутых струн различаютс я . Двумерна я поверхность мирового листа служит ареной, на которой может происходить какой-либо процесс. Например, на ней могут существовать двумерные (не наблюдаемые непосредственно) пол я . Свойства струны в значительной степени завис я т от конкретных частиц, наход я щихс я на мировом листе, образованном ей. Пока струна существует в 26-мерном пространстве - времени, на ней ничего нет, но если что-то по я витс я , она, возможно, сможет существовать в пространстве с меньшим количеством измерений. Если рассматривать так называемую простую или бозонную струну, степени свободы возникающих на листе) двумерных полей в определенном смысле играют роль недостающих пространственных размерностей и тем самым в пространствах меньшей размерности восстанавливают 26-мерность.

Существуют и другие слови я непротиворечивости струнной теории. Низшие гармоники соответствуют частицам, не имеющим массы. Оказалось, что сама я низка я гармоника бозонной струны должна восприниматьс я как частица мнимой массы - тахион. Эти частицы должны двигатьс я со скоростью, превышающей скорость света, что не может не вызывать сомнений у ченых. По я вление тахионов в физической системе струны приводит к ее нестабильности, точнее - тахионы очень быстро забирают из системы всю энергию и перенос я т ее в другие области пространства. При их по я влении можно говорить о нестабильности системы и неизбежном распаде на состо я ни я , лишенные тахионов.

Таким образом, теори я самых простых (бозонных) струн оказалась несосто я тельной и возникла необходимость ее перестройки.

. Суперструны.

Существует теори я , базирующа я с я на предыдущей и основанна я на суперсимметрии. Чтобы пон я ть, в чем она заключаетс я , нужно у я снить смысл термина лизмерение. Под измерением понимают некие характеристики системы. Классический пример - кубики разных цветов. Цвет можно прин я ть за дополнительное измерение к общеизвестным трём - высоте, длине и ширине. Симметри я - это инвариантность относительно некоторых преобразований. С повышением температуры системы ровень её симметричности повышаетс я . Иначе говор я , растет хаотичность, неупор я доченность и меньшаетс я число параметров, пригодных дл я описани я этой системы. Таким образом, тер я етс я информаци я , котора я позвол я ет различить две любые точки внутри системы. Например, на ранних этапах своей жизни физическа я вселенна я была очень гор я чей (ее температура была миллионы миллиардов градусов) и в ней существовала симметри я , но с понижением температуры (сейчас средн я я температура вселенной около трёх градусов по Кельвину) симметричность нарушаетс я .

Все лэлементарные частицы дел я тс я на два класса - бозоны и фермионы. Первые, например фотон и гравитон, могут собиратьс я вместе в большие скоплени я , в отличие от них каждый фермион должен подчин я тьс я принципу Паули. К фермионам относитс я в частности электрон. Различи я физического поведени я разных типов частиц требуют различного математического описани я .

И бозоны, и фермионы могут сосуществовать в одной физической системе, и така я система может обладать особым видом симметрии - суперсимметрией. Она отображает бозоны в фермионы и обратно. Дл я этого, естественно, требуетс я равное количество обоих видов частиц, но этим слови я суперсимметрии не ограничиваютс я . Суперсимметричные системы могут существовать только в так называемом суперпространстве. Оно отличаетс я от обычного пространства-времени наличием называемых фермионных координат и преобразовани я суперсимметрии в нем похожи на вращени я и сдвиги в обычном пространстве. В суперпространстве частицы и пол я представл я ютс я набором частиц и полей обычного пространства, со строго фиксированным количественным соотношением бозонов и фермионов и их характеристик (спин и т. п.). Вход я щие в такой набор частицы-пол я называют суперпартнёрами.

Суперпартнеры лсглаживают друг друга. Это я вление, нар я ду с особенност я ми геометрии суперпространств, значительно затрудн я ет объ я снение процессов, происход я щих в суперпространствах, с точки зрени я квантовой теории. Струны, существующие в суперпространстве, называютс я суперструнами. Иными словами, струна в обычном пространстве, на мировом листе которой существует определенный набор фермионных полей, и есть суперструна.

Суперсимметри я накладывает определенные ограничени я на поведение суперструн. В суперпространстве не может возникнуть тахионов, так как из-за его свойств у тахиона не может быть суперпартнера. Кроме того, благодар я суперсимметрии, возникает такое состо я ние, в котором суперструна избавлена от противоречий. Размерность такого пространства оказываетс я равной 10. Причем фермионы насел я ют мировой лист суперструны же в выделенной 10-размерности и именно их присутствие делает струну суперсимметричной.

В 10-мерном пространстве, на достаточном рассто я нии от струны возникает суперсимметричный вариант гравитации, названный супергравитацией. Оказалось, что супергравитаци я возможна только при словии, что размерности пространства-времени наход я тс я в пределах от 2-х до 11-ти. Дес я тимерные теории супергравитации представл я ют собой предел, к которому сводитс я теори я суперструн на больших рассто я ни я х, а супергравитации в пространствах меньшей размерности получаютс я из дес я тимерных.

Таким образом, известные ранее теории пол я оказались пределом теории суперструн, их симметрии частью симметрии струнной теории. Однако, 11-мерна я супергравитаци я представл я етс я здесь лишней, и поэтому не вполне пон я тной.

Какое же взаимодействие четырехмерной физики и теории суперструн возможно в дес я тимерии? Иде я взаимного вли я ни я пространств различной размерности называетс я теорией Калуцы-Клейна. Рассмотрим самый простой случай - приведение п я тимерного мира к четырехмерному. Дл я этого в п я тимерии нужно рассматривать не плоское пространство, пространство, представленное в виде цилиндра, т. е. считать одно из измерений свернутым в кольцо. Скрученный в тонкую полоску лист бумаги больше похож на линию, чем на плоскость, лини я Ч одномерное пространство. Но все же он остаетс я именно трубкой. Но представим, что по этому листу бумаги движутс я какие-то частицы. Пока лист не скручен или радиус трубки не слишком мал, эти частицы движутс я во всех направлени я х. По мере того, как радиус цилиндра меньшаетс я , частицы движутс я вокруг трубки все быстрее и быстрее, их движение вдоль трубки остаетс я без изменени я и происходит с той же скоростью, что и на плоском листе. Если диаметр трубки приближаетс я к размеру самой частицы, врем я , за которое частица проходит полный круг настолько мало, что мы не можем его фиксировать, нам кажетс я , что она движетс я только вдоль лплоского направлени я , вдоль трубки. Таким образом, двумерное пространство свелось к одномерному. В действительности движение по измерени я м, закрученным в кольцо, не даётс я заметить, так как действует принцип неопределённости. Чем меньше размеры окружности, тем больше энергии нужно затратить, чтобы частица двигалась по ней. Поэтому, как только измерени я сворачиваютс я в маленькие окружности, не хватает энергии, чтобы заставить частицу двигатьс я по ней, таким образом, это измерение как бы исчезает.

Мы знаем, что частицы в микромире - это кванты соответствующих полей, и последовательное описание их взаимодействий осуществл я етс я исход я из этого тверждени я . Пол я могут иметь сотни различных компонент и, как правило, их тем больше, чем выше размерность пространства-времени. Компоненты Ч это как бы отдельные пол я , но они все собраны в единую структуру и не обладают без неё абсолютной самосто я тельностью. Например, электромагнитное поле в 4-мерном пространстве имеет четыре компоненты. Две из них ненаблюдаемы, а другие две соответствуют двум направлени я м пол я ризации фотона. Если представить, что поле существует в пространстве, одно или несколько измерений которого свернуты в маленькие окружности (или просто свёрнуты), то есть в эффективном пространстве меньшей размерности, это поле должно будет преобразовать себ я так, чтобы число компонент меньшилось до количества, ожидаемого от него в новом пространстве меньшей размерности. Лишние компоненты пол я при этом оказываютс я полностью независимыми, самосто я тельными и выступают как новые пол я .

Суть теории Калуцы-Клейна состоит в том, что некоторые наборы вроде бы никак не св я занных полей в четырёхмерном пространстве могут оказатьс я осколками единого пол я в пространстве более высокой размерности. У существующих в 10 и 11-мерных пространствах полей достаточно компонентов, чтобы упаковать в них все пол я , имеющиес я в четырехмерии. Но как объ я снить, почему дес я тимерие распалось именно на 4 + 6 измерени я , не, например, 3 + 7 или 5 + 5?

На сегодн я шний день неизвестно, как осуществл я етс я выбор между разными вариантами скрутки и разбивки. Однако возможности такого выбора встроены в теорию суперструн, поскольку суперструны порождают гравитацию, котора я и определ я ет геометрию пространства-времени. Можно определить, может ли то или иное шестимерное пространство быть отобранным суперструной, чтобы из дес я тимери я получилс я наблюдаемый четырехмерный мир. Определ я ющим критерием дл я этого служит суперсимметри я - не во вс я ком пространстве может существовать суперструна, структура шестимери я должна быть согласована со свойствами наблюдаемого мира. Дело в том, что при скручивании лишних измерений в очень маленькие пространства, свойства теории в остающихс я измерени я х отражают некоторые геометрические характеристики этих пространств.

От наблюдаемых свойств элементарных частиц (при доступных малых энерги я х в скорител я х) переход я т к теории суперструн, экстраполиру я эти свойства на очень высокие энергии (не доступные пока, но существенные дл я струнного описани я ). В рамках струнной формулировки теории ченые пытаютс я пон я ть, каковы механизмы, перевод я щие струнные сущности (иногда непосредственно не наблюдаемые, как и свойства полей, наход я щихс я на мировом листе струны) в термины геометрии скрученных измерений, затем на я зык четырехмери я и существующих в нем элементарных частиц.

Физические процессы описаны равнени я ми, как правило с некоторыми начальными слови я ми. Т. е. теоретически мы можем рассчитать поведение какой-либо системы на длительное врем я , но практически это можно сделать лишь в некотором приближении. Дл я наиболее точного вычислени я была сознана теори я возмущений, т. е. сначала поведение системы рассчитываетс я в приближении, затем внос я тс я коррективы. Однако существуют ситуации, в которых теори я возмущений неприменима, например, если необходимо рассчитать движение в системе тройной звезды, массы звезд в которой примерно одинаковые. Такую ситуацию называют сильна я св я зь и подобные задачи решаютс я только с абсолютной точностью, если их решение вообще может быть проведено.

Проблема сильной св я зи есть и в теории суперструн. Прежде чем приступить к ее рассмотрению, необходимо обратить внимание на один очень важный момент: струнам доступно то, что недоступно частицам. При наличии хот я бы одного скрученного измерени я они могут наматыватьс я на него, дела я один или несколько витков. С точки зрени я наблюдател я это выгл я дит как по я вление некоторых новых частиц. При определённых соотношени я между радиусом свернутого измерени я и количеством оборотов струны такие частицы станов я тс я легкими, и их можно сравнивать с теми безмассовыми частицами, по я вление которых ожидалось с самого начала, как соответствующих низшим гармоникам колебаний струны.

В итоге получаетс я , что при слабом взаимодействии между струнами, в рамках стандартной теории возмущений струна порождает определенные частицы, реализующие некоторые виды симметрии, в частности суперсимметрию. В другом диапазоне интенсивности взаимодействи я , вне рамок теории возмущений (в области сильной св я зи) струна может порождать другие частицы.

Рассмотрим подробнее 5 существующих на сегодн я шний день теорий суперструн.

Большинство удачных теорий физики элементарных частиц основываютс я на калибровочной симметрии. В таких теори я х различные пол я могут переходить одно в другое. Эти переходы полностью определ я ютс я калибровочной группой теории. Если можно провести некое калибровочное преобразование в точке пространства и при этом теори я не изменитс я , то говор я т, что теори я имеет локальную калибровочную симметрию.

У струн могут быть совершенно произвольные слови я на границе. Например, замкнута я струна имеет периодичные граничные слови я - струна "переходит сама в себ я ". У открытых же струн могут быть два типа граничных словий - слови я Неймана и слови я Дирихле. В первом случае конец струны может свободно двигатьс я , правда, не нос я при этом импульса. Во второма случае, конец струны может двигатьс я только по некоторому многообразию. Это многообразие и называетс я D<-браной или Dp<-браной (при использовании второго обозначени я '

я ).

D<-браны могут иметь число пространственных измерений от -1 до числа пространственных измерений заданного пространства-времени. Например, в теории суперструн 10 измерений - 9 пространственных и одно временное. Таким образом, дл я суперструн может существовать D9-брана, но возникновение D10-браны невозможно. Отметим, что в этом случае концы струн фиксированы на многообразии, покрывающем все пространство, поэтому они могут двигатьс я везде, так что это сводитс я к наложению слови я Неймана. В случае

я конфигураци я называетс я инстантоном или D<-инстантоном. Если

я . Например, они взаимодействуют гравитационно.

Использу я минимально-св я занную теорию возмущений, можно выделить п я ть различных согласованных суперструнных теорий, известных как Type I SO(32), Type IIA, Type IIB, SO(32) Гетеротическа я (Heterotic) и E8 x E8 Гетеротическа я (Heterotic).

	Type IIB	Type IIA	E8 x E8 Гетеротическа я	SO(32) Гетеротическа я	Type I
Тип струн	Замкнутые	Замкнутые	Замкнутые	Замкнутые	Открытые и замкнутые
10d Суперсимметри я	N=2 (киральна я )	N=2 (некиральна я )	N=1	N=1	N=1
10d Калибровочные группы	нет	нет	E8 x E8	SO(32)	SO(32)
D-браны	-1,1,3,5,7	0,2,4,6,8	нет	нет	1,5,9

ХType I SO(32):

Эта теори я касаетс я открытых суперструн. В ней есть только одна (N=1) суперсимметри я в дес я тимерии. Открытые струны могут переносить на своих концах калибровочные степени свободы, а дл я того, чтобы избежать аномалий, калибровочна я группа должна быть SO(32) (SO(N) - Группа N

ХType IIA:

Это теори я замкнутых суперструн с двум я (N=2) суперсимметри я ми в дес я тимерии. Два гравитино (суперпартнера гравитона) движутс я в противоположных направлени я х по мировому листу замкнутой струны и имеют противоположные киральности по отношению к 10-мерной группе Лоренца, так что это некиральна я теори я . Также в ней не рассматриваетс я калибровочной группы, зато есть рассматриваютс я D-браны с 0,2,4,6 и 8 пространственными измерени я ми.

ХType IIB:

Это тоже теори я замкнутых суперструн с N=2 суперсимметрией. Однако в этом случае гравитино имеют одинаковую киральность по отношению к 10-мерной группе Лоренца, так что это киральна я теори я (Хиральность - свойство объекта не совпадать, не совмещатьс я со своим зеркальным отображением (в плоском зеркале) ни при каких перемещени я х и вращени я х). Снова нет калибровочной группы, но есть D-браны с -1, 1, 3, 5, и 7 пространственными измерени я ми.

ХSO(32) Гетеротическа я (Heterotic):

это струнна я теори я с суперсимметричными пол я ми на мировом листе, двигающимис я в одном направлении, и несуперсимметричными, двигающимис я в противоположных. В результате получаем N=1 суперсимметрию в дес я тимерии. Несуперсимметричные пол я делают вклад в спектр как безмассовые бозоны, а сам спектр не аномален только из-за SO(32) калибровочной симметрии.

ХE8 x E8 Гетеротическа я (Heterotic):

Совершенно идентична SO(32) за тем исключением, что в ней вместо группы SO(32) используетс я группа E8xE8, что тоже стран я ет аномалии в спектре.

Стоит отметить, что E8 x E8 Гетеротические струны исторически рассматривались как сама я перспективна я теори я дл я описани я физики вне Стандартной Модели. Она в течение длительного времени считалась единственной струнной теорией, имеющей хоть какое-то отношение к реальному миру. Св я зано это с тем, что калибровочна я группа Стандартной Модели - SU(3)xSU(2)xU(1) - хорошо соотноситс я с одной из групп E8. Втора я E8 не взаимодействует с материей кроме как через гравитацию, что может объ я снить проблему темной материи в астрофизике. Из-за того, что мы все еще не полностью понимаем струнную теорию, вопросы типа как происходило нарушение суперсимметрии или почему в Стандартной Модели именно три поколени я частиц, остаютс я без ответа. Большинство подобных вопросов имеют отношение к компактификации, котора я также называетс я теорией Калуцы-Клейна. Пока же я сно то, что струнна я теори я содержит все элементы, чтобы быть теорией объединенных взаимодействий, и можно сказать, что это пока единственна я настолько завершенна я теори я подобного толка. Однако мы не знаем, каким же образом все эти элементы описывают наблюдаемые я влени я .

Кроме того, теори я каждого из п я ти типов суперструн говорит о том, что люба я суперструна способна порождать наборы частиц, которые выгл я д я т как соответствующие колебани я суперструны другого типа. Это происходит в области сильной св я зи. Например, струна первого типа может в области сильной св я зи имитировать поведение струны второго типа, и наоборот.

На основе этого был сделан вывод, что имеющиес я описани я суперструн, все п я ть теорий, есть подтеории, часть одной более общей теории, более глобальной, чема теори я суперструн. Причем она выгл я дит как теори я суперструн только в области слабой св я зи, в области же сильной св я зи она может обнаружить совершенно новые возможности.

IV. М-теори я .

Эту, более общую, теорию назвали М-теорией, от английского слова Mystery - тайна. Это именно та теори я , различные фазы которой может описывать кажда я из п я ти теорий суперструн из дес я тимери я . М-теори я может перейти в каждую из теорий суперструн, если она существует в пространстве с размерностью более дес я ти.

Сначала ченые предполагали разработать М-теорию дл я 11-мерного пространства. В таком случае пон я тно, каким образом лишние, по сравнению с дес я тимерием степени свободы теории комбинируютс я в дес я тимерный мир, в котором существуют суперструны. Например, одна теори я получаетс я , когда 11-е измерение скручиваетс я в очень маленькую окружность - что-то вроде 10-мерного цилиндра. Друга я теори я возникает, когда М-теори я выдел я ет две дес я тимерные плоскости на некотором, очень малом, рассто я нии друг от друга. Эти плоскости, точнее гиперплоскости, параллельны друг другу. Тогда 10-мерный мир воспроизводитс я граничными эффектами чего-то более общего, происход я щего во всем объеме 11-мерного пространства.

Оказалось, что при слабой св я зи и малой энергии, М-теори я превращаетс я в 11-мерную теорию супергравитации. Таким образом, последн я я теори я , до этого сто я вша я особн я ком, включилась в общую картину мира. Однако 11-мерность может породить только две теории суперструн. Остальные три не смогли произойти из первых двух и был сделан шаг к величению размерности. Дл я вывода из одного источника всех теорий суперструн требуетс я 12-мерное пространство, где нар я ду с 10-пространственными измерени я ми имеютс я два времени. Но в то врем я как кажда я из п я ти теорий суперсимметрична, никакой суперсимметрии в 12-мерном пространстве нет.

П я ть описанных выше суперструнных теорий сильно различаютс я с точки зрени я слабо-св я занной пертурбативной теории (теории возмущений, описанной выше). Но на самом деле, как вы я снилось в последние несколько лет, они все св я заны между собой различными струнными дуальност я ми. (Назовем теории дуальными, если они описывают одну и ту же физику).

Первый тип дуальности, которую следует обсудить, - Т-дуальность. Такой тип дуальности св я зывает теорию, компактифицированную на окружности радиуса R, с теорией, компактифицированной на окружности радиуса 1/R. Таким образом, если в одной теории пространство свернуто в окружность малого радиуса, то в другой оно будет свернуто в окружность большого радиуса, но обе они будут описывать одну и ту же физику. Суперструнные теории типа IIA и типа IIB св я заны через Т-дуальность, SO(32) и E8 x E8 гетеротические теории также св я заны через нее.

Еще одна дуальность, которую мы рассмотрим - S-дуальность. Проще говор я , эта дуальность св я зывает предел сильной св я зи одной теории с пределом слабой св я зи другой теории. (Отметим, что при этом слабо св я занные описани я обеих теорий могут очень сильно различатьс я .) Например, SO(32) Гетеротическа я струнна я теори я и теори я Типа I S - дуальны в 10-мерии. Это означает, что в пределе сильной св я зи SO(32) Гетеротическа я теори я переходит в теорию Типа I в пределе слабой св я зи и наоборот. Найти же свидетельства дуальности между сильным и слабым пределами можно, сравнив спектры легких состо я ний в каждой из картин и обнаружив, что они согласуютс я между собой. Например, в струнной теории Типа I есть D-струна, т я жела я при слабой св я зи и легка я при сильной. Эта D-струна переносит те же легкие пол я , что и мировой лист SO(32) Гетеротической струны, так что когда теори я Типа I очень сильно св я зана, D-струна становитс я очень легкой и мы видим, что ее описание становитс я таким же, как и через слабо св я занную Гетеротическую струну. Другой S-дуальностью в 10-мерии я вл я етс я самодуальность IIB струн: сильно св я занный предел IIB струны это друга я IIB теори я , но слабо св я занна я . В IIB теории тоже есть D-струна (правда, более суперсимметрична я , нежели D-струны теории Типа I, так что и физика здесь друга я ), котора я становитс я легкой при сильной св я зи, но эта D-струна также я вл я етс я другой фундаментальной струной теории Типа IIB.

V. Заключение.

Наше современное представление о Вселенной и ее происхождении зависит не только от фундаментальных законов физики, но и от начальных словий во времена Большого взрыва. Например, движение брошенного м я ча определ я етс я законами гравитации. Однако, име я лишь законы гравитации, нельз я предсказать, где падет м я ч. Нужно еще знать начальные слови я , то есть величину и направление его скорости в момент броска. Дл я описани я начальных словий, существовавших при рождении Вселенной, используетс я модель Большого взрыва. В стандартной модели Большого взрыва начальные слови я задаютс я бесконечными значени я ми энергии, плотности и температуры в момент рождени я Вселенной. Иногда пытаютс я представить этот момент истории как взрыв некоей космической бомбы, порождающей материю в же существующей Вселенной. Однако этот образ несправедлив, так как когда взрываетс я бомба, она взрываетс я в определенном месте пространства и в определенный момент времени и ее содержимое просто разлетаетс я в разные стороны. Большой взрыв представл я ет собой порождение самого пространства. В момент Большого взрыва не было никакого пространства вне области взрыва. Или, если быть более точным, еще не было нашего пространства, возникавшего как раз в процессе взрыва и инфл я ционного расширени я

Теори я струн модифицирует стандартную космологическую модель в трех ключевых пунктах. Во-первых, из теории струн следует, что Вселенна я в момент рождени я имела минимально допустимый размер. Во-вторых, из теории струн следует дуальность малых и больших радиусов. В-третьих, число пространственно-временных измерений в теории струн и М-теории больше четырех, поэтому струнна я космологи я описывает эволюцию всех этих измерений. В начальный момент существовани я Вселенной все ее пространственные измерени я равноправны и свернуты в многомерный клубок планковского размера. И только потом, в ходе инфл я ции и Большого взрыва часть измерений освобождаетс я из оков суперструн и разворачиваетс я в наше огромное 4-мерное пространство-врем я .

Из теории струн (дуальности больших и малых размеров) следует, что сокращение радиусов пространств до и ниже планковского размера физически эквивалентно меньшению размеров пространства до планковских, с последующим их величением. Поэтому сжатие Вселенной до размеров, меньших планковских, приведет к прекращению роста температуры и ее последующему снижению, как после Большого взрыва, с точки зрени я внутреннего наблюдател я , наход я щегос я в этой Вселенной. Получаетс я достаточно интересна я картина, чем-то напоминающа я пульсирующую Вселенную, когда одна Вселенна я через своеобразный коллапс до клубка планковских размеров разворачиваетс я затем в новую расшир я ющуюс я Вселенную с теми же, по сути, физическими свойствами.

Теори я суперструн активно развиваетс я в последнее врем я , поскольку она может правильно описать всю нашу физику на всех энергетических масштабах. В ней есть все - квантова я физика, фермионы и бозоны, калибровочные группы и гравитаци я . В последние несколько лет произошел насто я щий прорыв в понимании сути теории, включа я D-браны и дуальность. Струнна я теори я успешно примен я етс я к исследованию черных дыр и квантовой гравитации. Хот я , как было пом я нуто выше, до полного понимани я теории еще далеко.

VI. Список использованной литературы.

1)     Бринк Л., Энно М. Принципы теории струн. М., 1991.

2)     В Рубаков В. Большие и бесконечные дополнительные измерени я // спехи физических наук. 2001. № 171.

3)     М. Сажин. Загадки космических струн // Наука и жизнь №4 1997