Комплексные числа
1. Введение.
1.1. ИСТОРИЧЕСКАЯ СПРАВКА
Комплексные числа были введены в математику для того, чтобы сделать возможной операцию извлечения квадратного корня из любого действительного числа. Это, однако, не является достаточным основанием для того, чтобы вводить в математику новые числа. Оказалось, что если производить вычисления по обычным правилам над выражениями, в которых встречаются квадратный корень из отрицательного числа, то можно прийти к результату, же не содержащему квадратный корень из отрицательного числа. В XVI в. Кардано нашел формулу для решения кубического равнения. Оказалось, когда кубическое равнение имеет три действительных корня, в формуле Кардано встречается квадратный корень из отрицательного числа. Поэтому квадратные корни из отрицательных чисел стали употреблять в математике и назвали их мнимыми числами - тем самым они как бы приобрели право на нелегальное существование. Полные гражданские права мнимым числам дал Гаусс, который назвал их комплексными числами, дал геометрическую интерпретацию и доказал основную теорему алгебры, тверждающую, что каждый многочлен имеет хотя бы один действительный корень.
2. Комплексные числа в алгебраической форме.
2.1. ПОНЯТИЕ КОМПЛЕКСНОГО ЧИСЛА
Решение многих задач математики, физики сводится к решению алгебраических равнений. Поэтому исследование алгебраических равнений является одним из важнейших вопросов в математике. Стремление сделать равнения разрешимыми - одна из главных причин расширения понятия числа.
Так для решимости равнений вида X<+A<=B X<+A<=B # "# ##0" положительных чисел недостаточно. Например, равнение X<+5=2а не имеет положительных корней. Поэтому приходится вводить отрицательные числа и нуль.
На множестве рациональных чисел разрешимы алгебраические равнения первой степени, т.е. равнения вид AX<+B<=0 (A а Однако алгебраические равнения степени выше первой могут не иметь рациональных корней. Например, такими являются равнения X2=2, X3=5. Необходимость решения таких равнений явилось одной из причин введения иррациональных чисел. Рациональные и иррациональные числа образуют множество действительных чисел.
а Однако алгебраические равнения степени выше первой могут не иметь рациональных корней. Например, такими являются равнения X2=2, X3=5. Необходимость решения таких равнений явилось одной из причин введения иррациональных чисел. Рациональные и иррациональные числа образуют множество действительных чисел.
Однако и действительных чисел недостаточно для того, чтобы решить любое алгебраическое равнение. Например, квадратное равнение с действительными коэффициентами и отрицательным дискриминантом не имеет действительных корней. Простейшее из них - равнение X2+1=0. Поэтому приходится расширять множество действительных чисел, добавляя к нему новые числа. Эти новые числа вместе с действительными числами образуют множество, которое называют множеством комплексных чисел.
Выясним предварительно, какой вид должны иметь комплексные числа. Будем считать, что на множестве комплексных чисел равнение X2+1=0 имеет корень. Обозначим этот корень буквой 2= Ц1.
Как и для действительных чисел, нужно ввести операции сложения и множения комплексных чисел так, чтобы сумма и произведение их были бы комплексными числами. Тогда, в частности, для любых действительных чисел A и B выражение A<+B
Комплексными числами аназывают выражения вида A<+B
Число A называется действительной частью комплексного числа A<+B Например, действительная часть комплексного числа 2+3< Для строгого определения комплексного числа нужно ввести для этих чисел понятие равенства. Два комплексных числа A<+B
Пусть дано комплексное число Z<=A<+B 2.2. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ КОМПЛЕКСНОГО ЧИСЛА Рисунок
SEQ Рисунок * ARABIC 1 Действительные числа геометрически изображаются точками числовой прямой. Комплексное число A<+B
Рисунок SEQ Рисунок * ARABIC 2< Не менее важной и добной является интерпретация комплексного числа A<+B
O(0;0) и с концом в точке М(A;B) (рисунок 2). Соответствие становленное между множеством комплексных чисел, с одной стороны, и множествами точек или векторов плоскости, с другой, позволяет комплексные числа точками или векторами. 2.3.МОДУЛЬ КОМПЛЕКСНОГО ЧИСЛА Пусть дано комплексное число Z<=A<+B Отметим, что Модулем комплексного числа Z<=A<+Bаи обозначается Это расстояние между точками либо длина. Множество комплексных чисел нельзя линейно упорядочить (сравнить). Из формулы (1) следует, что 2.4. СЛОЖЕНИЕ И МНОЖЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ Суммой двух комплексных чисел A<+B Произведением двух комплексных чисел A<+B (A + B Из формул вытекает, что сложение и умножение можно выполнять по правилам действий с многочленами, считая Переместительное свойство: Z1 +Z2=Z2+Z1, Z1Z2=Z2Z1
(A+B (A + B Сочетательное свойство: (Z1+Z2)+Z3=Z1+(Z2+Z3), (Z1Z2) ((A+B ((A + B Распределительное свойство: Z1(Z2+Z3)=Z1Z2+Z1Z3а (A + B
2.5. Геометрическое изображение суммы комплексных чисел Рисунок
SEQ Рисунок * ARABIC 3 Согласно определению сложения двух комплексных чисел, действительная часть суммы равна сумме действительных частей слагаемых, мнимая часть суммы равна сумме мнимых частей слагаемых. Точно также определяются координаты суммы векторов: Сумма двух векторов с координатами (A1;B1)
и (A2;B2) есть вектор с координатами (A1+A2;B1+B2). Поэтому, чтобы найти вектор, соответствующий сумме комплексных чисел Z1
и Z2 нужно сложить векторы,
соответствующие комплексным числама Z1 и Z2. 2.6. ВЫЧИТАНИЕ И ДЕЛЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ Вычитание комплексных чисел - это операция, обратная сложению: для любых комплексных чисел Z1 и Z2 существует, и притом только одно, число Z, такое, что: Z + Z2=Z1 Если к обеим частям равенства прибавить (ЦZ2), апротивоположное числу Z2: Z<+Z2+(ЦZ2)=Z1+(ЦZ2), откуда Z = Z1 Ц Z2 Число Z<=Z1+Z2 называют аразностью чисел Z1 и Z2, т.е. Z=(A+B Деление вводится как операция,
обратная множению: Z<×Z2=Z1 Разделив обе части на Z2 получим: Z<= Из этого равнения видно, что Z2 Z= E+ F< 2.7. Геометрическое изображение разности комплексных чисела Рисунок SEQ Рисунок * ARABIC 4 Разности Z2а
Ц Z1 комплексных чисел Z1 и Z2, соответствует разность векторов, соответствующих числам Z1 и Z2. Модуль Это важное геометрическое истолкование модуля разности двух комплексных чисел позволяет с спехом использовать простые геометрические факты. 2. 8. Возведение в степень и корень из комплексного числа. Комплексное число также можно возводить в степень, как и другие числа, выглядит это следующим образом: Квадратным корнем из комплексного числа называется выражение вида Возведем в квадрат и приравняем обе части, откуда и находятся
X и Y. 2.9. Свойства комплексного числа.
Операций сопряжения: 1. 2. 3. 4. 5.
Свойства модуля: 1. Если Z 2. 3. 4. 5. 3.ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА Запись комплексного числа Z в виде A<+B
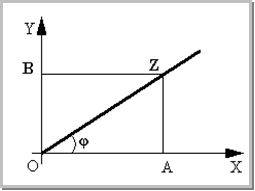
Рисунок SEQ Рисунок * ARABIC 1 A= r Число Z можно записать так: Z=
r Z = r( Эта запись называется тригонометрической формой комплексного числа. r = Число ргументом комплексного числа Z Для числа Z<=0 аргумент не определяется, и только в этом случае число задается только своим модулем. Как же говорилось выше A<+B cos Если Эту формулу добней использовать для нахождения аргумента Декартову плоскость, которая служит для изображения комплексных чисел называется комплексной плоскостью. Если комплексное число изобразить в полярной системе координат, то это будет выглядеть следующим образом: j при этом называется полярным глом, r - полярным радиусом, причем Совокупность точки О и оси ОР и единичного отрезка ОЕ называется полярной системой координат. 3.1.СВОЙСТВА МОДУЛЯ И АРГУМЕНТА КОМПЛЕКСНОГО ЧИСЛА Комплексные числа равны Z1 = Z2 С помощью тригонометрической формы удобно находить произведение и частное комплексных чисел. Пусть Z1=
r1(cos Z1Z2=
r1r2[cos = r1r2[ Таким образом, произведение комплексных чисел, записанных в тригонометрической форме, можно находить по формуле: Z1Z2= r1r2[cos( Из формулы (5) следует, что при умножении комплексных чисел их модули перемножаются, аргументы складываются. Вывод: Если Z1=Z2 то получим: Z2=[r(cos Z3=Z2Z= r2(cos2 = r3( Вообще для любого комплексного числа Z<= r( Zn =[
r(cos которую называют формулой Муавра. Частное двух комплексных чисел,
записанных в тригонометрической форме, можно находить по формуле: Используя формулу 5 cos( Вывод:
3.2. Показательная запись комплексного числа. Выражение вида:а Z=A+B При r =1, получим Ну сопряж.
ему Если их сложить или вычисть,
то получим следующее: cos При 4.ВОЗВЕДЕНИЕ В СТЕПЕНЬ И ИЗВЛЕЧЕНИЕ КОРНЯ. Многочлены деления круга. Из формулы 6 видно, что возведение комплексного числ r( [ r(cos Число Z называется корнем степени Из данного определения вытекает, что каждое решение равнения Zn = Z = r(cos Уравнение Zn =
rn<( cos n Два комплексных числа равны тогда и только тогда, когда равны их модули, аргументы отличаются слагаемыми,
кратными 2 n = и Итак, все решения могут быть записаны следующим образом: ZK= Формулу 8 называют второй формулой Муавра. Таким образом, если Символ 4.1. равнения высших степеней Формула 8 определяет все корни двучленного равнения степени an<×Znа + anЦ1<×ZnЦ1 +...+ a1<×Z1 + a0 =
0 (9) Где В курсе высшей математики доказывается теорема Гаусса:а каждое алгебраическое уравнение имеет в множестве комплексных чисел по крайней мере один корень. Эта теорема была доказана немецким математиком Карлом Гауссом в 1779 году. Опираясь на теорему Гаусса, можно доказать, что левая часть равнения 9 всегда может быть представлен в виде произведения: Где Z1, Z2,..., ZKа
Ц некоторые различные комплексные числа, a1 + Отсюда следует, что числ Z1, Z2,..., ZK являются корнями равнения 9. При этом говорят, что Z1 является корнем кратности Если словиться считать корень уравнения столько раз, какова его кратность, то можно сформулировать теорему:
каждое алгебраическое равнение степени Теорема Гаусса и только что сформулированная теорема дают решения о существовании корней, но ничего не говорят о том, как найти эти корни. Если корни первой и второй степени могут быть легко найдены, то для равнений третей и четвертой степеней формулы громоздки, для равнений степени выше четвертой таких формул вообще не существует. Отсутствие общего метода не мешает отыскивать все корни равнения.
Для решения равнения с целыми коэффициентами часто оказывается полезной следующая теорема: целые корни любого алгебраического равнения с целыми коэффициентами являются делителями свободного члена. Докажем эту теорему: Пусть Z = an<×Znа + anЦ1<×ZnЦ1
+...+ a1<×Z1 +
a0 = 0 с целыми коэффициентами. Тогда an<× a0 = -
При заданной прямоугольной декартовой системе координат на плоскоснти комплексному числу Число z тогда называют комплексной координатой точки М. Поскольку множество точек евклидовой плоскости находится во взаимнно однозначном соответствии с множеством комплексных чисел, то эту плоснкость называют также плоскостью комплексных чисел. Начало О декартовой системы координат называют при этом начальной или нулевой точкой плонскости комплексных чисел. При у=0 число Paccтoяниe от начала О плоскости до точки М(z) называется модулем комплексного числа
| аЕсли
откуда
Такое представление комплексного числа z называется его тригонометринческой формой. Исходное представление Если дано комплексное число Из равенства Точки с комплексными координатами Для любого числа z, очевидно, | Сумма и произведение двух сопряженных комплексных чисел являются действительными числами:а Число,
сопряженное с суммой, произведением или же частным комплекснных чисел, есть соответственно сумма, произведение или же частное чисел, сопряженных данным комплексным числам: Эти равенства можно легко проверить,
пользуясь формулами для опенраций над комплексными числами.а Каждой точке М( аРасстояние между точками А и В равно |АВ| = |а-
Так как | <|AB<|2=(a-b)( равнение
z откуд Если положить Условия (4) необходимы и достаточны для того, чтобы точки А, В, С были коллинеарны. При Тогда: c = Пусть имеем параллелограмм ABCD. Его центр имеет комплексную координату является необходимым и достаточным словием того, чтобы четырехугольнник ABCD был параллелограммом. 5.2. Параллельность и перпендикулярность. Коллинеарность трех точек ОПР: Пусть на плоскости комплексных чисел даны точки А(а) и
B(b). Векторы Очевидно также, что эти векторы направлены противоположно в том и только в том случае, если
arg a - arg b=arg Комплексные числа с аргументами 0,
Действительно,
так как в этом случае число
Возьмем теперь точки A(а), B( ОПР: Векторы Замечание:
1.
На основании (6) имеем:
2.
Если точки А, В, С, D принадлежат единичной окружности 3. Коллинеарность точек A, В, С характеризуется коллинеарностью векнторов Это критерий принадлежности точек A, B, С одной прямой. Его можно представить в симметричнома виде Если точки A и B принадлежат единичной окружности
Точки А и В фиксируем, точку С будем считать переменной, переобознанчив ее координату через
В частности, прямая ОА имеет равнение Переходим к выводу критериев перпендикулярности отрезков. Ясно, что Комплексные числа с аргументами Поэтому,
или
Отрезки АВ и
CD перпендикулярны тогда и только тогда, когда векторы точек с комплексными координатами Ч
В частности, когда точки А, В, С, D принадлежат единичной окружности
Выведем уравнение касательной к единичной окружности P(р). Если М (z) Ч произвольная точка этой касательной, то или Поскольку
Это частный случай равнения (12a) при а= 5.3. ПРЯМАЯ И ОКРУЖНОСТЬ НА ПЛОСКОСИа КОМПЛЕКСНЫХ ЧИСЕЛ Пусть произвольной точке М плоскости комплексных чисел соответнствует комплексное число Поэтому комплексные числа z и Формулы (1) позволяют осуществить переход от равнения геометринческой фигуры в декартовых координатах к ее равнению в сопряженных комплексных координатах. Однако сейчас мы предпочли непосредственное рассмотрение равнений в сопряженных комплексных координатах. Геометрический смысл равнения Найдем множество точек плоскости, сопряженные комплексные координнаты которых удовлетворяют равнению Сначала выделим особый случай, когда с=0. Тогда имеем систему отнонсительно второе уравнение которой получается из первого переходом к сопряжеым числам.
Уравнивая коэффициенты при задается прямая при Пусть теперь из которой получаем: Если
При
При
Если
Очевидно,
это множество есть прямая. При Таким образом, при Наконец,
отметим случай, когда приводит к противоречию: 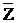
 A - B
A - B


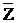
 A - B
A - B A<+B
A<+B


 (1)
(1) 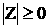 адля любого комплексного числа Z, причема
адля любого комплексного числа Z, причема  а Z<=0, т.е. когда A<=0 и B<=0.
а Z<=0, т.е. когда A<=0 и B<=0.

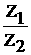


 аразности двух комплексных чисел Z2 и Z1 по определению модуля есть длина вектора Z2а
Ц Z1. Построим этот вектор, как сумму векторов Z2 и (ЦZ1) (рисунок 4). Таким образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости, которые соответствуют этим числам.
аразности двух комплексных чисел Z2 и Z1 по определению модуля есть длина вектора Z2а
Ц Z1. Построим этот вектор, как сумму векторов Z2 и (ЦZ1) (рисунок 4). Таким образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости, которые соответствуют этим числам.
 n = ZZZZZZЕ -
n = ZZZZZZЕ -
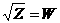 W2
= Z
W2
= Z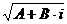 а<= X<+Y
а<= X<+Y
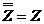




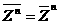
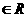 , то
, то  асовпадает с понятием действительного числа
асовпадает с понятием действительного числа

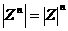
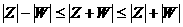
 Рассмотрим тригонометрическую форму записи комплексного числа. Действительная и мнимая части комплексного числа Z<=A<+B<= r и аргумент
Рассмотрим тригонометрическую форму записи комплексного числа. Действительная и мнимая части комплексного числа Z<=A<+B<= r и аргумент  Ц модуль комплексного числа.
Ц модуль комплексного числа.
 Z, причем величина гла считается положительной, если отсчет ведется против часовой стрелки, и отрицательной, если производится по часовой стрелке.
Z, причем величина гла считается положительной, если отсчет ведется против часовой стрелки, и отрицательной, если производится по часовой стрелке. <= r =
<= r =
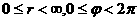
 а
а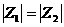 r1=r2 и
r1=r2 и 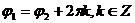

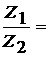
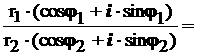
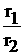
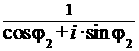
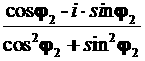
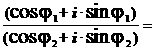

 аназывается формулой Эйлера, где r<-модуль,
аназывается формулой Эйлера, где r<-модуль, 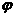 а<- аргумент.
а<- аргумент.

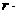
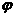 )=
)= 

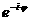 а<=
а<= 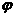
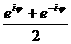 а,
а, 

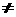 0, а,
следовательно, и Z и
0, а,
следовательно, и Z и  [cos(
[cos(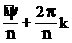 ) + i<
) + i<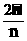
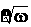 ане имеет однозначного смысла. Поэтому, потребляя его, следует четко представлять себе, что под этим символом подразумевается. Например, используя запись
ане имеет однозначного смысла. Поэтому, потребляя его, следует четко представлять себе, что под этим символом подразумевается. Например, используя запись 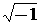
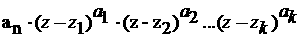 ,
,
5. Связь комплексных чисел с геометрией на плоскости.
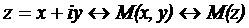 .
.
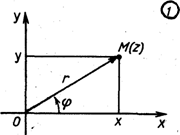
 Ч ориентированный гол, образованный вектором
Ч ориентированный гол, образованный вектором 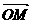 с осью х, то по определению функции синуса и косинуса
с осью х, то по определению функции синуса и косинуса 
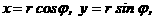 аи поэтому
аи поэтому  .
.

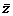 Точки М(z) и
Точки М(z) и  асимметричны относительно оси х (рис.2).
асимметричны относительно оси х (рис.2). 

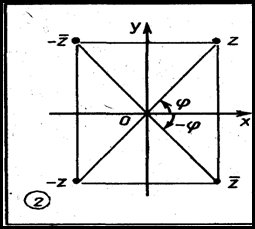
 .
.
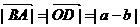
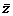 , то
, то  (2)
(2)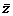 <= r2 определяет окружность с центром О радиуса r. Отношение
<= r2 определяет окружность с центром О радиуса r. Отношение  в котором точка С делит данный отрезок АВ, выражается через комплексные координаты этих точек так:
в котором точка С делит данный отрезок АВ, выражается через комплексные координаты этих точек так:
 (3)
(3) аи
аи  а
а (4)
(4) 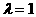 точк c является серединой отрезка AB, и обратно.
точк c является серединой отрезка AB, и обратно.  . (4
. (4
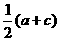 а<=
а<=  апри словии, что точки А, В, С, D имеют соответственно комплексные координаты а,
апри словии, что точки А, В, С, D имеют соответственно комплексные координаты а,
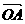 аи
аи асонаправлены тогда и только тогда, когда
асонаправлены тогда и только тогда, когда  .
.
 являются действительными. ТЕОРЕМА (Критерий коллинеарности точек О, А, В): Для того чтобы точки А(а) и В(
являются действительными. ТЕОРЕМА (Критерий коллинеарности точек О, А, В): Для того чтобы точки А(а) и В(
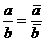 аили
аили 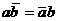 (6)
(6)
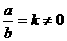 адействительное (
адействительное ( (7)
(7)
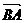 аи
аи  аколлиннеарны тогда и только тогда, когда точки, определяемые комплексными числами Чb и сЧd,
коллинеарны с началом О.
аколлиннеарны тогда и только тогда, когда точки, определяемые комплексными числами Чb и сЧd,
коллинеарны с началом О.
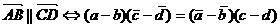 (8)
(8)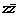
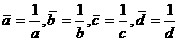 и поэтому словие (8) принимает вид:
и поэтому словие (8) принимает вид: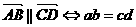 а;
(9)
а;
(9) аи
аи  . Используя (8), получаем:
. Используя (8), получаем: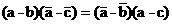 (10)
(10)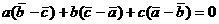 (11)
(11)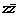
 (12)
(12)
 , (10а)
, (10а)  .
(12
.
(12

 аи
аи  являются чисто мнимыми.
являются чисто мнимыми.

 (13)
(13)  (14)
(14)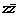
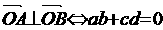 (15)
(15)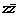
 аи обратно. На основании
(14) имеем:
аи обратно. На основании
(14) имеем: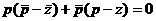

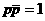 , то уравнение касательной становится таким:
, то уравнение касательной становится таким:  (16)
(16)
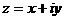 . Из равенств
. Из равенств 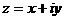 аи
аи  аодннозначно выражаются декартовы координаты х и у точки М через комплекснные числа
аодннозначно выражаются декартовы координаты х и у точки М через комплекснные числа 

 (1)
(1) аназываются сопряженными комплексными координатами этой точки.
аназываются сопряженными комплексными координатами этой точки.
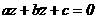
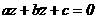 (2)
(2)  аи
аи 
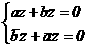
 , путем вычитания второго равнения из первого получаем:
, путем вычитания второго равнения из первого получаем: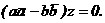
 Если
Если  , т.е.
, т.е. 
 абудет единственное число
абудет единственное число  анапишем в виде
анапишем в виде 

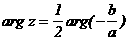 . Этому словию довлетнворяет каждая точка прямей
. Этому словию довлетнворяет каждая точка прямей  (3)
(3)  аи точка
аи точка 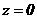 апри
апри  .
. (2) можно всегда сделать действительным числом путем мнонжения обеих частей уравнения на с. Поэтому сразу будем полагать
(2) можно всегда сделать действительным числом путем мнонжения обеих частей уравнения на с. Поэтому сразу будем полагать  Тогда имеем систему:
Тогда имеем систему: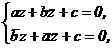
 . Рассмотрим возможные случаи.
. Рассмотрим возможные случаи.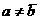 , то
, то 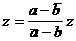 аи подстановкой в исходное равнение получаем:
аи подстановкой в исходное равнение получаем:  аили
аили 
 аего решение единственно:
аего решение единственно: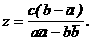
 арешений нет.
арешений нет.
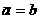 аи
аи 
 (2) при
(2) при  апрямая. В самом деле, возьмем точку
апрямая. В самом деле, возьмем точку 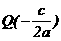 аи векнтор
аи векнтор  аточки В(
аточки В( (4)
(4) аи
аи  ауравнение (4) эквивалентно равнению (2).
ауравнение (4) эквивалентно равнению (2). аи
аи  ауравнение (2) есть равнение прямой, которая проходит через точку
ауравнение (2) есть равнение прямой, которая проходит через точку 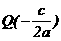 аперпендикулярно вектору
аперпендикулярно вектору 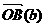 .
.  , но
, но  . Тогда система
. Тогда система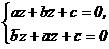
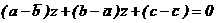



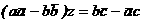 , которое:
, которое: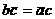 ;
; .
. а(5)
а(5)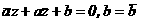 . Так как она перпендикулярна вектору
. Так как она перпендикулярна вектору 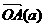
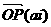 абудет ей параллелен
(рис.2). Следовательно, ориентированный угол от оси х до прямой т равен аргументу числа
абудет ей параллелен
(рис.2). Следовательно, ориентированный угол от оси х до прямой т равен аргументу числа 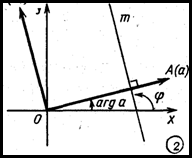
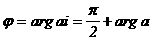 (6)
(6) аот прямойа
аот прямойа 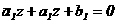 адо прямой
адо прямой 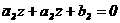 аравен глу между их направляющими векторами
аравен глу между их направляющими векторами 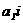 аи
аи 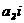 :
: . (7)
. (7)
 .
.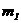 аи
аи 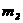 . В самом деле,
. В самом деле, 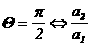 ачисто мнинмое число. Это значит, что
ачисто мнинмое число. Это значит, что 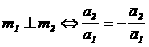
 (8)
(8) аили
аили  аполучаем:
аполучаем: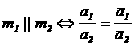 (9)
(9)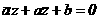 апроходит через точку
апроходит через точку 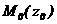
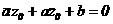 аи ее равнение можно написать в виде:
аи ее равнение можно написать в виде: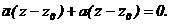 (10)
(10) . Поэтому на основании равнения (10) получаем уравнение
. Поэтому на основании равнения (10) получаем уравнение (11)
(11)
 (12)
(12)
 . (13)
. (13)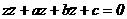
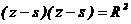 (14)
(14)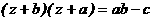 (16)
(16)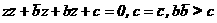 а(17)
а(17)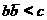 , то
, то 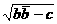 а<- чисто мнимое число.
Полагаем
а<- чисто мнимое число.
Полагаем  , тогда (16) можно записать так:
, тогда (16) можно записать так: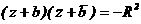 . а(18)
. а(18) , получающееся из (15) переходом к сопряженным комплексным числам.
Получаем:
, получающееся из (15) переходом к сопряженным комплексным числам.
Получаем: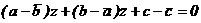

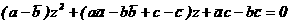 (19)
(19)
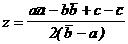
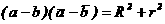 (20)
(20) 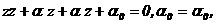
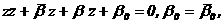
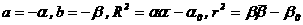 (20) их ортогональности трансформируется так:
(20) их ортогональности трансформируется так:  (21)
(21)